-
PDF
- Split View
-
Views
-
Cite
Cite
Jose Juan Lucena-Molina, Marina Gascon-Abellan, Virginia Pardo-Iranzo, Technical support for a judge when assessing a priori odds, Law, Probability and Risk, Volume 14, Issue 2, June 2015, Pages 147–168, https://doi.org/10.1093/lpr/mgu021
Close - Share Icon Share
Abstract
The Engineering Department of the Spanish Civil Guard has been using automatic speaker recognition systems for forensic purposes providing likelihood ratios since 2004. They are quantitatively much more modest than in the DNA field. In this context, it is essential a suitable calculation of the prior odds to figure out the posterior odds once the comparison result is expressed as likelihood ratio. These odds are under the responsibility of a Judge, and many consider unlikely that they can be quantitatively calculated in real cases. However, our experience defending in Court over 500 speaker recognition expert reports allows us to suggest how the expert may support Judges from a technical point of view to assess the odds. Technical support as referred should be preferentially provided in the preliminary investigation stage, after the expert report being issued by the laboratory, as in the course of oral hearings it is much more difficult for those who are not familiar with the new paradigm. It can be initiated upon request by the Examining Judge or any of the litigant parties. We consider this practice favourable to the equality of arms principle.
The use of Bayesian networks is proposed to provide inferential assistance to the Judge when assessing the prior odds. An example of the explanation above is provided by the case of the terrorist attack against Madrid-Barajas Airport Terminal 4 perpetrated in December 2006.
1. Introduction
Besides the DNA expert reports, there are hardly any other fields of criminalistics in which the Spanish official experts use Bayesian inference to scientifically interpret the results achieved by their analyses. And in the DNA expert report, the use of this inference in practice does not seem—in our opinion—to be an example to heed. If this was the case—and bearing in mind the years which have elapsed in which DNA techniques have been deployed in Justice—the majority of Spanish Judges and courts would have to have a clear idea of the difference between the logical basis of the conclusions of the DNA report—in which assertions never appear about the authorship of the traces as can be found in the reports of handwriting or fingerprints—and those from other fields of criminalistics in which it is necessary to carry out a comparison between known and unknown source samples. As it has been stressed before, our personal perception in this regard is that we are still far from deploying the Bayesian inference correctly.1
An outstanding exception in Spain is that of the Engineering Department of the ‘Guardia Civil’ police force (from now on Spanish Civil Guard) as regards to voice comparisons and audio or video recording authentication. The Department’s Acoustics’ Area has specific software for evaluating the likelihood ratio in a voice comparison developed by the AGNITIO company, the upshot of long uninterrupted, constant scientific research since 1997 with the university research group Area de Tratamiento de Voz y Señales (ATVS) belonging to the Further Polytechnical School of the Madrid Autonomous University and since 2004 with said company. As regards authentication, the Department assigns subjective probabilities using expert knowledge to inform likelihood ratios.2 Undoubtedly, this less known way of assessing the scientific evidence could be the immediate solution to avoid making the fallacy of the transposed conditional in conclusions.3
Within the logical framework of Bayesian inference, the prior odds are required—as well as obtaining likelihood ratio—to ascertain the posterior odds, in other words, the information really resolves the needs of the courts as regards to voice comparisons: calculating the posterior probabilities of the propositions put forward by the parties in the process regarding voice authorship questioned in the light of the results of the comparison and the context information at the disposal of the court.4 The expert’s aid is not only used to calculate likelihood ratios but it also might be used to quantify the prior odds and, on this latter assumption, it is specifically the court which has the information required so that the expert can do it.
However, during a BBfor25 (Bayesian Biometrics for Forensics) Workshop held in Martigny (France) in December 2011, N. Brümmer said in a presentation the following: ‘Let’s be realistic: In a real court case, it is unlikely that numbers will be assigned to the prior odds and cost ratio, and that the posterior will be explicitly calculated.’ It is believed that most forensic experts would agree with such a comment, but is there no room for possible solutions?
The purpose of the article here is to discuss what some scholars have proposed in the past as guidance (Section 2.1), the role of priors in a forensic evidence comparison within a Continental legal system as the Spanish one (Section 2.2), a case study illustrating why and how to use Bayesian networks to calculate priors (Sections 2.3 and 3.1), a more deeper study as regards to expert assistances to courts in terms of assessment of scientific evidence (Section 3.2), and conclusions (Section 4).
2. Material and methods
2.1 The analysis of evidence school
The work entitled ‘Analysis of Evidence’6 by Terence Anderson, David Schum and William Twining, is regarded as a classic in the rational assessment of evidence within the Anglo-US legal world, and could be a good starting point to face the challenges. These authors developed the thinking of John Henry Wigmore (1863–1943) who stated that neither common sense, intuition, nor experience, all of which are parts of the exercising of the skills inherent in inferential reasoning can replace what he called ‘principles of proof’.
These experts in the rational assessment of evidence have known how to describe a sound rational structure which helps to understand how, based on the evidence (whether tangible or physical or testimonial) a proposition may be proven which they call the ‘ultimate probandum’ (the last thing that needs to be proven) whose content is related with legal descriptions of a certain crime. A recent manuscript written by Paul Roberts and Colin Aitken7 on the logic of forensic proof says the following: ‘Wigmorean method is nothing more (or less) than an attempt to summarise the logic of inferential reasoning in graphical form, tailored to specific intellectual (analytic and decision) tasks. It is, in other words, a practical heuristic for litigation support designed specifically to assist those who need to formulate, evaluate, or respond to arguments to inferring factual conclusions from mixed masses of evidence to improve the quality of their intellectual output’.
Using the graphics’ method (Fig. 1), this reasoning method can be organized into a scheme whose key constructor elements are the concepts of proposition, generalization and evidence.
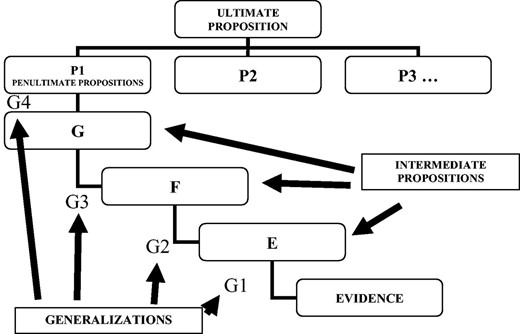
This methodology will be used in this article to make it easier for readers on how to understand the important distinction between ‘evidence’ and ‘background information’ in the case study (see paragraph 2.3), that is, certain propositions will be considered as ‘evidence’, and others as ‘background information’.8 The background information will be introduced in the notation using the capital letter I (see paragraph 3.1).
It is worth pointing out that although Anglo-Saxon and Continental legal systems have notable differences, what is set out in this article goes beyond them, as it is related with the reasoning logic bases which must be the background of these systems to be classified as rational.
2.2 The role of priors in forensic evidence comparisons
To make a decision at the end of the criminal proceedings it is first of all necessary ‘to prove facts’, those which are relevant to the criminal prosecution, and afterwards to apply to those facts the legal consequence according to the law for such a kind of facts. Let us remember that though it is said ‘to prove facts’ for our own convenience, in fact what are proved are not facts, but statements on facts.9 The proof of statements on facts is based on information provided to the proceedings through evidence. We call ‘prior probability’ to the subjective probability assigned to a statement on facts bearing in mind certain information or piece of evidence at that moment.
Priors of any statements on facts are changing as the proceedings are going on. Therefore, there will be different priors depending on the moment of the procedural stage. Some of them could be useful to justify investigative actions (e.g. phone tapping, house search, e-mail examination and so on). Once has the trial stage finished, the court has to determine which facts have been proven and justify their factual decisions in the sentence.
There are two stages in the Spanish Code of Criminal Procedure: the investigative and trial stages. The former is mainly addressed to finding out the circumstances around a crime and its authorship. During this phase, investigative actions (e.g. scene examination or questioning) and precautionary measures (e.g. pre-trial custody), are undertaken, but these activities do not actually constitute legal evidence and therefore they cannot invalidate the presumption of innocence, nor be enough to convict. At the second stage, under a different Judge, the prosecutor makes a decision to charge and the evidence is provided.
Experts can help Judges in both stages according to the Spanish Code of Criminal Procedure. In accordance with case law, a Judge cannot yield or relinquish his/her evaluating responsibility. Judges are responsible for determining prior and posterior odds of the Bayes’ Theorem in a real case, although they can be assisted by experts to do that scientifically (maintaining ‘coherence’ in probabilistic reasoning10) and combine both of them with likelihood ratios. While the investigative stage allows experts to explain much better the procedure and conclusion of their reports to both the investigating Judge and parties, the trial is the exclusive legal stage in which the report will be converted into scientific evidence. Though the Court is made up of different magistrates from those who acted in the first stage, the parties are the same. Therefore, the assistance given by experts quantifying prior odds in the investigative stage will reinforce the principle of equality of arms in the proceedings.11 Besides, the expert will never give such assistance to the Court without knowing the alleged relevant information submitted by the parties in the proceedings, something that only Judges can determine and authorize. A wider and specific legal study as regards to expert assistance in terms of the appraisal of a scientific test will be presented in Section 3.
2.3 Case study: a voice comparison
As a practical example of the application of the graphic method proposed by Wigmore, we have based ourselves on the Report 08/10279/AI-01 by the Acoustics and Image Department of the Spanish Civil Guard (voice comparison) and information taken from Sentence 18/2010 of Section 3 of the Criminal Division of the High Court dated 21 May 2010 regarding the investigation into the attack which occurred at parking D of Terminal T-4 of the Madrid-Barajas Airport on 30 December 2006.12 The graphic (Fig. 2) may help the Court to carry out an assessment of prior odds in favour of the prosecution thesis before the forensic voice comparison provides its technical information. At the root of the graphic, art and science have to be combined as its creators specifically recognize. The quoted example is not intended to be anything other than an academic example—illustrative—because in reality it should be completed by the evidence, propositions and generalizations deriving from the defence.
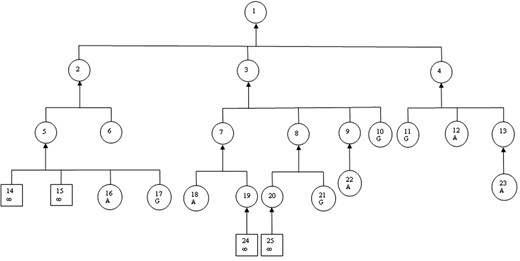
Graphic of the case study.
Key:
1: IP made a phone call to the DYA Exchange in S. Sebastián, in ETA’s name, at 7:53 a.m. of 30 December 2006 from the mobile phone XXX warning that a van bomb had been planted with a large amount of explosives at parking D of T-4, being a Renault Traffic model, dark red, registration plate YYY which would go off at 9:00 a.m.
2: IP made a phone call to the DYA Exchange in S. Sebastián at 7:53 a.m. of 30 December 2006 from the mobile phone XXX.
3: IP was aware that the Renault Trafic van bomb, dark red colour, YYY registration plate, was loaded with big quantities of explosives, which was parked at parking D of T-4, and would explode at 9:00 a.m.
4: IP was aware that it was acting in the name of ETA.
5: IP bought the phone XXX.
6: The S. Sebastián DYA received a call from the phone XXX at 07:53 a.m. on 30 December 2006.
7: IP knew that the van bomb was loaded with a large amount of explosive.
8: IP knew that the van bomb was parked at parking D of T-4.
9: The explosion was scheduled for 9:00 a.m. on 30 December 2006.
10: The warnings regarding the planting of bombs by ETA in public places are usually carried out with a sufficient time margin for an urgent evacuation and preventing deactivation by putting at serious risk the deactivators’ safety.
11: ETA usually claims the more notorious attacks in similar media shortly after the occurrence of the facts.
12: ETA claimed the T-4 attack in a press release published in the daily paper GARA in its digital edition dated 9 January 2007 and in the normal edition dated 10 January.
13: The upshot of this handwriting comparison supporting the authorship by IP of the handwriting of the telephone number of the Madrid Fire Brigade in a note seized from IP clothes when he was arrested.
14: Statement by MS saying that IP bought the phone with the number XXX.
15: Statement by the Phone vendor describing the physionomical characteristics of the purchaser of the phone XXX on 23 December 2006.
16: Invoice for the purchase of the phone XXX dispatched by Phone vendor on 23 December 2006.
17: The miscreants use prepaid phones so as not to leave any trace of their involvement in the committing of any offences over the phone.
18: The Renault Trafic van, dark red in colour, registration YYY was stolen in France by hooded individuals on 27 December 2006. His driver was released by 9:40 a.m. of December 30th 2006.
19: The Renault Trafic van, dark red in colour, registration plate YYY, was collected by MS and MSS, with the explosive charge already prepared for activation on 29 December 2006.
20: IP took part in the operation thought up for the transfer of the van bomb to T-4.
21: The members of a terrorist command co-ordinate with each other to undertake an attack.
22: The explosion of the van bomb took place at 08:59:29 a.m. on 30 December 2006.
23: IP and MS were arrested by the Spanish Civil Guard in Mondragón (Guipúzcoa) in a road check on 6 January 2007. In the IP’s napsack two guns stolen in France on 26 October 2006 were found. IP’s personal documentation contained a handwritten note with the phone number of the Madrid Fire Brigade and the S. Blas Police Park (Madrid). The Madrid Fire Brigade received a call from the phone XXX at 7:55 a.m. on 30 December 2006 warning that the van bomb had been placed at T-4.
24: Statement by MS describing the collection of the van bomb in France on 29 December 2006.
25: Statement by MS describing the method of operation for moving the van bomb to Madrid-Barajas Airport.
Abbreviations: DYA: Road Assistance Service of the Basque Country; ETA: Euzkadi Ta Askatasuna; IP: terrorist no. 1; MS: terrorist no. 2; MSS: terrorist no. 3; T-4: Terminal 4 of the Madrid-Barajas Airport.
Signs: ∞: testimony which the Court can hear directly in the courtroom or evidence which may be directly inspected in the same way; A: proposition assumed to be right; G: generalization; witness evidence; O: circumstantial evidence or inferred propositions.
The graphics’ method helps to reason with logic and it proves particularly useful and even necessary when the case is complex. However, it is not suitable to calculate prior odds in accordance with the laws of probability and Jeffrey’s rule, laws and the rule which ensure rationality when estimating such odds without any doubt.
In addition to the information provided in the previous graphic by Wigmore—limited so as not to make the example too lengthy—it is worth stressing that the court is aware that: All this information (far from what was described known by the Court in the case in hand) can be used to evaluate—in odds form—the propositions defended by the parties to the process with regard to the voice comparison: that it was IP who made the phone calls on the mobile XXX on 30 December, warning of the planting of the van bomb in contrast to that it was not done.
The members of the ETA command kept an appointment with their managers MGAR and JAA who proposed to them to take a van to T-4, requesting that they should first check the route. In actual fact, to undertake the work route survey they rented a vehicle in Irún (Guipúzcoa) in the name of IP (the Court has the rental contract for the vehicle Volkswagen Polo registration VVV, signed in Irún in the name of IP for 21 and 22 October 2006). The vehicle travelled a distance of 963 Km (the distance between Irún and Barajas is 928 km).
The van bomb was stolen in France at gunpoint and its owner—Spanish—was released by an ETA command 40 minutes after committing the terrorist attack on the T-4.
The ETA command police record from its inception given by the Information Service of the Spanish Civil Guard.
We can use a Bayesian network to evaluate the prior odds so that in this way—as has already been indicated previously—the laws and theorems of the probability theory and Jeffrey’s rule are respected. Furthermore, we are interested in exploring to what extent these odds can be changed when the Court considers some of the information on which the evaluation of the odds is based right.
To this end, the first task which the expert has to carry out in this regard is to consider the propositions which must be inserted in the network and the relations between them and we will do so showing the following network as shown in Fig. 3 (it is a very simplified network to promote the teaching purpose of the article):
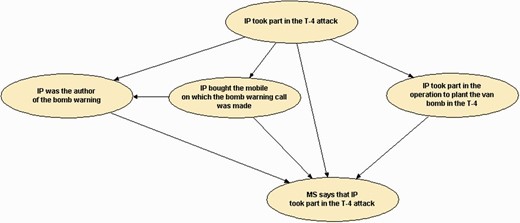
The propositions are defined inside the ellipses which we call nodes. From top to bottom we discover what we could call the ‘ultimate proposition’: the participation of IP in the terrorist act perpetrated at T-4 of Madrid-Barajas Airport. The possible statuses of this proposition would be as follows: principal/accessory/non-participation—including in this status merely material or innocent participation if possible. This proposition is said to be ‘relevant’ for the four directly linked to it in descending order: ‘Relevance’ is one of the main concepts used to construct Bayesian networks.13 It is said that a proposition B is relevant for another A if and only if the answer to the following question is positive: if it is supposed that B is true, does that supposition change the degree of believe in the truth of A? The ‘relevance’, as can be gleaned from the definition provided, is commutative: if A is relevant to B, B is to A. This commutative property of relevance is the necessary consequence of the axiom which constitutes the third law of probability.
that IP carried out the bomb warning to the DYA exchange (questioned voice inspected by the Spanish Civil Guard);
that the mobile use in the bomb warnings was bought by IP;
that he actively participated in the transport of a van bomb from Irún to T-4; and
that the statement by MS about the participation of IP in the T-4 attack was true.
Henceforth, capital letters will be used instead of describing the enunciations of the propositions on the network with a view to facilitating the use of mathematical notation when developing argumentation.
The new network thus has the following appearance as shown in Fig. 4.
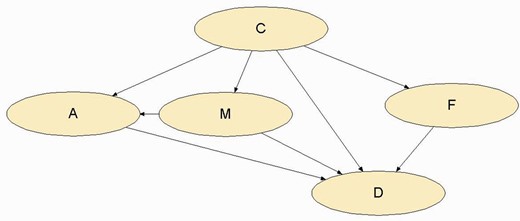
Network of the case study to facilitate the use of mathematical notation.
We can illustrate the commutatively of relevance by concentrating at the nodes C and M, e.g. Knowing that IP took part in the T-4 attack is relevant to establish whether it was he who bought the mobile used to make the bomb warning and, on the other hand, knowing that he bought the mobile used to make the bomb warning is relevant for knowing whether he took part in the T-4 attack.
On a network, only the direct dependencies between the nodes should be reflected. On the network in Fig. 4, not all the nodes are linked to each other. Nodes C and D are linked to all of them but, e.g. F is only linked to C and D and M to C, A and D. This network has the virtue of containing all the possible ways of making connections between nodes: ‘divergences’ (between node C and nodes A, M, D and F; and between node M and nodes A and D); ‘series’ (between nodes C, M and D; between C, A and D; between C, M, A and D; and between C, F and D); and ‘convergences’ (between nodes A, M, C, F and node D; between nodes C, M and node A).
The Bayesian networks use the property of conditional independence to optimize the calculation of the probabilities which may prove to be of interest within the network. The connections of Fig. 4 allow the assurance of conditional independence where necessary.
The network of Fig. 4 has a high degree of interdependence: if IP had taken part in the T-4 attack, the network propositions in intermediate position could be related with his criminal activity. On the other hand, the statement by MS, very lengthy on details, contains the intermediate propositions. This leads to the fact that the network connects the node C to all the others and the node D as well. While the former connects by means of a divergence, the latter is achieved by means of a convergence.
The divergences between node C and nodes A, M, D and F complies with that which is believed that if you do not know the status of C, the knowledge of the state of one of the other nodes (A, M, D or F) may change the belief about the probabilities of the statuses of the other nodes which are in brackets. For example, if it is not known for sure whether IP took part in the T-4 attack, knowing that he acted as the driver of a shuttle vehicle when moving the van bomb to parking D of T-4 from Irún may change the belief about whether it was him who provided the bomb warning, bought the mobile used in the warning or whether the statement by MS was right. We could provide the same reasoning knowing A with regard to M, D and F, knowing M with regard to A, D and F or knowing D with regard to A, M and F.
Analyzing the compliance of the property of the conditional independence in the divergence between node C and nodes A, M, D, F, the following occurs (whenever the status of node D is not known) if the status of C (C1, C2 or C3) is known: Convergence indicates that if there is a certain idea whether any of the uses of the statement by MS (D) is known definitely, a change in the belief of any of the statuses of nodes A, M, C and F brings about a change in the statuses of the others.
a change in the belief of the statuses of F does not cause any change in the belief about the statuses of nodes A and/or M and vice versa.
With the aid of the Hugin programme,14 it is possible to verify all the comments about the conditional independence and dependence in the network of Fig. 4.
It is very important to establish that on Bayesian networks only uncertain propositions can be included (in the form of nodes). Everything about which there is confidence it has occurred cannot be introduced therein. It is a logical reasoning structure under uncertainty.
3. Results and legal discussion
3.1 Running the Bayesian network
The next step in our argument consists of checking the usefulness of the network for calculating prior odds about whether IP made the bomb warning. To illustrate that it is not necessary to deploy figures to prior odds, we commence our probabilistic reasoning by comparing probabilities with each other, simply considering to what extent some may be bigger than others.
Exclusively based on general information about the case (we designate this information with the letter I), in other words, the information which the Court may have about whether IP may have committed the T-4 attack with the absence of any of that written on the network, we can determine the following statuses of the proposition C: ‘IP took part in the T-4 attack’, mutually exclusive and exhaustive:15 It is possibly not hard to be in agreement with the following assignment of prior probabilities from the background information explicitly mentioned in the paragraph 2.3: P(C1 | I) > P(C2 | I). Let us imagine that the Court initially is just in the sceptical doubt: P(C1 ∪ C2 | I) = P(C3 | I), in other words: P(C1 | I) + P(C2 | I) = P(C3 | I). The Court has no reasons to believe more the prosecutor hypothesis than the defence one. These probabilities are those of the propositions in view of the information of a general context.
C1: as principal in the first degree
C2: as accessory or principal in the second degree
C3: did not take part or did so innocently
We can make numerical assignments to the different statuses of proposition C, respecting the aforementioned qualitative assignment of probability (Table 1).
The numerical values actually chosen serve as guidelines and are justified in the light of the general information available about the case by the Court. The most important is not the numerical assignment chosen for each status, but rather the numerical proportions between these assignments. As these are mutually exclusive and exhaustive events, the sum of their probabilities must be equal to the whole number to meet the first two probability theory laws. These figures indicate that the Court estimates there is a 50% probability that IP took part in the T-4 attack and that, in turn, it is believed to be more likely that he did so as an offender rather than as an accomplice.
Other probabilities which we can estimate in qualitative form are those technically called likelihoods. These are probabilities of events considered on the network, in other words, of the propositions which are under the ultimate proposition which we have called C since it is regarded as right any specific state of this proposition and, where applicable, other propositions. As an example: P(A | C1), P(A | C2)… P(M | C1)… P(F | C1)… P(D | C1)… P(D | A, M, C1)… P(D | A, F, C1)… P(D | A, M, F, C1)…
A numerical assignment respecting the previous considerations may be shown as given in Table 2.
| C: . | C1 . | C2 . | C3 . |
|---|---|---|---|
| P(C | I) | 0.45 | 0.05 | 0.5 |
| C: . | C1 . | C2 . | C3 . |
|---|---|---|---|
| P(C | I) | 0.45 | 0.05 | 0.5 |
| C: . | C1 . | C2 . | C3 . |
|---|---|---|---|
| P(C | I) | 0.45 | 0.05 | 0.5 |
| C: . | C1 . | C2 . | C3 . |
|---|---|---|---|
| P(C | I) | 0.45 | 0.05 | 0.5 |
| C: . | C1 . | C2 . | C3 . |
|---|---|---|---|
| M: P(M = t | C, I) | 0.2 | 0.2 | 0.1 |
| M: P(M = f | C, I) | 0.8 | 0.8 | 0.9 |
| C: . | C1 . | C2 . | C3 . |
|---|---|---|---|
| M: P(M = t | C, I) | 0.2 | 0.2 | 0.1 |
| M: P(M = f | C, I) | 0.8 | 0.8 | 0.9 |
| C: . | C1 . | C2 . | C3 . |
|---|---|---|---|
| M: P(M = t | C, I) | 0.2 | 0.2 | 0.1 |
| M: P(M = f | C, I) | 0.8 | 0.8 | 0.9 |
| C: . | C1 . | C2 . | C3 . |
|---|---|---|---|
| M: P(M = t | C, I) | 0.2 | 0.2 | 0.1 |
| M: P(M = f | C, I) | 0.8 | 0.8 | 0.9 |
If we translate the above in numerical assignment, Table 3 respects the aforementioned qualitative assignments.
| M: . | t . | f . | ||||
|---|---|---|---|---|---|---|
| C: . | C1 . | C2 . | C3 . | C1 . | C2 . | C3 . |
| A: P(A = t | C, M, I) | 0.8 | 0.4 | 0.01 | 0.1 | 0.1 | 0.001 |
| A: P(A = f | C, M, I) | 0.2 | 0.6 | 0.99 | 0.9 | 0.9 | 0.999 |
| M: . | t . | f . | ||||
|---|---|---|---|---|---|---|
| C: . | C1 . | C2 . | C3 . | C1 . | C2 . | C3 . |
| A: P(A = t | C, M, I) | 0.8 | 0.4 | 0.01 | 0.1 | 0.1 | 0.001 |
| A: P(A = f | C, M, I) | 0.2 | 0.6 | 0.99 | 0.9 | 0.9 | 0.999 |
| M: . | t . | f . | ||||
|---|---|---|---|---|---|---|
| C: . | C1 . | C2 . | C3 . | C1 . | C2 . | C3 . |
| A: P(A = t | C, M, I) | 0.8 | 0.4 | 0.01 | 0.1 | 0.1 | 0.001 |
| A: P(A = f | C, M, I) | 0.2 | 0.6 | 0.99 | 0.9 | 0.9 | 0.999 |
| M: . | t . | f . | ||||
|---|---|---|---|---|---|---|
| C: . | C1 . | C2 . | C3 . | C1 . | C2 . | C3 . |
| A: P(A = t | C, M, I) | 0.8 | 0.4 | 0.01 | 0.1 | 0.1 | 0.001 |
| A: P(A = f | C, M, I) | 0.2 | 0.6 | 0.99 | 0.9 | 0.9 | 0.999 |
Translating the previous considerations into numerical form, we get the following results as shown in Table 4.
| C: . | C1 . | C2 . | C3 . |
|---|---|---|---|
| F: P(F = t | C, I) | 0.8 | 0.2 | 0 |
| F: P(F = f | C, I) | 0.2 | 0.8 | 1 |
| C: . | C1 . | C2 . | C3 . |
|---|---|---|---|
| F: P(F = t | C, I) | 0.8 | 0.2 | 0 |
| F: P(F = f | C, I) | 0.2 | 0.8 | 1 |
| C: . | C1 . | C2 . | C3 . |
|---|---|---|---|
| F: P(F = t | C, I) | 0.8 | 0.2 | 0 |
| F: P(F = f | C, I) | 0.2 | 0.8 | 1 |
| C: . | C1 . | C2 . | C3 . |
|---|---|---|---|
| F: P(F = t | C, I) | 0.8 | 0.2 | 0 |
| F: P(F = f | C, I) | 0.2 | 0.8 | 1 |
The numerical assignments we can carry out become complicated in this case because the number of variables to be borne in mind and their statuses mean that the number of assignments required attains 24 (with their corresponding assignments of complementary probabilities).
The probabilities which it is wished to calculate regarding the truthfulness of the statement by MS, once the values of the statuses of the other variables and their complementarities are known. The criteria in selected order are as shown in Table 5 and the 48 assignments are shown in Table 6.
| P(D = t | M, F, A, C) . | Variable statuses . |
|---|---|
| 0.999 | When all the binary restrictive events have the value ‘true’ and the variable C = C1 |
| 0.99 | When all the binary restrictive events have the value ‘true’ except for M and the variable C = C1 |
| 0.9 | When all the binary restrictive events have the value ‘true’ except for A and the variable C = C1; also on the assumption that all the binary events considered have the value ‘true’ and the variable C = C2 |
| 0.8 | When C = C2 and A and F have the value ‘true’ |
| 0.7 | Both when C = C1 and only F has the value ‘true’ as well as when C = C2 and only A has the value ‘false |
| 0.6 | when C = C2 and only F has the value ‘true’ |
| 0.3 | When C = C1 and only F has the value ‘false’ |
| 0.2 | Both when C = C1 and only A has the value ‘true’ as well as when C = C2 and only F has the value ‘false’ |
| 0.1 | When C = C1 and only M has the value ‘true’ and when C = C2 and only A or M have the value ‘true’ |
| 0.01 | When C = C3 and only F has the value ‘false’ |
| 0.001 | When C = C3 and only A or M have the value ‘true’ |
| 0 | When all the other restrictive events have the value ‘false’ regardless of the status of C and when C = C3 and F has the value ‘true’ |
| P(D = t | M, F, A, C) . | Variable statuses . |
|---|---|
| 0.999 | When all the binary restrictive events have the value ‘true’ and the variable C = C1 |
| 0.99 | When all the binary restrictive events have the value ‘true’ except for M and the variable C = C1 |
| 0.9 | When all the binary restrictive events have the value ‘true’ except for A and the variable C = C1; also on the assumption that all the binary events considered have the value ‘true’ and the variable C = C2 |
| 0.8 | When C = C2 and A and F have the value ‘true’ |
| 0.7 | Both when C = C1 and only F has the value ‘true’ as well as when C = C2 and only A has the value ‘false |
| 0.6 | when C = C2 and only F has the value ‘true’ |
| 0.3 | When C = C1 and only F has the value ‘false’ |
| 0.2 | Both when C = C1 and only A has the value ‘true’ as well as when C = C2 and only F has the value ‘false’ |
| 0.1 | When C = C1 and only M has the value ‘true’ and when C = C2 and only A or M have the value ‘true’ |
| 0.01 | When C = C3 and only F has the value ‘false’ |
| 0.001 | When C = C3 and only A or M have the value ‘true’ |
| 0 | When all the other restrictive events have the value ‘false’ regardless of the status of C and when C = C3 and F has the value ‘true’ |
| P(D = t | M, F, A, C) . | Variable statuses . |
|---|---|
| 0.999 | When all the binary restrictive events have the value ‘true’ and the variable C = C1 |
| 0.99 | When all the binary restrictive events have the value ‘true’ except for M and the variable C = C1 |
| 0.9 | When all the binary restrictive events have the value ‘true’ except for A and the variable C = C1; also on the assumption that all the binary events considered have the value ‘true’ and the variable C = C2 |
| 0.8 | When C = C2 and A and F have the value ‘true’ |
| 0.7 | Both when C = C1 and only F has the value ‘true’ as well as when C = C2 and only A has the value ‘false |
| 0.6 | when C = C2 and only F has the value ‘true’ |
| 0.3 | When C = C1 and only F has the value ‘false’ |
| 0.2 | Both when C = C1 and only A has the value ‘true’ as well as when C = C2 and only F has the value ‘false’ |
| 0.1 | When C = C1 and only M has the value ‘true’ and when C = C2 and only A or M have the value ‘true’ |
| 0.01 | When C = C3 and only F has the value ‘false’ |
| 0.001 | When C = C3 and only A or M have the value ‘true’ |
| 0 | When all the other restrictive events have the value ‘false’ regardless of the status of C and when C = C3 and F has the value ‘true’ |
| P(D = t | M, F, A, C) . | Variable statuses . |
|---|---|
| 0.999 | When all the binary restrictive events have the value ‘true’ and the variable C = C1 |
| 0.99 | When all the binary restrictive events have the value ‘true’ except for M and the variable C = C1 |
| 0.9 | When all the binary restrictive events have the value ‘true’ except for A and the variable C = C1; also on the assumption that all the binary events considered have the value ‘true’ and the variable C = C2 |
| 0.8 | When C = C2 and A and F have the value ‘true’ |
| 0.7 | Both when C = C1 and only F has the value ‘true’ as well as when C = C2 and only A has the value ‘false |
| 0.6 | when C = C2 and only F has the value ‘true’ |
| 0.3 | When C = C1 and only F has the value ‘false’ |
| 0.2 | Both when C = C1 and only A has the value ‘true’ as well as when C = C2 and only F has the value ‘false’ |
| 0.1 | When C = C1 and only M has the value ‘true’ and when C = C2 and only A or M have the value ‘true’ |
| 0.01 | When C = C3 and only F has the value ‘false’ |
| 0.001 | When C = C3 and only A or M have the value ‘true’ |
| 0 | When all the other restrictive events have the value ‘false’ regardless of the status of C and when C = C3 and F has the value ‘true’ |
| C: . | C1 . | C2 . | C3 . | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A: . | t . | f . | t . | f . | t . | f . | ||||||||||||||||||
| F: . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | ||||||||||||
| M: . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . |
| D: P(D = t | M, F, A, C) | 0.999 | 0.99 | 0.3 | 0.2 | 0.9 | 0.7 | 0.1 | 0 | 0.9 | 0.8 | 0.2 | 0.1 | 0.7 | 0.6 | 0.1 | 0 | 0 | 0 | 0.01 | 0.001 | 0 | 0 | 0.001 | 0 |
| D: P(D = f | M, F, A, C) | 0.001 | 0.01 | 0.7 | 0.8 | 0.1 | 0.3 | 0.9 | 1 | 0.1 | 0.2 | 0.8 | 0.9 | 0.3 | 0.4 | 0.9 | 1 | 1 | 1 | 0.99 | 0.999 | 1 | 1 | 0.999 | 1 |
| C: . | C1 . | C2 . | C3 . | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A: . | t . | f . | t . | f . | t . | f . | ||||||||||||||||||
| F: . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | ||||||||||||
| M: . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . |
| D: P(D = t | M, F, A, C) | 0.999 | 0.99 | 0.3 | 0.2 | 0.9 | 0.7 | 0.1 | 0 | 0.9 | 0.8 | 0.2 | 0.1 | 0.7 | 0.6 | 0.1 | 0 | 0 | 0 | 0.01 | 0.001 | 0 | 0 | 0.001 | 0 |
| D: P(D = f | M, F, A, C) | 0.001 | 0.01 | 0.7 | 0.8 | 0.1 | 0.3 | 0.9 | 1 | 0.1 | 0.2 | 0.8 | 0.9 | 0.3 | 0.4 | 0.9 | 1 | 1 | 1 | 0.99 | 0.999 | 1 | 1 | 0.999 | 1 |
In the numerical assignment of probabilities, the general criterion has been established of not exceeding an assessment which entails more than three decimals.
| C: . | C1 . | C2 . | C3 . | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A: . | t . | f . | t . | f . | t . | f . | ||||||||||||||||||
| F: . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | ||||||||||||
| M: . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . |
| D: P(D = t | M, F, A, C) | 0.999 | 0.99 | 0.3 | 0.2 | 0.9 | 0.7 | 0.1 | 0 | 0.9 | 0.8 | 0.2 | 0.1 | 0.7 | 0.6 | 0.1 | 0 | 0 | 0 | 0.01 | 0.001 | 0 | 0 | 0.001 | 0 |
| D: P(D = f | M, F, A, C) | 0.001 | 0.01 | 0.7 | 0.8 | 0.1 | 0.3 | 0.9 | 1 | 0.1 | 0.2 | 0.8 | 0.9 | 0.3 | 0.4 | 0.9 | 1 | 1 | 1 | 0.99 | 0.999 | 1 | 1 | 0.999 | 1 |
| C: . | C1 . | C2 . | C3 . | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A: . | t . | f . | t . | f . | t . | f . | ||||||||||||||||||
| F: . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | ||||||||||||
| M: . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . | t . | f . |
| D: P(D = t | M, F, A, C) | 0.999 | 0.99 | 0.3 | 0.2 | 0.9 | 0.7 | 0.1 | 0 | 0.9 | 0.8 | 0.2 | 0.1 | 0.7 | 0.6 | 0.1 | 0 | 0 | 0 | 0.01 | 0.001 | 0 | 0 | 0.001 | 0 |
| D: P(D = f | M, F, A, C) | 0.001 | 0.01 | 0.7 | 0.8 | 0.1 | 0.3 | 0.9 | 1 | 0.1 | 0.2 | 0.8 | 0.9 | 0.3 | 0.4 | 0.9 | 1 | 1 | 1 | 0.99 | 0.999 | 1 | 1 | 0.999 | 1 |
In the numerical assignment of probabilities, the general criterion has been established of not exceeding an assessment which entails more than three decimals.
The usefulness of the network is appreciated when in the Hugin programme, the Edit mode (the mode in which the nodes and their links are devised and the initial probabilistic values are completed in the tables) passes to the Run mode (the information flow is activated in the network). The example network has been shown in Fig. 5 when the Run mode is commenced (the probabilistic values are those of each proposition).
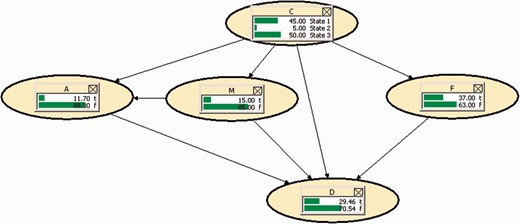
We can carry out an initial Bayesian inferential reasoning exercise with the information we have available: However, the network provides us with the possibility of applying Jeffrey’s rule,16 in other words these are related to the changes in the information flow within the network. For example, if the Court was certain that IP took part in the operation to plant the van bomb, it could be estimated how much influence that belief would have on the probability which we wish to ascertain: that IP gave the bomb warning. Let us observe the result as shown in Fig. 6.
With the general context information available (I), the probabilistic estimates carried out, at the first instance, of the explanatory facts which appear on the network and in accordance with the probability laws, an initial estimate can be made that there is a 11.7% estimate that IP could be who gave the bomb warning.
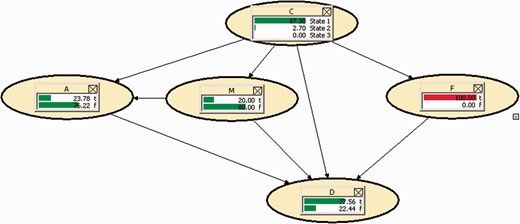
The influence of node F has not been highly significant in terms of increasing the probability that IP was the one who gave the bomb warning. Even so, the network estimates that this probability increases up to 23.78%. It is worth observing that the probability that IP took part in the T-4 attack increased from around 45% to about 97.3%.
Maybe we could assume that it could be more important for our purposes that the Court should be certain that IP bought the mobile on which the bomb warning call was made. This being the case, the results are as follows as shown in Fig. 7.
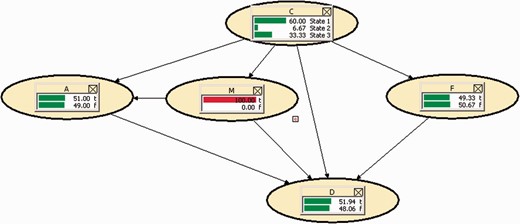
Against this backdrop, the increase in the probability we are seeking is much more important than before: we attain 51%. However, the probability that IP took part in the attack rose from 45% to 60%.
And if we consider that the Court estimated that the events M and F are right, in what way would these certainties influence which we have in hand? (Fig. 8).
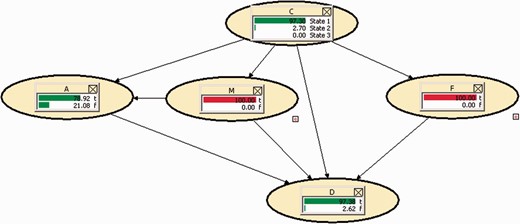
The rise has now been much more important: we almost reach 78.92%. The probability that IP has participated in the attack has attained 97.3%, the same as the figure obtained with just bearing in mind the certainty about F. What has risen a lot is the probability that the statement by MS is right: it has reached 97.38%, starting at 29.46% in the initial Run mode status.
Finally, on the assumption that the Court was right about what was stated by MS, we would obtain the following result as shown in Fig. 9.
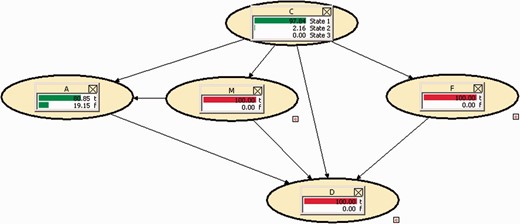
In this way a figure of 80.85% has been attained. In turn, the probability of C1 has been estimated at 97.84%.
Carrying out a summary exercise, the Court could argue in favour of prior probability that IP had carried out the bomb warning that around 80% of the assumption which considered the propositions looked at in the network right except for the so-called ‘ultimate proposition’ in this network (node C). However, the Court could adopt a more realistic position—which in this case would favour the accused party—considering that the explanatory events featuring in the network could never be entirely demonstrated and that the statement by MS—like no other evidence of a testimonial nature—may not be exact. In Hugin language, it is called entering likelihood evidence and in this case Hugin performs updating on uncertain evidence.
The Bayesian network only endeavoured to help the Court with the calculation of the prior odds before the expert in voices had intervened. The results of their analysis will modify the aforementioned initial bet and allow the probabilities to be found which are being searched for. In our example, we tried to find the probability if IP were the author of the bomb warning once the result of the voice recognition was obtained.
The experts of Spanish Civil Guard in voice comparison who acted in court regarding the attack on T-4 argued, before the Court, that to properly interpret the information provided by them in the expert opinion about the voice comparison (‘Evidence shows a moderately strong support towards the hypothesis which points at the defendant IP as the source of questioned voice versus the hypothesis of the authorship by other people recorded in similar acoustic conditions’, wherein the likelihood ratio was equal to 213 and the Evett verbal scale was used) required a calculation of the prior odds within the Bayesian inference framework used by them to attain an estimate about the probability of attributing to IP the bomb warning. Making it clear to the Court that this prior odds was an exclusive competence of the jurisdictional body, they wished to illustrate this as carrying this out in practice if the members of such a body had the confidence that one of the command was the one who made the call. The experts wished to stay out of the actual case in point and there were four members of the so-called ‘legal command’ (as has been seen, in reality the ETA command was made up of only three ‘legal’ members—non-fugitive members of the terrorist band from Spain). In this way, IP was able to attain 25% of a priori probability of being the author thereof. As can be seen, this figure can always be classified as conservative with regard to the maximum calculated with the network.
Applying the odds form of Bayes’ Theorem, the calculated posterior probability that IP was the author of the bomb warning once the result of the voice expertise had been attained, having approximately reached 98%. This figure is what stood out in the media as provided by the experts after their appearance in court to defend their expert report, but the patient reader of this article will have noticed that the journalists were far from reality as they had properly understood the information conveyed by the Spanish Civil Guard experts.
If we work out the posterior odds in favour of the proposition that IP made the bomb warning based on the maximum a priori probability for this proposition with the Bayesian network, the figure of around 99.9% would be reached for the posterior probability that IP was the author of the bomb warning.
This was not set out in the provisions of the sentence regarding the voice test be regarded as brilliant. Without any doubt, there is a difficulty of understanding both in that stated by the experts in trial as well as that written in the expert report.
3.2 On the expert assistance to Courts in assessing forensic expert testimony
The assessment of evidence is at the core of the judicial decision-making. It consists of determining whether the evidence before the Judge or Court supports (and how strongly) the statements about disputed issues of fact, which implies to evaluate the reliability and helpfulness of the available evidence as well as to ascribe appropriate weight to it in support of such statements. Assessing evidence consists, in other words, in determining, through a chain of ‘reasoning’ from the evidence submitted in the courtroom, whether the statements about disputed factual issues can be taken as true.
So far as evidential reasoning is essentially made up of inductive inferences based on probabilistic laws or even on social generalizations without any scientific foundation, the results that said reasoning produces cannot be taken as conclusive but rather they must be read in terms of simple ‘probability’.17 Self-evidently, the above does not mean that such results cannot be treated as true; what’s more, there are good reasons to expect that the results of a sound process of assessment will be accurate. This only means that, strictly speaking, the most that can be said is that the evidential reasoning concludes with a ‘hypothesis’, a statement which we accept as true though we do not know with absolute certainty whether it is or not, and that the degree of probability will provide a good criterion for its justification. The consequence of the just mentioned is clear: the main task of a rational assessment is that of ‘measuring probability’. And that’s why the objective of the evidence assessment models must be to provide rational schemes to assign the probability of the hypotheses.
Two major models for assessing evidence may be adopted18: (a) those based on confirmation schemes, which use the logical or inductive notion of probability (which applies to propositions and corresponds to the common use of ‘probably’, ‘possibly’, ‘presumably’ something is true); and (b) those based on the application of mathematical tools to the appraisal process, which use the mathematical concept of probability (which applies to events and it is interpreted either in terms of the relative frequency of the class of events to which they belong or in terms of the degree of belief in the occurrence of an event or in the veracity of a proposition). The first model is by far the one prevailing in the legal field but there are also abundant approaches which propose to apply the mathematical methods of the probability calculus to the evidence assessment process.
This work is actually inserted into the second model: the use of the Bayes’ Theorem as a tool to rationalize the assessment of scientific evidence; in other words, ‘to rationally determine what is to be believed’ about the hypothesis to be proved when a scientific test has been carried out.19 A task that—we should remember—is undertaken by combining the result of the expert report on the occurrence of the disputed hypothesis compared with its alternative (which is expressed by means of a ‘likelihood ratio’) with the ‘prior odds’ of these hypotheses in view of all the evidence that the judge has before him apart from (and on the sidelines of) the expert report.
However a remark must be made in this regard. Bayesianism, as a ‘general’ model for evaluating the support that all the available evidence provides to a hypothesis on disputed issues of fact has been subject to criticism.20 Most of the criticism is driven by practical considerations. In particular they highlight how difficult it may be for the judge to quantify its prior appraisal (the ‘prior odds’); or draw attention to the inevitable subjectivity of said quantification, or to the risk which entails putting it in the hands of judges statistical instruments which most of the times are incomprehensible to them: perhaps not all the experts—it is argued—would actually be capable of presenting the ‘likelihood ratio’ with the necessary accuracy for its correct understanding; moreover, even if they were able to, the judges could still get confused.21 Furthermore, the Bayesian formula—they say—entails a relatively simple mathematical calculation in the base case of having to evaluate a ‘single’ item of evidence which ‘directly’ deals with the hypothesis to be tested, which in turn is a ‘simple’ hypothesis. However the difficulty of the calculation increases strikingly when it is used to resolve more complex situations such as the ‘plurality’ of evidence relating to a hypothesis, the ‘cascaded inference’ (or indirect evidence) or the proof of a hypothesis relating to a ‘complex’ fact.
To counter this criticism the following should be noted. First, the criticism stated does not take into account the advances which have been made in the last few decades to optimize and simplify the probabilistic calculations (e.g. by means of the deployment of Bayesian networks) and it actually reveals the traditional aversion of jurists to open up to extralegal knowledge. Secondly, this article is not focused on the adoption of the Bayes’ Theorem as a general evidence assessment model, but rather only as a way of determining (by quantifying) the probative value to be assigned to the statistical data supplied in the forensic expert report. We consider that to be particularly appropriate as in recent years the evolution of ‘forensic science’ has provided a very wide range of scientific proofs with a statistical structure which can be used in all the proceedings.22 Finally, what is specifically proposed here is the use of a tool (the Bayesian networks) to quantify Court’s prior subjective assessment (the ‘prior odds’), which is fairly—as mentioned above—one of the main difficulties indicated by critics to use the Bayes’ Theorem in Courts. And there can be no objections to this proposal: there is no reason to assume that the result of this operation is of higher quality when the judge carries it out ‘subjectively’, without the aid for reasoning provided by the logic and the mathematics.
There is no doubt that the use of Bayesian networks is—as it has been endeavoured to show here—a good way to rationally quantify the ‘prior odds’. But there is no doubt either that, in practice, use of this tool requires the assistance of expert staff, which in principle may appear as ‘problematic’. The objection could be raised that, by using such assistance, the risk is run that it is the expert and not the Judge who ultimately determines what is to be believed about the disputed factual issues under consideration, thus converting the expert into the decision-maker of the case. In that way, however,—here is the ‘problem’—the principle of ‘free’ assessment of evidence, whereby it is for judges and no one else to assess the evidence, would be breached and a system based on the Judge’s authority would have been replaced by another based on expert’s authority.
In our opinion though, there would be no grounds for the stated objection. The assistance provided by the expert to the judge is ‘merely technical’ and consists of using his knowledge to help the latter, turning his degree of belief into figures; in other words, quantifying that which he is unable to quantify by himself. That is all. It is the Judge who has to provide the pieces of evidence that form the basis for this degree of belief which has to be quantified. More specifically, contrary to the conclusions stated in the above-mentioned expert report (see paragraph 2.3), which are the entire responsibility of the expert as it is something which only he can reach with his tools and knowledge, the ‘prior odds’ (which—we should recall—expresses the degree of belief assigned by the Judge to the ‘ultimate probandum’ in odds form before the expert test is carried out and the results thereof are known) is something which is entirely based on the knowledge that only the Judge has; and, in actual fact, the Judge could find it himself if he just had the necessary training to do that. The expert merely helps him to quantify this degree of belief in probabilistic fashion.
Precisely because the expert aid provided to the Judge in this task is merely technical, this cooperation does not entail that it is the expert who ends up carrying out a function (that of judging and previously stating the facts of the case) which has been institutionally granted to the Judge, nor is it at odds with the principle of free assessment of evidence; quite the opposite, in fact. This principle has been traditionally interpreted in extremely subjective and irrational terms. In actual fact, it has been customary—and unfortunately it still is—to understand ‘free assessment’ as a private, firm, non-transferable, subjective conviction; as a kind of ineffable ‘quid’, a hunch which cannot be exteriorized nor controlled. The widespread expression ‘intimate conviction’ clearly expresses this irrational way of conceiving it. However, this interpretation proves to be unacceptable. The Court’s assessment of evidence must indeed be free from legal obstacles but clearly ‘not free from reasons’. Otherwise we would be proclaiming the purest judicial decisionism. This is why when a scientific test has been carried out with the aid of the expert to calculate the ‘prior odds’ and determine from that juncture—using the Bayes’ Theorem—the probative value that should be assigned thereunto, not only does it prove incompatible with the principle of free assessment of evidence but rather it is also ‘required’. There would be no point in deploying the complex expertise that technical-scientific advances put at the disposal of the proceeding if the determination of its probative value were totally left in the hands of an unskilled Judge who does not know its correct interpretation and scope. The expert assistance provided to the Judge who has to assess the evidence is thus highly important to rationally determine the value of the ‘prior odds’. Moreover, it could be said to constitute an ‘epistemological guarantee’ required by any rational conception of the assessment of evidence. It’s something else deciding ‘when’ and ‘how’ this assistance can be provided.
The Spanish criminal procedural model, which is adversarial, is structured around two major stages, both of them assigned to different judges or magistrates23 because the Constitutional Court Judgement dated on 12 July 1988 declared it to be unconstitutional for the same court to hear the case and pass sentence on it—to ensure the court’s impartiality.
The main aim of the first stage—preliminary investigation—as far as possible and never at any price, is to search for the truth. Acts are carried out which are intended to establish something which is not known (the circumstances relating to the offence and the identity of their perpetrator—Article 299 LECrim (Spanish Code of Criminal Procedure); its implementation would result, among other aspects, in the Judge’s decision as regards to the alternative dismissal-opening of the trial. These actions thus do not, as a general rule, have any evidential value nor do they serve as the basis for any sentence regarding the guilt or innocence of the accused.
During preliminary investigation the Judge enjoys broad powers to agree, at the request of either party or on his own initiative, such diligences as he sees fit, including expert reports which he will agree ‘when, to establish or assess any important circumstance or fact in the summary, scientific or artistic knowledge proves necessary or appropriate’ (Article 456 LECrim). Once the expert has provided expertise, the Judge may—also on his own initiative or at the request of either party—ask the experts such questions as he deems relevant and/or ask them for the necessary clarifications (Article 483 LECrim).
Two things become clear that being said up to now: The second stage, the trial, is the one at which, inter alia, the evidence is presented with a view to delivering judgement. This is subjected to the principles of oral procedure, contradiction, immediacy and publicity, but not by chance, but rather because they constitute the mechanism to more appropriately ensure the rights of the defendant, the powers of the accusers and the correctness of the court decision. The elements required to justify the sentence must be acquired by the court in the trial.
Leaving aside the debate about the nature of the expert report and assuming that the expertise is just another means of proof or diligences of the investigation—depending on the procedural stage we are at—what is for sure is that the expert helps the Judge in his function, providing the process with knowledge that the magistrate does not possess. In this regard, inter alia, the TS (Supreme Court) Judgement on 5 May 2010 states that: expert reports contain ‘technical opinions about certain matters or about certain facts by those who have special training in this area with a view to making the Court’s job easier when appraising the evidence. It is not evidence which provides factual aspects but rather criteria which help the magistrate to interpret and appraise the facts without changing its attendant to appraise the evidence’.
The Judge’s powers at this stage to request an expert report and to ask the expert those questions and clarifications the Judge deems opportune are broad. Should this be the case, self-evidently there is no legal impediment—at the request of the Judge and bearing in mind, obviously, that it is the latter (or the requesting party) who states ‘clearly and decisively to the experts the object of their report’ (Article 475 LECrim)—to the expert also helping him/her with the work to establish the ‘prior odds’ required within a logical framework of Bayesian inference to obtain the ‘posterior odds’. Let’s bear in mind that the expert will issue his/her report with regard to facts—to be precise, statements about factual data which he is informed.
The above, applied to the expertise, means that for the expert report carried out during the preliminary investigation 24 to have evidential value, there needs to be a statement by the experts at the trial.25 And here, although the material powers of the Judge are much more limited, there does not seem to be any impediment for the Court to request the expert to provide clarifications about the answers given to the questions posed by the parties or even to formulate new questions. Nevertheless, we deem it crucial to bear the following in mind:
(a) First, there is no doubt that as regards to the expert’s testimony, there is no article such as Article 708 LECrim—regarding the testimony—which specifically enables the president of the Court to ask the witnesses those questions he sees fit to ascertain the facts regarding which statements are being made. By contrast, Article 724 LECrim regarding the expertise indicates that the experts will answer the questions and the cross-examination of the parties without any reference to the Judge. Nevertheless, and always considering questions conducive to ascertaining the facts about which statements are being made, it makes no sense for there to be a different treatment between both types of proof.26
(b) Secondly, we are aware that in criminal proceedings, the evidence presented in trial is that requested by the parties which the Judge deems to be relevant (Article 728 LECrim); evidence requested on the initiative of the Court has an exceptional nature and is limited to the assumptions set out in Article 729 LECrim. Number 2 of the previous provision enables the Judge to ‘agree the examination of evidence not proposed by either party which the Court deems to be necessary to prove any of the facts which have been subject to qualification documents'. This section has been redefined by the TS (TS Judgements dated December 1st 1993), establishing that evidence requested on the initiative of the Court is solely possible if aimed at verifying whether the evidence about the facts are reliable or not from the perspective of article 741 LECrim (which is known as proof upon proof).
It thus seems that those who have great powers can also make use of lesser ones. In other words, if, for the purposes of proving any of the facts which have been subject to qualification documents the Judge is able to agree the examination of evidence, he has all the more reason to ask questions or clarifications from the experts who, proposed by the parties, have spoken at the trial.
4. Conclusions
This research provides reasoning to justify the assistance of forensic experts to Judges and Courts to assign prior odds when the evaluation of scientific evidence has been made by likelihood ratios. We consider it very relevant that the judicial reasoning used to defend a result related with a criminalistic comparison is based on logic laws which are used in science and not in hunches.
The mathematical tool proposed for such assistance is a Bayesian network, because it is a logical structure of reasoning under uncertainty based mainly on the Bayes’ Theorem and Jeffrey’s rule. These rules ensure that the subjective estimation of the probabilities required in the inferential process strictly respects the probability laws. No one can reasonably say that the probabilistic estimations which we have come to are arbitrary, unfounded, unscientific, intentionally skewed or random.
The prior odds which have to be estimated in a Bayesian inference framework related with an expert report can be assigned numerically in line with generalizations and common sense in many cases. A real case has been discussed in detail to illustrate how to implement in practice the inferential assistance suggested.
Legal implications of the proposed expert assistance to Judges and Courts in a Continental judicial system as the Spanish one have also been discussed. In accordance with the applicable Spanish law and jurisprudence, we believe that there are grounds to assist them in this way. On the one hand, this technical support could be thought as an ‘epistemological guarantee’ to preserve a rational conception of the assessment of scientific evidence. On the other hand, this kind of forensic practice could reinforce the principle of equality of arms in the legal procedure.
Future practical research will be needed to make good use of the possibilities that Bayesian networks can offer to Judges and Courts (and the parties to the proceedings) to make inferences, not only to assess coherently the evidence but also to make decisions in the same way (i.e. using utility functions) along the procedural stages. This work is only a first of such possibilities.
Funding
Partial support by Fullbright Commission and Spanish Ministry of Science under the program Salvador de Madariaga-2013 (to M.G.-A.). Partial support by Spanish Ministry of Science and Innovation under the project DER2011-27970 to (to V.P.-I.)
1 J.J. Lucena-Molina, V. Pardo-Iranzo & J. Gonzalez-Rodriguez, Weakening Forensic Science in Spain: From Expert Evidence to Documentary Evidence, J Forensic Sci, Vol. 57(4), July 2012, 952–963.
2 A. O’Hagan et al. (2006). Uncertain judgments: eliciting expert’s probabilities. Wiley, Hoboken NJ (USA).
3 C. Aitken & F. Taroni (2004). Statistics and the evaluation of evidence for forensic scientists. Second edition. J. Wiley & Sons, Chichester (UK), pp. 79ff.
4 Ibid.
5http://bbfor2.net/ (accessed August, 2014).
6 T. Anderson, D. Schum & W. Twining (2010). Analysis of Evidence. Second edition. Cambridge University Press, Cambridge (UK).
7 P. Roberts & C. Aitken, The Logic of Forensic Proof: Inferential Reasoning in Criminal Evidence and Forensic Science, Guidance for Judges, Lawyers, Forensic Scientists and Expert Witnesses, prepared under auspices of the Royal Statistical Society s Working Group on Statistics and the Law, UK, 2012.
8 This is an important point because on one hand ‘when a proposition’s degree of belief is evaluated, there is always exploitation of available background information, even though it is not explicit’ and, on the other hand ‘A relevant proposition is taken to mean a proposition which is not included in the background information’, and besides it should be assumed that, for the evaluation of forensic evidence, ‘the distinction between the background knowledge of the Court or of the expert, and the findings submitted for judgment, is clear from the context’ (F. Taroni, C. Aitken, P. Garbolino & A. Biedermann (2006). Bayesian Networks and Probabilistic Inference in Forensic Science. J. Wiley & Sons, Chichester (UK).
9 M. Gascon-Abellan (2010). Los hechos en el derecho. 3a edición. Marcial Pons, Barcelona (Spain).
10 D.V. Lindley (2007). Understanding Uncertainty. John Wiley & Sons, New Jersey (USA).
11 C. Champod & J. Vuille, Scientific evidence in Europe – Admissibility, Appraisal and Equality of Arms, European Committee on Crime Problems (CDCP), Strasbourg, May, 2010.
12http://en.wikipedia.org/wiki/2006_Madrid-Barajas_Airport_bombing (accessed August 2014).
13 F. Taroni, C. Aitken, P. Garbolino & A. Biedermann (2006). Bayesian Networks and Probabilistic Inference in Forensic Science. J. Wiley & Sons, Chichester (UK).
14http://www.hugin.com (accessed August 2014).
15 Art. 28 of the Spanish Penal Code (SPC): Principals are those who perpetrate the act themselves, alone, jointly, or by means of another used to aid and abet. The following shall also be deemed principals: (a) Whoever directly induces another or others to commit a crime; (b) Whoever co-operates in the commission thereof by an act without which a crime could not have been committed.
Art. 29 SPC: Accessories are those who, not being included in the preceding Article, co-operate in carrying out the offence with prior or simultaneous acts.
16 Ibid. 15.
17 Cfr. M. Gascon-Abellan, Los hechos en el derecho, cit.
18 Ibíd. pp. 92 ff.
19 R. Royall, Statistical evidence, a likelihood paradigm, Monographs on Statistics and Applied Probability, Chapman&Hall/CRC, London/New York, 1997. See also M. Gascón Abellan, J.J. Lucena-Molina & J. Gonzalez-Rodriguez, Razones científico-jurídicas para valorar la prueba científica: una argumentación multidisciplinar, Diario La Ley, 4 Oct. 2010, n° 7481, Sección Doctrina.
20 For the deficiencies assigned to Bayesianism applied in criminal procedural law, see M. Gascón-Abellán, J.J. Lucena-Molina & J. Gonzalez-Rodriguez Ibid. See also L.H. Tribe, Trial by Mathematics, Harvard Law Rev, 84, 1971, M. Taruffo, La prueba de los hechos, Trotta, Madrid, 2004, and H.L.Cohen (1977). The Probable and the Provable. Oxford, Clarendon Press..
21 The main problem here is the possible confusion of P (E/H) with P (H/E) and P (E/no-H) with P (no-H/E). It is really hard for experts to express the proposition ‘P (E/H) is much bigger than P (E/no-H)’ in a verbal form which does not make it sound like ‘P (H/E) is much bigger than P (no-H/E)’. That is why those who defend the use of this appraisal model in the courts consider that it will not attain its purposes whilst judges and lawyers are not familiar with the most elementary probability theory. See R.D. Friedman, Assessing Evidence, Michigan Law Rev, 94, 1996, pp.1836-37, and footnote no. 5.
22 In actual fact, the Bayes’ Theorem constitutes the logical reasoning structure to resolve the appraisal problem that the specialized scientific forensic community has claimed as the most appropriate for decades. See S.E. Fienberg & D.H. Kaye (1991) Legal and statistical aspects of some mysterious clusters J. R. Stat. Soc, Ser A, 154.
23 It is important to carry out this precision because in many countries around us the preliminary investigation falls within the competence of the Public Prosecutor. In Spain the only exception is assumed in the Criminal Procedure for Minors (LO 5 issued on 12 January 2000).
24 Though, by way of exception, the carrying out of the expertise in a trial stage may be agreed, it is more common to be carried out during the preliminary investigation.
25 In this regard two points must be pointed out: first, the law—Art. 788.2 LECrim—has ‘converted’ into a document some specific expert reports (the analysis about the nature, quantity and purity of narcotic substances carried out by official laboratories), attributing evidential value to the document which includes the report without said statement by the expert at the trial. On the other hand, without legal backing other expert reports (in addition to those legally known as scientifically objective) are sometimes receiving this same treatment, at least when they are not challenged. In both cases there is sometimes some doubt as to whether the right to defense is being fully respected (see, V. Pardo-Iranzo, La prueba documental en el proceso penal, Tirant lo Blanch, colección <<abogacía práctica>> no. 37, Valencia, 2008, and J.J. Lucena-Molina, V. Pardo-Iranzo & M.A. Escola-Garcia, Elementos para el debate sobre la valoración de la prueba científica en España: hacia un estándar acreditable bajo la norma 17.025 sobre conclusiones de informes periciales, www.riedpa.com (accessed August 2014)).
26 In actual fact, in trials with a jury, jurors are specifically allowed, through the presiding judge and subject to a relevance statement, to pose to the experts in writing such questions as they deem fit to ascertain and clarify the facts with which the evidence is connected (Article 46 Organic Law 5 enacted on 22 May 1995 regarding Courts with a Jury).


