-
PDF
- Split View
-
Views
-
Cite
Cite
B. Beikircher, T. Ameglio, H. Cochard, S. Mayr, Limitation of the Cavitron technique by conifer pit aspiration, Journal of Experimental Botany, Volume 61, Issue 12, July 2010, Pages 3385–3393, https://doi.org/10.1093/jxb/erq159
Close - Share Icon Share
Abstract
The Cavitron technique facilitates time and material saving for vulnerability analysis. The use of rotors with small diameters leads to high water pressure gradients (ΔP) across samples, which may cause pit aspiration in conifers. In this study, the effect of pit aspiration on Cavitron measurements was analysed and a modified ‘conifer method’ was tested which avoids critical (i.e. pit aspiration inducing) ΔP. Four conifer species were used (Juniperus communis, Picea abies, Pinus sylvestris, and Larix decidua) for vulnerability analysis based on the standard Cavitron technique and the conifer method. In addition, ΔP thresholds for pit aspiration were determined and water extraction curves were constructed. Vulnerability curves obtained with the standard method showed generally a less negative P for the induction of embolism than curves of the conifer method. Differences were species-specific with the smallest effects in Juniperus. Larix showed the most pronounced shifts in P50 (pressure at 50% loss of conductivity) between the standard (–1.5 MPa) and the conifer (–3.5 MPa) methods. Pit aspiration occurred at the lowest ΔP in Larix and at the highest in Juniperus. Accordingly, at a spinning velocity inducing P50, ΔP caused only a 4% loss of conductivity induced by pit aspiration in Juniperus, but about 60% in Larix. Water extraction curves were similar to vulnerability curves indicating that spinning itself did not affect pits. Conifer pit aspiration can have major influences on Cavitron measurements and lead to an overestimation of vulnerability thresholds when a small rotor is used. Thus, the conifer method presented here enables correct vulnerability analysis by avoiding artificial conductivity losses.
Introduction
Vulnerability analyses substantially contribute to our knowledge of plant water relations, and, according to Cochard et al. (2005), they may be increasingly applied in ecological studies as well as in breeding programmes (Mayr et al., 2006; Cochard et al., 2008; McDowell et al., 2008; West et al., 2008; Beikircher and Mayr, 2009; Beikircher et al., 2010). A vulnerability curve shows a species’ resistance to drought-induced embolism. It is a plot of per cent loss of hydraulic conductivity (PLC) versus the xylem pressure (P; Tyree and Sperry, 1988, 1989; Tyree and Zimmermann, 2002). Until recently, they have mainly been obtained via hydraulic measurements after inducing a defined P by dehydration (Sperry et al., 1988; Mayr et al., 2002; Tyree and Zimmermann, 2002), air-injection (Cochard et al., 1992; Sperry and Saliendra, 1994), or centrifugation (Holbrook et al., 1995; Pockman et al., 1995; Alder et al., 1997). By contrast with these methods, the Cavitron technique allows the induction and measurement of PLC in rapid succession while samples are enclosed in the centrifuge, and thus enables the construction of an entire vulnerability curve within a short space of time (Cochard, 2002; Cochard et al., 2005, 2007).
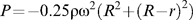

whereby r1 and r2 are the differences in water levels between the reservoirs at the times t1 and t2, respectively. Thus, the smaller a rotor, the higher are the required ω (see above) and, in consequence, the higher is ΔP (Fig. 1)—unless the water levels in the reservoirs are balanced. In that case ΔP is 0 and does not depend on ω or P.
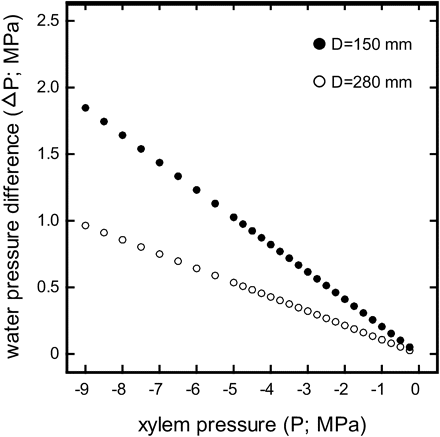
Maximum water pressure difference across the sample (ΔP; MPa) versus xylem pressures (P; MPa) induced by different spinning velocities calculated according to equation 2. ΔP and corresponding P were calculated for a rotor with 280 mm (open symbols) and 150 mm in diameter (closed symbols), respectively. Water levels in the reservoirs were assumed to be 0.8 cm and 1.6 cm from the inner rotor wall (see Materials and methods section). Please note that this figure concerns only the standard method. In the case of the conifer method ΔP is maximal at 0.05 MPa regardless of P (for explanation see paragraph ‘conifer method’ in the Materials and methods section).
To understand the background of the Cavitron technique as well as the interrelationship with pit aspiration presented in this study, it is essential to distinguish carefully between the parameters P and ΔP and their impact on xylem function. The former is a measure of the availability of water at a certain point in a plant or a sample and is physically equivalent to a tension (Tyree and Ewers, 1991). When it exceeds species-specific thresholds, embolism occurs due to air-seeding (Sperry and Tyree, 1990; Tyree and Ewers, 1991; Tyree and Zimmermann, 2002; Cochard et al., 2009). The ΔP is the difference in water pressure between two points in a plant or sample, respectively. High ΔP is known to cause pit aspiration in conifers, whereby the pressure drop across each pit membrane is relevant (Sperry and Tyree, 1990). The inter-tracheid pits of conifers typically have a torus-margo pit membrane. This architecture allows water to flow between two water-filled tracheids as water passes through the thin and porous margo driven by moderate ΔP. When a tracheid is filled with air (embolism), the pressure difference between the water-filled (negative pressure) and the air-filled conduit (ambient pressure) increases considerably, the thickened torus is aspirated against the pit opening and seals the air-filled tracheid as long as the pressure difference is lower than the species-specific vulnerability threshold for air-seeding (Chapman et al., 1977; Tyree and Zimmermann, 2002; Hacke et al., 2004; Domec et al., 2006, 2008; Hölttä et al., 2007). Theoretically, this sealing of the tracheid can also happen between two water-filled tracheids when ΔP is high enough. In nature this may rarely be the case as the pressure difference over the pit membrane due to normal transpiration is far too small to cause pit aspiration (Gregory and Petty, 1973; Chapman et al., 1977; Hölttä et al., 2007). Although Hammel (1967) and Robson et al. (1988) found that, at the boundary between frozen and unfrozen tracheids, the pressure difference can be sufficient to cause pit aspiration.
So far, the rotor diameter has only been known to influence cavitron measurements of angiosperms negatively (Choat et al., 2010; Cochard et al., 2010,a): When mean conduit length exceeds the sample length, water in cut conduits may be thrown out by the rotational motion (Alder et al., 1997) or, due to the lack of filtration of microscopic particles or air bubbles at the pit membranes, embolism may be induced, causing a strongly altered vulnerability curve (Cochard et al., 2005; but also see Li et al., 2008). This should not concern measurements on conifers, as tracheids are mostly only few millimetres long (Tyree and Zimmermann, 2002). Accordingly, Cochard et al. (2005) and Li et al. (2008) demonstrated that vulnerability curves of conifers obtained with conventional methods and the Cavitron technique corresponded well, which would also indicate that pit aspiration does not play any role in Cavitron measurements. However, they used a rotor of about 280 mm in diameter which might be sufficient to avoid critical ΔP. It is hypothesized that the use of smaller rotors can be problematic when high ΔP causes pit closure and, consequently, conductivity losses independent of embolism formation. Species-specific differences in the sensitivity to ΔP effects were also expected.
In this study, a small rotor was used with a diameter of 150 mm to measure vulnerability to drought-induced embolism. The influence of ΔP on vulnerability curves was analysed, based on two different measurement approaches. First, measurements were carried out at stepwise increasing ω and, consequently, increasing ΔP according to measurement protocols in Cochard (2002), Cochard et al. (2005 2008), and Li et al. (2008). This method is referred to as the ‘standard method’. Second, ΔP was kept low by a reduction of ω during conductivity measurements and balancing the water levels in the reservoirs before increasing ω to attain the desired P (see Materials and methods section). This measuring method is referred to as the ‘conifer method’.
Vulnerability curves obtained with both methods were compared on four conifer species, and ΔP thresholds determined by measurement of hydraulic conductivity at increasing ΔP. Furthermore, water extraction curves were made with the centrifuge to test if spinning itself affect pits by induced gravitiy forces.
Materials and methods
Plant material
All measurements were made on the following four conifers: Juniperus communis L., Picea abies (L.) Karsten, Pinus sylvestris L., and Larix decidua Mill. The latter three species were harvested in a natural forest in Natters (47°14′ N, 11°22′ E; 783 m a.s.l., Tyrol, Austria, Central European Alps), while J. communis was growing in the Botanical Garden of Innsbruck (47° 16′ N, 11 24′ E; 754 m a.s.l., Tyrol, Austria, Central European Alps). Branches were cut from plants, wrapped in dark plastic bags and transported to the laboratory. There, they were re-cut twice under water and saturated for 24 h.
Vulnerability analyses
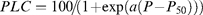
where PLC is the per cent loss of conductivity, P is the corresponding xylem pressure (Pa), and a is related to the slope of the curve. P50 is the P value corresponding to 50% loss of conductivity. In addition, P at 10% PLC (P10) and 90% PLC (P90) were determined. PLC was calculated from the ratio of actual (after inducing a given P) to maximum (i.e. first measurement at –0.25 MPa) hydraulic conductance (k).
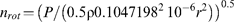
where ρ is the density of water (kg m−3), 0.1047198 is the conversion factor of angular velocity (ω; rad s−1) in nrot (1 s−1) and r (m) is the radius of the rotor less the distance to the outlet of the downstream reservoir. In the case of the conifer method, where the water reservoirs were emptied, r was the radius of the rotor less the wall thickness of the reservoirs (3 mm).
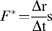
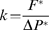
Two different approaches were chosen for Cavitron measurements:
Standard method
For measurements with the standard method the rotational speed (nrot; and thus the angular velocity ω) was set to the target pressure (according to equation 4) and maintained constant for 1 min. This time was assumed to be sufficient to generate the maximum level of cavitation as (i) it has been reported that cavitation is formed within a few seconds after exposure to the respective P (Cochard et al., 2005), and (ii) during the water extraction analyses (see below) it has been observed that water was released only within the first seconds after increasing P and that the meniscus was stable afterwards. After setting P, the flow rate (F*) was measured and hydraulic conductance (k) was calculated as described above (see equations 5 and 6). The first measurement was done at –0.25 MPa and the following at successively lower pressures. In the case that the meniscus was moving too rapidly at high speed, after setting P nrot was lowered for conductivity measurements. However, in contrast to the conifer method (see below), water levels in the reservoirs were never balanced before increasing nrot and thus high ΔP values were achieved at low pressures. For example, at a P of –6 MPa, ΔP was 1.25 MPa (Fig. 1).
Conifer method
In the conifer method, ΔP was always kept low by (i) doing all k measurements at –0.25 MPa and (ii) balancing the water levels before increasing P as described in the following. First, P was set to –0.25 MPa (equals ΔP of 0.05 MPa for our rotor diameter) and after 1 min, k was measured in a similar way to the standard method. In contrast to the standard method, water levels in the reservoirs were balanced before P was decreased to the next desired value. This was done either by waiting until the water levels were balanced due to the water flow itself, or (as conductivity was rather low in most samples and thus a lot of time, often more than 1 h, was required to balance the water levels) by stopping the centrifuge briefly. By stopping the centrifuge for a few seconds, reservoirs were emptied except for a small amount of water. This remaining water caused a 1 mm thick water film at the reservoir bottom during spinning so that sample ends were still submerged. Then, nrot was set to the next desired P for 1 min. Due to the balanced water levels, ΔP was thus nearly zero regardless of nrot (also see Introduction). After inducing P, nrot was decreased again to –0.25 MPa before the reservoirs were refilled for the next conductivity measurement. Thus, in the conifer method ΔP never exceeded 0.05 MPa. A problem with this measuring method could have arisen if conduits refilled during spinning at low nrot. At least for our study this can be excluded, because k was always constant during the measurement phase. Also Cochard (2002) did not observe a conductance recovery in Laurus nobilis when, after spinning at –3.1 MPa, samples where spun at –0.8 MPa for 4 h.
Pressure–conductivity analyses
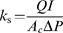
where Q is the volume flow rate (m3 s−1), l is the sample length (m), Ac is the xylem cross-sectional area (sapwood less heartwood; m2), and ΔP in this case corresponds to the water pressure (Pa) applied with the pressure bomb.
Curves were fitted similar to vulnerability curves (equation 3) whereby PLC was substituted by percentage loss of ks. ΔP at 10, 50, and 90% loss of ks corresponded to 10, 50, and 90% pit aspiration (ΔPasp10, ΔPasp50, ΔPasp90).
This method may cause problems when the solution in the chamber is saturated with gas and, subsequently, gas comes out of the solution in the stem section protruding from the bomb. However, this was only observed at pressures where PLC was already up to 100%. Furthermore, this effect would be similar on all measured species and thus could not explain the variation shown in Fig. 3. Also, Cochard et al. (2010b, who did a similar experiment on Fagus sylvatica, observed no decrease in conductance.
Critical sample length
Critical sample length was defined as the minimum length at which less than 10% pit aspiration occurred at P50. It was calculated by plotting ΔP versus P for various diameters (as in Fig. 1) and subsequently inserting of the respective ΔPasp10 (y-value) in the linear equations obtained. The diameter at which the thereby calculated x-value corresponded to P50 was taken as the critical sample length.
Water extraction curves
Water extraction curves (also see Cochard et al., 2010b) were made with the Cavitron. Therefore, two reservoirs with outlets at 1.6 cm from the bottom were used. Samples were first spun at –0.25 MPa until water levels were balanced and menisci overlapped. Then, nrot was increased successively to different P and the respective distances travelled by the meniscus noted. For the calculation of P (equation 1), R was taken as the distance from the rotational axis to the actual water level. The percentage of extracted water was calculated as the ratio of actual (at a given P) to maximum distance travelled. Curves were fitted similar to vulnerability curves (equation 3) whereby PLC was substituted by percentage extracted water. ΔPex50 is the ΔP at 50% of total water extraction.
Number of samples and statistics
Vulnerability analyses, water extraction curves, and pressure–conductivity analyses were made on 4–10 samples, originating from at least three individual plants per species, and method. For conductivity measurements with the Cavitron at least five k values were taken per measurement and means calculated. Differences between methods were tested with the Welch-test at a probability level of 5%.
Results
In all four conifers, vulnerability curves analysed with the standard and conifer methods, respectively, differed. Vulnerability thresholds, i.e. xylem pressure at 10, 50, and 90% loss of conductivity (P10, P50, P90) were higher (i.e. less negative) when measured with the standard method (Table 1; Fig. 2). The greatest differences were found in L. decidua, where P50 of the standard method was 2.08 MPa higher than that measured with the conifer method. Differences were lower in P. sylvestris and P. abies and lowest in J. communis (0.66 MPa; Table 1). In general, P50 measured with the conifer method corresponded well to P50 values obtained with conventional hydraulic methods (Table 1).
Vulnerability curve parameters (parameter a, xylem pressure at 10, 50, and 90% loss of conductivity: P10, P50, P90) and xylem pressure at 50% water extraction (Pex50) of Juniperus communis, Picea abies, Pinus sylvestris, and Larix decidua
| Juniperus communis | Picea abies | Pinus sylvestris | Larix decidua | |
| Parameter a | ||||
| Standard method | 0.77±0.04 | 1.25±0.09 | 1.65±0.14 | 2.00±0.18 |
| Conifer method | 0.77±0.04 | 1.01±0.06* | 2.64±0.32* | 1.61±0.09 |
| P10 | ||||
| Standard method | –2.10±0.22 | –1.18±0.18 | –0.83±0.17 | –0.36±0.15 |
| Conifer method | –2.78±0.20 | –1.80±0.18* | –2.54±0.15* | –2.18±0.43* |
| P50 | ||||
| Standard method | –4.96±0.07 | –2.93±0.06 | –2.17±0.05 | –1.46±0.05 |
| Conifer method | –5.62±0.06* | –3.98±0.05* | –3.37±0.05* | –3.54±0.04* |
| 280 mm rotor diameter | –6.37±0.18 | –3.97±0.04 | –3.20±0.02 | –3.87±0.10 |
| Conventional | –5.60±0.181 | –3.39±0.032 | –2.53; –2.78±0.114 | –3.66±0.052 |
| P90 | ||||
| Standard method | –7.82±0.09 | –4.68±0.07 | –3.50±0.06 | –2.56±0.05 |
| Conifer method | –8.47±0.09* | –6.16±0.07* | –4.21±0.06* | –4.90±0.27* |
| Pex50 | –5.61±0.06 | –4.08±0.02 | –3.24±0.05 | –3.93±0.06 |
| Juniperus communis | Picea abies | Pinus sylvestris | Larix decidua | |
| Parameter a | ||||
| Standard method | 0.77±0.04 | 1.25±0.09 | 1.65±0.14 | 2.00±0.18 |
| Conifer method | 0.77±0.04 | 1.01±0.06* | 2.64±0.32* | 1.61±0.09 |
| P10 | ||||
| Standard method | –2.10±0.22 | –1.18±0.18 | –0.83±0.17 | –0.36±0.15 |
| Conifer method | –2.78±0.20 | –1.80±0.18* | –2.54±0.15* | –2.18±0.43* |
| P50 | ||||
| Standard method | –4.96±0.07 | –2.93±0.06 | –2.17±0.05 | –1.46±0.05 |
| Conifer method | –5.62±0.06* | –3.98±0.05* | –3.37±0.05* | –3.54±0.04* |
| 280 mm rotor diameter | –6.37±0.18 | –3.97±0.04 | –3.20±0.02 | –3.87±0.10 |
| Conventional | –5.60±0.181 | –3.39±0.032 | –2.53; –2.78±0.114 | –3.66±0.052 |
| P90 | ||||
| Standard method | –7.82±0.09 | –4.68±0.07 | –3.50±0.06 | –2.56±0.05 |
| Conifer method | –8.47±0.09* | –6.16±0.07* | –4.21±0.06* | –4.90±0.27* |
| Pex50 | –5.61±0.06 | –4.08±0.02 | –3.24±0.05 | –3.93±0.06 |
Data (mean ±SE) show parameters of vulnerability curves measured with the standard and the conifer method and P50 values measured with a rotor with 280 mm in diameter (published in Cochard, 2006) as well as conventional hydraulic methods (conventional; (1) Beikircher et al., 2010; (2) Mayr et al., 2006; (3) Cochard, 1992; (4) Poyatos et al., 2008). Asterisks indicate significant intraspecific differences between standard and conifer method (P >0.05, Welch test).
Vulnerability curve parameters (parameter a, xylem pressure at 10, 50, and 90% loss of conductivity: P10, P50, P90) and xylem pressure at 50% water extraction (Pex50) of Juniperus communis, Picea abies, Pinus sylvestris, and Larix decidua
| Juniperus communis | Picea abies | Pinus sylvestris | Larix decidua | |
| Parameter a | ||||
| Standard method | 0.77±0.04 | 1.25±0.09 | 1.65±0.14 | 2.00±0.18 |
| Conifer method | 0.77±0.04 | 1.01±0.06* | 2.64±0.32* | 1.61±0.09 |
| P10 | ||||
| Standard method | –2.10±0.22 | –1.18±0.18 | –0.83±0.17 | –0.36±0.15 |
| Conifer method | –2.78±0.20 | –1.80±0.18* | –2.54±0.15* | –2.18±0.43* |
| P50 | ||||
| Standard method | –4.96±0.07 | –2.93±0.06 | –2.17±0.05 | –1.46±0.05 |
| Conifer method | –5.62±0.06* | –3.98±0.05* | –3.37±0.05* | –3.54±0.04* |
| 280 mm rotor diameter | –6.37±0.18 | –3.97±0.04 | –3.20±0.02 | –3.87±0.10 |
| Conventional | –5.60±0.181 | –3.39±0.032 | –2.53; –2.78±0.114 | –3.66±0.052 |
| P90 | ||||
| Standard method | –7.82±0.09 | –4.68±0.07 | –3.50±0.06 | –2.56±0.05 |
| Conifer method | –8.47±0.09* | –6.16±0.07* | –4.21±0.06* | –4.90±0.27* |
| Pex50 | –5.61±0.06 | –4.08±0.02 | –3.24±0.05 | –3.93±0.06 |
| Juniperus communis | Picea abies | Pinus sylvestris | Larix decidua | |
| Parameter a | ||||
| Standard method | 0.77±0.04 | 1.25±0.09 | 1.65±0.14 | 2.00±0.18 |
| Conifer method | 0.77±0.04 | 1.01±0.06* | 2.64±0.32* | 1.61±0.09 |
| P10 | ||||
| Standard method | –2.10±0.22 | –1.18±0.18 | –0.83±0.17 | –0.36±0.15 |
| Conifer method | –2.78±0.20 | –1.80±0.18* | –2.54±0.15* | –2.18±0.43* |
| P50 | ||||
| Standard method | –4.96±0.07 | –2.93±0.06 | –2.17±0.05 | –1.46±0.05 |
| Conifer method | –5.62±0.06* | –3.98±0.05* | –3.37±0.05* | –3.54±0.04* |
| 280 mm rotor diameter | –6.37±0.18 | –3.97±0.04 | –3.20±0.02 | –3.87±0.10 |
| Conventional | –5.60±0.181 | –3.39±0.032 | –2.53; –2.78±0.114 | –3.66±0.052 |
| P90 | ||||
| Standard method | –7.82±0.09 | –4.68±0.07 | –3.50±0.06 | –2.56±0.05 |
| Conifer method | –8.47±0.09* | –6.16±0.07* | –4.21±0.06* | –4.90±0.27* |
| Pex50 | –5.61±0.06 | –4.08±0.02 | –3.24±0.05 | –3.93±0.06 |
Data (mean ±SE) show parameters of vulnerability curves measured with the standard and the conifer method and P50 values measured with a rotor with 280 mm in diameter (published in Cochard, 2006) as well as conventional hydraulic methods (conventional; (1) Beikircher et al., 2010; (2) Mayr et al., 2006; (3) Cochard, 1992; (4) Poyatos et al., 2008). Asterisks indicate significant intraspecific differences between standard and conifer method (P >0.05, Welch test).

Per cent loss of conductivity (PLC) versus xylem pressure (P; MPa) for Juniperus communis, Picea abies, Pinus sylvestris, and Larix decidua. Open symbols and dashed lines show vulnerability curves achieved with the standard method, closed symbols and solid lines those achieved with the conifer method. Vertical lines show P at 50% loss of conductivity (P50) for the standard (dashed line) and the conifer method (solid line). The upper x-axis gives the maximum water pressure difference across the sample (ΔP; MPa) corresponding to the respective P in the used rotor.

Per cent loss of specific conductivity (ks) versus pressure gradient (ΔP) applied with the pressure chamber for Juniperus communis, Picea abies, Pinus sylvestris, and Larix decidua. Vertical lines show pressure at 50% pit aspiration (ΔPasp50).
According to the findings of the vulnerability analysis, L. decidua was also most susceptible in the pressure–conductivity analysis. In this species, 10% pit aspiration occurred already at an applied water pressure of 0.32 MPa (ΔPasp10). Table 2 lists ΔP thresholds for pit aspiration and ΔP induced with the standard method at a P causing 50% of embolism. Thereby P50 was taken from curves obtained with the conifer method as these P50 values were similar to the results of conventional methods and thus suggested to be close to the actual P50. J. communis was the only species which showed the onset of pit aspiration (ΔPasp10) at a ΔP higher than the ΔP corresponding to 50% embolism. In all other species, pit aspiration had already occurred at the ΔP where embolization took place (ΔPasp10 was lower than ΔP at P50; see Table 2), and thus both pit aspiration and embolism formation contributed to conductivity losses. Accordingly, ΔPasp50 of L. decidua is less negative than its ΔP at P50. In P. sylvestris both values are identical and in P. abies, ΔPasp50 is slightly above ΔP at P50. In J. communis, ΔPasp50 was 1.25 MPa higher than ΔP at P50. Critical sample length, i.e. minimum length at which less than 10% pit aspiration occurs at P50 ranged from 116 mm for J. communis up to 324 mm for L. decidua (Table 2).
Parameters of the pressure–conductivity analysis (parameter a, water pressure difference causing 10, 50, and 90 % pit aspiration: ΔPasp10, ΔPasp50, ΔPasp90), water pressure difference (ΔP) obtained with the standard method at P50 of the conifer method and critical sample length of Juniperus communis, Picea abies, Pinus sylvestris, and Larix decidua; mean ±SE.
| Juniperus communis | Picea abies | Pinus sylvestris | Larix decidua | |
| Parameter a | –2.49±0.20 | –6.12±0.84 | –11.36±1.20 | –6.64±0.58 |
| ΔPasp10 | 1.52±0.11 | 0.59±0.10 | 0.50±0.03 | 0.32±0.04 |
| ΔPasp50 | 2.40±0.04 | 0.95±0.05 | 0.69±0.01 | 0.65±0.01 |
| ΔPasp90 | 3.29±0.04 | 1.31±0.00 | 0.88±0.01 | 0.98±0.02 |
| ΔP at P10 | 1.15 | 0.81 | 0.69 | 0.73 |
| Critical sample length (mm) | 116 | 204 | 206 | 324 |
| Juniperus communis | Picea abies | Pinus sylvestris | Larix decidua | |
| Parameter a | –2.49±0.20 | –6.12±0.84 | –11.36±1.20 | –6.64±0.58 |
| ΔPasp10 | 1.52±0.11 | 0.59±0.10 | 0.50±0.03 | 0.32±0.04 |
| ΔPasp50 | 2.40±0.04 | 0.95±0.05 | 0.69±0.01 | 0.65±0.01 |
| ΔPasp90 | 3.29±0.04 | 1.31±0.00 | 0.88±0.01 | 0.98±0.02 |
| ΔP at P10 | 1.15 | 0.81 | 0.69 | 0.73 |
| Critical sample length (mm) | 116 | 204 | 206 | 324 |
Parameters of the pressure–conductivity analysis (parameter a, water pressure difference causing 10, 50, and 90 % pit aspiration: ΔPasp10, ΔPasp50, ΔPasp90), water pressure difference (ΔP) obtained with the standard method at P50 of the conifer method and critical sample length of Juniperus communis, Picea abies, Pinus sylvestris, and Larix decidua; mean ±SE.
| Juniperus communis | Picea abies | Pinus sylvestris | Larix decidua | |
| Parameter a | –2.49±0.20 | –6.12±0.84 | –11.36±1.20 | –6.64±0.58 |
| ΔPasp10 | 1.52±0.11 | 0.59±0.10 | 0.50±0.03 | 0.32±0.04 |
| ΔPasp50 | 2.40±0.04 | 0.95±0.05 | 0.69±0.01 | 0.65±0.01 |
| ΔPasp90 | 3.29±0.04 | 1.31±0.00 | 0.88±0.01 | 0.98±0.02 |
| ΔP at P10 | 1.15 | 0.81 | 0.69 | 0.73 |
| Critical sample length (mm) | 116 | 204 | 206 | 324 |
| Juniperus communis | Picea abies | Pinus sylvestris | Larix decidua | |
| Parameter a | –2.49±0.20 | –6.12±0.84 | –11.36±1.20 | –6.64±0.58 |
| ΔPasp10 | 1.52±0.11 | 0.59±0.10 | 0.50±0.03 | 0.32±0.04 |
| ΔPasp50 | 2.40±0.04 | 0.95±0.05 | 0.69±0.01 | 0.65±0.01 |
| ΔPasp90 | 3.29±0.04 | 1.31±0.00 | 0.88±0.01 | 0.98±0.02 |
| ΔP at P10 | 1.15 | 0.81 | 0.69 | 0.73 |
| Critical sample length (mm) | 116 | 204 | 206 | 324 |
Water extraction curves in all four species showed a course very similar to vulnerability curves (Figs 2, 4) and 50% water extraction (Pex50) in all species was reached close to P50 (Table 1). No indications for any direct influence of spinning, like pit aspiration at higher ω, which would alter position and shape of the curve by slowing down the release of water, were observed.
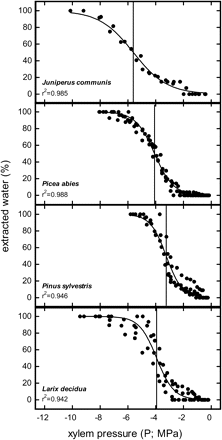
Per cent extracted water at different xylem pressure (P; MPa) in the Cavitron. Vertical lines show P at which 50% water was extracted (Pex50).
Discussion
The main advantage of the Cavitron technique over other methods of vulnerability analysis lies in its time-efficiency and low material requirement: Embolism induction and conductivity measurements are achieved in parallel, and an entire curve can be measured on a single sample independent of season and foliage (Cochard et al., 2005, 2007; Li et al., 2008). However, our study clearly demonstrates that pit aspiration can limit measurements on conifers and that rotor diameter may thus be critical.
According to the hypothesis formulated in the Introduction, vulnerability curves made with the standard method, where high ΔP can occur (see Materials and methods), were significantly shifted to less negative P compared to curves made with the conifer method (Fig. 2; Table 1). Effects of ΔP were found to be highly species-specific, with the most pronounced shift in vulnerability thresholds in L. decidua, and slightest differences in J. communis (Table 1; Fig. 2). With the conifer method, it was possible to avoid high ΔP by equilibration of water contents in the water reservoirs. In all four species, xylem pressure at 50% loss of conductivity (P50) measured with the conifer method was similar to the P50 measured using conventional hydraulic methods (Table 1).
The reason for shifts in vulnerability curves was pit aspiration. As demonstrated in our pressure–conductivity analysis (Fig. 3), pit aspiration in three out of the four species studied induced considerable conductivity losses at ΔP corresponding to P inducing embolism in the standard method (Table 2). At P50 (actual P50, see Results), the ΔP induced by the 150 mm rotor caused pit aspiration resulting in conductivity losses of c. 60% in L. decidua and c. 40% in P. abies and P. sylvestris. Only in J. communis, pit aspiration contributed hardly to overall PLC (4% at P50) and thus showed the smallest shift in vulnerability curves obtained with the standard and the conifer methods (Fig. 2; Table 1). Critical sample length (i.e. minimum sample length at which less than 10% pit aspiration occurs in the range of P50) showed that a considerably bigger rotor would be required to achieve similarly good conformities between the vulnerability curves for the other measured species (Table 2). Accordingly, in the study of Cochard (2006)P50 values achieved with a bigger rotor (280 mm in diameter) correspond well to those achieved with conventional methods (see Table 2).
The differences are very obvious when differences between ΔPasp50 and ΔP at P50 are compared. Table 2 clearly indicates that the overlapping of the two processes, embolism formation and pit aspiration, was most relevant in L. decidua, followed by P. sylvestris and P. abies and hardly relevant in J. communis. Pit aspiration upon experimentally increased pressure gradients was already demonstrated by Sperry and Tyree (1990). The authors found a decrease in hydraulic conductivity (at a ΔP less than –1 MPa) only in conifers and the effect was reversed when the pressure was decreased again. They hypothesized that observed differences between species may be due to the flexibility of the inter-tracheid pit membrane. The lower the flexibility the higher is the pressure required to get the torus in a sealing position. On the other hand, a high rigidity may also hold the torus in a sealing position even at large pressure differences and thus account for a high resistance to air-seeding (but also see Cochard et al., 2009). Accordingly, species of the genus Juniperus, which has an extraordinarily high resistance to drought-induced embolism (Pockman and Sperry, 2000; Martinez-Vilalta et al., 2004; Mayr et al., 2006; Willson and Jackson, 2006; West et al., 2007; Beikircher and Mayr, 2008; Willson et al., 2008) showed pit aspiration at lowest P in the study of Sperry and Tyree (1990) and this study, respectively. Besides interspecific differences in susceptibility to pit aspiration, variation between early- and late-wood pits may also play a role (Gregory and Petty, 1973; Bolton and Petty, 1977; Cochard et al., 2009). Furthermore, pit aspiration is not only of interest in experimental approaches, but also in applied sciences and to the timber industry as it influences the permeability of sapwood (Comstock and Côté, 1968).
An attempt was made to compute the combined effect of P-induced embolism formation and ΔP-induced pit aspiration from vulnerability curves (conifer method) and pit aspiration analysis. Interestingly, the calculated effects (data not shown) were much lower than the measured differences (i.e. the standard vulnerability curves deviated much more from the curves obtained with the conifer method as indicated by pit aspiration thresholds (Figs 2, 3), which indicates that both processes were interrelated and, in consequence, effects on conductivity amplified. It is suggested that cavitation of a tracheid might lead to an increase of ΔP at surrounding pits and induce their aspiration. Furthermore, pit margo elasticity is known to be strongly increased after pressure treatments (Cochard et al., 2010b), which might also influence xylem vulnerability to air seeding. A rapid increase in ΔP may cause high local pressure differences and pit aspiration before pressures are equilibrated within the sample. It is also not known if a pit, when already aspirated to one pit opening by ΔP, can prevent air seeding when sealing to the other pit opening would be required.
In our centrifuge experiments, pits might also have been influenced by the spinning procedure itself. It was unclear if the centrifugal forces can cause displacement or even a sealing of the torus. In Cavitron vulnerability measurements (Fig. 2), embolism and pit aspiration influence the measured variable (hydraulic conductivity) and can thus not be distinguished. We therefore made water extraction experiments, where embolism was estimated by the release of water from broken water columns (Fig. 4). As these measurements were made at zero ΔP, ΔP related pit aspiration played no role. Any other change at the pits would be obvious in differences of shape or position in the water extraction curve compared with the vulnerability curve (with the conifer method or obtained by conventional methods). Figure 4 clearly indicates that the direct effects of spinning forces on pit structures did not play a role. Also Cochard et al. (2010b) reported a close correlation between P50 and P at 50% water extraction. Thus, water extraction curves may even be a simplified alternative to vulnerability measurements as long as the amount of extracted water caused by embolism linearly correlates to conductivity losses.
In summary, use of a small rotor, although advantageous for small samples, may be unsuitable for vulnerability analysis of conifers. The high rotational speeds required to reach low P can cause high ΔP and, in consequence, pit aspiration, when water levels in the reservoirs are unbalanced. In large rotors, spinning velocities and ΔP are lower. Thus, the effect of pit aspiration overall negatively correlates with rotor size but the remarkably species-specific differences in pit aspiration thresholds have to be considered. We recommend use of the conifer method for Cavitron measurements on conifers unless test experiments prove that rotor diameter and species-specific thresholds for pit aspiration allow the use of the faster standard Cavitron method.
Abbreviations
- P
xylem pressure (Pa)
- P10, P50, P90
xylem pressure at 10, 50, and 90% loss of hydraulic conductivity (Pa)
- Pex50
xylem pressure at 50% water extraction (Pa)
- ΔP
water pressure difference across the sample (Pa)
- ΔP*
water pressure difference across the sample averaged over time (Pa)
- ΔPasp10, ΔPasp50, ΔPasp90
water pressure difference at 10, 50, and 90% pit aspiration (Pa)
- k
hydraulic conductance (cm3 s−1 Pa−1)
- ks
specific hydraulic conductivity (cm2 s−1 Pa−1)
- PLC
per cent loss of hydraulic conductivity (%)
This study was supported by Forschungsförderung für die Leopold-Franzens-Universität durch die Südtiroler Landesregierung 2008 and Österreichischer Austauschdienst ÖAD (Amadee 2009).




Comments