-
PDF
- Split View
-
Views
-
Cite
Cite
Xian Wu, Xiangping Wang, Yulian Wu, Xinli Xia, Jingyun Fang, Forest biomass is strongly shaped by forest height across boreal to tropical forests in China, Journal of Plant Ecology, Volume 8, Issue 6, December 2015, Pages 559–567, https://doi.org/10.1093/jpe/rtv001
Close - Share Icon Share
Abstract
Forest height is a major factor shaping geographic biomass patterns, and there is a growing dependence on forest height derived from satellite light detecting and ranging (LiDAR) to monitor large-scale biomass patterns. However, how the relationship between forest biomass and height is modulated by climate and biotic factors has seldom been quantified at broad scales and across various forest biomes, which may be crucial for improving broad-scale biomass estimations based on satellite LiDAR.
We used 1263 plots, from boreal to tropical forest biomes across China, to examine the effects of climatic (energy and water availability) and biotic factors (forest biome, leaf form and leaf phenology) on biomass–height relationship, and to develop the models to estimate biomass from forest height in China.
(i) Forest height alone explained 62% of variation in forest biomass across China and was far more powerful than climate and other biotic factors. (ii) However, the relationship between biomass and forest height were significantly affected by climate, forest biome, leaf phenology (evergreen vs. deciduous) and leaf form (needleleaf vs. broadleaf). Among which, the effect of climate was stronger than other factors. The intercept of biomass–height relationship was more affected by precipitation while the slope more affected by energy availability. (iii) When the effects of climate and biotic factors were considered in the models, geographic biomass patterns could be well predicted from forest height with an r2 between 0.63 and 0.78 (for each forest biome and for all biomes together). For most biomes, forest biomass could be well predicted with simple models including only forest height and climate. (iv) We provided the first broad-scale models to estimate biomass from forest height across China, which can be utilized by future LiDAR studies. (v) Our results suggest that the effect of climate and biotic factors should be carefully considered in models estimating broad-scale forest biomass patterns with satellite LiDAR.
INTRODUCTION
Monitoring the geographic patterns of forest biomass is a basic way to identify forest carbon sources and sinks (Fang et al. 2001, 2014; Myneni et al. 2001; Piao et al. 2005; Schimel et al. 2001). However, uncertainty in mapping the distributions of forest biomass is still a major source of uncertainty in carbon flux estimation (Baker et al. 2004; Goodale et al. 2002; Myneni et al. 2001). Compared with field-based forest inventory, biomass estimation based on remote sensing is not only much more time and efforts saving, but also allow for mapping global biomass patterns at finer grain sizes and shorter intervals (e.g. Boudreau et al. 2008; Houghton 2005; Wang et al. 2013). Light detecting and ranging (LiDAR) is perhaps the most promising remote sensing technology for monitoring the broad-scale patterns of forest biomass (Boudreau et al. 2008; Lefsky et al. 2005; Saatchi et al. 2011). LiDAR has a unique capability for estimating forest canopy height, which has close relationship with not only aboveground biomass (e.g. Drake et al. 2002; Dubayah and Drake 2000; Lefsky et al. 2002, 2005), but also belowground biomass (Næsset and Gobakken 2008; Wang et al. 2013). With the availability of satellite LiDAR data in recent years, rapid progresses have been achieved in mapping forest height from regional (Lefsky et al. 2005; Zhang et al. 2014) to global scales (Lefsky 2010; Los et al. 2012; Simard et al. 2011). At the same time, regional to global biomass patterns have also been estimated based on forest height retrieved from satellite LiDAR (e.g. Lefsky et al. 2005; Saatchi et al. 2011; Zhang et al. 2014).
Quantifying the relationship between biomass and forest height is the base for estimating biomass from LiDAR retrieved height (e.g. Lefsky et al. 2005; Saatchi et al. 2011; Zhang et al. 2014). Probably because early studies were based on airborne LiDAR at relative small scales, previous analyses generally did not include climatic factors in their models to predict biomass from forest height. This is true even in satellite-based studies that estimate large to global-scale forest biomass (Lefsky et al. 2005; Saatchi et al. 2011; Zhang et al. 2014). However, recently Wang et al. (2013) found that large-scale biomass patterns could not be well predicted from forest height, if the influences of climate and biotic factors were not considered. This suggests that understanding how the biomass–height relationships are modulated by abiotic and biotic factors may be crucial for improving broad-scale biomass estimations with LiDAR. Nevertheless, the study of Wang et al. (2013) included only temperate and boreal forests in northeast China, and thus their findings need further tests in other forest biomes. This is important because relationships between biomass and abiotic/biotic factors obtained at restricted geographic/climatic extents may not hold at broader scales (Stegen et al. 2011).
In this study, we used 1263 plots from boreal to tropical forests and from humid to arid regions across China (Fig. 1) to examine biomass–height relationship and its’ abiotic and biotic modulators, and to explore the method to estimate large-scale biomass patterns from forest height. We tested whether there is still a close biomass–height relationship for forests over broad-scale across boreal to tropical climates. If true, this will provide strong support to mapping global biomass patterns with satellite LiDAR. We also tested a hypothesis to explain why forest biomass is closely related to forest height (Fang et al. 2006; Wang et al. 2013). The hypothesis suggests that the biomass per unit of forest space (i.e. the ratio of biomass to forest height) is similar for closed-canopy forests, and thus, biomass per area can be roughly explained by differences in forest height. The hypothesis may provide a biological basis for mapping forest biomass patterns with LiDAR, and has been supported by boreal and temperate forests in northeast China (Wang et al. 2013). However, it has not yet been tested for other important biomes, such as warm-temperate and (sub)tropical forests. We then tested the findings of Wang et al. (2013) to examine if climate (water and energy availability), leaf phenology (evergreen vs. deciduous), leaf form (needleleaf vs. broadleaf) and forest biomes showed significant influence on biomass–height relationship. Nowadays there is growing dependence on LiDAR-derived forest height to map geographic biomass patterns. However, the data on both forest height and biomass is still rather limited, at least in China (Wang et al. 2013). This may greatly prevent the wide application of biomass estimation based on satellite LiDAR. The present study also aims to provide calibrated models for estimating biomass from forest height, which can be utilized by future studies using satellite LiDAR to map geographic biomass patterns in China.
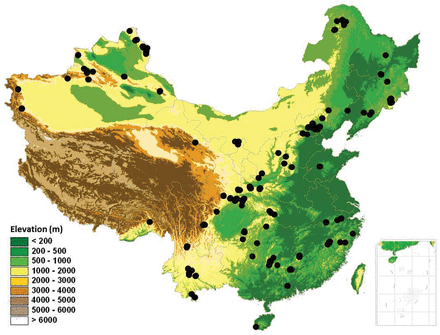
forest plots across mountains of China used in this study, covering tropical to boreal forests along the latitudinal gradients and humid to arid regions from eastern to western China. Many plots overlap each other and are thus not visible.
Specifically, we asked four questions as follows. (i) Does the close relationship between forest biomass and height found at smaller scales still hold at a broad scale? (ii) Is the ratio of total biomass to forest height similar for boreal to tropical forests, and for evergreen/deciduous and needleleaf/broadleaf forests? (iii) Among different climatic and biotic variables (leaf form and phenology, biome), which are the major factors modulating biomass–height relationship? (iv) Can geographic biomass patterns be well predicted from forest height, when the influences of climate and biotic factors are considered in the model?
MATERIALS AND METHODS
The dataset on forest height and biomass
We developed a large dataset on forest height and biomass for 1263 plots across China (Fig. 1), which documented the following information for each plot: (i) total biomass (aboveground + belowground); (ii) forest height (maximum tree height); (iii) forest biome, i.e. boreal, temperate, warm-temperate, subtropical or tropical forest; (iv) leaf phenology: i.e. evergreen, deciduous or mixed forest; (v) leaf form: needleleaf, broadleaf or mixed forest; (vi) geographic coordinates (latitude, longitude and altitude); (vii) climate variables. Monthly mean temperature and precipitation for each plot were estimated based on latitude, longitude and altitude, using the method described in Fang et al. (2012). Various climatic indices were calculated for each plot using the monthly mean temperature and precipitation data, including potential evapotranspiration (PET), mean annual precipitation (MAP) and temperature, warmth index, and annual biotemperature, etc. (Fang et al. 2012).
The dataset came from two major sources:
(1) In Wang et al. (2013), we have reported a dataset on forest biomass across the northeast part of China. The dataset included 230 plots that have both forest height and total biomass data. Since then another 85 plots from literatures were appended into the dataset, mainly from Ma (1988) which documented biomass for Pinus tabuliformis forests across China. The final dataset used here included 315 plots that documented forest height and biomass. The methods for data collection have been described in details in Wang et al. (2013) and thus not repeated here. Briefly, for the literature data we extracted the abovementioned information (biomass, forest height, etc.) for each plot from the literatures. For the 166 plots that were sampled by us, across all the major mountain ranges and forest types of the northeast part of China, we used the methods described below.
(2) The other plots came from the project of ‘Peking University Plant Species Diversity Survey for China’s Mountains (abbreviated as PKU-PSD)’, which investigated forests in mountains across China (Fang et al. 2012). Here we used 948 plots in which tree heights were measured. In each plot, we documented diameter at breast height (DBH) and height for stems with a DBH >3cm. The geographic coordinates of the plots were recorded for estimation of climatic indices. For details on sampling protocols see Fang et al. (2012).
Total biomass for each of the 948 plots was estimated from stock volume using the biomass expansion factor method (Fang et al. 2001), which has been repeatedly proved to be the most accurate way for large-scale estimation of forest biomass (e.g. Brown 2002; Fang et al. 1998; Wang et al. 2006, 2013). We first calculated the total timber volume for each plot. The volume for each tree in a plot was calculated as:
where, v is stem volume (m3), D is DBH (cm), H is tree height (m), and a, b and c are coefficients. The national technology standard of China, Tree Volume Tables (LY 208–77), provided equations for major species of China. These equations were developed based on 197000 samples from 180 tree species across the nation, and were recommended as the best method to calculate stock volume by the national technology standard (State Forestry Administration of China 1977).
In a second step, the total biomass of each plot was estimated with:
where, B is the total (above and below ground) dry biomass (Mg/ha), V the stock volume of a plot (m3/ha) and a and b are coefficients. We used the models of Fang et al. (2001, 2007), which were developed separately for 21 major forest types across China. These models were based on 594 field measurements of timber volume and total biomass across China, and are the most widely used method to estimate forest biomass from stock volume across China (e.g. Fang et al. 2014; Guo et al. 2010, 2013; Piao et al. 2005, 2009).
As shown in Fig. 1, the 1263 plots used in this study covered most major mountain systems across China. They spanned a geographic range from 18.6 to 51.9°N in latitude, 75.2 to 128.9°E in longitude, and from 190 to 4250 m a.s.l. in altitude. In another word, our plots covered a variety of natural forest types in China, including: (i) boreal forest (337 plots); (ii) temperate forest (242 plots); (iii) warm-temperate forest (465 plots); (iv) subtropical forest (173 plots) and (v) tropical forest (46 plots). In the data analyses, subtropical and tropical forests were merged because plots from tropical forest were limited. Our plots also included different leaf form and phenology types in each biome. For plot numbers within each leaf form and phenology category, see supplementary Appendix 1.
Statistic analyses
Previous studies showed that energy and water availability are key climatic factors affecting geographic patterns of forest biomass (e.g. Stegen et al. 2011; Wang et al. 2006, 2008). Consequently, we selected PET and MAP for statistic analyses, which were commonly used indices for energy and water availability, respectively (e.g. Fang et al. 2012; O’Brien 2006; Wang et al. 2006, 2012). Other climatic variables in our dataset were similar in biological meanings with PET and MAP and thus were not used to avoid collinearity.
The relationship between biomass and forest height could be well described by a power function (Saatchi et al. 2011; Wang et al. 2013):
where, B is the plot biomass (Mg/ha), H the forest height (m) and a and b are coefficients.
To analyse the potential factors affecting biomass–height relationship, we used general linear model (GLM) to explain log (biomass) with log (height) and several abiotic and biotic factors together: (i) climate (PET and MAP), (ii) leaf phenology (evergreen, deciduous or mixed forest), (iii) leaf form (needleleaf, broadleaf or mixed forest), and (iv) biome (boreal, temperate, warm-temperate or subtropical forest). The interaction terms between log (height) and other explanatory terms were also included in GLMs to examine whether the regression slopes between log (biomass) and log (height) were affected by climate and biotic factors (leaf phenology, leaf form and biome) (e.g. Wang et al. 2008, 2013). Variables were transformed when necessary to increase the normality and homoscedasticity of residuals, which is a common practice in statistic analyses (Crawley 2007; He et al. 2009; Quinn and Keough 2002; Wang et al. 2009). As a result, MAP was log-transformed while PET was remained untransformed.
To identify the major factors affecting biomass–height relationship, we used the model selection approach based on Bayesian Information Criterion (BIC), to drop unnecessary variables (Johnson and Omland 2004). We did not use the commonly used Akaike Information Criterion because BIC is more conservative in retaining variables. Thus BIC is well suited for our purpose to obtain the most parsimonious model to predict biomass, which may reduce large amount of efforts in the practical works of large-scale biomass estimation (Wang et al. 2013).
To validate the models thus obtained, we randomly extracted 10% plots from each forest biome. The resulting 126 plots were used for model validation, while other plots in the dataset were used to construct GLMs for estimating forest biomass from height. We calculated predicted biomass for the 126 validation plots with each GLM. Predicted values were fitted against observed biomass to obtain the regression r2, the 95% confidential intervals (CIs) for regression slope and interception. If the r2 was high enough, and the 95% CI for slope and interception enclosed 1 and 0, respectively, then the model was judged as acceptable (e.g. Wang et al. 2013).
All statistic analyses were performed with R 2.10 (R Development Core Team 2007).
RESULTS
Factors regulating the relationship between biomass and forest height
Forest biomass was closely related to forest height at a broad scale (Fig. 2). Forest height alone explained 62% of variation in biomass for all plots together, and explained 49–71% of variation for various forest groups (Table 1). Analysis of covariance showed that the biomass–height relationship differed significantly among forest biomes, and among forests with different leaf phenology and leaf form (P < 0.05).
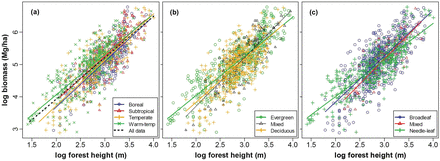
relationships between stand total biomass and forest height, (a) for each forest biome and all biome together; (b) for evergreen, deciduous and mixed forests and (c) for broadleaf, needleleaf and mixed forests. All regressions were significant at P < 0.001. For r2s, sample sizes, slopes and intercepts of the relationships, see Table 1.
relationships between biomass and forest height (both log-transformed) for plots across China, for each biome, and for forests with different leaf phenology and leaf form. The mean ratio of biomass to forest height (B/H) was also reported for each forest group.
| Forest group . | Biomass–height relationship (log-log) . | Mean B/H (Mg/ha/m) . | |||
|---|---|---|---|---|---|
| Slope . | Intercept . | r2 . | n . | ||
| Overall | 1.28 | 1.37 | 0.62 | 1137 | 9.53 |
| Biomes | |||||
| Boreal | 1.41 | 0.87 | 0.61 | 304 | 8.59 |
| Temperate | 1.42 | 0.89 | 0.70 | 218 | 8.89 |
| Warm-temperate | 1.25 | 1.56 | 0.62 | 420 | 10.13 |
| Subtropical | 1.37 | 1.14 | 0.59 | 195 | 10.45 |
| Leaf phenology | |||||
| Evergreen | 1.22 | 1.61 | 0.70 | 509 | 9.98 |
| Mixed | 1.51 | 0.68 | 0.68 | 167 | 9.67 |
| Deciduous | 1.33 | 1.16 | 0.49 | 461 | 8.99 |
| Leaf form | |||||
| Broadleaf | 1.42 | 0.99 | 0.58 | 623 | 10.05 |
| Mixed | 1.53 | 0.58 | 0.71 | 77 | 9.39 |
| Needleleaf | 1.13 | 1.75 | 0.68 | 437 | 8.82 |
| Forest group . | Biomass–height relationship (log-log) . | Mean B/H (Mg/ha/m) . | |||
|---|---|---|---|---|---|
| Slope . | Intercept . | r2 . | n . | ||
| Overall | 1.28 | 1.37 | 0.62 | 1137 | 9.53 |
| Biomes | |||||
| Boreal | 1.41 | 0.87 | 0.61 | 304 | 8.59 |
| Temperate | 1.42 | 0.89 | 0.70 | 218 | 8.89 |
| Warm-temperate | 1.25 | 1.56 | 0.62 | 420 | 10.13 |
| Subtropical | 1.37 | 1.14 | 0.59 | 195 | 10.45 |
| Leaf phenology | |||||
| Evergreen | 1.22 | 1.61 | 0.70 | 509 | 9.98 |
| Mixed | 1.51 | 0.68 | 0.68 | 167 | 9.67 |
| Deciduous | 1.33 | 1.16 | 0.49 | 461 | 8.99 |
| Leaf form | |||||
| Broadleaf | 1.42 | 0.99 | 0.58 | 623 | 10.05 |
| Mixed | 1.53 | 0.58 | 0.71 | 77 | 9.39 |
| Needleleaf | 1.13 | 1.75 | 0.68 | 437 | 8.82 |
The 126 plots used for model validation were not included in this analysis.
relationships between biomass and forest height (both log-transformed) for plots across China, for each biome, and for forests with different leaf phenology and leaf form. The mean ratio of biomass to forest height (B/H) was also reported for each forest group.
| Forest group . | Biomass–height relationship (log-log) . | Mean B/H (Mg/ha/m) . | |||
|---|---|---|---|---|---|
| Slope . | Intercept . | r2 . | n . | ||
| Overall | 1.28 | 1.37 | 0.62 | 1137 | 9.53 |
| Biomes | |||||
| Boreal | 1.41 | 0.87 | 0.61 | 304 | 8.59 |
| Temperate | 1.42 | 0.89 | 0.70 | 218 | 8.89 |
| Warm-temperate | 1.25 | 1.56 | 0.62 | 420 | 10.13 |
| Subtropical | 1.37 | 1.14 | 0.59 | 195 | 10.45 |
| Leaf phenology | |||||
| Evergreen | 1.22 | 1.61 | 0.70 | 509 | 9.98 |
| Mixed | 1.51 | 0.68 | 0.68 | 167 | 9.67 |
| Deciduous | 1.33 | 1.16 | 0.49 | 461 | 8.99 |
| Leaf form | |||||
| Broadleaf | 1.42 | 0.99 | 0.58 | 623 | 10.05 |
| Mixed | 1.53 | 0.58 | 0.71 | 77 | 9.39 |
| Needleleaf | 1.13 | 1.75 | 0.68 | 437 | 8.82 |
| Forest group . | Biomass–height relationship (log-log) . | Mean B/H (Mg/ha/m) . | |||
|---|---|---|---|---|---|
| Slope . | Intercept . | r2 . | n . | ||
| Overall | 1.28 | 1.37 | 0.62 | 1137 | 9.53 |
| Biomes | |||||
| Boreal | 1.41 | 0.87 | 0.61 | 304 | 8.59 |
| Temperate | 1.42 | 0.89 | 0.70 | 218 | 8.89 |
| Warm-temperate | 1.25 | 1.56 | 0.62 | 420 | 10.13 |
| Subtropical | 1.37 | 1.14 | 0.59 | 195 | 10.45 |
| Leaf phenology | |||||
| Evergreen | 1.22 | 1.61 | 0.70 | 509 | 9.98 |
| Mixed | 1.51 | 0.68 | 0.68 | 167 | 9.67 |
| Deciduous | 1.33 | 1.16 | 0.49 | 461 | 8.99 |
| Leaf form | |||||
| Broadleaf | 1.42 | 0.99 | 0.58 | 623 | 10.05 |
| Mixed | 1.53 | 0.58 | 0.71 | 77 | 9.39 |
| Needleleaf | 1.13 | 1.75 | 0.68 | 437 | 8.82 |
The 126 plots used for model validation were not included in this analysis.
These differences among forest groups were confirmed by analyses on biomass/height ratio (Table 1, Fig. 3). The mean ratio increased slightly from 8.59 to 10.45 Mg/ha/m from boreal to subtropical forests. Biomass/height ratios did not differed significantly between boreal and temperate forests, and not between warm-temperate and subtropical forests, but differed between the two groups. The ratio also differed significantly between evergreen and deciduous forests (9.98 vs. 8.99 Mg/ha/m), and between broadleaf and needleleaf forests (10.05 vs. 8.82 Mg/ha/m) (Fig. 3).
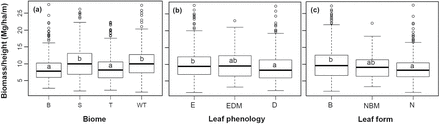
comparison of biomass/height ratio among forest groups. (a) Among boreal (B), temperate (T), warm-temperate (WT) and subtropical (S) forests; (b) Among evergreen (E), deciduous (D), and evergreen and deciduous mixed (EDM) forests; (c) Among broadleaf (B), needleleaf (N), and needleleaf and broadleaf mixed (NBM) forests. Forest groups that shared a same letter did not showed significant difference at P < 0.05. For mean biomass/height ratio of each forest group, see Table 1.
Models for estimating forest biomass from height
The abovementioned results (Figs 2 and 3, Table 1) suggest that climate, leaf phenology and leaf form may have significant influence on the relationship between forest height and biomass. In the GLM including all biomes (‘overall GLM’ hereafter), these variables were indeed retained in the model and showed significant explanatory power (Table 2). However, various climate and biotic variables, and their interactions with height, explained only 7.2% of variation in addition to the 62.3% explained by height, confirming the predominant role of forest height in shaping geographic biomass patterns. MAP was more powerful in explaining biomass than PET (3.3 vs. 0.4%). On the other hand, the interaction term between height and PET was significant while that of MAP was excluded from the final model. This means that the intercept of biomass–height relationship was more affected by precipitation, while the slope of the relationship was more affected by energy availability.
summary of GLMs for the effects of forest height (H), climate (PET and MAP), leaf phenology (LP), leaf form (LF) and biome on forest biomass (log-transformed)
| Variable . | df . | MS . | P . | %SS . | Variable . | df . | MS . | P . | %SS . |
|---|---|---|---|---|---|---|---|---|---|
| All biomes . | Boreal forests . | ||||||||
| log(H) | 1 | 353.17 | 0.000 | 62.26 | log(H) | 1 | 69.64 | 0.000 | 61.23 |
| PET | 1 | 2.13 | 0.000 | 0.38 | PET | 1 | 1.34 | 0.001 | 1.18 |
| log(MAP) | 1 | 18.95 | 0.000 | 3.34 | log(MAP) | 1 | 5.28 | 0.000 | 4.64 |
| LP | 2 | 1.32 | 0.000 | 0.47 | LP | 2 | 0.95 | 0.000 | 1.68 |
| LF | 2 | 0.99 | 0.002 | 0.35 | log(H):PET | 1 | 1.74 | 0.000 | 1.53 |
| Biome | 3 | 3.31 | 0.000 | 1.75 | Residuals | 297 | 0.11 | 29.75 | |
| log(H):PET | 1 | 1.71 | 0.001 | 0.30 | |||||
| log(H):LF | 2 | 1.14 | 0.001 | 0.40 | |||||
| log(H):Biome | 3 | 0.47 | 0.029 | 0.25 | |||||
| Residuals | 1120 | 0.15 | 30.51 | ||||||
| Temperate forests | Warm-temperate forests | ||||||||
| log(H) | 1 | 90.87 | 0.000 | 70.03 | log(H) | 1 | 131.69 | 0.000 | 61.63 |
| log(MAP) | 1 | 1.05 | 0.015 | 0.81 | PET | 1 | 0.60 | 0.063 | 0.28 |
| Residuals | 215 | 0.18 | 29.16 | log(MAP) | 1 | 7.41 | 0.000 | 3.47 | |
| log(H):PET | 1 | 1.82 | 0.001 | 0.85 | |||||
| Residuals | 415 | 0.17 | 33.77 | ||||||
| Subtropical forests | |||||||||
| log(H) | 1 | 51.55 | 0.000 | 59.33 | |||||
| PET | 1 | 6.87 | 0.000 | 7.91 | |||||
| log(MAP) | 1 | 5.03 | 0.000 | 5.79 | |||||
| Residuals | 191 | 0.12 | 26.97 | ||||||
| Variable . | df . | MS . | P . | %SS . | Variable . | df . | MS . | P . | %SS . |
|---|---|---|---|---|---|---|---|---|---|
| All biomes . | Boreal forests . | ||||||||
| log(H) | 1 | 353.17 | 0.000 | 62.26 | log(H) | 1 | 69.64 | 0.000 | 61.23 |
| PET | 1 | 2.13 | 0.000 | 0.38 | PET | 1 | 1.34 | 0.001 | 1.18 |
| log(MAP) | 1 | 18.95 | 0.000 | 3.34 | log(MAP) | 1 | 5.28 | 0.000 | 4.64 |
| LP | 2 | 1.32 | 0.000 | 0.47 | LP | 2 | 0.95 | 0.000 | 1.68 |
| LF | 2 | 0.99 | 0.002 | 0.35 | log(H):PET | 1 | 1.74 | 0.000 | 1.53 |
| Biome | 3 | 3.31 | 0.000 | 1.75 | Residuals | 297 | 0.11 | 29.75 | |
| log(H):PET | 1 | 1.71 | 0.001 | 0.30 | |||||
| log(H):LF | 2 | 1.14 | 0.001 | 0.40 | |||||
| log(H):Biome | 3 | 0.47 | 0.029 | 0.25 | |||||
| Residuals | 1120 | 0.15 | 30.51 | ||||||
| Temperate forests | Warm-temperate forests | ||||||||
| log(H) | 1 | 90.87 | 0.000 | 70.03 | log(H) | 1 | 131.69 | 0.000 | 61.63 |
| log(MAP) | 1 | 1.05 | 0.015 | 0.81 | PET | 1 | 0.60 | 0.063 | 0.28 |
| Residuals | 215 | 0.18 | 29.16 | log(MAP) | 1 | 7.41 | 0.000 | 3.47 | |
| log(H):PET | 1 | 1.82 | 0.001 | 0.85 | |||||
| Residuals | 415 | 0.17 | 33.77 | ||||||
| Subtropical forests | |||||||||
| log(H) | 1 | 51.55 | 0.000 | 59.33 | |||||
| PET | 1 | 6.87 | 0.000 | 7.91 | |||||
| log(MAP) | 1 | 5.03 | 0.000 | 5.79 | |||||
| Residuals | 191 | 0.12 | 26.97 | ||||||
Unnecessary variables were dropped based on BIC. The analysis was conducted for all biomes together, and for each biome separately (for model coefficients, see supplementary Appendix 2 and Supplementary Data, respectively). %SS = percentage of sum of squares explained; df = degree of freedom; MS = mean square.
summary of GLMs for the effects of forest height (H), climate (PET and MAP), leaf phenology (LP), leaf form (LF) and biome on forest biomass (log-transformed)
| Variable . | df . | MS . | P . | %SS . | Variable . | df . | MS . | P . | %SS . |
|---|---|---|---|---|---|---|---|---|---|
| All biomes . | Boreal forests . | ||||||||
| log(H) | 1 | 353.17 | 0.000 | 62.26 | log(H) | 1 | 69.64 | 0.000 | 61.23 |
| PET | 1 | 2.13 | 0.000 | 0.38 | PET | 1 | 1.34 | 0.001 | 1.18 |
| log(MAP) | 1 | 18.95 | 0.000 | 3.34 | log(MAP) | 1 | 5.28 | 0.000 | 4.64 |
| LP | 2 | 1.32 | 0.000 | 0.47 | LP | 2 | 0.95 | 0.000 | 1.68 |
| LF | 2 | 0.99 | 0.002 | 0.35 | log(H):PET | 1 | 1.74 | 0.000 | 1.53 |
| Biome | 3 | 3.31 | 0.000 | 1.75 | Residuals | 297 | 0.11 | 29.75 | |
| log(H):PET | 1 | 1.71 | 0.001 | 0.30 | |||||
| log(H):LF | 2 | 1.14 | 0.001 | 0.40 | |||||
| log(H):Biome | 3 | 0.47 | 0.029 | 0.25 | |||||
| Residuals | 1120 | 0.15 | 30.51 | ||||||
| Temperate forests | Warm-temperate forests | ||||||||
| log(H) | 1 | 90.87 | 0.000 | 70.03 | log(H) | 1 | 131.69 | 0.000 | 61.63 |
| log(MAP) | 1 | 1.05 | 0.015 | 0.81 | PET | 1 | 0.60 | 0.063 | 0.28 |
| Residuals | 215 | 0.18 | 29.16 | log(MAP) | 1 | 7.41 | 0.000 | 3.47 | |
| log(H):PET | 1 | 1.82 | 0.001 | 0.85 | |||||
| Residuals | 415 | 0.17 | 33.77 | ||||||
| Subtropical forests | |||||||||
| log(H) | 1 | 51.55 | 0.000 | 59.33 | |||||
| PET | 1 | 6.87 | 0.000 | 7.91 | |||||
| log(MAP) | 1 | 5.03 | 0.000 | 5.79 | |||||
| Residuals | 191 | 0.12 | 26.97 | ||||||
| Variable . | df . | MS . | P . | %SS . | Variable . | df . | MS . | P . | %SS . |
|---|---|---|---|---|---|---|---|---|---|
| All biomes . | Boreal forests . | ||||||||
| log(H) | 1 | 353.17 | 0.000 | 62.26 | log(H) | 1 | 69.64 | 0.000 | 61.23 |
| PET | 1 | 2.13 | 0.000 | 0.38 | PET | 1 | 1.34 | 0.001 | 1.18 |
| log(MAP) | 1 | 18.95 | 0.000 | 3.34 | log(MAP) | 1 | 5.28 | 0.000 | 4.64 |
| LP | 2 | 1.32 | 0.000 | 0.47 | LP | 2 | 0.95 | 0.000 | 1.68 |
| LF | 2 | 0.99 | 0.002 | 0.35 | log(H):PET | 1 | 1.74 | 0.000 | 1.53 |
| Biome | 3 | 3.31 | 0.000 | 1.75 | Residuals | 297 | 0.11 | 29.75 | |
| log(H):PET | 1 | 1.71 | 0.001 | 0.30 | |||||
| log(H):LF | 2 | 1.14 | 0.001 | 0.40 | |||||
| log(H):Biome | 3 | 0.47 | 0.029 | 0.25 | |||||
| Residuals | 1120 | 0.15 | 30.51 | ||||||
| Temperate forests | Warm-temperate forests | ||||||||
| log(H) | 1 | 90.87 | 0.000 | 70.03 | log(H) | 1 | 131.69 | 0.000 | 61.63 |
| log(MAP) | 1 | 1.05 | 0.015 | 0.81 | PET | 1 | 0.60 | 0.063 | 0.28 |
| Residuals | 215 | 0.18 | 29.16 | log(MAP) | 1 | 7.41 | 0.000 | 3.47 | |
| log(H):PET | 1 | 1.82 | 0.001 | 0.85 | |||||
| Residuals | 415 | 0.17 | 33.77 | ||||||
| Subtropical forests | |||||||||
| log(H) | 1 | 51.55 | 0.000 | 59.33 | |||||
| PET | 1 | 6.87 | 0.000 | 7.91 | |||||
| log(MAP) | 1 | 5.03 | 0.000 | 5.79 | |||||
| Residuals | 191 | 0.12 | 26.97 | ||||||
Unnecessary variables were dropped based on BIC. The analysis was conducted for all biomes together, and for each biome separately (for model coefficients, see supplementary Appendix 2 and Supplementary Data, respectively). %SS = percentage of sum of squares explained; df = degree of freedom; MS = mean square.
We also constructed GLMs for each biome separately (‘biome GLMs’ hereafter) (Table 2). Interestingly, the variables retained in the final model included only height and climate for most biomes, except that leaf phenology was retained in the model for boreal forests. Again, MAP was more powerful than PET in explaining biomass expect for subtropical forests, while the interaction between height and PET was retained in the model for boreal and warm-temperate forests, confirming the different roles of energy and water availabilities in affecting the relationship between biomass and height.
Model validation
The two sets of GLMs, i.e. the ‘overall GLM’ and the ‘biome GLMs’ (Table 3), predicted stand biomass for the 126 validation plots with an r2 of 0.70 and 0.73, respectively. When tested for each biome separately, the GLMs predicted plot biomass with an r2 between 0.63 and 0.81. In most cases the slopes between predicted and observed values were not significantly different from 1 (see the 95% CIs), while the intercepts were also not significantly different from 0. These results suggest that the empirical data were well predicted, not only for the overall patterns, but also for each biome except subtropical forests. Interestingly, the ‘overall GLM’ and the biome-specific GLMs showed similar ability in predicting forest biomass, no matter measured by r2s or slopes and intercepts.
testing two set of GLMs for estimating biomass from forest height, using 126 plots remained for model validation
| Biome . | n . | Overall GLM . | Biome GLMs . | ||||
|---|---|---|---|---|---|---|---|
| Slope (CI) . | Intercept (CI) . | r2 . | Slope (CI) . | Intercept (CI) . | r2 . | ||
| All | 126 | 0.96 (0.87 to 1.06) | 0.20 (−0.27 to 0.68) | 0.70 | 0.92 (0.84 to 1.01) | 0.41 (−0.02 to 0.85) | 0.73 |
| Boreal | 33 | 1.04 (0.85 to 1.27) | −0.24 (−1.32 to 0.84) | 0.70 | 0.93 (0.76 to 1.15) | 0.32 (−0.68 to 1.31) | 0.68 |
| Temperate | 24 | 0.94 (0.76 to 1.16) | 0.33 (−0.67 to 1.34) | 0.77 | 0.92 (0.75 to 1.13) | 0.44 (−0.51 to 1.39) | 0.78 |
| Warm-temperate | 45 | 1.00 (0.83 to 1.21) | −0.03 (−0.97 to 0.91) | 0.63 | 0.97 (0.81 to 1.15) | 0.17 (−0.68 to 1.03) | 0.67 |
| Subtropical | 24 | 0.73 (0.58 to 0.91) | 1.52 (0.64 to 2.41) | 0.74 | 0.79 (0.65 to 0.95) | 1.18 (0.35 to 2.01) | 0.81 |
| Biome . | n . | Overall GLM . | Biome GLMs . | ||||
|---|---|---|---|---|---|---|---|
| Slope (CI) . | Intercept (CI) . | r2 . | Slope (CI) . | Intercept (CI) . | r2 . | ||
| All | 126 | 0.96 (0.87 to 1.06) | 0.20 (−0.27 to 0.68) | 0.70 | 0.92 (0.84 to 1.01) | 0.41 (−0.02 to 0.85) | 0.73 |
| Boreal | 33 | 1.04 (0.85 to 1.27) | −0.24 (−1.32 to 0.84) | 0.70 | 0.93 (0.76 to 1.15) | 0.32 (−0.68 to 1.31) | 0.68 |
| Temperate | 24 | 0.94 (0.76 to 1.16) | 0.33 (−0.67 to 1.34) | 0.77 | 0.92 (0.75 to 1.13) | 0.44 (−0.51 to 1.39) | 0.78 |
| Warm-temperate | 45 | 1.00 (0.83 to 1.21) | −0.03 (−0.97 to 0.91) | 0.63 | 0.97 (0.81 to 1.15) | 0.17 (−0.68 to 1.03) | 0.67 |
| Subtropical | 24 | 0.73 (0.58 to 0.91) | 1.52 (0.64 to 2.41) | 0.74 | 0.79 (0.65 to 0.95) | 1.18 (0.35 to 2.01) | 0.81 |
The ‘Overall GLM’ was developed using data from all biomes (supplementary Appendix 2), while the ‘Biome GLMs’ were developed for each biome separately (supplementary Appendix 3). For each method, we tested its ability to predict the biomass for each biome and also for all biomes together. For each test, the r2, slope and intercept between predicted and observed biomass were reported. The slopes and intercepts were boldfaced, if the 95% CI of slope included 1 and the intercept CI included 0. n = sample size.
testing two set of GLMs for estimating biomass from forest height, using 126 plots remained for model validation
| Biome . | n . | Overall GLM . | Biome GLMs . | ||||
|---|---|---|---|---|---|---|---|
| Slope (CI) . | Intercept (CI) . | r2 . | Slope (CI) . | Intercept (CI) . | r2 . | ||
| All | 126 | 0.96 (0.87 to 1.06) | 0.20 (−0.27 to 0.68) | 0.70 | 0.92 (0.84 to 1.01) | 0.41 (−0.02 to 0.85) | 0.73 |
| Boreal | 33 | 1.04 (0.85 to 1.27) | −0.24 (−1.32 to 0.84) | 0.70 | 0.93 (0.76 to 1.15) | 0.32 (−0.68 to 1.31) | 0.68 |
| Temperate | 24 | 0.94 (0.76 to 1.16) | 0.33 (−0.67 to 1.34) | 0.77 | 0.92 (0.75 to 1.13) | 0.44 (−0.51 to 1.39) | 0.78 |
| Warm-temperate | 45 | 1.00 (0.83 to 1.21) | −0.03 (−0.97 to 0.91) | 0.63 | 0.97 (0.81 to 1.15) | 0.17 (−0.68 to 1.03) | 0.67 |
| Subtropical | 24 | 0.73 (0.58 to 0.91) | 1.52 (0.64 to 2.41) | 0.74 | 0.79 (0.65 to 0.95) | 1.18 (0.35 to 2.01) | 0.81 |
| Biome . | n . | Overall GLM . | Biome GLMs . | ||||
|---|---|---|---|---|---|---|---|
| Slope (CI) . | Intercept (CI) . | r2 . | Slope (CI) . | Intercept (CI) . | r2 . | ||
| All | 126 | 0.96 (0.87 to 1.06) | 0.20 (−0.27 to 0.68) | 0.70 | 0.92 (0.84 to 1.01) | 0.41 (−0.02 to 0.85) | 0.73 |
| Boreal | 33 | 1.04 (0.85 to 1.27) | −0.24 (−1.32 to 0.84) | 0.70 | 0.93 (0.76 to 1.15) | 0.32 (−0.68 to 1.31) | 0.68 |
| Temperate | 24 | 0.94 (0.76 to 1.16) | 0.33 (−0.67 to 1.34) | 0.77 | 0.92 (0.75 to 1.13) | 0.44 (−0.51 to 1.39) | 0.78 |
| Warm-temperate | 45 | 1.00 (0.83 to 1.21) | −0.03 (−0.97 to 0.91) | 0.63 | 0.97 (0.81 to 1.15) | 0.17 (−0.68 to 1.03) | 0.67 |
| Subtropical | 24 | 0.73 (0.58 to 0.91) | 1.52 (0.64 to 2.41) | 0.74 | 0.79 (0.65 to 0.95) | 1.18 (0.35 to 2.01) | 0.81 |
The ‘Overall GLM’ was developed using data from all biomes (supplementary Appendix 2), while the ‘Biome GLMs’ were developed for each biome separately (supplementary Appendix 3). For each method, we tested its ability to predict the biomass for each biome and also for all biomes together. For each test, the r2, slope and intercept between predicted and observed biomass were reported. The slopes and intercepts were boldfaced, if the 95% CI of slope included 1 and the intercept CI included 0. n = sample size.
DISCUSSION
The relationship between forest height and biomass
Previous studies have widely found that forest biomass is closely related to forest height at local to regional scales (e.g. Drake et al. 2002; Dubayah and Drake 2000; Lefsky et al. 2002). However, seldom studies have examined whether this strong biomass–height relationship still hold at broad scales and across various forest biomes, which is important for global-scale mapping of forest biomass with LiDAR.
Our result showed that forest biomass across China was closely related to forest height. This is also true for forests from boreal to subtropical climates, and for forests with different leaf phenology and leaf form (Fig. 2 and Table 1). In the multivariate models (Table 2), forest height is also the strongest predictor of biomass and accounted for most of the model explanatory power. These results extend previous findings at smaller spatial scales (Drake et al. 2002; Lefsky et al. 2005; Saatchi et al. 2011; Wang et al. 2013), and confirm that the broad-scale patterns of forest biomass are also strongly shaped by forest height.
The overall mean of biomass/height ratio was 9.53 Mg/ha/m for Chinese forests. The mean biomass/height ratios for various forest types felled into a very narrow range between 8.59 and 10.45 Mg/ha/m, and were similar as the overall mean (Table 1). This result supports the hypothesis that the biomass per unit of forest space was similar for closed-canopy forests, and thus, geographic forest biomass patterns could be roughly explained by forest height (Fang et al. 2006; Wang et al. 2013). The best evidence of the hypothesis is that: the overall mean of 9.53 Mg/ha/m can predict the biomass for the validation data (126 plots) with an r2 of 0.61, which was not much lower than that of the GLMs in Table 3 (0.70 and 0.73). Thus the hypothesis provides a simple but sound explanation for why biomass is closely related to forest height, even when data from different parts (climates) of China were pooled together (Figs 1 and 2). Note that the hypothesis cannot be interpreted as that the biomass/height ratio is invariant. In fact, the mean biomass/height ratios did increase slightly but regularly from 8.59 in boreal forests to 10.45 Mg/ha/m in subtropical forests (Table 1). This regular change suggests that the biomass–height relationship is influenced by climatic factors. However, it is clear that this effect plays a much weaker role in shaping geographic biomass patterns, compared with forest height (Table 2). Previous studies have shown that forest and tree height changes markedly along climatic gradients (Aiba and Kitayama 1999; Fang et al. 2012; Moles et al. 2009; Wang et al. 2006), this may be one of the reasons why the explanatory power of climate is weak in our study. It is possible that climate drives geographic biomass patterns also through its influence on forest height, which need further studies.
Factors modulating the relationship between forest height and biomass
In this analysis, climate showed significant effect in regulating biomass–height relationship (Table 2), confirming our previous findings in northeast China (Wang et al. 2013) and suggest that climate factor should be considered in broad-scale biomass estimation based on LiDAR. Meanwhile, using a much larger dataset than that study, here we obtained findings unrevealed before. We found that water and energy availability has different effect on biomass–height relationship: the intercept is more affected by MAP, while the slope is more affected by PET (Table 2). We also showed that the explanatory power of PET (including its interaction terms) is generally lower than MAP. This is true for all biomes together, and also for most biomes (except subtropical forests). In northeast China, the effect of climate on biomass–height relationship was weaker than leaf phenology (Wang et al. 2013). However, here we found that the effect of climate was clearly stronger than leaf phenology, leaf form and biome (Table 2), probably because the climatic gradients in this study is much larger than that in Wang et al. (2013). These results highlight the importance of broad-scale studies across various biomes, because relationships obtained in a region may be specific to that region and cannot be easily extrapolated to broader scales.
We found that leaf phenology has significant effect on biomass–height relationship for forests across China (Figs 2b and 3b, Table 2). This confirms previous findings in temperate and boreal forests (Wang et al. 2013), and in tropical forests (Drake et al. 2003). Thus it seems that now we can conclude that the effect of leaf phenology on biomass–height relationship is a general one across various forest biomes. Wang et al. (2013) found that biomass–height relationship did not differ between deciduous broadleaf and deciduous needleleaf forests in northeast China. However, in this analysis we found significant effect of leaf form on biomass–height relationship (Figs 2c and 3c, Table 2). Previous studies that estimate forest parameters with LiDAR have noticed the importance of discriminating needleleaf and broadleaf forests (van Leeuwen and Nieuwenhuis 2010). Some LiDAR studies have also found that estimating the biomass of broadleaf trees is more difficult than for conifers (Næsset 2004; Nelson et al. 2004; Popescu et al. 2003). Tree heights are generally more strongly related to biomass for needleleaf species because they show strong apical dominance (i.e. the main stem is dominant over other side stems). However, many broadleaf species allocate more biomass into lateral branches, which cause the height–biomass relationship noisier (Boudreau et al. 2008). Our results did show that the r2 between forest biomass and height is higher for needleleaf than for broadleaf forests (0.68 vs. 0.58, Table 1). Thus the different biomass–height relationship between needleleaf and broadleaf forests (Fig. 2c) may be a result of different stem and canopy structures of needleleaf and broadleaf trees.
However, leaf phenology and leaf form were generally excluded from the ‘biome GLMs’ (except for leaf phenology in boreal forests), though they were both included in the ‘overall GLM’ (Table 2). Within a same biome, the explanatory power of leaf phenology and leaf form should be weaker than analysed with data from all biomes, because most needleleaf forests and deciduous forests were distributed in cold weather while evergreen broadleaf forests were confined to subtropical and tropical climate. This also means that climate variables have already included some effects of leaf phenology and leaf from. Thus, the results did not refute the effect of leaf phenology and leaf form on biomass–height relationship within a same biome, but suggest that their effects were weaker compared with climatic gradients and thus were excluded from the ‘biome GLMs’.
Models predicting forest biomass from height
Consistent with Wang et al. (2013), the present analysis showed that observed forest biomass patterns could be well predicted from forest height (Table 3), if the effects of climate and biological factors (biome, leaf phenology, etc.) were considered appropriately in the models.
Interestingly, while the ‘biome GLMs’ involves fewer parameters (supplementary Appendix 3) compared with the ‘overall GLM’ (supplementary Appendix 2), the two sets of GLMs showed similar ability to predict biomass patterns (Table 3). This means that for most biomes the geographic biomass patterns can be well estimated with only forest height and climate, without knowing the distributions of evergreen/deciduous and needleleaf/broadleaf forests. We suggest that the ‘biome GLMs’ may be more useful in the practical works of forest biomass monitoring, because monitoring the distributions of these forest types with remote sensing images can be a great task at the broad scales (Wang et al. 2013).
In this analysis, both the ‘biome GLMs’ and the ‘overall GLM’ tend to underestimate the biomass for subtropical forests (Table 3). Thus more studies are still needed to develop better biomass–height models for this biome. However, data on both forest height and biomass are rare in China. Our tests showed that the overall patterns across different biomes were well predicted by the models (Table 3). Thus, before new data and models for subtropical forests appear, our models can still be used to map the overall biomass patterns across China with satellite LiDAR, though the results of subtropical forests should be viewed with caution.
In summary, our results suggest that the effect of climate and biotic factors should be considered in models predicting biomass from height at a large scale, for a more accurate mapping of geographic biomass patterns with satellite LiDAR.
FUNDING
National Natural Science Foundation of China (31370620, 31200146, 31321061); the State Scholarship Fund of China (2011811457).
Conflict of interest statement. None declared.
REFERENCES




