-
PDF
- Split View
-
Views
-
Cite
Cite
Vera Kempe, Nicolas Gauvrit, Alison Gibson, Margaret Jamieson, Adults are more efficient in creating and transmitting novel signalling systems than children, Journal of Language Evolution, Volume 4, Issue 1, January 2019, Pages 44–70, https://doi.org/10.1093/jole/lzy012
Close - Share Icon Share
Abstract
Iterated language learning experiments have shown that meaningful and structured signalling systems emerge when there is pressure for signals to be both learnable and expressive. Yet, such experiments have mainly been conducted with adults using language-like signals. Here we explore whether structured signalling systems can also emerge when signalling domains are unfamiliar and when the learners are children with their well-attested cognitive and pragmatic limitations. In Experiment 1, we compared iterated learning of binary auditory sequences denoting small sets of meanings in chains of adults and 5- to 7-year-old children. Signalling systems became more learnable even though iconicity and structure did not emerge despite applying a homonymy filter designed to keep the systems expressive. When the same types of signals were used in referential communication by adult and child dyads in Experiment 2, only the adults, but not the children, were able to negotiate shared iconic and structured signals. Referential communication using their native language by 4- to 5-year-old children in Experiment 3 showed that only interaction with adults, but not with peers resulted in informative expressions. These findings suggest that emergence and transmission of communication systems are unlikely to be driven by children, and point to the importance of cognitive maturity and pragmatic expertise of learners as well as feedback-based scaffolding of communicative effectiveness by experts during language evolution.
1. Introduction
Languages are shaped by two sets of constraints: the need to be learnable so that they can be transmitted to the next generation and the need to be expressive to ensure successful communication (Tamariz 2017). Empirical evidence for this insight comes from experimental semiotics studies of novel signalling systems (Garrod and Galantucci 2011), which comprise iterated language learning experiments, where the outcome of learning a mini-language by one participant serves as input for the next participant in a chain (Cornish et al. 2013; Kirby et al. 2008, 2015; Silvey et al. 2015; Verhoef et al. 2011, 2014, 2015, 2016; Verhoef 2012), as well as referential communication tasks and signalling games, where multiple participants negotiate meanings of novel signals over several rounds of communicative interaction (Dingemanse et al. 2015; Fay et al. 2014; Garrod et al. 2007; Roberts et al. 2015; Selten and Warglien 2007). These studies have shown that unstructured stimuli become increasingly easier to learn and to use because innovations are shaped by learners’ implicit biases towards simpler, more transparent (Dingemanse et al. 2015; Jones et al. 2014; Roberts et al. 2015) and more compressible (Kirby et al. 2014; Tamariz and Kirby 2015, 2016; Xu and Griffiths 2010) languages. To date, these types of laboratory experiments have been conducted mainly with adults. It is conceivable that adults, especially when presented with language-like signals, albeit artificial ones, will invoke their considerable meta-linguistic knowledge about what language ought to be like. Yet, language is primarily acquired by children who lack this meta-linguistic knowledge and are subject to a range of cognitive constraints that differ from those operating in adults. To gain a better understanding of the generalizability of findings from experimental semiotics, and to explore the role of the cognitive and pragmatic constraints imposed by child learners, this study compares transmission and creation of unfamiliar signalling systems between adults and children.
To predict in what ways children may alter the way consistent and communicatively efficient signalling systems emerge, we first need to consider what research in experimental semiotics tells us about how such systems emerge in adults. The findings can be summarized with respect to three crucial features of language: iconicity, combinatorial structure, and compositional structure. Iconicity emerges when adult learners are faced with novel signal-meaning mappings, and attempts to exploit transparent links between physical properties of the signals and dimensions of the associated meanings (Dingemanse et al. 2015; Roberts et al. 2015), capitalizing either on abundant neonatal cross-modal connections or acquired knowledge about statistical regularities or cross-modal co-occurrences (Spence 2011). Emergence of iconicity has been demonstrated not just when learners negotiate novel signalling systems during communication but also in simple iterated learning experiments without communication (Jones et al. 2014). Iconic signal-meaning mappings are subsequently aligned and refined during communicative interaction, resulting in conventionalized signals that become increasingly arbitrary (Garrod and Galantucci 2011; Lister and Fay 2017).
Emergence of combinatorial structure can be demonstrated in iterated learning experiments with novel stimuli that are not linked to referents, e.g. whistle sounds (Verhoef 2012; Verhoef et al. 2014, 2015), colour sequences (Cornish et al. 2013), doodles (Del Giudice 2012; Tamariz and Kirby 2015), or random dot patterns (Kempe et al. 2015). As a result of iterations through consecutive cycles of learning, such meaningless stimuli become more systematic and structured as sub-components like pitch contour segments or small colour sequences are recombined to generate potentially unlimited sets, in the same way as phonemes are combined to form morphemes and words in natural languages. When such unfamiliar stimuli are linked to meaning, combinatorial structure can also arise from the pressure to minimize confusion between signals as an increase in the number of signals renders them increasingly difficult to discriminate (Nowak et al. 1999; Zuidema and De Boer 2009), but also from intrinsic signal features such as rapid fading (Galantucci et al. 2010), or limited iconic affordances of the signalling domain (Roberts et al. 2015).
Compositional structure has been shown to emerge when the signals are not only subjected to iterated learning, but also used to communicate meaning (Kirby et al. 2015), when meaning spaces undergo expansion (Selten and Warglien, 2007), when communication involves multiple interlocutors in social networks (Raviv et al. 2019), or when context-based predictability of referents is low (Winters et al. 2018). In these situations, sub-components of the signals become systematically associated with dimensions of the meanings, akin to morpho-syntactic rules in natural languages (Del Giudice 2012; Kirby et al. 2008, 2015; Silvey et al. 2015; Verhoef et al. 2015).
In the present study, we ask if and how these basic results would change when novel signals are learned and used by children. Children differ from adults with respect to cognitive capacities, pragmatic abilities, pre-existing real-world knowledge, and prior linguistic experience.1 It is therefore important to investigate more directly how children create and transmit novel signalling systems in order to gain a better understanding of the underlying constraints operating in this process and the role that children may play in language change, especially in light of claims that diversity of linguistic structure is linked to the proportion of child vs. adult learners of a language and the differences in learning constraints this may impose on the process of language transmission (Dale and Lupyan 2012; Lupyan and Dale 2010).
Predictions about what constraints children impose on the emergence of communicatively efficient signalling systems and in what ways these constraints differ from those imposed by adults should address both emergence of iconicity and emergence of structure. Findings from child language development research suggest that such predictions will not necessarily be straightforward: with respect to the emergence of iconicity, the Iconic Bootstrapping Hypothesis (Imai and Kita 2014) proposes that children benefit from iconic signal-meaning mappings because such mappings are transparent and hence easier to comprehend, thereby alleviating the burden of learning. Consequently, children should be more predisposed than adults to capitalize on transparent cross-modal associations between signal features and meaning dimensions. However, the developmental origins of transparent cross-modal association are not clear. A recent meta-analysis of the emergence of the kiki-bouba effect in infancy and early childhood (Fort et al., 2018) suggested that some cross-model correspondences (e.g. the bouba effect that refers to the association of round shapes with back vowels and voiced consonants) are present early on while others (e.g. the kiki effect that refers to the association of spiky shapes with front vowels and voiceless consonants) tend to emerge over time. This would lead to fairly complex predictions according to which some iconic mappings may be preferred by children while others should more easily be accessible to adults based on their greater experience with statistical regularities in the environment; yet, the literature at present does not allow us to make predictions with regards to specific age-dependent cross-modal preferences.
Predictions are also inconsistent with respect to the emergence of structure. On the one hand, in accordance with the Less-Is-More-hypothesis (Newport 1990), children have been credited with superior language learning capabilities precisely because their limited cognitive capacity has been implicated in the injection of structure into language (Hudson Kam and Newport 2005, 2009; Senghas and Coppola 2001; Senghas et al. 2004; Thompson-Schill et al. 2009). Based on this view, structure should emerge more readily in children than in adults during iterated language learning. However, it is not clear whether cognitive immaturity per se aids structure-inducing innovations as attempts to demonstrate experimentally that cognitive limitations lead to superior decomposition (Cochran et al. 1999) or regularization of input (Perfors 2012a) have proved unsuccessful or are open to alternative interpretations (Perfors 2012b; Rohde and Plaut 1999, 2003).
On the other hand, considerable evidence suggests that children fail consistently in referential communication tasks (Garrod and Clark 1993; Glucksberg and Krauss 1967; Matthews et al. 2007; Nilsen and Graham 2009; Sonnenschein and Whitehurst 1984), especially in unfamiliar referential domains for which easily accessible word labels are not available (Glucksberg et al. 1966; Krauss and Glucksberg 1969). Despite attested perspective-taking abilities (Liebal et al. 2009; Moll et al. 2008) such communicative failure may be the result of children’s cognitive limitations, which hinder systematic monitoring of the environment for potential sources of ambiguity and of the informativeness of their own expressions (Rabagliati and Robertson 2017). Consequently, during creation of novel signalling systems, emergence of systematic and reliable signal-meaning mappings should be less likely in children than in adults. Because of these complex and somewhat contradictory predictions, the present study must remain exploratory in nature.
To our knowledge, so far only two other studies have attempted to experimentally study language transmission in children. First, Flaherty and Kirby (2008) compared transmission chains of 7-year-old children and adults learning a small artificial language consisting of bisyllabic pseudo-words denoting objects in a two-dimensional meaning space. The results showed that compositional structure emerged only in the adults but not in the children. Second, Raviv and Arnon (2018) trained 6- to 12-year-old children and adults to orally reproduce bisyllabic pseudo-words presented as signals for twelve meanings that varied on three dimensions. To encourage productivity, participants were trained on only nine out of the twelve signal-meaning pairs, and subsequently tested on the entire set. While compositional structure did not increase over the course of transmission to reach above-chance levels in either age group, it was nonetheless significantly higher in the adults. These two studies constitute preliminary evidence that emergence of structure is less likely in child learners.
While iterated language learning studies with adults typically present typed input, the studies with children used pseudo-words assembled from syllables in a syllable bank, to accommodate children’s still fragile literacy abilities. Producing signals in such a way is a fairly unnatural task. To test the suitability of using more natural stimuli with children, we conducted a pilot study with an oral artificial language denoting a simple meaning space of stars differing in colour, shape, and size in iterated language learning with 4- to 5-year-old children. The results revealed persistent intrusions of familiar words such as ‘Mummy’, ‘Daddy’, and ‘baby’, which emerged early in the transmission chains, regardless of seed stimuli. Apparently, at this age, children’s use of native phonology in pseudo-words is strongly constrained by transfer from prior linguistic knowledge, presumably due to their limited inhibitory control abilities, which preclude suppression of easily accessible, familiar labels (Kahan and Richards 1986). Thus, to put children and adults on a level-playing field in terms of prior experience with the signals, the present study used an entirely unfamiliar signalling domain that did not resemble natural languages, to study iterated language learning (Experiment 1) and creation of novel communication systems (Experiment 2). In addition, to distinguish children’s referential ability from their ability to learn novel signals, Experiment 3 examined children’s referential communication in their native language. All experiments were approved by the Ethics Committee of the School of Health and Social Sciences at Abertay University.
2. Experiment 1
The aim of our first experiment was to compare iterated learning of a novel signalling system between adults and children. Although unfamiliar signalling systems, e.g. slide whistles or Leap Motion (Eryilmaz and Little 2017; Little et al. 2017; Verhoef 2012; Verhoef et al. 2014, 2015, 2016), have been explored before, they either may invoke biases based on pre-existing musical experience or are difficult to execute with small children. We therefore decided to use binary auditory sequences consisting of high and low fixed-length buzzer tones, which are easy and very pleasurable for children to produce. This is an entirely novel signalling domain that has not been explored in the literature. It is unfamiliar to adult and child participants alike, not even resembling music due to its simplicity, yet shares the property of fading with auditory signals of oral language. The binary auditory sequences were combined with eight referents varying in the dimensions of shape, size, and brightness (Fig. 1). This meaning space comprising dark and bright kiki- and bouba-type objects of different size had considerable iconic affordances that are known to affect children’s word learning during natural language acquisition (Maurer et al. 2006; Ozturk et al. 2013). To keep experiment duration and task demands manageable for small children, we did not include a communication task in addition to the learning task but introduced pressure for expressivity by applying a homonymy filter (Kirby et al. 2008), i.e. by removing ambiguous signals from the transmission process to prevent languages from degenerating into uninformative systems.

While we expected learnability to increase over the course of transmission in both adults and children, the more interesting question is whether it does so to a similar extent in both age groups and what strategies children and adults use to encode and retrieve the unfamiliar signals. One strategy learners might adopt is to reduce the number of signals in a way that exceeds the cap imposed by the homonymy filter, which would result in a loss of expressivity. Children may be more prone to this strategy given their smaller working memory capacity. Another strategy would be to forge more transparent, iconic links that help to retrieve a signal given its meaning, and children might be more likely to use this strategy according to predictions from the Iconic Bootstrapping Hypothesis (Imai and Kita 2014). For the meaning space used here, signal dimensions that potentially afford iconic mappings are the auditory features of sequence length, pitch, and the number of pitch alternations. These features can be mapped onto the meaning dimensions of size (big vs. small), shape (spiky vs. fluffy), and brightness (dark vs. light), resulting in nine possible sound-symbolic mappings. The lack of familiarity with the physical properties of the signals provides a unique opportunity to find out how readily children vs. adults can exploit these various iconic affordances. However, of the nine possible cross-modal mappings, only a subset is attested in the literature on iconicity and cross-modal associations, and these are the ones we will explore in this study:
given evidence for magnitude symbolism, larger referents might be associated with longer signals (Dingemanse et al. 2015);
research on cross-modal associations has established associations between pitch height and brightness (Spence 2011), suggesting that brighter referents might be associated with auditory sequences containing a higher proportion of high-pitched sounds;
similarly, research on cross-modal associations has also established links between pitch height and shape such that higher pitch is associated with more angular, spiky shapes (Spence 2011). Consequently, spiky objects might be associated with sequences with a higher proportion of high-pitched sounds;
studies of whistled tone signals, which are characterized by continuous pitch changes, have indicated that pitch contour can be used to mimic object shape (Verhoef et al. 2015). With respect to the referents in this study, this means that more pitch alternations within a sequence (e.g. 01010101 as opposed to 00001111, where 0 represents the high and 1 the low tone) might be used to indicate spiky shapes.
In addition to exploiting iconicity to aid learning and transmission, there are several ways in which learners can also introduce structure: First, learners can attempt to make individual signals easier to remember and reproduce by shortening them (Zipf 1949) and by reducing their algorithmic complexity. Children’s limited working memory capacity should predispose them more than adults towards creating shorter signals but also towards decomposition into smaller sub-components, which then can be recombined using simple production algorithms. For example, a binary sequence consisting of high and low tones represented as 0 and 1 that takes the form 010001011 is considerably more complex than the sequence 000111000, which can be produced according to a simple production rule ‘alternate triplets’, or the sequence 01010101, which simply requires repeating the sub-component 01 four times. This intuition is formally captured by Kolmogorov complexity, which for small binary sequences can be quantified based on the coding theorem method (Gauvrit et al. 2014; Zenil et al. 2015). As algorithmic complexity increases with sequence length, we provide estimates normalized for sequence length.2
Second, on the level of the entire system, learners can try to systematically map sub-components of the signals and salient dimensions of the meanings, thereby inducing compositional structure. Compositional structure can be quantified following the procedure outlined in Kirby et al. (2008) where similarities between all possible pairs of signals are correlated with similarities in the associated pairs of meanings: the stronger these correlations, the higher the compositional structure. However, such a general measure of compositional structure could obscure the fact that participants may focus on certain dimensions of the meanings but not others, as observed in previous research (Beckner et al. 2017). We therefore also compute and analyse correlations between similarities in signals and similarities in various meaning dimensions separately, which will be reported in Appendix A1.
One problem with exploring differences between adults and children in these various manifestations of iconicity and structure is that it necessitates testing a considerable number of dependent variables, thereby inflating the possibility of Type-I errors. Yet, this approach is not uncommon in the experimental semiotics literature: iterated language learning studies typically measure a range of outcomes that capture complexities of the emerging systems. This attests to the still exploratory nature of this research, and the present study is no exception. We hope that our results will contribute to the formulation of more specific hypotheses that in the future can be tested in more targeted confirmatory studies.
2.1 Methods
2.1.1 Participants
A total of 72 adults (51 men, age range 18–51 years) and 72 children (42 boys, all primary grade Levels 1, 2, and 3,3 age range 5–7 years) participated in the study. In each age group, participants were assembled into 6 transmission chains of 12 generations each, with the number of generations chosen simply to accommodate all children who were eager to participate in the experiment. The number of generations of adult participants was chosen to match that of the children. Child transmission chains were assembled controlling for grade level within chains, with two chains each for primary grade Levels 1, 2, and 3. Adult participants were recruited on campus, provided informed consent and were debriefed after the experiment; child participants were pupils of a Primary school, and received a sticker as reward for participation. Parental consent was obtained for all children.
2.1.2 Materials
The referents were eight coloured objects (Fig. 1) differing in shape (spiky kiki-type vs. fluffy bouba-type), size (2 × 2 cm vs. 4 × 4 cm), and brightness (25% vs. 75% saturation), printed onto 5 × 8 cm laminated cards. All referents also had unique properties that arose from variation in the particular shapes of each individual object as well as in the individual hues. Two 500 ms sine-wave tones (high: 440 Hz = musical note a; low: 293.7 Hz = musical note d) were synthesized and recorded onto two buzzers (Learning Resources Recordable Answer Buzzers) of 9 cm in diameter. Note that pressing the buzzers always generated tones of the same duration, making it impossible to modify individual tone duration. Buzzers differed in colour; due to the need to replace the buzzers from time to time, their actual colours changed throughout the study.
2.1.3 Procedure
Children and adults received the same child-appropriate instruction, which for adults was prefaced with the comment that they were invited to test a game designed to be suitable for 5- to 7-year-old children. Participants were told that they would learn a language used by aliens who had no mouth and hence operated buzzers as a means of communication. Participants were further told that they would learn the ‘buzzing words’ for a set of shapes, and were shown all eight cards. Unbeknownst to the participants, two cards were then withheld according to the criteria described below, resulting in training sets of six cards. Training proceeded in incremental fashion such that participants learned signal-meaning pairs one-at-a-time. In the training phase, the experimenter placed the buzzers in front of the participant, shuffled the preselected six cards, and showed them to the participant one by one, accompanying the demonstration by buzzing the associated binary sequence of high and low tones at an even pace with one hand using a prepared script. Participants were asked to repeat the sequence also using only one hand to operate the buzzers, to avoid the overlapping of sounds. Before proceeding to the next card, the experimenter demonstrated the buzzer sequence again, and the participants repeated it for a second time. In the testing phase, participants were shown all eight cards one at a time in a randomized order, and were asked to produce the associated buzzer sequence to the best of their ability. If participants felt unsure, they were encouraged to produce what they thought the appropriate alien ‘buzzer word’ should be, given their acquired knowledge of the alien language. During testing, hand movements and buzzed tone sequences were video-recorded, and then coded for subsequent reproduction by the experimenter during training of the next participant in the chain. Coding accuracy was ensured through double coding.
Generation 1 participants in each chain were trained with random 6-bit or 8-bit binary sequences such that the average length was 7-bits, yet participants experienced some length variation. There were six different random seed languages, each used for one child and one adult chain. As indicated above, only six out of the total of eight cards and the associated buzzer tone sequences were presented during training. For the seed languages, these six cards were selected at random. Modifying the procedure introduced by Kirby et al. (2008) to preserve equal size of the training set, we applied a homonymy filter by removing two cards in the subsequent generations using the following criteria, designed to minimize degeneration of languages to maintain expressivity: If two signals had been duplicated by the learner (i.e. the buzzer language contained only six unique signals), then one of the two cards associated with each duplicate signal was removed at random; if one signal was duplicated (i.e. the buzzer language contained only seven unique signals), then one of the cards associated with the duplicate signal was removed at random, as was one additional randomly chosen card. As the training set contained six cards, any further duplicate signals that occurred were transmitted to the next generation (and the duplicate signals that were withheld were selected at random), to ensure equal size of the training set for all participants. A single session lasted ∼10 min. At the end of each session, adult participants were debriefed; child participants were given the opportunity to choose a reward sticker.
2.2 Results
Appendix A2 provides the final generation binary auditory sequences for adult and child chains. Our analyses explored whether children and adults differed in the trajectories of change in expressivity, learnability, signal length, signal structure, and compositional structure, which are depicted in Fig. 2. Expressivity was operationalized as the number of distinct signals within a language; the more signals there are, the more expressive a language is, with fully expressive languages containing the same number of signals as there are meanings. Learnability, i.e. transmission fidelity, of each buzzer language was measured as the average normalized Levenshtein edit distance between trained and produced signals for each meaning, which constitutes an inverse similarity measure, and was calculated as the number of tone substitutions, insertions, and deletions at each position in the sequence required to change one signal into the other, divided by the length of the longer signal. Signal length was measured as the total number of high and low tones produced for each meaning. Signal structure was operationalized as length-normalized algorithmic complexity (Gauvrit et al. 2014; Zenil et al. 2014, 2015), which constitutes an inverse measure of the degree of structure of individual signals. Finally, compositional structure of each language was computed following the procedure outlined in Kirby et al. (2008): For all possible signal pairings, we determined the dissimilarity based on edit distances and correlated this with dissimilarity between the associated meanings based on Hamming distances, which indicate the number of divergent meaning dimensions (out of three: shape, size, brightness). We report standardized scores for these correlations within the distribution of correlations obtained from 10,000 random permutations of all possible pairings using a Monte Carlo process (Mantel 1967) to determine whether these correlations exceeded the level of chance.
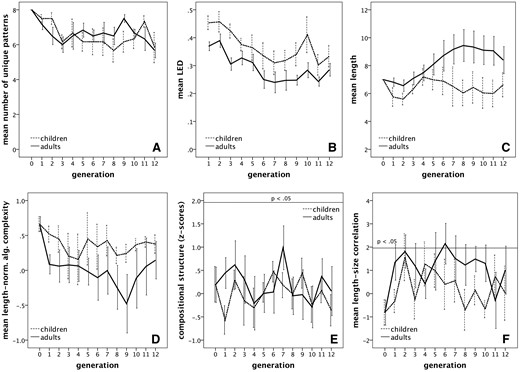
Means for numbers of signals (out of eight) as a measure of degeneration of the language (A), length-normalized Levenshtein edit distance (mean LED) between signals denoting the same meanings in consecutive generations as an inverse measure of learnability (B), signal length (C), length-normalized Kolmogorov complexity as a measure of signal structure (D), z-scores of correlations between similarity of signal pairs and meaning pairs as a measure of compositional structure (E) and iconic mapping indicated by z-scores for the correlation between sequence length and referent size (F), for six adult and six child chains consisting of twelve generations of learners in Experiment 1. Solid lines in (E) and (F) demarcate the z > 1.96, P < 0.05 area. Error bars represent ±1 S.E.M aggregated by participants.
Finally, to estimate iconicity, occurrence of each of the hypothesized iconic mappings was quantified by calculating measures of association between differences in the relevant feature of the auditory sequences (e.g. length, proportion of high-pitched tones, number of pitch alternations) and Hamming distances between the target meaning dimensions across all signal pairings using the Mantel test (Mantel 1967). Proportion of high-pitched tones was calculated to determine the predominant pitch of an auditory sequence, e.g. sequences like 011 and 001111 were assigned the same proportion of high-pitch tones of 0.33. The rationale behind this relative measure was to capture the overall pitch of a sequence regardless of its length. Similarly, to determine pitch alternations, we computed the proportion of all alternations among all tone transitions.
All dependent variables in this and the subsequent experiments were subjected to Growth Curve Analyses (GCAs) with mixed-effect models using the lmer and glmer functions of the R package lme4 in R version 3.4.3. We included fixed effects of Age Group and Generation as well as their interaction, and a maximal random effect structure (Barr et al. 2013) that included random effects of participants, chains, and of items (i.e. referents) where appropriate, as well as all relevant random intercepts, slopes, and slope interactions (Winter and Wieling 2016).4 For all models, P-values were obtained using the Satterthwaite approximation to degrees of freedom provided by the lmerTest package. All fixed effects were centred in order to reduce multicollinearity. Model coefficients and associated t-test for all dependent variables are given in Table 1.
Coefficients for intercepts and fixed effects in the linear mixed-effect models for all dependent variables in Experiment 1
| DV . | Intercept . | Age Group . | Generation . | Age Group × Generation . | |
|---|---|---|---|---|---|
| Model: lmer (DV ∼ Age Group * Generation + (1 + Generation | Chain)) | |||||
| Unique signals | |||||
| β | 6.63 | 0.05 | −0.35 | 0.08 | |
| T | 34.27*** | 0.23 | −2.90* | 0.63 | |
| Compositional structure | |||||
| β | 0.10 | 0.09 | −0.04 | −0.05 | |
| T | 1.20 | 1.15 | −0.51 | −0.55 | |
| Iconicity—correlations between: | |||||
| Length—size | |||||
| β | 0.64 | 0.42 | 0.02 | 0.05 | |
| T | 2.37* | 1.54 | 0.09 | 0.32 | |
| Pitch—shape | |||||
| β | 0.20 | −0.32 | 0.06 | 0.13 | |
| T | 1.17 | −1.91 | 0.34 | 0.70 | |
| Pitch—brightness | |||||
| β | 0.04 | 0.18 | −0.02 | 0.04 | |
| T | 0.19 | 0.94 | −0.14 | 0.20 | |
| Pitch changes—shape | |||||
| β | −0.13 | 0.21 | 0.02 | 0.08 | |
| T | −0.79 | 1.31 | 0.11 | 0.34 | |
| Model: lmer (DV ∼ Age Group * Generation + (1 + Generation | Chain) + (1 + Age Group * Generation | Referent)) | |||||
| Length-normalized edit distance | |||||
| β | 0.33 | −0.04 | −0.04 | −0.00 | |
| T | 21.49*** | −2.48* | −5.17*** | −0.11 | |
| Signal length | |||||
| β | 7.53 | −0.99 | −0.24 | 0.10 | |
| T | 11.79*** | −1.58 | −1.15 | 0.49 | |
| Algorithmic complexity | |||||
| β | 0.09 | 0.25 | 0.12 | −0.05 | |
| T | 0.45 | 1.28 | 1.74 | −0.76 | |
| DV . | Intercept . | Age Group . | Generation . | Age Group × Generation . | |
|---|---|---|---|---|---|
| Model: lmer (DV ∼ Age Group * Generation + (1 + Generation | Chain)) | |||||
| Unique signals | |||||
| β | 6.63 | 0.05 | −0.35 | 0.08 | |
| T | 34.27*** | 0.23 | −2.90* | 0.63 | |
| Compositional structure | |||||
| β | 0.10 | 0.09 | −0.04 | −0.05 | |
| T | 1.20 | 1.15 | −0.51 | −0.55 | |
| Iconicity—correlations between: | |||||
| Length—size | |||||
| β | 0.64 | 0.42 | 0.02 | 0.05 | |
| T | 2.37* | 1.54 | 0.09 | 0.32 | |
| Pitch—shape | |||||
| β | 0.20 | −0.32 | 0.06 | 0.13 | |
| T | 1.17 | −1.91 | 0.34 | 0.70 | |
| Pitch—brightness | |||||
| β | 0.04 | 0.18 | −0.02 | 0.04 | |
| T | 0.19 | 0.94 | −0.14 | 0.20 | |
| Pitch changes—shape | |||||
| β | −0.13 | 0.21 | 0.02 | 0.08 | |
| T | −0.79 | 1.31 | 0.11 | 0.34 | |
| Model: lmer (DV ∼ Age Group * Generation + (1 + Generation | Chain) + (1 + Age Group * Generation | Referent)) | |||||
| Length-normalized edit distance | |||||
| β | 0.33 | −0.04 | −0.04 | −0.00 | |
| T | 21.49*** | −2.48* | −5.17*** | −0.11 | |
| Signal length | |||||
| β | 7.53 | −0.99 | −0.24 | 0.10 | |
| T | 11.79*** | −1.58 | −1.15 | 0.49 | |
| Algorithmic complexity | |||||
| β | 0.09 | 0.25 | 0.12 | −0.05 | |
| T | 0.45 | 1.28 | 1.74 | −0.76 | |
P < 0.001,
P < 0.05.
Coefficients for intercepts and fixed effects in the linear mixed-effect models for all dependent variables in Experiment 1
| DV . | Intercept . | Age Group . | Generation . | Age Group × Generation . | |
|---|---|---|---|---|---|
| Model: lmer (DV ∼ Age Group * Generation + (1 + Generation | Chain)) | |||||
| Unique signals | |||||
| β | 6.63 | 0.05 | −0.35 | 0.08 | |
| T | 34.27*** | 0.23 | −2.90* | 0.63 | |
| Compositional structure | |||||
| β | 0.10 | 0.09 | −0.04 | −0.05 | |
| T | 1.20 | 1.15 | −0.51 | −0.55 | |
| Iconicity—correlations between: | |||||
| Length—size | |||||
| β | 0.64 | 0.42 | 0.02 | 0.05 | |
| T | 2.37* | 1.54 | 0.09 | 0.32 | |
| Pitch—shape | |||||
| β | 0.20 | −0.32 | 0.06 | 0.13 | |
| T | 1.17 | −1.91 | 0.34 | 0.70 | |
| Pitch—brightness | |||||
| β | 0.04 | 0.18 | −0.02 | 0.04 | |
| T | 0.19 | 0.94 | −0.14 | 0.20 | |
| Pitch changes—shape | |||||
| β | −0.13 | 0.21 | 0.02 | 0.08 | |
| T | −0.79 | 1.31 | 0.11 | 0.34 | |
| Model: lmer (DV ∼ Age Group * Generation + (1 + Generation | Chain) + (1 + Age Group * Generation | Referent)) | |||||
| Length-normalized edit distance | |||||
| β | 0.33 | −0.04 | −0.04 | −0.00 | |
| T | 21.49*** | −2.48* | −5.17*** | −0.11 | |
| Signal length | |||||
| β | 7.53 | −0.99 | −0.24 | 0.10 | |
| T | 11.79*** | −1.58 | −1.15 | 0.49 | |
| Algorithmic complexity | |||||
| β | 0.09 | 0.25 | 0.12 | −0.05 | |
| T | 0.45 | 1.28 | 1.74 | −0.76 | |
| DV . | Intercept . | Age Group . | Generation . | Age Group × Generation . | |
|---|---|---|---|---|---|
| Model: lmer (DV ∼ Age Group * Generation + (1 + Generation | Chain)) | |||||
| Unique signals | |||||
| β | 6.63 | 0.05 | −0.35 | 0.08 | |
| T | 34.27*** | 0.23 | −2.90* | 0.63 | |
| Compositional structure | |||||
| β | 0.10 | 0.09 | −0.04 | −0.05 | |
| T | 1.20 | 1.15 | −0.51 | −0.55 | |
| Iconicity—correlations between: | |||||
| Length—size | |||||
| β | 0.64 | 0.42 | 0.02 | 0.05 | |
| T | 2.37* | 1.54 | 0.09 | 0.32 | |
| Pitch—shape | |||||
| β | 0.20 | −0.32 | 0.06 | 0.13 | |
| T | 1.17 | −1.91 | 0.34 | 0.70 | |
| Pitch—brightness | |||||
| β | 0.04 | 0.18 | −0.02 | 0.04 | |
| T | 0.19 | 0.94 | −0.14 | 0.20 | |
| Pitch changes—shape | |||||
| β | −0.13 | 0.21 | 0.02 | 0.08 | |
| T | −0.79 | 1.31 | 0.11 | 0.34 | |
| Model: lmer (DV ∼ Age Group * Generation + (1 + Generation | Chain) + (1 + Age Group * Generation | Referent)) | |||||
| Length-normalized edit distance | |||||
| β | 0.33 | −0.04 | −0.04 | −0.00 | |
| T | 21.49*** | −2.48* | −5.17*** | −0.11 | |
| Signal length | |||||
| β | 7.53 | −0.99 | −0.24 | 0.10 | |
| T | 11.79*** | −1.58 | −1.15 | 0.49 | |
| Algorithmic complexity | |||||
| β | 0.09 | 0.25 | 0.12 | −0.05 | |
| T | 0.45 | 1.28 | 1.74 | −0.76 | |
P < 0.001,
P < 0.05.
These analyses yielded effects of Generation only for the number of unique patterns and for the edit distances indicating that both of these measures declined over the course of transmission. For edit distances, we also found an effect of Age Group suggesting that transmission fidelity was higher in adults.5 No effects of Generation and Age Group were found for measures of signal length, signal structure, or compositional structure.6
2.3 Discussion
Experiment 1 investigated differences between adults and 5- to 7-year-old children in the iterated reproduction of binary auditory sequences associated with a three-dimensional meaning space with eight referents differing in shape, size, and brightness. We found that the emerging languages degenerated by losing some of the unique patterns, and became easier to learn over the course of transmission, as indicated by a decrease in edit distance. Although decreasing edit distances indicated significant gains in fidelity of transmission in both children and adults, particularly in the earlier generations, transmission overall tended to be more faithful in adults. Notably, compositional structure and iconicity did not emerge in either age group. Thus, whatever advantages adults may have had in their ability to learn the unfamiliar signals, they were not due to increased structuring of the individual signals nor of the entire languages but most likely just a reflection of their greater working memory capacity that enabled them to retain a larger number of sequences. This is in line with the findings from immediate serial recall of unfamiliar 4-colour sequences produced by 6- to 10-year old children in the SIMON®-game (Mathy et al. 2016), which demonstrated that age-related increase in memory capacity was not associated with formation of larger chunks, which could potentially introduce greater structure, but with the ability to store more of them.
The null effects for structure obtained here differ from previous findings comparing iterated reproduction of random dot patterns between adults and children (Kempe et al. 2015), where structure emerged more rapidly in the children. The different results may be due to differences in familiarity: In the visuo-spatial domain, children will only have acquired a simple repertoire of representations such as straight lines or blobs, and hence fall back on these algorithmically simpler structures during reproduction. Adults, on the other hand, are likely to possess a larger repertoire of more complex representations like triangles, diamonds, squares, zigzags, and crosses, etc., thus being able to introduce patterns with greater algorithmic complexity. However, sequences of high and low tones are likely to be equally unfamiliar for both age groups so that no such different prior representations can bias children’s and adults’ reproductions. Under these conditions, adults simply benefit from their larger memory capacity allowing them to retain more unstructured chunks.
Our findings are in line with the study by Raviv and Arnon (2018), where learnability of meaningful signals was also higher in adults than 6- to 12-year-old children. Moreover, as in the present study, compositional structure did not exceed chance levels in that study either although it was significantly higher in adults. There are at least two possible reasons for why structure and iconicity did not emerge reliably in these experiments: First, both in Raviv and Arnon (2018) and in the present study, the training phase was considerably shorter than in many previous iterated learning studies, a methodological constraint that was necessary to sustain children’s attention on the task. A shorter training phase may have simply not provided enough opportunity to explore the iconic and structural potential of the signalling domains. Second, introducing a homonymy filter may not have imposed a sufficiently strong expressivity pressure to avoid ambiguous signals (Carr et al. 2017; Flaherty and Kirby 2008). A better way of directing learners’ attention to the requirement for having unique signals for all meanings would have been to combine iterated learning with a referential communication task, as in Kirby et al. (2015). This, however, would have required administering a fairly complex and elaborate learning and communication procedure to a large number of dyads, which is a considerable logistical challenge for research with small children. As a result, it is not clear whether the failure of iconicity and structure to emerge was a consequence of insufficient pressure for expressivity or whether it reflects general limitations of this signalling domain, either because it is unfamiliar or because it is unsuitable for structuring. To clarify this issue, the next experiment compared children and adults in their ability to exploit iconicity and induce structure when trying to create a novel signalling system for referential communication.
3. Experiment 2
The goal of this experiment was to examine how children differ from adults in their ability to create an expressive communication system based on an unfamiliar signalling domain like the binary auditory sequences used in Experiment 1. The results will provide insights into the extent to which children are motivated and capable to be sufficiently expressive to create shared signalling systems from scratch.
3.1. Method
3.1.1 Participants
Twenty-four adults (twelve men, overall age range 20–26 years) and twenty-four monolingual children with English as native language (sixteen boys, all Primary grade Level 3, which in Scotland typically comprises ages 6–7 years) were assembled into twelve same-sex pairs within each age group. Recruitment, consent, and reward conditions were the same as in Experiment 1.
3.1.2 Materials
We duplicated the eight cards used in Experiment 1 to create two identical sets, and used the same buzzers as in Experiment 1. In addition, each interlocutor received a coloured cup to collect reward tokens.
3.1.3 Procedure
Children and adults were given the same child-appropriate instruction, which for adults were prefaced with the comment that they were invited to test a game designed to be suitable for 6- to 7-year-old children. Participants sat on opposite sides of a table with the buzzers placed within equal reach in between them. After brief familiarization with the cards, they were told that they would be using the buzzer language used by a species of aliens with no mouth, to communicate the identity of the cards to each other, switching between the roles of Director and Matcher. The interaction phase was preceded by a brief training phase, in which participants were exposed to the ‘alien language’, i.e. to random binary auditory sequences similarly to the ones used at the outset of the iterated learning in Experiment 1. In the training phase, children took turns to repeat the signal provided by the experimenter for each referent such that each child repeated half of the signals. The purpose of this very brief familiarization was not for the participants to learn the sequences, but simply to expose them to an array of possible sequences to provide them with an understanding of the variation in the signals that could be used.
In the interaction phase, participants were invited to take turns signalling all referents so that their interlocutors were able to identify the cards correctly. For the first half of the adult and child dyads (i.e. dyads 1–6), the Matchers’ cards were placed face up on the table by the Experimenter, taking special care that the random, unstructured spatial arrangement of cards would preclude a strategy of signalling cards by location, i.e. avoiding arrangements in rows, squares, rectangles, or circles. The Directors then shuffled their cards and placed them face down on the table, drawing from the deck one by one. Placing the Matcher cards on the table had the advantage that participants were continuously reminded of all the three relevant meaning dimensions, but had the disadvantage that participants could attempt positional coding despite instructions to avoid this strategy (i.e. indicating referents by the number of buzzes depending on position). To check whether positional coding could have influenced the results, the second half of adult and child dyads (i.e. in dyads 7–12) underwent a slight change in procedure such that Matchers placed their eight cards away from the Director’s view on a cardboard stand resembling an oversized Scrabble tile holder. This prevented positional coding but had the disadvantage that Directors did not have a reminder of the meaning dimensions in front of them. To control for this variation in procedure, the factor of Card Position (visible vs. hidden) was included in all analyses.
Once the cards were in place, Directors selected the first card keeping its face out of the Matcher’s view, and signalled the depicted meaning using the buzzers to generate a sequence of tones. The Matcher then picked up the selected the card and both participants placed the target cards in the middle of the table in view of the video camera, and received a reward token every time their cards matched. It was stressed that rewards would only be awarded jointly so Directors were encouraged to be cooperative in their signalling. The Matcher then returned the selected card to its previous position before the Director buzzed the sequence denoting the next card. After signals for all eight cards had been communicated, participants switched roles. This interaction continued for a total of five rounds after which participants counted up their reward tokens. Adults were debriefed and thanked for their participation; children were allowed to choose several different reward stickers. While players operated the buzzers, their hands were video-recorded for subsequent coding. Each session lasted between 35 and 45 min.
3.2 Results
In addition to the variables examined in Experiment 1, we also analysed the following variables (see Fig. 3): (1) a measure of alignment, determined as length-normalized Levenshtein edit distance between binary sequences of both participants produced for the same meaning by the interlocutor on the previous turn; (2) consistency, defined as length-normalized Levenshtein edit distance between binary sequences produced by the same participant for the same meaning on two consecutive rounds; and (3) accuracy of card identifications as an indicator of communicative efficiency. With respect to this latter dependent variable, it should be noted that the random sampling of cards without replacement rendered the Matchers’ referent choices dependent on their memory capacity, and not just on the Directors’ expressivity, as participants could attempt to remember which cards had already been signalled by the Director.7
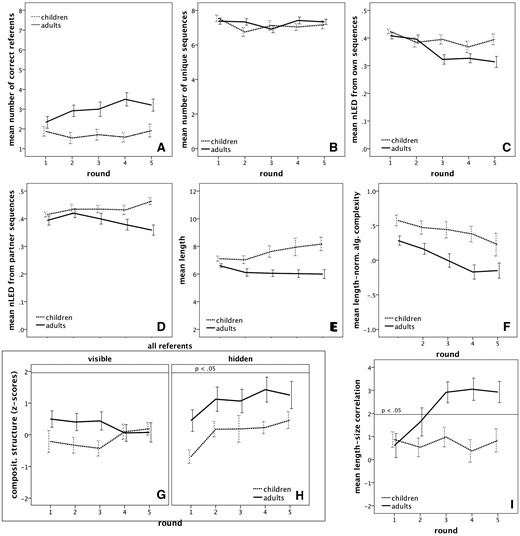
Number of correctly identified referents (A), number of different signals (out of eight) as an inverse measure of degeneration of the language (B), length-normalized Levenshtein edit distance from own binary sequences produced on the previous round (C) and from binary sequences produced by interlocutor on the previous turn (D), binary sequence length (E), length-normalized algorithmic complexity of binary sequences as a measure of signal structure (F), z-scores of correlations between similarity of sequence pairs and meaning pairs indicating compositional structure as a function of Card Position (G and H), and iconic mapping between sequence length and referent size measured as z-scores of length-size correlations (I) for twelve child and twelve adult dyads interacting over five rounds in Experiment 2. Solid lines indicate z = 1.96, P = 0.05. Values represent means across dyads; error bars represent ±1 S.E.M aggregated by participants.
All dependent variables were analysed with GCAs using a mixed-effect model with Card Position (visible vs. hidden), Age Group (adults vs. children), and Round (1–5) and their interactions as fixed effects, and Participants nested within dyads as random effects. To control for the variation of the spatial position of the Matcher cards, we included the factor of Card Position (i.e. matcher cards were either visible or hidden) in all analyses. As in Experiment 1, we included items (i.e. individual meanings) as another random effect where appropriate.8 The results are given in Table 2.
Coefficients for intercepts and fixed effects in the linear mixed-effect models for all dependent variables in Experiment 2
| DV . | Intercept . | Card Pos . | Age Group . | Round . | Card Pos × Age Group . | Card Pos × Round . | Age Group × Round . | 3-Way . |
|---|---|---|---|---|---|---|---|---|
| Model: DV ∼ CardPosition * AgeGroup * Round + (1+Round | Dyad/Participant) | ||||||||
| Unique patterns | ||||||||
| β | 7.21 | −0.21 | −0.06 | −0.04 | −0.08 | 0.09 | −0.04 | −0.05 |
| t | 52.87*** | −1.54 | −0.47 | −0.58 | −0.56 | 1.33 | −0.58 | −0.80 |
| Compositional structure | ||||||||
| β | 0.27 | −0.19 | −0.39 | 0.18 | 0.12 | −0.18 | 0.12 | 0.08 |
| t | 2.66* | −1.89 | −3.86*** | 2.34* | 1.13 | −2.28* | 1.54 | 1.06 |
| Iconicity—correlations between | ||||||||
| Length—size | ||||||||
| β | 1.33 | −0.43 | −0.60 | 0.50 | 0.22 | 0.01 | −0.54 | −0.05 |
| t | 5.23*** | −1.66 | −2.36* | 2.63* | 0.85 | 0.06 | −2.84* | −0.28 |
| Pitch—shape | ||||||||
| β | 0.27 | −0.15 | 0.04 | 0.05 | 0.05 | 0.29 | 0.03 | −0.30 |
| t | 1.06 | −0.60 | 0.17 | 0.28 | 0.18 | 1.60 | 0.19 | −1.64 |
| Pitch—brightness | ||||||||
| β | −0.15 | 0.19 | −0.02 | −0.16 | −0.35 | 0.08 | 0.19 | 0.14 |
| t | −0.77 | 0.95 | −0.13 | −0.94 | −1.76 | 0.47 | 1.11 | 0.81 |
| Pitch change—shape | ||||||||
| β | −0.07 | −0.06 | 0.26 | 0.10 | −0.04 | −0.07 | 0.17 | −0.03 |
| T | −0.49 | −0.41 | 1.93 | 0.82 | −0.27 | −0.57 | 1.35 | −2.18 |
| Model: DV ∼ CardPos * AgeGroup * Round + (1 + Round | Dyad/Participant) + (1 + Experiment * Age * Round | Item)) | ||||||||
| Accuracy | ||||||||
| β (logit) | −1.00 | 0.13 | −0.40 | 0.11 | 0.11 | −0.01 | −0.10 | −0.02 |
| z | −8.66*** | 1.22 | −4.48*** | 1.51 | 1.30 | −0.08 | −1.34 | −0.29 |
| Signal length | ||||||||
| β | 6.89 | −0.01 | 0.62 | 0.13 | −0.08 | −0.09 | 0.34 | −0.00 |
| T | 27.16*** | −0.57 | 3.55*** | 1.00 | −0.49 | −0.70 | 2.75** | −0.01 |
| LEDown | ||||||||
| β | 0.38 | −0.00 | 0.02 | −0.03 | −0.01 | 0.01 | 0.01 | −0.01 |
| T | 35.00*** | −0.01 | 2.24* | −3.43** | −1.14 | 0.84 | 2.34* | −2.08* |
| LEDother | ||||||||
| β | 0.41 | 0.00 | 0.02 | −0.00 | −0.00 | 0.01 | 0.02 | 0.00 |
| T | 33.33*** | 0.09 | 2.12* | −0.19 | −0.53 | 0.52 | 2.36* | −1.98 |
| Algorithmic complexity | ||||||||
| β | 0.26 | 0.02 | 0.17 | −0.15 | 0.04 | −0.03 | 0.03 | 0.03 |
| t | 4.03** | 0.37 | 3.01** | −3.70** | 0.95 | −0.88 | 0.91 | 0.95 |
| DV . | Intercept . | Card Pos . | Age Group . | Round . | Card Pos × Age Group . | Card Pos × Round . | Age Group × Round . | 3-Way . |
|---|---|---|---|---|---|---|---|---|
| Model: DV ∼ CardPosition * AgeGroup * Round + (1+Round | Dyad/Participant) | ||||||||
| Unique patterns | ||||||||
| β | 7.21 | −0.21 | −0.06 | −0.04 | −0.08 | 0.09 | −0.04 | −0.05 |
| t | 52.87*** | −1.54 | −0.47 | −0.58 | −0.56 | 1.33 | −0.58 | −0.80 |
| Compositional structure | ||||||||
| β | 0.27 | −0.19 | −0.39 | 0.18 | 0.12 | −0.18 | 0.12 | 0.08 |
| t | 2.66* | −1.89 | −3.86*** | 2.34* | 1.13 | −2.28* | 1.54 | 1.06 |
| Iconicity—correlations between | ||||||||
| Length—size | ||||||||
| β | 1.33 | −0.43 | −0.60 | 0.50 | 0.22 | 0.01 | −0.54 | −0.05 |
| t | 5.23*** | −1.66 | −2.36* | 2.63* | 0.85 | 0.06 | −2.84* | −0.28 |
| Pitch—shape | ||||||||
| β | 0.27 | −0.15 | 0.04 | 0.05 | 0.05 | 0.29 | 0.03 | −0.30 |
| t | 1.06 | −0.60 | 0.17 | 0.28 | 0.18 | 1.60 | 0.19 | −1.64 |
| Pitch—brightness | ||||||||
| β | −0.15 | 0.19 | −0.02 | −0.16 | −0.35 | 0.08 | 0.19 | 0.14 |
| t | −0.77 | 0.95 | −0.13 | −0.94 | −1.76 | 0.47 | 1.11 | 0.81 |
| Pitch change—shape | ||||||||
| β | −0.07 | −0.06 | 0.26 | 0.10 | −0.04 | −0.07 | 0.17 | −0.03 |
| T | −0.49 | −0.41 | 1.93 | 0.82 | −0.27 | −0.57 | 1.35 | −2.18 |
| Model: DV ∼ CardPos * AgeGroup * Round + (1 + Round | Dyad/Participant) + (1 + Experiment * Age * Round | Item)) | ||||||||
| Accuracy | ||||||||
| β (logit) | −1.00 | 0.13 | −0.40 | 0.11 | 0.11 | −0.01 | −0.10 | −0.02 |
| z | −8.66*** | 1.22 | −4.48*** | 1.51 | 1.30 | −0.08 | −1.34 | −0.29 |
| Signal length | ||||||||
| β | 6.89 | −0.01 | 0.62 | 0.13 | −0.08 | −0.09 | 0.34 | −0.00 |
| T | 27.16*** | −0.57 | 3.55*** | 1.00 | −0.49 | −0.70 | 2.75** | −0.01 |
| LEDown | ||||||||
| β | 0.38 | −0.00 | 0.02 | −0.03 | −0.01 | 0.01 | 0.01 | −0.01 |
| T | 35.00*** | −0.01 | 2.24* | −3.43** | −1.14 | 0.84 | 2.34* | −2.08* |
| LEDother | ||||||||
| β | 0.41 | 0.00 | 0.02 | −0.00 | −0.00 | 0.01 | 0.02 | 0.00 |
| T | 33.33*** | 0.09 | 2.12* | −0.19 | −0.53 | 0.52 | 2.36* | −1.98 |
| Algorithmic complexity | ||||||||
| β | 0.26 | 0.02 | 0.17 | −0.15 | 0.04 | −0.03 | 0.03 | 0.03 |
| t | 4.03** | 0.37 | 3.01** | −3.70** | 0.95 | −0.88 | 0.91 | 0.95 |
LEDown: length-normalized Levenshtein edit distance to previous signal used for a given meaning by the same participant, LEDother: length-normalized Levenshtein edit distance to signal used for the same meaning by the other participant in the preceding round, alg. comp.: length-normalized algorithmic complexity of individual signals.
P < 0.001,
P < 0.01,
P < 0.05.
Coefficients for intercepts and fixed effects in the linear mixed-effect models for all dependent variables in Experiment 2
| DV . | Intercept . | Card Pos . | Age Group . | Round . | Card Pos × Age Group . | Card Pos × Round . | Age Group × Round . | 3-Way . |
|---|---|---|---|---|---|---|---|---|
| Model: DV ∼ CardPosition * AgeGroup * Round + (1+Round | Dyad/Participant) | ||||||||
| Unique patterns | ||||||||
| β | 7.21 | −0.21 | −0.06 | −0.04 | −0.08 | 0.09 | −0.04 | −0.05 |
| t | 52.87*** | −1.54 | −0.47 | −0.58 | −0.56 | 1.33 | −0.58 | −0.80 |
| Compositional structure | ||||||||
| β | 0.27 | −0.19 | −0.39 | 0.18 | 0.12 | −0.18 | 0.12 | 0.08 |
| t | 2.66* | −1.89 | −3.86*** | 2.34* | 1.13 | −2.28* | 1.54 | 1.06 |
| Iconicity—correlations between | ||||||||
| Length—size | ||||||||
| β | 1.33 | −0.43 | −0.60 | 0.50 | 0.22 | 0.01 | −0.54 | −0.05 |
| t | 5.23*** | −1.66 | −2.36* | 2.63* | 0.85 | 0.06 | −2.84* | −0.28 |
| Pitch—shape | ||||||||
| β | 0.27 | −0.15 | 0.04 | 0.05 | 0.05 | 0.29 | 0.03 | −0.30 |
| t | 1.06 | −0.60 | 0.17 | 0.28 | 0.18 | 1.60 | 0.19 | −1.64 |
| Pitch—brightness | ||||||||
| β | −0.15 | 0.19 | −0.02 | −0.16 | −0.35 | 0.08 | 0.19 | 0.14 |
| t | −0.77 | 0.95 | −0.13 | −0.94 | −1.76 | 0.47 | 1.11 | 0.81 |
| Pitch change—shape | ||||||||
| β | −0.07 | −0.06 | 0.26 | 0.10 | −0.04 | −0.07 | 0.17 | −0.03 |
| T | −0.49 | −0.41 | 1.93 | 0.82 | −0.27 | −0.57 | 1.35 | −2.18 |
| Model: DV ∼ CardPos * AgeGroup * Round + (1 + Round | Dyad/Participant) + (1 + Experiment * Age * Round | Item)) | ||||||||
| Accuracy | ||||||||
| β (logit) | −1.00 | 0.13 | −0.40 | 0.11 | 0.11 | −0.01 | −0.10 | −0.02 |
| z | −8.66*** | 1.22 | −4.48*** | 1.51 | 1.30 | −0.08 | −1.34 | −0.29 |
| Signal length | ||||||||
| β | 6.89 | −0.01 | 0.62 | 0.13 | −0.08 | −0.09 | 0.34 | −0.00 |
| T | 27.16*** | −0.57 | 3.55*** | 1.00 | −0.49 | −0.70 | 2.75** | −0.01 |
| LEDown | ||||||||
| β | 0.38 | −0.00 | 0.02 | −0.03 | −0.01 | 0.01 | 0.01 | −0.01 |
| T | 35.00*** | −0.01 | 2.24* | −3.43** | −1.14 | 0.84 | 2.34* | −2.08* |
| LEDother | ||||||||
| β | 0.41 | 0.00 | 0.02 | −0.00 | −0.00 | 0.01 | 0.02 | 0.00 |
| T | 33.33*** | 0.09 | 2.12* | −0.19 | −0.53 | 0.52 | 2.36* | −1.98 |
| Algorithmic complexity | ||||||||
| β | 0.26 | 0.02 | 0.17 | −0.15 | 0.04 | −0.03 | 0.03 | 0.03 |
| t | 4.03** | 0.37 | 3.01** | −3.70** | 0.95 | −0.88 | 0.91 | 0.95 |
| DV . | Intercept . | Card Pos . | Age Group . | Round . | Card Pos × Age Group . | Card Pos × Round . | Age Group × Round . | 3-Way . |
|---|---|---|---|---|---|---|---|---|
| Model: DV ∼ CardPosition * AgeGroup * Round + (1+Round | Dyad/Participant) | ||||||||
| Unique patterns | ||||||||
| β | 7.21 | −0.21 | −0.06 | −0.04 | −0.08 | 0.09 | −0.04 | −0.05 |
| t | 52.87*** | −1.54 | −0.47 | −0.58 | −0.56 | 1.33 | −0.58 | −0.80 |
| Compositional structure | ||||||||
| β | 0.27 | −0.19 | −0.39 | 0.18 | 0.12 | −0.18 | 0.12 | 0.08 |
| t | 2.66* | −1.89 | −3.86*** | 2.34* | 1.13 | −2.28* | 1.54 | 1.06 |
| Iconicity—correlations between | ||||||||
| Length—size | ||||||||
| β | 1.33 | −0.43 | −0.60 | 0.50 | 0.22 | 0.01 | −0.54 | −0.05 |
| t | 5.23*** | −1.66 | −2.36* | 2.63* | 0.85 | 0.06 | −2.84* | −0.28 |
| Pitch—shape | ||||||||
| β | 0.27 | −0.15 | 0.04 | 0.05 | 0.05 | 0.29 | 0.03 | −0.30 |
| t | 1.06 | −0.60 | 0.17 | 0.28 | 0.18 | 1.60 | 0.19 | −1.64 |
| Pitch—brightness | ||||||||
| β | −0.15 | 0.19 | −0.02 | −0.16 | −0.35 | 0.08 | 0.19 | 0.14 |
| t | −0.77 | 0.95 | −0.13 | −0.94 | −1.76 | 0.47 | 1.11 | 0.81 |
| Pitch change—shape | ||||||||
| β | −0.07 | −0.06 | 0.26 | 0.10 | −0.04 | −0.07 | 0.17 | −0.03 |
| T | −0.49 | −0.41 | 1.93 | 0.82 | −0.27 | −0.57 | 1.35 | −2.18 |
| Model: DV ∼ CardPos * AgeGroup * Round + (1 + Round | Dyad/Participant) + (1 + Experiment * Age * Round | Item)) | ||||||||
| Accuracy | ||||||||
| β (logit) | −1.00 | 0.13 | −0.40 | 0.11 | 0.11 | −0.01 | −0.10 | −0.02 |
| z | −8.66*** | 1.22 | −4.48*** | 1.51 | 1.30 | −0.08 | −1.34 | −0.29 |
| Signal length | ||||||||
| β | 6.89 | −0.01 | 0.62 | 0.13 | −0.08 | −0.09 | 0.34 | −0.00 |
| T | 27.16*** | −0.57 | 3.55*** | 1.00 | −0.49 | −0.70 | 2.75** | −0.01 |
| LEDown | ||||||||
| β | 0.38 | −0.00 | 0.02 | −0.03 | −0.01 | 0.01 | 0.01 | −0.01 |
| T | 35.00*** | −0.01 | 2.24* | −3.43** | −1.14 | 0.84 | 2.34* | −2.08* |
| LEDother | ||||||||
| β | 0.41 | 0.00 | 0.02 | −0.00 | −0.00 | 0.01 | 0.02 | 0.00 |
| T | 33.33*** | 0.09 | 2.12* | −0.19 | −0.53 | 0.52 | 2.36* | −1.98 |
| Algorithmic complexity | ||||||||
| β | 0.26 | 0.02 | 0.17 | −0.15 | 0.04 | −0.03 | 0.03 | 0.03 |
| t | 4.03** | 0.37 | 3.01** | −3.70** | 0.95 | −0.88 | 0.91 | 0.95 |
LEDown: length-normalized Levenshtein edit distance to previous signal used for a given meaning by the same participant, LEDother: length-normalized Levenshtein edit distance to signal used for the same meaning by the other participant in the preceding round, alg. comp.: length-normalized algorithmic complexity of individual signals.
P < 0.001,
P < 0.01,
P < 0.05.
Only one dependent variable, compositional structure, showed an interaction between Card Position and Round, which we explored in separate analyses for both conditions. When cards were visible, there was an effect of AgeGroup, β = −0.28, t = −2.30, P = 0.039, confirming greater compositional structure in adults. When cards were hidden, there was also an effect of Age Group, β = −0.51, t = −3.03, P = 0.011, as well as an effect of Round, β = 0.37, t = 3.19, P < 0.003, indicating that while higher in adults, compositional structure also increased over consecutive rounds of the interaction. This indicates that despite our attempts to prevent positional coding in the condition where cards were visible, some participants might have attempted it despite instructions to the contrary, which may have reduced occurrences of compositional innovations in later rounds. However, despite these effects, it is important to reiterate that most z-scores were <1.96, indicating that even in the adults, compositional structure did not emerge reliably.
3.3 Discussion
In Experiment 2, pairs of adults and children communicated over five rounds using binary auditory sequences to signal a set of eight meanings differing in shape, size, and brightness. Not unexpectedly, we found that adults outperformed the children in terms of communicative success. As expected for communicative interactions (Kirby et al. 2015), languages did not degenerate or shorten over repeated rounds. We also found that over the course of repeated interactions, individual signals were reproduced more consistently, especially in the adults who more frequently than the children reused the signals they had created previously. In contrast to Experiment 1, communicative interaction over five rounds led to increasingly structured individual signals, as indicated by a reduction in algorithmic complexity in both age groups; algorithmic complexity in general was lower in the adults than in the children. This suggests that more frequent production of the same signals compared to Experiment 1 can drive an increase in signal structure, which, in turn, facilitates consistency of reproduction, as more structured sequences are easier to remember. As expected, without the learnability pressures that arise from inter-generational transmission (Kirby et al. 2015), interlocutors did not spontaneously introduce sufficient compositional structure that would have correlations between similarities in signals and meanings exceed chance levels, even though overall compositional structure was higher in adults.
Most notably, we observed that alignment between interlocutors increased in the adults but not in the children, as evidenced by the decreasing edit distance to signals produced by the interlocutor on the previous turn. Even at the end of the interaction, children took little notice of the signals produced by their interlocutor, while adults increasingly matched their interlocutors’ productions. Note that simply imitating the interlocutor’s most recent signals does not lead to alignment; interlocutors need to align signals with the corresponding meanings. There are three ways in which such alignment can be achieved. First, participants can memorize and reproduce the individual signals produced by their interlocutors, a strategy that is taxing on memory resources and therefore favours adults. Second, participants can discover and reproduce any systematicity in their interlocutor’s way of linking signals to meanings, i.e. compositional structure. Our findings showed greater compositionality in adults, but not in children, in line with findings from Raviv and Arnon (2018), even if compositional structure still did not exceed chance. This age effect was mainly carried by the dimension of shape. Finally, alignment can be achieved through discovery and sharing of transparent, iconic links between signals and meanings. We found that adults, but not children, established such links by consistently and reliably associating bigger referents with longer sequences. The observation that magnitude symbolism emerged as the preferred cross-modal association lends further support to the notion that links between linguistic features that differ in magnitude (e.g. pitch or word length) and meaning dimensions that express quantity (e.g. size or complexity) appear to be fundamental and perhaps universal (Dingemanse et al. 2015). However, it should be pointed out that mapping signal length onto size per se is not sufficient to achieve alignment. For example, the hypothetical sequences 000000 and 111111 are perfectly matched in length but bear no resemblance in terms of their structure and are therefore not aligned. The facts that edit distance to interlocutor signals, the inverse measure of alignment, decreased in the adults suggests that they pursued other ways of linking signals to meanings in addition to relying on magnitude symbolism. Misalignment in children, then, may have been either due to a lack of understanding that mappings between signal and meaning need to be shared, inability to discover cross-modal links or inability to monitor form and communicative efficiency of their own and their interlocutor’s productions, a task that is difficult for children of this age group, as it requires considerable processing capacity (Rabagliati and Robertson 2017).
Two factors may be responsible for why sound-symbolic mappings between signal length and referent size did not emerge in the children, counter to predictions from the Iconic Bootstrapping Hypothesis (Imai and Kita 2014). First, children’s processing limitations may restrict their capacity to systematically scan the novel signalling space for iconic affordances, and to monitor their own signals as well as interlocutor responses. Second, children may lack the fundamental insight that novel signals need to be informative, in the same way in which monolingual children often lack the meta-linguistic understanding that the same meanings can be expressed unambiguously by different signals in different languages (Bialystok 1986). To distinguish between these options—the cognitive cost associated with using a novel signalling system vs. the lack of insight that signals need to be informative—Experiment 3 tested children’s expressivity in a communication task that allowed them to use their native language.
4. Experiment 3
To establish whether children are capable of the expressivity that would be needed to create novel communication systems when not hampered by lack of familiarity with the signalling domain, we examined pre-schoolers’ referential communication with peers and adults in their native language. Although there is evidence that children are able to monitor knowledge states of their addressees (Bahtiyar and Küntay 2009; Liebal et al. 2009; Moll et al. 2008; Nadig and Sedivy 2002; O'Neill 1996), communication is generally unsuccessful when children do not have labels for referents readily available (Garrod and Clark 1993; Glucksberg and Krauss 1967; Glucksberg et al. 1966; Kahan and Richards 1986; Krauss and Glucksberg 1969; Nilsen and Graham 2009; Sonnenschein and Whitehurst 1984). There is also evidence that children show limited understanding of communicative failure (Robinson and Robinson 1978) and require adult scaffolding to repair communicative breakdown (Matthews et al. 2007), which otherwise presents problems in peer interaction up until about 11–12 years of age (Garrod and Clark 1993; Girbau 2001). A second goal of Experiment 3 was therefore to explore how children adjust their communication strategies in response to such scaffolding to shed light on the conditions under which children are able to succeed in negotiating meaningful signalling systems.
To remain compatible with Experiments 1 and 2, we compared children’s referential communication about nameable referents varying on three dimensions, so that informative expressions required production of a set of three modifiers. The need to produce modifiers created a situation that would discourage referential pacts (Brennan and Clark 1996) so that unlike other studies (e.g. Krauss and Glucksberg 1969), our stimuli allowed us to quantify informativeness of referring expressions directly by counting up the mentions of attributes. If children are unable to produce informative, unambiguous referential expressions under these circumstances, then this would suggest that their inferior performance in transmitting and negotiating meaningful signals in Experiments 1 and 2 was not just due to lack of familiarity with the signalling domain but a reflection of their more general pragmatic limitations that impair communicative expressivity.
4.1 Method
4.1.1 Participants
Thirty monolingual children with English as native language (13 boys) aged between 4; 0 and 5; 1 years (mean age 4; 5 years) were tested in a nursery. Note that the age was 1–2 years below that of the participants in Experiments 1 and 2. This was a pragmatic decision owed to the fact that it was only possible to recruit children with their mothers in a nursery but not in a school setting, and the implications for the comparison with Experiments 1 and 2 will be discussed below. Ten children were paired with their mother; the other children were paired with each other based on play preferences reported by nursery staff. Written parental consent was obtained for all children.
4.1.2 Materials
In order to present children with a readily nameable object for which attributes would then have to be specified in the children’s native language, we used stars as referents rather than the unfamiliar objects from Experiments 1 and 2, but preserved the size of the meaning space and the number of meaning dimensions. We created four identical sets of laminated cards sized 5 × 8 cm depicting five-pointed stars on white background. Within each set, stars varied on the dimensions of size (big vs. small), colour (red vs. blue), and shape (‘spiky’ vs. ‘fat’, depending on whether the angles of the points were acute or obtuse), resulting in eight different stars per set.
4.1.3 Procedure
Participants were informed that they would play four rounds of a game that required them to instruct each other to find specific cards. The number of rounds was reduced to accommodate the fact that children were slightly younger than in Experiment 2. In the child–adult dyads, the child was always given the role of Director (i.e. the one to describe the cards) for the first half of the interaction. In the child–child dyads, roles were assigned at random. In all dyads, roles were reversed in the second half of each round.
Because performance in referential communication tasks depends not only on the ability to appreciate the interlocutor’s point of view, but also on task demands associated with processing the meaning dimensions that may distinguish referents (Bishop and Adams 1991), we thought it important to make sure that participants attended to the relevant identifying features of the stars. The experimenter therefore first presented each participant with minimal pairs of stars differing only on one dimension, accompanied by questions about the three critical dimensions (e.g. ‘Show me the big/small one’, etc.). Both adults and children were successful at selecting the correct stars under these conditions. Next, both participants were seated at a table at opposite sides of a barrier, and were given two sets of cards each, placed face up on the table in no particular order. The experimenter then selected four of the Director’s cards according to a pre-determined pseudo-randomized order such that all four cards were always different, and placed them in a row in front of the remaining twelve cards. The rationale behind having participants select from two, rather than just one, set of cards was to discourage identification of cards by elimination (i.e. to prevent participants from realizing that if the big, red, spiky star had already been selected, the only other big red star would have to be the fat one, rendering the shape attribute over-informative). Using two sets ensured that all three attributes were always required to be informative (i.e. even if one big, red, spiky star had already been mentioned, there was still another one).
The Director was then asked to describe the four cards in the order they were laid out so that the Matcher would be able to find the described targets in their set of cards. The Matcher was asked to identify the cards based on the Director’s description and to arrange them in a row. No restrictions were imposed on the amount and type of communication. If children were reluctant to provide verbal descriptions, then one experimenter, seated behind the Director, would gently encourage them to do so with prompts like ‘Tell Mummy/X what the star is like’. After the four cards had been described and identified by the Matcher, the barrier was lifted to enable the Director and Matcher to see whether the selected cards matched, and an experimenter to take a photograph of the cards. All children received a yellow smiley sticker for each correctly matched card. The barrier was then replaced, and the cards were returned to the overall pool, before the roles of Director and Matcher were reversed. Next, one experimenter helped the Director to select four different cards, which again were placed in a row in front of the other cards, before the game continued in the same way as before the role reversal. The subsequent check of the matched cards concluded one round of the game. Participants then completed the remaining three other rounds of the game so that each participant served as Director four times.
4.1.4 Coding
Audio recordings were transcribed and two coders independently coded Directors’ mentions of the three relevant features. Discrepancies arose only in 2.6% of cases and were resolved by jointly re-coding the utterances. To establish informativeness of the Director’s utterances, we coded, for each star, whether Directors mentioned each of the features (colour, shape, and size) on their first utterance that was produced without any prior communication from the Matcher, as a measure of informativeness of Directors’ spontaneous expressions before receiving any feedback or clarification requests. We also coded the number of features that were mentioned over the course of an entire exchange pertaining to one card. We did not code whether the Matcher selected the correct card because accuracy is not a suitable measure of referential efficiency due to differences in comprehension ability between adults and children. Because the interaction was unconstrained, the information provided by the Director could be distributed over a number of conversational exchanges that the dyad engaged in until the Matcher selected a star. We therefore also coded the number of turns the Director took and whether utterances produced on those turns were volunteered by the Director, i.e. produced without any prompting or clarification requests from the Matcher. This measure enabled us to determine to what extent children provided information on their own accord without feedback from their addressee.
4.2 Results
Our analyses had to take into account that performance was dependent on role position: Participants acting as Directors second could produce more informative expressions because they may have gained prior communicative experience when performing the role of Matcher. Because the adults always acted as Directors second, a comparison of this role position would thus entail comparing performance between adults and children which would reveal trivial results given the adults’ undoubtedly superior performance in the task. We therefore only analysed the data for the children who acted as Directors first, interacting either with a peer or with their mother. We analysed the following dependent variables, depicted in Fig. 4:
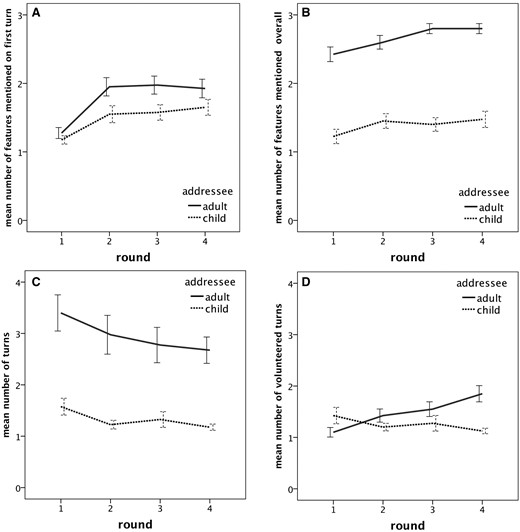
Mean number of features per referent (out of three) mentioned on first turn (A) and during the entire conversational episode (B), mean number of turns taken per referent (C) and mean number of volunteered turns per referent (D) for children addressing either a peer or an adult (their mother) in Experiment 3 error bars represent ±1 S.E.M aggregated by participants.
(a) Informativeness of the first referring expression indicates how much information children produced on their very first utterance on their own accord before the addressee provided any feedback. Because all stars were present twice in the entire set (see Section 4.1.3), Directors always had to mention all three attributes on every trial, i.e. describe a star as ‘big, red, and spiky’. Informativeness was therefore quantified as number of mentioned modifiers, i.e. referent features (out of three).
(b) Informativeness of the entire communicative episode. The number of features produced over the course of an entire communicative episode does not just indicate the child’s referential competence, but also depends on the feedback from the Matcher. It is therefore a measure of the communicative efficiency that children can achieve as a part of a dyad, and is instructive about the communicative strategies that children adopt in response to Matcher feedback.
(c) Number of turns within a communicative episode pertaining to a single referent is a measure of the overall amount of communication that took place.
(d) Number of volunteered turns indicates how many turns children took without prompting or clarification requests from their interlocutor. After the children had provided their initial descriptions, subsequent turns could have been either volunteered if the addressee did not request further information, or could have been prompted by specific (e.g. ‘What colour is the star?’) or general (e.g. ‘Tell me more!’) clarification requests. The number of unprompted (volunteered) turns is a measure for children’s attempts to provide information spontaneously, and how it changes over the course of interaction.
We performed GCAs using linear mixed-effect models with Addressee (child vs. adult) and Round (1–4) as centred fixed effects and crossed random effects of participants and items (i.e. the eight star types). We used maximal random effect structure as permitted by the data (see Supplementary Materials at https://osf.io/rqpd5/).9 We also fitted models with a fixed effect of Round to the data from each group separately when there was an interaction between Addressee and Round.
The results, provided in Table 3, showed that at the outset of the interaction, 1.2 out of 3 features produced by children interacting with a peer were not significantly different from the 1.3 features produced by children interacting with an adult, and there was no significant increase over the course of the interaction. However, there was a dramatic difference in how much information children were able to provide as a result of the interaction: at the end of a communicative episode, children interacting with a peer showed no improvement mentioning on average still only 1.4 features, compared with the dramatic improvement resulting on average of 2.7 features provided by children interacting with adults. This difference was due to feedback and clarification requests from the adult as indicated by the significantly larger average number of 3.0 turns taken in child–adult dyads, compared with only 1.3 turns in child–child dyads. The analysis also showed that the number of volunteered turns increased only in the children who interacted with adults, suggesting that these children were learning from the interaction with the adult to provide more information on their own accord.
Coefficients for intercepts and fixed effects in the linear mixed-effect models for all dependent variables in Experiment 3
| Dependent variable . | . | Intercept . | Addressee . | Round . | Addressee × Round . |
|---|---|---|---|---|---|
| Model: lmer (DV ∼ Addressee * Round + (1 + Round | Participant) + (1 + Addressee * Round | Item) | |||||
| # features first utterance | β | 1.66 | −0.15 | 0.15 | −0.02 |
| t | 14.84*** | −1.39 | 2.03 | −0.35 | |
| # features overall | β | 2.02 | −0.64 | 0.12 | −0.04 |
| t | 19.76*** | −6.22*** | 2.73* | −0.92 | |
| # turns | β | 2.13 | −0.82 | −0.19 | 0.07 |
| t | 8.26*** | −3.17** | −2.23 | 0.85 | |
| # volunteered turns | β | 1.36 | −0.12 | 0.09 | −0.18 |
| t | 16.35*** | −1.42 | 1.36 | −2.52* | |
| Child–adult | β | 1.48 | 0.27 | ||
| t | 11.39*** | 2.50* | |||
| Child–child | β | 1.25 | −0.08 | ||
| t | 11.38*** | −0.10 | |||
| Dependent variable . | . | Intercept . | Addressee . | Round . | Addressee × Round . |
|---|---|---|---|---|---|
| Model: lmer (DV ∼ Addressee * Round + (1 + Round | Participant) + (1 + Addressee * Round | Item) | |||||
| # features first utterance | β | 1.66 | −0.15 | 0.15 | −0.02 |
| t | 14.84*** | −1.39 | 2.03 | −0.35 | |
| # features overall | β | 2.02 | −0.64 | 0.12 | −0.04 |
| t | 19.76*** | −6.22*** | 2.73* | −0.92 | |
| # turns | β | 2.13 | −0.82 | −0.19 | 0.07 |
| t | 8.26*** | −3.17** | −2.23 | 0.85 | |
| # volunteered turns | β | 1.36 | −0.12 | 0.09 | −0.18 |
| t | 16.35*** | −1.42 | 1.36 | −2.52* | |
| Child–adult | β | 1.48 | 0.27 | ||
| t | 11.39*** | 2.50* | |||
| Child–child | β | 1.25 | −0.08 | ||
| t | 11.38*** | −0.10 | |||
P < 0.001,
P < 0.01,
P < 0.05.
Coefficients for intercepts and fixed effects in the linear mixed-effect models for all dependent variables in Experiment 3
| Dependent variable . | . | Intercept . | Addressee . | Round . | Addressee × Round . |
|---|---|---|---|---|---|
| Model: lmer (DV ∼ Addressee * Round + (1 + Round | Participant) + (1 + Addressee * Round | Item) | |||||
| # features first utterance | β | 1.66 | −0.15 | 0.15 | −0.02 |
| t | 14.84*** | −1.39 | 2.03 | −0.35 | |
| # features overall | β | 2.02 | −0.64 | 0.12 | −0.04 |
| t | 19.76*** | −6.22*** | 2.73* | −0.92 | |
| # turns | β | 2.13 | −0.82 | −0.19 | 0.07 |
| t | 8.26*** | −3.17** | −2.23 | 0.85 | |
| # volunteered turns | β | 1.36 | −0.12 | 0.09 | −0.18 |
| t | 16.35*** | −1.42 | 1.36 | −2.52* | |
| Child–adult | β | 1.48 | 0.27 | ||
| t | 11.39*** | 2.50* | |||
| Child–child | β | 1.25 | −0.08 | ||
| t | 11.38*** | −0.10 | |||
| Dependent variable . | . | Intercept . | Addressee . | Round . | Addressee × Round . |
|---|---|---|---|---|---|
| Model: lmer (DV ∼ Addressee * Round + (1 + Round | Participant) + (1 + Addressee * Round | Item) | |||||
| # features first utterance | β | 1.66 | −0.15 | 0.15 | −0.02 |
| t | 14.84*** | −1.39 | 2.03 | −0.35 | |
| # features overall | β | 2.02 | −0.64 | 0.12 | −0.04 |
| t | 19.76*** | −6.22*** | 2.73* | −0.92 | |
| # turns | β | 2.13 | −0.82 | −0.19 | 0.07 |
| t | 8.26*** | −3.17** | −2.23 | 0.85 | |
| # volunteered turns | β | 1.36 | −0.12 | 0.09 | −0.18 |
| t | 16.35*** | −1.42 | 1.36 | −2.52* | |
| Child–adult | β | 1.48 | 0.27 | ||
| t | 11.39*** | 2.50* | |||
| Child–child | β | 1.25 | −0.08 | ||
| t | 11.38*** | −0.10 | |||
P < 0.001,
P < 0.01,
P < 0.05.
4.3 Discussion
Our final experiment examined informativeness of modifying expressions used to describe a meaning space of the same size and complexity as used in Experiments 1 and 2. The findings showed that 4- to 5-year-old children have extremely limited ability to produce informative and unambiguous referential expressions in peer interaction in accord with previous findings (e.g. Krauss and Glucksberg 1969). Despite the fact that the signalling domain—their native language—was familiar to them, children typically mentioned less than half of the defining features in their first, unprompted utterances. Only children interacting with adults, but not children interacting with peers, ended up supplying the required information as illustrated in (1). Children interacting with peers, on the other hand, produced considerably less informative expressions than were needed to identify the cards. Thus, at this age, children require feedback and scaffolding for communication to be efficient, yet their peers do not provide such feedback: the small amount of turns in the child–child dyads indicates that peer interlocutors did not request the missing information when they found themselves on the receiving end of uninformative referential expressions as illustrated in (2). This shows that in order to develop communicative efficiency, children require scaffolding through clarification requests and feedback that only adults can provide (Matthews et al. 2007). As a result of such scaffolding, children learn to volunteer the required information on their own accord.
1. Child: …
Adult: What colour is it?
Child: Erm—red.
Adult: And is it a big star or a small star?
Child: Erm—a big star.
Adult: And is it a fat one or a skinny one?
Child: A skinny one.
2. Child 1: A skinny one.
Child 2: …
Child 1: (whispers) A skinny one.
Child 2: …
Child 1: Skinny.
Child 2: …
It could be argued that the results of Experiment 3 are not relevant as a potential explanation for the inability to negotiate a novel signalling system because the children tested in this experiment were about 1–3 years younger than the children in Experiments 1 and 2. However, the literature on children’s difficulties with communicating about unfamiliar referents in their native language suggests that development of referential communication is long and protracted, and certainly not concluded until children reach middle childhood (e.g. Garrod and Clark 1993; Krauss and Glucksberg 1969). The findings of Experiment 3 therefore support the notion that it is the lack of pragmatic insight necessary for efficient communication, rather than the lack of familiarity with novel signalling domains, which prevented children from learning and creating novel communication systems in Experiments 1 and 2.
4.4 General discussion
In this study, we found that iterated learning of an entirely novel signalling system in Experiment 1 did not readily lead to emergence of iconicity or structure, at least not under limited learning conditions and without a strong pressure to communicate. As a result, adults outperformed children in terms of learning and transmitting the system faithfully based mainly on their more mature cognitive abilities, which enabled them to memorize more of the unfamiliar signals. However, when the novel signals were used for referential communication in Experiment 2, adults, but not children, developed shared systems by exploiting iconic mappings between referent size and signal length, as well as by inducing signal structure and, to some extent, compositional structure. One possible reason for why compositional structure was not as pronounced in the adults to reliably exceed chance levels is that lack of familiarity with the signalling system may have prevented adults from applying their meta-linguistic knowledge of linguistic structure. This invites some caution with respect to findings based on language-like stimuli reported elsewhere, which may bias participants towards the use of meta-linguistic knowledge. It is also possible that binary auditory sequences may just be very difficult to learn, not the least because of their fading nature. However, the crucial finding is that under communicative pressure, adults were able to align their productions and to negotiate a system based on iconicity whereas children were not. Experiment 3 found that even when given the opportunity to use their native language, children were unable to produce informative expressions that would enable interlocutors to identify the intended meanings. This points to substantial pragmatic limitations in children as one of the possible causes for their inability to negotiate meaning and to produce motivated signs, be it iconic or compositional ones. Children only attained communicative efficiency when adult expert language users provided scaffolding through feedback and clarification questions to elicit missing information. Although these findings clearly call for further research that explores factors like length of training or frequency of signal use, they so far provide no indication that children are more likely than adults to introduce the kind of innovations that could drive the emergence of structure during cultural transmission and use of language. Below, we provide further suggestions for what may prevent children from creating and transmitting novel communication systems, what this implies for the role of children in language change, and what conditions may allow children to overcome those limitations.
4.5 The nature of children’s limitations in creating and transmitting novel signalling systems
When learning and using a novel signalling system, children did not compensate for their lower cognitive capacity by imposing structure more readily than the adults. Thus, our results do not suggest that ‘less is more’ (Newport 1990) with respect to emergence of structure during language transmission. Instead, they are in line with the evidence that larger processing capacity benefits language processing and language learning in general (e.g. Braine et al. 1990; Brooks et al.1993; Daneman and Merikle 1996; Snow and Hoefnagel 1978). We suggest several pathways by which more mature cognitive abilities may actually benefit creation and transmission of novel signalling systems.
One possibility is that adults have a better insight into the pragmatic requirement that interlocutors need to be able to map signals onto meanings, which is likely to drive what Lister and Fay (2017) termed the creation of ‘motivated signs’. This insight may be linked to mentalizing abilities that arise from a more mature Theory of Mind. In contrast, children may not yet understand that motivated signs are needed in the first place, by assuming that meaning is an intrinsic property of a signal rather than a negotiated convention.
Another possibility is that children appreciate the need for motivated signs but have insufficient means to create them—either because they lack more sophisticated aspects of Theory of Mind necessary to predict which signal-meaning mappings are transparent enough for an addressee to recover, or because they have insufficient processing capacity to monitor whether their own and their addressee’s signals express the newly established meanings in a consistent way. Thus, to create motivated iconic signal-meaning mappings, interlocutors need to systematically scan the signalling domain for iconic affordances, and monitor the communicative efficiency of the selected iconic mappings. Although children are sensitive to statistical regularities in the linguistic form from a very early age, linking novel forms to meanings is cognitively very demanding (Naigles 2002), even if the signalling domain affords considerable potential for iconic mappings. However, while the Iconic Bootstrapping Hypothesis suggests that children benefit from iconicity in early word learning (Imai and Kita 2014), this does not necessarily imply that children are also more predisposed towards using iconicity in innovative ways in novel signalling systems, an ability that may require considerable processing capacity, especially when it relies on careful appraisal of the structure of the meaning space—a demand that may have limited ecological validity in heavily contextualized day-to-day communicative interactions (Bishop and Adams 1991).
Finally, children may be less adept at aligning their own signals with those of their interlocutor, as our findings suggest. Lister and Fay (2017) propose that behavioural alignment drives cognitive alignment such that when interlocutors copy signals produced by their communication partners, this will gradually lead to the establishment of shared cognitive representations. However, behavioural alignment requires monitoring of the match between one’s own and the interlocutor’s productions, to compute an error term in cases of mismatch, and to adjust subsequent productions to minimize this error term. Given the evidence for children’s limitations in monitoring the informativeness of their own and their interlocutor’s expressions (Rabagliati and Robertson 2017), it is not surprising that behavioural alignment seems to be difficult for children.
4.6 The role of children’s processing limitations in language change
The finding that motivated and structured signal-meaning mappings did not emerge in 4- to 7-year-old children challenges the idea that processing limitations make children important agents of language evolution and language change (Bickerton 1981; Dale and Lupyan 2012; Hudson Kam and Newport 2005,, 2009; Lumsden 1999). One domain in which the role for children has been demonstrated empirically is the spontaneous emergence of grammatical structure in the home sign systems of deaf children (Goldin-Meadow 2003), and the observation that younger cohorts of deaf children were responsible for introducing structure into the newly emerging Nicaraguan Sign Language (Senghas and Coppola 2001; Senghas et al. 2004). These younger cohorts tended to grammaticize holistic gestures, either by linearizing simultaneously occurring elements of gestural signs, or by restricting the meaning of certain aspects of the signs, such as using spatial location to denote a specific type of co-reference. How can these observations be reconciled with children’s inability to induce structure and create motivated signs in the present experiments?
One important difference between our findings and the findings from Nicaraguan Sign Language is that the signalling domain of gesture was already familiar to the sign-learning children, as they all had used home sign systems before encountering sign language for the first time. Pre-existing gestural representations may have supported decomposition of gestural input. If such easily decomposable signals are then transmitted from cohort to cohort of learners, just like artificial languages are transmitted in iterated learning studies (e.g. Kirby et al. 2008, 2015), then structure is likely to emerge. Consequently, emergence of structure in subsequent cohorts cannot be taken as evidence that it was the children’s age and the associated limited processing capacity, rather than their position in the transmission chain, which is the driving factor.
Our findings are more in line with sociophonetic observations and associated models of diachronic change, which suggest that linguistic innovations are introduced and sustained by cognitively more mature agents, specifically female adolescents and young adults (Labov 2001). Children, on the other hand, at least up to the age of 5 years, display distributions of form variants that are similar to their caregivers’, and only start to engage in vernacular reorganization later in childhood (Kerswill and Williams 2000), reaching peak usage of novel variants by approximately at the age of 17 years (Cedergren 1988). Such a trajectory of change is not confined to phonetic changes, but extends to morphological, syntactic, and discourse-pragmatic features (Tagliamonte and D'Arcy 2009) as well. On this account, young children are conservative learners unlikely to introduce or take up innovation beyond what it is they are able to retain from the input (Tomasello 1992). Moreover, children’s alleged propensity to regularize does not necessarily lead to language change either: agent-based simulations of factors that govern the spread of linguistic innovations within social networks also demonstrate a very limited role of regularizing, as opposed to probability matching, biases (Pierrehumbert et al. 2014). These simulations show that in the face of inconsistent input where traditional forms and innovations coexist, the latter are only able to spread through the population if agents adopt decision rules that are closer to the probability matching, rather than the dichotomizing end of the continuum of decision-making biases. Thus, some of the evidence points in the direction of adults as the innovators responsible for emergence and change of linguistic structure.
4.7 Overcoming children’s limitations
Experiment 3 demonstrated that children’s expressivity improved dramatically through scaffolding provided by expert language users (Matthews et al. 2007). This points to an important caveat in studies exploring iterated language learning and referential communication: Inter-generational transmission of language does not occur between adults, who are expert language users, as simulated in previous studies (e.g. Kirby et al. 2008, 2015), nor does it occur between children, who are cognitively constrained novices, as examined in this study. Instead, language is transmitted from adults to children, and a vast body of research on the nature of child-directed speech (for reviews, see Golinkoff et al. 2015; Saint-Georges et al. 2013; Soderstrom 2007) has documented that adults adjust their communication to accommodate children’s cognitive and linguistic limitations although the universality of this adjustment is debated (e.g. Cristia et al. 2017; Lieven 1994; Schieffelin and Ochs 1983). Moreover, not only do adults pre-select the input provided to children in a manner that may aid learning (Eaves et al. 2016; Ferguson 1964; Fernald et al. 1989) but also, as Matthews et al. (2007) and Experiment 3 of this study suggest, they provide feedback that teaches children how to monitor the communicative efficiency of their productions.
Recently, the role of accommodation to novices in the cultural transmission of language has started to receive some attention in empirical (Atkinson et al. 2018) and computational (Frank and Smith 2018) research. This work shows that adult experts modify their language for the benefit of adult novices, and, thus, constitutes a simulation of foreigner-directed rather than child-directed speech. The findings presented here suggest that input enhancement and scaffolding of communication strategies for child learners may be an important factor that complements the constraints imposed by the nature of the signalling domain, the cognitive capacity of the learner, and the social environment in which communication takes place. Given the growing interest in how teaching as a universal behaviour (Kline 2015) may have shaped cultural evolution in general (Csibra and Gergely 2009), future research should attempt to integrate insights from the vast body of research on the role of child-directed communication in language development with those from research on the creation and transmission of novel signalling systems to add another interesting facet to our understanding of how human language might have evolved.
Supplementary data
Supplementary Materials can be found online on the Open Science Framework https://osf.io/rqpd5/.
Footnotes
It has been argued that imposing a transmission bottleneck, i.e. presenting learners with only a sub-set of the signal-meaning mappings during learning (Smith et al. 2003), can be taken as a simulation of the role of child learners in this process (Vogt 2005). The underlying rationale is that children have to induce structure based on much more limited input than adults. Yet, poverty of the stimulus is intrinsic to any language learning situation, regardless of age. Thus, merely imposing a transmission bottleneck is insufficient to study the constraints imposed by child learners.
Note that this operationalization of signal structure is different from combinatorial structure as described in the Introduction, i.e. from the extent to which the signals within an entire signalling system (i.e. a language) consist of re-combinations of smaller sub-components (e.g. doubles, triplets, quadruplets), which can be taken as a loose analogy to phonemes in natural languages. For other novel signalling systems, combinatorial structure has been estimated either through measures of entropy (Verhoef, 2012; Verhoef et al., 2014), through a Form Recombination Index which captures how often a sub-component of a signal is re-used in other signals of that language (Roberts et al., 2015), by applying compression algorithms (Cornish et al., 2013) or by computing Associative Chunk Strength (Cornish et al., 2017). The first two methods rely on individual components being easily discriminable, e.g. through periods of silence in auditory signals or through interruptions in continuous lines. This is not possible in our case: Even though binary auditory sequences can be decomposed into smaller units like doubles or triplets, we are unable to determine how an individual learner might have decomposed a given sequence, e.g. whether the sequence 000111 (where 0 represents the high and 1 the low tone) was decomposed as 00-01-11 or 000-111. The third measure, size of the entire language after compression, is suitable to compare amount of structure across languages with identical numbers of signals but is heavily influenced by degeneration such that languages with fewer signals will be more compressible thereby obscuring degree of combinatoriality. Finally, Associative Chunk Strength is uninformative given the limited number of possible bigrams contained in binary sequences. So even though inverse algorithmic complexity is not a measure of combinatorial structure for entire languages because we cannot tell to what extent the sub-components or chunks from any given signal were also used in the other signals, it still provides a proxy for how efficiently learners were able to chunk individual signals.
Consent conditions did not allow us to gain access to the records of the children to ascertain their exact ages, but all children were within the normal age range expected for their grade level.
Because primary grade level was controlled within chains, we were also able to explore developmental trajectories within the children by performing separate GCAs with the fixed effects of grade level (first vs. second vs. third) and Generation and their interactions for the children only, which did not yield any significant effects (see Supplementary Materials at https://osf.io/rqpd5/).
Following Beckner et al. (2017), we also explored the shape of the trajectory of generational change by including a quadratic term of Generation to capture potential non-linearity, but only when the effect of Generation was significant. For the number of unique patterns, the model AgeGroup + Generation + Generation2 + AgeGroup: Generation + AgeGroup: Generation2 + (1 + Generation + Generation2| Chain) yielded a better overall fit than the linear model in Table 1, χ2 = 17.78, df = 5, P = 0.003, and confirmed the declining linear trend over Generations, β = −0.35, t = 2.72, P = 0.02. However, neither the quadratic term nor the interactions with Age Group showed significant effects based on t-tests, all P’s > 0.11; it therefore seems warranted not to make strong claims about whether the declining number of unique patterns levelled off in later generations or not. For the length-normalized Levenshtein edit distance, we fitted the model AgeGroup + Generation + Generation2 + AgeGroup: Generation + AgeGroup: Generation2 + (1 + Generation + Generation2|Chain) + (1 + AgeGroup + Generation + Generation2 + AgeGroup: Generation + AgGroupe: Generation2|Referent) which failed to converge. Uncorrelating the intercept from the slopes and slope interactions by Referents showed an improved model fit to the model with the linear term of Generation (see Table 1), χ2 = 32.71, df = 1, P < 0.001, and yielded main effects of the linear, β = −0.04, t = −4.38, P = 0.001, and the quadratic, β = 0.03, t = 2.82, P = 0.018, term of Generation, while the effect of Age Group was now no longer significant, P = 0.09. This suggests that the decline in edit distance levelled out in both age groups, thereby presumably somewhat reducing the difference between children and adults as both groups reached a similar asymptote in learnability.
To estimate the extent to which signal structure represented individual semantic dimensions, we analysed within-category measures of structure. For all pairs of signals and their associated meanings, we computed signal similarity based on Levenshtein edit distance and Pearson product-moment correlations with differences in just one dimension of interest—size, shape, or brightness—using the Mantel test (Mantel 1967) as described for overall compositional structure. There were no effects of Generation or Age Group on these within-category measures of structure (see Appendix A1).
As in Experiment 1, we also tested whether any of the individual meaning dimensions were given preference when linking individual meaning dimensions to signals. This was again computed over correlations between similarity in the binary sequences and similarity in referent size, shape, and brightness separately using the Mantel test (Mantel 1967). These analyses showed an effect of Age Group on shape-based structure, indicating that there was more structure associated with the dimension of shape in the languages produced by adults, as well as an overall increase in size-based structure, even though none of the dimension-specific signal-meaning correlations exceeded the level of chance (see Appendix A1).
As in Experiment 1, we only included a quadratic term of Round to examine nonlinear trends over the five rounds when the linear effect of Round was significant. In cases where more complex models containing the quadratic term did not converge, we eliminated slope interactions by items until the models converged. The dependent variables that showed significant effects of Round were overall compositional structure, size-based structure, length-size correlation, and edit distance from own previous pattern. Adding the quadratic term of Round as well as its interaction with Age Group provided a significantly better fit of the model to the data only in the case of size-based compositional structure, χ2 = 10.97, df = 4, P = 0.026 even though the quadratic effect of Round did not reach significance, P = 0.150.
In this experiment, we only modelled linear effects of Round as having only four rounds of interaction that made the inclusion of a quadratic term in analogy to the previous experiments superfluous.
Acknowledgement
We gratefully acknowledge funding by the Max-Planck-Institute of Psycholinguistics in Nijmegen for a research visit to the Language and Cognition Group, which supported the writing of this paper, and helpful discussions with Limor Raviv, Mark Dingemanse, Monica Tamariz, Seán Roberts and Stephen Levinson. We also wish to express our gratitude to the Croft Nursery, Arduthie Primary School and Mill O’Forest Primary School, Stonehaven, for their support in running the experiments.
References
Appendix 1: Analysis of category-specific measures of structure based on the individual dimensions of shape, size, and brightness
Table 1.1: Coefficients for intercepts and fixed effects in the linear mixed-effect models for within-category compositional structure in Experiment 1
| DV . | Intercept . | Age Group . | Generation . | Age Group × Generation . |
|---|---|---|---|---|
| Model: lmer (DV ∼ AgeGroup * Generation + (1 + Generation | Chain)) | ||||
| Compositional structure: | ||||
| Shape | ||||
| β | 0.01 | 0.05 | −0.05 | −0.05 |
| t | 0.11 | 0.63 | −0.45 | −0.39 |
| Size | ||||
| β | 0.21 | 0.11 | 0.01 | 0.04 |
| t | 2.30 | 1.27 | 0.07 | 0.50 |
| Brightness | ||||
| β | 0.08 | −0.04 | −0.02 | −0.07 |
| t | 1.14 | 0.52 | 0.24 | −1.00 |
| DV . | Intercept . | Age Group . | Generation . | Age Group × Generation . |
|---|---|---|---|---|
| Model: lmer (DV ∼ AgeGroup * Generation + (1 + Generation | Chain)) | ||||
| Compositional structure: | ||||
| Shape | ||||
| β | 0.01 | 0.05 | −0.05 | −0.05 |
| t | 0.11 | 0.63 | −0.45 | −0.39 |
| Size | ||||
| β | 0.21 | 0.11 | 0.01 | 0.04 |
| t | 2.30 | 1.27 | 0.07 | 0.50 |
| Brightness | ||||
| β | 0.08 | −0.04 | −0.02 | −0.07 |
| t | 1.14 | 0.52 | 0.24 | −1.00 |
P < 0.001,
P < 0.01,
P < 0.05.
Table 1.1: Coefficients for intercepts and fixed effects in the linear mixed-effect models for within-category compositional structure in Experiment 1
| DV . | Intercept . | Age Group . | Generation . | Age Group × Generation . |
|---|---|---|---|---|
| Model: lmer (DV ∼ AgeGroup * Generation + (1 + Generation | Chain)) | ||||
| Compositional structure: | ||||
| Shape | ||||
| β | 0.01 | 0.05 | −0.05 | −0.05 |
| t | 0.11 | 0.63 | −0.45 | −0.39 |
| Size | ||||
| β | 0.21 | 0.11 | 0.01 | 0.04 |
| t | 2.30 | 1.27 | 0.07 | 0.50 |
| Brightness | ||||
| β | 0.08 | −0.04 | −0.02 | −0.07 |
| t | 1.14 | 0.52 | 0.24 | −1.00 |
| DV . | Intercept . | Age Group . | Generation . | Age Group × Generation . |
|---|---|---|---|---|
| Model: lmer (DV ∼ AgeGroup * Generation + (1 + Generation | Chain)) | ||||
| Compositional structure: | ||||
| Shape | ||||
| β | 0.01 | 0.05 | −0.05 | −0.05 |
| t | 0.11 | 0.63 | −0.45 | −0.39 |
| Size | ||||
| β | 0.21 | 0.11 | 0.01 | 0.04 |
| t | 2.30 | 1.27 | 0.07 | 0.50 |
| Brightness | ||||
| β | 0.08 | −0.04 | −0.02 | −0.07 |
| t | 1.14 | 0.52 | 0.24 | −1.00 |
P < 0.001,
P < 0.01,
P < 0.05.
Coefficients for intercepts and fixed effects in the linear mixed-effect models for within-category compositional structure in Experiment 2
| DV . | Inter-cept . | Card Pos . | Age Group . | Round . | Card Pos × Ag Group . | Card Pos × Round . | Age Group ×Round . | 3-way . |
|---|---|---|---|---|---|---|---|---|
| Model: (DV ∼ CardPosition * AgeGroup * Round + (1+Round|Dyad/Participant)) | ||||||||
| Compositional structure: | ||||||||
| Shape | ||||||||
| β | 0.13 | −0.14 | −0.39 | 0.02 | 0.08 | −0.06 | 0.12 | 0.02 |
| t | 1.11 | −1.15 | −3.29** | 0.17 | 0.69 | −0.60 | 1.34 | 0.16 |
| Size | ||||||||
| β | 0.26 | −0.05 | 0.19 | 0.21 | −0.01 | −0.12 | 0.02 | −0.04 |
| t | 2.63* | 0.52 | −1.95 | 2.59* | −0.10 | −1.41 | 0.21 | −0.47 |
| Brightness | ||||||||
| β | −0.01 | −0.08 | 0.03 | 0.03 | 0.09 | −0.08 | 0.03 | 0.14 |
| t | −0.08 | −0.72 | 0.29 | 0.32 | 0.80 | −0.81 | 0.28 | 1.40 |
| DV . | Inter-cept . | Card Pos . | Age Group . | Round . | Card Pos × Ag Group . | Card Pos × Round . | Age Group ×Round . | 3-way . |
|---|---|---|---|---|---|---|---|---|
| Model: (DV ∼ CardPosition * AgeGroup * Round + (1+Round|Dyad/Participant)) | ||||||||
| Compositional structure: | ||||||||
| Shape | ||||||||
| β | 0.13 | −0.14 | −0.39 | 0.02 | 0.08 | −0.06 | 0.12 | 0.02 |
| t | 1.11 | −1.15 | −3.29** | 0.17 | 0.69 | −0.60 | 1.34 | 0.16 |
| Size | ||||||||
| β | 0.26 | −0.05 | 0.19 | 0.21 | −0.01 | −0.12 | 0.02 | −0.04 |
| t | 2.63* | 0.52 | −1.95 | 2.59* | −0.10 | −1.41 | 0.21 | −0.47 |
| Brightness | ||||||||
| β | −0.01 | −0.08 | 0.03 | 0.03 | 0.09 | −0.08 | 0.03 | 0.14 |
| t | −0.08 | −0.72 | 0.29 | 0.32 | 0.80 | −0.81 | 0.28 | 1.40 |
P < 0.001,
P < 0.01,
P < 0.05.
Coefficients for intercepts and fixed effects in the linear mixed-effect models for within-category compositional structure in Experiment 2
| DV . | Inter-cept . | Card Pos . | Age Group . | Round . | Card Pos × Ag Group . | Card Pos × Round . | Age Group ×Round . | 3-way . |
|---|---|---|---|---|---|---|---|---|
| Model: (DV ∼ CardPosition * AgeGroup * Round + (1+Round|Dyad/Participant)) | ||||||||
| Compositional structure: | ||||||||
| Shape | ||||||||
| β | 0.13 | −0.14 | −0.39 | 0.02 | 0.08 | −0.06 | 0.12 | 0.02 |
| t | 1.11 | −1.15 | −3.29** | 0.17 | 0.69 | −0.60 | 1.34 | 0.16 |
| Size | ||||||||
| β | 0.26 | −0.05 | 0.19 | 0.21 | −0.01 | −0.12 | 0.02 | −0.04 |
| t | 2.63* | 0.52 | −1.95 | 2.59* | −0.10 | −1.41 | 0.21 | −0.47 |
| Brightness | ||||||||
| β | −0.01 | −0.08 | 0.03 | 0.03 | 0.09 | −0.08 | 0.03 | 0.14 |
| t | −0.08 | −0.72 | 0.29 | 0.32 | 0.80 | −0.81 | 0.28 | 1.40 |
| DV . | Inter-cept . | Card Pos . | Age Group . | Round . | Card Pos × Ag Group . | Card Pos × Round . | Age Group ×Round . | 3-way . |
|---|---|---|---|---|---|---|---|---|
| Model: (DV ∼ CardPosition * AgeGroup * Round + (1+Round|Dyad/Participant)) | ||||||||
| Compositional structure: | ||||||||
| Shape | ||||||||
| β | 0.13 | −0.14 | −0.39 | 0.02 | 0.08 | −0.06 | 0.12 | 0.02 |
| t | 1.11 | −1.15 | −3.29** | 0.17 | 0.69 | −0.60 | 1.34 | 0.16 |
| Size | ||||||||
| β | 0.26 | −0.05 | 0.19 | 0.21 | −0.01 | −0.12 | 0.02 | −0.04 |
| t | 2.63* | 0.52 | −1.95 | 2.59* | −0.10 | −1.41 | 0.21 | −0.47 |
| Brightness | ||||||||
| β | −0.01 | −0.08 | 0.03 | 0.03 | 0.09 | −0.08 | 0.03 | 0.14 |
| t | −0.08 | −0.72 | 0.29 | 0.32 | 0.80 | −0.81 | 0.28 | 1.40 |
P < 0.001,
P < 0.01,
P < 0.05.
Appendix 2: Final generation patterns in Experiment 1 for chains of adults and children with Primary School grade level in parentheses
| Brightness . | Size . | Shape . | Adult chains . | |||||
|---|---|---|---|---|---|---|---|---|
| 1 . | 2 . | 3 . | 4 . | 5 . | 6 . | |||
| Dark | Big | Fluffy | 0001010 | 010101010011 | 1011101 | 101101 | 001010 | 1100110011000 |
| Light | Big | Fluffy | 0010110 | 10101010101100 | 100010 | 00111010 | 01001 | 1100110011000 |
| Dark | Small | Fluffy | 0011010 | 01010101 | 100010 | 0011100011010 | 01001 | 001100111 |
| Light | Small | Fluffy | 0011010 | 010101010011 | 10110 | 11011001 | 0011010 | 0011000 |
| Dark | Big | Spiky | 0011010 | 101010101100 | 101101 | 00111000110 | 011010 | 001100110011000 |
| Light | Big | Spiky | 001010 | 101010100 | 1011101 | 000110101 | 0011010 | 1100110011000 |
| Dark | Small | Spiky | 0010110 | 10101010 | 101001 | 00111000110 | 001011 | 0011001100111 |
| Light | Small | Spiky | 0010101 | 010101010011 | 101101 | 00110101 | 011010 | 0011000 |
Child chains | ||||||||
| 1 (P1) | 2 (P1) | 3 (P2) | 4 (P2) | 5 (P3) | 6 (P3) | |||
| Dark | Big | Fluffy | 001100 | 1010 | 1111000010101 | 0001111 | 1100101 | 0101001 |
| Light | Big | Fluffy | 101100 | 1010 | 01010101 | 00011111 | 0010101 | 10010 |
| Dark | Small | Fluffy | 0011000 | 0101 | 0101100 | 00001111 | 10101 | 01001 |
| Light | Small | Fluffy | 0010001 | 0101 | 110010 | 000011111 | 10010 | 10101 |
| Dark | Big | Spiky | 01001 | 0101 | 1010011 | 000011111 | 101101 | 100101 |
| Light | Big | Spiky | 001100 | 0101 | 0101000111010111 | 000111 | 10010110 | 10101 |
| Dark | Small | Spiky | 1010100 | 1010 | 010110011001010011 | 00001111 | 10110 | 101001 |
| Light | Small | Spiky | 001001 | 0101 | 0101100 | 000111 | 10110 | 101001 |
| Brightness . | Size . | Shape . | Adult chains . | |||||
|---|---|---|---|---|---|---|---|---|
| 1 . | 2 . | 3 . | 4 . | 5 . | 6 . | |||
| Dark | Big | Fluffy | 0001010 | 010101010011 | 1011101 | 101101 | 001010 | 1100110011000 |
| Light | Big | Fluffy | 0010110 | 10101010101100 | 100010 | 00111010 | 01001 | 1100110011000 |
| Dark | Small | Fluffy | 0011010 | 01010101 | 100010 | 0011100011010 | 01001 | 001100111 |
| Light | Small | Fluffy | 0011010 | 010101010011 | 10110 | 11011001 | 0011010 | 0011000 |
| Dark | Big | Spiky | 0011010 | 101010101100 | 101101 | 00111000110 | 011010 | 001100110011000 |
| Light | Big | Spiky | 001010 | 101010100 | 1011101 | 000110101 | 0011010 | 1100110011000 |
| Dark | Small | Spiky | 0010110 | 10101010 | 101001 | 00111000110 | 001011 | 0011001100111 |
| Light | Small | Spiky | 0010101 | 010101010011 | 101101 | 00110101 | 011010 | 0011000 |
Child chains | ||||||||
| 1 (P1) | 2 (P1) | 3 (P2) | 4 (P2) | 5 (P3) | 6 (P3) | |||
| Dark | Big | Fluffy | 001100 | 1010 | 1111000010101 | 0001111 | 1100101 | 0101001 |
| Light | Big | Fluffy | 101100 | 1010 | 01010101 | 00011111 | 0010101 | 10010 |
| Dark | Small | Fluffy | 0011000 | 0101 | 0101100 | 00001111 | 10101 | 01001 |
| Light | Small | Fluffy | 0010001 | 0101 | 110010 | 000011111 | 10010 | 10101 |
| Dark | Big | Spiky | 01001 | 0101 | 1010011 | 000011111 | 101101 | 100101 |
| Light | Big | Spiky | 001100 | 0101 | 0101000111010111 | 000111 | 10010110 | 10101 |
| Dark | Small | Spiky | 1010100 | 1010 | 010110011001010011 | 00001111 | 10110 | 101001 |
| Light | Small | Spiky | 001001 | 0101 | 0101100 | 000111 | 10110 | 101001 |
0: high tone; 1: low tone.
| Brightness . | Size . | Shape . | Adult chains . | |||||
|---|---|---|---|---|---|---|---|---|
| 1 . | 2 . | 3 . | 4 . | 5 . | 6 . | |||
| Dark | Big | Fluffy | 0001010 | 010101010011 | 1011101 | 101101 | 001010 | 1100110011000 |
| Light | Big | Fluffy | 0010110 | 10101010101100 | 100010 | 00111010 | 01001 | 1100110011000 |
| Dark | Small | Fluffy | 0011010 | 01010101 | 100010 | 0011100011010 | 01001 | 001100111 |
| Light | Small | Fluffy | 0011010 | 010101010011 | 10110 | 11011001 | 0011010 | 0011000 |
| Dark | Big | Spiky | 0011010 | 101010101100 | 101101 | 00111000110 | 011010 | 001100110011000 |
| Light | Big | Spiky | 001010 | 101010100 | 1011101 | 000110101 | 0011010 | 1100110011000 |
| Dark | Small | Spiky | 0010110 | 10101010 | 101001 | 00111000110 | 001011 | 0011001100111 |
| Light | Small | Spiky | 0010101 | 010101010011 | 101101 | 00110101 | 011010 | 0011000 |
Child chains | ||||||||
| 1 (P1) | 2 (P1) | 3 (P2) | 4 (P2) | 5 (P3) | 6 (P3) | |||
| Dark | Big | Fluffy | 001100 | 1010 | 1111000010101 | 0001111 | 1100101 | 0101001 |
| Light | Big | Fluffy | 101100 | 1010 | 01010101 | 00011111 | 0010101 | 10010 |
| Dark | Small | Fluffy | 0011000 | 0101 | 0101100 | 00001111 | 10101 | 01001 |
| Light | Small | Fluffy | 0010001 | 0101 | 110010 | 000011111 | 10010 | 10101 |
| Dark | Big | Spiky | 01001 | 0101 | 1010011 | 000011111 | 101101 | 100101 |
| Light | Big | Spiky | 001100 | 0101 | 0101000111010111 | 000111 | 10010110 | 10101 |
| Dark | Small | Spiky | 1010100 | 1010 | 010110011001010011 | 00001111 | 10110 | 101001 |
| Light | Small | Spiky | 001001 | 0101 | 0101100 | 000111 | 10110 | 101001 |
| Brightness . | Size . | Shape . | Adult chains . | |||||
|---|---|---|---|---|---|---|---|---|
| 1 . | 2 . | 3 . | 4 . | 5 . | 6 . | |||
| Dark | Big | Fluffy | 0001010 | 010101010011 | 1011101 | 101101 | 001010 | 1100110011000 |
| Light | Big | Fluffy | 0010110 | 10101010101100 | 100010 | 00111010 | 01001 | 1100110011000 |
| Dark | Small | Fluffy | 0011010 | 01010101 | 100010 | 0011100011010 | 01001 | 001100111 |
| Light | Small | Fluffy | 0011010 | 010101010011 | 10110 | 11011001 | 0011010 | 0011000 |
| Dark | Big | Spiky | 0011010 | 101010101100 | 101101 | 00111000110 | 011010 | 001100110011000 |
| Light | Big | Spiky | 001010 | 101010100 | 1011101 | 000110101 | 0011010 | 1100110011000 |
| Dark | Small | Spiky | 0010110 | 10101010 | 101001 | 00111000110 | 001011 | 0011001100111 |
| Light | Small | Spiky | 0010101 | 010101010011 | 101101 | 00110101 | 011010 | 0011000 |
Child chains | ||||||||
| 1 (P1) | 2 (P1) | 3 (P2) | 4 (P2) | 5 (P3) | 6 (P3) | |||
| Dark | Big | Fluffy | 001100 | 1010 | 1111000010101 | 0001111 | 1100101 | 0101001 |
| Light | Big | Fluffy | 101100 | 1010 | 01010101 | 00011111 | 0010101 | 10010 |
| Dark | Small | Fluffy | 0011000 | 0101 | 0101100 | 00001111 | 10101 | 01001 |
| Light | Small | Fluffy | 0010001 | 0101 | 110010 | 000011111 | 10010 | 10101 |
| Dark | Big | Spiky | 01001 | 0101 | 1010011 | 000011111 | 101101 | 100101 |
| Light | Big | Spiky | 001100 | 0101 | 0101000111010111 | 000111 | 10010110 | 10101 |
| Dark | Small | Spiky | 1010100 | 1010 | 010110011001010011 | 00001111 | 10110 | 101001 |
| Light | Small | Spiky | 001001 | 0101 | 0101100 | 000111 | 10110 | 101001 |
0: high tone; 1: low tone.
Category-specific compositional structure for shape, size, and brightness over twelve generations of transmission in Experiment 1. Error bars represent ± 1 S.E.M aggregated by participants.
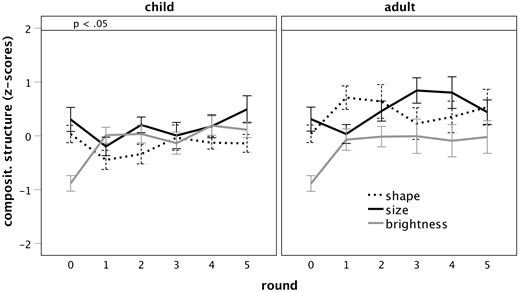
Category-specific compositional structure for shape, size, and brightness over five rounds of interaction in Experiment 2. Error bars represent ± 1 S.E.M aggregated by participants.


