-
PDF
- Split View
-
Views
-
Cite
Cite
Courtney L Fitzpatrick, Michael J Wade, When is Offspring Viability Fitness a Measure of Paternal Fitness and When is it not?, Journal of Heredity, Volume 113, Issue 1, January 2022, Pages 48–53, https://doi.org/10.1093/jhered/esab055
Close - Share Icon Share
Abstract
We use population genetics to model the evolution of a gene with an indirect effect owing to paternal care and with a second pleiotropic, direct effect on offspring viability. We use the model to illustrate how the common empirical practice of considering offspring viability as a component of parent fitness can confound a gene’s direct and indirect fitness effects. We investigate when this confounding results in a distorted picture of overall evolution and when it does not. We find that the practice has no effect on mean fitness, W, but it does have an effect on the dynamics of gene frequency change, ∆q. We also find that, for some regions of parameter space associated with fitness trade-offs, the distortion is not only quantitative but also qualitative, obscuring the direction of gene frequency change. Because it affects the evolutionary dynamics, it also affects the expected amount of genetic variation at mutation-selection balance, an important consideration in molecular evolution. We discuss empirical techniques for separating direct from indirect effects and how field studies measuring the value of male paternal care might be improved by using them.
It is common practice to treat offspring viability as a component of parental fitness in the empirical analysis of field data investigating the evolution of parental rearing strategies (Clutton-Brock 1988; Fitzpatrick et al. 2014). The practice has been recommended for several reasons. For example, Smiseth et al. (2012, p. 11) argue for it because “… parental care has a strong causal effect on offspring fitness,” and because (Clutton-Brock 1988, p. 473) “…differences in offspring survival are one of the most important components of life time reproductive success in breeding females.” However, phenotypic selection theory recommends against this common practice in the analysis of data for 2 reasons. First, it confounds selection and inheritance (Lande and Arnold 1983; Cheverud and Moore 1994). Second, it confounds within and between generation measures of selection (Wolf and Wade 2001). Wolf and Wade (2001) argued that it also confounds direct effects on offspring fitness with parental indirect genetic effects and which evolve very differently. Despite these concerns, the quantitative effects of considering offspring viability a component of parental fitness have not been derived. How bad an approximation of natural selection is it to consider offspring viability a component of parental fitness? Are there conditions under which it is a better approximation than others?
In this article, we use a population genetic model to revisit the consequences of including offspring viability as a component of parental fitness. Specifically, we focus on a model of paternal effects on offspring viability. We focus on paternal care here not because the mathematical formulation is different from maternal care (it is not), but because paternal effects—while common—are less well-studied and many untested hypotheses exist for why males might either harm or help their offspring. We address 2 questions: (1) If we consider offspring viability fitness as a component of paternal fitness, what quantitative affect does it have on our interpretation of the evolution of paternal care? And, (2) How can multiple, simultaneous causal effects on offspring viability (e.g., paternal care and good genes) be distinguished empirically, measured, and then reassembled to give an evolutionary perspective that better conforms to best theoretical practice? The first question is of evolutionary interest because the evolution of paternal care is often conceptualized as a trade-off between increased offspring survival versus increased mating success (Maynard-Smith 1977). If genetic causes of offspring viability are confounded with those of paternal care, then the evolutionary balance between caring for offspring and mating may be erroneously skewed in favor of or against paternal care. When are these effects small enough to be ignored? When is it large enough that it becomes worthwhile to expend the experimental effort to separate the simultaneously acting causes of offspring viability? These are practical questions, readily addressable and quantifiable with explicit population genetic models, and their answers may be useful in the analysis of data.
The Model
We investigate these questions using a single-locus, 2-allele population genetic model. We consider a locus that has 2 different, simultaneously acting genetic influences on mean offspring viability, one is a direct effect and the other, an indirect effect (Wade 1998; Wolf, Jason B. 2009; Fitzpatrick et al. 2021). One pleiotropic allele causes both effects. This type of pleiotropy is well documented in the empirical literature on genetic correlations between direct and indirect genetic effects in the empirical literature. Although pleiotropy is not the sole explanation for such correlations, it is a common one and the numerous examples of such correlations provide sound justification for this assumption of our model (Riska et al. 1985; Robinson 1996; Ligda et al. 2000; Wilson and Réale 2006; Head 2012; Pires et al. 2016).
The indirect effect arises when a male parent genotype bearing a c allele provides care to (or harms) its offspring, increasing (or reducing) their mean viability. The direct effect arises when an offspring of either sex bearing a c allele enjoys enhanced (or suffers diminished) viability. The model allows us to explore combinations of simultaneously acting direct and indirect effects on offspring viability. In our model, we can treat offspring viability as a component of paternal fitness by lumping together the direct and indirect effects of a c allele and treating them together as an attribute of certain paternal genotypes. This allows us to investigate quantitatively how attributing genetic fitness effects to a parent instead of an offspring affects our perception of adaptation. That is, when we treat offspring viability as a component of paternal fitness, we are studying evolution as though genes in the offspring genome were instead in the genome of the male parent of the previous generation. When does this misattribution bias our view of adaptation and how large a bias is it, when it occurs?
We simplify the model of Fitzpatrick et al. (2021), which considered a single locus with pleiotropic effects, 2 of them affecting offspring viability: an indirect effect of paternal offspring care (sI) and a direct effect (sD). An allele expressed in the paternal genome that affects the viability of a male’s offspring (regardless of offspring genotype) is said to have an indirect genetic effect. In contrast, an allele has a direct effect when it is expressed by the offspring’s own genotype and increases or decreases that offspring’s viability. In our model, the paternal, indirect effect on offspring viability is transgenerational; the focal allele is expressed by the members of one generation (fathers), but the effect is on the viability phenotype of members of the subsequent generation (offspring). The direct effect is manifest within a generation; the focal allele is expressed by the offspring that carry it and, when expressed, affects offspring viability. Direct and indirect genetic effects can evolve differently despite effects of similar magnitude on mean offspring fitness (Wolf and Wade 2001, 2016; Dury and Wade 2019). It is the transgenerational fitness effect of paternal care on the offspring phenotype that fosters the practice of considering offspring fitness a component of paternal fitness.
Let a c allele in males have an additive indirect effect, sI, on the viability of offspring. That is, males of genotype cc increment the viability fitness of their offspring via paternal care by the quantity, 2sI, and Cc heterozygous males increment the fitness of their offspring by sI. Also, let the c allele have an additive, direct effect, sD, on offspring viability fitness. Thus, cc offspring of Cc fathers have viability fitness, 1 + 2sD + sI. Males bearing the c allele care for (sI > 0) or harm (sI < 0) their offspring. Similarly, offspring bearing the c allele have increased (sD > 0) or decreased (sD < 0) viability (Figure 1).
The simultaneous direct (SD) and indirect (S1) effects. The allele has a direct effect on viability of SD Males, with the allele increment the viability of their offspring by S1.
In Table 1 (après Table 1 of Fitzpatrick et al. 2021), we use these effects on viability to assign fitnesses. Family fitness (Table 1, column 7) is the viability averaged across offspring and paternal genotypes. Genotypes are denoted P, H, and Q (CC, Cc, and cc, respectively.) If we assign all offspring viability to paternal genotype and average across the different mates of each paternal genotype, we obtain the values in column 8 of Table 1. Taking the average fitness values of either column 7 or 8 in Table 1, we find that W, mean offspring viability fitness, equals
| . | . | . | Offspring genotypes . | . | . | ||
|---|---|---|---|---|---|---|---|
| Male . | Female . | Family frequency . | CC . | Cc . | cc . | Offspring mean fitness . | Mean offspring fitness by male parent genotype . |
| CC | CC | P2 | 1 | -- | -- | 1 | 1 + sDq |
| CC | Cc | PH | 1/2 | 1/2 | -- | 1 + sD/2 | |
| CC | cc | PQ | -- | 1 | -- | 1 + sD | |
| Cc | CC | HP | 1/2 | 1/2 | -- | 1 + sD/2 +sI | 1 + sD(q+1/2) + sI |
| Cc | Cc | H2 | 1/4 | 1/2 | 1/4 | 1 + sD + sI | |
| Cc | cc | HQ | -- | 1/2 | 1/2 | 1 + 3 sD /2 + sI | |
| cc | CC | QP | -- | 1 | -- | 1 + sD + 2 sI | 1 + sD (q+1) + 2sI |
| cc | Cc | QH | -- | 1/2 | 1/2 | 1 + 3sD /2 + 2 sI | |
| cc | cc | Q2 | -- | -- | 1 | 1 + 2sD + 2 sI | |
| . | . | . | Offspring genotypes . | . | . | ||
|---|---|---|---|---|---|---|---|
| Male . | Female . | Family frequency . | CC . | Cc . | cc . | Offspring mean fitness . | Mean offspring fitness by male parent genotype . |
| CC | CC | P2 | 1 | -- | -- | 1 | 1 + sDq |
| CC | Cc | PH | 1/2 | 1/2 | -- | 1 + sD/2 | |
| CC | cc | PQ | -- | 1 | -- | 1 + sD | |
| Cc | CC | HP | 1/2 | 1/2 | -- | 1 + sD/2 +sI | 1 + sD(q+1/2) + sI |
| Cc | Cc | H2 | 1/4 | 1/2 | 1/4 | 1 + sD + sI | |
| Cc | cc | HQ | -- | 1/2 | 1/2 | 1 + 3 sD /2 + sI | |
| cc | CC | QP | -- | 1 | -- | 1 + sD + 2 sI | 1 + sD (q+1) + 2sI |
| cc | Cc | QH | -- | 1/2 | 1/2 | 1 + 3sD /2 + 2 sI | |
| cc | cc | Q2 | -- | -- | 1 | 1 + 2sD + 2 sI | |
Genotype frequencies are denoted as P (homozygous CC), H (heterozygous Cc), and Q (homozygous cc).
| . | . | . | Offspring genotypes . | . | . | ||
|---|---|---|---|---|---|---|---|
| Male . | Female . | Family frequency . | CC . | Cc . | cc . | Offspring mean fitness . | Mean offspring fitness by male parent genotype . |
| CC | CC | P2 | 1 | -- | -- | 1 | 1 + sDq |
| CC | Cc | PH | 1/2 | 1/2 | -- | 1 + sD/2 | |
| CC | cc | PQ | -- | 1 | -- | 1 + sD | |
| Cc | CC | HP | 1/2 | 1/2 | -- | 1 + sD/2 +sI | 1 + sD(q+1/2) + sI |
| Cc | Cc | H2 | 1/4 | 1/2 | 1/4 | 1 + sD + sI | |
| Cc | cc | HQ | -- | 1/2 | 1/2 | 1 + 3 sD /2 + sI | |
| cc | CC | QP | -- | 1 | -- | 1 + sD + 2 sI | 1 + sD (q+1) + 2sI |
| cc | Cc | QH | -- | 1/2 | 1/2 | 1 + 3sD /2 + 2 sI | |
| cc | cc | Q2 | -- | -- | 1 | 1 + 2sD + 2 sI | |
| . | . | . | Offspring genotypes . | . | . | ||
|---|---|---|---|---|---|---|---|
| Male . | Female . | Family frequency . | CC . | Cc . | cc . | Offspring mean fitness . | Mean offspring fitness by male parent genotype . |
| CC | CC | P2 | 1 | -- | -- | 1 | 1 + sDq |
| CC | Cc | PH | 1/2 | 1/2 | -- | 1 + sD/2 | |
| CC | cc | PQ | -- | 1 | -- | 1 + sD | |
| Cc | CC | HP | 1/2 | 1/2 | -- | 1 + sD/2 +sI | 1 + sD(q+1/2) + sI |
| Cc | Cc | H2 | 1/4 | 1/2 | 1/4 | 1 + sD + sI | |
| Cc | cc | HQ | -- | 1/2 | 1/2 | 1 + 3 sD /2 + sI | |
| cc | CC | QP | -- | 1 | -- | 1 + sD + 2 sI | 1 + sD (q+1) + 2sI |
| cc | Cc | QH | -- | 1/2 | 1/2 | 1 + 3sD /2 + 2 sI | |
| cc | cc | Q2 | -- | -- | 1 | 1 + 2sD + 2 sI | |
Genotype frequencies are denoted as P (homozygous CC), H (heterozygous Cc), and Q (homozygous cc).
(see also, Fitzpatrick et al. 2021, equation 1). Note that the indirect effect makes a contribution, 2qsD, to mean fitness, W, in a manner similar to the contribution of the direct effect, 2qsI, whether we assign offspring viability to sires (column 8 average) or not (column 7 average).
Fitzpatrick et al. (2021, equation 3) demonstrated that the rate of gene frequency change with a direct effect and an indirect effect (through one parent) equals:
Equation 2 (here forward denoted as Δqtrue) is an approximation, because we substituted the Hardy-Weinberg value, q2 for the exact cc genotype frequency, Q. This is a standard approximation in evolutionary genetic models and the difference between the exact and approximate solutions is smaller than sI2.
The attribution of offspring viability fitness to paternal genotypes does not affect the mean fitness function (Equation 1). However, does such attribution correctly capture the direction and magnitude of gene frequency change? One approach when considering the evolution of traits with social salience among related individuals is to apply a kinship coefficient. For example, in the dynamical equations for our example, the indirect effect is discounted by a simple kinship factor of ½, while the direct effect is not. However, whenever there is nonrandom mating, either through inbreeding (Wolf and Wade 2016), a sexually selected male mating advantage (Fitzpatrick et al. 2021), or nonrandom extra-pair matings (EPCs; Fitzpatrick et al. 2021), the difference between sD and sI is no longer so simple. Most importantly, for the problem at hand, sD and sI are simultaneously acting genetic effects on offspring viability, so that, in the natural world, we often can measure only their sum (sD + sI), and not their separate magnitudes. This makes it impossible in principle to correctly apply a kinship coefficient to sI but not to sD. In the next section, we quantitatively evaluate this issue.
Treating Offspring Viability as a Component of Paternal Genotypic Fitness
Is offspring viability as a component of paternal fitness a reliable guide to how paternal care will evolve? To address this question, we take the 3 values for paternal genotypic fitness in column 8 of Table 1 and use them as paternal genotypic selection values in a population genetic model. In column 7 of Table 1, the mean offspring fitness is a function of both sD and sI. For example, note the mean offspring fitness in rows 3 and 7, both of which are families where all offspring are heterozygotes. Because heterozygotes have a fitness (1 + sD), that term appears in both mean family fitnesses (rows 3 and 7 in column 8). However, the family of row 3 has a non-caregiving sire, CC, while the family of row 7 has a caregiving sire, cc. As a result, mean offspring fitness in the latter family is increased by 2sI, while the former is not.
Using the paternal means (Table 1, column 8), we find that the frequency of heterozygous males after selection, H’, equals H (the frequency before selection) multiplied by the relative fitness (1 + sDq + [sD/2] + sI)/W and, similarly, after selection, Q’ is Q(1 + sDq + sD + 2sI)/W. With these, we find q’ in males as (Q’ + H’/2), giving the change in the frequency of the c allele owing to selection among sires, i.e., considering offspring fitness as a component of sire fitness. Under the same degree of approximation as above, we find:
By comparing Equations 3 and 2, the weightings, ½ and 1, of sD and sI in Equation 3 are the reverse of the weightings in Equation 2 (from here forward, we refer to Equation 2 as Δqtrue). The weightings are reversed because the sire average of offspring viability is changed by (sD/2), owing to offspring inheriting a paternal c allele with a direct effect on offspring viability, while each c allele in the paternal genotype increments average offspring viability by sI, owing to paternal care. Note that inheriting a c allele from the dam also changes the expected offspring viability fitness, but, with random mating, offspring of each paternal genotype, on average, have the same dam contribution, sDq. Differently put, with random mating, c alleles inherited through the mother have no differential effect on average paternal genotypic fitness. Thus, in our sire-based perspective with random mating, the dam genetic contribution to offspring viability is not differential among sires and thus cannot influence selection response. In summary, the weightings of sD and sI remain the same and equal to one another in the calculation of W, so that the results of models based on maximization of mean absolute fitness remain the same. However, the weightings of sD and sI in the expressions for Δqtrue and Δqsire are reversed.
The difference between Δqsire and Δqtrue sheds light on the magnitude of the effect of treating offspring fitness as a component of paternal fitness. This difference measures the underestimate, when negative, or the over-estimate, when positive, of the rate of evolution. The difference between Δqsire and Δqtrue equals
When the direct and indirect effects are equal, sD = sI, Δqsire = Δqtrue and the difference is zero. So, when the effects are equal in magnitude and of the same sign, attributing offspring viability to paternal fitness does not bias our interpretation of the evolutionary process through either W or Δqtrue.
Whenever sD and sI are of opposite sign but equal in magnitude, Δqtrue and Δqsire (Equations 3 and 2) are necessarily of opposite sign. Here, the direction of selection is wrongly inferred by treating mean offspring fitness as male parental fitness. That is, we infer that Δqtrue is positive, when in fact it is negative or vice versa. We illustrate this dichotomy of inference in Figure 2. Here, there is a range where Δqsire is negative, suggesting that the a allele is lost, while the actual Δqtrue is positive so it is spreading to fixation. Considering offspring viability as a component of parental fitness in cases like this leads to inferring the wrong direction of evolutionary change.
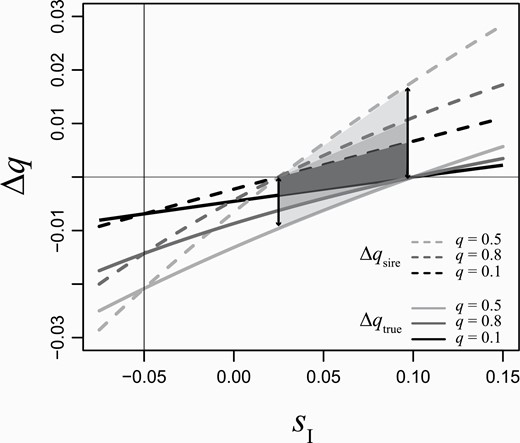
The change in allele frequency per generation (Δq) when offspring survival is considered a component of parental fitness (Δqsire, dashed lines) and when it is not (Δqtrue, solid lines) as a function of the indirect genetic effect (SI) for 3 different allele frequencies (q = 0.1, dark gray; q = 0.5, black; q = 0.8, light gray) when SD = −0.5. Note that Δqsire = Δqtrue when SD = SI (vertical line in this example). However, when the direct and indirect effects are not the same, Δqsire deviates from Δqtrue. The magnitude of this deviation represents an error in inference. The magnitude of the error increases as a function of the absolute difference between the 2 effects (compare each pair of solid vs. dashed lines increases as SI >> SD) and as a function of genetic variation (difference between dashed and solid line is larger when q = 0.5 than either when q = 0.1 or when q = 0.8). For some values of SI, not only is value of Δqsire incorrect, but also the sign (shaded regions).
Empirical Separation of Indirect From Direct Effects on Fitness
In order to obtain the correct equation for gene frequency change, the direct (sD) and indirect (sI) causes of offspring viability must be separated (see Head et al. 2012 for an example). Empirically, this separation can be achieved by cross-fostering if the offspring with each of the genotypes produced by the mating system are distributed randomly across the 3 male genotypes. (Note that, with cross-fostering, CC males can raise cc cross-fostered offspring, an otherwise impossibility with diploid Mendelian inheritance.) This manipulation distributes the direct effect (sD) of c alleles inherited by offspring across sires equally among all 3 male genotypes and therefore removes the differential offspring viability among sire broods that results from sD. In this type of cross-fostering scenario, offspring viability differs among male parental genotypes only by an increment (sI) for every c allele in the paternal genome. We can thus use the mean viabilities of offspring cross-fostered across sires and the genotypic identity of the sires to estimate the value of sI.
Once this empirical separation of sD and sI is accomplished, then we can recognize that dams, as well as sires, transmit the c allele to offspring, so that Δqdams ~ (sD/2)pqW. That is, we can better account for this component of gene frequency change. Moreover, because the indirect effect of paternal care is limited to sires, the correct fraction of gene frequency change owing to paternal care is Δqsire ~ (sI/2)pqW. Thus, the total gene frequency change is the sum of that from direct effects of the c allele on offspring viability as transmitted by both sexes (i.e., Δqdam + Δqsire ~ sDpq/W) plus the indirect effect owing to single-sex paternal care (i.e., Δqsire ~ sI/2)pqW). Indeed, the sum of these 2 components is the total gene frequency change; it equals Equation 1.
We have emphasized that, when empirical studies investigate any type of indirect effect, such as paternal care, it is important to use a research design that disentangles the direct and indirect effects on offspring fitness (see Linksvayer 2006 and 2007 for experimental studies of multiple indirect genetic effects using cross-fostering within and among populations and within and among species). Cross-fostering is one such approach (e.g., Velando et al. 2005; Quesada and Senar 2009), but may not be feasible in some cases. For instance, such experiments are intractable in some study organisms (e.g., highly social mammals with paternal care like marmosets, where removing neonates from caregiving parents would be prohibitively disruptive). Moreover—even if feasible—cross-fostering may not always achieve the desired separation of effects if, for example, the indirect effects take place prenatally or before embryos can be redistributed across paternal genotypes (but see Atchley et al. 1991). Such empirical challenges go beyond our case of paternal care; they are characteristic of indirect genetic effects in general. For example, RNA transcripts of maternal origin are often sequestered in ova prior to fertilization and these maternal transcripts influence early offspring development (see Wade 2021 this volume). These transcripts are derived from a different genome than the zygotic genome and so represent an indirect effect. However, many of these same genes also have direct effects when zygotically expressed in early development (Demuth and Wade 2007; Cruickshank and Wade 2008). With these types of very early indirect effects (especially those occurring pre-fertilization), cross-fostering fails to separate completely direct from the indirect effects. Under such conditions, one alternative approach, is to use the so-called “animal model” of quantitative genetics. This statistical technique requires multi-generational pedigrees but, when they are available, it permits the estimation of additive direct genetic effects as well as indirect genetic effects without cross-fostering (Maniatis and Pollott 2003). We note that such an approach is not a panacea and that there are caveats to consider when using the animal model (e.g., see Hill 2010). Nevertheless, whether through cross-fostering or statistical techniques like the “animal model”, partitioning the direct and indirect genetic effects is necessary for accurate empirical measurements of the fitness effects and subsequent evolutionary genetic inferences.
Mutation-Selection Balance: Expected Genetic Diversity With Opposing Levels of Selection
Here we deviate briefly from our focus on paternal care to demonstrate that separating direct and indirect effects can also strengthen predictions about the expected patterns of gene sequence diversity. Indeed, population genetic models are commonly used for this purpose (e.g., Barker et al. 2005; Linksvayer and Wade 2005, 2009; Demuth and Wade 2007; Cruickshank and Wade 2008; Wade et al. 2009; Van Dyken and Wade 2010; Dapper and Wade 2020). However, even though it is common to posit transgenerational effects of a gene with opposing indirect and direct effects on fitness (like those in our model), the influence of such an effect on sequence diversity at mutation-selection balance has not been investigated.
At mutation-selection balance in an infinite population with weak selection, we find the equilibrium value of p, p*, by setting the total change in allele frequency, the sum of the changes by selection and by mutation, equal to zero. We assume that net selection favors the ‘c’ allele so that it is near fixation, where q is near 1 and p is near 0. Weak selection means that W is also essentially equal to 1. Mutation introduces deleterious alleles by altering ‘c’ to other states, which we lump into the frequency, p. Together, selection and mutation with the assumptions above give us the following approximation,
Setting Equation 5 equal to 0, we find that p* = u/(sD + [sI/2]). Clearly, the relative values of sD and sI affect the expected value of p* and thus gene diversity at equilibrium. When both sD and sI > 0, p* is smaller than if they are of opposite sign. When of opposite sign (but still net positive), net selection is weakened by the opposing selective forces, so that p* is higher and gene diversity is increased. This is a general feature of fitness trade-offs: it can weaken total selection acting on a gene when it leads to opposing types or levels of selection.
Discussion
Using a model with direct and indirect effects on offspring viability, we have shown that the practice of counting offspring survival as paternal fitness can lead to distorted evolutionary conclusions. This distortion occurs because, even when direct and indirect effects may make similar contributions to mean fitness, they do not contribute equally to allele frequency change. In other words, the surface of mean fitness becomes separated from the adaptive landscape.
This separation between the surface of mean fitness and the adaptive landscape is more than a technicality; our model demonstrates that in some cases, it can lead to erroneous conclusions that are substantial. In particular, the size of the error is exacerbated as 1) genetic variation increases and as 2) the difference between the size of the direct and indirect effects increases. These findings have implications beyond the basic principles we are emphasizing here. For instance, it suggests that in systems where the genetic variation for paternal care is substantial, the misattribution of offspring viability to paternal fitness will result in a larger error than when genetic variation for paternal care is lower. Substantial variation for paternal care is quite plausible and there is empirical support for it in sticklebacks (Bell et al. 2018). Moreover, although direct and indirect genetic effects may be equal in size at times, it strains credulity to posit that this condition should be the rule rather than the exception. Differently put, we expect the conditions that exacerbate the size of the inferential error to be common. Finally, our model demonstrates that, under some conditions, measuring offspring survival as paternal fitness results in an error not only in magnitude, but also in sign.
So, in a scenario like the one we model here, when is offspring viability a measure of paternal fitness? The answer from theory is: only when the indirect effect of paternal care on offspring viability and the direct effect on offspring viability are equal or approximately so. It appears to be an especially bad idea when there are trade-offs such that the direct and indirect effects are of opposite sign, a condition that has been shown to be common by the empirical research on IGEs (Bijma 2014).
Our model illustrates quantitatively the risks of ignoring the challenges associated with measuring the separate effects on fitness of simultaneously acting causes. Indeed, we recognize the substantial empirical challenge that empiricists face when trying to measure the separate effects on fitness of simultaneously acting causes. We hope that our findings will help motivate more empiricists to grapple with the potential confounds when measuring paternal care and to include cross-fostering experiments and the “animal model” to their methodological tool kit for the study of indirect genetic effects of all kinds.
On a final note, in this paper, we did not address issues of internal versus external fertilization, paternity assurance, post-copulatory sperm competition, cryptic female choice, or extra-pair copulation. We have examined many of these other issues in an earlier paper (Fitzpatrick et al. 2021). Indeed, the model discussed here is based on that earlier work.
Funding
This work was supported by National Institutes of Health (NIH) award 5T32HD049336-12 (C.L.F.) and The John Templeton Foundation (M.J.W.) and a sabbatical fellowship by the Wissenschafts Kollege zu Berlin (M.J.W.).
Acknowledgments
We thank Kimberly Hughes for the invitation to participate in the American Genetics Association 2020 Presidents Symposium on Genes As Environment, Anjanette Baker for coordinating the symposium and special issue, and 2 anonymous reviewers whose comments improved this manuscript.
References



