-
PDF
- Split View
-
Views
-
Cite
Cite
Marco Galaverni, Romolo Caniglia, Pietro Milanesi, Silvana Lapalombella, Elena Fabbri, Ettore Randi, Choosy Wolves? Heterozygote Advantage But No Evidence of MHC-Based Disassortative Mating, Journal of Heredity, Volume 107, Issue 2, March 2016, Pages 134–142, https://doi.org/10.1093/jhered/esv090
Close - Share Icon Share
Abstract
A variety of nonrandom mate choice strategies, including disassortative mating, are used by vertebrate species to avoid inbreeding, maintain heterozygosity and increase fitness. Disassortative mating may be mediated by the major histocompatibility complex (MHC), an important gene cluster controlling immune responses to pathogens. We investigated the patterns of mate choice in 26 wild-living breeding pairs of gray wolf (Canis lupus) that were identified through noninvasive genetic methods and genotyped at 3 MHC class II and 12 autosomal microsatellite (STR) loci. We tested for deviations from random mating and evaluated the covariance of genetic variables at functional and STR markers with fitness proxies deduced from pedigree reconstructions. Results did not show evidences of MHC-based disassortative mating. Rather we found a higher peptide similarity between mates at MHC loci as compared with random expectations. Fitness values were positively correlated with heterozygosity of the breeders at both MHC and STR loci, whereas they decreased with relatedness at STRs. These findings may indicate fitness advantages for breeders that, while avoiding highly related mates, are more similar at the MHC and have high levels of heterozygosity overall. Such a pattern of MHC-assortative mating may reflect local coadaptation of the breeders, while a reduction in genetic diversity may be balanced by heterozygote advantages.
Mate choice is one of the main mechanisms through which sexual selection influences genetic diversity, inbreeding avoidance and adaptability in wild populations (Tregenza and Wedell 2000). The major histocompatibility complex (MHC) is viewed as a key element in mate choice (Eizaguirre et al. 2009). MHC genes encode for glycoprotein receptors that trigger biological pathways in response to pathogens and infectious diseases. MHC proteins may also affect the composition of the bacterial flora of the host and the pleasantness of individual odor cues. In this way, MHC peptides can be perceived via olfaction or pheromone detection (Brennan and Kendrick 2006; Spehr et al. 2006; Janeš et al. 2010; Sturm et al. 2013) and can function as signals of similarity between individuals, possibly driving active mate choice.
The effects of MHC-mediated signals in mate choice have been hypothesized in several sexual selection models. In the inbreeding avoidance hypothesis (Potts and Wakeland 1990), selection should favor unrelated parents, whose offspring will not be exposed to inbreeding depression. Parallel, heterozygote individuals can have higher fitness (heterozygote advantage) due to higher resistance to multiple parasites (Hedrick 2012). In the moving target model (Penn and Potts 1999), sexual selection could enhance the ability of the host to keep its defenses up-to-date with the continuing evolution of the “parasite weapons” thanks to a rare-allele advantage (Landry et al. 2001). In the honest signal model (Hamilton and Zuk 1982), MHC may be linked to other secondary sexual characteristics that indicate the levels of pathogen resistance and the general fitness of potential mates (Ditchkoff et al. 2001). These 3 hypotheses have been documented in a number of species (Kamiya et al. 2014), including humans (Wedekind et al. 1995; Havlicek and Roberts 2009).
However, other studies failed to detect any deviation from random mating (Huchard et al. 2010; Yang et al. 2014; Kuduk et al. 2014) and a number of works also reported cases of assortative (hereafter intended as positive-assortative) matings (Sin et al. 2015 and references therein). The theoretical models to explain assortative matings assume the reduction of outbreeding (e.g., in hybrid zones between divergent populations, where selection can act against genetic incompatibility; Tregenza and Wedell 2000), or the maintenance of allele compatibility or optimal allele combinations linked to local adaptation (Neff 2004). Preferences for partners with intermediate levels of dissimilarity can otherwise be expected to balance the costs of expressing numerous MHC alleles, which can lead to an increased chance of autoimmune diseases (Penn and Potts 1999), representing an intermediate case between disassortative and assortative mating.
Gray wolves (Canis lupus) offer an interesting case to study interactions between MHC variability and mate choice due to their complex social structure. The classical vision of a dominance hierarchy, once used to describe the relationships within a pack, was typically derived from observations of large groups in captivity and is mostly overcome (Packard 2003). In smaller, wild-living packs, family-like relationships can better illustrate the interactions among pack members, which are regulated by a combination of leadership skills, individual temperament, and experiences (Packard 2003). However, the mating system in wolves is strictly monogamous (Geffen et al. 1996), with a single pair that reproduces in a pack once a year (Mech and Boitani 2003). Polygamy and multiple litters per year are rare exceptions (Vonholdt et al. 2008). Breeding pairs can establish in newly colonized territories by loner or dispersing individuals, whereas in already existing packs one or both mates can be replaced by immigrant wolves, or by their own progeny (Vonholdt et al. 2008; Caniglia et al. 2014). Active inbreeding avoidance has been described within, but not across, packs (Geffen et al. 2011). Moreover, genetic diversity in wolf populations can also be maintained by heterozygote advantage or balancing selection (Bensch et al. 2006; Hagenblad et al. 2009).
The genetic organization of the canine MHC is well known (Kennedy et al. 2001; Berggren and Seddon 2005; Wayne and Ostrander 2007; Yuhki et al. 2007). MHC variability has been investigated in domestic and wild canids (Hedrick et al. 2002; Angles et al. 2005; Kennedy et al. 2007b; Fliegner et al. 2008; Galaverni et al. 2013), where a few cases of MHC-mediated resistance to pathogen outbreaks have been described (Hedrick et al. 2003; Kennedy et al. 2011). However, the role of MHC variation on mate choice in gray wolves yet has to be explored, also because obtaining data on wild-living individuals is no easy task. The extensive use of combined field and molecular monitoring tools is limited to a few cases (Vonholdt et al. 2008; Stahler et al. 2013). Nonetheless, the possibility to derive good-quality genetic data even from noninvasive samples can be successfully exploited (Yang et al. 2014).
In this study, we used wolf genotypes and pack genealogies, obtained in a long-term monitoring project based on extensive noninvasive genetic sampling, which allowed to infer the most likely reproductive parent pairs and their offspring (Caniglia et al. 2014). These wolves were genotyped at both putatively nonfunctional microsatellites (STR) and functional MHC class II loci, and fitness proxies were deduced from the reconstructed pedigrees. We aimed to identify the prevalent mate choice patterns, as well as to investigate the relations between MHC and STR variability, and individuals’ fitness in wild-living wolf packs. Expecting high genetic diversity (Seddon and Ellegren 2004), inbreeding avoidance (Adams et al. 2011; Geffen et al. 2011) and heterozygote advantage or balancing selection (Bensch et al. 2006; Hagenblad et al. 2009), we assumed that the prevalent mate choice patterns can be aimed to select the maximum MHC diversity and dissimilarity between reproductive pack partners.
Materials and Methods
Sampling and Pack Reconstructions
We used DNA samples that were collected during an extensive noninvasive genetic monitoring program of the Italian wolf population carried out in the northern Apennines (Italy) from 2001 to 2011 (Caniglia et al. 2014). Biological samples (n = 5065, 99% scats) were genotyped at 12 nonfunctional and putatively neutral autosomal STRs, which allowed to identify 414 distinct wolf individual genotypes. Familial relationships were identified after Caniglia et al. (2014) using a maximum-likelihood approach implemented in the software Colony 2.0 (Wang and Santure 2009). All the genotypes that were sampled in restricted ranges (<100 km2) at least 4 times and for periods longer than 24 months were selected. Their spatial distributions were determined by 95% kernel analysis using the adehabitathr package for R (Calenge 2006) and mapped in ArcGis 10.0 (ESRI). According to spatial overlaps, individuals were split into distinct groups that might correspond to packs, for which parentage analyses were performed. All the individuals sampled in the first year of sampling and more than 4 times in the same area were considered as candidate parents of each group. All the individuals collected within the 95% kernel spatial distribution of each pack and in a surrounding buffer area of approximately 17-km radius from the kernel were considered as candidate offspring (Caniglia et al. 2014). Colony was run with allele frequencies and PCR error rates as estimated from all the genotypes, assuming a 0.5 probability of including fathers and mothers in the candidate parental pairs. Genealogies were then compared to those obtained by an open parentage analysis, using all the males and females as candidate parents, and all the wolves sampled in the study area as candidate offspring. The best maximum-likelihood genealogies reconstructed by Colony were then compared also with those obtained by a likelihood approach in Cervus (Kalinowski et al. 2007), based on the Mendelian inheritance of the alleles, accepting only parent–offspring combinations with at most 1/24 allele incompatibilities, and father–son combinations with no incongruities at Y-STR haplotypes. Whenever available, additional field information such as snow-tracking, wolf-howling, camera-trapping, and occasional direct observations were used to evaluate the reliability of the inferred pack structure and locations. Reliable pedigrees were identified for 26 packs, which sometimes extended over multiple years and generations (Caniglia et al. 2014). None of the alternative genealogies was supported by sampling dates, frequency, or location. Moreover, from 2/24 to 5/24 allele incompatibilities and incongruities at Y-haplotypes occurred in 93 (95%) of 98 father–son combinations of the alternative trios with significant natural log of likelihood ratio scores (for details see also Supporting Information S7 from Caniglia et al. 2014). Multiple litters per year in a pack, or extra-pair reproductions were never detected in any pack. Details on the metrics of the STR loci used to genotype the samples are reported in Supplementary Table S1 online.
For each breeding pair, we then calculated an overall fitness proxy derived from pedigree information, namely the total number of offspring of a pair (total offspring, TO), which reflects the number of pups that survived until they were detected through noninvasive genetic sampling. In addition, to better highlight different contributions to fitness, we also considered the 2 main components of TO, namely the number of years a breeding pair was sampled (hereafter: years as reproducer, YR) and the average number of identified offspring per year, or litter size per year (LSY).
We then computed the correlations between all the pairs of fitness proxies (Pearson’s correlation test) and tested for the normal distribution of data with a Shapiro–Wilk normality test.
MHC Amplification and Genotyping
For each of the 63 identified breeders (32 males, 31 females; Caniglia et al. 2014), the best available DNA sample was PCR-amplified and sequenced at the second exon of 3 class II MHC genes: DRB1, DQA1, and DQB1, using the intronic and locus-specific primers DRB1F (5′ –ccg tcc cca cag cac att tc– 3′) and DRB1R (5′ –tgt gtc aca cac ctc agc acc a– 3′; Hedrick et al. 2002, after Kennedy et al. 1998); DQAin1 (5′ –taa ggt tct ttt ctc cct ct– 3′) and DQAin2 (5′ –gga cag att cag tga aga ga– 3′); DQB1B (5′ –ctc act ggc ccg gct gtc tc– 3′), and DQBR2 (5′ –cac ctc gcc gct gca acg tg– 3′; Kennedy et al. 2006, after Wagner et al. 1996). Amplifications were carried out in a 10-μL mix, including 2 μL genomic DNA solution, 1 μL bovine serum albumin (2%), and 0.2 μL of each primer (10 μM) plus 0.25 units of Taq, at conditions specific for each primer pair (Galaverni et al. 2013). PCR products were purified with Exo/SAP and sequenced in both directions using BigDye Terminator 1.1, according to the manufacturer’s protocol. Sequences were analyzed in an automated sequencer ABI 3130XL, corrected and aligned with the software Seqscape 2.5, using the sequences DLA-DRB1*03101 (AF336108.1), DLA-DQA1*014012 (AJ316220.1), and DLA-DQB1*05601 (FM246843.1) as references.
MHC alleles were reconstructed in DnaSp 5.10 (Librado and Rozas 2009) using the software PHASE (Stephens and Donnelly 2003), which allows to avoid the cloning step, applying the “recombination” model (−MR0) and running 1000 iterations after 100 burn-ins (Berggren and Seddon 2008; Galaverni et al. 2013). Alleles were matched to sequences available in GenBank via Blastn (Johnson et al. 2008) and also compared with those included in the Immuno Polymorphism-MHC Database (IPD; http://www.ebi.ac.uk/ipd/mhc/dla/index.html; Robinson et al. 2010). Three-locus MHC haplotypes were then identified with a subtractive approach described in Kennedy et al. (2007a) and computationally verified in PHASE (Berggren and Seddon 2008; Galaverni et al. 2013).
The MHC genotypes of 5 individuals were independently derived from 2 different fecal samples in order to check for robustness in the sequencing and genotyping procedure. To further verify the congruent reconstruction of the alleles through trio comparisons, we also sequenced and phased MHC alleles in 15 known offspring of the analyzed breeders. In addition, 22 nonreproductive pack members unrelated to the breeding pair (hereafter “adoptees”) were included for testing for preferences toward alternative mates.
Random Mating and Allele Sharing
We computed the mean value of the asymmetrical Queller and Goodnight’s estimator of relatedness (r) between the members of each observed breeding pair at the 3 MHC loci [r(MHC)] in GenAlEx (Peakall and Smouse 2006). Similarly, r was computed also at the 12 STRs [r(STR)] to control for genome-wide effects.
We then empirically assessed the probability of deviations from random mating by comparing the breeding pairs’ relatedness values, both at MHC and STR loci, to those between the members of all the potential pairs of male–female breeders. This was done by a permutation procedure implemented in PERM 1.0 (Duchesne et al. 2006), with 5000 permutations of the breeding pair members repeated for 10 iterations.
Additionally, we tested for deviations from random mating probabilities by observing the levels of allele sharing at the MHC in the breeding pairs, both at each locus (in these cases considering a Bonferroni-corrected alpha of 0.05/3, or ~0.017, to adjust for multiple comparisons) and for the 3-locus haplotypes. We hypothesized an excess of pairs where the mates shared a lower number of MHC alleles than expected by random. At each locus, there are 3 possible classes of matings: pairs where the members share no alleles (e.g., 01 01×12 12), 1 allele (01 01×01 12, or 01 16×01 12), or both (01 01×01 01). The expected frequency of a given mating (mating probability, PM) was then calculated as ∑Pij(f)Pij(m), where Pij(f) and Pij(m) are the observed frequencies of the genotype with alleles i and j in females and males, respectively (Hedrick and Black 1997). We then evaluated the difference between the observed and expected number of mating events in these 3 classes (χ2 test) at each locus and at the 3-locus haplotypes. To avoid inflating the frequency of alleles that could be more frequent among breeders than in the whole population, genotypic allele frequencies were computed only across breeding individuals. We then carried out a power analyses to verify the robustness of the results and the possibility to detect significant differences between groups (Faul et al. 2007). The power of a statistical test is the complement of β, which denotes the Type II (or beta-error) probability of falsely retaining an incorrect null hypothesis. Thus, the power of a test ranges between 1 and 0, which indicate high or low statistical power, respectively (Faul et al. 2007).
Functional Similarity Analyses
In order to better incorporate the levels of functional similarity in our analyses (Landry et al. 2001; Miller et al. 2009), we calculated the mean number of amino acid (AA) differences between female and male alleles at each MHC locus, and in total across the 3 loci. AA differences were then compared in observed versus potential pairs of breeders with the same permutation procedure used above, expecting a higher difference within actual pairs in case of disassortative matings.
To further test for preferences toward alternative mates, we finally compared AA differences between observed mates to those between a given breeder and any unrelated wolf of the opposite sex that was eventually present in the pack in the same period (adoptee), but who had no access to reproduction (Caniglia et al. 2014), with a Bonferroni-corrected t-test.
Heterozygote Advantage and Correlations to Fitness Proxies
We correlated the genetic measures of diversity and dissimilarity with the fitness proxies derived from pedigree information.
First, the observed heterozygosity of each breeder and the mean heterozygosity for each breeding pair were calculated in GenAlEx, both at MHC [Ho(MHC)] and STR loci [Ho(STR)]. Then we compared the average fitness values in MHC-heterozygous versus MHC-homozygous breeders and between breeders with higher- versus lower-than-average Ho(STR) through a Welch 2-sample t-test.
Finally, we related each fitness proxy to the main genetic metrics deduced from the genotypes of the breeding pair members: the relatedness estimates r(STR) and r(MHC), also re-computed according to Lynch and Ritland (1999) [r(STR-LR) and r(MHC-LR)], the mean heterozygosity of the breeders Ho(MHC) and Ho(STR), the mean heterozygosity of the breeders calculated across all the polymorphic sites at the MHC loci [Ho(MHC-SNPs)], the average number of AA differences between mates (AAdist) and their normalized values (AAdist-N). These variables were used as fixed factors in generalized linear mixed models (GLMM), while geographic locations in the study area (“Eastern,” “Central,” and “Western”), elevations (higher vs. lower than 800 m above sea level) and year of breeding (from 2001 to 2009, grouped in 3 classes: 2001–2003; 2004–2006; 2007–2009) were considered as random factors. We also entered quadratic terms for the genetic variables to test if they could show higher relation with each fitness proxy, as expected under an optimal allele diversity model (Thoss et al. 2011).
Model selection was based on the Akaike’s information criterion corrected for sample size (AICc; Akaike 1974), where models that better fit the data produce lower AICc values. According to Anderson et al. (2001), multi-model inference was performed for models with ΔAICc < 2. All these analyses were performed in R 3.2.0 (R Development Core Team 2009; www.R-project.org).
Data Archiving
In fulfillment of data archiving guidelines (Baker 2013), we have deposited the primary data underlying these analyses as follows:
Genetic metrics for the microsatellite used for genotyping: Supplementary Table S1 online.
Allele frequency for the 3 MHC loci analyzed and their combined haplotypes: Supplementary Tables S2 and S3 online, respectively.
MHC genotypes for all the breeders analyzed: Dryad.
Results
Sequencing Success and MHC Variability
We successfully sequenced and phased the alleles at all the 3 MHC loci in DNA samples from 47/63 identified wolf breeders, belonging to 19 packs and 26 breeding pairs, plus 10/15 of their offspring and 10/22 adoptees (67% of the tested individuals, overall). All the genotypes of the 5 individuals that were reconstructed from 2 independent fecal samples regularly matched one another (100%). We detected 7 alleles at DRB1, 6 at DQA1, and 7 at DQB1 (Supplementary Table S2 online), combined into 16 different MHC haplotypes (Supplementary Table S3 online). We were able to reconstruct 10 full parent-offspring trios, in all cases confirming the Mendelian inheritance of the alleles.
Random Mating and Allele Sharing
The observed relatedness between breeders at microsatellite loci [r(STR) = 0.026±0.237] was not significantly deviating from random mating expectations [r(STR) = −0.023±0.252; P = 0.218±0.005), as well as the relatedness at MHC loci [r(MHC) = 0.066±0.688 versus −0.090±0.641, respectively, P = 0.080±0.004].
Similarly, no signals of disassortative matings were detected from the allele sharing analysis. Actually, we found a nonsignificant excess of cases where the pair members shared one or both alleles compared to random mating expectations at each locus and MHC haplotype (Table 1). Results were associated to a high statistical power for the test at DQA1, but just to a moderate power for DRB1, DQB1, and haplotypes (Table 1), indicating that for these loci a larger sample size could have provided more significant results.
| Allele combination . | DRB1 . | DQA1 . | DQB1 . | Haplotypes . | ||||
|---|---|---|---|---|---|---|---|---|
| obs. . | exp. . | obs. . | exp. . | obs. . | exp. . | obs. . | exp. . | |
| 0 shared | 8 | 12.8 | 4 | 5.8 | 10 | 13.3 | 11 | 15.2 |
| 1 shared | 14 | 10.6 | 10 | 11.9 | 12 | 10.4 | 13 | 9.3 |
| 2 shared | 4 | 2.6 | 12 | 8.3 | 4 | 2.3 | 2 | 1.5 |
| χ2P value | 0.164 | 0.287 | 0.299 | 0.247 | ||||
| Statistical power | 0.406 | 0.999 | 0.563 | 0.509 | ||||
| Allele combination . | DRB1 . | DQA1 . | DQB1 . | Haplotypes . | ||||
|---|---|---|---|---|---|---|---|---|
| obs. . | exp. . | obs. . | exp. . | obs. . | exp. . | obs. . | exp. . | |
| 0 shared | 8 | 12.8 | 4 | 5.8 | 10 | 13.3 | 11 | 15.2 |
| 1 shared | 14 | 10.6 | 10 | 11.9 | 12 | 10.4 | 13 | 9.3 |
| 2 shared | 4 | 2.6 | 12 | 8.3 | 4 | 2.3 | 2 | 1.5 |
| χ2P value | 0.164 | 0.287 | 0.299 | 0.247 | ||||
| Statistical power | 0.406 | 0.999 | 0.563 | 0.509 | ||||
The number of breeding pairs (n = 26) sharing 0, 1, or 2 alleles at each MHC locus and haplotype (obs.) was compared to what expected under a random chance of mating based on the breeders’ allele frequencies (exp.). The P values were computed by a χ2 test.
| Allele combination . | DRB1 . | DQA1 . | DQB1 . | Haplotypes . | ||||
|---|---|---|---|---|---|---|---|---|
| obs. . | exp. . | obs. . | exp. . | obs. . | exp. . | obs. . | exp. . | |
| 0 shared | 8 | 12.8 | 4 | 5.8 | 10 | 13.3 | 11 | 15.2 |
| 1 shared | 14 | 10.6 | 10 | 11.9 | 12 | 10.4 | 13 | 9.3 |
| 2 shared | 4 | 2.6 | 12 | 8.3 | 4 | 2.3 | 2 | 1.5 |
| χ2P value | 0.164 | 0.287 | 0.299 | 0.247 | ||||
| Statistical power | 0.406 | 0.999 | 0.563 | 0.509 | ||||
| Allele combination . | DRB1 . | DQA1 . | DQB1 . | Haplotypes . | ||||
|---|---|---|---|---|---|---|---|---|
| obs. . | exp. . | obs. . | exp. . | obs. . | exp. . | obs. . | exp. . | |
| 0 shared | 8 | 12.8 | 4 | 5.8 | 10 | 13.3 | 11 | 15.2 |
| 1 shared | 14 | 10.6 | 10 | 11.9 | 12 | 10.4 | 13 | 9.3 |
| 2 shared | 4 | 2.6 | 12 | 8.3 | 4 | 2.3 | 2 | 1.5 |
| χ2P value | 0.164 | 0.287 | 0.299 | 0.247 | ||||
| Statistical power | 0.406 | 0.999 | 0.563 | 0.509 | ||||
The number of breeding pairs (n = 26) sharing 0, 1, or 2 alleles at each MHC locus and haplotype (obs.) was compared to what expected under a random chance of mating based on the breeders’ allele frequencies (exp.). The P values were computed by a χ2 test.
Functional Similarity
Up to 22 variable AA sites were found at DRB1, 5 at DQA1, and 22 at DQB1 (68%, 20%, and 59% of which fall within putative antigen-binding sites, respectively).
The trend toward an excess of allele sharing was stronger when looking at the mean number of pairwise AA differences between mates at the MHC genes. The number of AA differences was significantly lower between actual mates than among random combinations of breeders at DQA1 (P = 0.030) and DQB1 (P = 0.026), and in total across the 3 loci (P = 0.039, Table 2), as deduced from PERM permutations.
Average number of pairwise amino acid differences at 3 MHC loci between the members of the 26 breeding pairs compared to that expected between all the possible random pairs of breeders (after 10×5000 permutations in Perm; upper part). Average number of pairwise amino acid differences between 10 breeders and their actual mates, versus the same 10 breeders and 10 alternative mates, defined as unrelated individuals present in their same pack, but not reproducing (t-test, Bonferroni corrected; lower part). Significant values are indicated with an asterisk.
| . | Mean number of amino acid differences . | |||
|---|---|---|---|---|
| DRB1 . | DQA1 . | DQB1 . | Total . | |
| Within observed pairs | 6.6 | 1.5 | 6.7 | 14.8 |
| Within random pairs | 7.0 | 1.7 | 7.8 | 16.6 |
| PermP value | 0.221 | 0.030* | 0.026* | 0.039* |
| Actual mates | 5.1 | 1.9 | 5.2 | 12.3 |
| Alternative mates | 8.3 | 2.6 | 6.7 | 17.6 |
| t-Test P | 0.079 | 0.067 | 0.204 | 0.097 |
| . | Mean number of amino acid differences . | |||
|---|---|---|---|---|
| DRB1 . | DQA1 . | DQB1 . | Total . | |
| Within observed pairs | 6.6 | 1.5 | 6.7 | 14.8 |
| Within random pairs | 7.0 | 1.7 | 7.8 | 16.6 |
| PermP value | 0.221 | 0.030* | 0.026* | 0.039* |
| Actual mates | 5.1 | 1.9 | 5.2 | 12.3 |
| Alternative mates | 8.3 | 2.6 | 6.7 | 17.6 |
| t-Test P | 0.079 | 0.067 | 0.204 | 0.097 |
Average number of pairwise amino acid differences at 3 MHC loci between the members of the 26 breeding pairs compared to that expected between all the possible random pairs of breeders (after 10×5000 permutations in Perm; upper part). Average number of pairwise amino acid differences between 10 breeders and their actual mates, versus the same 10 breeders and 10 alternative mates, defined as unrelated individuals present in their same pack, but not reproducing (t-test, Bonferroni corrected; lower part). Significant values are indicated with an asterisk.
| . | Mean number of amino acid differences . | |||
|---|---|---|---|---|
| DRB1 . | DQA1 . | DQB1 . | Total . | |
| Within observed pairs | 6.6 | 1.5 | 6.7 | 14.8 |
| Within random pairs | 7.0 | 1.7 | 7.8 | 16.6 |
| PermP value | 0.221 | 0.030* | 0.026* | 0.039* |
| Actual mates | 5.1 | 1.9 | 5.2 | 12.3 |
| Alternative mates | 8.3 | 2.6 | 6.7 | 17.6 |
| t-Test P | 0.079 | 0.067 | 0.204 | 0.097 |
| . | Mean number of amino acid differences . | |||
|---|---|---|---|---|
| DRB1 . | DQA1 . | DQB1 . | Total . | |
| Within observed pairs | 6.6 | 1.5 | 6.7 | 14.8 |
| Within random pairs | 7.0 | 1.7 | 7.8 | 16.6 |
| PermP value | 0.221 | 0.030* | 0.026* | 0.039* |
| Actual mates | 5.1 | 1.9 | 5.2 | 12.3 |
| Alternative mates | 8.3 | 2.6 | 6.7 | 17.6 |
| t-Test P | 0.079 | 0.067 | 0.204 | 0.097 |
Similarly, the comparison with the 10 alternative potential mates from the same packs showed that actual mates differed on average for 12.3±7.1 AA in total across loci versus 17.6±10.2 AA differences for alternative mates, although not significantly (t-test, P = 0.097).
Heterozygote Advantage and Correlations to Fitness Proxies
Results of the correlations between our fitness proxies showed that the values of litter size per year (LSY) were not significantly correlated to the years as reproducers (YR; Pearson’s correlation c = 0.09, P = 0.561), whereas the total offspring (TO) was significantly correlated to both YR (c = 0.76, P = 1.024e−09) and LSY (c = 0.63, P = 3.652e−06), as expected. When comparing MHC and genome-wide STR diversity, we found that Ho(MHC) and Ho(STR) were not significantly correlated (Pearson’s correlation c = −0.08, P = 0.598).
Breeders that were heterozygote at MHC haplotypes and DQB1 had significantly higher LSY than the homozygotes, on average (respectively, 2.83±1.28 versus 1.79±0.95, P = 0.003; 2.92±1.34 versus 1.96±0.91, P = 0.004; t-test). No significant differences were found for other fitness proxies and loci (Figure 1). Breeders with higher-than-average heterozygosity at STR loci had also higher values of TO (7.2±5.5 versus 4.7±4.4) and LSY (2.9±1.2 versus 2.4±1.3), but these differences were not significant per se (t-test, P = 0.072 and P = 0.156, respectively).
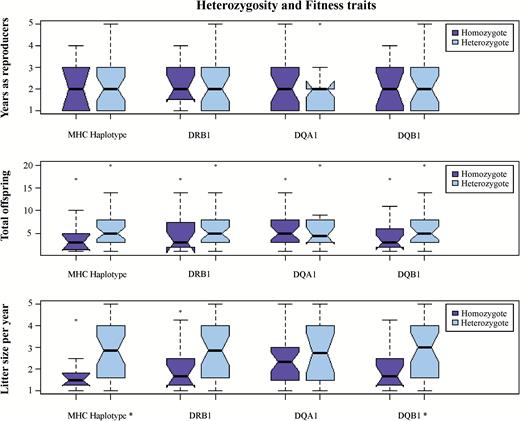
Comparison of the average values of fitness between homozygote and heterozygote breeding wolves at MHC haplotypes, DRB1, DQA1, and DQB1 loci. Outlier values are indicated as dots outside the boxes. Notches that do not overlap represent a 95% probability for the median values to be different. Significant differences are indicated with an asterisk next to the label.
By applying GLMMs, we identified a single model with ΔAICc < 2 for each fitness proxy, characterized by the same 4 explanatory genetic variables, namely the average heterozygosity Ho(STR) and Ho(MHC) of the pair members, and their relatedness r(STR) and r(MHC) (Figure 2, Table 3). The model with the lowest AICc for YR (AICc = 82.63; R2 = 0.35) showed a significant and negative effect of r(STR) (β = −2.795, P = 0.0056), while LSY (AICc = 85.68; R2 = 0.39) was mostly explained by Ho(STR) and Ho(MHC), both with positive effects (β = 1.631, P = 0.0372; and β = 7.089, P = 0.0115, respectively). Finally, we identified also for TO only one model with ΔAICc < 2 (AICc = 139.38; R2 = 0.32) in which r(STR) showed the most significant, negative effect (β = −8.881, P = 0.0273), confirming its correlation to our fitness proxies.
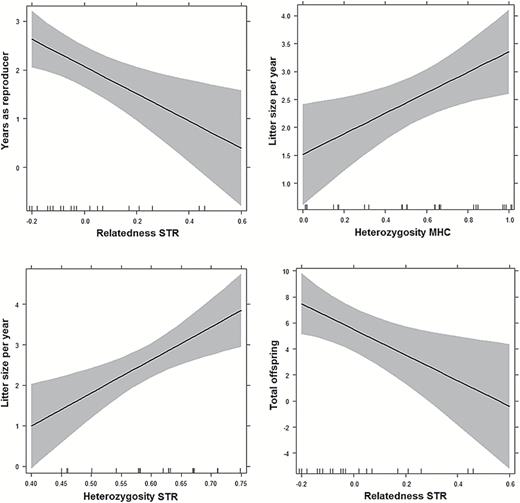
Effect plots of the multiple regressions between fitness proxies of breeding wolves (Y axis) and their significant explanatory genetic variables (X axis), as deduced from the best generalized linear mixed models (Table 3). Tic marks on horizontal axes indicate observations and shaded areas underlie 95% confidence intervals. The number of years as reproducers (top-left) was significantly correlated to the relatedness at the 12 microsatellites, with a negative effect. The average litter size per year (top-right and bottom-left) was positively correlated to the heterozygosity at MHC and STR loci, whereas the total offspring (bottom-right) was correlated to the relatedness at STR loci, with a negative effect.
Generalized linear mixed models correlating 3 fitness proxies (YR = years as reproducers, LSY = litter size per year, TO = total offspring) to relatedness (r) and heterozygosity (Ho) of the breeding pair members at the 12 microsatellites and 3 MHC loci
| Model . | Y ~ Ho(MHC) + Ho(STR) + r(MHC) + r(STR) . | ||||||
|---|---|---|---|---|---|---|---|
| Fitness proxy . | AICc . | R2 . | Variable . | β . | SE . | t . | P . |
| YR | 82.63 | 0.35 | Intercept | 3.334 | 1.509 | 2.209 | 0.0389* |
| Ho(MHC) | 0.494 | 0.677 | 0.731 | 0.4741 | |||
| Ho(STR) | −2.664 | 2.361 | −1.128 | 0.2724 | |||
| r(MHC) | 0.491 | 0.374 | 1.311 | 0.2047 | |||
| r(STR) | −2.795 | 0.902 | −3.099 | 0.0056** | |||
| LSY | 85.68 | 0.39 | Intercept | −2.583 | 1.629 | −1.586 | 0.1284 |
| Ho(MHC) | 1.631 | 0.731 | 2.232 | 0.0372* | |||
| Ho(STR) | 7.089 | 2.547 | 2.783 | 0.0115* | |||
| r(MHC) | 0.633 | 0.404 | 1.568 | 0.1325 | |||
| r(STR) | −1.052 | 0.973 | −1.081 | 0.2928 | |||
| TO | 139.38 | 0.32 | Intercept | −3.737 | 6.237 | −0.599 | 0.5559 |
| Ho(MHC) | 4.567 | 2.799 | 1.632 | 0.1184 | |||
| Ho(STR) | 10.981 | 9.756 | 1.126 | 0.2737 | |||
| r(MHC) | 2.862 | 1.547 | 1.851 | 0.0591 | |||
| r(STR) | −8.881 | 3.728 | −2.382 | 0.0273* | |||
| Model . | Y ~ Ho(MHC) + Ho(STR) + r(MHC) + r(STR) . | ||||||
|---|---|---|---|---|---|---|---|
| Fitness proxy . | AICc . | R2 . | Variable . | β . | SE . | t . | P . |
| YR | 82.63 | 0.35 | Intercept | 3.334 | 1.509 | 2.209 | 0.0389* |
| Ho(MHC) | 0.494 | 0.677 | 0.731 | 0.4741 | |||
| Ho(STR) | −2.664 | 2.361 | −1.128 | 0.2724 | |||
| r(MHC) | 0.491 | 0.374 | 1.311 | 0.2047 | |||
| r(STR) | −2.795 | 0.902 | −3.099 | 0.0056** | |||
| LSY | 85.68 | 0.39 | Intercept | −2.583 | 1.629 | −1.586 | 0.1284 |
| Ho(MHC) | 1.631 | 0.731 | 2.232 | 0.0372* | |||
| Ho(STR) | 7.089 | 2.547 | 2.783 | 0.0115* | |||
| r(MHC) | 0.633 | 0.404 | 1.568 | 0.1325 | |||
| r(STR) | −1.052 | 0.973 | −1.081 | 0.2928 | |||
| TO | 139.38 | 0.32 | Intercept | −3.737 | 6.237 | −0.599 | 0.5559 |
| Ho(MHC) | 4.567 | 2.799 | 1.632 | 0.1184 | |||
| Ho(STR) | 10.981 | 9.756 | 1.126 | 0.2737 | |||
| r(MHC) | 2.862 | 1.547 | 1.851 | 0.0591 | |||
| r(STR) | −8.881 | 3.728 | −2.382 | 0.0273* | |||
AIC, Akaike’s Information Criterion; df, degrees of freedom.
Significance “**” = 0.01 and “*” = 0.05.
Generalized linear mixed models correlating 3 fitness proxies (YR = years as reproducers, LSY = litter size per year, TO = total offspring) to relatedness (r) and heterozygosity (Ho) of the breeding pair members at the 12 microsatellites and 3 MHC loci
| Model . | Y ~ Ho(MHC) + Ho(STR) + r(MHC) + r(STR) . | ||||||
|---|---|---|---|---|---|---|---|
| Fitness proxy . | AICc . | R2 . | Variable . | β . | SE . | t . | P . |
| YR | 82.63 | 0.35 | Intercept | 3.334 | 1.509 | 2.209 | 0.0389* |
| Ho(MHC) | 0.494 | 0.677 | 0.731 | 0.4741 | |||
| Ho(STR) | −2.664 | 2.361 | −1.128 | 0.2724 | |||
| r(MHC) | 0.491 | 0.374 | 1.311 | 0.2047 | |||
| r(STR) | −2.795 | 0.902 | −3.099 | 0.0056** | |||
| LSY | 85.68 | 0.39 | Intercept | −2.583 | 1.629 | −1.586 | 0.1284 |
| Ho(MHC) | 1.631 | 0.731 | 2.232 | 0.0372* | |||
| Ho(STR) | 7.089 | 2.547 | 2.783 | 0.0115* | |||
| r(MHC) | 0.633 | 0.404 | 1.568 | 0.1325 | |||
| r(STR) | −1.052 | 0.973 | −1.081 | 0.2928 | |||
| TO | 139.38 | 0.32 | Intercept | −3.737 | 6.237 | −0.599 | 0.5559 |
| Ho(MHC) | 4.567 | 2.799 | 1.632 | 0.1184 | |||
| Ho(STR) | 10.981 | 9.756 | 1.126 | 0.2737 | |||
| r(MHC) | 2.862 | 1.547 | 1.851 | 0.0591 | |||
| r(STR) | −8.881 | 3.728 | −2.382 | 0.0273* | |||
| Model . | Y ~ Ho(MHC) + Ho(STR) + r(MHC) + r(STR) . | ||||||
|---|---|---|---|---|---|---|---|
| Fitness proxy . | AICc . | R2 . | Variable . | β . | SE . | t . | P . |
| YR | 82.63 | 0.35 | Intercept | 3.334 | 1.509 | 2.209 | 0.0389* |
| Ho(MHC) | 0.494 | 0.677 | 0.731 | 0.4741 | |||
| Ho(STR) | −2.664 | 2.361 | −1.128 | 0.2724 | |||
| r(MHC) | 0.491 | 0.374 | 1.311 | 0.2047 | |||
| r(STR) | −2.795 | 0.902 | −3.099 | 0.0056** | |||
| LSY | 85.68 | 0.39 | Intercept | −2.583 | 1.629 | −1.586 | 0.1284 |
| Ho(MHC) | 1.631 | 0.731 | 2.232 | 0.0372* | |||
| Ho(STR) | 7.089 | 2.547 | 2.783 | 0.0115* | |||
| r(MHC) | 0.633 | 0.404 | 1.568 | 0.1325 | |||
| r(STR) | −1.052 | 0.973 | −1.081 | 0.2928 | |||
| TO | 139.38 | 0.32 | Intercept | −3.737 | 6.237 | −0.599 | 0.5559 |
| Ho(MHC) | 4.567 | 2.799 | 1.632 | 0.1184 | |||
| Ho(STR) | 10.981 | 9.756 | 1.126 | 0.2737 | |||
| r(MHC) | 2.862 | 1.547 | 1.851 | 0.0591 | |||
| r(STR) | −8.881 | 3.728 | −2.382 | 0.0273* | |||
AIC, Akaike’s Information Criterion; df, degrees of freedom.
Significance “**” = 0.01 and “*” = 0.05.
Discussion
Contrary to sexual selection models assuming advantages for disassortative matings (Kamiya et al. 2014), our study did not show evidences of MHC-based disassortative mate choice in 26 breeding pairs from 19 packs of wild-living gray wolves from the Italian population. Conversely, we found that wolves preferentially chose mates who had less amino acid differences at MHC class II loci than expected under random mating. Although not significantly, an excess of MHC similarity appeared also when comparing the number of AA differences between observed versus alternative possible mates, or when considering the levels of allele sharing at MHC loci between observed breeders. Overall, these results indicate the absence of an MHC-based disassortative pattern, but are rather compatible with signals of positive-assortative mating. Although the most popular hypotheses on the benefits of sexual selection assume a disassortative mate choice (Piertney and Oliver 2006; Ejsmond et al. 2014), a number of studies failed to document such a scheme in wild and captive populations (with exhaustive examples presented in (Huchard et al. 2010). Assortative mating was conversely observed in a wild population of house sparrow, where mates shared more MHC alleles than expected by random (Bonneaud et al. 2006). A higher reproductive success for MHC-similar mates was documented in the tiger salamander (Bos et al. 2009). Assortative mating was also recently documented in the European badger, with a smaller amino acid distance between actual breeders compared with random mates at MHC class II loci (Sin et al. 2015). Benefits of an assortative mate choice have been so far demonstrated to reduce outbreeding in hybrid zones and limit autoimmune disorders caused by genetic incompatibilities (Tregenza and Wedell 2000), maximize the adaptation to local pathogen pressures (Sin et al. 2015) and avoid the disruption of linked and co-adapted genes (Roberts 2009). Moreover, Lewis (1998) argued that in social species a preferential association with MHC-similar individuals should decrease the probability of infection with unfamiliar pathogens that could be carried by immigrant individuals who do not share the same immunological variants. Consequently, choosing an MHC-similar mate would be directly beneficial for the breeders, that will more likely avoid interaction with potential disease carriers, as long as this does not increase the general inbreeding levels (Drury 2010). Parallel, inbreeding avoidance may not be necessary in expanding populations (Jamieson et al. 2009), such as the Italian wolf, where the probability to encounter related individuals outside the natal pack is relatively low (Geffen et al. 2011). In fact, when analyzing several wolf populations at neutral loci, Geffen et al. (2011) did not find any evidence of inbreeding avoidance between mates, except within natal groups. Moreover, inbreeding in wolves can be also prevented by other commonly adopted behaviors, such as long-distance dispersals (Caniglia et al. 2014).
However, when considering the correlation of MHC and STR diversity and dissimilarity of mates to fitness proxies deduced from pedigree data, we found a significant effect of the genome-wide relatedness r(STR) of mates on the number of years they reproduced (YR) and on the total offspring they produced (TO): the lower the relatedness, the higher the fitness proxy (Figure 2). These findings suggest that positive assortative mating at the MHC (highlighted by the lower AA difference between mates) may be balanced by a greater fitness of mates with a higher genome-wide dissimilarity (inbreeding avoidance).
Moreover, the average litter size per year (LSY) was positively correlated to the average heterozygosity of mates, both at the MHC and STRs, as also shown by the comparisons between MHC-homozygous versus heterozygous breeders (Figure 1). These results confirm the presence of a heterozygote advantage demonstrated in a number of studies on wolves and other vertebrate species, both at neutral (García-Navas et al. 2009) and MHC loci (Setchell and Huchard 2010; Thoss et al. 2011; Knafler et al. 2012; Niskanen et al. 2014). Despite the possible presence of MHC-based assortative mating schemes, MHC polymorphism can thus be maintained via a heterozygote advantage hypothesis, by providing resistance to a wider range of diseases or pathogens and possibly resulting in a higher individual survival (Hedrick 2012).
Such a panel of potential benefits likely reflects the social structure of wolves, the pack, where a single pair of well-fit mates can reproduce each year, with few exceptions (Vonholdt et al. 2008). This mechanism allows for a constant adaptation to the environment, which includes both its resources and its pathogens. Therefore, MHC-based assortative mating could be explained by a local co-adaptation of the breeders and would allow to constantly keep up with the local environmental changes, including pathogens (Penn and Potts 1999), while reducing the interactions with possibly sick or pathogen-carrying individuals (Drury 2010). This could be especially true in expanding populations, where a significant portion of packs is founded by dispersing individuals that establish themselves in new territories (Vonholdt et al. 2008; Caniglia et al. 2014). Of course, our study would greatly benefit from a wider sampling of the studied population. However, obtaining genetic and reproductive information on elusive carnivore species such as the wolf is far from trivial, especially in populations where active management strategies or trapping of individuals are not applied. Thus, we sought to exploit a large source of non-invasive samples (Caniglia et al. 2014), although fecal DNA has been seldom used in MHC gene sequencing (Yang et al. 2014). Our study represents the first application of noninvasive genetic sampling to investigate the role of MHC on sexual selection in canids. Our procedure showed a good MHC genotyping success (comparable to values reported in other noninvasive genetic studies on MHC; Yang et al. 2014) and reliability (as confirmed by the double-sequencing controls), and promises to be extended to future large-scale monitoring projects.
In conclusion, although contrasting with the most common research results reporting dissimilar mating schemes, our models were able to explain part of the variance of multiple fitness proxies in an expanding wolf population and to elucidate the genetic bases driving the observed mating patterns.
This type of information could be also useful to increase the chance of success of active management actions such as reintroduction projects or the release of rescued individuals.
Supplementary Material
Supplementary material can be found at http://www.jhered.oxfordjournals.org/
Funding
Italian Ministry of Environment; the Emilia-Romagna Region (thanks to Dr. M. L. Bargossi and Dr. M. L. Zanni) sponsored the genotyping work at the Laboratorio di Genetica, Istituto Superiore per la Protezione e la Ricerca Ambientale; and University of Bologna (to M.G. and S.L.).
Acknowledgments
We kindly thank Phil Hedrick (University of Arizona), Edoardo Velli (University of Roma 3), and Aritz Ruiz-Gonzales (University of the Basque Country) for their useful comments, and many collaborators that contributed to collect the wolf samples in Italy. We also thank the Associated Editor and 2 anonymous reviewers for their useful comments that helped to considerably improve the manuscript.
References
Anderson DR, Link WA, Johnson DH, Burnham KP. 2001. Suggestions for presenting the results of data analyses. J Wildl Manag. 65:373–378.
Kennedy LJ, Carter SD, Barnes A, Bell S, Bennett D, Ollier WE, Thomson W. 1998. Nine new dog DLA-DRB1 alleles identified by sequence-based typing. Immunogenetics. 48:296–301.
Mech LD, Boitani L. 2003. Wolf social ecology. In: Mech LD, Boitani L, editors. Wolves: behavior, ecology and conservation. Chicago (IL): The University of Chicago Press. p. 1–34.
Packard JM. 2003. Wolf behavior: reproductive, social and intelligent. In: Mech LD, Boitani L, editors. Wolves: behavior, ecology and conservation. Chicago (IL): The University of Chicago Press. p. 35–65.
Author notes
Address correspondence to Marco Galaverni at the address above, or e-mail: [email protected].
Data deposited at Dryad: http://dx.doi.org/doi:10.5061/dryad.t6n8h
Corresponding Editor: Robert Wayne



