Abstract
Worldwide inequalities in vaccine availability are expected to affect the spread and spatial distribution of infectious diseases. It is unclear, however, how spatial variation in vaccination coverage can affect the long-term evolution of pathogens. Here we use an analytical model and numerical simulations to analyse the influence of different imperfect vaccines on the potential evolution of pathogen virulence in a two-population model where vaccination coverage varies between populations. We focus on four vaccines, with different modes of action on the life cycle of a pathogen infecting two host populations coupled by migration. We show that, for vaccines that reduce infection risk or transmissibility, spatial heterogeneity has little effect on pathogen prevalence and host mortality, and no effect on the evolution of pathogen virulence. In contrast, vaccines that reduce pathogen virulence can select for more virulent pathogens and may lead to the coexistence of different pathogen strains, depending on the degree of spatial heterogeneity in the metapopulation. This heterogeneity is driven by two parameters: pathogen migration and the difference in the vaccination rate between the two populations. We show that vaccines that only reduce pathogen virulence select mainly for a single pathogen strategy in the long term, while vaccines that reduce both transmission and virulence can favor the coexistence of two pathogen genotypes. We discuss the implications and potential extensions of our analysis.
Introduction
A major challenge when designing public health measures is to balance the often urgent need to manage epidemic and endemic infectious diseases with potential long-term evolutionary side effects (Day et al., 2020; Dieckmann et al., 2005). Vaccines that reduce pathogen spread or harmfulness are a key tool for the management of infectious diseases in human and animal populations. At the same time, vaccination, like other public health measures, may trigger an evolutionary response that could lead to pathogen adaptation and the erosion of vaccine efficacy. Even though vaccination has been shown to be more durable than other therapeutic interventions (Kennedy and Read, 2017, 2018), the use of imperfect vaccines may promote the evolution of pathogen traits, such as virulence, transmission or immune escape (Gandon and Day, 2008; McLeod and Gandon, 2022; Read et al., 2015). Evidence of vaccine-driven pathogen evolution is mixed, with some vaccines causing little or no vaccine adaptation (such as the anti-measles vaccine), and other vaccines having been tied with increases in pathogen virulence (such as the various vaccines against Marek’s disease in poultry, Day et al., 2022; Gandon and Day, 2008; Read et al., 2015). Previous theoretical studies have shed light on this dichotomy, showing that the evolution of pathogen life-history traits in response to vaccination can be favoured when the vaccine is imperfect and acts by reducing the cost of virulence (Gandon et al., 2001, 2003; Read et al., 2015), compared to vaccines that solely target pathogen reproduction by decreasing the susceptibility and transmissibility of hosts. This pattern has also been shown to be broadly preserved in the presence of spatial structure (Zurita-Gutiérrez and Lion, 2015) or temporal heterogeneity (Walter and Lion, 2021).
However, human and animal populations are often characterized by heterogeneity in vaccination coverage and complex patterns of dispersal between local populations. For instance, in human populations, different regions, even geographically close, may have very different vaccination coverages, as exemplified by regional differences in vaccination against measles in the Netherlands (Knol et al., 2013) or the worldwide inequality of access to COVID-19 vaccines (Mathieu et al., 2021; Rydland et al., 2022). Furthermore, the globalization of travel and trade tends to increase the connections between local populations and facilitate the dispersal of hosts and pathogens, with potentially worrying consequences for pathogen spread and evolution (Boots and Sasaki, 1999; Memish et al., 2015). Hence, host populations are best viewed as metapopulations of local patches with different epidemiological characteristics, coupled by host or pathogen migration. It is not clear how the interplay between migration and spatial heterogeneity in vaccine coverage will affect the epidemiology and evolution of pathogens.
As a first step towards answering this question, we analyse a theoretical model to understand the combined effects of migration and vaccine distribution on the long-term evolution of pathogen virulence in a metapopulation. We consider the simple case of a metapopulation of two host populations connected by pathogen dispersal. Each population is characterized by a distinct vaccination coverage, which may lead to different local optima for the pathogen. As such, the problem we investigate is reminiscent of classical local adaptation models that have shown that a metapopulation with migration between populations with different optima can select for generalist or specialist strategies depending on migration and the degree of similarity between the populations (Day, 2000; Débarre et al., 2013; Meszéna et al., 1997; Mirrahimi and Gandon, 2020; Ronce and Kirkpatrick, 2001). Here, we extend these models to an epidemiolgoical context and ask how these factors may affect the evolution of pathogen polymorphism and what are the implications of such polymorphism for the epidemiological and evolutionary management of diseases.
Following Gandon et al. (2001), we assume the vaccine is imperfect and can have different modes of action on the pathogen’s life cycle. Moreover, we consider a heterogeneous vaccine distribution across the two populations and explore the epidemiological and evolutionary consequences of different vaccine distributions, ranging from homogeneous distributions (i.e., equal distribution between the two populations) to fully heterogeneous distributions (i.e., one population is completely vaccinated and the other completely naive). We investigate, both analytically and numerically, the long-term effects of spatial heterogeneity on the evolution of pathogen virulence, either for vaccines with a single mode of action or for vaccines combining different modes of action on the pathogen’s life cycle. We present and discuss the epidemiological and evolutionary consequences of these different scenarios, as well as the broader implications of our study for infectious disease management.
Epidemiological model
We consider a metapopulation composed of two populations and , coupled by parasite migration (life cycle depicted in Figure 1, see Table 1 for notations). In each population, the host–pathogen interaction is described by a susceptible-infected epidemiological model. Susceptible hosts are produced in each population at rate and vaccinated with a habitat-specific probability. In population , a proportion of new hosts receive the vaccine and enter the vaccinated class , while a proportion enter the unvaccinated class . Likewise, in population , a proportion of new hosts enter the class, and a proportion enter the class. Note that this can be interpreted as a model of vaccination at birth, but we show in Supplementary Material S.7 that an alternative model where adults are vaccinated leads to qualitatively identical results. All hosts die at a natural rate . The metapopulation is infected by a pathogen that can migrate between the two populations at rate , which varies between and . For , there is only local transmission of pathogens and susceptible hosts of population (respectively ) are only infected by infected hosts from population (respectively ). For , susceptible hosts can be equally infected by hosts from population or . We consider that scenarios where is greater than , meaning that susceptible hosts would be more infected by hosts from the other population, would be unrealistic (Park et al. 2015). Infected hosts in a given population transmit the pathogen at a rate that differs for naive ( and ) or vaccinated ( and ) hosts. Similarly, infected hosts in population and immunity state have an additional disease induced mortality . Note that we only consider pathogen migration, and, as a result, host densities are not directly altered by migration. A susceptible host can be infected either by a philopatric pathogen (with probability ) or by an allopatric pathogen (with probability ). This could correspond to at least three scenarios: (a) direct pathogen propagule dispersal, (b) environmental transmission through abiotic or biotic factors or (c) rapid to-and-fro host movements between the two populations (e.g., with workers commuting between two cities). In addition, we assume for simplicity that migration is symmetric between the two populations.
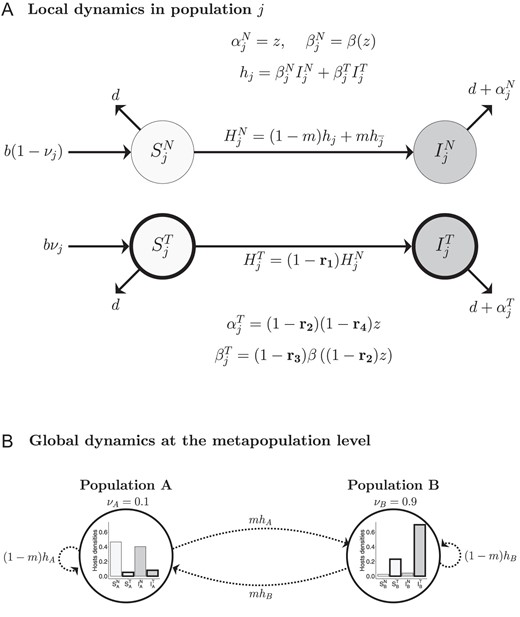
Figure 1.
Schematic presentation of the model. (A) Life cycle of the host–pathogen interaction in the population , showing transition rates between classes. Susceptible hosts are represented in light grey and infected hosts in dark grey, vaccinated hosts are in thick circle and naive hosts in thin. Four types of vaccines are considered: (1) anti-infection vaccines that reduce susceptibility to the pathogen (with efficacy ), (2) anti-growth vaccines that reduce within-host replication and act on both transmission and virulence (with efficacy ), (3) vaccines that only reduce transmissibility (with efficacy ) and (4) vaccines that only reduce virulence (with efficacy ). As shown in the figure, these vaccines affect the force of infection , and the life history traits in the treated class ( and ). See the main text for more details about the mathematical expressions. (B) Transition rates in the metapopulation show how pathogens migration affects the forces of infection and the prevalence in each population. Barplots of hosts densities are shown as examples of population structure at equilibrium with an anti-virulence vaccine, where , , , , and .
Table 1.Table of parameters and variables (k stands for naive (N) or vaccinated (T) hosts; j stands for population A or B).
| Parameter
. | Definition
. |
|---|
| Life-history traits | |
| Disease-induced mortality caused by the pathogen strain in population and class |
| Transmission of the disease of the pathogen strain in population and class |
| Production of propagules by hosts in population |
| Force of infection caused by hosts in population on susceptible hosts in class |
| Reproductive values | |
| Class reproductive value in population |
| Ecology | |
| Influx of susceptible hosts |
| Natural death rate |
| Parasite migration rate |
| Vaccines | |
| Probability of vaccinating new hosts in population |
| |
| Efficacy of anti-infection vaccine |
| Efficacy of anti-growth vaccine |
| Efficacy of anti-transmission vaccine |
| Efficacy of anti-virulence vaccine |
| Susceptibility of hosts () |
| Parameter
. | Definition
. |
|---|
| Life-history traits | |
| Disease-induced mortality caused by the pathogen strain in population and class |
| Transmission of the disease of the pathogen strain in population and class |
| Production of propagules by hosts in population |
| Force of infection caused by hosts in population on susceptible hosts in class |
| Reproductive values | |
| Class reproductive value in population |
| Ecology | |
| Influx of susceptible hosts |
| Natural death rate |
| Parasite migration rate |
| Vaccines | |
| Probability of vaccinating new hosts in population |
| |
| Efficacy of anti-infection vaccine |
| Efficacy of anti-growth vaccine |
| Efficacy of anti-transmission vaccine |
| Efficacy of anti-virulence vaccine |
| Susceptibility of hosts () |
Table 1.Table of parameters and variables (k stands for naive (N) or vaccinated (T) hosts; j stands for population A or B).
| Parameter
. | Definition
. |
|---|
| Life-history traits | |
| Disease-induced mortality caused by the pathogen strain in population and class |
| Transmission of the disease of the pathogen strain in population and class |
| Production of propagules by hosts in population |
| Force of infection caused by hosts in population on susceptible hosts in class |
| Reproductive values | |
| Class reproductive value in population |
| Ecology | |
| Influx of susceptible hosts |
| Natural death rate |
| Parasite migration rate |
| Vaccines | |
| Probability of vaccinating new hosts in population |
| |
| Efficacy of anti-infection vaccine |
| Efficacy of anti-growth vaccine |
| Efficacy of anti-transmission vaccine |
| Efficacy of anti-virulence vaccine |
| Susceptibility of hosts () |
| Parameter
. | Definition
. |
|---|
| Life-history traits | |
| Disease-induced mortality caused by the pathogen strain in population and class |
| Transmission of the disease of the pathogen strain in population and class |
| Production of propagules by hosts in population |
| Force of infection caused by hosts in population on susceptible hosts in class |
| Reproductive values | |
| Class reproductive value in population |
| Ecology | |
| Influx of susceptible hosts |
| Natural death rate |
| Parasite migration rate |
| Vaccines | |
| Probability of vaccinating new hosts in population |
| |
| Efficacy of anti-infection vaccine |
| Efficacy of anti-growth vaccine |
| Efficacy of anti-transmission vaccine |
| Efficacy of anti-virulence vaccine |
| Susceptibility of hosts () |
These assumptions lead to the following ODE system for the population :
where represents the population or , and (resp. ) is the force of infection experienced by a naive (resp. vaccinated) susceptible host in population . This force of infection depends on pathogen migration and is a weighted average of the contributions of infected hosts in populations and , so that , where we use the notation to refer to the non-focal population (i.e., if ), and is the force of infection due to hosts in population :
where (resp. ) is the pathogen’s transmission rate in class (resp. ) in population . Furthermore, we assume that the force of infection on a vaccinated susceptible host in population , , is reduced by a factor compared to that on a naive susceptible host, so that . The full 8-equation ODE system is given in Supplementary Material S.1.
Following Gandon et al. (2001, 2003), we consider four imperfect vaccines with different modes of actions on the pathogen’s life cycle. We assume that the vaccine can either (a) reduce the susceptibility of hosts (anti-infection vaccine, noted ), (b) reduce the within-host growth rate of pathogens (anti-growth vaccine, noted ), (c) reduce pathogen transmission (anti-transmission vaccine, noted ) or (d) reduce disease-induced mortality in infected hosts (anti-virulence vaccine, noted ). Biological examples of each type of vaccine are presented in Walter and Lion (2021), and the relationship between the vaccine efficacy parameters and the epidemiological parameters is given in Figure 1A.
With these assumptions, the typical epidemiological behaviour of our model is either pathogen extinction or convergence to an endemic state where the densities of all classes of susceptible and infected hosts settle on equilibrium values. In the next section, we use adaptive dynamics theory to analyse how the migration rate , and the probabilities of vaccination and affect the long-term evolutionary outcome of the pathogen population, before applying the results to specific epidemiological scenarios.
Evolutionary dynamics
Assuming that the metapopulation infected by a resident strain of the pathogen has reached an epidemiological equilibrium, we consider a scenario where a mutant strain of the pathogen appears with different life-history traits and investigate the invasion success of this mutant using the adaptive dynamics framework (Dieckmann et al., 2005; Geritz et al., 1998).
Mutant invasion fitness
Consider that the resident pathogen has trait and that a mutant strain appears in the metapopulation with a different trait value, noted . We assume that both transmission and virulence are functions of the trait (we will provide explicit examples for these functions in the “Numerical exploration of the effect of migration and spatial heterogeneity” section) and, consequently, the mutation leads to different life-history traits for the mutant pathogen, denoted by a prime (e.g., is the virulence caused by the mutant pathogen in naive infected hosts in population ). The mutant can either die out or invade and replace the resident strain. Mutant success depends on its invasion fitness, , that represents the number of surviving mutant offspring per mutant parent when the mutant allele is rare (Hurford et al., 2009; Otto and Day, 2011). Note that this invasion fitness is measured per generation (i.e., it measures the expected number of secondary infections over the duration of a primary infection by the mutant), but an equivalent invasion fitness could be derived per unit of time. In our model, this takes the form (Supplementary Material S.2):
with
the mutant reproduction number in the population ( or ), where
are, respectively, the mutant reproduction numbers in naive or vaccinated hosts in population . In other words, the reproduction numbers and quantify the overall productivity of the mutant in each population. Note that the invasion fitness of the mutant, , depends both on the resident trait through susceptible densities at equilibrium and (included in and ), and on the mutant trait through the transmissibility ( and ) and virulence ( and ) traits, which are included in and . The mutant invades if and dies out if . For completeness, we note that expression (3) is also valid for a mutant arising in a polymorphic resident population (i.e., when the trait is a vector), as the resident environment only acts through the densities of susceptible hosts.
Selection gradient
In order to gain analytical insight into the long-term evolution of the trait of interest, which governs the virulence and the transmission of the pathogen, we calculate the selection gradient, . This amounts to calculating the partial derivative of the mutant invasion fitness with respect to evaluated at . The zeros of the selection gradient correspond to the evolutionary singularities, noted . In our model, it can be expressed as (Supplementary Information S.2):
where is a short-hand notation for the derivative of the mutant reproduction number in population , calculated with respect to and evaluated at (see Supplementary Material S.2 for a full expression), and are the local reproduction numbers in the resident population at equilibrium (defined as in Equation 4, but without the primes), and
are the class reproductive values of pathogens in populations and , respectively. The class reproductive values sum to 1 (e.g., , see Supplementary Material S.2) and can therefore be interpreted as measures of host quality for the pathogen which weigh the effects of selection in the two populations (Gandon, 2004; Lion, 2018; Lion and Gandon, 2022; Rousset, 1999; Walter and Lion, 2021). When the two populations are isolated (), there are two distinct singularities for each population, and , which corresponds to the zeros of and , respectively. In the extreme case where a population (say, ) represents a habitat of very poor quality for pathogens (e.g., tends towards ), then, at the metapopulation level, the singularity will tend towards the singularity of the good habitat, . On the other hand, when the two populations have similar qualities, the singularity at the metapopulation level will be intermediate between and .
Using Equation 7, we can rewrite condition as
Equation 8 is reminiscent of fitness set representation that have been used to obtain a geometric understanding of adaptation in heterogeneous environments (Gandon et al., 2003; Levins, 1962), although here the graphical analysis is complicated by the fact that the pathogen’s fitness set is not fixed because it depends on epidemiological feedbacks via the densities of susceptible hosts. Yet, this expression can be used to understand how the evolutionary outcome depends on the interplay between the local productivity of each population and migration. When migration is maximal (), the right-hand side of (9) is equal to , so that, at an evolutionary singularity, an increase in pathogen reproductive success in population must be exactly compensated by a decrease in population . However, when decreases, the balance will depend on migration and on the relative productivity of the two populations. If a population has a higher productivity (i.e., ) it will drive evolution towards a specialization to this population (i.e., evolves towards ). In other words, this source–sink evolutionary dynamics is driven by the source. Yet, since , epidemiological feedbacks can affect the number of singularities and their positions with respect to and , as we shall see in our numerical analysis below.
Stability of evolutionary equilibria
After convergence by successive mutations towards an evolutionary singularity, two different outcomes are possible. If the singularity cannot be invaded by nearby mutants, it corresponds to an evolutionarily stable strategy (ESS). If nearby mutants can invade, the singularity is called a branching point (BP), and the population can split into two coexisting morphs. The stability of the singularity can be investigated by calculating the second-order derivative of the invasion fitness, , near the singularity . If , the evolutionary singularity is stable. If , the singularity is unstable. In our model, takes the form
where is the second order derivative of the mutant reproduction number in population with respect to evaluated at (see Supplementary Material S.2 for a full expression), and
It is useful to interpret Equations 9 by using the analogy of the fitness landscape. The first two terms on the right-hand side of Equation 9 are a weighted average of the local curvature of the fitness landscapes in populations and , while in Equation 10 depends on the squared difference of the slopes of the fitness landscapes, locally near the singularity. Thus, is always positive and therefore acts as a destabilizing force. In particular, this means that, even if the selection is locally stabilizing around the singularity in both populations, so that the partial derivatives in Equation 9 are both negative, selection can be disruptive at the metapopulation level when is large enough. This effect is due to divergent directional selection on the trait in the two populations, as captured by the difference . In general, the singular strategies will be evolutionarily stable if and unstable otherwise.
With a concave-down, monotonically increasing transmission–virulence trade-off, the sign of the second derivatives is negative unless the vaccine has a strong anti-growth component (Gandon et al., 2003). Hence, when tends towards zero, we expect the evolutionarily singularity to be always an ESS. From Equation 10, we see that will be vanishingly small when (a) the class reproductive value of the pathogen is zero in one of the populations (e.g., ); (b) the direction of selection is the same in both habitats (e.g., ); and (c) the metapopulation is well mixed ().
On the other hand, Equation 10 shows that a low migration rate will cause to increase and lead to evolutionarily unstable singularities. Hence, the singularity will tend to be unstable at low migration rates, unless the two populations resemble a single population (either because directional selection is equal in both [] or because one of the populations does not contribute to selection [ or ]).
Numerical exploration of the effect of migration and spatial heterogeneity
So far, our general adaptive dynamics analysis of pathogen evolution in a monomorphic resident population predicts that, in general, we expect a high migration rate to lead to a single ESS, whereas unstable singularities, potentially leading to polymorphism, can exist in the limit of low migration. In this section, we investigate different biological scenarios to make more specific predictions on the evolutionary outcomes, using both our monomorphic AD anaytical results and numerical simulations, which allow us to explore the polymorphic dynamics of the population and to relax the assumption of mutation-limited evolution used in AD.
We quantify the spatial heterogeneity of the metapopulation using the parameter , which captures the variation in vaccination coverage between the two populations. Without loss of generality, we assume that the vaccination coverage is always higher in population , so that takes values between 0 (homogeneous distribution, ) and 1 (maximal heterogeneity, and ). For simplicity, we also assume in the main text that the average probability of vaccination at birth is , so that and ), an assumption that we relax in Supplementary Material S.7.
In line with previous theoretical studies on virulence evolution (Alizon et al., 2009), our results rely on a positive correlation between transmission and virulence, captured by an increasing and saturating transmission–virulence trade-off function. More specifically, we use the functional form in all our simulations.
Anti-infection and anti-transmission vaccines
For anti-infection () or anti-transmission () vaccines, we show that spatial structure does not affect pathogen evolution (Supplementary Material S.2). Indeed, even though the and components of the vaccine affect the efficacy of vaccination and the reproductive value of the pathogen in vaccinated hosts, the optimal virulence is independent of these parameters in the absence of coinfections (Gandon et al., 2001, 2003; Walter and Lion, 2021). Indeed, as discussed in previous studies in well-mixed single-population models, the ES virulence is only affected by vaccination if the vaccine acts on virulence directly. Since the optimal virulence (i.e., the ES virulence in the absence of migration) does not vary between the two populations, the ES virulence depends neither on the migration rate nor on the variation in vaccination coverage . In the following, we therefore focus on anti-growth () and anti-virulence () vaccines.
Anti-growth and anti-virulence vaccines
Non-spatial models have shown that anti-growth () and anti-virulence () vaccines can select for increased virulence (Gandon et al., 2001, 2003; Read et al., 2015; Walter and Lion, 2021). Our results show that, in line with these earlier results, both and vaccines select for higher virulence, but that this effect is modulated by the migration rate and the heterogeneity in vaccination coverage . In particular, there is a marked difference between and vaccines: Anti-growth vaccines () allow for the coexistence of a low- and a high-virulence pathogen when migration is below a threshold (Figures 2A and 3A). In contrast, anti-virulence vaccines () are less conducive to the emergence of polymorphism (Figures 2B and 3B).
![Effect of migration and vaccination on the long-term evolution of the pathogen. The plain and dotted black lines represent the monomorphic singularities calculated by the adaptive dynamics. Plain black lines represent locally evolutionarily stable singularities, while dotted black lines represent locally evolutionarily unstable singularities (BPs or repellor). The upper plain grey line represents the ESS in a population fully vaccinated, and the lower plain grey line represents the ESS in a population without vaccination. The black crosses represent the virulence strategies of the globally stable polymorphic equilibrium (see Supplementary Material S.4 for further information). (A) For the anti-growth vaccine, when m∈[0,0.33] we observe bistatility (pink area), with m∈[0.33,0.38], there is a unique branching point (yellow area), and with m∈[0.38,0.5], there is a unique ESS (blue area). For the anti-vrulence vaccine, when m∈[0,0.02], the monomorphic singularity is a branching point (yellow area) and with m∈[0.02,0.5], the singularity is an ESS (blue area). Here δ=0.75, μ=0.01, Vm=0.001 and for (a) r2=0.9 and (b) r4=0.9 and all the other parameters as in Figure 3.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/jeb/37/2/10.1093_jeb_voad016/1/m_voad016_fig2.jpeg?Expires=1749736571&Signature=oeje81hNAKkl1HK4TyRPFTJIBTRX~4ZYIdTIv6VL~s-FkON-aHdCnXaT3sz5CFbRxJJ6P-6JGCG8NoPOOh6-tvw8INSxpTVPrB8edA19jtXHV4-PadamxBdfnkk3fN2vwFoKtYYNEGnMMr7FK2B3HLSQFiSvJzHI9o3tSjuM~Gy3kwEnkKsu90wxGEOlL3~pZpdq6DquMIoF17he7tK081eSf1W5-G-O7jyMmOjt3SPzZM4wypBqMu2b-F8dDznMSd1qKiG34T0DUDuehn9GI3qkpMenJVwRz3YWrhYUJ1g739arWRdwaZlkWz1sd4fKjzhZiKVOh520WbcEyI5Eug__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Figure 2.
Effect of migration and vaccination on the long-term evolution of the pathogen. The plain and dotted black lines represent the monomorphic singularities calculated by the adaptive dynamics. Plain black lines represent locally evolutionarily stable singularities, while dotted black lines represent locally evolutionarily unstable singularities (BPs or repellor). The upper plain grey line represents the ESS in a population fully vaccinated, and the lower plain grey line represents the ESS in a population without vaccination. The black crosses represent the virulence strategies of the globally stable polymorphic equilibrium (see Supplementary Material S.4 for further information). (A) For the anti-growth vaccine, when we observe bistatility (pink area), with , there is a unique branching point (yellow area), and with , there is a unique ESS (blue area). For the anti-vrulence vaccine, when , the monomorphic singularity is a branching point (yellow area) and with , the singularity is an ESS (blue area). Here , , and for (a) and (b) and all the other parameters as in Figure 3.
For anti-growth vaccines (), our results predict that, at low migration, polymorphism arises due to local adaptation within the low- and high-coverage habitats. As migration increases, the breakdown of spatial structure interferes with local adaptation, which favours a single generalist strategy. Overall, this corresponds to our general intuitive understanding of the interplay between migration and local adaptation in metapopulation models. More precisely, our AD analysis allows us to tease apart the effect of migration () vs. heterogeneity () and predicts three distinct long-term evolutionary outcomes: (i) convergence towards a single ESS, (ii) evolutionary branching or (iii) evolutionary bistability, with convergence towards different ESSs depending on the initial conditions. Both outcomes (ii) and (iii) can potentially lead to polymorphism. To see this, we first explore the effect of the migration , on the singularities, for a fixed value of the vaccination heterogeneity (Figure 2). At high migration (), we have a single evolutionary stable virulence. As migration decreases and the two populations become less connected, the monomorphic singularity turns into a BP, leading to the splitting of the population into two morphs that evolve towards a dimorphic ESS (the crosses in Figure 2). As migration further decreases, we enter the bistability region, where the monomorphic singularity becomes an evolutionary repellor (central dotted line), surrounded by two other singularities. Near , these two singularities are BPs and the dynamics eventually converge towards the dimorphic ESS (crosses). For lower migration, the two singularities are evolutionarily stable, and evolutionary dynamics can evolve towards three distinct ESSs depending on the initial conditions: either one of two monomorphic ESSs (plain lines) or a dimorphic ESS (crosses). A similar pattern was observed in previous studies (Débarre et al., 2013; Mirrahimi and Gandon, 2020) that analysed the joint evolution of local adaptation and demography in a two-population model. Importantly, as in these previous studies, we find that the dimorphic ESS is always globally stable in the bistability region, whereas the monomorphic ESS are only locally stable (Supplementary Material S.2). Hence, with enough mutation and standing variation, the population dynamics will eventually converge to the globally stable dimorphic attractor. To numerically calculate the dimorphic ESS, we do not use the AD analysis, but rather directly use numerical simulations where we track the dynamics of a continuous trait distribution under selection and mutation (Supplementary Material S.4). However, even if, for simplicity, we do not explicitly explore the dimorphic adaptive dynamics in our model, the AD analysis presented in the previous section is sufficient to shed light on the key factors (e.g., migration and habitat heterogeneity) that cause the shift from a single stable ESS to a dimorphic evolutionary outcome.
Interestingly, for anti-virulence () vaccines, decreasing migration does not promote polymorphism, except when pathogen migration is completely local (Figure 2B). We only observe a single ES virulence, which increases as migration becomes more local. This is because, in population B, which has a higher coverage of anti-virulence vaccine, infected hosts have a longer infection period, but no reduction in transmission. This leads to a higher productivity () and a higher prevalence (see Figure 1B). As discussed above, Equation 8 shows that when migration becomes local, the evolutionary outcome is increasingly driven by the source. This explains why the ESS gets closer to the optimum of population , which corresponds to higher virulence (Gandon et al., 2001, 2003). As explained in Discussion, the discrepancy between the predictions for and vaccines can be explained by the specific epidemiological feedbacks that take place in each scenario.
In Figure 3, we explore the interaction between the effects of the heterogeneity in vaccination coverage and migration on pathogen evolution, for both anti-growth and anti-virulence vaccines. In each of these figures, the bottom right corner corresponds to the most heterogeneous metapopulation (low migration and maximal difference in vaccination coverage). In contrast, the upper-left corner represents a completely homogeneous metapopulation ( and ), and corresponds to the results of Gandon et al. (2001) (without superinfection) or Walter and Lion (2021) (without temporal fluctuations). As expected, when increases (i.e., as the populations become more different), polymorphism emerges more readily, although again there is a clear difference between anti-growth and anti-virulence vaccines. We note however that this difference may be partly dependent on the specific transmission–virulence trade-off shape we assume in this study.
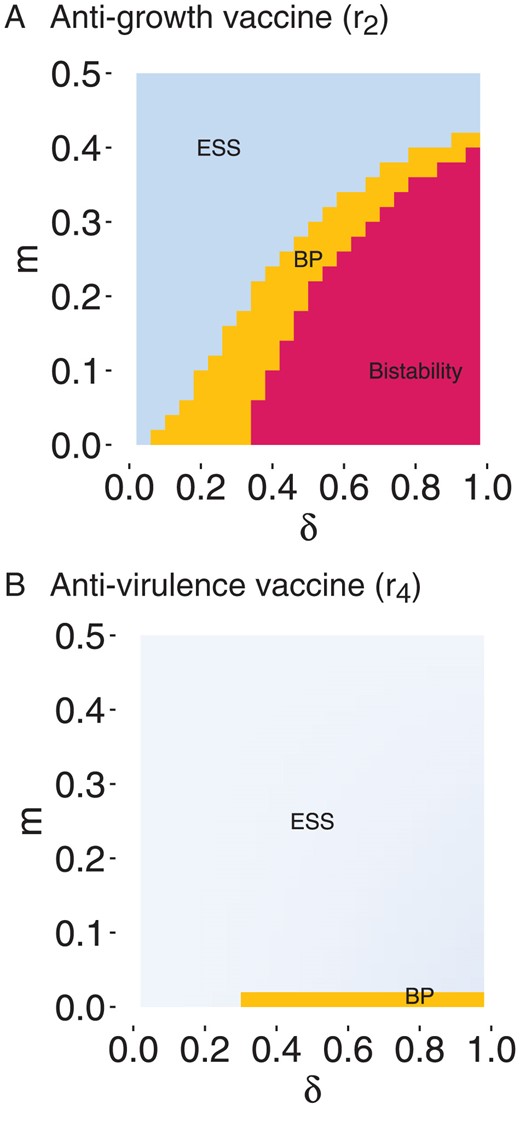
Figure 3.
Effect of migration and heterogeneity in vaccination coverage on long-term evolutionary outcome. Long-term evolutionary state calculated using adaptive dynamics, for (A) anti-growth and (B) anti-virulence vaccines. Evolutionary stable virulence (ESS) is represented in blue, following the gradient shown in Figure 4, branching point (BP) in orange and bistability in pink, according to and . Here and the other parameters are as in Figure 3.
In Figure 4, we explore the effects of a vaccine that combines multiple components on the evolution of the pathogen. In particular, Figure 4A shows that the combination of and effects can further expand the parameter space where polymorphism is expected to emerge and be stably maintained in the long term. In Figure 4B, we also explore the effect of a vaccine with a combination of and effects. Figure 4B shows that even if is expected to have no effect on pathogen evolution, we see a major interaction with the effect of since reduces the possibility of bistability and branching. A similar effect is observed in a combination between and (see Supplementary Material S.3).
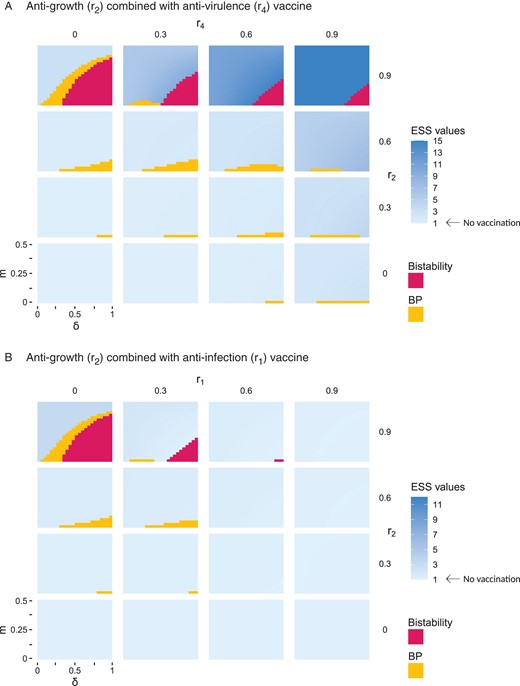
Figure 4.
Long-term evolutionary outcome for different combinations of vaccines. We plot the long-term evolutionary state calculated using adaptive dynamics, for anti-growth vaccine combined with anti-virulence, as a function of and . Branching points (BP) are represented in yellow, bistability in pink, and ESS values in a gradient of blue. Other parameters as in Figure 3
Discussion
Here, we study the long-term evolution of pathogen life-history traits in a metapopulation, in response to the selective pressures caused by imperfect vaccines with different modes of action. Our analysis confirms the general message of earlier non-spatial models (Gandon et al., 2001, 2003; Walter and Lion, 2021) that there is a sharp dichotomy between vaccines that only have an effect on pathogen reproduction (e.g., anti-infection and anti-transmission vaccines) and vaccines that reduce the cost of virulence for the pathogen (i.e., anti-growth and anti-virulence vaccines). With the first type of vaccine, we predict no effect of vaccination on the long-term evolution of pathogen virulence (or potentially even a decrease in virulence when multiple infections are taken into account, see e.g. Gandon et al. 2001). In contrast, for anti-growth and anti-virulence vaccines, we show that pathogen virulence can evolve in response to vaccination. In addition, we show that the long-term evolutionary outcome crucially depends on the degree of spatial heterogeneity of the metapopulation, which we quantify using two parameters: the migration rate and the asymmetry in vaccine coverage . For high migration () and low asymmetry (), the metapopulation behaves like a single homogeneous population, and we recover the results of previous non-spatial models (Gandon et al., 2001, 2003; Walter and Lion, 2021). However, when migration is low and asymmetry is high, pathogen polymorphism becomes possible, leading to coexistence between two specialist strains, one that is adapted to the less vaccinated population and the other that is adapted to the population with higher coverage. In other words, as in classical metapopulation models, (Day, 2000; Débarre et al., 2013; Meszéna et al., 1997; Mirrahimi and Gandon, 2020; Ronce and Kirkpatrick, 2001), heterogeneity in selection (as measured by the asymmetry ) and low migration favour the coexistence between genotypes locally adapted to each habitat. When the degree of heterogeneity of the metapopulation is below a threshold, our model predicts a single generalist ES strategy.
However, in contrast to classical local adaptation models that tend to assume Gaussian fitness functions maximized at fixed and externally determined optima, the effects we observe in our vaccination model are all mediated by epidemiological feedbacks, through the densities of vaccinated and unvaccinated infected hosts in each population. Interestingly, these epidemiological feedbacks act differently for anti-growth () and anti-virulence () vaccines: Increasing the degree of heterogeneity in the metapopulation selects for more diversification with anti-growth vaccines, while polymorphism is only observed for maximal heterogeneity with anti-virulence vaccines. This occurs because vaccines increase the duration of infection and boost the productivity of the highly vaccinated population, which causes asymmetric migration between the two populations. In contrast, vaccines do not increase the productivity of the highly vaccinated population because the increased duration of infections is balanced by the reduction in transmission. With vaccines, the asymmetric influx of pathogens from the highly vaccinated population has two consequences on the long-term evolutionary outcome. First, it prevents the coexistence between two specialist genotypes because local selection to the unvaccinated population is swamped by migration from the vaccinated population. Second, asymmetric migration promotes adaptation to the more productive population (i.e., the highly vaccinated population) and selects for high ES virulence. This source–sink interpretation is similar to the findings of earlier analyses of adaptation in two-population models (Day, 2000; Débarre et al., 2013; Meszéna et al., 1997; Mirrahimi and Gandon, 2020; Ronce and Kirkpatrick, 2001). Interestingly, this source–sink dynamics is very different with the anti-growth () vaccine because pathogen prevalence drops in the vaccinated population. Hence, different vaccines have different consequences on the asymmetry between the populations. As discussed by Mirrahimi and Gandon (2020), this source–sink dynamics could be exacerbated by additional asymmetries in migration rates between populations but the exploration of these effects is beyond the scope of the present work.
It is interesting to compare the predictions of our two-patch model to previous analyses of the impact of spatial structure on the evolution of pathogen virulence. Using a lattice model, Zurita-Gutiérrez and Lion (2015) have shown that, for all types of vaccines, lower pathogen dispersal tends to select for lower ES virulence, except for high-efficacy anti-growth vaccines. In addition, they do not observe polymorphism. Although this prediction is consistent with the result that selection should favour more “prudent” pathogen strains in spatially structured populations (Haraguchi and Sasaki, 2000; Lion and van Baalen, 2008; van Baalen, 2002), it could appear at odds with our result that pathogen migration either has no or little effect on the ES virulence (for , and vaccines) or leads to increased ES virulence (for vaccines) or polymorphism. However, it is important to note that, although the model of Zurita-Gutiérrez and Lion (2015) does incorporate spatial structure by allowing a mixture of global and local transmission, it does not allow for heterogeneity in vaccination coverage as all new hosts have the same probability of being vaccinated, irrespective of their location. Furthermore, the effects observed in Zurita-Gutiérrez and Lion (2015) are mostly driven by kin competition for susceptible hosts. In our model, local populations are well mixed, and there is no kin selection.
Although the results in the main text assume a high vaccine efficacy (90%) and that the mean vaccination coverage at birth is 1/2 (and thus, ), we have relaxed these assumptions in Supplementary Material S.5, where we generalize our results to all the possible combinations of vaccine coverage and efficacy. We show that an increase in pathogen migration, a decrease in vaccination asymmetry and a decrease in vaccine efficacy makes polymorphism less likely. This is consistent with our general message that, as the metapopulation becomes increasingly homogeneous, the potential for diversification weakens. In Supplementary Material S.7, we also show that a model where adults (and not newborns) are vaccinated yields qualitatively similar predictions.
There are several interesting potential extensions of this work. First, our model assumes that hosts either cannot recover and therefore does not take into account natural immunity. We do not expect our qualitative results to be affected if recovery is total, but taking into account more realistic patterns of natural immunity would be technically more challenging and potentially impact our predictions. We note however that our model is a good approximation of many chronic diseases, and particularly of Marek’s disease in poultry, where evolution in response to vaccination has been well studied (Gimeno, 2008; Read et al., 2015). Second, our model does not account for coinfections, and we know that within-host competition could potentially alter the effect of vaccination on the evolution of virulence (Gandon et al., 2001). Third, although we have framed our results in the context of vaccination against a pathogen infecting a single species of hosts, our analytical results are more general because they allow the pathogen’s life-history traits to depend on different types of host ( and in the present model). This implies that the same analytical expressions capture the direction of selection and the condition of evolutionary stability for a pathogen infecting two host species (Gandon, 2004). Moreover, the focus on vaccines is by no means exclusive, as the four modes of action we distinguish can also be used to describe the action of other forms of heterogeneity, such as genetic resistance in the host or other treatments. In the context of chronic diseases, there are potentially interesting parallels to draw with imperfect antiretroviral therapies in HIV, although the complexity of HIV dynamics would require an adaptation of our epidemiological assumptions. Third, a limitation of our study is that it relies on a separation of time-scale assumption to make predictions on the long-term evolutionary outcome. However, for many practical purposes, what matters most is the joint dynamics of strain diversity and epidemiological dynamics over shorter time scales (Gandon and Lion, 2022). Hence, it would be interesting to extend this model to take into account both spatial heterogeneity and epidemic dynamics on the transient spread of new pathogen variants. Fourth, our adaptive dynamics framework is not well suited to capture the inherently stochastic nature of the spread of new mutations (Day et al., 2022; Gandon et al., 2022; Restif and Grenfell, 2006, 2007). In a similar two-patch stochastic model, Gerrish et al. (2021) have shown that heterogeneity in vaccine distribution promotes the emergence of vaccine escape mutants. It would be interesting to explore how demographic stochasticity could alter the emergence and the spread of new pathogenvariants.
From an applied point of view, the consequences of the evolution of pathogen polymorphism on long-term infectious disease management are not obvious. On the one hand, our model does not predict that polymorphism affects the cumulative number of deaths (see Supplementary Material S.6), although this specific prediction is probably sensitive to epidemiological assumptions. On the other hand, the circulation of two variants instead of one is a major challenge for the design of effective control strategies. For instance, this may require the development of vaccines targeting all strains, or specifically the most virulent variants as in the vaccination against Streptococcus pneumoniae (Masomian et al., 2020; Musher et al., 2022) or against human papillomavirus (Koutsky and Harper, 2006; Schiller and Lowy, 2012). Further studies are thus required to investigate how strain coexistence, which is expected to be a qualitatively robust outcome of pathogen evolution in populations with a high degree of spatial heterogeneity, needs to be taken into account in public health strategies. In addition, our results suggest that the risk of high-virulence evolution can be mitigated by the use of vaccines that combine both anti-infection and anti-growth effects. This is reassuring as most vaccines are unlikely to squarely fall into one of the four categories we distinguish in this study.
At a conceptual level, there is a parallel between our present investigation of the effect of spatial heterogeneity in vaccination coverage, and our previous analysis of the effect of temporal heterogeneity through periodic vaccination coverage (Walter and Lion, 2021). In this previous study, the pathogen sequentially experiences two very different habitats (corresponding to maximal or minimal coverage, respectively), which corresponds to in our spatial model, and the period of fluctuations allows for varying the amount of time spent in each habitat (much like the migration parameter ). Both studies predict that heterogeneity in vaccination coverage (whether it is spatial or temporal) has no effect on the ES virulence for anti-infection and anti-transmission vaccines. However, for anti-growth and anti-virulence vaccines, the parallel between temporal and spatial heterogeneity is not straightforward. First, the model with periodic fluctuations in vaccination coverage never predicts strain coexistence. Second, for the anti-virulence vaccine, increasing the period of temporal fluctuations leads to lower virulence, whereas decreasing migration leads to higher virulence in the spatial model. Hence, the effect of increased heterogeneity is markedly different in the spatial and temporal models. This calls for further exploration of the consequences of a combination of both spatial and temporal variations in vaccine coverage on the evolution of pathogen traits. For instance, in the context of the COVID-19 pandemic, Kortessis et al. (2020) have used a similar metapopulation model to study the effect of asynchronous public health measures on disease prevalence. A very interesting avenue for future research would be to extend this analysis to explore how spatio-temporal fluctuations of the environment affect the short- and long-term evolution of pathogens. Understanding both the epidemiological and the evolutionary consequences of different deployment strategies of vaccination may help identify more effective vaccination strategy that minimize both the cumulated number of cases and the speed at which the pathogen adapts to vaccination.
Data availability
The Mathematica notebooks and code used to generate the figures in this study are available on Zenodo at https://dx.doi.org/10.5281/zenodo.10212665.
Author contributions
Alicia Walter (Formal analysis [Lead], Investigation [Lead], Software [Lead], Writing—original draft [Lead], Writing—review & editing [Equal]), Sylvain Gandon (Conceptualization [Equal], Investigation [Equal], Methodology [Equal], Supervision [Equal], Writing—review & editing [Equal]), and Sébastien Lion (Conceptualization [Equal], Investigation [Equal], Methodology [Equal], Supervision [Equal], Writing—review & editing [Equal]).
Funding
This work was funded by grants ANR-16-CE35-0012 “STEEP” to S.L. and ANR-17-CE35-0012 “EVO-MALWILD” to S.G. from the Agence Nationale de la Recherche.
Acknowledgment
We thank two anonymous reviewers for their critical reading and helpful comments.
Conflicts of interest
None declared.
References
Alizon
,
S.
,
Hurford
, A.
,
Mideo
, N.
, &
van Baalen
, M.
(
2009
).
Virulence evolution and the trade-off hypothesis: History, current state of affairs and the future
.
Journal of Evolutionary Biology
,
22
(
2
),
245
–
259
.
https://doi.org/10.1111/j.1420-9101.2008.01658.x
Boots
,
M.
, &
Sasaki
, A.
(
1999
).
‘Small worlds’ and the evolution of virulence: Infection occurs locally and at a distance
.
Proceedings of the Royal Society of London. Series B: Biological Sciences
,
266
(
1432
),
1933
–
1938
.
https://doi.org/10.1098/rspb.1999.0869.
Day
,
T.
(
2000
).
Competition and the effect of spatial resource heterogeneity on evolutionary diversification
.
The American Naturalist
,
155
(
6
),
790
–
803
.
https://doi.org/10.1086/303356
Débarre
,
F.
,
Ronce
, O.
, &
Gandon
, S.
(
2013
).
Quantifying the effects of migration and mutation on adaptation and demography in spatially heterogeneous environments
.
Journal of Evolutionary Biology
,
26
(
6
),
1185
–
1202
.
https://doi.org/10.1111/jeb.12132
Dieckmann
,
U.
,
Metz
, J. A.
, &
Sabelis
, M. W.
(
2005
).
Adaptive dynamics of infectious diseases: In pursuit of virulence management
.
Cambridge Studies in Adaptive Dynamics, Series Number 2
.
Cambridge University Press
.
Gandon
,
S.
(
2004
).
Evolution of multihost parasites
.
Evolution
,
58
(
3
),
455
–
469
.
Gandon
,
S.
,
Day
, T.
, &
Lambert
, A.
(
2022
).
The speed of vaccination rollout and the risk of pathogen adaptation
. medRxiv. 2022.08.01.22278283.
Gandon
,
S.
, &
Lion
, S.
(
2022
).
Targeted vaccination and the speed of SARS-CoV-2 adaptation
.
Proceedings of the National Academy of Sciences of the United States of America
,
119
(
3
),
e2110666119
.
https://doi.org/10.1073/pnas.2110666119
Gandon
,
S.
,
Mackinnon
, M.
,
Nee
, S.
, &
Read
, A.
(
2003
).
Imperfect vaccination: Some epidemiological and evolutionary consequences
.
Proceedings Biological Sciences
,
270
(
1520
),
1129
–
1136
.
https://doi.org/10.1098/rspb.2003.2370.
Gandon
,
S.
,
Mackinnon
, M. J.
,
Nee
, S.
, &
Read
, A. F.
(
2001
).
Imperfect vaccines and the evolution of pathogen virulence
.
Nature
,
414
(
6865
),
751
–
756
.
https://doi.org/10.1038/414751a
Geritz
,
S. A.
,
Mesze
, G.
,
Metz
, J. A.
, &
Metz
, J. A. J.
(
1998
).
Evolutionarily singular strategies and the adaptive growth and branching of the evolutionary tree
.
Evolutionary Ecology
,
12
,
35
–
57
.
Gerrish
,
P. J.
,
Saldana
, F.
,
Galeota-Sprung
, B.
, …
Hernández
, J. X. V.
(
2021
).
How unequal vaccine distribution promotes the evolution of vaccine escape
. medRxiv. 2021.03.27.21254453.
Haraguchi
,
Y.
, &
Sasaki
, A.
(
2000
).
The evolution of parasite virulence and transmission rate in a spatially structured population
.
Journal of Theoretical Biology
,
203
(
2
),
85
–
96
.
https://doi.org/10.1006/jtbi.1999.1065
Hurford
,
A.
,
Cownden
, D.
, &
Day
, T.
(
2009
).
Next-generation tools for evolutionary invasion analyses
.
Journal of the Royal Society Interface
,
7
(
45
),
561
–
571
.
https://doi.org/10.1098/rsif.2009.0448
Kennedy
,
D. A.
, &
Read
, A. F.
(
2017
).
Why does drug resistance readily evolve but vaccine resistance does not
?
Proceedings Biological Sciences
,
284
(
1851
),
20162562
.
https://doi.org/10.1098/rspb.2016.2562.
Kennedy
,
D. A.
, &
Read
, A. F.
(
2018
).
Why the evolution of vaccine resistance is less of a concern than the evolution of drug resistance
.
Proceedings of the National Academy of Sciences of the United States of America
,
115
(
51
),
12878
–
12886
.
https://doi.org/10.1073/pnas.1717159115
Kortessis
,
N.
,
Simon
, M. W.
,
Barfield
, M.
, …
Holt
, R. D.
(
2020
).
The interplay of movement and spatiotemporal variation in transmission degrades pandemic control
.
Proceedings of the National Academy of Sciences of the United States of America
,
117
(
48
),
30104
–
30106
.
https://doi.org/10.1073/pnas.2018286117
Levins
,
R.
(
1962
).
Theory of fitness in a heterogeneous environment. I. The fitness set and adaptive function
.
The American Naturalist
,
96
(
891
),
361
–
373
.
https://doi.org/10.1086/282245
Lion
,
S.
(
2018
).
Class structure, demography, and selection: Reproductive-value weighting in nonequilibrium, polymorphic populations
.
The American Naturalist
,
191
(
5
),
620
–
637
.
https://doi.org/10.1086/696976
Lion
,
S.
, &
van Baalen
, M.
(
2008
).
Self-structuring in spatial evolutionary ecology
.
Ecology Letters
,
11
,
277
–
295
.
Masomian
,
M.
,
Ahmad
, Z.
,
Ti Gew
, L.
, &
Poh
, C. L.
(
2020
).
Development of next generation Streptococcus pneumoniae vaccines conferring broad protection
.
Vaccines
,
8
(
1
),
132
.
McLeod
,
D. V.
, &
Gandon
, S.
(
2022
).
Effects of epistasis and recombination between vaccine-escape and virulence alleles on the dynamics of pathogen adaptation
.
Nature Ecology & Evolution
,
6
(
6
),
786
–
793
.
https://doi.org/10.1038/s41559-022-01709-y
Memish
,
Z. A.
,
Assiri
, A.
,
Turkestani
, A.
, …
Gautret
, P.
(
2015
).
Mass gathering and globalization of respiratory pathogens during the 2013 Hajj
.
Clinical Microbiology and Infection
,
21
(
6
),
571.e1
–
571.e8
.
https://doi.org/10.1016/j.cmi.2015.02.008
Meszéna
,
G.
,
Czibula
, I.
, &
Geritz
, S.
(
1997
).
Adaptive dynamics in a 2-patch environment: A toy model for allopatric and parapatric speciation
.
Journal of Biological Systems
,
05
(
02
),
265
–
284
.
https://doi.org/10.1142/s0218339097000175
Mirrahimi
,
S.
, &
Gandon
, S.
(
2020
).
Evolution of specialization in heterogeneous environments: Equilibrium between selection, mutation and migration
.
Genetics
,
214
(
2
),
479
–
491
.
https://doi.org/10.1534/genetics.119.302868
Musher
,
D. M.
,
Anderson
, R.
, &
Feldman
, C.
(
2022
).
The remarkable history of pneumococcal vaccination: An ongoing challenge
.
Pneumonia
,
14
(
1
),
1
–
15
.
Otto
,
S. P.
, &
Day
, T.
(
2011
).
A biologist’s guide to mathematical modeling in ecology and evolution
.
Princeton University Press
.
Park
,
A. W.
,
Haven
, J.
,
Kaplan
, R.
, &
Gandon
, S.
(
2015
).
Refugia and the evolutionary epidemiology of drug resistance
.
Biology Letters
,
11
(
11
),
20150783
.
https://doi.org/10.1098/rsbl.2015.0783
Restif
,
O.
, &
Grenfell
, B. T.
(
2006
).
Integrating life history and cross-immunity into the evolutionary dynamics of pathogens
.
Proceedings Biological Sciences
,
273
(
1585
),
409
–
416
.
https://doi.org/10.1098/rspb.2005.3335.
Rydland
,
H. T.
,
Friedman
, J.
,
Stringhini
, S.
, …
Eikemo
, T. A.
(
2022
).
The radically unequal distribution of covid-19 vaccinations: A predictable yet avoidable symptom of the fundamental causes of inequality
.
Humanities and Social Sciences Communications
,
9
(
1
),
1
–
6
.
Schiller
,
J. T.
, &
Lowy
, D. R.
(
2012
).
Understanding and learning from the success of prophylactic human papillomavirus vaccines
.
Nature Reviews Microbiology
,
10
(
10
),
681
–
692
.
https://doi.org/10.1038/nrmicro2872
van Baalen
,
M.
(
2002
).
Contact networks and the evolution of virulence
. In
U.
Dieckmann
, J. A. J.
Metz
, M. W.
Sabelis
, & K.
Sigmund
(Eds.),
Adaptive dynamics of infectious diseases: In pursuit of virulence management
, (pp.
85
–
103
).
Cambridge University Press
.
Walter
,
A.
, &
Lion
, S.
(
2021
).
Epidemiological and evolutionary consequences of periodicity in treatment coverage
.
Proceedings Biological Sciences
,
288
(
1946
),
20203007
.
https://doi.org/10.1098/rspb.2020.3007.
Zurita-Gutiérrez
,
Y. H.
, &
Lion
, S.
(
2015
).
Spatial structure, host heterogeneity and parasite virulence: Implications for vaccine-driven evolution
.
Ecology Letters
,
18
(
8
),
779
–
789
.
https://doi.org/10.1111/ele.12455
© The Author(s) 2023. Published by Oxford University Press on behalf of the European Society of Evolutionary Biology. All rights reserved. For permissions, please e-mail: journals.permissions@oup.com
PDF

![Effect of migration and vaccination on the long-term evolution of the pathogen. The plain and dotted black lines represent the monomorphic singularities calculated by the adaptive dynamics. Plain black lines represent locally evolutionarily stable singularities, while dotted black lines represent locally evolutionarily unstable singularities (BPs or repellor). The upper plain grey line represents the ESS in a population fully vaccinated, and the lower plain grey line represents the ESS in a population without vaccination. The black crosses represent the virulence strategies of the globally stable polymorphic equilibrium (see Supplementary Material S.4 for further information). (A) For the anti-growth vaccine, when m∈[0,0.33] we observe bistatility (pink area), with m∈[0.33,0.38], there is a unique branching point (yellow area), and with m∈[0.38,0.5], there is a unique ESS (blue area). For the anti-vrulence vaccine, when m∈[0,0.02], the monomorphic singularity is a branching point (yellow area) and with m∈[0.02,0.5], the singularity is an ESS (blue area). Here δ=0.75, μ=0.01, Vm=0.001 and for (a) r2=0.9 and (b) r4=0.9 and all the other parameters as in Figure 3.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/jeb/37/2/10.1093_jeb_voad016/1/m_voad016_fig2.jpeg?Expires=1749736571&Signature=oeje81hNAKkl1HK4TyRPFTJIBTRX~4ZYIdTIv6VL~s-FkON-aHdCnXaT3sz5CFbRxJJ6P-6JGCG8NoPOOh6-tvw8INSxpTVPrB8edA19jtXHV4-PadamxBdfnkk3fN2vwFoKtYYNEGnMMr7FK2B3HLSQFiSvJzHI9o3tSjuM~Gy3kwEnkKsu90wxGEOlL3~pZpdq6DquMIoF17he7tK081eSf1W5-G-O7jyMmOjt3SPzZM4wypBqMu2b-F8dDznMSd1qKiG34T0DUDuehn9GI3qkpMenJVwRz3YWrhYUJ1g739arWRdwaZlkWz1sd4fKjzhZiKVOh520WbcEyI5Eug__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)





