-
PDF
- Split View
-
Views
-
Cite
Cite
Manoj Thomas, Ellie J Kyung, Slider Scale or Text Box: How Response Format Shapes Responses, Journal of Consumer Research, Volume 45, Issue 6, April 2019, Pages 1274–1293, https://doi.org/10.1093/jcr/ucy057
Close - Share Icon Share
Abstract
Consumer payments elicited on slider scales can be systematically different from those elicited through text boxes because of the end point assimilation effect. When people use text boxes to make payments, they evaluate monetary values relative to the starting point of the response range. In contrast, when people use slider scales, they evaluate monetary values relative to the starting point as well as the end point of the response range. Consequently, payments elicited on slider scales tend to be assimilated toward the end point of the response range. This slider scale end point assimilation effect varies for ascending and descending payment formats. For ascending payment formats (e.g., eBay bids), slider scales elicit higher payments than text boxes. But for descending payment formats (e.g., Priceline bids), slider scales elicit lower payments than text boxes. This research not only documents how slider scales alter consumer payments, but also explains how the mental number line affects financial decisions.
Are payment responses elicited through slider scales different from those elicited through open-ended text boxes? This question is relevant for organizations that use participative pricing strategies and researchers interested in measuring contingent valuations. The proliferation of online transactions has increased the popularity of participative pricing models where customers choose what they want to pay. Online bidding has become quite commonplace. eBay allows customers to bid on listed items. WineBid allows customers to bid on wines of their choosing. Even charity websites, such as Doctors Without Borders, allow donors to enter a donation amount of their choice. With the increasing popularity of transactions on handheld devices such as mobile phones and tablets, organizations are increasingly using slider scales rather than text boxes to allow people to enter values with the swipe of a finger rather than laboriously typing values with their thumbs. For example, Priceline—the online retailer of travel services that allows its customers to bid on hotel rooms—uses text boxes on its web page and slider scales on its mobile application. Do payment responses elicited through text boxes versus slider scales differ from each other in systematic ways? And if so, how? And why?
The answers to these questions also have implications for academic research. Researchers often measure monetary constructs such as contingent valuation, willingness to pay (WTP), internal reference prices, and latitude of price acceptance (Adaval and Monroe 2002; Burson, Larrick, and Lynch 2009; Monroe 1971), but the extant literature is silent on the effect of these response formats on measurement. To measure these constructs, some researchers have used open-ended text boxes (Ward and Dahl 2014), some have used discrete semantic differential scales (O’Guinn, Tanner, and Maeng 2015), and others have used continuous slider scales (Galak et al. 2014). We examined experiments measuring willingness to pay in the Journal of Consumer Research from 2011 to 2017 and found that from 2011 to 2014, 100% of the experiments employed text boxes. However, from 2015 to 2017, 64% employed text boxes, while 23% employed slider scales, and 10% employed discrete semantic differential scales. The increasing use of different response formats is based on the assumption that the amount a consumer is willing to pay is unaffected by response format; the axiom of procedural invariance implied in standard utility theories suggests that people’s willingness to pay should be invariant to response format. In this research, we question and empirically test this assumption.
To presage our results, we find that relative to text boxes, slider scales elicit more extreme responses assimilated toward the end point of the response range. This occurs because slider scales recalibrate the mental number line that people use to judge price magnitudes. When people use text boxes to submit numeric responses, they evaluate numeric magnitudes relative to the starting point of a response range. In contrast, when people use slider scales, they evaluate numeric magnitudes by considering the visual distance from both the starting point and the end point of the response range. Because of this tendency to use visual distance from the end point as a magnitude cue, numeric responses on slider scales are more likely to be assimilated toward this end point. This end point assimilation effect can cause numeric responses on slider scales to be systematically higher or lower than those of text boxes, depending on the direction of the response adjustment. It also renders slider scale responses more susceptible to the size and salience of the response range end point. Thus, this research not only documents how scale visualization can influence consumer payments but also characterizes the role of the mental number line in price perception, which is emerging as one of the most fundamental theoretical constructs in the numerical cognition literature (Dehaene 2001; Dehaene et al. 2008).
MENTAL NUMBER LINE RECALIBRATION
The mental number line recalibration account begins with two foundational assumptions. First, we assume that consumers have stable valuations for only a few basic things that they frequently encounter, and that for most real-world situations they construct valuations during decision making. Second, we assume that people use a nonlinear mental number line to evaluate monetary values.
Constructing Price Judgments
The constructivist account of valuations (Bettman, Luce, and Payne 1998; Burson et al. 2009; Fischhoff 1991) posits that people’s valuations of goods are subjective, entailing several intuitive judgments and decisions that happen in quick succession. A prospective buyer begins by assessing the desirability of a potential product or service. If the buyer considers the product or service very desirable, she should be willing to pay a high price for it. If she considers it less desirable, she should want to pay a lower price. Next, contingent on the first decision, she will have to decide what specific price is considered low or high. A price of $500 might be high for a bottle of wine, but low for a new laptop. Per this constructivist account, the prospective buyer will have to, given a particular context, come up with thresholds for implicitly categorizing prices as low, medium, or high on the spur of the moment. For example, a person considering the purchase of a laptop on eBay will have to first decide—based on an evaluation of its attractiveness—whether the price she is willing to pay for it is relatively low, medium, or high. If she evaluates the laptop as very attractive, she has to judge what numeric value constitutes a high bid. On the other hand, if she considers the laptop only somewhat attractive, she must judge what numeric value constitutes a low bid. Thus, when evaluating prices, consumers create implicit markers or boundaries of price magnitude categories—such as low, medium, and high—along their mental number line.
The Nonlinear Mental Number Line
Psychologists studying the mental representation of numbers (Dehaene 2001; Dehaene et al. 2008; Izard and Dehaene 2008) as well as consumer researchers (Adaval 2013; Adaval and Monroe 2002; Bagchi and Davis 2016; Biswas et al. 2013; Lembregts and Pandelaere 2013; Monroe and Lee 1999; Schley, Lembregts, and Peters 2017; Thomas and Morwitz 2009a, 2009b; Valenzuela and Raghubir 2015) agree that numbers are represented not only symbolically as arithmetic and verbal codes, but also as asymbolic semantic representations best conceptualized as a nonlinear mental number line. In their dual-process model of price cognition, Thomas and Morwitz (2009a) have explained how everyday price judgments are influenced by the interplay of conscious symbolic representations and the nonconscious asymbolic representations on the mental number line. This mental number line does not resemble the linear arithmetic ruler. Unlike a linear arithmetic ruler with evenly spaced markers, the mental ruler in our minds is not calibrated linearly or with uniformly spaced markers. Instead, it is an unbounded line with diminishing discriminability: the same objective numerical difference is seen as larger when closer to the starting point of the mental number line than if it is away from the starting point. Just as Ernst Weber and his student Gustav Fechner postulated that the ability to recognize a just-noticeable difference with sensory stimuli depends on the magnitude of the initial stimuli (e.g., people easily detect the difference between a 15- vs. 30-watt lamp, but not the difference between a 120- vs. 135-watt lamp), numerical cognition researchers have posited that the mental number line used to evaluate numeric stimuli follows a similar response function. Specifically, Dehaene et al. (2008) suggested that our brain perceives the change between 10 and 20 as greater than that between 20 and 30, and the change between 20 and 30 as greater than that between 30 and 40, even though the arithmetic differences are identical. Thus, the psychological impact of increasing a price from $10 to $20 will be greater than that of increasing it from $30 to $40. This has implications for calibration of the mental number line: the positions of the boundaries between evaluative categories that serve as discrimination thresholds between low, medium, and high values are not uniformly spaced. To use a term from psychophysics (Johnson 1944), these category limens are compressed toward the starting value of the mental number line as depicted in figure 1.

ASCENDING PAYMENT FORMATS
NOTE.—In an ascending payment format, in the text box condition, because payment values are compared to the lowest possible response, the limens that separate categories are assimilated toward the starting point (top line). In the slider scale condition, where the visual distances from both the starting and end points are more salient, the limens that separate internal categories tend to assimilate toward the highest possible response (bottom line). Furthermore, the shift in category limens is more pronounced for higher values that are visually closer to the end point.
Recalibrating the Mental Number Line
We propose that category limens on the mental number line are not only nonlinear but also context dependent—specifically, that the natural category limens on the mental number line can unconsciously shift depending on response format. When people use a text box to submit a price response, they are likely to rely on the natural nonlinear number line in their mind. Their judgments about the boundaries between low, medium, and high prices are calibrated with respect to the starting price, with responses anchored on this starting point (see figure 1). For example, if a buyer can bid anywhere between $200 (starting price) and $1,000 (retail price) for a laptop using an open-ended text box, then her low bid might be around $300, her medium bid might be around $400, and her high bid around $600. Note that all of these values are assimilated toward the starting price on the lefthand side of the mental number line.
In contrast, slider scales provide a visual representation of a line with salient starting and end points. We propose that when using a slider scale, people judge price magnitudes by assessing the visual distance from the starting as well as from the end point of the slider scale. Consistent with a dual-process model of price cognition (Monroe and Lee 1999; Thomas and Morwitz 2009a, 2009b), we propose that while the reflective part of the brain deals with deliberative numeric comparisons, the reflexive part of the brain spontaneously assesses the visual distances from the starting and end points of the slider scale. Price magnitude judgments are influenced by the distance from the starting point (“how far is it from the lowest possible value”) as well as the distance from the end point of the scale (“how close is it to the highest possible value”). Thus, slider scales change the boundaries between evaluative categories—the category limens—on the mental number line. Relative to the category limens elicited by a text box, the category limens elicited by a slider scale are more stretched toward the end point of the slider. Continuing with the illustrative bidding example introduced earlier, if a buyer can bid anywhere between $200 and $1,000 using a slider scale, then a low bid might be around $300, a medium bid might be around $600, and a high bid around $800.
More generally, we propose that when people use a text box for an ascending payment format, where price magnitudes input are higher than some starting point, if Pmin is the lowest possible price that one can pay, then category limens Plow, Pmedium, and Phigh will be marked relative to Pmin, such that these limens are assimilated toward Pmin. However, when people use a slider scale for an ascending payment format, the visual distances from both starting point Pmin and end point Pmax are perceptually more salient, reducing the assimilation toward Pmin and increasing the assimilation toward Pmax. People submitting a high price response will consider not only whether the value is far enough from Pmin but also whether it is close enough to Pmax. This shift in category limens caused by the slider format is depicted in figure 1. Therefore, in an ascending payment format, where payment values are higher than the starting point (e.g., eBay), people are likely to submit higher values when they use a slider scale versus a text box because the markers that identify categories are shifted to the right toward the end point. We refer to this as the slider scale end point assimilation effect. Formally,
H1a: In ascending payment formats, values elicited through a slider scale will be higher than those elicited through a text box.
Our theorizing does not suggest that slider scales will always elicit higher values; in fact, our theory posits that the direction of the end point assimilation effect will reverse for descending payment formats. In a descending payment format, where prices submitted are lower than a starting price (e.g., Priceline), people adjust the prices downward from the list or retail price. In such cases, the category limens on the mental number line will be marked relative to this highest possible response. As depicted in figure 2, when people use a text box for descending payment formats, if Pmax is the starting price, then the category limens Phigh, Pmedium, and Plow will be marked relative to Pmax and assimilated toward Pmax. However, when people use a slider scale, the visual distances from Pmax (starting point) and Pmin (end point) are salient, reducing the assimilation toward Pmax and increasing the assimilation toward Pmin. Thus, in a descending payment format, values elicited through a slider scale will be lower than those elicited through a text box. Formally,
H1b: In descending payment formats, values elicited through a slider scale will be lower than those elicited through a text box.

DESCENDING PAYMENT FORMATS
NOTE.—In a descending payment format, in the text box condition, people use a mental number line where the limens that separate categories are assimilated toward the starting point that is the highest possible response (top line). In the slider scale condition, where the visual distances from both the starting point (right) and end point (left) are salient, the limens that separate internal categories are more assimilated toward the end point—the lowest possible response (bottom line). Furthermore, the shift in category limens is more pronounced for lower values that are closer to the end point.
Proximity to the End Point
The novel insight that underlies our conceptualization is that slider scales create a bias in magnitude judgments by increasing the salience of the visual distance to the end point of the response scale.1 If visual distance from the end point is the root cause of more extreme responses on slider scales, then it follows that the extent of the bias will depend on proximity to the slider end point. Proximity to an end point can make visual distance from that end point perceptually more salient. This postulate suggests that the end point assimilation effect will depend on the response magnitude. For ascending payment formats (figure 1) category limens for higher price values, which are visually closer to the end point (right), are more likely to assimilate toward this perceptually salient end point than lower price values. Thus, the end point assimilation effect will be strongest for those willing to pay higher prices. For descending payment formats (figure 2) category limens for lower price values, which are visually closer to the end point (left), are more likely to assimilate toward this perceptually salient end point than higher price values. Thus, the end point assimilation effect will be strongest for those willing to pay the least. Formally,
H2: The end point assimilation effect will be stronger for values that are closer to the end point of the slider scale. For ascending payment formats, the end point assimilation effect will be stronger for higher price values; for descending payment formats, the end point assimilation effect will be stronger for lower price values.
Visual Distance from the End Point
The key difference between the slider scale and text box formats is that with the former, people rely on visual distance for magnitude judgments, whereas with the latter, they rely on numeric comparisons. When people use a text box, they evaluate magnitudes by comparing values to the starting point of the response range. This is a numeric comparison process. But when people use slider scales, they consider visual distances from the starting point as well as the end point of the response continuum as cues for magnitude judgment. This postulate suggests that relative to text box responses, slider scale responses should be more susceptible to contextual factors that alter the visual distances from the end point of the response range. We consider two such factors that can change the visual distance from end points and thus moderate the slider scale end point assimilation effect.
The first factor is distance calibration of the slider scale—that is, the change in numeric response when the slider knob moves by a unit distance. Note that slider scales usually have a linear calibration, such that when the slider knob moves by one unit, the numeric response changes by a fixed amount. The change in numeric response per unit distance remains constant throughout the length of the slider scale. It is this linear calibration of the slider scales that makes it different from the mental number, which is inherently nonlinear in nature. This postulate suggests that a nonlinear slider scale wherein numerical values are a convex function of distance from the starting point should mimic the natural mental number line and attenuate the slider scale end point assimilation effect.
A second factor that can influence the visual distances from the end points of the slider is the response range. If the length of a slider scale in an ascending payment format remains the same but the value of the end point increases from $1,000 to $1,800, then payment values will increase for the slider scale with the larger range. Responses will seem farther from this new, higher end point value on the slider scale with the larger range, and therefore people will adjust their response upward until it is close enough to the new end point. However, because people using text box formats are less influenced by the end point of the response range, increasing the end point value should matter less for text box responses. Formally, we predict:
H3: Contextual factors that alter the visual distance of the response from the end point of the slider scale will moderate the slider scale end point assimilation effect.
ALTERNATIVE ACCOUNTS
As we embarked on this research, in addition to the metal number line recalibration account, we considered several alternative accounts for why slider scales might elicit different responses from text boxes. Two of them are particularly plausible and pertinent: the response momentum account and the asymmetric range awareness account. While the mental number line recalibration account is based on the numerical cognition literature, the response momentum account is inspired by the notion of psychological momentum in human kinetics (Markman and Guenther 2007), which suggests that slider scales might intensify responses because of a natural inclination to continue the physical sliding movement once it has started in a particular direction. People may end up pulling the slider knob farther than they intended relative to a starting point, and past a value they might indicate in a text box, because they are caught up in the momentum of the movement itself. Like the mental number line recalibration account, the response momentum account also predicts that responses elicited on a slider scale will be more extreme than those elicited through a text box. But unlike the previous account, the response momentum account suggests that the effect will be restricted to scales that entail a sliding response and will not generalize to discrete scales that simulate line visualization, but do not entail a sliding response (e.g., response scales with radio buttons).
The asymmetric range awareness account suggests that the difference between slider scale and text box responses stems not from the use of visual distance as magnitude cues, but instead from varying awareness of the response range information. It is conceivable that when people use text boxes, they might not be aware of the full response range, particularly the end point. If the effect of response format is caused only by such information asymmetry, then making text box users mindful of the response range should easily alleviate it. However, our conceptualization suggests that even when text box users are aware of the response range, responses elicited through slider scales can be different from text box responses because of inherent differences in the cognitive and perceptual processes employed by the two response formats. When text boxes are used to submit responses, respondents can volitionally and deliberately choose the more diagnostic reference point to compare and judge numeric responses: in most cases, this will be the starting price. However, when slider scales are used to submit responses, the choice of reference points is less volitional and more spontaneous, driven by the visual distance of the response from the starting and end points. The automatic processing of visual distance as a magnitude cue influences their price magnitude judgments and price responses. Tzelgov and Ganor-Stern (2005; also see Tzelgov, Meyer, and Henik 1992) argued many of the day-to-day human cognitive processes are partially automatic because people are not aware of the processes, because the processes cannot be controlled, or because the process is not volitional. Similarly, we posit that the use of visual distances from the end points of slider scales as magnitude cues is a partially automatic process that occurs spontaneously without respondents’ awareness rather than due to information asymmetry.
OVERVIEW OF EXPERIMENTS AND ANALYSES
For all experiments, in order to ensure that our results are not contingent on distributional assumptions, we used both parametric and nonparametric approaches to analyze the data. We analyzed all the data with PROC GLIMMIX in SAS using both the normal and Poisson distributions. The comparison of results assuming normal and Poisson distributions are available in web appendix B. To ensure that the results are not driven by a few outliers, we conducted the same analyses after removing participants with responses more than three standard deviations from the mean. The means without these outliers are reported in web appendix C. The model-free means, standard deviations, and standard errors for all conditions are reported in table 1. Note that because our primary interest is in the average values that participants are willing to pay, in all studies we report model-free means that are not contingent on model fit and distributional assumptions. In addition, we analyzed the results of all studies by comparing the medians by conditions using nonparametric methods. Condition medians and the results of these analyses are reported in table 2. These supplementary analyses demonstrate that the results of the studies are robust to modeling and distributional assumptions. In the following sections we discuss results from 11 studies. Because of space constraints, we describe results from only seven studies in detail. The results of the remaining studies are summarized in the meta-analysis and web appendixes G and H.
| 1A: Mug auction(ascending payment format) | ||||||||||||||||||||||||||||
| Text box | Slider | |||||||||||||||||||||||||||
| n | Mean | STDV | SE | n | Mean | STDV | SE | |||||||||||||||||||||
| Mug bid price | 62 | 8.01 | 6.64 | 0.84 | 65 | 11.40 | 9.77 | 1.21 | ||||||||||||||||||||
| 1B: Veteran’s Day donations(ascending payment format) | ||||||||||||||||||||||||||||
| Text box | Slider | |||||||||||||||||||||||||||
| n | Mean | STDV | SE | n | Mean | STDV | SE | |||||||||||||||||||||
| Donation | 105 | 24.04 | 30.61 | 2.99 | 99 | 37.76 | 39.13 | 3.93 | ||||||||||||||||||||
| 2. eBay bids(ascending payment format: laptops) | ||||||||||||||||||||||||||||
| Text box | Slider | |||||||||||||||||||||||||||
| Starting bid | n | Mean | STDV | SE | n | Mean | STDV | SE | ||||||||||||||||||||
| $239 | 97 | 268.02 | 55.54 | 5.64 | 102 | 276.71 | 42.79 | 4.24 | ||||||||||||||||||||
| $259 | 97 | 281.85 | 36.32 | 3.69 | 102 | 293.70 | 40.24 | 3.98 | ||||||||||||||||||||
| $279 | 97 | 290.42 | 28.07 | 2.86 | 102 | 301.36 | 40.30 | 3.99 | ||||||||||||||||||||
| 3. Priceline bids(descending payment format: hotel rooms) | ||||||||||||||||||||||||||||
| Text box | Slider left-to-right | Slider right-to-left | ||||||||||||||||||||||||||
| Starting price | n | Mean | STDV | SE | n | Mean | STDV | SE | n | Mean | STDV | SE | ||||||||||||||||
| Level 1 | 100 | 128.59 | 22.80 | 2.28 | 101 | 117.81 | 23.45 | 2.33 | 103 | 123.89 | 21.09 | 2.08 | ||||||||||||||||
| Level 2 | 100 | 142.22 | 25.27 | 2.53 | 101 | 130.06 | 26.02 | 2.59 | 103 | 136.72 | 23.92 | 2.36 | ||||||||||||||||
| Level 3 | 100 | 154.54 | 28.02 | 2.82 | 101 | 143.90 | 29.52 | 2.94 | 103 | 145.95 | 29.04 | 2.86 | ||||||||||||||||
| 4. Moderation by distance to end point(ascending payment format: laptops) | ||||||||||||||||||||||||||||
| Response magnitude | Text box | Slider | Scale | |||||||||||||||||||||||||
| n | Mean | STDV | SE | n | Mean | STDV | SE | n | Mean | STDV | SE | |||||||||||||||||
| Low | 110 | 289.33 | 64.38 | 6.14 | 111 | 297.82 | 72.03 | 6.84 | 112 | 298.64 | 61.76 | 5.84 | ||||||||||||||||
| Medium | 110 | 395.17 | 114.12 | 10.88 | 111 | 437.47 | 110.98 | 10.53 | 112 | 439.00 | 93.66 | 8.85 | ||||||||||||||||
| High | 110 | 560.62 | 214.19 | 20.42 | 111 | 621.20 | 183.93 | 17.46 | 112 | 621.68 | 167.04 | 15.78 | ||||||||||||||||
| 5. A convex slider(ascending payment format: laptops) | ||||||||||||||||||||||||||||
| Response magnitude | Text box | Convex slider | Slider | |||||||||||||||||||||||||
| n | Mean | STDV | SE | n | Mean | STDV | SE | n | Mean | STDV | SE | |||||||||||||||||
| Low | 86 | 276.80 | 41.02 | 4.42 | 88 | 284.43 | 45.43 | 4.84 | 88 | 303.80 | 63.35 | 6.75 | ||||||||||||||||
| Medium | 86 | 380.79 | 99.22 | 10.70 | 88 | 397.78 | 103.61 | 11.04 | 88 | 435.19 | 115.59 | 12.32 | ||||||||||||||||
| High | 86 | 551.22 | 188.83 | 20.36 | 88 | 564.63 | 200.93 | 21.42 | 88 | 595.92 | 177.03 | 18.87 | ||||||||||||||||
| 6. Moderation by end point size(ascending payment format: wine) | ||||||||||||||||||||||||||||
| Range × response magnitude | Text box | Slider | ||||||||||||||||||||||||||
| n | Mean | STDV | SE | n | Mean | STDV | SE | |||||||||||||||||||||
| $500 range | ||||||||||||||||||||||||||||
| Low | 107 | 29.39 | 18.07 | 1.75 | 99 | 50.78 | 62.80 | 6.31 | ||||||||||||||||||||
| Medium | 107 | 59.41 | 59.66 | 5.77 | 99 | 84.68 | 80.50 | 8.09 | ||||||||||||||||||||
| High | 107 | 102.98 | 115.01 | 11.12 | 99 | 125.31 | 112.75 | 11.33 | ||||||||||||||||||||
| $1,000 range | ||||||||||||||||||||||||||||
| Low | 103 | 29.14 | 14.07 | 1.39 | 104 | 62.90 | 96.63 | 9.48 | ||||||||||||||||||||
| Medium | 103 | 65.08 | 72.97 | 7.19 | 104 | 128.77 | 160.53 | 15.74 | ||||||||||||||||||||
| High | 103 | 122.64 | 160.97 | 15.86 | 104 | 219.83 | 262.26 | 25.72 | ||||||||||||||||||||
| 1A: Mug auction(ascending payment format) | ||||||||||||||||||||||||||||
| Text box | Slider | |||||||||||||||||||||||||||
| n | Mean | STDV | SE | n | Mean | STDV | SE | |||||||||||||||||||||
| Mug bid price | 62 | 8.01 | 6.64 | 0.84 | 65 | 11.40 | 9.77 | 1.21 | ||||||||||||||||||||
| 1B: Veteran’s Day donations(ascending payment format) | ||||||||||||||||||||||||||||
| Text box | Slider | |||||||||||||||||||||||||||
| n | Mean | STDV | SE | n | Mean | STDV | SE | |||||||||||||||||||||
| Donation | 105 | 24.04 | 30.61 | 2.99 | 99 | 37.76 | 39.13 | 3.93 | ||||||||||||||||||||
| 2. eBay bids(ascending payment format: laptops) | ||||||||||||||||||||||||||||
| Text box | Slider | |||||||||||||||||||||||||||
| Starting bid | n | Mean | STDV | SE | n | Mean | STDV | SE | ||||||||||||||||||||
| $239 | 97 | 268.02 | 55.54 | 5.64 | 102 | 276.71 | 42.79 | 4.24 | ||||||||||||||||||||
| $259 | 97 | 281.85 | 36.32 | 3.69 | 102 | 293.70 | 40.24 | 3.98 | ||||||||||||||||||||
| $279 | 97 | 290.42 | 28.07 | 2.86 | 102 | 301.36 | 40.30 | 3.99 | ||||||||||||||||||||
| 3. Priceline bids(descending payment format: hotel rooms) | ||||||||||||||||||||||||||||
| Text box | Slider left-to-right | Slider right-to-left | ||||||||||||||||||||||||||
| Starting price | n | Mean | STDV | SE | n | Mean | STDV | SE | n | Mean | STDV | SE | ||||||||||||||||
| Level 1 | 100 | 128.59 | 22.80 | 2.28 | 101 | 117.81 | 23.45 | 2.33 | 103 | 123.89 | 21.09 | 2.08 | ||||||||||||||||
| Level 2 | 100 | 142.22 | 25.27 | 2.53 | 101 | 130.06 | 26.02 | 2.59 | 103 | 136.72 | 23.92 | 2.36 | ||||||||||||||||
| Level 3 | 100 | 154.54 | 28.02 | 2.82 | 101 | 143.90 | 29.52 | 2.94 | 103 | 145.95 | 29.04 | 2.86 | ||||||||||||||||
| 4. Moderation by distance to end point(ascending payment format: laptops) | ||||||||||||||||||||||||||||
| Response magnitude | Text box | Slider | Scale | |||||||||||||||||||||||||
| n | Mean | STDV | SE | n | Mean | STDV | SE | n | Mean | STDV | SE | |||||||||||||||||
| Low | 110 | 289.33 | 64.38 | 6.14 | 111 | 297.82 | 72.03 | 6.84 | 112 | 298.64 | 61.76 | 5.84 | ||||||||||||||||
| Medium | 110 | 395.17 | 114.12 | 10.88 | 111 | 437.47 | 110.98 | 10.53 | 112 | 439.00 | 93.66 | 8.85 | ||||||||||||||||
| High | 110 | 560.62 | 214.19 | 20.42 | 111 | 621.20 | 183.93 | 17.46 | 112 | 621.68 | 167.04 | 15.78 | ||||||||||||||||
| 5. A convex slider(ascending payment format: laptops) | ||||||||||||||||||||||||||||
| Response magnitude | Text box | Convex slider | Slider | |||||||||||||||||||||||||
| n | Mean | STDV | SE | n | Mean | STDV | SE | n | Mean | STDV | SE | |||||||||||||||||
| Low | 86 | 276.80 | 41.02 | 4.42 | 88 | 284.43 | 45.43 | 4.84 | 88 | 303.80 | 63.35 | 6.75 | ||||||||||||||||
| Medium | 86 | 380.79 | 99.22 | 10.70 | 88 | 397.78 | 103.61 | 11.04 | 88 | 435.19 | 115.59 | 12.32 | ||||||||||||||||
| High | 86 | 551.22 | 188.83 | 20.36 | 88 | 564.63 | 200.93 | 21.42 | 88 | 595.92 | 177.03 | 18.87 | ||||||||||||||||
| 6. Moderation by end point size(ascending payment format: wine) | ||||||||||||||||||||||||||||
| Range × response magnitude | Text box | Slider | ||||||||||||||||||||||||||
| n | Mean | STDV | SE | n | Mean | STDV | SE | |||||||||||||||||||||
| $500 range | ||||||||||||||||||||||||||||
| Low | 107 | 29.39 | 18.07 | 1.75 | 99 | 50.78 | 62.80 | 6.31 | ||||||||||||||||||||
| Medium | 107 | 59.41 | 59.66 | 5.77 | 99 | 84.68 | 80.50 | 8.09 | ||||||||||||||||||||
| High | 107 | 102.98 | 115.01 | 11.12 | 99 | 125.31 | 112.75 | 11.33 | ||||||||||||||||||||
| $1,000 range | ||||||||||||||||||||||||||||
| Low | 103 | 29.14 | 14.07 | 1.39 | 104 | 62.90 | 96.63 | 9.48 | ||||||||||||||||||||
| Medium | 103 | 65.08 | 72.97 | 7.19 | 104 | 128.77 | 160.53 | 15.74 | ||||||||||||||||||||
| High | 103 | 122.64 | 160.97 | 15.86 | 104 | 219.83 | 262.26 | 25.72 | ||||||||||||||||||||
| 1A: Mug auction(ascending payment format) | ||||||||||||||||||||||||||||
| Text box | Slider | |||||||||||||||||||||||||||
| n | Mean | STDV | SE | n | Mean | STDV | SE | |||||||||||||||||||||
| Mug bid price | 62 | 8.01 | 6.64 | 0.84 | 65 | 11.40 | 9.77 | 1.21 | ||||||||||||||||||||
| 1B: Veteran’s Day donations(ascending payment format) | ||||||||||||||||||||||||||||
| Text box | Slider | |||||||||||||||||||||||||||
| n | Mean | STDV | SE | n | Mean | STDV | SE | |||||||||||||||||||||
| Donation | 105 | 24.04 | 30.61 | 2.99 | 99 | 37.76 | 39.13 | 3.93 | ||||||||||||||||||||
| 2. eBay bids(ascending payment format: laptops) | ||||||||||||||||||||||||||||
| Text box | Slider | |||||||||||||||||||||||||||
| Starting bid | n | Mean | STDV | SE | n | Mean | STDV | SE | ||||||||||||||||||||
| $239 | 97 | 268.02 | 55.54 | 5.64 | 102 | 276.71 | 42.79 | 4.24 | ||||||||||||||||||||
| $259 | 97 | 281.85 | 36.32 | 3.69 | 102 | 293.70 | 40.24 | 3.98 | ||||||||||||||||||||
| $279 | 97 | 290.42 | 28.07 | 2.86 | 102 | 301.36 | 40.30 | 3.99 | ||||||||||||||||||||
| 3. Priceline bids(descending payment format: hotel rooms) | ||||||||||||||||||||||||||||
| Text box | Slider left-to-right | Slider right-to-left | ||||||||||||||||||||||||||
| Starting price | n | Mean | STDV | SE | n | Mean | STDV | SE | n | Mean | STDV | SE | ||||||||||||||||
| Level 1 | 100 | 128.59 | 22.80 | 2.28 | 101 | 117.81 | 23.45 | 2.33 | 103 | 123.89 | 21.09 | 2.08 | ||||||||||||||||
| Level 2 | 100 | 142.22 | 25.27 | 2.53 | 101 | 130.06 | 26.02 | 2.59 | 103 | 136.72 | 23.92 | 2.36 | ||||||||||||||||
| Level 3 | 100 | 154.54 | 28.02 | 2.82 | 101 | 143.90 | 29.52 | 2.94 | 103 | 145.95 | 29.04 | 2.86 | ||||||||||||||||
| 4. Moderation by distance to end point(ascending payment format: laptops) | ||||||||||||||||||||||||||||
| Response magnitude | Text box | Slider | Scale | |||||||||||||||||||||||||
| n | Mean | STDV | SE | n | Mean | STDV | SE | n | Mean | STDV | SE | |||||||||||||||||
| Low | 110 | 289.33 | 64.38 | 6.14 | 111 | 297.82 | 72.03 | 6.84 | 112 | 298.64 | 61.76 | 5.84 | ||||||||||||||||
| Medium | 110 | 395.17 | 114.12 | 10.88 | 111 | 437.47 | 110.98 | 10.53 | 112 | 439.00 | 93.66 | 8.85 | ||||||||||||||||
| High | 110 | 560.62 | 214.19 | 20.42 | 111 | 621.20 | 183.93 | 17.46 | 112 | 621.68 | 167.04 | 15.78 | ||||||||||||||||
| 5. A convex slider(ascending payment format: laptops) | ||||||||||||||||||||||||||||
| Response magnitude | Text box | Convex slider | Slider | |||||||||||||||||||||||||
| n | Mean | STDV | SE | n | Mean | STDV | SE | n | Mean | STDV | SE | |||||||||||||||||
| Low | 86 | 276.80 | 41.02 | 4.42 | 88 | 284.43 | 45.43 | 4.84 | 88 | 303.80 | 63.35 | 6.75 | ||||||||||||||||
| Medium | 86 | 380.79 | 99.22 | 10.70 | 88 | 397.78 | 103.61 | 11.04 | 88 | 435.19 | 115.59 | 12.32 | ||||||||||||||||
| High | 86 | 551.22 | 188.83 | 20.36 | 88 | 564.63 | 200.93 | 21.42 | 88 | 595.92 | 177.03 | 18.87 | ||||||||||||||||
| 6. Moderation by end point size(ascending payment format: wine) | ||||||||||||||||||||||||||||
| Range × response magnitude | Text box | Slider | ||||||||||||||||||||||||||
| n | Mean | STDV | SE | n | Mean | STDV | SE | |||||||||||||||||||||
| $500 range | ||||||||||||||||||||||||||||
| Low | 107 | 29.39 | 18.07 | 1.75 | 99 | 50.78 | 62.80 | 6.31 | ||||||||||||||||||||
| Medium | 107 | 59.41 | 59.66 | 5.77 | 99 | 84.68 | 80.50 | 8.09 | ||||||||||||||||||||
| High | 107 | 102.98 | 115.01 | 11.12 | 99 | 125.31 | 112.75 | 11.33 | ||||||||||||||||||||
| $1,000 range | ||||||||||||||||||||||||||||
| Low | 103 | 29.14 | 14.07 | 1.39 | 104 | 62.90 | 96.63 | 9.48 | ||||||||||||||||||||
| Medium | 103 | 65.08 | 72.97 | 7.19 | 104 | 128.77 | 160.53 | 15.74 | ||||||||||||||||||||
| High | 103 | 122.64 | 160.97 | 15.86 | 104 | 219.83 | 262.26 | 25.72 | ||||||||||||||||||||
| 1A: Mug auction(ascending payment format) | ||||||||||||||||||||||||||||
| Text box | Slider | |||||||||||||||||||||||||||
| n | Mean | STDV | SE | n | Mean | STDV | SE | |||||||||||||||||||||
| Mug bid price | 62 | 8.01 | 6.64 | 0.84 | 65 | 11.40 | 9.77 | 1.21 | ||||||||||||||||||||
| 1B: Veteran’s Day donations(ascending payment format) | ||||||||||||||||||||||||||||
| Text box | Slider | |||||||||||||||||||||||||||
| n | Mean | STDV | SE | n | Mean | STDV | SE | |||||||||||||||||||||
| Donation | 105 | 24.04 | 30.61 | 2.99 | 99 | 37.76 | 39.13 | 3.93 | ||||||||||||||||||||
| 2. eBay bids(ascending payment format: laptops) | ||||||||||||||||||||||||||||
| Text box | Slider | |||||||||||||||||||||||||||
| Starting bid | n | Mean | STDV | SE | n | Mean | STDV | SE | ||||||||||||||||||||
| $239 | 97 | 268.02 | 55.54 | 5.64 | 102 | 276.71 | 42.79 | 4.24 | ||||||||||||||||||||
| $259 | 97 | 281.85 | 36.32 | 3.69 | 102 | 293.70 | 40.24 | 3.98 | ||||||||||||||||||||
| $279 | 97 | 290.42 | 28.07 | 2.86 | 102 | 301.36 | 40.30 | 3.99 | ||||||||||||||||||||
| 3. Priceline bids(descending payment format: hotel rooms) | ||||||||||||||||||||||||||||
| Text box | Slider left-to-right | Slider right-to-left | ||||||||||||||||||||||||||
| Starting price | n | Mean | STDV | SE | n | Mean | STDV | SE | n | Mean | STDV | SE | ||||||||||||||||
| Level 1 | 100 | 128.59 | 22.80 | 2.28 | 101 | 117.81 | 23.45 | 2.33 | 103 | 123.89 | 21.09 | 2.08 | ||||||||||||||||
| Level 2 | 100 | 142.22 | 25.27 | 2.53 | 101 | 130.06 | 26.02 | 2.59 | 103 | 136.72 | 23.92 | 2.36 | ||||||||||||||||
| Level 3 | 100 | 154.54 | 28.02 | 2.82 | 101 | 143.90 | 29.52 | 2.94 | 103 | 145.95 | 29.04 | 2.86 | ||||||||||||||||
| 4. Moderation by distance to end point(ascending payment format: laptops) | ||||||||||||||||||||||||||||
| Response magnitude | Text box | Slider | Scale | |||||||||||||||||||||||||
| n | Mean | STDV | SE | n | Mean | STDV | SE | n | Mean | STDV | SE | |||||||||||||||||
| Low | 110 | 289.33 | 64.38 | 6.14 | 111 | 297.82 | 72.03 | 6.84 | 112 | 298.64 | 61.76 | 5.84 | ||||||||||||||||
| Medium | 110 | 395.17 | 114.12 | 10.88 | 111 | 437.47 | 110.98 | 10.53 | 112 | 439.00 | 93.66 | 8.85 | ||||||||||||||||
| High | 110 | 560.62 | 214.19 | 20.42 | 111 | 621.20 | 183.93 | 17.46 | 112 | 621.68 | 167.04 | 15.78 | ||||||||||||||||
| 5. A convex slider(ascending payment format: laptops) | ||||||||||||||||||||||||||||
| Response magnitude | Text box | Convex slider | Slider | |||||||||||||||||||||||||
| n | Mean | STDV | SE | n | Mean | STDV | SE | n | Mean | STDV | SE | |||||||||||||||||
| Low | 86 | 276.80 | 41.02 | 4.42 | 88 | 284.43 | 45.43 | 4.84 | 88 | 303.80 | 63.35 | 6.75 | ||||||||||||||||
| Medium | 86 | 380.79 | 99.22 | 10.70 | 88 | 397.78 | 103.61 | 11.04 | 88 | 435.19 | 115.59 | 12.32 | ||||||||||||||||
| High | 86 | 551.22 | 188.83 | 20.36 | 88 | 564.63 | 200.93 | 21.42 | 88 | 595.92 | 177.03 | 18.87 | ||||||||||||||||
| 6. Moderation by end point size(ascending payment format: wine) | ||||||||||||||||||||||||||||
| Range × response magnitude | Text box | Slider | ||||||||||||||||||||||||||
| n | Mean | STDV | SE | n | Mean | STDV | SE | |||||||||||||||||||||
| $500 range | ||||||||||||||||||||||||||||
| Low | 107 | 29.39 | 18.07 | 1.75 | 99 | 50.78 | 62.80 | 6.31 | ||||||||||||||||||||
| Medium | 107 | 59.41 | 59.66 | 5.77 | 99 | 84.68 | 80.50 | 8.09 | ||||||||||||||||||||
| High | 107 | 102.98 | 115.01 | 11.12 | 99 | 125.31 | 112.75 | 11.33 | ||||||||||||||||||||
| $1,000 range | ||||||||||||||||||||||||||||
| Low | 103 | 29.14 | 14.07 | 1.39 | 104 | 62.90 | 96.63 | 9.48 | ||||||||||||||||||||
| Medium | 103 | 65.08 | 72.97 | 7.19 | 104 | 128.77 | 160.53 | 15.74 | ||||||||||||||||||||
| High | 103 | 122.64 | 160.97 | 15.86 | 104 | 219.83 | 262.26 | 25.72 | ||||||||||||||||||||
| 1A: Mug auction(ascending payment format) | ||||||||||||||||||
| Text box | Slider | Wilcoxon two-sample test | ||||||||||||||||
| Median | Median | Z | p | |||||||||||||||
| Mug bid price | 6.0 | 10.0 | –1.56 | .06 | ||||||||||||||
| 1B: Veteran’s Day donations(ascending payment format) | ||||||||||||||||||
| Text box | Slider | Wilcoxon two-sample test | ||||||||||||||||
| Median | Median | Z | p | |||||||||||||||
| Donation amount | 10.0 | 20.0 | –2.31 | .01 | ||||||||||||||
| 2. eBay bids(ascending payment format: laptops) | ||||||||||||||||||
| Text box | Slider | Wilcoxon two-sample test | ||||||||||||||||
| Starting price | Median | Median | Z | p | ||||||||||||||
| $239 | 250.0 | 256.0 | –2.80 | .003 | ||||||||||||||
| $259 | 270.0 | 278.0 | –3.43 | <.001 | ||||||||||||||
| $279 | 280.5 | 287.0 | -3.81 | <.001 | ||||||||||||||
| 3. Priceline bids(descending payment format: hotel rooms) | ||||||||||||||||||
| Text box | Slider L-to-R | Slider R-to-L | Wilcoxon two-sample tests | |||||||||||||||
| Text box vs. L-to-R | Text box vs. R-to-L | L-to-R vs. R-to-L | ||||||||||||||||
| Starting price | Median | Median | Median | Z | p | Z | p | Z | p | |||||||||
| Level 1 | 130.0 | 116.0 | 127.5 | 3.48 | <.001 | 1.89 | .03 | –1.87 | .03 | |||||||||
| Level 2 | 145.0 | 130.0 | 140.0 | 3.35 | <.001 | 1.78 | .04 | –2.04 | .02 | |||||||||
| Level 3 | 157.5 | 142.0 | 151.0 | 2.66 | .004 | 2.07 | .02 | –.68 | .25 | |||||||||
| 4. Moderation by distance to end point(ascending payment format: laptops) | ||||||||||||||||||
| Response magnitude | Text box | Slider | Scale | Wilcoxon two-sample tests | ||||||||||||||
| Text box vs. slider | Text box vs. scale | Slider vs. scale | ||||||||||||||||
| Median | Median | Median | Z | p | Z | p | Z | p | ||||||||||
| Low | 260.0 | 270.0 | 289.0 | –.26 | .40 | .12 | .45 | –.03 | .49 | |||||||||
| Medium | 370.0 | 401.0 | 424.0 | –3.07 | .001 | –3.14 | <.001 | –.38 | .35 | |||||||||
| High | 500.0 | 605.0 | 619.0 | –2.40 | .008 | –2.30 | .01 | .05 | .48 | |||||||||
| 5. A convex slider(ascending payment format: laptops) | ||||||||||||||||||
| Response magnitude | Text box | Convex slider | Slider | Wilcoxon two-sample tests | ||||||||||||||
| Text box vs. slider | Text box vs. convex slider | |||||||||||||||||
| Median | Median | Median | Z | p | Z | p | ||||||||||||
| Low | 260.0 | 269.5 | 287.5 | –3.67 | <.001 | –.86 | .20 | |||||||||||
| Medium | 350.0 | 373.0 | 425.0 | –3.39 | <.001 | –1.27 | .10 | |||||||||||
| High | 500.0 | 550.0 | 600.0 | –1.81 | .04 | –.40 | .34 | |||||||||||
| 6. Moderation by end point size(ascending payment format: wine) | ||||||||||||||||||
| Range × response magnitude | Text box | Slider | Wilcoxon two-sample test | |||||||||||||||
| Median | Median | Z | p | |||||||||||||||
| $500 range | ||||||||||||||||||
| Low | 25.0 | 30.0 | –4.24 | <.001 | ||||||||||||||
| Medium | 40.0 | 50.0 | –3.81 | <.001 | ||||||||||||||
| High | 60.0 | 75.0 | –2.85 | .002 | ||||||||||||||
| $1,000 range | ||||||||||||||||||
| Low | 25.0 | 27.0 | –2.76 | .003 | ||||||||||||||
| Medium | 40.0 | 56.0 | –3.59 | <.001 | ||||||||||||||
| High | 60.0 | 97.0 | –3.47 | <.001 | ||||||||||||||
| 1A: Mug auction(ascending payment format) | ||||||||||||||||||
| Text box | Slider | Wilcoxon two-sample test | ||||||||||||||||
| Median | Median | Z | p | |||||||||||||||
| Mug bid price | 6.0 | 10.0 | –1.56 | .06 | ||||||||||||||
| 1B: Veteran’s Day donations(ascending payment format) | ||||||||||||||||||
| Text box | Slider | Wilcoxon two-sample test | ||||||||||||||||
| Median | Median | Z | p | |||||||||||||||
| Donation amount | 10.0 | 20.0 | –2.31 | .01 | ||||||||||||||
| 2. eBay bids(ascending payment format: laptops) | ||||||||||||||||||
| Text box | Slider | Wilcoxon two-sample test | ||||||||||||||||
| Starting price | Median | Median | Z | p | ||||||||||||||
| $239 | 250.0 | 256.0 | –2.80 | .003 | ||||||||||||||
| $259 | 270.0 | 278.0 | –3.43 | <.001 | ||||||||||||||
| $279 | 280.5 | 287.0 | -3.81 | <.001 | ||||||||||||||
| 3. Priceline bids(descending payment format: hotel rooms) | ||||||||||||||||||
| Text box | Slider L-to-R | Slider R-to-L | Wilcoxon two-sample tests | |||||||||||||||
| Text box vs. L-to-R | Text box vs. R-to-L | L-to-R vs. R-to-L | ||||||||||||||||
| Starting price | Median | Median | Median | Z | p | Z | p | Z | p | |||||||||
| Level 1 | 130.0 | 116.0 | 127.5 | 3.48 | <.001 | 1.89 | .03 | –1.87 | .03 | |||||||||
| Level 2 | 145.0 | 130.0 | 140.0 | 3.35 | <.001 | 1.78 | .04 | –2.04 | .02 | |||||||||
| Level 3 | 157.5 | 142.0 | 151.0 | 2.66 | .004 | 2.07 | .02 | –.68 | .25 | |||||||||
| 4. Moderation by distance to end point(ascending payment format: laptops) | ||||||||||||||||||
| Response magnitude | Text box | Slider | Scale | Wilcoxon two-sample tests | ||||||||||||||
| Text box vs. slider | Text box vs. scale | Slider vs. scale | ||||||||||||||||
| Median | Median | Median | Z | p | Z | p | Z | p | ||||||||||
| Low | 260.0 | 270.0 | 289.0 | –.26 | .40 | .12 | .45 | –.03 | .49 | |||||||||
| Medium | 370.0 | 401.0 | 424.0 | –3.07 | .001 | –3.14 | <.001 | –.38 | .35 | |||||||||
| High | 500.0 | 605.0 | 619.0 | –2.40 | .008 | –2.30 | .01 | .05 | .48 | |||||||||
| 5. A convex slider(ascending payment format: laptops) | ||||||||||||||||||
| Response magnitude | Text box | Convex slider | Slider | Wilcoxon two-sample tests | ||||||||||||||
| Text box vs. slider | Text box vs. convex slider | |||||||||||||||||
| Median | Median | Median | Z | p | Z | p | ||||||||||||
| Low | 260.0 | 269.5 | 287.5 | –3.67 | <.001 | –.86 | .20 | |||||||||||
| Medium | 350.0 | 373.0 | 425.0 | –3.39 | <.001 | –1.27 | .10 | |||||||||||
| High | 500.0 | 550.0 | 600.0 | –1.81 | .04 | –.40 | .34 | |||||||||||
| 6. Moderation by end point size(ascending payment format: wine) | ||||||||||||||||||
| Range × response magnitude | Text box | Slider | Wilcoxon two-sample test | |||||||||||||||
| Median | Median | Z | p | |||||||||||||||
| $500 range | ||||||||||||||||||
| Low | 25.0 | 30.0 | –4.24 | <.001 | ||||||||||||||
| Medium | 40.0 | 50.0 | –3.81 | <.001 | ||||||||||||||
| High | 60.0 | 75.0 | –2.85 | .002 | ||||||||||||||
| $1,000 range | ||||||||||||||||||
| Low | 25.0 | 27.0 | –2.76 | .003 | ||||||||||||||
| Medium | 40.0 | 56.0 | –3.59 | <.001 | ||||||||||||||
| High | 60.0 | 97.0 | –3.47 | <.001 | ||||||||||||||
| 1A: Mug auction(ascending payment format) | ||||||||||||||||||
| Text box | Slider | Wilcoxon two-sample test | ||||||||||||||||
| Median | Median | Z | p | |||||||||||||||
| Mug bid price | 6.0 | 10.0 | –1.56 | .06 | ||||||||||||||
| 1B: Veteran’s Day donations(ascending payment format) | ||||||||||||||||||
| Text box | Slider | Wilcoxon two-sample test | ||||||||||||||||
| Median | Median | Z | p | |||||||||||||||
| Donation amount | 10.0 | 20.0 | –2.31 | .01 | ||||||||||||||
| 2. eBay bids(ascending payment format: laptops) | ||||||||||||||||||
| Text box | Slider | Wilcoxon two-sample test | ||||||||||||||||
| Starting price | Median | Median | Z | p | ||||||||||||||
| $239 | 250.0 | 256.0 | –2.80 | .003 | ||||||||||||||
| $259 | 270.0 | 278.0 | –3.43 | <.001 | ||||||||||||||
| $279 | 280.5 | 287.0 | -3.81 | <.001 | ||||||||||||||
| 3. Priceline bids(descending payment format: hotel rooms) | ||||||||||||||||||
| Text box | Slider L-to-R | Slider R-to-L | Wilcoxon two-sample tests | |||||||||||||||
| Text box vs. L-to-R | Text box vs. R-to-L | L-to-R vs. R-to-L | ||||||||||||||||
| Starting price | Median | Median | Median | Z | p | Z | p | Z | p | |||||||||
| Level 1 | 130.0 | 116.0 | 127.5 | 3.48 | <.001 | 1.89 | .03 | –1.87 | .03 | |||||||||
| Level 2 | 145.0 | 130.0 | 140.0 | 3.35 | <.001 | 1.78 | .04 | –2.04 | .02 | |||||||||
| Level 3 | 157.5 | 142.0 | 151.0 | 2.66 | .004 | 2.07 | .02 | –.68 | .25 | |||||||||
| 4. Moderation by distance to end point(ascending payment format: laptops) | ||||||||||||||||||
| Response magnitude | Text box | Slider | Scale | Wilcoxon two-sample tests | ||||||||||||||
| Text box vs. slider | Text box vs. scale | Slider vs. scale | ||||||||||||||||
| Median | Median | Median | Z | p | Z | p | Z | p | ||||||||||
| Low | 260.0 | 270.0 | 289.0 | –.26 | .40 | .12 | .45 | –.03 | .49 | |||||||||
| Medium | 370.0 | 401.0 | 424.0 | –3.07 | .001 | –3.14 | <.001 | –.38 | .35 | |||||||||
| High | 500.0 | 605.0 | 619.0 | –2.40 | .008 | –2.30 | .01 | .05 | .48 | |||||||||
| 5. A convex slider(ascending payment format: laptops) | ||||||||||||||||||
| Response magnitude | Text box | Convex slider | Slider | Wilcoxon two-sample tests | ||||||||||||||
| Text box vs. slider | Text box vs. convex slider | |||||||||||||||||
| Median | Median | Median | Z | p | Z | p | ||||||||||||
| Low | 260.0 | 269.5 | 287.5 | –3.67 | <.001 | –.86 | .20 | |||||||||||
| Medium | 350.0 | 373.0 | 425.0 | –3.39 | <.001 | –1.27 | .10 | |||||||||||
| High | 500.0 | 550.0 | 600.0 | –1.81 | .04 | –.40 | .34 | |||||||||||
| 6. Moderation by end point size(ascending payment format: wine) | ||||||||||||||||||
| Range × response magnitude | Text box | Slider | Wilcoxon two-sample test | |||||||||||||||
| Median | Median | Z | p | |||||||||||||||
| $500 range | ||||||||||||||||||
| Low | 25.0 | 30.0 | –4.24 | <.001 | ||||||||||||||
| Medium | 40.0 | 50.0 | –3.81 | <.001 | ||||||||||||||
| High | 60.0 | 75.0 | –2.85 | .002 | ||||||||||||||
| $1,000 range | ||||||||||||||||||
| Low | 25.0 | 27.0 | –2.76 | .003 | ||||||||||||||
| Medium | 40.0 | 56.0 | –3.59 | <.001 | ||||||||||||||
| High | 60.0 | 97.0 | –3.47 | <.001 | ||||||||||||||
| 1A: Mug auction(ascending payment format) | ||||||||||||||||||
| Text box | Slider | Wilcoxon two-sample test | ||||||||||||||||
| Median | Median | Z | p | |||||||||||||||
| Mug bid price | 6.0 | 10.0 | –1.56 | .06 | ||||||||||||||
| 1B: Veteran’s Day donations(ascending payment format) | ||||||||||||||||||
| Text box | Slider | Wilcoxon two-sample test | ||||||||||||||||
| Median | Median | Z | p | |||||||||||||||
| Donation amount | 10.0 | 20.0 | –2.31 | .01 | ||||||||||||||
| 2. eBay bids(ascending payment format: laptops) | ||||||||||||||||||
| Text box | Slider | Wilcoxon two-sample test | ||||||||||||||||
| Starting price | Median | Median | Z | p | ||||||||||||||
| $239 | 250.0 | 256.0 | –2.80 | .003 | ||||||||||||||
| $259 | 270.0 | 278.0 | –3.43 | <.001 | ||||||||||||||
| $279 | 280.5 | 287.0 | -3.81 | <.001 | ||||||||||||||
| 3. Priceline bids(descending payment format: hotel rooms) | ||||||||||||||||||
| Text box | Slider L-to-R | Slider R-to-L | Wilcoxon two-sample tests | |||||||||||||||
| Text box vs. L-to-R | Text box vs. R-to-L | L-to-R vs. R-to-L | ||||||||||||||||
| Starting price | Median | Median | Median | Z | p | Z | p | Z | p | |||||||||
| Level 1 | 130.0 | 116.0 | 127.5 | 3.48 | <.001 | 1.89 | .03 | –1.87 | .03 | |||||||||
| Level 2 | 145.0 | 130.0 | 140.0 | 3.35 | <.001 | 1.78 | .04 | –2.04 | .02 | |||||||||
| Level 3 | 157.5 | 142.0 | 151.0 | 2.66 | .004 | 2.07 | .02 | –.68 | .25 | |||||||||
| 4. Moderation by distance to end point(ascending payment format: laptops) | ||||||||||||||||||
| Response magnitude | Text box | Slider | Scale | Wilcoxon two-sample tests | ||||||||||||||
| Text box vs. slider | Text box vs. scale | Slider vs. scale | ||||||||||||||||
| Median | Median | Median | Z | p | Z | p | Z | p | ||||||||||
| Low | 260.0 | 270.0 | 289.0 | –.26 | .40 | .12 | .45 | –.03 | .49 | |||||||||
| Medium | 370.0 | 401.0 | 424.0 | –3.07 | .001 | –3.14 | <.001 | –.38 | .35 | |||||||||
| High | 500.0 | 605.0 | 619.0 | –2.40 | .008 | –2.30 | .01 | .05 | .48 | |||||||||
| 5. A convex slider(ascending payment format: laptops) | ||||||||||||||||||
| Response magnitude | Text box | Convex slider | Slider | Wilcoxon two-sample tests | ||||||||||||||
| Text box vs. slider | Text box vs. convex slider | |||||||||||||||||
| Median | Median | Median | Z | p | Z | p | ||||||||||||
| Low | 260.0 | 269.5 | 287.5 | –3.67 | <.001 | –.86 | .20 | |||||||||||
| Medium | 350.0 | 373.0 | 425.0 | –3.39 | <.001 | –1.27 | .10 | |||||||||||
| High | 500.0 | 550.0 | 600.0 | –1.81 | .04 | –.40 | .34 | |||||||||||
| 6. Moderation by end point size(ascending payment format: wine) | ||||||||||||||||||
| Range × response magnitude | Text box | Slider | Wilcoxon two-sample test | |||||||||||||||
| Median | Median | Z | p | |||||||||||||||
| $500 range | ||||||||||||||||||
| Low | 25.0 | 30.0 | –4.24 | <.001 | ||||||||||||||
| Medium | 40.0 | 50.0 | –3.81 | <.001 | ||||||||||||||
| High | 60.0 | 75.0 | –2.85 | .002 | ||||||||||||||
| $1,000 range | ||||||||||||||||||
| Low | 25.0 | 27.0 | –2.76 | .003 | ||||||||||||||
| Medium | 40.0 | 56.0 | –3.59 | <.001 | ||||||||||||||
| High | 60.0 | 97.0 | –3.47 | <.001 | ||||||||||||||
EXPERIMENT 1A: MUG AUCTION
In this experiment, participants bid on a mug with the clear understanding that the highest bidder would have to pay the bid amount. We manipulated the response format for bid submissions: half the participants submitted their bids using a slider scale, while the other half used an open-ended text box. Will bids elicited through a slider scale be higher than those elicited through a text box (hypothesis 1a)?
In addition, we controlled for awareness of range information to rule out the possibility that the effect is driven by participants in the text box condition who do not consider range information. Range information—lowest and highest possible bid values—was explicitly made salient in both conditions to rule out that the effect of response format is caused by information asymmetry. Furthermore, participants were provided with the retail price of the product.
Method
Participants
One hundred twenty-seven undergraduates from a US university (49% female, Mage = 21.4 years) participated in this study in exchange for course credit.
Procedure
The computer-based experiment was created in Adobe Flash and administered in a laboratory in sessions of eight to 15 participants. This was the first study in a series of unrelated studies. Participants were told that they would be presented with the opportunity to bid on a Japanese insulated travel mug in a real auction. A research assistant showed the real mug to the participants before they bid on it.
To ensure that the participants were serious about the bids, before they submitted the bids we asked if they understood that they would be contacted to pay the bid amount to the experimenter in exchange for the mug (yes/no), and those participants that clicked “no” were given the option of not participating in the study. No participant chose this option.
The participants were then presented with an instruction screen for placing their bid, with a reminder that they would have to pay the bid price if they won the auction. They were informed that the retail price is $24 and that they could enter any response from $0 to $150. Thus, the range information was made equally salient for both the conditions. They were asked, “Do you understand how to submit your bid?” (yes/no). Once they confirmed they understood the instructions, they were shown the product information for the insulated mug and asked to enter their bid. The participants then entered their response on a slider scale or text box and clicked on the “Place Bid” button (see figure 3). Finally, participants were asked, “In the instructions that you just read about placing your bid, you were told that you could enter any response between which two numbers?” ($0 to $100, $0 to $150, $0 to $200) and answered demographic questions.
Results
Bids
We conducted the analysis using PROC GLIMMIX specifying a Poisson distribution with response format as the independent measure and bid price as the dependent measure. It revealed a significant effect of response format where participants in the slider condition bid more on the insulated mug (M = $11.40) than those in the text box condition (M = $8.01, F(1, 125) = 37.05, p < .001, see table 1).
The results are robust to distributional assumptions and the type of statistical test. The median values in the two conditions and the nonparametric test are reported in table 2. The results from a similar analysis assuming normal distribution are available in web appendix B. The means without the outliers are reported in web appendix C.
The highest bid, $35, was submitted by two participants in the slider condition. One of these two participants was chosen as the winner and asked to buy the product for the bid amount. The participant met with the experimenter and exchanged $35 for the mug. However, because this was an undergraduate student from the subject pool, after the transaction was completed, we returned the money and let the participant keep the mug as a token of goodwill.
Confound Check: Range Information
The vast majority of participants (90%) correctly identified the range outlined in the experiment stimuli as $0 to $150, confirming that attention to range information did not vary across the two conditions. Furthermore, removing participants that incorrectly identified the range did not change the results. Thus, the slider scale end point assimilation effect does not stem from participants in the text box condition being unaware of the response range.
EXPERIMENT 1B: DONATIONS TO CHARITY
In the previous experiment, some participants may not have felt invested in the exercise or that they were bidding with real money. Does the effect still hold when transactions involve real money for every individual? In experiment 1b, following the procedure used by Berman and Small (2012), we gave every participant a $1 bonus at the beginning of the study and the choice of donating any portion of their bonus to the Intrepid Fallen Heroes Fund, a nonprofit serving US military personnel injured during active duty and their families. The donations were elicited through either a slider scale or text box. The amount they did not donate was theirs to keep.
Method
Participants
Two hundred four US-based panelists on Amazon Mechanical Turk (MTurk), verified by IP address, participated in this study (52% female, Mage = 36.3 years). To avoid confounds from differences in screen size, participants were able to complete the study only if they were on a computer; mobile users were automatically blocked from responding to the study. These procedures were followed for all subsequent experiments.
Procedure
Participants recruited were told that they would be paid 45 cents for completing a brief study about their interest in “donating to a particular charity for US veterans.” The study was run on Veteran’s Day to make the charity more relevant for all individuals. After starting the study, they received the following additional instructions about receiving a $1 bonus amount, in addition to the 45 cents:
You will be paid 45 cents for completing this brief study. You will also be paid an additional $1 (as a bonus). This study is about your interest in donating to a particular charity for US veterans. You will then be asked how much you are interested in donating to this charity.
They were then given a description of the Intrepid Fallen Heroes Fund (see web appendix A.1B) and asked, “Please enter the number of cents from the $1 that you would like to donate to the Intrepid Fallen Heroes Fund. You can enter any value from 0 to 100 cents.” All participants were also given the average donation value: “In a previous version of this study, the average donation was 17 cents.”2 Thus, the range information and the average donation value were made clear in both conditions. Underneath, participants were shown either a text box or a slider scale to enter their response. The end points of the slider scales were not numbered to rule out the possibility that the slider format increases awareness of the numeric range. Finally, participants answered demographic questions.
Results
Donations
The total value of donations collected from all the participants was $62.61, and this amount was donated to the charity by the experimenter. The analysis conducted with PROC GLIMMIX, specifying a Poisson distribution with response format as the independent measure and donation amount as the dependent measure, revealed a significant effect of response format, where participants in the slider condition donated significantly more of their $1 (M = 37.8 cents) than those in the text box condition (M = 24.0 cents, F(1, 202) = 307.29, p < .001; see table 1). The results are robust to distributional assumptions and the type of statistical test (see table 2, web appendixes B and C).
Discussion
The results from experiments 1a and 1b provide evidence that response formats can change valuations. Experiment 1a used an auction administered on students in a laboratory. Experiment 1b used a donation task administered to a more general population as an online study. Experiment 1a entailed amounts involving dollars ($0 to $150), whereas experiment 1b entailed amounts involving cents (0 to 100). Yet the results from the two studies were convergent in showing that slider scales elicit more intense bids than text boxes, supporting hypothesis 1a—bids were 42% higher for experiment 1a and donations were 57% higher for experiment 1b (effect sizes for each study are summarized in web appendix H). Note that although the economic values are quite different across the two studies, the effect sizes are comparable, suggesting that participants were responding to the numerosity of the prices rather than to economic values (Bagchi and Davis 2016; Burson et al. 2009). The range information was made clear in both experiments; in experiment 1a, participants knew that their bid had to be between $0 and $150, and in experiment 1b participants knew that their donation value had to be between 0 and 100 cents. In addition, in experiment 1b all participants who chose to donate had to spend real money. Thus, the absence of range information or inconsequentiality of the response is not a necessary condition for the observed effect. In the next two experiments, we take a closer look at the plausible mechanisms causing end point assimilation when using slider scales—ruling out several potential alternative explanations—and use a more externally valid participative pricing context similar to that used by companies.
EXPERIMENT 2: ASCENDING PAYMENT FORMAT ON EBAY
In this experiment, we used a more externally valid decision context by giving people the scenario of bidding on items offered by the popular auction website eBay. We asked participants who recently purchased laptops or were planning to purchase laptops to bid on three used laptops using either a slider scale or a text box. Each participant offered three bids, one for each laptop. We varied the starting bids for three laptops as a within-subjects factor. This enabled us to address whether the effect of response format holds even when participants make several consecutive responses in the same product category. The range information was not explicitly provided for either format to further test the external validity of the effect, as firms typically do not provide such range information. To rule out other possible alternative accounts, we measured ease of response, format preference, and awareness of format influence.
Method
Participants
One hundred ninety-nine US-based participants on MTurk, verified by IP address, participated in this experiment in exchange for $1 (47% women; Mage = 37.1 years). To ensure the effect is not restricted to people who are uninvolved or unfamiliar with the product category, we recruited only participants familiar with the category. All potential participants were asked two screening questions—only participants who had purchased a laptop computer in the past 24 months or intended to purchase one in the next 24 months were allowed to participate in the study. Participants who answered “no” to both of these questions were screened out at the beginning of the study and did not continue.
Procedure
The experiment used a 2 × 3 mixed-factorial design with response format (text box, slider) as the randomly assigned between-subjects factor and starting bid ($239, $259, $279) as a within-subjects factor. Participants were told they would be asked to imagine bidding on eBay. The first screen informed them how the bidding process works on eBay. They were then asked to submit their bids on three used laptops with different starting bid prices shown in randomized order one at a time. The information format design was as close as possible to eBay: each bid page included a photograph of the product, the current bid price, the number of prior bids, and detailed product information. The only difference between conditions was that participants were randomly assigned to submit their bids either via an open-ended text box or a slider scale anchored at the starting bid price (see web appendix A.2). Ranges were not provided in either condition. The bid amounts were the primary dependent variable.
Process Measures
After submitting their bids, participants were asked how easy or difficult it was to submit the bids (1 = extremely easy, 5 = extremely difficult). To assess whether participants were mindful of the biasing influence of response formats, we asked them to describe how they arrived at the bid values for the three computers. They described their thought process in an open-ended text box. They were also asked direct questions about response formats. Participants were shown the response formats side by side and asked to indicate which they preferred (slider/text box). Then they were asked whether response format could change their responses (i: “No, my bid values will not be affected by the response format”; ii: “Yes, my bid values will be higher when I use the slider format”; iii: “Yes, my bid values will be higher when I use the text box format”). Finally, participants submitted their demographic information.
Results
Willingness to Pay
The analysis was conducted with PROC GLIMMIX specifying a Poisson distribution with response format (slider vs. text box) as a between-subjects factor and starting bid ($239, $259, $279) as a within-subjects factor. The main effect of response format was significant, F(1, 197) = 5.61, p = .02, where values submitted by text box (M = $280) were lower than those submitted by slider (M = $291). Participants’ WTP for all three laptops was higher when submitted via a slider scale relative to a text box (all ps < .01), supporting hypothesis 1a (see figure 4, table 1). There was also a main effect of the starting bid, F(2, 393) = 98.49, p < .001, but the two-way interaction was not significant (F < 1). These results are robust to distributional assumptions and the type of statistical test (see table 2, web appendixes B and C).
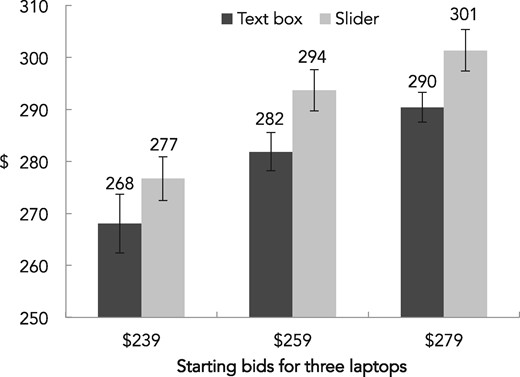
EXPERIMENT 2: EFFECT OF RESPONSE FORMAT FOR ASCENDING PAYMENT FORMAT
Ease of Responding
Participants’ self-reported ease of responding was reverse-scored such that higher scores indicated greater ease. There was no effect of response format on self-reported ease (F < 1) and the average scores on the five-point scale were very high in both conditions (Mtext box = 4.59, Mslider = 4.65).
Awareness of Bias
Were participants aware of a biasing influence of response format? In their open-ended responses, participants mentioned that their bids were influenced by product specifications, bid prices, initial bids, how the product looked, how much they wanted it, and more, but none of them mentioned influence by response format. For the direct question about the influence of response formats, the vast majority of participants (73%) reported that their bid values would not be affected by the response format. Some (22%) suspected that their bids would be higher when they used a slider scale, and a very small proportion (5%) believed that their bids would be higher when they used text boxes. These proportions did not differ by response format (p = .19). These results suggest that most participants do not suspect that response format could change their answers, but when directly prompted to consider this possibility, a small proportion suspect that they might be indicating higher values when using slider scales.
Preference for Response Formats
Participants’ preference for response format (1 = prefer slider, 0 = prefer text box) was submitted to a one-way ANOVA with response format as the predictor and revealed a significant effect of response format (F(1, 197) = 29.13, p < .001). Participants were more likely to prefer the slider scale response format after having used a slider scale (37%) versus a text box (7%). These results suggest that people do not have stable preferences for response format and adapt to the response format they use.
Discussion
These results suggest that response format manipulation can influence consumer behavior even in more externally valid shopping situations. If eBay—a popular online shopping forum—starts using a slider scale instead of a text box to elicit bids, then shoppers are likely to offer higher bids, supporting hypothesis 1a. More importantly, the process measures from this experiment suggest that we can rule out that the effect is caused by ease of use: participants found both response formats—slider scales and text boxes—equally easy to use. Furthermore, most participants were unaware of the surreptitious influence of response formats on their bid values. Even when asked directly after making their judgments whether response formats might have influenced their bids, only a small minority considered this possibility. This suggests that the psychological mechanism underlying the slider scale effect is implicit in nature, operating outside of people’s awareness.
Also, we employed a within-subjects factor with three different levels of starting bids. The effect manifested for all three randomized replicates, ruling out the possibility that the effect wears out with familiarity with the response format. Finally, this study shows that the end point assimilation effect manifests both when range information is and is not provided.
To further test the number line recalibration account, in the next study, we employed a descending payment format and also varied the placement of the slider knob starting point.
EXPERIMENT 3: DESCENDING PAYMENT FORMAT ON PRICELINE
This experiment had two objectives. First, we wanted to test the effect of response format in the context of a descending payment format. Thus far, all experiments used ascending payment formats where buyers submit responses higher than the starting price. In this experiment, participants had to submit responses lower than the starting price. Participants were informed that Priceline, an online travel reservation company, allows customers to bid for hotel rooms. For example, a night at an expensive downtown New York City hotel room has a rack rate of $400, but a Priceline customer could bid lower, say $300 or even $150. If the end point assimilation effect stems from consideration of the visual distance from the end point in relation to the starting point, per hypothesis 1b, then in a descending payment format, slider scales should result in lower numeric values than text boxes.
Second, in this experiment we introduced two slider scale conditions—one where the slider knob moved from left to right (slider left-to-right) and one where it moved from right to left (slider right-to-left). This allows us to address the possibility that the effect of slider scale could be an idiosyncratic effect of the left-to-right hand movement. If the effect of slider scale is because of the left-to-right hand movement, then reversing the direction of the hand movement from right to left should alleviate the effect. However, if the effect is due to the visual distance from end points and not because of the direction of the hand movement, then the responses in both slider scale conditions should be lower than in the text box condition.
Note that in this study, we used the same process measures and replicated the results of experiment 2, but the explication and results of these measures are included in web appendix D for the sake of brevity.
Method
Participants
Three hundred four US-based participants on MTurk participated in this computer experiment in exchange for $1 (38% women; Mage = 33.4 years). To ensure the applicability to the relevant customer base, only participants who had made online hotel reservations and stayed in a hotel in the past 24 months were allowed to participate in this study.
Procedure
The experiment used a 3 (response format) × 2 (hotel city) × 3 (starting price level) mixed-factorial design with response format (text box, slider-left-to-right, slider-right-to-left) as a randomly assigned between-subjects factor and hotel city and starting price level as within-subjects factors to create six hotel replicates.
Participants were informed that Priceline.com’s Name Your Own Price® system (popularly referred to as NYOP) allows travelers to bid on hotel rooms. They read that over the last 12 months, a substantial percentage of accepted offers have resulted in savings of up to 60% in comparison to the lowest published rates on other leading online travel sites for the same itinerary. Participants were randomly assigned to one of three conditions: text box, left-to-right-slider, or right-to-left-slider. They were given information about six hotels (two cities, three starting price levels), one at a time, and for each they submitted their bid per room, per night, in US dollars. For each hotel, they saw the city, general location of the hotel, star rating, and median retail price of a similar hotel. (For Atlanta, the three starting prices were $161, $194, and $199; for New York, the three starting prices were $179, $183, and $214). Note that this procedure matches Priceline’s actual NYOP bidding process where customers do not see the name of the specific hotel until their bid is accepted. Examples of the stimuli are shown in appendix A.3. In the left-to-right slider condition, the knob on the slider scale was set at the lowest possible bid value and participants had to drag it to a higher value to submit their bid. Conversely, in the right-to-left slider condition, the knob was set at the highest possible bid value.
Results
Willingness to Pay
The analysis was conducted with PROC GLIMMIX specifying a normal distribution with response format (left-to-right-slider, right-to-left-slider, text box) as a between-subjects factor and hotel replicates (city, starting price level) as within-subjects factors. We specified a normal distribution because, unlike in the other studies, the descending payment format did not result in a skewed distribution of responses.
The main effect of response format was significant, F(2, 301) = 5.30, p < .01. Participants’ average WTP value in the left-to-right-slider condition (M = $131) was lower than that in the text box condition (M = $142; t(301) = –3.25, p = .001). Participants’ average WTP value in the right-to-left-slider condition (M = $135) was also lower than that in the text box condition, although this contrast was marginally significant (t(301) = –1.84, p = .07). The two slider conditions were not significantly different from each other (t(301) = –1.43, p = .15). Thus, in a descending payment format, slider scales always reduced the WTP values regardless of the positioning of the slider knob. The mean WTP values for starting price level by response format, collapsed across city for simplicity, are depicted in figure 5 and table 1. (There are no significant interactions between response format and city.) There were also significant main effects of the city, F(1, 1504) = 265.35, p < .001, and starting price level, F(2, 1504) = 558.22, p < .001, and a two-way interaction between response format and starting price level, F(4, 1504) = 2.40, p = .05. The three-way interaction and two-way interactions between response format and city were not significant (p > .30). These results are robust to distributional assumptions and the type of statistical test (see table 2, web appendixes B and C).
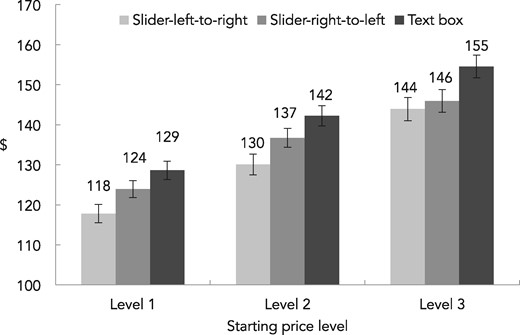
EXPERIMENT 3: EFFECT OF RESPONSE FORMAT FOR DESCENDING PAYMENT FORMAT
Discussion
The results from experiment 3 are illuminating in several ways. First, this experiment clearly demonstrates that slider scales do not always increase bid values. Instead, slider scales assimilate responses to the end point of the response range. Participants had to respond by bidding an amount lower than the retail price. Those who used slider scales submitted bids lower than those using text boxes.
Second, because the starting point of the slider knob was explicitly manipulated, some participants moved the knob to the left from the starting point (highest bid, right-to-left slider), while others moved it to the right from the end point (lowest bid, left-to-right slider). Consistent with prior research on anchoring effects in valuations (Adaval and Monroe 2002; Mussweiler and Strack 1999), results from these studies show that starting points do serve as anchors and influence final bids. However, manipulations of starting points did not wipe out the effect of response format. Bids elicited through slider scales—regardless of the starting point—were significantly lower than those elicited through text boxes. These results rule out the possibility that the slider effect stems simply from the location of the slider anchor point or an idiosyncratic effect of spatial left-to-right orientation.
EXPERIMENT 4: LOW, MEDIUM, AND HIGH BID VALUES ON A NONSLIDING SCALE
Hypothesis 2 posits that proximity to end point is an important moderator of the slider scale end point assimilation effect. As depicted in figures 1 and 2, a visual linear number line makes the distance from the end point more conspicuous, and this is more pronounced for response magnitudes that are closer to the end point. Therefore, bids elicited through slider scales and text boxes are more likely to diverge when participants consider numerical values that are closer to the end point rather than when the values are closer to the starting point. To test this hypothesis, we elicited three values that exemplified low, medium, and high bids from each participant. We predicted that for ascending payment formats, the effect of slider scales would be stronger for high values than for low values.
This study also had a second objective—namely, to rule out the response momentum account that the sliding movement (the physical action of sliding the slider knob and the concomitant sensory responses) is responsible for the results. A priori we had to acknowledge the possibility that the proposed effect could be idiosyncratic to the slider scale itself because of the sliding movement in response generation, rather than because of a mental recalibration of the number line. Slider scales might be intensifying responses because the momentum of the sliding response makes the final response end up farther away than the intended point. To test this alternative account, we added a new nonsliding scale condition where responses were elicited by a scale arrayed with a large number of points in $30 increments. The starting and end points of the scale exactly matched the slider scale and visually formed an evenly spaced number line, but did not entail the sliding movement; participants had to click on a point on the scale. If bid intensification stems only from the sliding movement, then it should not occur in the nonsliding scale condition, which does not require any sliding movement for a response. Conversely, if the effect stems from recalibration of the mental number line because of visual distance from the end points, then the nonsliding scale condition should result in end point assimilation similar to the slider condition.
Method
Participants
Three hundred thirty-three US-based participants on MTurk participated in this experiment in exchange for 51 cents (48% women; Mage = 35.1 years).
Procedures
The experiment used a 3 × 3 mixed-factorial design with response format (text box, slider, nonsliding scale) as a randomly assigned between-subjects factor and response magnitude (low, medium, high) as a within-subjects factor. The procedures for this experiment were identical to experiment 2 with the following exceptions. First, participants evaluated only one laptop with the $259 starting price and were asked to generate a low, medium, and high bid for the item. Second, in order to keep the response range information identical across all conditions, the bidding range was explicitly provided with a starting bid of $259 and an ending bid of $949, the retail price for a new computer. Third, a new nonsliding scale condition was added to the text box and slider condition. In the nonsliding scale condition, participants could select any bid from $259 to $949 in $30 increments where the bid values were arrayed on top of a series of radio buttons that visually formed a number line (see figure 6 for the nonsliding condition and web appendix A.4 for all conditions). The primary dependent measures were the three bid values submitted by each participant: low, medium, and high.

Results
Willingness to Pay
The analysis was conducted with PROC GLIMMIX specifying a Poisson distribution with response format (text box, slider, nonsliding scale) as a between-subjects factor, response magnitude (low, medium, high) as a within-subjects factor, and the bid amount as the dependent measure. The effects of response format (F(2, 330) = 5.66, p < .001), response magnitude (F(2, 660) = 17, 232.30, p < .001), and the interaction between the two (F(4, 660) = 22.08, p < .001) were all significant (see figure 7, table 1). The average bid in the text box condition ($415) was lower than that in the slider ($452, t(330) = –2.79, p < .01) and nonsliding scale ($453, t(330) = –3.03, p < .01) conditions, but the slider and nonsliding scale conditions were nearly identical to each other (t(330) = –.23, p =.82).
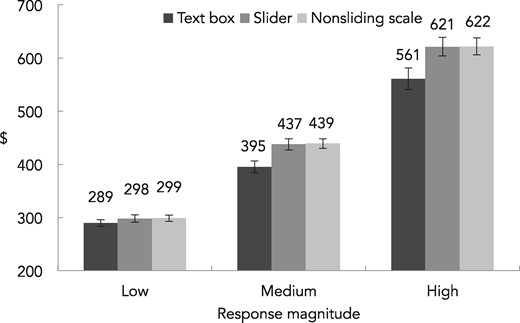
Furthermore, consistent with hypothesis 2, the end point assimilation effect for the slider and scale conditions was stronger for higher bid values. In the low response magnitude condition, the text box ($289), slider ($298), and scale ($299) bids were not significantly different from each other (all ps > .13). However, in the medium response magnitude condition, the average bid in the text box condition ($395) was lower than those in the slider ($437, t(660) = –3.47, p < .001) and nonsliding scale ($439, t(660) = –3.75, p < .001) conditions, but the slider and nonsliding scale conditions were nearly identical (t(660) = –.26, p = .79). In the high response magnitude condition, the average bid in the text box condition ($561) was lower than those in the slider ($621, t(660) = –3.52, p < .001) and nonsliding scale ($622, t(660) = –3.71, p < .001) conditions, but the slider and nonsliding scale conditions were nearly identical (t(660) = –.18, p =.85). These results are robust to distributional assumptions and the type of statistical test (see table 2, web appendixes B and C).
EXPERIMENT 5: A CONVEX SLIDER SCALE
This study was designed to delineate the role of distance visualization in the slider scale end point assimilation effect. If the bias in magnitude judgments is caused by the use of visual distance from the end point as a magnitude cue, then if we are able to surreptitiously change the visual distance of a bid value from the end point of the scale, then consumers’ evaluation of that bid value should change. For example, on a linear slider scale that ranges from $259 to $949, where the numeric values are a linear function of the distance from the starting point, a value of $604 would fall squarely in the middle of the starting and end points. But if we make the numeric values a convex function of the distance from the starting point, then $604 would appear to be closer to the end point than to the starting point of the scale. Thus, the same bid value should be perceived to be higher on a convex slider scale than on a linear slider scale. Therefore, a convex slider scale can mimic the responses elicited through a text box format. The present experiment was designed to test this hypothesis.
Method
Participants
Two hundred sixty-two US-based participants on MTurk participated in this experiment in exchange for 51 cents (58% women; Mage = 36.2 years).
Procedures
The experiment used a 3 × 3 mixed-factorial design with response format (text box, linear slider, convex slider) as a randomly assigned between-subjects factor and response magnitude (low, medium, high) as a within-subjects factor. The procedures for this experiment were identical to experiment 4; we used the laptop bidding context, and the linear slider and the text box conditions were exactly the same as in the previous study. The only point of departure was the addition of the convex slider condition in place of the nonsliding scale condition. Participants in the convex slider condition saw a slider scale that looked very much like the slider in the linear condition. However, unbeknownst to them, the values on the slider scale were a convex function of the distance from the starting point. In the linear slider scale condition, the bid value y was a linear function of the distance from the starting point.
The two functions are depicted in figure 8. As shown there, the midpoint of the linear slider scale is $604. But on the convex slider, $604 appears between markers 6 and 7, much closer to the end point (see web appendix A.5 for screenshots of the slider conditions). More generally, all values on the convex slider scales appear closer to the end point relative to how they appear on the linear slider scale. Therefore, we expected responses on the convex slider scale to be less extreme and more closely match the responses on the text box format. Note that operationally the linear slider scale and the convex slider scale appear very similar to each other, and it is difficult for the participants in the convex slider condition to discern that the response format they are using is unusual. As in the previous study, the primary dependent measures were the three bid values submitted by each participant: low, medium, and high.
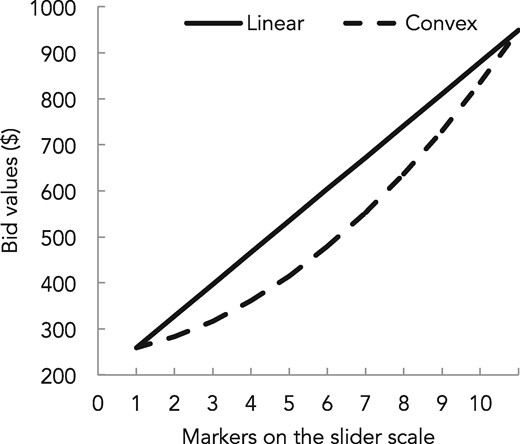
Results
Willingness to Pay
The analysis was conducted with PROC GLIMMIX specifying a Poisson distribution with response format (text box, linear slider, convex slider) as a between-subjects factor, response magnitude (low, medium, high) as a within-subjects factor, and the bid amount as the dependent measure. The effects of response format (F(2, 259) = 3.92, p = .02), response magnitude (F(2, 518) = 12, 157.10, p < .001), and the interaction between the two (F(4, 518) = 8.47, p < .001) were all significant (see figure 9, table 1). The average bid in the linear slider condition ($445) was higher than in the text box condition ($403, t(259) = 2.71, p < .01) and the convex slider condition ($416, t(259) = –1.96, p = .05), while the average bids in the text box and convex slider conditions were not significantly different from each other (t(259) = .76, p = .45). A nonparametric test of medians also demonstrated the same pattern (see table 2). However, this is the only study in the set of studies wherein the results were contingent on distributional assumptions (see web appendix B). We conducted follow-up analyses for this study to validate the robustness of our results and also ran another post hoc condition with a concave slider scale, details of which are reported in web appendixes E and F, respectively.
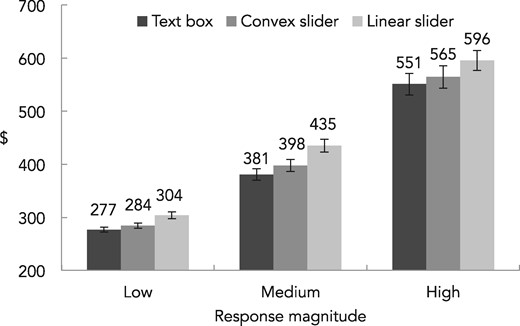
EXPERIMENT 6: BIASING EFFECT OF RESPONSE RANGE
The final study in this research delineates the influence of visual distance from end points by manipulating the response range (hypothesis 3). We used wines as the stimuli in this study because wine prices have a wide range, allowing us to manipulate the price range without arousing suspicion in the participants. Participants bid on a bottle of wine being sold by an online wine retailer; half of them were told that the bid values could range from $20 to $500, whereas the other half were told that the range is $20 to $1,000. We expected this range manipulation to change the visual distance from the end point when participants use slider scales to submit bids. A bid of $260 would be equidistant from the two end points for the smaller range slider, but it would appear farther from the end point on the larger range slider. Thus, the same bid would appear smaller on the larger range scale. The text box responses, in contrast, would be less affected by this range manipulation because of the absence of visual distance as a magnitude cue.
Additionally, we also tested whether participants in the slider scale conditions are less aware of the effect of the range manipulations relative to those in the text box conditions. Because we conceptualize the slider scale end point assimilation effect as automatic, we predicted that participants would be less aware of the influence of response range in the slider scale conditions.
Method
Participants
Four hundred thirteen US-based participants on MTurk participated in this experiment in exchange for 51 cents (51% women; Mage = 37.1 years).
Procedures
The experiment used a 2 × 2 × 3 mixed-factorial design with response format (text box, slider) and response range (small, large) as randomly assigned between-subjects factors and response magnitude (low, medium, high) as a within-subjects factor. Participants were told that an online store has enabled consumers to bid on wines and they could bid whatever they wanted, and that sellers would honor bids that they find reasonable. Several screens then explained the information they would receive about the wines—this information included the vintage of the wine, its name, the Wine Spectator rating, and a brief description with the starting bid price. Those in the small range condition were told “You will see the starting bid for the wines. The starting bid is the amount suggested by the seller to open the bid. Your bid has to be higher than the starting bid. The maximum bid anyone can submit is $500. So you can bid up to $500, if you want to.” Those in the large range condition were given the exact same information except they were told that the maximum bid they could submit is $1,000. (See web appendix A.6 for screenshots). They were then told that they would be asked to place a low, medium, and high bid for the described wine. Next, they were presented with information on the wine to bid on, a 2007 Farmlands Pinot Noir with a Wine Spectator rating of 97 and a starting bid of $20, described as “Vibrant ruby with a garnet core, expresses black cherry cola, red plum, and dry underbrush on the nose. The palate…shows some nice complexity and depth. It’s biodynamic.”
Participants then placed low, medium, and high bids for this wine either using text boxes or slider scales. After that, they were presented with a series of confound check questions. They were asked, “What was the starting bid for the wine?” and “What was the maximum bid anyone could submit?” as open-ended text boxes, and “To what extent was your highest bid influenced by the maximum possible bid value?” (“A great deal,” “A lot,” “A moderate amount,” “A little,” or “None at all”), followed by demographic questions.
Results
Willingness to Pay
The analysis was conducted with PROC GLIMMIX specifying a Poisson distribution with response format (text box, slider) and response range (small, large) as between-subjects factors, response magnitude (low, medium, high) as a within-subjects factor, and the bid amount as the dependent measure. The pattern of means is depicted in figure 10. The effects of response format (F(1, 409) = 28.97, p < .001) and response magnitude (F(2, 818) = 9, 752.79, p < .001) were both significant, as were the two-way interactions between response magnitude and response format (F(2, 818) = 123.51, p < .001) and response magnitude and response range (F(2, 818) = 116.53, p < .001) and the three-way interaction (F(2, 818) = 10.75, p < .001). For ease of exposition, first consider the WTP values in the two between-subjects conditions averaged across low, medium, and high bids. For low range conditions, the average WTP in the slider condition was somewhat higher than in the text box condition (Mtext-$500 = 64 vs. Mslider-$500 = 87, t(409) = 3.16, p < .01); however, as predicted this response format effect was stronger for the large range conditions (Mtext-$1000 = 72 vs. Mslider-$1000 = 137, t(409) = 4.45, p < .01). The pattern is depicted in figure 10.
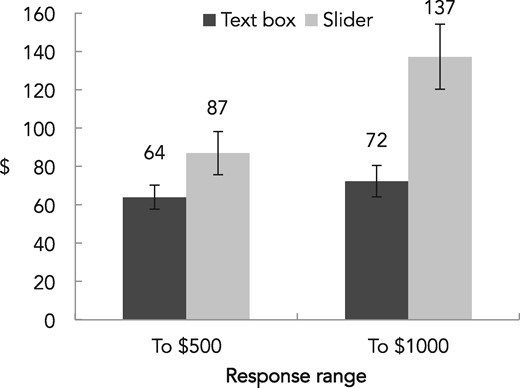
The WTP values for the three response magnitudes—low, medium, and high—are also consistent with our expectations. For low response magnitude, there was no effect of response range in either the text box (Mtext-$500 = 29 vs. Mtext-$1000 = 29, t(818) = .59, p = .56) or slider (Mslider-$500 = 51 vs. Mslider-$1000 = 63, t(818) = .15, p = .88) conditions. For medium response magnitude, there was no effect of response range in the text box conditions (Mtext-$500 = 59 vs. Mtext-$1000 = 65, t(818) = –.32, p = .75) and a marginally significant effect in slider conditions (Mslider-$500 = 85 vs. Mslider-$1000 = 129, t(818) = –1.71, p = .09). However, in the high response magnitude condition, while there was no effect of response range in the text box conditions (Mtext-$500 = 103 vs. Mtext-$1000 = 123, t(818) = –1.09, p = .28), in the slider conditions, bids for the larger response range (Mslider-$1000 = 220) were higher than those for the smaller response range (Mslider-$500 = 125, t(818) = –3.01, p < .01). These results are robust to distributional assumptions and the type of statistical test (see table 2, web appendixes B and C).
End Point Influence
After being asked the minimum and maximum possible bids that could be placed, participants were asked to what extent the maximum possible bid influenced their high bids. These values were reverse-coded from 1 to 5 such that higher numbers indicate greater stated influence by the end point. A two-way ANOVA with response range and format as independent variables revealed only a significant interaction effect (F(1, 409) = 7.01, p < .01). Participants in the slider conditions for both the small (M = 1.74) and large (M = 1.96) response range indicated that the end point of the response range had little effect on their high bid response (F(1, 409) = 2.00, p = .16). However, in the text box conditions, participants in the large response range condition (M = 1.68) indicated that the end point had less of an influence on their high bid response than those in the small response range condition (M = 2.03, F(1, 409) = 5.48, p = .02). These results suggest that participants in the text box conditions, who were presumably relying on deliberative numeric comparisons, were conscious of the influence of the end points, whereas those in the slider condition, who were influenced by automatic visual distance comparisons, were oblivious to the influence of the end points.
The results support hypotheses 2 and 3. Consistent with hypothesis 3, the results show that slider scales, compared to text boxes, are more susceptible to the manipulation of response range. Furthermore, consistent with hypothesis 2, the effect was stronger for numeric values that were closer to the end point.
ADDITIONAL STUDIES AND META-ANALYSIS
We conducted a single-paper meta-analysis across the seven studies outlined in this article and an additional four studies detailed in web appendix G. The four studies included in the web appendix were excluded from this article for brevity, but provide further evidence for the mental number line recalibration explanation. Experiment A1 replicates the real donation results of experiment 1B. The only differences between experiment 1B and experiment A1 are that in the latter version the slider scales were not anchored on the numeric values, we did not specify an average donation reference point, and the study was run on Memorial Day. Experiment A2 uses a paradigm similar to experiment 2 and introduced an additional condition, text box + slider. The text box + slider condition was identical to the original text box condition, but a slider scale was included beneath the text box with instructions for participants to confirm their bid from the text box after it was entered. The results from this study suggest that using a slider scale after responding through a text box does not result in the same end point assimilation as when the slider scale is actively used in the response generation process. Experiment A3 demonstrates a result similar to experiment 6, that range can moderate the end point assimilation effect, but in a much more bounded and narrow domain—the amount of tip given on a taxi ride can be influenced by the response range when slider scales are used to record payments. Experiment A4 demonstrates that the end point assimilation effect is attenuated for participants who were told they can pay only with cash versus credit cards—the pain of paying by cash prompted participants to focus on the starting point rather than the end point of the response range (Prelec and Loewenstein 1998; Prelec and Simester 2001; Raghubir and Srivastava 2008; Soman 2003).
Using the process outlined by Lipsey and Wilson (2001), we find that the effect size across these 11 studies is .38, a medium effect size, with a z-test value of 9.59, p < .001, indicating that this mean sample size effect is statistically significant. The 95% confidence interval is .31 to .46. The details around the descriptive statistics used in the meta-analysis are summarized in web appendix G.
GENERAL DISCUSSION
Organizations and researchers have been using text boxes and bounded scales—specifically slider scales—interchangeably to record consumers’ participative pricing decisions. The tacit assumption underlying this practice is that consumers’ innate valuations are invariant to cosmetic changes in response formats. Although prior research has examined the effect of slider formats on response rates and response times (Funke 2016; Funke, Reips, and Thomas 2011; Roster, Lucianetti, and Albaum 2015), no one has empirically tested this assumption. In the present research, we examine whether there is a systematic difference in valuations elicited by text boxes and slider scales.
Experiment 1a demonstrated that undergraduate students offered higher bids for a mug when the bid was elicited on a slider scale relative to a text box. Experiment 1b demonstrated, using real money, that people donate more money when donating using a slider scale than when donating using a text box. In both experiments, the range of possible responses was equally salient for all participants; thus, the slider scale end point assimilation effect cannot be attributed to differences in knowledge of range information or the highest possible response. Experiment 2 demonstrated that if eBay or other firms using ascending payment formats were to use slider scales instead of text boxes to elicit bids, they are likely to elicit higher bid amounts. Experiment 3 showed that slider scales do not always increase bid values. Instead, slider scales assimilate responses to the end point of the response range and decrease responses in descending payment formats. Experiments 4, 5, and 6 demonstrate that the effect of slider scales is due to the salience of the visual distance from the end point of the response range. Experiment 4 shows that values that are considered high are more affected by response formats; low and medium values are less affected by response formats. In experiment 5 we manipulated the visual distance from the end points of the slider by using a convex slider scale. In this experiment we found that responses on a convex slider scale are more similar to text box responses than to those on a linear slider scale. In experiment 6 we altered distance from end points by manipulating the response range. As predicted, the manipulation of response range had a larger effect on slider scale response than on text box responses because visual distance from end points does not play a role for text boxes.
Substantive Implications
Our results suggest that managers in organizations as well as consumers engaging in participative pricing decisions should be more mindful of the response format used for eliciting monetary payments. In situations where consumers might consider offering higher prices, using a slider scale instead of a text box can elicit higher payments from consumers. Retailers that auction products, such as eBay or WineBid, are likely to see higher revenues if they use a slider scale with a wide response range. In a similar vein, service providers, such as taxi services and restaurants, are likely to realize higher revenues when they use a slider scale instead of a text box. However, in situations where consumers adjust their prices downward from the listed prices, using a slider scale can backfire. Companies like Priceline are more likely to elicit higher bids if they use a text box instead of a slider scale. From a consumer welfare perspective, it is important for consumers to realize that response formats can alter their monetary payments and their subjective magnitude perceptions of monetary values, without their awareness.
Theoretical Implications
Although our interest in this research question was triggered by the current practices used to elicit valuations in participative pricing contexts, the results from this research have had a profound effect on our perspectives on numerical cognition. Although the notion of a compressed internal mental number line with a nonlinear calibration is now widely accepted by researchers (Dehaene 2001; Dehaene et al. 2008), to the best of our knowledge nobody has examined how the calibration of this mental number line could be affected by response formats. Our research complements previous work that has shown how the range of anchors (Beattie and Baron 1991; Kahneman 1992) or response ranges (Janiszewski and Lichtenstein 1999; Parducci 1965) can influence consumer responses by demonstrating the importance of visualization of these ranges. Our results suggest that for some response formats, beyond the range itself, visual distances from end points can become a cue for magnitude judgments and this cue can change the calibration of the mental number line. Salience of the visual distance from end points tends to linearize the internal number line, which is usually nonlinear and compressed for higher values. These results call for new theoretical models that can account for dynamic, context-dependent calibration of the mental number line. Identifying and characterizing the determinants of such a dynamic interplay of the contextual factors and the intrinsic representational systems is important for the evolution of numerical cognition theories.
DATA COLLECTION INFORMATION
All study designs and analyses were discussed and agreed upon by both authors. The first author supervised data collection for experiments 2 and 3 through the MTurk online panel. The second author supervised the data collection for experiment 1a through Dartmouth College, and experiments 1b, 4, 5, 6, and web appendix experiments A1, A2, A3, A4, and F, through the MTurk online panel. Data were collected in 2015 through 2017. The first and second authors separately and jointly analyzed the data from these studies, confirming all results.
This was a truly collaborative experience; both authors contributed equally to this research, and they equally enjoyed the collaboration. Supplemental materials, including experiment stimuli, additional graphs, and supplementary analyses, are included in the web appendix accompanying the online version of this article. This research has benefited from feedback at various seminars and conferences, including Effect of Numerical Markers on Consumer Judgment and Decision Making at Moore School of Business, University of South Carolina; the New Directions in Pricing Management Research and Practice at University of Illinois; the Northeast Marketing Conference at Harvard Business School; the Marketing Department at IDC Herzliya; the Marketing Seminar at Texas A&M May’s School; The Wharton School Decision Processes Colloquia; and the Cornell University Marketing Seminar. The authors are grateful to Kevin Keller for his thoughtful feedback; Matthew Paronto, Brad Turner, and Geoff Gunning for helping them write clearly; Yifan He for her research assistance; Sachin Gupta, Kusum Ailawadi, Scott Neslin, Blake McShane, and Paul Wolfson for their advice on statistical analyses; and Maxine Park and Roxane Park for pretesting stimuli. The authors thank Bob Burnham for his programming genius creating the convex slider scale used in experiment 5, and anonymous reviewer C and John Hauser for making this suggestion. Finally, the authors thank the JCR review team—the editors, three reviewers, and two trainee reviewers—for their thoughtful and constructive feedback, which greatly strengthened their research.
Footnotes
Here the term bias refers to the difference between the perceived magnitude primed by the slider scale and that primed by the text box.
The results are robust to omission of this information. A similar experiment was run on Memorial Day without including this information. The results of this experiment are summarized in web appendix G.


