-
PDF
- Split View
-
Views
-
Cite
Cite
Yong Yang, Xiaotong Ren, Yiqiao Li, Ning Wang, Kun Zhang, Shengqiang Shen, Similarity characteristics of qualitative and quantitative regulation for adjustable ejector, International Journal of Low-Carbon Technologies, Volume 18, 2023, Pages 423–432, https://doi.org/10.1093/ijlct/ctad030
Close - Share Icon Share
Abstract
In the new era of ejector technology entering into system scale from device scale. The methodology of regulation mode of an adjustable ejector has been summarized in this paper. The similarity in characteristics of qualitative and quantitative regulation under different operating modes are researched. The results show that both qualitative and quantitative regulation have the characteristics of ‘constant capacity’. Three different ‘constant-capacity’ phenomena in ejectors have been found, and the similarity indicates that the turbulent flow in ejectors has some statistical invariances in the form of mass flow rate of jetting flow. The ejector has the similar entrainment ability by increasing primary pressure by 43% in the qualitative regulation mode or enlarging the nozzle throat opening by 47% in the quantitative regulation mode under critical mode with similar underexpanded state. The advantages of adjustable ejectors have been promoted, in particular ±5% regulation accuracy or constant regulation ability, discharging improved ability by 80% in flow rate or 10% in pressure lifting ability in subcritical mode or primary flow rate saving ability by 25% or 13% in pressure lifting ability in critical mode.
1 INTRODUCTION
Ejectors can be widely used in thermodynamic systems, acting as compressors, vacuum generators, heat and mass exchangers or flow adapters. It needs limited maintenance, is low cost and has no constraints regarding the work fluids. Owing to these advantages, ejector technology enters a new era with research gradually entering into the system scale from a device scale [1]. With a movable spindle controlling the mass flow rate and pressure, the adjustable ejector is the best choice in air conditioning and refrigeration [2, 3], desalination [4, 5], fuel cells [6, 7], vapour compression units [8, 9], etc. to maintain high efficiency of the thermodynamic system in the long history of ‘Carbon Peak’ and ‘Carbon Neutrality’.
In 1858, Giffard invented the condensing ejector to solve the feeding-water problem of boilers by lifting the pressure of replenishment with steam, as shown in Figure 1. The adjustable ejector with integrated spindle valve for control of motive flow rate has been used [10]. Around 1901, as the heart of the jet refrigeration system, the ejector was invented by Sir Charles Parsons to remove air from a steam engine’s condenser. In 1910, Maurice Leblanc combined an ejector to the first steam jet refrigeration system [11]. This system experienced a wave of popularity during the early 1930s for air conditioning in large buildings [12]. Later, steam jet refrigeration systems were always the competitive technology compared with compression refrigeration [13]. With the development of solar energy and carbon usage, the jet refrigeration system comes into the combination and hybridization stage [14, 15]. As an improving technology, an ejector acts as an essential adjustable compressor to keep the system adapting to load changes varying with solar energy or operating conditions, generally through valve controlling [16], biejector controlling [17, 18], bypass controlling [19] or combined with frequency conversion controlling of the mechanical compressors [20]. The adjustable ejector, with a spindle valve in the primary nozzle controlling the flow distribution in the system, becomes a research hotspot again [21–24].
Besides air conditioning and refrigeration systems, the ejector is also the essential part that governs overall process of MED-TVC (Multieffect Distillation with Thermal Vapour Compression) system. It recycles low-pressure vapour from the rear-effect evaporator to obtain steam with suitable pressure entering the first-effect evaporator to decrease consumption of high-pressure motive steam, maximizing the performance ratio of the system [25]. To adapt to the variation of water production load of the system, especially to improve the regulation ability for steam extraction pressure from turbines in a dual-purpose plant, an adjustable ejector is usually the best choice [26, 27].
Meanwhile, as an excess fuel recirculation and water management equipment, the ejector is a recycle unit in fuel cells, especially for solid oxide fuel cell (SOFC) and proton exchange membrane fuel cell (PEMFC) [28, 29]. Generally, the fixed-structure ejector has only one optimum operating point. Deviations from the design point mostly result in reduced efficiency for the ejector and the system. Thus, the adjustable ejector has been discussed to apply for improving efficiency in partial operating conditions for fuel cells [6, 7]. In addition, the compressed air energy storage system is a fast-growing interdisciplinary research area in which the adjustable ejector also has wide application prospects [30].
With ejector technology entering the system scale, understanding the regulation principle and mechanism of ejectors with the changing of operating conditions and structures is very important. To make the performance characteristics of an adjustable ejector clearer, the performance of a steam ejector on varying primary pressure based on the Sokolov aerodynamics theory is analysed in this paper. In particular, the similarity characteristics of qualitative and quantitative regulation for the adjustable ejector is researched, and the statistical invariances of turbulence flow in the ejector is discovered in the form of entrainment characteristics. Based on critical states transferring characteristics of adjustable ejectors in qualitative and quantitative regulation mode, the advantages of adjustable ejectors are revealed.
2 MATHEMATICAL MODELLING FOR ADJUSTABLE EJECTORS
2.1 Regulation mechanism of adjustable ejectors
As shown in Figure 2, an adjustable ejector construction includes a convergent–divergent primary nozzle, a suction chamber, a mixing chamber and a diffuser. The difference with a fixed-structure ejector is that it uses an adjustment spindle, which axially extends into the primary steam nozzle and is actuated either manually or by an electric positioner.
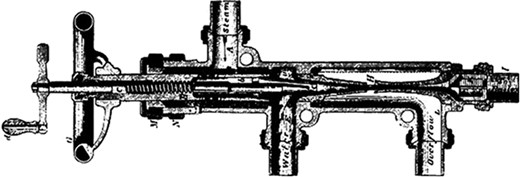
Henri Giffard’s ejector from 1864 with integrated spindle valve for control of motive flow rate (Kranakis, 1982).
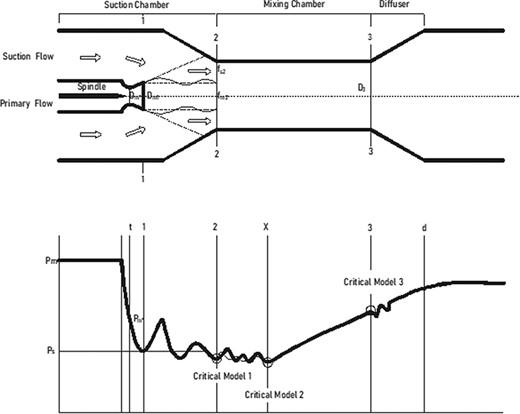
Structure diagram of the adjustable ejector construction and analysis model.
Based on the definition by Sokolov and Zinger [31], the regulation mechanisms of ejectors are mainly qualitative regulation with varying operating pressure and quantitative regulation with varying structure of the ejector. The advantage of an adjustable ejector is that it has three different regulation modes. Besides qualitative and quantitative regulation, it can achieve qualitative and quantitative combined regulation by adjusting the primary nozzle throat combined with varying operating pressure. An adjustable ejector can achieve higher efficiency in quantitative regulation with higher entrainment ratio. Notably, it can always work at its critical operating points by adjusting the primary nozzle throat combined with varying operating conditions in qualitative and quantitative combined regulation mode, which means that the adjustable ejector can always operate with the highest efficiency under different conditions.
2.2 The mathematical model for adjustable ejectors
In the aforementioned equations (3) to (9), Pm, Ps, and Pd are pressures of primary, suction and discharging flow, respectively; subscript * denotes the critical value; k is the specific heat ratio; v is the specific capacity; φ3 is the velocity efficiency of the diffuser, K1 is the velocity efficiency of primary flow; and K2 is velocity efficiency of suction flow.
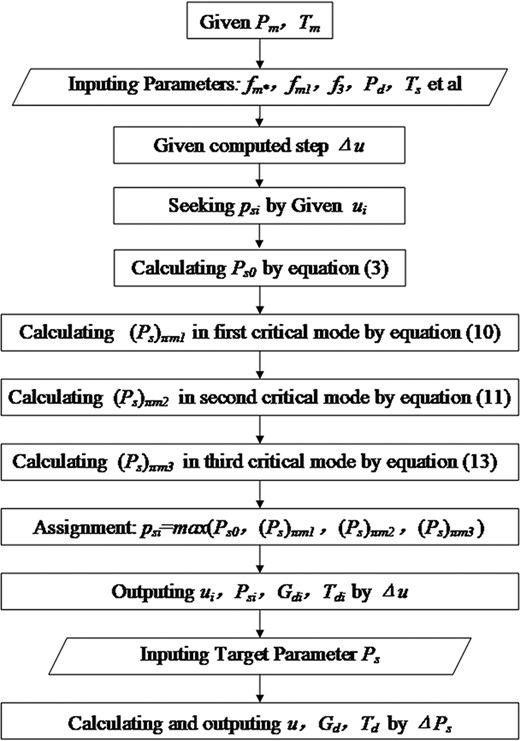
Calculation flow chart of variable characteristics for adjustable ejector.
Design parameters of the ejector.
| Primary pressure, Pm . | 0.55 MPa . |
|---|---|
| Primary fluid temperature, Tm | 185°C |
| Suction pressure, Ps | 0.015 MPa |
| Suction fluid temperature, Ts | Saturated temperature |
| Discharging pressure, Pd | 0.028 MPa |
| Rated discharging flow rate, Gd | 13.89 kg/s |
| Discharging flow rate regulation range | Up to 120% |
| Primary nozzle throat diameter, Dm* | 102.65 mm |
| Primary nozzle outlet diameter, Dm1 | 225.30 mm |
| Mixing chamber diameter, D3 | 667.84 mm |
| Mixing chamber structure | Cylindrical |
| Primary pressure, Pm . | 0.55 MPa . |
|---|---|
| Primary fluid temperature, Tm | 185°C |
| Suction pressure, Ps | 0.015 MPa |
| Suction fluid temperature, Ts | Saturated temperature |
| Discharging pressure, Pd | 0.028 MPa |
| Rated discharging flow rate, Gd | 13.89 kg/s |
| Discharging flow rate regulation range | Up to 120% |
| Primary nozzle throat diameter, Dm* | 102.65 mm |
| Primary nozzle outlet diameter, Dm1 | 225.30 mm |
| Mixing chamber diameter, D3 | 667.84 mm |
| Mixing chamber structure | Cylindrical |
| Primary pressure, Pm . | 0.55 MPa . |
|---|---|
| Primary fluid temperature, Tm | 185°C |
| Suction pressure, Ps | 0.015 MPa |
| Suction fluid temperature, Ts | Saturated temperature |
| Discharging pressure, Pd | 0.028 MPa |
| Rated discharging flow rate, Gd | 13.89 kg/s |
| Discharging flow rate regulation range | Up to 120% |
| Primary nozzle throat diameter, Dm* | 102.65 mm |
| Primary nozzle outlet diameter, Dm1 | 225.30 mm |
| Mixing chamber diameter, D3 | 667.84 mm |
| Mixing chamber structure | Cylindrical |
| Primary pressure, Pm . | 0.55 MPa . |
|---|---|
| Primary fluid temperature, Tm | 185°C |
| Suction pressure, Ps | 0.015 MPa |
| Suction fluid temperature, Ts | Saturated temperature |
| Discharging pressure, Pd | 0.028 MPa |
| Rated discharging flow rate, Gd | 13.89 kg/s |
| Discharging flow rate regulation range | Up to 120% |
| Primary nozzle throat diameter, Dm* | 102.65 mm |
| Primary nozzle outlet diameter, Dm1 | 225.30 mm |
| Mixing chamber diameter, D3 | 667.84 mm |
| Mixing chamber structure | Cylindrical |
2.3 The critical model of ejectors
2.4 Calculation method for characteristics of adjustable ejectors
Based on the mathematical models built in sections 2.2 and 2.3, the performance of an ejector with variable operating condition and structure can be exactly predicted as shown in Figure 3. The calculation steps of critical states transferring characteristics for an adjustable ejector is as follows:
1) For ejector characteristics prediction, the structure parameters fm*, fm1 and f3 should be set originally.
2) Select the operating condition for Pm, Tm, Pd or Ts if the suction flow is not saturated vapour.
3) Obtain suction pressure Ps0 for given entrainment ratio u0 by calculation step △u for each ui through equation (3) in subcritical mode.
4) Calculate |${\left({P}_s\right)}_{\varPi m1}$|, |${\left({P}_s\right)}_{\varPi m2}$| and |${\left({P}_s\right)}_{\varPi m3}$| in different critical modes for each ui by equation (10), (11) and (13). Because the third critical mode always occurs combined with the first or the second critical modes under the same calculated suction pressure Ps., therefore when calculating the third critical mode as shown in the flowchart in Figure 3, the first and the second critical modes should be considered at the same time; for example, considering |${q}_{s2}$|=1 to calculate the first critical mode when predicting the third critical mode.
5) Select the maximum value of the suction pressure Psi in Ps0, |${\left({P}_s\right)}_{\varPi m1}$|, |${\left({P}_s\right)}_{\varPi m2}$| and |${\left({P}_s\right)}_{\varPi m3}$| as the obtained parameter to match the subcritical or critical mode for ui.
6) Output the variable characteristics of the ejector for different suction pressure Psi by calculation step of Δu.
7) Calculate the needed value for definite Ps based on the interpolation method.
8) Calculate different operating condition for Pm and Pd.
An alternative method is to calculate the minimum value of ui for the selected Psi. In addition, the variable condition characteristics of the adjustable ejector can be calculated by changing the throat area of the primary nozzle fm*.
3 SIMILARITY CHARACTERISTICS OF REGULATION MODE FOR ADJUSTABLE EJECTORS
3.1 Validation of the mathematical model
Even though the performance of ejectors has been reported by numerous researchers, the similarity characteristics of ejectors under different modes has not been reported. Because the special characteristic of ‘constant capacity’ is always the basic property and fundamental theory in ejectors [32], the main purpose of this paper is to find different similarity characteristics and statistical invariances in ejectors based on performance research for adjustable ejectors under variable operating conditions and structures [33].
Based on the aerodynamic model proposed previously, an adjustable steam ejector is designed in this paper, and its similarity characteristics and statistical invariances under different modes are simulated and analysed. The design conditions of the ejector are shown in Table 1. The performance prediction of an adjustable ejector can be obtained by changing the primary nozzle throat area.
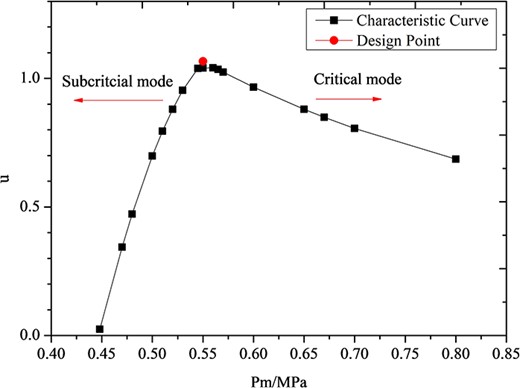
Figure 4 shows the performance characteristic curve of an ejector with variable primary pressure Pm. It reveals that the prediction value is in agreement with the design point, where the ejector has the best operating performance, indicating the accuracy and reliability of the calculation model. Figure 5 shows the comparison between the entrainment ratio in critical mode obtained by the calculation model and the experimental data by Chen, who has got the optimal critical entrainment ratios of the ejector with part of the long, cylindrical mixing chamber and an overdesigned conical suction chamber [34], which means the first or the second critical mode can occur in the mixing duct with combination of the third critical mode as prediction in part 2.4. The result shows that the relative error is <5%, indicating that the calculation model has high prediction accuracy for critical mode.
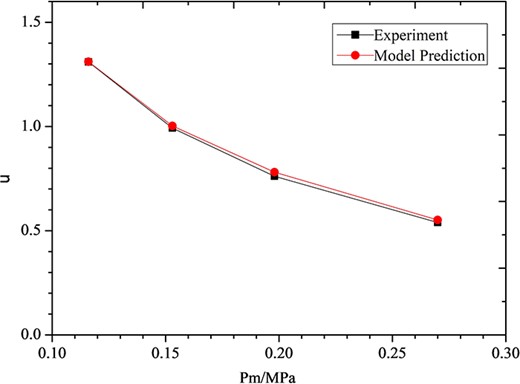
Experimental verification of calculation model under critical mode of ejector.
3.2 Similarity of ejectors with variable operating condition in qualitative regulation mode
As shown in Figure 4, the entrainment ratio at the design point is the highest, indicating that the structure designed by the aerodynamic model is the optimal structure. When primary pressure Pm is <0.55 MPa, the ejector operates in subcritical mode and the entrainment ratio decreases rapidly with the drop of Pm. When Pm is higher than the design pressure, the ejector operates in critical mode and the entrainment ratio decreases with the increase of Pm.
As shown in Figure 6, when adjusting the discharging pressure Pd, operating characteristics of the ejector in critical mode has strong similarity and the critical entrainment ratio under different Pd converges on a curve that is in an approximately exponential relationship with the Pm. This indicates that above the critical primary pressure Pm* (the red star), reducing Pd has nearly no effect on the entrainment ratio in critical mode, with the primary holding the performance of the ejector in critical mode, which is same with classic double-choking mode with varying Pd pointed out by Huang [35], shown in Figure 7 obtained by the similar variable Pd model proposed in the literature [5].
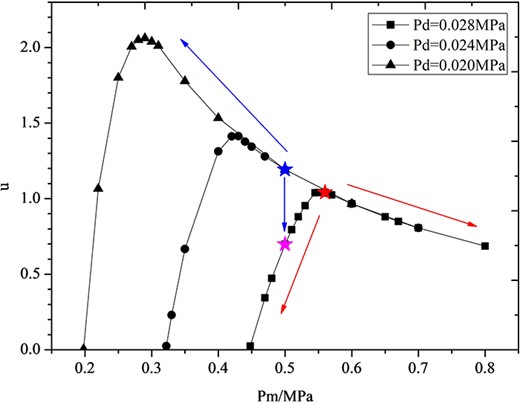
Similarity in qualitative regulation mode of ejector with variable Pm.
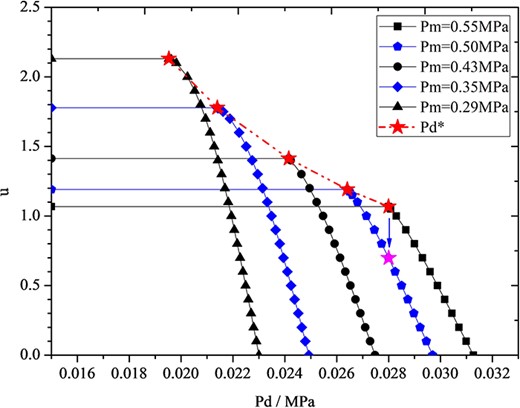
Similarity in qualitative regulation mode of ejector with variable Pd.
However, reducing Pd can enlarge the working range of the critical mode. When the ejector drops to subcritical mode as Pm drops to the value below the critical value Pm*, the ejector will enter subcritical mode without changing the discarding pressure Pd, shown as the pink star in Figure 6. Regardless of reduced Pd, the ejector can still operate in critical mode with lower Pm, shown as the blue star in Figure 6. That means the performance of the ejector can be improved significantly when reducing Pm matches well with the decreasing Pd. In the system scale, when the discharging load of the ejector reduces, it obviously has advantage to reduce Pm and Pd because the suction flow rate Gs remains nearly constant (as shown in Figure 8), even increasing slightly. In addition, the results show that in qualitative regulation mode, the benefit of increasing Pm is negative for the performance and efficiency of the ejector. When the needing load for discharging flow rate increases, the increasing part in qualitative regulation is mainly from the increase of the primary flow and not the suction flow. This phenomenon shows the limitations of qualitative regulation in system scales.

Constant-capacity characteristic of suction flow rate in qualitative regulation mode.
Significantly, the profile of the converging curve for the critical entrainment ratio obtained by the model promoted in this paper with varying Pm, as shown in Figure 6, and the profile of critical value captured by the mode promoted in the literature [5], with varying Pd on the red dotted line in Figure 7, is similar with same critical entrainment value. Moreover, the entrainment ratio on subcritical mode also has the same value, as shown by the two pink stars in the figures. The results reveal that the model promoted in this paper is correct, with high prediction accuracy, which reveals that the assumption about the model built in part 2.4 is right: that the third critical mode always occurs combined with the first or the second critical mode.
The results in this paper show the similarity of ejectors in qualitative regulation with varying Pm and Pd. In addition, two well-known ‘constant-capacity’ characteristics of ejectors have been revealed: that the entrainment ratio will obviously drop from critical to subcritical mode when the discharging pressure increases, but when the ejector operates in critical mode, the entrainment ratio remains constant with characteristics of ‘constant capacity’ with decreasing of Pd. A new expression for the constant entrainment ratio under double-choking mode with decreasing Pd is shown in Figure 6; it is similar to the expression of Huang as shown in Figure 7 [35]. The ‘constant-capacity’ characteristic in suction flow rate Gs is shown in Figure 8. As shown in the figure, above the point of subcritical mode transferring to critical mode, the suction flow remains nearly constant, with a slight decrease with higher Pm., with ~10% reduction from 0.3 to 0.8 MPa. The simulation results match well with Sun’s experiment [36]. The two ‘constant-capacity’ characteristics match well with Munday’s explanation, that the capacity of an ejector is proportional to motive pressure up to a point beyond which suction flow actually falls slightly [32].
3.3 Similarity in quantitative regulation mode of ejectors with variable structure
Different from the fixed-structure ejector, which has the best performance only under the design operating condition, the advantage of the adjustable ejector is that it can make the ejector adapt to the change of operating condition by adjusting the structure, which enables the adjustable ejector to obtain higher operating performance in a much wider working range. Notably, the adjustable ejector has three different regulation modes as mentioned in section 2.1.
Figure 9 and Figure 10 show the similarity of regulation characteristics of the adjustable ejector under different primary nozzle throat opening ψ, which is the ratio of the primary nozzle throat area at the adjustment position to the primary nozzle throat area under the design structure. As shown in the figures, the adjustable ejector can obviously enlarge the working range of the critical mode. With the nozzle throat opening ψ > 1, the critical Pm* where the performance of the ejector enters the critical mode from subcritical mode decreases, which means the ejector can hold critical states in the low-Pm region, but with smaller critical entrainment ratio and suction flow rate. On the other hand, when the nozzle throat opening ψ < 1, the critical Pm* increases but with higher entrainment ratio, which means the ejector can obtain higher critical states in the high-Pm region and with increase of suction flow rate. The adjustable ejector can hold critical performance with Pm reducing by 16% when enlarging the nozzle throat opening ψ by 20% and can improve the critical entrainment ratio by 24% when reducing the nozzle throat opening ψ by 20%. Generally, the ejector with different throat area fm* but with same structure mixing chamber, the performance of the ejector under both subcritical and critical modes has strong similarity. In the ideal regulation state, the adjustable ejector can always work at the optimal critical mode with the highest entrainment ratio and efficiency.
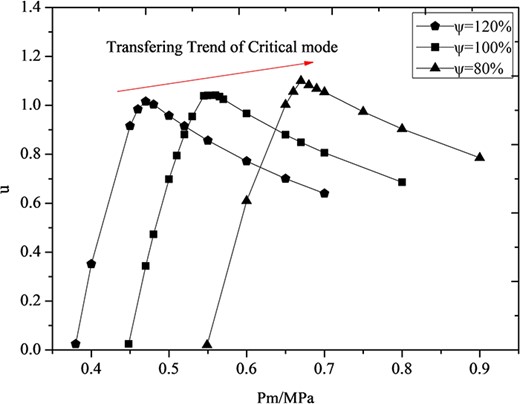
Similarity of critical mode transferring characteristics of the adjustable ejector.
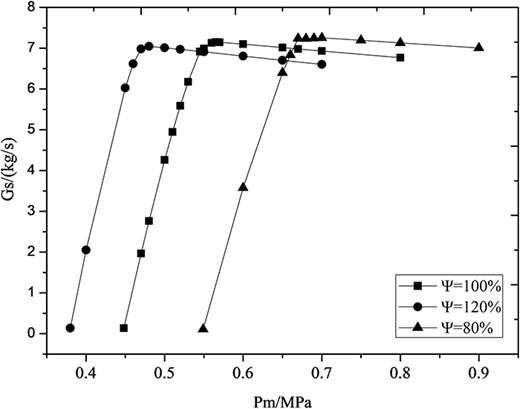
Similarity of suction flow rate transferring characteristics of the adjustable ejector.
Different from the qualitative regulation mode, in which the suction flow rate Gs converges on a curve with increasing of Pm, adjusting Pm can only change the flow rate of the suction flow ~10% by increasing Pm 0.5 MPa. The adjustable ejector can obviously change the suction flow rate Gs. Similar to the experiment results of Chen [21], the suction flow rate Gs increases with decrease of the throat opening of the primary nozzle in critical mode. With the nozzle throat opening ψ > 1, the suction flow rate Gs decreases, whereas with the nozzle throat opening ψ < 1, the suction flow increases. Therefore, the adjustable ejector can flexibly adjust the suction flow rate Gs, and the adjustable range is ~±5% at same Pm, or keep the suction flow rate constant combined with varying of Pm. As shown in Figure 10, the flow rate characteristics of the suction flow also have strong similarities under different throat opening ψ. Moreover, the suction flow rate Gs retains the similar ‘constant capacity’ with the increase of primary pressure under different primary nozzle throat areas.
3.4 Similarity of qualitative and quantitative regulation of ejectors
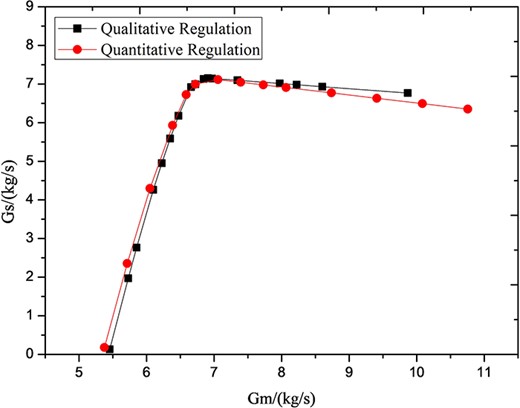
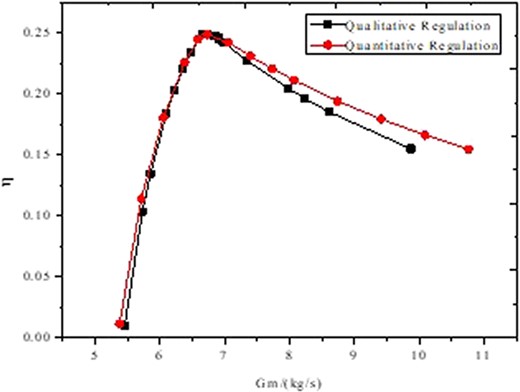
Figures 11 and 12 show the similarities of qualitative and quantitative regulation modes, in the form of suction flow rate Gs and efficiency with varying primary flow rate Gm. With the similar primary flow rate, the similarity in primary flow rate is shown in Figure 11, when the primary pressure Pm increases from 0.45 to 0.8 MPa in qualitative regulation mode, and the nozzle throat opening ψ increases from 80 to 160% in quantitative regulation mode. The suction flow rate Gs is nearly same with equal primary flow rate Gm. In addition, both qualitative and quantitative regulation modes show subcritical and critical characteristics based on primary flow rate Gm.
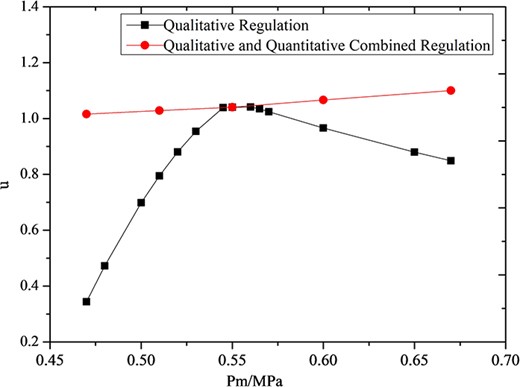
Ideal regulation state in qualitative and quantitative combined regulation of adjustable ejector.
In subcritical regulation mode, the suction flow rate and efficiency of the ejector obviously drops with decrease of primary flow rate Gm, caused by decreasing Pm in qualitative regulation mode or by decreasing the nozzle throat opening ψ in qualitative regulation mode. In critical mode, suction flow rate Gs decreases slightly with increase of Gm, caused by increasing Pm or increasing the nozzle throat opening ψ. The third special characteristic of ‘constant capacity’ occurs in both qualitative and quantitative regulation in critical mode. The similarity indicates that the turbulent flow in the ejector has some statistical invariances in the form of mass flow rate of jetting flow. The difference is that the suction flow rate in qualitative regulation mode is slightly higher than the quantitative regulation mode because the pressure is higher in qualitative rather than quantitative regulation mode at the same Gm, which means the turbulent flow is a little stronger than the latter.
The efficiency of the ejector under the same primary mass flow rate Gm also has strong similarity in qualitative and quantitative regulation modes. In subcritical mode, the efficiency obviously drops with the decrease in Gm. In critical mode, the efficiency decreases slightly with the increase in Gm. However, the efficiency in qualitative regulation mode is lower than that in quantitative regulation mode because turbulence loss is higher in qualitative regulation mode with same Gm and a slightly higher Gs. Generally, the ejector has a similar entrainment ability by increasing Pm by 43% or enlarging the nozzle throat opening ψ by 47% in critical mode with similar underexpanded state. Based on comparison in Figure 11 and Figure 12, the regulation ability of qualitative and quantitative regulation mode is nearly the same measure by Gm, which means it is not necessary to use an adjustable ejector when a fixed-structure ejector is adequate. However, an adjustable ejector can achieve more flexible regulation.
3.5 Advantage of adjustable ejectors
The advantage of an adjustable ejector is that it has three different regulation modes. The fixed-structure ejector has only one optimum operating point at the design condition, deviations that mostly result in a reduced performance for the ejector in qualitative regulation mode by changing the primary pressure. An adjustable ejector can achieve higher performance in quantitative regulation by adjusting the primary nozzle throat with higher entrainment ratio. Notably, it can always work at its critical operating points by adjusting the primary nozzle throat combined with varying operating conditions in qualitative and quantitative combined regulation mode.
Figure 13 shows the ideal regulation state in qualitative and quantitative combined regulation. Within the range of throat opening ψ from 80 to 120%, compared with the fixed-structure ejector, an adjustable ejector can promote the performance of the ejector from subcritical to critical mode, with the entrainment ability increasing 195.6% and discharging ability increasing 80% in discharging flow rate or 10% in discharging pressure when primary pressure decreases. In addition, entrainment ability can be promoted by 29.6% in critical mode with primary flow rate saving 25% or discharging ability saving 13% in discharging pressure lift when primary pressure increases [37]. The results reveal the effectiveness of the autotuning area ratio ejector invented by Gu [4]. Furthermore, with the increase of primary pressure, the ideal entrainment ratio of the adjustable ejector increases at the same time.
4 CONCLUSIONS
With ejector technology entering into the system scale from device scale, the methodology of regulation mode of an adjustable ejector has been summarized in this paper. Based on aerodynamic theory, a performance prediction model for an adjustable ejector under variable operating conditions and variable structures has been presented. The advantages of the adjustable ejector with three regulation modes have been compared with the fixed-structure ejector. In addition, the similarity of performance characteristics of adjustable ejectors under varying operating conditions and structures has been found. The main conclusions are obtained as follows:
(1) The ejector has similar performance under different pressures and different structures. The similarity of qualitative and quantitative regulation modes has been presented. The ejector has a similar entrainment ability by increasing Pm by 43% in qualitative regulation mode or enlarging the nozzle throat opening ψ by 47% in quantitative regulation mode under critical mode with similar underexpanded state.
(2) Three special characteristics of ‘constant capacity’ have been revealed in new expression for both fixed-structure and adjustable ejectors, including entrainment ratio in double-choking mode, suction flow rate in critical mode and suction flow rate distribution trend with varying primary flow.
(3) The advantages of adjustable ejectors have been promoted, including flexible regulation for the suction flow rate with ~±5% accuracy at the same Pm or constant suction flow rate combined with varying of Pm and improving ability in three regulation modes. Principally in qualitative and quantitative combined regulation, within the range of throat opening ψ from 80 to 120%, the entrainment ability can increase 195.6% in subcritical mode and discharging ability increases 80% in discharging flow rate or 10% in discharging pressure when primary pressure decreases. In addition, entrainment ability can be promoted by 29.6% in critical mode with primary flow rate saving 25% or discharging ability saving 13% in discharging pressure lift.
Acknowledgements
This research is supported by the Key Project of National Natural Science Foundation of China (NO.51936002) and the Science and Technology Innovation Foundation of Dalian (NO.2020JJ26SN063).


