-
PDF
- Split View
-
Views
-
Cite
Cite
Gil Marom, Luca Paolo Weltert, Ehud Raanani, Ilaria Chirirchilli, Christian Giebels, Francesco Giosuè Irace, Ruggero De Paulis, Hans-Joachim Schäfers, Systematic adjustment of root dimensions to cusp size in aortic valve repair: a computer simulation, Interdisciplinary CardioVascular and Thoracic Surgery, Volume 38, Issue 2, February 2024, ivae024, https://doi.org/10.1093/icvts/ivae024
Close - Share Icon Share
Abstract
Aortic valve repair requires the creation of a normal geometry of cusps and aortic root. Of the different dimensions, geometric cusp height is the most difficult to change while annular and sinotubular dimensions can be easily modified. The objective of this study was to investigate, by computer simulation, ideal combinations of annular and sinotubular junction size for a given geometric height.
Based on a literature review of anatomical data, a computational biomechanics model was generated for a tricuspid aortic valve. We aimed to determine the ideal relationships for the root dimensions, keeping geometric height constant and creating different combinations of the annular and sinotubular junction dimensions. Using this model, 125 virtual anatomies were created, with 25 different combinations of annulus and sinotubular junction. Effective height, coaptation height and mechanical cusp stress were calculated with the valves in closed configuration.
Generally, within the analysed range of geometric heights, changes to the annular diameter yielded a stronger impact than sinotubular junction diameter changes for optimal valve configuration. The best results were obtained with the sinotubular junction being 2–4 mm larger than the annulus, leading to higher effective height, normal coaptation height and lower stress. Within the range tested, stenosis did not occur due to annular reduction.
In tricuspid aortic valves, the geometric height can be used to predict ideal post-repair annular and sinotubular junction dimensions for optimal valve configuration. Such an ideal configuration is associated with reduced cusp stress.
INTRODUCTION
For the past 6 decades, aortic valve replacement has been the standard treatment for both stenosis and regurgitation. Mechanical and biological substitutes have low morbidity and mortality at implantation [1]. They are effective in improving haemodynamics and prognosis [2], but carry substantial long-term risks of valve-related complications and mortality [3]. In the past 20 years, reconstructive procedures for treatment of aortic regurgitation with or without an aortic root aneurysm have become an increasingly practiced alternative to replacement. A durable repair will result in a low incidence of valve-related complications [4] and probably improved survival [5].
The key in aortic valve repair is restoration of normal aortic valve geometry, resulting in a normalization of aortic valve function. Initially, the procedures focused on the correction of root dilatation [6, 7]; others aimed at restoration of normal cusp configuration [8]. Combined procedures addressing cusps and root were also proposed [9]; the traditional concept consisted of a visual inspection of the valve, ensuring all free margins were aligned at identical level.
With time, it has become apparent that the aortic valve must be considered as a functional unit of cusps and root [10, 11], where the geometric relationships between root and cusps [12, 13] are critical. Aortic regurgitation may be due to root dilatation or cusp pathology, such as prolapse, retraction or perforation. A tailored surgical repair is needed, taking the relationship between root and cusp dimensions into consideration.
Of the root dimensions determining valve configuration, sinotubular junction (STJ) and annular diameters are the most important [14–16]. The cusp dimensions can be essentially defined by commissural height, amount of cusp tissue and free margin length. Of these, geometric height (gH; the maximal length of the cusp from the nadir to its free margin) has been used as surrogate parameter for cusp tissue [17, 18]. In an anatomical study, it ranged from 16 to 23 with a mean of 20 mm [19]. Very little information is available on commissural height and free margin length. The effective height (eH)—i.e. height difference between annular plane and cusps free margin in diastole—has been introduced as a configuration parameter [13]. It has been found to be 9–10 mm in adults, or roughly 45–50% of the gH [13, 19, 20].
Current techniques of aortic valve repair in specialized centres are increasingly based on these parameters. Treatment of cusp prolapse by shortening the free cusp margin has proven easy and reproducible [21, 22]. The use of a dedicated calliper for intraoperative measurement of eH [20] has been shown to improve post-repair valve durability [23]. Cusp retraction, however, remains a challenge and predictor of lesser durability; cusp augmentation using pericardial patches is possible; nevertheless, the durability of such procedure has been suboptimal.
With given cusp dimensions, alterations of STJ and annular diameter influence cusp coaptation and eH [15, 16]. STJ reduction improves aortic valve function, as does annuloplasty or the combined approach of root replacement. On the other hand, it is conceivable that lower than normal ranges of gH could be successfully repaired if root dimensions are adjusted appropriately. The precise relationship between these parameters as a function of gH, however, is yet unknown.
We aimed to determine the relationships for the root dimensions by computer simulation, keeping gH constant and creating different combinations of the annular and STJ dimensions. Ideal and suboptimal configurations were identified using eH, coaptation height (cH) and diastolic stress as end-points. These simulations may be an intellectual trigger to stimulate the debate and guide the aortic valve surgeon to perform a more ‘geometrically perfect’ root reconstruction that possibly will translate to a more durable aortic valve.
MATERIALS AND METHODS
Study design
First step was to quantitatively describe the range of normal human anatomies to create a working model of a normal aortic root. We used data from the 2018 study of De Kerchove et al. [19], providing comprehensive information about normal dimensions of aortic root complex and reciprocal relationships derived from anatomical specimens.
Next step was to describe these ranges as ratios of one dimension relative to another. Three key dimensions were considered: cusp gH as the primary measure, annular and STJ diameters as derived measurements. For each set of calculations, we assumed gH to be constant (being the most difficult to modify during surgery).
We determined a range of acceptable annular and STJ dimensions for any gH. The calculated dimensions were rounded to 2-mm increments.
The model is designed to be simple and focused on the fundamental dimensions of the aortic root components only. Thus, variations of other dimensions, particularly commissural height and free margin length of the cusp, were not included.
Computational models of the anatomy and mechanical function
We created 125 possible scenarios, 25 for each given gH, ranging from 16 to 24 mm in accordance with the standard literature range [24]. For each gH, normal annular diameter was defined as 1.28⋅gH and normal STJ diameter was defined as 1.41⋅gH [19]. A range of 4 mm below and above the normal diameters was considered.
To generate the anatomical geometries, we used the mathematical description we previously proposed [25], based on a parametric description of the geometry and an algorithm that generates it for a given combination of dimensions.
These generated geometries were in an almost closed configuration to geometrically describe each cusp separately. When diastolic pressure closes them, they come in contact and are pushed towards the ventricle. Therefore, a mechanical response of the valve closure is required to calculate the eH, cH and cusp stress in the diastolic configuration (Fig. 1).

Schematic representation of finite elements model creation of the aortic root and valve, starting from computed tomography reconstruction through geometric mesh.
To model valve closure, our algorithm created meshes for finite element analysis. The algorithms were implemented with our in-house Matlab (Mathworks Inc.) and TrueGrid (XYZ Scientific Applications Inc.) codes. The models were based on previously published work with the same material properties and collagen fibre architecture [26]. Boundary conditions were simplified, and cusps were closed with a prescribed pressure difference of 100 mmHg instead of solving the blood flow and coupling it with the structural kinematics. These finite element models were solved in Simulia Abaqus (Dassault Systèmes); eH of fully closed valve was defined as vertical distance between free margin of cusp and its interface with annular plane. Average cH was calculated as coaptation area divided by length of free margin. Representative stress in cusps is equal to maximum stress in elastin, assuming that elastin is more susceptible to injury than collagen fibres. Finally, the ratio between eH and gH was calculated, and defined as repair aortic index (RAI). Post-processing algorithm was implemented with in-house Matlab code.
Four parameters were calculated, each representing 1 aspect of the problem:
eH: difference between annular plane and cusp free margins in diastole.
cH: height of contact of the leaflets in diastole. It has been investigated in human cohorts, albeit not reaching the level of consensus of the eH.
Stress: representing the maximum stress in elastin when cusps are exposed to maximum pressure loads of diastole.
RAI: defined as ratio between eH and gH as an indexed parameter, accommodating the variability of gH.
For any of these parameters, we set threshold values to classify them in ‘optimal’, ‘sub-optimal’ or ‘inadequate’. The classification of optimal values was based on the anatomical work of De Kerchove et al. [19], but precise thresholds were defined as made post hoc with the purpose of having discrete and handleable values.
Based on normal values and clinical data [15, 16], we defined the following optimal, sub-optimal and inadequate values:
eH: ‘optimal’ between 8.1 and 10 mm, ‘suboptimal’ between 7 and 8 mm and ‘inadequate’ below 7 mm.
cH: ‘optimal’ above 5 mm, ‘suboptimal’ between 4 and 4.9 mm and ‘inadequate’ below 4 mm.
cusp stress: for the analysis of mechanical stress in the aortic cusps, no established stress level is available to classify the results. Thus, the general concept of ‘lower is better’ applies.
RAI: The ratio between eH and gH (RAI) was classified as ‘optimal’ (>0.4), ‘suboptimal’ (0.35–0.4) and ‘inadequate’ when <0.35.
Statistical methods
Statistical methods less prominently apply in general to computational models. The results are consistent due to the methodology (every time one tries to solve a case with the same parameters, he will get the same results), unlike experiments in general and clinical studies in particular. The variables considered in the study were all continuous scalar in nature; in order to test and confirm correlations of involved variables, Pearson Correlation Analysis was carried out, showing very significant correlation, either positive or negative depending on which variable was considered. Details are provided in the Supplementary Material. Data entry was carried out in Microsoft Excel, while statistical tests were performed in IBM SPSS 22.0 and Stata (Supplementary Material Figs S1–S3).
RESULTS
Effective height
In general, eH was strongly influenced by the annular size and relatively less prominently by STJ measure (Fig. 2). For any given gH value, eH decreased with increasing annular size. For high gH (22 and 24 mm), most combinations yielded optimal eH results, even though eH was exceedingly high with annular and STJ diameters <25 mm. In the presence of marked annular dilatation (>33 mm) and sinotubular dilatation (>36 mm), eH was suboptimal. For gH of 20 mm, optimal results were obtained with an annular size of up to 28 mm. For a STJ diameter >26 mm, annular size had to be <26 mm for optimal configuration. Marked annular dilatation (>30 mm) or STJ >30 mm led to suboptimal eH. For a gH of 18 mm, optimal eH was obtained with low annular and STJ sizes (annular ≤25 mm and STJ <27 mm). For a gH of 16 mm, only small annular (<20 mm) and STJ (<25 mm) resulted in a normal eH.
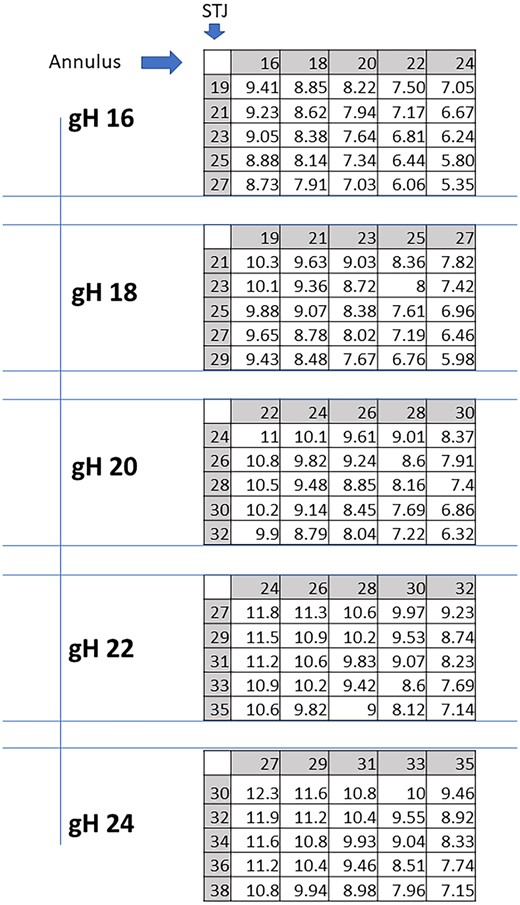
Expected cusps effective height (eH) in mm for each combination of STJ and annular sizes, per any given geometric height (gH). STJ: sinotubular junction.
Coaptation height
Furthermore, for cH, the impact of the annular size was more pronounced than that of the STJ within the range studied (Fig. 3). For any given gH, the cH decreased as the annulus increased and remained stable with increasing STJ. For large gH (22 and 24 mm), all combinations led to optimal cH results. For gH of 20 mm, most combinations yielded optimal results, except for a large annulus (>29 mm). For gH of 18 mm, optimal results were obtained with annulus ≤23 mm in all combinations. For gH of 16 mm, only an annulus ≤18 mm produced optimal cH values except for a 20-mm annulus combined with STJ >22 mm. No optimal result was found when annulus exceeded 22 mm.
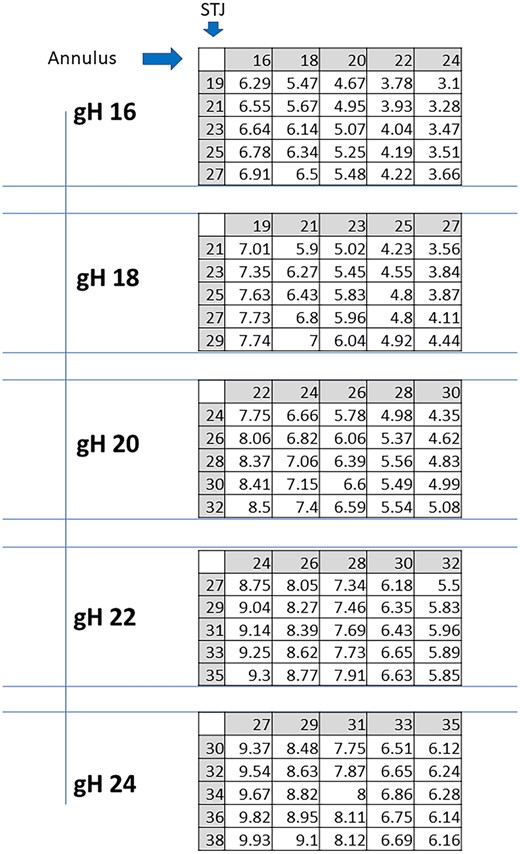
Expected cusp coaptation height (cL) in mm for each combination of STJ and annular sizes, per any given geometric height (gH). STJ: sinotubular junction.
Cusp stress
Unlike in the other parameters, the relative impact of the annular size and the STJ on stress was similar (Fig. 4). In general, stress increased with increasing annular and STJ size. The lowest stress was calculated for a gH of 16 mm in the combination of a 16-mm annulus and 19-mm STJ. Stress doubled with a combined increase of annular and STJ diameters.
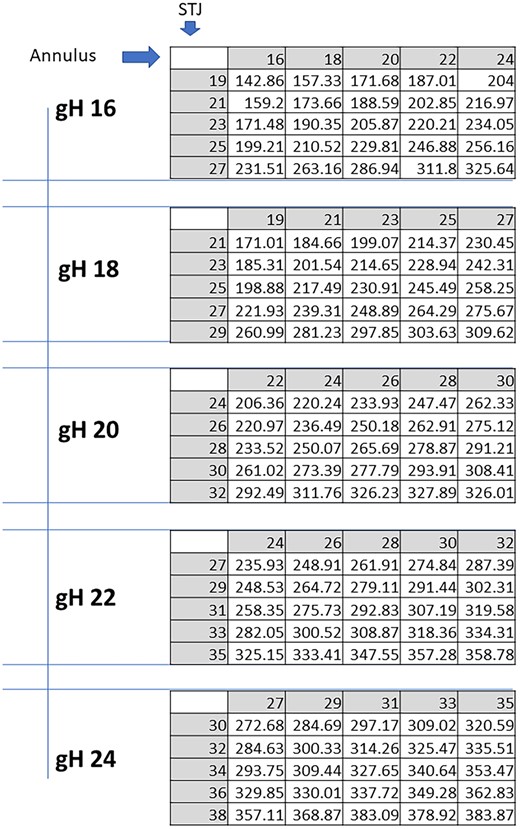
Expected cusps mechanical stress in kPa for each combination of STJ and annular sizes, per any given cusp geometric height (gH). STJ: sinotubular junction.
Repair aortic index
In general, the observations are similar to eH, with a lower impact of the STJ diameter than the annular size (Fig. 5). For any given gH, RAI decreased with increasing annular and STJ sizes. For a gH of 24 mm, optimal RAI values were obtained with an annular size <33 mm. With a larger STJ diameter (>32 mm), only 27 and 29 mm STJ yielded an optimal resulting value. A gH of 22 mm showed an optimal RAI value for all tested annular diameters when STJ was <31 mm. Larger STJ sizes required smaller annular diameters to achieve an optimal configuration. A gH of 20 mm showed a similar behaviour. Both had inadequate configuration when annular and STJ dilatation was present. The gH of 18 mm required even smaller annular and STJ diameters to achieve optimal configuration. This was even more pronounced with a gH of 16 mm, which required an annular diameter ≤24 mm and/or STJ ≤25 mm.
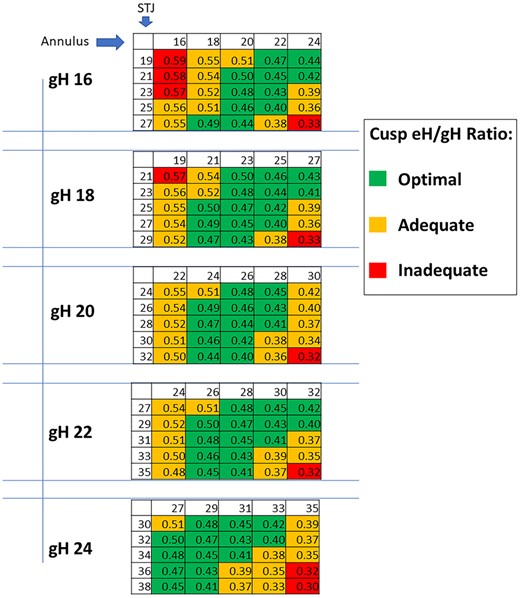
Expected cusps effective height (eH)/geometric height (gH) (RAI—repair aortic index) for each combination of STJ and annulus sizes, per any given geometric height (gH). STJ: sinotubular junction.
DISCUSSION
While aortic valve replacement has long been the standard treatment for aortic stenosis and regurgitation, its drawbacks have become increasingly recognized [3]. The Ross operation has recently been revived due to excellent long-term haemodynamic results, durability and survival. Its complexity and the non-negligible rate of reoperations still limit its use. For these reasons, aortic valve repair is an appealing option with favourable haemodynamics, a low rate of complications [4] and good survival [5].
The practice of aortic valve repair has changed in the past 20 years. The introduction of geometric parameters, such as geometric [17] and effective cusp height [13, 23], or cH [34], has made the procedures more widely applicable and improved reproducibility and durability [18]. It has also become clearer that the aortic valve is a functional unit whose form (and function) depends not only on cusp size and shape but also on root dimensions [13, 17]. In mathematical terms, the form of an aortic valve is a function of different variables that incorporate cusp and root dimensions. To gain a better knowledge of ideal valve form, control of the variables, including its morphology must be achieved. This is not yet common knowledge, since different operative details are proposed without adequate control of all the variables involved.
To shorten the learning curve, we have initiated a series of investigations in which we used computer simulation to determine the role of single variables on aortic valve form. Using a given and constant cusp size, we could confirm the assumed influence of STJ and annular diameters on valve configuration [20, 21]. We could also demonstrate that cH—which may be difficult to measure intraoperatively—correlates with eH. These investigations, however, were performed with only 1 given cusp size. In real life, cusp size varies; this is true for geometric cusp height [18] and probably also for the length of the free margin [24]. Of the different geometric determinants of the aortic valve, gH is the easiest to measure intra-operatively but the most difficult to change. A low gH requires augmentation of the cusp, e.g. with pericardial tissue; this practice, however, has been associated with reduced valve durability [27]. Other parameters, such as length of free margin (if redundant), and annular or STJ diameters, can be modified using established techniques [14].
Thus, as proposed by Komiya et al. [24], the best combination of root and valve dimensions should be determined to create an ‘ideal’ valve configuration. We therefore created the current model, simplified compared to the previous one [21], allowing us to stepwise modify annular and STJ diameters. To represent the normal variations of root dimensions, the variability of annular and STJ diameter was limited to a range of 8 mm. We primarily used eH as the end-point; in addition, we added cH and calculated mechanical stress on the cusps. To accommodate the variations in valve form with variable gHs, we used a normalized parameter, i.e. the ratio between eH and gH, which we named RAI. Previous investigations suggest that its normal range should be between 0.45 and 0.5 [19].
One of the advantages of a computational method over empirical experience is the ability to accommodate for scenarios that are less frequent in practice. It also allows for the prediction of certain scenarios, which otherwise would require many operations and years of follow-up. Our computational model included both a mathematical and geometrical description of the morphology and a mechanical model of the diastolic closure. The unique parametric description of the anatomy [25, 26] and a novel iterative algorithm that can generate different morphologies with constant gH allowed us to consider 125 scenarios, with a variety of cases that cannot be found in clinical databases. It is important to emphasize that these models are three-dimensional, and they account for out-of-plane effects. The mechanical model allowed us to further investigate how the valve will look when it is closed. This is obviously important for the evaluation of the procedure by metrics such as eH and cH, and it also provided us with information on the mechanical stress that the cusp tissue is exposed to. The internal stresses are the highest during diastole and in the collagen fibres, which carry most of the load. However, collagen can withstand high stress, being less prone to injury than the elastin. Therefore, our focus on the elastin exposure to diastolic stress is an important indicator of injury.
The results showed that annular diameter within the range analysed was more important than STJ diameter. A smaller annulus predicted higher eH, higher RAI, normal cH and lower stress. It thus confirmed current clinical assumptions and surgical practice [19]. Interestingly, both eH and RAI were unusually high with small annular sizes. While these are abnormal, it is currently unclear whether this abnormality is of clinical relevance. A minor degree of bulging (<2 mm) may have contributed to this phenomenon, much less than in previous studies [15, 16]. It can be expected to be higher with a more pronounced annular reduction.
By comparison, STJ size was of lesser importance. In general, however, best results were obtained, with the STJ being a few mm larger than the annulus. Within the range tested, stenosis did not occur with annular reduction. Thus, it should be considered that STJ dimensions could be correlated with the longitudinal stretching stress of the ascending aorta [28].
The practical implications of the results at the surgical table are as follows: the gH is measured at the time of surgery with a ruler. The size of the annulus ring is assessed with a Hegar dilator and STJ is best measured by echocardiography with the aorta being pressurized. For optimal configuration, predicted eH, annulus, and STJ diameters are chosen based on the RAI table. Annular dilatation is corrected by an annuloplasty and dilatation of the STJ may be corrected by STJ remodelling or an annuloplasty placed at STJ level. The eH can be further adjusted by cusp plication when appropriate.
Limitations
The model is based on previous anatomical studies [19] and on the mathematical relationships between the aortic root components they indicate. We decided to utilize these already confirmed data, instead of directly collecting new measurements on cadaveric aortas or computed tomography images for building our model. Though it might be argued to be a limitation in the model creation, it simplifies the model while still being reasonably accurate in the core components and allows modelling 125 cases. For the sake of simplification, we also chose to reduce haemodynamics to only a static pressure load that represents the diastolic pressure difference between aorta and ventricle. Future research could investigate fluid–structure interaction, similar to our previous work. Also, dealing with the already large number of models led to the choice not to consider other less dominant and less easily manipulated parameters, such as the length of the free margin and the commissural height of the cusp.
From the medical point of view, precise estimation of the involved measures is proposed here intraoperatively, leading to often exact millimetric numbers that do not find immediate correlation in the tables. Presentation of results in 2-mm steps, as usual in cardiac surgery (prosthetic valve measures, vascular grafts measures), was chosen to maximize readability of tables and might involve interpolation to the nearest value at the time of surgery. Finally, it should be noted that we chose the aortic cusp gH as a reference parameter to build our model. Nonetheless, other groups have also considered other features, such as the free margin length, as a reference element to start the repair [29] with comparable results.
The simulation results will have to be confirmed by clinical data. The results are only applicable to tricuspid aortic valves; anatomical information currently has the best database for this entity. Finally, the results relate to intraoperative measurements of gH; the correlation between intra- versus preoperative determination (using echocardiography or computed tomography) has yet to be determined.
It should be noted that the simulation simplifies the complexity of the real aortic anatomy, where the shape of the annulus is usually elliptical (and not circular) and the cups’ sizes are not always symmetrical; this work should be considered as a 1st step towards a more precise and even personalized patient-tailored model.
CONCLUSIONS
gH of an aortic cusp is easily measured at the time of aortic valve repair. Using the calculations presented by this computer simulation study, annular and STJ diameters can be adjusted to achieve good valve configuration in a predictable fashion. In this model of tricuspid aortic valves, annular reduction was more important than STJ reduction for cusp configuration and cusp stress.
SUPPLEMENTARY MATERIAL
Supplementary material is available at ICVTS online.
Conflict of interest: none declared.
DATA AVAILABILITY
The data underlying this article will be shared on reasonable request to the corresponding author.
Author contributions
Gil Marom: Conceptualization; Data curation; Formal analysis; Investigation; Methodology; Writing—original draft. Luca Paolo Weltert: Conceptualization; Data curation; Writing—original draft. Ehud Raanani: Methodology; Writing—review and editing. Ilaria Chirirchilli: Validation; Writing—review and editing. Christian Giebels: Conceptualization; Writing—review and editing. Francesco Giosuè Irace: Visualization; Writing—original draft. Ruggero De Paulis: Supervision; Validation. Hans-Joachim Schäfers: Conceptualization; Supervision; Validation; Writing—review and editing.
Reviewer information
Interdisciplinary CardioVascular and Thoracic Surgery thanks Marek Jasinski, Marc W. Gerdisch and the other anonymous reviewers for their contribution to the peer review process of this article.
Ethics statement
Ethics statement does not apply to computerized model studies.
REFERENCES
ABBREVIATIONS
- cH
Coaptation height
- eH
Effective height
- gH
Geometric height
- RAI
Repair aortic index
- STJ
Sinotubular junction
Author notes
Gil Marom and Luca Paolo Weltert authors contributed equally to this study.





