Abstract
This manuscript discusses the benefits of having a stock assessment model that is intuitively close to a linear model. It creates a case for the need of such models taking into account the increase in data availability and the expansion of stock assessment requests. We explore ideas around the assessment of large numbers of stocks and the need to make stock assessment easier to run and more intuitive, so that more scientists from diverse backgrounds can be involved. We show, as an example, the model developed under the European Commission Joint Research Center’s ‘Assessment for All’ Initiative (a4a) and how it fits the a4a strategy of making stock assessment simpler and accessible to a wider group of scientists.
Background
This paper explores the advantages and disadvantages of having a stock assessment model based on linear modelling techniques. The argument is made that having such a model will promote the engagement of more scientists, which will result in an increase in capacity to perform stock assessments, and will make performing assessments less time demanding allowing more stocks to be analysed in the same time frame.
The volume and availability of data useful for fisheries stock assessment is continually increasing. Time series of ‘traditional’ sources of information, such as surveys and landings data are not only getting longer, but also cover an increasing number of species.
For example, in Europe the 2009 revision of the Data Collection Regulation (EU, 2008a) has changed the focus of fisheries sampling programmes away from providing data for individual assessment of ‘key’ stocks (i.e. those that are economically important) to documenting fishing trips, thereby shifting the perspective to a large coastal monitoring programme. The result has been that data on growth and reproduction of fish stocks are being collected for more than 300 stocks in waters where the European fleets operate. Catches from all major fisheries are monitored with on-board and market sampling programmes, collecting length structures of all species caught by commercial fisheries. Moreover, a large network of scientific surveys monitor Europe’s coastal fish resources, collecting information about the size of several fish stocks, their length structure, biology and geophysical characteristics of the area.
Another example is the Nansen project, run by FAO and Norway (http://www.eaf-nansen.org), that has been surveying the African coast since 1975 (Sætersdal et al., 1999). The project collects information about the size and length structure of several fish stocks, with and without commercial relevance, as well as biological information.
Despite the increase in data availability, Beddington et al. (2007) calculated the proportion of major stocks and stock complexes that were in an undetermined state in several regions to be 48% in Australia, 78% in New Zealand, and 61% in the Northeast Atlantic. In the European Union (EU) coastal waters, only about 100 stocks are currently assessed with analytical methods by either ICES or the GFCM (Le Quesne et al., 2013). In the United States over half of the identified stocks and stock complexes are either not assessed or have unknown status (NRC, 2013).
The increasing volume and breadth of data provide the opportunity for assessing the status of not just the economically important stocks, but also of stocks that may become economically important in the future, or those that play other important roles, such as in ecosystem function. Assessing an increasing number of stocks within an ecosystem brings us closer to ecosystem-based fisheries management (FAO, 1995; Pikitch, 2004) by allowing a wider scale analysis to be performed.
Initiatives like the European Marine Strategy Framework Directive (EU, 2008b), the UNESCO initiative on biodiversity (http://www.unesco.org/new/en/natural-sciences/special-themes/biodiversity-initiative), and the Intergovernmental Platform on Biodiversity and Ecosystem Services—IPBES (http://www.ipbes.net) will benefit from having information about the abundance and exploitation of more fish populations.
The investment required to make use of the additional data that have already been collected outweighs the opportunity costs of not using it. However, having more data do not necessarily translate directly into having more information. There will be problems of inconsistency between the datasets, for example time series with different time and space aggregations. Putting together the necessary tools to make it possible to explore the data efficiently is therefore an important objective.
This manuscript explores the option of making stock assessment more accessible by making use of linear models, so that more analysts get involved and more stocks can be accessed.
The assessment for all initiative (a4a)
Recognizing that the context above required new methodological developments, the European Commission Joint Research Centre (JRC) started its ‘Assessment for All’ Initiative (a4a), with the aim to develop, test, and distribute methods to assess a large numbers of stocks in an operational time frame, and to build the necessary capacity/expertise on stock assessment and advice provision.
The long-term strategy of a4a is to increase the number of stock assessments by reducing the workload required to run each analysis and by bringing more scientists/analysts into fisheries management advice. The first is achieved by developing a working framework with the methods required to run all the analyses a stock assessment needs. Such an approach should make the model exploration and selection processes easier, as well as decreasing the burden of moving between software platforms. The second can be achieved by making the analysis more intuitive, thereby attracting more experts to join stock assessment teams.
One major step to achieve the a4a goals was the development of a stock assessment model that could be applied rapidly to a large number of stocks and for a wide range of applications: traditional stock assessment, conditioning of operating models, forecasting, or informing harvest control rules in MSE algorithms.
Stock assessment framework
The model chosen was a statistical catch-at-age model implemented in R (R Core Team, 2014), making use of the FLR platform (Kell et al., 2007), and using automatic differentiation implemented in ADMB (Fournier et al., 2012) as the optimization engine. The framework is fully open source and free to use and modify, to better promote the required transparency, transferability, and repeatability that should form the basis of scientific advice on public natural resources. The R language provides a strong platform, with already implemented state-of-the-art statistical analysis tools. ADMB is a sophisticated package for finding optimal solutions in highly non-linear models, supported by solid statistical theory, that allows estimation of the statistical characteristics of the parameters. Having a fully statistical approach allows the usage of the common statistical tools for post-processing of model results, like diagnostics, model comparison (e.g. AIC, BIC, cross validation), model averaging (Millar et al., 2014), simulation, etc.
Submodels can incorporate linear functions of age and year, as well as fixed degrees of freedom splines which can vary with age, year, or both age and year. Additionally, the submodels can include covariates like environmental indicators. The recruitment submodel can also use stock–recruitment models, with the option to specify linear models for its parameters.
Setting up each submodel is done using R’s syntax for equations, which is based on the notation for model building developed by Chambers and Hastie (1992).
Example
To show the flexibility provided by the a4a framework, a case study is presented based on the North Sea cod (Gadus morhua) stock. The code, data, and R packages required to repeat this analysis are provided as Supplementary material.
The dataset, as used by ICES, contains 15 age classes, from 1 to 15, and 48 years, from 1963 to 2011. The plus group of the catch data is set at age 10. The abundance index comes from a single survey, which covers five ages (1–5) and years from 1983 to 2011. Note that in this example we are showing the statistical modelling flexibility of the framework, but in a real situation the model choice must be based on plausible models, supported by knowledge of the biology of the stock, environmental conditions of the region, fishing gears, major management events, etc.
The following models use different smoothers and interactions on age and year to model fishing mortality. Note that using the R language makes available a large number of modelling methods that can be applied without requiring a long process of implementation. In this case we will use the R library ‘mgcv’ (Wood, 2006) to set up the smoothers based on splines.
where k is related to the smoothness of the spline’s basis (for more details, see Wood, 2006).
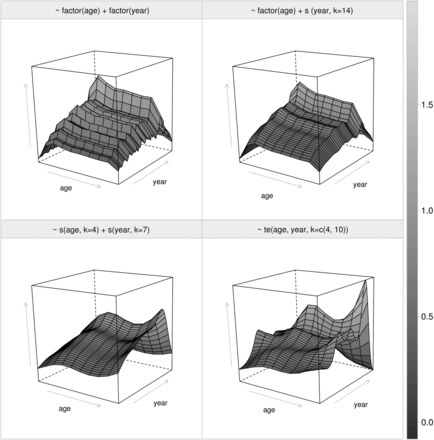
A graphical depiction of four fishing mortality models. Top left: the basic model which considers fishing mortality to have a year and an age effect, independent from each other, with one coefficient for each age and year (analogous to a separable model). Bottom left: a smooth version of the basic model where each effect, age and year, is modelled with thin plate splines which introduces correlation along age and year. Top right: a mixture of the previous two, allowing the fishing mortality at age to vary independently while a thin plate spline is used to smoothly model the fishing mortality over the years. k is related with the smoothness of the spline’s basis (for more details, see Wood, 2006). Bottom right: using a tensor product of cubic splines over age and year, introducing correlation along the age and year effects, but also cross-correlation between ages and years.
Limitations of the a4a approach
Conceptually, the biggest limitation comes from the use of single species analyses. When compared with multispecies assessments, the a4a approach is looking sideways to obtain a global view of the system. Instead of trying to incorporate all the elements in the ecosystem in one single model, it approaches the problem in different stages, by breaking down the analysis into single species, and then providing the framework to build on top of these. Having a coherent dataset of estimates of population dynamics and fishing mortalities will still allow the exploration of relationships between species, between species and the environment, technical interactions between fleets, etc.
The trade-off is thus in complexity vs. insight, between a more complex model dealing with the ecosystem as a whole, or a simpler model that deals with parts of the ecosystem leaving the global analysis downstream. The complex model approach may give more insight of the system, by explicitly including processes that the simple model approach ignores or aggregates. Having identified those processes will force the analysts to make their assumptions explicit. The downside is that the complex model approach requires information that often does not exist, driving analysts to parameterize a part of their model based on personal guesses. The simple model will ignore those relationships, but by having less complexity it will require less information and assumptions to be made, because part of these are less explicit. The global analysis will then be carried out afterwards, by exploring the relationships previously not considered but now apparent. It can still be argued that this ‘shortcut’ is not as thorough as the complex model, which is true. But it is also true that this approach may allow us to start looking at the system on a scale that is difficult to get right now.
A similar approach, of breaking down the system into smaller parts, is taken for individual growth and natural mortality models. These are taken upstream of the model fit, allowing uncertainty to be incorporated by the model and reflected on the results, even if not estimated within the model fit.
The strategy of assessing all the stocks in a sea basin is debatable and open to criticism. From a fisheries management perspective, we might risk doing unnecessary work, if the fishery can be successfully managed by taking into account just one species, or a small group of “key species”. The costs associated with such ambitious objective may be too high in some cases, taking into account the commercial value of the catches from a single basin. Our expectation is that the gain in efficiency obtained by having an accessible solid framework will balance out the increase in work time necessary for such a number of stocks to be assessed. On the other hand, the cost–benefit analysis can not only be monetary, and the full benefits, in risks and knowledge, should also be considered.
There are technical limitations in the a4a approach, mainly related to modelling assumptions. These are, for example, the assumption of lognormality of catches and abundance indices errors, annual and single space dynamics, Baranov’s equation for catches, and the exponential decay of population numbers.
The flexibility introduced in the model can be seen both as an advantage and as a limitation, in particular due to the possibility of over-parameterization. We are working on developing model wrappers to make the model building and exploration process more intuitive, and distance the user from the details of specifying more complex linear model formulations, such as smoothers with breakpoints or time varying smoothers, and decreasing it this way the temptation to over-parameterize. For example setting up a separable model could be done with a syntax like ‘log F ∼ separable(age, year)’ instead of the more verbose ‘log F ∼ factor(age)+ factor(year)’. Although such formulations will still not make the models bullet-proof against over-parameterization, they should reduce that possibility.
The choice of R to implement the methods can also be seen as a limitation, in the sense that the users will need to know how to operate R to be able to use the a4a methods. However, the advantages in terms of easier collaboration, transparency, repeatability, and the large number of methods already implemented, greatly compensates the costs of the learning curve associated with this platform. Linear models are nowadays an essential part of basic statistical training, and their use and familiarity has been greatly expanded by the adoption of the S/R language (Becker and Chambers, 1984). Although we do not expect most scientists to be experts in linear modelling, they should be familiar with many of the concepts, so the barriers to learning a linear model-based assessment method are bound to be low.
Final comments
The outcomes of WCSAM (ICES, 2013) show that there is still a long way to go before multispecies space-time stock assessments become routine. In the meantime we, as a community, should focus on getting the most out of single stock assessments, in particular when data are already available.
So, why not aim to assess all species in a sea basin or ecosystem?
The pressure to provide information about the stock status of large numbers of stocks already exists in the EU and US. The EU’s Common Fisheries Policy (EU, 2013) and the Magnuson–Stevens Fishery Conservation and Management Reauthorization Act (USC, 2006) in the USA require scientific advice for a lot more stocks than previous regulations.
The a4a initiative is tackling this problem by putting together a group of statistically robust standard methods that can be applied rapidly and without requiring a strong statistical technical background, but allowing scientists to make the best use of the available technical knowledge of fisheries, stocks, and ecosystems. The methods being developed are subject to extensive testing to evaluate their performance and to identify the appropriate configurations for different situations, as well as robust default settings.
Clearly, there will be advantages in dealing simultaneously with stocks that are being caught by the same fleets, inhabiting the same areas and being exposed to the same management actions. Information can be shared across stocks, and modelling under a single framework will create the necessary environment to do so efficiently. The so-called “key” stocks, or those of special concern, will still be subject to more thorough analyses, performed with more complex stock assessment models like SS3 (Methot and Wetzel, 2013) and CASAL (Bull et al., 2012), or tailor-made models developed using ADMB (Fournier et al., 2012), JAGS (Plummer, 2003), or other suitable tools.
Finally, to make progress understanding the natural processes and the human behaviour associated with the fishing activity, we need to diversify our knowledge base, and bring into the process a wider range of disciplines: biology, ecology, economy, engineering, etc. In our opinion, one possible way to bring quantitative fisheries science closer to all those fields is to provide tools that scientists with different backgrounds can understand. Linear models could be the common language that is able to lower the barriers currently limiting the ability of fisheries science to establish stronger links with those disciplines.
Supplementary data
Supplementary material is available at the ICESJMS online version of the manuscript.
References
Author notes
Handling editor: Dr Mark Maunder
