-
PDF
- Split View
-
Views
-
Cite
Cite
Alf Harbitz, Michael Pennington, Comparison of shortest sailing distance through random and regular sampling points, ICES Journal of Marine Science, Volume 61, Issue 1, 2004, Pages 140–147, https://doi.org/10.1016/j.icesjms.2003.11.002
Close - Share Icon Share
Abstract
The shortest sailing distance through n sampling points is calculated for simple theoretical sampling domains (square and circle) as well as for a rather irregular and concavely shaped real sampling domain in the Barents Sea. The sampling sites are either located at the nodes of a square grid (regular sampling) or they are randomly distributed. For n less than ten, the exact shortest sailing distance is derived. For larger n, a traveling salesman algorithm (simulated annealing) was applied, and its bias (distance from true minimum) was estimated based on a case where the true minimum distance was known. In general, the average minimum sailing distance based on random sampling was considerably shorter than for regular sampling, and the difference increased with sample size until an asymptotic value was reached at about n=60 for a square domain. For the sampling domain in the Barents Sea used for shrimp (Pandalus borealis) abundance surveys (n=118 stations), the cruise-track lengths based on random sampling were approximately normally distributed. The mean sailing distance was 18% shorter than the cruise track for regular sampling and the standard deviation equalled 2.6%.
1 Introduction
Abundance surveys at sea are expensive, where the major cost for trawl sampling and other “point” sample equipment is due to the sailing time between sampling sites. For a given set of n sampling locations, it is therefore important to find the shortest sailing distance through the n points, typically with some constraints, such as a given entrance and departure point and available survey time. A related question is which sampling design (Cochran, 1977; Thompson, 1992; Thompson and Seber, 1996) provides the shortest sailing distance.
This paper considers regular sampling at the nodes of a square grid and sampling at random locations. A major motivation for this work was the discovery that random locations tended to have considerably shorter minimum sailing distances as compared with a regular design, which was a surprising result for us as well as for a range of other scientists concerned with the design of marine resource surveys. This paper is an attempt to quantify this difference, with emphasis on a real sampling domain with a rather irregular border and a concave shape used for shrimp (Pandalus borealis) abundance surveys in the Barents Sea.
It should be noted that the sailing distance is just one of several factors that needs to be taken into account when determining an optimal sampling design. A logistic problem related to random sampling is, for example, the handling of the samples if two or more adjacent sampling sites are very close to each other (Harbitz et al., 1998). Another important aspect is the spatial correlation between samples that is commonly present. In this case, regular sampling may provide more precise abundance estimates than random sampling. Nevertheless, the minimum sailing distance is definitely an important factor when designing a survey (Pennington and Vølstad, 1994).
For small sample sizes (n<10), the exact shortest sailing distance is easily found by comparing all possible alternatives. Realistic n-values are considerably larger, however, and a numerical search method is needed, but there is generally no guarantee that the exact shortest distance is found. This is a typical traveling salesman problem (TSP), named after the problem of finding the cheapest tour or cycle through n cities.
In this paper, a TSP algorithm based on simulated annealing (Kirkpatrick et al., 1983) is used to find the shortest cruise track. The algorithm is taken from Press et al. (1994) and translated to Matlab code that is freely available from either of the authors.
2 Length of cruise track
Surveys of marine resources generally are based on either systematic or random selection of sampling sites within the survey area. For systematic surveys, a grid is laid over the survey region and a sample is taken at each grid node that lies within the survey region. We refer to this as a “regular” sampling scheme. For random surveys, the survey region is usually stratified, and sampling sites are chosen at random in each stratum.
2.1 The minimum sailing distance for regular sampling
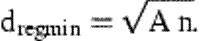
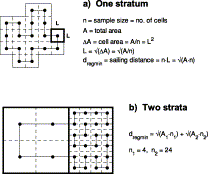
Illustration of the theoretically shortest sailing distance, dregmin, through n points at the nodes in a regular square grid: (a) one stratum and (b) two strata.
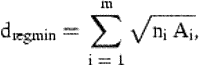
For fixed Ais and fixed n=n1+n2+⋯+nm, it can be deduced from Equation (2) that the maximum value of dregmin is obtained with proportional allocation, i.e. with ni∝Ai. Any stratification thus results in a shorter theoretical minimum sailing distance. Note, however, that in practice the theoretical minimum will be even harder to obtain in the stratified case than in the non-stratified situation.
An example where the theoretical minimum distance is obtainable is shown in Figure 1b with m=2 and n=28. With A=1, dregmin in this case equals  . For no stratification,
. For no stratification,  , i.e. dregmin is about 12% shorter in the stratified design.
, i.e. dregmin is about 12% shorter in the stratified design.
To understand intuitively why stratified sampling provides shorter minimum sailing distances compared with evenly distributed sampling points, one can imagine stratification as synonymous with a certain degree of clustering, where strata with dense points are clusters compared to strata with sparse densities. For random points, the clustering effect is even more enhanced, and one can imagine that a cluster of close points can be replaced by the average location of the points, thus reducing the effective number of points with respect to distance.
2.2 Sailing distance for random surveys
Let x and y denote the horizontal and vertical coordinates, respectively, in a 2D Cartesian coordinate system. Further, let xmin and xmax denote the minimum and maximum x-values in the x-direction, and let ymin and ymax denote the extension in the y-direction. A random location (X, Y) in the domain is generated by drawing X and Y as independent and uniformly distributed variables on [xmin, xmax] and [ymin, ymax], respectively, until the location is within the area. The procedure is repeated until n locations are generated in the actual domain.
For a rectangular area, any location by the above procedure will be within the area. This is also the case for a circular domain, but in this case the procedure is slightly modified by adjusting the values of ymin and ymax dependent on the generated x-value.
If the domain is partitioned into m strata, the procedure is applied separately in each stratum. Other sampling options considered were one random location per unit cell in a regular grid and the inclusion of the transport distance to and from the sampling field.
The minimum sailing distance, drnd, through n random locations in a closed cycle was determined exactly for n<10. For larger n, it was estimated using the TSP algorithm (see Appendix A). To compare random and regular sampling, simulations were used to estimate the distribution of the random variable f=drnd/dreg or f=drnd/dregmin. Because the iterative simulated annealing algorithm chose permutations of the chronological order of sample point visits in a random fashion, repetitions of the algorithm on a given realization of n random sampling points provide different results. The estimated variance of drnd (and f) therefore will contain one component due to different sampling point realizations, and one component due to the stochastic nature of the simulated annealing procedure.
Three major properties of the TSP algorithm examined were the bias (distance from true minimum distance), the standard deviation of minimum traveling distance found by repeating the TSP algorithm on a given realization of n random points, and the efficiency in terms of CPU time.
The bias of the algorithm was estimated as the difference between the mean and the minimum shortest distance found by a number of TSP-runs for the same realization of sampling points. In order to examine how many runs were needed in order to obtain the exact minimum, a test case with 100 random locations in a square where the exact solution is known was run (Reinelt, 1991). The success rate, i.e. the relative number of simulations where the exact solution was found was then used as a rough guideline for how many repeated simulations for a given realization were needed in order to obtain the exact minimum, or a minimum negligibly larger than the exact solution. Note that the bias can be reduced by adjusting the parameters in the TSP algorithm at the cost of increased CPU time. A rough goodness criterion to assess the found minimum is to verify that the tour does not intersect itself, which is inconsistent with the optimal solution (Flood, 1956).
With regard to dispersion, the standard deviation of minimum sailing distance due to different realizations of the n random locations is of major interest. It is assumed that this standard deviation is independent of the standard deviation of the TSP algorithm for a given realization. It is further assumed that the standard deviation of the TSP algorithm is independent of realization. By subtracting the variance of the TSP algorithm from the variance of minimum distance found by a number of different realizations with one TSP simulation per realization, the standard deviation due only to different realizations can be estimated.
2.3 The Barents Sea shrimp survey
This trawl-based survey has been conducted in April/May on an annual basis with a fixed regular sampling design since 1992. The square sampling grid is oriented in an N–S (and E–W) direction with 20 nautical miles (nm) between closest neighbors. A rather irregular border encloses the concavely shaped domain, including 118 regular sampling sites, close to the actual number of trawl hauls conducted in each survey. Recently, some modifications were made by applying the diagonals in the N–S grid as a regular square grid in the least abundant area (south-western part), i.e. a regular square grid oriented NW–SE with ca. 28 nm spacing between neighbor sampling sites.
In several surveys, one and the same location has been sampled several times in order to study diurnal effects. An ideal coverage of the entire study area has also rarely been obtained, due to ice coverage in the north, bad weather, gear problems, or other complications. In 1996, a pilot study was performed by applying a regular square N–S grid in part of the abundant Hopen area (northern stratum) with 10 nm distances between closest neighbors.
At each station, a standard trawl haul is conducted with a vessel speed of 3 nm/h (kn) for 20 min, and the trawling operation typically takes about 1 h, varying with depth. This includes the slowing down of the vessel from the cruising speed of 12 kn between stations, the setting, towing, and retrieval of the trawl and the speeding up to 12 kn towards the next station. The vessel is heading towards the next station during the trawl operation with an average speed of approximately 3 kn. Thus for each station approximately 3 nm of the sailing distance is covered. The remaining average distance of 17 nm takes 1 h 25 min. The time spent on cruising thus dominates the time spent on sampling, but the latter could not be neglected.
The following sampling schemes were examined with n=118 sampling points: Case studies 1 through 4 were based on 200 realizations and case 5 was based on 400 realizations. For case 1, some small random values were added to the 118 regular sites to obtain only one unique solution. In this regular case, it is easier to judge subjectively if the exact minimum distance is obtained, compared to the situation with random locations.
Regular distance. The minimum regular sailing distance, dreg, that is possible as compared to the theoretical minimum distance.
Random sampling. The distribution of f=drnd/dreg when the sampling points are randomly distributed over the entire sampling domain (one stratum).
Cell simulation. The distribution of f=drnd/dreg when one random location is chosen within each of the 118 regular unit cells in the sampling domain.
Transport included. The ratio between shortest random and shortest regular distance when the transport distance to and from the port (Tromsø) is included.
Stratified sampling. The distribution of f=drnd/dregmin with six strata and the number of sampling sites within each stratum proportional to stratum area and average stratum standard deviation of historical shrimp (Pandalus borealis) samples. The stratification is ignored in the simulations of shortest sailing distance.
Case study 3 was chosen to examine if random sampling gives shorter sailing distance than regular sampling under the strong restriction of having one random location in each regular unit cell. This option can be seen as a hybrid combining regular and random sampling.
Case study 4 includes the traveling distance to and from the sampling field. If the traveling distance dominates the sailing distance within the field, the f-ratio would be very close to one (no difference between minimum sailing distance by random and regular sampling). However, the sailing distance within the sampling field may be much larger than the transport distance to and from the field, even if the latter is comparable to the extension of the sampling field. This is the case for the Barents Sea sampling domain, where the transport distance is about 15% of the total sailed distance.
As noted previously, stratified sampling is expected to provide shorter regular sailing distance than non-stratified sampling. This is also the expected result for random sampling, but it is hard to deduce theoretically how stratified sampling will influence the f-ratio. This is the reason why case 5 is included.
3 Sailing distance and survey precision
Which survey design, random or regular, is preferable for abundance surveys of a stock depends on, among other factors, the precision of the abundance estimates generated by the two methods for a survey of fixed duration. The precision of a random survey is a function of sample size, while the precision of a regular survey depends on the sample size and the spatial structure of the stock.
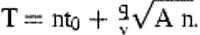
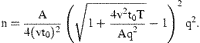
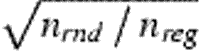 is larger than CVrnd/CVreg, where the first ratio is calculated for fixed T and the latter is calculated for fixed n≈nreg.
is larger than CVrnd/CVreg, where the first ratio is calculated for fixed T and the latter is calculated for fixed n≈nreg.Note that Equations (3) and (4) can be slightly modified to take into account other factors. For example, to examine the effect of different constant tow durations, t0 can be replaced by c1+t, where c1 is the average trawl operation time excluding the tow duration, t (Pennington and Vølstad, 1991). If the vessel is heading towards the next station during the sampling process with an average speed of v0, and the “sampling distance” v0t0 is not negligible compared with the average distance between adjacent stations, then this can be accounted for by replacing t0 with (1−v0/v)t0 in Equations (3) and (4).
4 Results
4.1 Square and circular domains
Exact minimum distances were calculated for n<10. For all n, the circular domain provided smaller mean values and standard deviations of f and the average ratios were always smaller than 1 for both shapes (Figure 2). Except for n=4, f decreased with increasing n, and for n=9 the average result for the circular and square domain nearly merged. These results are based on rather extensive simulations: for n=4, 5 and 6, nsim=100 000 realizations of random locations were conducted, while nsim=10 000 for n=7 and 8 and nsim=2000 for n=9.
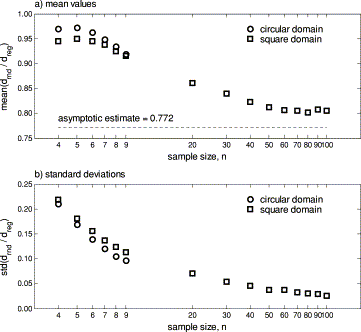
The mean of the estimated distribution of the minimum distance through n random points divided by minimum distance based on n regular points (a) and the estimated standard deviation of the distribution (b) for a square and a circle vs. sample size, n. The exact minimum is calculated for n<10, and minimum distances were estimated by simulated annealing for n>10. The asymptotic estimate is based on bias estimates of the simulated annealing procedure.
For n larger than ten, the average ratio for a square domain based on 200 realizations for each n appeared to converge to an asymptotic constant for n larger than 60 (Figure 2a). The asymptotic estimate f=0.772 is below the points because it takes into account the bias of the simulated annealing procedure. The bias estimate is based on the result of 400 repetitions of the simulated annealing algorithm applied to a case study with n=100 random locations in a square where the exact minimum solution f=0.7910 is known (see the files rd100.tsp and rd100.opt.tour at http://elib.zib.de/pub/Packages/mp-testdata/tsp/tsplib/tsp/). This minimum value was found in two of the 400 simulations, and the difference Δf=0.0304 between the average f and the minimum f was used as the estimate of bias for n=100.
4.2 The Barents Sea survey
The shortest distance found by the simulated annealing procedure through the 118 regular sampling sites in the Barents Sea is shown in Figure 3. Note that the minimum distance, dreg, is 3.86% larger than the theoretical minimum distance  . When the 118 sampling points were randomly distributed within the sampling domain, the minimum sailing distance through the 118 points tended to be considerably smaller than for regular sampling. An example is shown in Figure 4a, where the minimum distance through the random points is 25% smaller than the regular minimum distance shown in Figure 3. Based on 200 random realizations, the minimum sailing distance was found to be approximately normally distributed and the mean was 18% smaller than the regular minimum distance. The estimated standard deviation of the sampling distribution equalled 2.6%, after a minor adjustment that took the dispersion of the TSP algorithm into account. The bias Δf of the TSP algorithm was in this case estimated to be 0.0161, i.e. considerably smaller than for the square domain. This is probably due to the use of more iterations in the TSP algorithm in the Barents Sea simulations. As a rough estimate, each TSP simulation required approximately 3 min CPU time in the Barents Sea case, as compared to about half the time required for the square domain setting.
. When the 118 sampling points were randomly distributed within the sampling domain, the minimum sailing distance through the 118 points tended to be considerably smaller than for regular sampling. An example is shown in Figure 4a, where the minimum distance through the random points is 25% smaller than the regular minimum distance shown in Figure 3. Based on 200 random realizations, the minimum sailing distance was found to be approximately normally distributed and the mean was 18% smaller than the regular minimum distance. The estimated standard deviation of the sampling distribution equalled 2.6%, after a minor adjustment that took the dispersion of the TSP algorithm into account. The bias Δf of the TSP algorithm was in this case estimated to be 0.0161, i.e. considerably smaller than for the square domain. This is probably due to the use of more iterations in the TSP algorithm in the Barents Sea simulations. As a rough estimate, each TSP simulation required approximately 3 min CPU time in the Barents Sea case, as compared to about half the time required for the square domain setting.
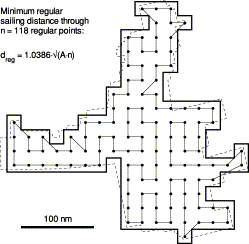
Minimum regular sailing distance, dreg, through the n=118 regular sampling sites in the Barents Sea, as found by the use of the simulated annealing procedure. Note that this minimum distance is 3.86% larger than the theoretical minimum distance  . The dotted contour shows the actual sampling domain, while the solid contour shows the approximation by assigning one square cell to each regular sampling site.
. The dotted contour shows the actual sampling domain, while the solid contour shows the approximation by assigning one square cell to each regular sampling site.
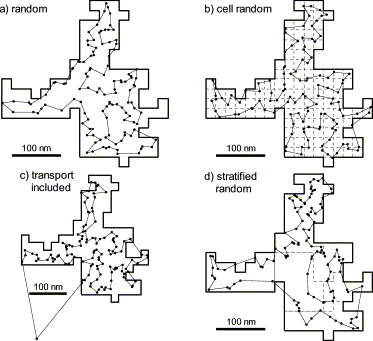
Examples of ratios between random and regular cruise tracks in the Barents Sea with n=118 sampling points. (a) Random sampling, f=drnd/dreg=0.7514, (b) one random location per unit cell, f=drnd/dreg=0.8859, (c) random sampling with transport to and from field included, f=drnd/dreg=0.7899, and (d) stratified sampling, drnd/dregmin=0.7879.
Even when one random point was chosen within each square cell defined by the regular sampling scheme, the random distance tended to be shorter than the regular one. An example is shown in Figure 4b, where the random distance was 11.4% shorter than the regular one. Based on 200 random realizations, the distance with one random point per cell was estimated on average to be 6.5% shorter than the regular distance, when no bias correction of the TSP-procedure was applied. When applying the same TSP-bias correction as for unconstrained random locations, the average random distance was estimated to be 8.1% shorter than the regular distance.
Including the transport distance to and from the sample field appeared to have a small effect on the relative difference between random and regular sampling, even though the transport distance was comparable with the extension of the area. An example is shown in Figure 4c, where the random distance is 21.0% shorter than the regular one. On average, based on 200 realizations, a 16.4% shorter sailing distance was obtained with random sampling, applying the same TSP-bias correction as before.
The last factor examined was stratified sampling, where the number of sample points in each stratum was chosen approximately proportional to stratum area and mean of stratum standard deviation over years. For the six strata, the number of sample points were: 10 (18), 9 (11), 14 (12), 14 (24), 51 (30), and 20 (23) in stratum 1 through 6, respectively, with the sample size in the non-stratified case in parentheses. In this case, the theoretical regular minimum distance by applying Equation (2) is 97.6% of the theoretical non-stratified regular minimum distance. An example is shown in Figure 4d, where the random distance was 21.2% shorter than the theoretical regular minimum. On average, based on 200 realizations, a 14.0% shorter sailing distance was obtained by random vs. regular sampling. To determine the actual shortest distance compared to the theoretical one in the stratified case is rather tedious and was not done, but a factor larger than 1.0386 obtained for the non-stratified case is expected. If the factor 1.0386 is applied, the average random distance is 17.3% shorter than the regular distance, i.e. very close to the non-stratified case.
To find out if a random design provides a smaller CV than a regular design, t0 in Equations (3) and (4) was replaced by (1−v0/v)t0=0.75 h. If nreg=118 stations are sampled, then C=285 h (Equation (3)). For a random survey of the same duration, q=0.82, and therefore, nrnd=143 (Equation (4)).
Using geostatistic methods, Harbitz and Aschan (in press) estimated that the coefficient of variation (CV) for these shrimp surveys would be on average 8.2% if random sampling were employed (nrnd=118) and 6.4% for regular sampling. If instead of 118 stations, 143 stations were sampled randomly, then the average CV would be  . Given the validity of the assumptions underlying the geostatistic estimates, it would then appear that the regular design is the preferred design for these surveys at least for estimating abundance.
. Given the validity of the assumptions underlying the geostatistic estimates, it would then appear that the regular design is the preferred design for these surveys at least for estimating abundance.
5 Discussion
One may ask why the drdn/dreg results incorporated the bias of the TSP algorithm, because in practice a bias can hardly be avoided for realistic sampling sizes and one must live with the fact that the exact minimum distance normally will not be found. Note, however, that to provide the results in the present study, several realizations of the n sampling locations were needed (typically 200 realizations were run for the different settings). In a practical situation, only one realization is needed, and thus far more extensive TSP-runs can be performed. It is therefore realistic to expect that the bias in practice is negligible, at least for sample sizes that are not much larger than n=118 used in this work.
The existence of the asymptotic result  for sufficiently large n, where k is a universal constant, was proven by Beardwood et al. (1958), but the exact value of k is to our knowledge unknown. As outlined in the present paper, the theoretical minimum distance for regular sampling points (at the nodes in a square grid) is
for sufficiently large n, where k is a universal constant, was proven by Beardwood et al. (1958), but the exact value of k is to our knowledge unknown. As outlined in the present paper, the theoretical minimum distance for regular sampling points (at the nodes in a square grid) is  . This is also an asymptotic result, at least for all realistic sampling domains. Thus asymptotically, f=drnd/dreg converges to the constant k, and k<1 implies a shorter minimum sailing distance by random than by regular locations.
. This is also an asymptotic result, at least for all realistic sampling domains. Thus asymptotically, f=drnd/dreg converges to the constant k, and k<1 implies a shorter minimum sailing distance by random than by regular locations.
Though the exact value of k is not known, it has been estimated based on simulations. Beardwood et al. (1958) estimated that k is equal to 0.75 with 95% confidence interval (0.66, 0.84). Christofides and Eilon (1969) graphically show that their simulations fit quite well with k=0.75 for n in the range of 70–100, the interval in which the results for a circular, square, and triangular square coincided.
An asymptotic result by itself does not say how large n should be in order to be close to its asymptotic limit. For n=118 and the Barents Sea sampling domain, the estimated mean f based on 200 realizations was 0.85 when corrected for bias, which is rather far from the asymptotic estimate of k=0.77. When adjusting the estimate for the minimum realizable regular distance, the mean f-ratio was 0.82.
It is interesting that our results appear to be rather independent of whether a stratified sampling design is or is not applied, and also rather independent of including the traveling distance to and from the sampling area. Note, however, that if the vessel starts in one port and ends in another, the sailing route is no longer closed, and the traveling salesman algorithm needs to be modified. How this will influence the f-ratio is a task for future investigations, along with the influence of, e.g., particular constraints, such as the minimum time required to handle the sample at each sampling site before a new sample is taken. The simulated annealing algorithms in general are quite flexible with regard to including constraints (Press et al., 1994).
It appears that for the shrimp surveys, a regular survey would generate more precise abundance estimates than random surveys, even though considerably more stations could be sampled randomly. Note, however, that determining an appropriate estimate of the CV for systematic designs is a complicated issue. Even if a correct model for the correlation structure is applied, it is often a great challenge to find appropriate estimators of the model parameters. For example, a critical parameter for the geostatistic estimator is the nugget parameter, which determines how much of the sampling variance is caused by random variation and how much is due to the spatial structure. A regular design will not have any sampling pairs at zero or small distances. Such pairs are often crucial to estimate adequately the nugget effect and, therefore, the estimated CV for a pure regular survey may be rather imprecise and biased. In contrast, for random surveys it is straightforward to estimate the precision of the abundance estimates, and these CV-estimates will tend to be more precise than CV-estimates obtained for a regular design.
To conclude, the major goal of this work has been to document that random sampling provides considerably shorter sailing distances than regular sampling, and that this is one of the several aspects that should be considered in the much wider challenge of finding an optimal sampling design.
We thank Richard McGarvey and an anonymous reviewer for their comments, which helped us significantly to improve this paper. This research was done under the shrimp assessment project, which is financed by the Norwegian Fisheries Department.
Appendix A
The traveling salesman algorithm
The applied traveling salesman algorithm is taken from Press et al. (1994). Two simple techniques for changing the order of the n sampling locations were used: The reverse or transport alternative was chosen with equal probability. If the new change of visiting order gave a shorter total sailing distance, then the new order replaced the old one, and the simulations continued. To avoid being stuck in one of the many local minima, the algorithm sometimes uses the previous order even if the sailing distance of the new order is shorter. The probability for this happening is controlled by a clever analogy to thermodynamics and is given by exp(−Δd/dit), where Δd is the change in sailing distance by the reverse order or transport alternative, and dit is initially a large value. Thus the probability of jumping out of a local minimum is high at the start and then dit is gradually decreased exponentially.
Reverse order: choose a random segment of succeeding sites along the present route, and reverse the order of the segment.
Transport: choose a random segment of succeeding sites along the present route studied, and transport the whole segment between two succeeding sites outside the segment, one of them chosen randomly.
The following parameters control the algorithm, where a success either means that the reverse order or transport gives a shorter sailing distance or that by chance the new route should be chosen: d0 is determined by first generating a set of 100 realizations of random locations of the n sampling points within the study area. For each realization, the sailing distance is calculated by visiting the random locations in the order they are generated. Then d0 is calculated as the standard deviation of the 100 distances, multiplied by two, the latter factor being determined from numerical experimentation. The values used for the other three parameters were as follows: succeeding values for dit were chosen by the rule di+1=0.9di, nt=100, nsuccmax=10n, and nitmax=100n, according to the codes given by Press et al. (1994).
| d0 | initial value of dit, |
| nt | number of dit iterations, |
| nsuccmax | maximum number of successes before a new iteration, |
| nitmax | maximum number of path trials before a new iteration |
| d0 | initial value of dit, |
| nt | number of dit iterations, |
| nsuccmax | maximum number of successes before a new iteration, |
| nitmax | maximum number of path trials before a new iteration |
| d0 | initial value of dit, |
| nt | number of dit iterations, |
| nsuccmax | maximum number of successes before a new iteration, |
| nitmax | maximum number of path trials before a new iteration |
| d0 | initial value of dit, |
| nt | number of dit iterations, |
| nsuccmax | maximum number of successes before a new iteration, |
| nitmax | maximum number of path trials before a new iteration |



