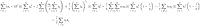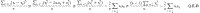Abstract
A stratified random sample survey has been carried out since 1988 as a component of the assessment of the stock of northern shrimp Pandalus borealis in offshore West Greenland waters. In 1999, the placing of stations independently and randomly was replaced by buffered random sampling, in which stations were randomly placed but prevented from being closer together than a prescribed limit. Buffered random sampling gave a more even distribution of stations within strata, and nearest-neighbour distances were on average increased by 50%. The statistical effects were difficult to determine, but did not appear to be large, and the estimated standard errors did not change much from previous years. However, the buffered sampling method generated designs in which stations were evenly distributed over the strata, and did away with the need for subjective manual adjustment of the positions of stations which independent random sampling sometimes placed too close to another station.
1 Introduction
Probability-based surveys of resource density are an integral component of fishery resource assessments. Many stocks are fished by trawling, and trawl surveys, for which swept-area calculations yield a convenient and relatively precise index of effort, provide fishery-independent estimates of at least relative abundance; absolute abundance estimates depend on accurate knowledge of gear performance. Trawl, and other, surveys are commonly used to gather data for reinforcing assessments based on fishery records of catch and effort.
Correlation between sample members is a common problem in both design and execution of sampling schemes. As the average positive correlation between members of a sample increases, the sample mean becomes in reality less precise as an estimate of the population mean, while its standard error calculated by conventional methods (based on deviations from the sample mean) decreases so it becomes more precise in appearance. Fishery resources are often distributed such that there is positive correlation between results at closely spaced sampling stations. In sampling from such populations, the most direct method for reducing the average correlation, and thereby making the sample mean a more precise estimate of the population mean, is to ensure that highly correlated pairs of closely spaced stations do not occur in the sampling design.
Stratified random sampling is the basic standard sampling technique for trawl surveys, and complete spatial randomness (CSR) provides the statistical standard method of placing stations within strata (Doubleday, 1981). It gives unbiased estimates, the sampling error variance of which can also be estimated without bias. In practice, it has undesirable characteristics. In a CSR design, some stations will be close to their nearest neighbours while large spaces elsewhere may be left blank. These drawbacks to CSR sampling may be – often are – mitigated by dividing the survey area into many small strata and fixing the number of stations per stratum, so as to obtain a more even distribution of survey effort (Gunderson, 1993), by further dividing strata into substrata of approximately equal area and randomly placing one station in each member of a random sample of these substrata (Doubleday, 1981), or by manually adjusting the positions of stations that randomly fall too close together. Any of these methods incurs a statistical cost, and subjective manual adjustment of station positions without closely defined rules of procedure, which depends on the personal idiosyncrasy of survey designers, should certainly be avoided in favour of objective methods. More controlled methods of efficient sampling design are desirable; these include systematic sampling and the method that will be described here, buffered random sampling.
The northern shrimp (Pandalus borealis) is fished off West Greenland in NAFO Divisions 0A and 1A–1F, mostly in water between 150 and 600 m deep. A trawl survey is a component of the assessment process for the stock, which places some emphasis on the year-on-year change in the swept-area biomass index estimate from the survey. The survey has been carried out annually since 1988 (Carlsson and Kanneworff, 1998a, b). It is based on a stratified design. The survey area – waters from 150 to 600 m deep between the southern tip of Greenland and 72°30′N on the west coast – is divided into geographical areas and subareas, and those for which good bathymetry is available are further divided into four strata with depth ranges of 150–200, 200–300, 300–400, and 400–600 m (Figure 1, Table 1). The design of the survey and the analysis of the resulting data were reviewed in 1998 and 1999, and a number of changes were suggested (Carlsson et al., 1998). For the reasons given above it was suggested inter alia that buffered random sampling should be used to place survey stations instead of the existing method of independent random sampling with subjective manual re-adjustment. This suggestion, as well as others, was implemented in the 1999 and subsequent surveys (Carlsson et al., 2000a).
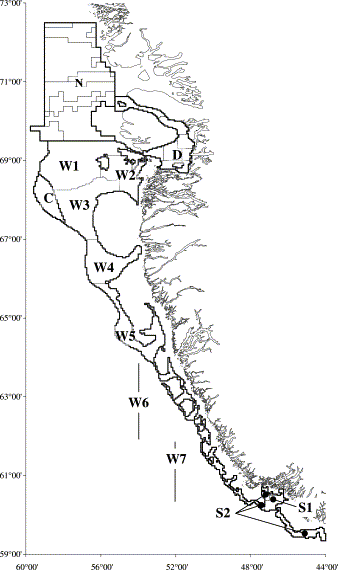
Study area and stratification for the West Greenland trawl survey for northern shrimp Pandalus borealis.
Regions and stratification of the West Greenland shrimp survey.
| Region | Description | No. of areas | Depth sub-stratification | Total area (km2) |
|---|---|---|---|---|
| N | Offshore waters from 69°30′N to 72°30′N, from the coast to 59°W | 9 | No | 38 517 |
| D | Inshore waters of Disko Bay and Vaigat, lying roughly between 68°45′N and 70°40′N | 9 | No | 9 364 |
| W | Offshore waters from 150 m to 600 m deep, east of the dividing line, from 69°30′N south and east to 48°20′W at about 60°25′N | 7 | Yes | 66 853 |
| C | Greenlandic continental shelf waters to 600 m deep west of the dividing line with Canada, near 68°N; contiguous with region W | 2 | Yes | 3 442 |
| S | Southern offshore waters from 150 to 600 m deep, east of 48°20′W, south of about 60°25′N, south and east to 44°00′W at about 59°15′N | 2 | No | 6 519 |
| Region | Description | No. of areas | Depth sub-stratification | Total area (km2) |
|---|---|---|---|---|
| N | Offshore waters from 69°30′N to 72°30′N, from the coast to 59°W | 9 | No | 38 517 |
| D | Inshore waters of Disko Bay and Vaigat, lying roughly between 68°45′N and 70°40′N | 9 | No | 9 364 |
| W | Offshore waters from 150 m to 600 m deep, east of the dividing line, from 69°30′N south and east to 48°20′W at about 60°25′N | 7 | Yes | 66 853 |
| C | Greenlandic continental shelf waters to 600 m deep west of the dividing line with Canada, near 68°N; contiguous with region W | 2 | Yes | 3 442 |
| S | Southern offshore waters from 150 to 600 m deep, east of 48°20′W, south of about 60°25′N, south and east to 44°00′W at about 59°15′N | 2 | No | 6 519 |
Regions and stratification of the West Greenland shrimp survey.
| Region | Description | No. of areas | Depth sub-stratification | Total area (km2) |
|---|---|---|---|---|
| N | Offshore waters from 69°30′N to 72°30′N, from the coast to 59°W | 9 | No | 38 517 |
| D | Inshore waters of Disko Bay and Vaigat, lying roughly between 68°45′N and 70°40′N | 9 | No | 9 364 |
| W | Offshore waters from 150 m to 600 m deep, east of the dividing line, from 69°30′N south and east to 48°20′W at about 60°25′N | 7 | Yes | 66 853 |
| C | Greenlandic continental shelf waters to 600 m deep west of the dividing line with Canada, near 68°N; contiguous with region W | 2 | Yes | 3 442 |
| S | Southern offshore waters from 150 to 600 m deep, east of 48°20′W, south of about 60°25′N, south and east to 44°00′W at about 59°15′N | 2 | No | 6 519 |
| Region | Description | No. of areas | Depth sub-stratification | Total area (km2) |
|---|---|---|---|---|
| N | Offshore waters from 69°30′N to 72°30′N, from the coast to 59°W | 9 | No | 38 517 |
| D | Inshore waters of Disko Bay and Vaigat, lying roughly between 68°45′N and 70°40′N | 9 | No | 9 364 |
| W | Offshore waters from 150 m to 600 m deep, east of the dividing line, from 69°30′N south and east to 48°20′W at about 60°25′N | 7 | Yes | 66 853 |
| C | Greenlandic continental shelf waters to 600 m deep west of the dividing line with Canada, near 68°N; contiguous with region W | 2 | Yes | 3 442 |
| S | Southern offshore waters from 150 to 600 m deep, east of 48°20′W, south of about 60°25′N, south and east to 44°00′W at about 59°15′N | 2 | No | 6 519 |
2 Methods
Buffered random sampling was implemented for the West Greenland shrimp survey in 1999 (Carlsson et al., 1999). Stations were allocated to strata based on the stratum area and on predictions, from past surveys, of the variability in catch. The allocation was algorithmically optimized to give the lowest standard error of the total survey biomass estimate given the predicted stratum variances.
Systematic sampling – placing sample units equal distances apart (Bellhouse and Rao, 1975) – is statistically efficient for autocorrelated populations (Cochran, 1977). It is also operationally convenient. It is readily applied in surveying large areas at a uniform sampling density, and for such surveys it is frequently preferred to random placement of sampling units. It is the usual design basis for transect surveys, both aerial and ship-borne. However, systematic design is operationally inconvenient to apply to stratified point-station surveys if the strata are based on a habitat mosaic – and are therefore of irregular shapes – while the target sampling density varies from stratum to stratum and induces corresponding changes in the scale of a sampling grid.
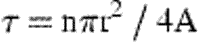
To select station positions for the West Greenland shrimp survey, the survey area was divided into small elements, 1/32 of a degree of latitude by 1/12 of a degree of longitude (roughly a 2-n.mi. square). A 30-min trawl station is about 1.5 n.mi. long, so one trawl station could be placed in a selected element. The elements in the entire study area, and in a margin around it, were placed in a single list in random order.
For each stratum in order, the selection procedure was as follows. A buffering distance was set equal to √2 times the diameter of a circle of area equal to the stratum area divided by the required number of stations (equivalent to a packing intensity τ of 0.5). The elements in each stratum were considered in the random order into which they had been placed. Each successive element was rejected from the sample if it was closer than the buffering distance to a previously selected element, either in the current stratum or in a stratum already dealt with. So that there would not be a bias toward selecting stations close to the boundaries of the stratum, elements in a suitable margin outside the stratum were also considered in the sample selection process. Elements selected in this margin were not counted in the sample, but were held as temporary buffering stations, so that the stratum boundary should be invisible to the process of selecting elements.
When the required number of stations in the stratum had been found, sampling stopped, and the process went on to the next stratum. The sample stations within the stratum were retained, but elements selected as temporary buffering stations in the margin around the stratum were deleted before proceeding.
If the required number of stations within the stratum was not found by the time all the elements had been considered, the selection for the stratum was cancelled, the buffering distance was reduced by 10%, and another attempt was made.
The distance between two stations that were in adjacent strata had to be greater than the buffering radius appropriate to the stratum that was sampled, the later of the two. In strata with small buffering radii, stations could be expected to lie close to the stratum boundary – on average, within half a buffering radius. If a stratum with a low density of stations, and therefore a large buffering radius, was considered after a neighbouring stratum with a smaller buffering radius, many elements close to its edge would be close to the already-selected stations in the neighbouring stratum and could not be selected, leading to a sampling bias (Figure 2a). Therefore, strata were sampled in increasing order of sampling density. In this way, any neighbouring stratum that had already been sampled would have a larger buffering radius and would not bias station selection in neighbouring strata sampled later (Figure 2b). Because buffering distances were observed not only within strata, but also between stations in adjacent strata, the precision not only of individual stratum results, but also of the overall survey, was expected to be enhanced.
Buffered sampling in contiguous strata with different sampling densities: (a) densely sampled stratum before sparsely sampled stratum; sampling in the sparse stratum is biased against regions close to the interface; and (b) sampling the low-density stratum first; subsequent sampling in the high-density stratum is unbiased. (Open symbols: buffering points; filled symbols: sample points; circles: sampling for the high-density stratum; triangles: sampling for the low-density stratum.)
Stratum biomass estimates were based on the unweighted mean biomass density for all the stations in the stratum. No weightings were applied based on tesselation areas or variograms. This simplified the calculation of appropriate standard errors.
The standard error of the estimate was calculated by two methods. One was the standard expression based on the sum of squares of deviations from the sample mean. The other was based on near-neighbour differences. “Near neighbours” were defined as those joined by the links in a Delaunay triangulation of the sample. An estimate of error variance was based on the sum of squares of differences between catches at “near neighbours”, and compared with the result of the conventional expression based on the sum of squares of deviations from the mean.
3 Discussion and results
Sampling from structured populations is a recurring problem. Three approaches are often considered and compared. These are simple random sampling, stratified random sampling, and systematic sampling. For populations in which the structure takes the form of autocorrelation, with an autocorrelation function that is everywhere concave upwards, it is concluded that systematic sampling is an acceptable technique, and more precise than random sampling. (e.g. Quenouille, 1947; Blight, 1973; Jessen, 1978).
The exact statistical properties of buffered random sampling are intractable, especially when it is applied to irregular areas. In one dimension, buffered random sampling on a closed loop is unbiased, because the probability of any set of distances between members of the sample is independent of the orientation of the sample with respect to the loop, so all points have equal probability of being selected. This extends to two dimensions, so buffered random sampling on the surface of a sphere is unbiased: a sampling design, defined as a set of distances between sample points, will be selected with a probability that is independent of its orientation with respect to the sphere. All points have equal probability of being selected in any design considered alone, and therefore in all designs considered together. By extension again, buffered random sampling on an infinite sphere, and therefore on an infinite plane, are unbiased.
However, when sampling from a finite population, bias is possible. Points near the ends or edges of a bounded finite population have fewer neighbours, and as sampling proceeds they are less likely to be inhibited than points in the interior of the population. Therefore, in a naiı̈ve application of buffered random sampling from a bounded population, there will be a point-selection bias toward points on or near the ends or edges of the sampled area, and a bias against points that are about one buffering distance away from the edges. This bias is difficult to estimate quantitatively, especially when sampling from an area of irregular shape. However, it appears from simulations that this edge-related bias decays within about twice the buffering distance from the edges of a bounded sampling area.
In applying buffered random sampling to any given stratum in the West Greenland shrimp survey, a margin around the stratum, with a minimum width of twice the buffering distance, was included in the area being sampled. The sampling bias related to the edge of the sampling area, which was thus made sufficiently larger than the stratum, therefore took effect only outside the stratum and the sample in the stratum was unbiased.
There is another source of bias, which is a feature of systematic sampling, and which affects buffered random sampling when, owing to a high packing intensity, it tends toward systematic sampling. Large samples are easier to fit into a stratum if they contain points near its edge, and if by chance a buffered random sample contains few edge points, the sampling process may terminate before a sample of the required size has been found. This failure is more likely if the target packing intensity is high.
The resulting bias depends on how this problem is resolved. If the process were terminated and the incomplete sample used, larger samples would tend to contain edge points, but smaller samples would contain inefficient points distant just less than one buffering radius from the edge. Edge points would on average be associated with larger samples, and would therefore, on average, be under-weighted in estimations.
If, on the contrary, incomplete samples were rejected and the process restarted over and over again at the same packing intensity until a sample of the required size was finally obtained, resulting designs would tend to include more edge points, because such designs would be easier to squeeze into the stratum. There would then be a bias toward edge points, associated with well-fitting designs, and away from points that were just less than one buffering distance from the edge, associated with inefficient designs that fitted badly into the stratum.
This design-selection bias is a feature of systematic sampling, but has not usually been considered a reason to reject systematic sampling. It affects buffered random sampling when a high packing intensity, which causes it to approximate systematic sampling, is used. It cannot be avoided by including a margin round the stratum in the area to be sampled. It could be avoided by using a packing intensity of 0.3023 or less, which would guarantee success first time, but this small packing intensity would produce rather random designs and would partly forgo the expected advantages of buffered sampling. It would not avoid the point-selection bias towards edge points due to their having fewer neighbours, and a margin around the stratum would still be necessary during the sampling process.
In applying buffered random sampling to the West Greenland survey, sampling in each stratum was started at a target packing intensity of 0.5, which was found to give about a 70% chance of success first time in a given stratum. If a sampling attempt in a stratum was unsuccessful, the incomplete sample was rejected. The packing intensity was reduced before trying again – so the sampling was shifted in the direction of greater randomness – but the same random ordering of sampling elements was retained. The reduction was effected in moderately large steps, rather than nibbling away until a design could be squeezed into the stratum. This did not completely avoid design-selection bias, which is associated with any non-zero probability of failure on the first round, so points near the edges of the survey area and of individual strata are slightly over-weighted in these results.
It was expected that biomass density would be estimated more precisely by using buffered random sampling as a consequence of reducing the average correlation between stations relative to random sampling. If two unbiased estimates (say xi and xj) have common variance of estimation σ2 and correlation r, the overall estimate – the mean of xi and xj – has error variance σ2(1+r)/2. For n such estimates, the true error variance of their mean is 
or 
where r̄ is the average pairwise correlation coefficient between the n estimates. The efficiency of a sample survey can be compromised by positive correlation between sample members, especially if samples are large, and significant gains in precision can be expected if the average correlation can be reduced.
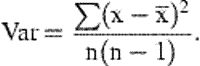
The expectation of this estimate is 
where r̄ is the expected average pairwise correlation between sample members. While positive correlation between sample members makes a survey less precise in reality, it causes it to appear more precise as measured by its conventionally calculated standard error. If the average positive correlation between members of an (unbiased) sample can be reduced by changing the sampling method, the survey can be expected to become more precise – but this will not be apparent from standard expressions for calculating error variance.
Compared with complete spatial randomness at a given sampling intensity, buffered random sampling reduces the frequency of small distances between stations and increases the frequency of moderate distances between stations. The average frequency of large distances between stations only depends on the mean sampling density and is not affected. Catches of northern shrimp at stations that are close to one another are positively correlated (Carlsson et al., 2000b; Kingsley et al., 2002). By reducing the frequency of positively correlated close neighbours relative to CSR, buffered random sampling is expected to reduce the average positive correlation between sample members and improve the precision of survey estimates of biomass.
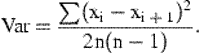
This estimate tends toward unbiasedness as the serial autocorrelation tends to zero and the population becomes random. It overestimates the error in systematic samples if the population has positive autocorrelation. If this serial-difference method were applied to an independent random sample from a serially correlated population, the resulting estimate of error variance would be incorrect and biased downwards: it is less than the estimate based on all paired differences, which for random samples is known to be unbiased. Therefore, a serial-difference method of estimating error variance should be applied with caution if sampling is not systematic or nearly so.
Sampling designs may have a primary objective of estimating a parameter of the target population as precisely as possible, with the estimate of its true precision subordinated to this. An alternative priority may be that an unbiased estimate of the precision must be ensured even at some cost in precision itself. In the context of fishery resource assessments, little formal use is made of estimated standard errors, while the behaviour of time-series of annual survey results is invariably seen as important. Consequently, for this application, greater emphasis should be placed on precise estimation; unbiased estimates of true precision are less important.
For large samples in strata that had regular shapes, neither very elongated nor disjunct, buffered random sampling in 1999 reduced the frequency of closely spaced pairs of stations (Figure 3), increased nearest-neighbour distances, and gave a more regular triangulation, as compared with CSR sampling.
Sampling designs with Delaunay triangulations for stratum W1, 300–400 m depth, in 1998 by manually adjusted random sampling and in 1999 by buffered random sampling, with a 24-station CSR sample for comparison.
Previous surveys, up to 1998, had nominally used CSR sampling, although stations had been manually adjusted if they were too close to another. In the 1998 survey, small distances between stations were on average associated with smaller differences between catch rates (Figure 4). However, the statistical effect of buffered sampling in 1999 as compared with the 1998 design did not appear to be large, as few closely spaced pairs of stations had been retained in the earlier year. The distribution of nearest-neighbour distances in the 1998 survey was intermediate between that obtained in a CSR design and that given by a buffered random design (Figure 5).
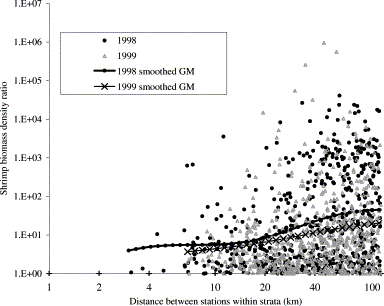
Biomass density ratio vs. distance between stations, within strata, in the West Greenland shrimp survey.
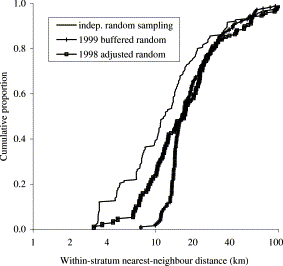
Cumulative distribution of nearest-neighbour distances within strata in the West Greenland shrimp survey in 1998 (manually adjusted random sampling) and in the 1999 design (buffered sampling) compared with completely random sampling.
The standard error calculated from the mean squared difference between the catch densities at “near neighbours” was not consistently less than the value obtained from the conventional method based on squared deviations from the sample mean. Reasons for this include
- –
distance between stations is not closely related to difference in biomass densities, except at the small distances that are removed from the design by the use of buffered sampling (Figure 4);
- –
some strata in this survey are very elongated or disjunct and have extended perimeters relative to their areas. The final sampling pattern in such strata is often far from systematic, and Delaunay triangulations in such strata defined pairs of “near neighbours” that were often not close together (see e.g. Figure 6).
- –
many strata had few (e.g. 3 or 4) stations, and then all were “near neighbours” to all the others and the two expressions were equivalent.
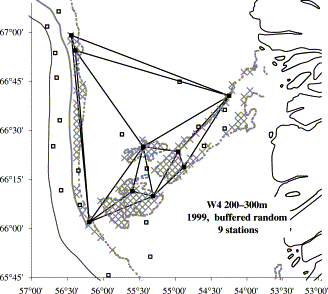
Sampling design with Delaunay triangulation for buffered random sampling from a disjunct stratum, W4, 200–300 m depth.
For the few strata that were large and coherent and had reasonably large numbers of stations, so that the buffered sampling design gave a uniform triangulation with numerous links of approximately equal length, the standard deviation estimated from nearest-neighbour differences was usually less than that estimated from the conventional expression (Table 2).
Stratum standard deviation of biomass density from buffered random samples, estimated from near-neighbour differences obtained from Delaunay triangulation and from deviations from the sample mean, for coherent strata with seven or more stations in the West Greenland shrimp survey in 1999 and 2000.
| Biomass density s.d. (t/km2) calculated from | ||||
|---|---|---|---|---|
| Year | Stratum | No of stations | (n) Near-neighbour differences | Deviations from the sample mean |
| 1999 | W1, 300–400 m | 24 | (59) 1.395 | 1.949 |
| 1999 | W2, 200–300 m | 7 | (12) 3.927 | 4.153 |
| 1999 | W3, 200–300 m | 14 | (34) 1.495 | 1.733 |
| 2000 | S1 | 16 | (40) 9.643 | 11.097 |
| 2000 | W1, 300–400 m | 11 | (25) 6.410 | 6.191 |
| 2000 | W3, 200–300 m | 11 | (24) 13.085 | 14.250 |
| Biomass density s.d. (t/km2) calculated from | ||||
|---|---|---|---|---|
| Year | Stratum | No of stations | (n) Near-neighbour differences | Deviations from the sample mean |
| 1999 | W1, 300–400 m | 24 | (59) 1.395 | 1.949 |
| 1999 | W2, 200–300 m | 7 | (12) 3.927 | 4.153 |
| 1999 | W3, 200–300 m | 14 | (34) 1.495 | 1.733 |
| 2000 | S1 | 16 | (40) 9.643 | 11.097 |
| 2000 | W1, 300–400 m | 11 | (25) 6.410 | 6.191 |
| 2000 | W3, 200–300 m | 11 | (24) 13.085 | 14.250 |
Stratum standard deviation of biomass density from buffered random samples, estimated from near-neighbour differences obtained from Delaunay triangulation and from deviations from the sample mean, for coherent strata with seven or more stations in the West Greenland shrimp survey in 1999 and 2000.
| Biomass density s.d. (t/km2) calculated from | ||||
|---|---|---|---|---|
| Year | Stratum | No of stations | (n) Near-neighbour differences | Deviations from the sample mean |
| 1999 | W1, 300–400 m | 24 | (59) 1.395 | 1.949 |
| 1999 | W2, 200–300 m | 7 | (12) 3.927 | 4.153 |
| 1999 | W3, 200–300 m | 14 | (34) 1.495 | 1.733 |
| 2000 | S1 | 16 | (40) 9.643 | 11.097 |
| 2000 | W1, 300–400 m | 11 | (25) 6.410 | 6.191 |
| 2000 | W3, 200–300 m | 11 | (24) 13.085 | 14.250 |
| Biomass density s.d. (t/km2) calculated from | ||||
|---|---|---|---|---|
| Year | Stratum | No of stations | (n) Near-neighbour differences | Deviations from the sample mean |
| 1999 | W1, 300–400 m | 24 | (59) 1.395 | 1.949 |
| 1999 | W2, 200–300 m | 7 | (12) 3.927 | 4.153 |
| 1999 | W3, 200–300 m | 14 | (34) 1.495 | 1.733 |
| 2000 | S1 | 16 | (40) 9.643 | 11.097 |
| 2000 | W1, 300–400 m | 11 | (25) 6.410 | 6.191 |
| 2000 | W3, 200–300 m | 11 | (24) 13.085 | 14.250 |
The design laid out for the West Greenland bottom-trawl survey – like many others – is not always exactly followed. Stations are sometimes omitted or moved, usually because the selected fishing grounds do not permit trawling with a large, heavy offshore shrimp trawl. Stations omitted are often omitted in clusters, and stations that are moved may converge on restricted areas of good trawlable bottom. Such departures from a design that was originally regular tended to increase the aggregation of station positions, and often produced a greater number of closely spaced neighbours than the design originally contained. In such circumstances using nearest-neighbour differences may under-estimate standard errors. It was concluded that we should continue to estimate standard errors using the conventional expression based on deviations from the sample mean.
Data from the West Greenland survey show that small distances between stations tend to be associated with small differences in density (Kingsley et al., 2002), and as the use of buffered sampling reduces the occurrence of small distances (Figure 5), buffered sampling is expected to give more precise survey estimates than random sampling.
The present design of the West Greenland shrimp survey uses a total of 53 strata, ranging in area from 12 000 km2 down to about 240 km2. This stratification has been used to control the spatial distribution of stations and is now used in an optimal allocation routine based on past variability in the stratum. Having so many strata may not yield large gains in survey precision (Folmer and Pennington, 2000). It is normally considered that having more than about six strata produces little benefit (Cochran, 1977), and a habitat-based stratification scheme did not improve precision in groundfish surveys on the Scotian shelf (Gavaris and Smith, 1987). Within the survey strata in the West Greenland survey the standard deviation of catch per tow is on average as large as the stratum mean. Buffered sampling could permit survey strata to be pooled into larger units, while still ensuring an even distribution of stations.
In the design of fishery resource surveys, systematic sampling is sometimes used, such as the rectangular station grid that has been used in the Norwegian trawl survey in the Barents Sea (Aschan, 2000). When systematic surveys are repeated in succeeding years, it is common practice to repeat the same station positions, because systematic sampling gives such uniform coverage that the survey designer typically feels that there is no good reason for selecting a new design every year. Survey stations based on CSR sampling can be fixed from year to year, but fixing station positions is in practice so closely associated with systematic sampling that in fisheries survey parlance, “fixed stations” is often used when “systematic sampling” is meant (see e.g. Deriso et al., 1998).
If station catches are correlated from year to year, fixing the positions of some or all of the stations can improve estimates of total biomass and of the change of biomass from year to year (Patterson, 1950). In connection with the implementation of buffered random sampling, 50% of the stations were fixed. Catches at fixed stations were found to be correlated from year to year, and we expect to discuss the size of these correlations and the effect of fixing stations on the properties of the series of survey biomass estimates in a later article.
4 Conclusion
Buffered random sampling is an advantageous method of placing stations for surveys of fishery resources. With appropriate algorithms for selecting station positions, it avoids the worst defects of designs obtained by independent random sampling, in particular the occurrence of closely spaced pairs of stations, and it makes an approximation to systematic sampling available for stratified surveys with sampling intensity variable between strata. It is more efficient than independent random sampling. When applied to sampling in a survey for northern shrimp, in which densities are apparently correlated only at short distances, its statistical effects appear to be small.
A great advantage of using buffered random sampling is that because it approximates systematic sampling, fixed station positions can be used. In the West Greenland shrimp survey, fixed stations have significant statistical advantages for detecting biomass changes between years. Within strata, catches at fixed stations were well correlated between years, and a stratified analysis of the year-to-year differences by station significantly enhanced the ability of the survey to measure change in stock biomass.
Appendix A
Sum of squared pairwise differences identical to the standard corrected sum of squares
