-
PDF
- Split View
-
Views
-
Cite
Cite
E. Rodríguez-Marín, H. Arrizabalaga, M. Ortiz, C. Rodríguez-Cabello, G. Moreno, L.T. Kell, Standardization of bluefin tuna, Thunnus thynnus, catch per unit effort in the baitboat fishery of the Bay of Biscay (Eastern Atlantic), ICES Journal of Marine Science, Volume 60, Issue 6, 2003, Pages 1216–1231, https://doi.org/10.1016/S1054-3139(03)00139-5
Close - Share Icon Share
Abstract
Relative indices of abundance by age class for bluefin tuna from 1975 to 2000 were estimated using generalized linear mixed models. Age class was included as a fixed factor within the model specifications, with the Year×Age interaction as a fixed factor component in order to obtain annual indices by age. Catch and effort data on bluefin tuna were available from two sources, catches by trip, and daily catches from logbooks. Catches were modelled using the delta-lognormal model. The model finally selected included the following explanatory factors: Year, Age, Year×Age, Month, number of Crew, number of Bait Tanks, and with the Year×Month interaction as a random component. Overall, year trends and coefficients of variation were similar from both datasets by age class. In general, the standardization procedure showed that vessel characteristics and technological advances related to fishing have a relatively minor explanatory effect on the observed catch rates of bluefin tuna in the fishery. Neither geographical distribution nor type of bait had an explanatory effect on the observed catch rates. The 1994 cohort stands out as an exceptionally large year class; it can be followed through the standardized series. This standardized catch rate index at age of bluefin tuna is the most complete yet available and is the only one currently used for juvenile fish in calibrating population models to evaluate the Eastern Atlantic and Mediterranean stock. It is particularly valuable because, apart from improvements in electronic technology, there are no changes in the method of exploitation during the entire series.
Introduction
Bluefin tuna (Thunnus thynnus) are much in demand commercially owing to a strong market for the species in Japan. The demand has led to a considerable increase in catches in the Mediterranean in the past two decades. The International Commission for the Conservation of Atlantic Tunas (ICCAT) currently assumes the existence of two discrete stock units: in the Western and in the Eastern Atlantic, the latter including the Mediterranean Sea. Recent (1998–2000) reported landings for the Eastern Atlantic and Mediterranean Sea are around 35 000 t, but “unreported catches seem to be high”, leading ICCAT scientists to express concern about potential overexploitation (Anon., 1999, 2001, 2003).
The Eastern stock spawns in the Mediterranean Sea (Richards, 1976), generally between June and July (Piccinetti and Piccinetti-Manfrin, 1970; Dicenta and Piccinetti, 1978; Garcia et al., 2002). Once spawning has finished, some of the adults leave the Mediterranean and migrate to their feeding areas between the northwestern coast of Africa and Cape Verde in the south, and the coast of Norway in the north, even making trans-Atlantic migrations (Rodríguez-Roda, 1964; Sarà, 1973; Cort, 1990; Mather et al., 1995; Block et al., 2001). Some 0-year-old tuna also leave the Mediterranean and winter along the Atlantic coast of Morocco until, on attaining age 1 the next summer, they migrate into the Bay of Biscay, before returning to Moroccan waters in autumn. Tuna make these trophic migrations up to an age of 4 or 5 years (Aloncle, 1964; Cort, 1990; Mather et al., 1995), and the migratory behaviour means that different age classes are vulnerable to exploitation by many different gears of the Spanish fleet. Spawners are caught by traps and baitboats in waters around the Strait of Gibraltar during their spawning migration into the Mediterranean, as well as on their return trophic migration out of the Mediterranean. They are also caught by longline and purse-seine between the Balearic Islands and the Iberian Peninsula. Juvenile tuna are caught by baitboats in the Bay of Biscay.
Baitboat catches of bluefin tuna in the Bay of Biscay are dominated by fish of 70–140 cm fork length (1–5 years of age); specimens around 80 cm (2 years of age) are the most abundant in the catch. This has allowed the development of a nominal catch per unit effort (cpue) index (of age class 2), that has been used as a relative abundance index for juvenile bluefin tuna of the Eastern stock (Cort and Bard, 1980; Cort, 1995; Anon., 1999).
The Standing Committee for Research and Statistics of ICCAT assesses the status of the Eastern Atlantic stock of bluefin tuna through virtual population analysis (VPA ADAPT), a procedure that is calibrated to a set of indices of relative abundance. These cpue series include: the Spanish baitboat fishery of the Bay of Biscay, the Spanish trap index in the Atlantic, the French purse-seine index in the Mediterranean, and the Japanese longline index in the eastern Atlantic and Mediterranean. Of these series, only the Spanish baitboat index is not standardized. The assessment session for this stock in 1998 concluded that cpue indices caused large uncertainty in the results of the ADAPT VPA analyses (Anon., 1999).
The main objective of the current work is to understand the influence of factors related to fishing practice on catch rate (cpue), and then to standardize the index of cpue of bluefin tuna by age for the baitboat fishery in the Bay of Biscay. To this end it was necessary to use new information, additional to and different from that used to date, in order to obtain the nominal index of age 2 bluefin tuna. New catch and effort data on bluefin tuna from two sources were used in this study: catches by trip from port landings, and daily catches from logbooks. The processing of these two relational databases, together with a revision of fleet characteristics, permitted changes in fishing power to be taken into account in the cpue indices from 1975 to 2000.
The fishery
The bluefin tuna baitboat fishery of the Bay of Biscay takes place from June to October in the southeast corner of the Bay, 43–47°N, 2–6°W, near the coast (Figure 1). Bluefin tuna are caught by a specialized fleet based mainly in the port of Hondarribia (Fuenterrabía), although since 1996 some boats from the port of Getaria (Guetaria) also target the species early in the fishing season. The catches at these two ports constitute more than 80% of the total bluefin tuna catch in the Bay of Biscay. The balance is from incidental troll and baitboat fishing for albacore, Thunnus alalunga, in the Cantabrian Sea.
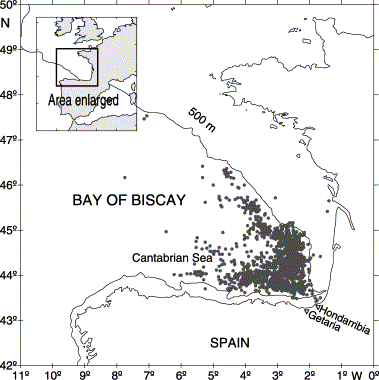
The study area, and bluefin tuna fishing locations based on logbook data.
For baitboat fishing, live bait is caught at dusk by purse-seine in shallow waters near the coast, e.g. in bays and off beaches. The bait is collected with brailers and loaded into tanks subjected to continuous water circulation. Horse mackerel (Trachurus trachurus), bogue (Boops boops), sardine (Sardina pilchardus), and anchovy (Engraulis encrasicholus) are the preferred bait species for bluefin tuna. Horse mackerel is considered “best”, because it survives best in tanks and because, when cast into the water, it does not swim away, but hides under the shadow of the boat, enticing the tuna to feed close to the boat.
Fishing is with single rods for tuna <10 kg, and with rods supported at the top by a cable leading to a pulley on the boat for larger tuna. This system permits the use of long rods (5 m), but it requires two fishers, one handling the rod and one pulling on the pulley cable. For bluefin >30 kg, the pulley cables are doubled, each cable requiring one or two operators (Cort, 1990). The fishing procedure consists of attracting the bluefin tuna schools to the side of the boat with live bait, and then, when the fish are nearby, spraying a water-jet curtain over the water surface in an attempt to hide the rods and the vessel and simulating a school of small fish splashing at the surface. The rods are then lowered and fishing begins. During the fishing operation the vessel follows the movement of the bluefin tuna using a special slow-ahead gear introduced into the fleet at the beginning of the 1970s. Schools are located by watching for signs of their presence, including sightings of tuna as well as the proximity of birds or whales in areas of krill. Since the mid-1970s, sonar has been used in addition to these traditional methods of detection.
Material and methods
Databases
Catch and effort data for the bluefin baitboat fishery in the Bay of Biscay were collected from the ports of Hondarribia and Getaria between 1975 and 2000. Data from the port of Hondarribia were collected from landing returns, and logbooks were used to check the number of fishing days (excluding days of bad weather and time employed in bait fishing). Information from the port of Getaria was collected by port agents, through interviews. The information collected for each vessel included: date of landing, number of specimens by commercial category, and number of fishing days. This database represents almost a census of landings by trip and vessel during the study period. In all, 7545 trips (22 303 fishing days) are included in the database. Each trip lasted one to seven fishing days, with an average of three days. The mean number of days per trip remained practically constant throughout the study period, though with a slightly declining trend. The mean number of trips by boat and year was 10, generally varying between 6 and 17 (the maximum for the study period was 30), depending on the duration of the fishing season and the number of days of inclement weather.
A review of the catch by boat and year shows that, from 1975 to 2000, 78 different boats caught bluefin tuna in the baitboat fishery. Of these, 37 generated 5 or more years of consecutive catches. The subset of 37 boats accounts for up to 92% of the total cumulative catch (Figure 2). In terms of fishing skippers, 82 different ones were identified in the database from 1975 to 2000, of which 48 had 5 or more years with consecutive catches of bluefin tuna. Those 48 skippers accounted for 94% of the cumulative catch. As a test, a criterion of skippering for 5 or more years of the catch history in the time-series was used for data selection. Applying that criterion also restricted the data to those skippers that accounted for most of the cumulative catch of bluefin tuna. Avoiding vessels that worked opportunistically tended to remove the variation most likely associated with “learning the fishery”, i.e. gaining skippering experience.
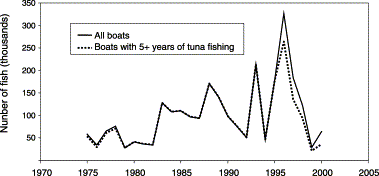
Annual catch of baitboats with 5 or more years of bluefin catch, compared with the total catch of the entire baitboat fleet from 1975 to 2000.
Information on daily catch and effort was obtained from logbooks supplied by baitboat skippers. Logbook data were available from 1987 to 2000 and provided the following information on a daily basis: name of vessel, date of capture, position of catch (latitude and longitude), number of specimens by commercial category, type of bait used, and sea surface temperature. For standardization purposes when data from several positions on the same day were available, the position and the temperature were averaged, and catches were totalled to obtain the daily cpue. In all, 4346 records were collected, 2573 being daily data.
Conversion from commercial catch category to catch at age
Catches of bluefin tuna at the ports of Hondarribia and Getaria were available by number and detailed by weight (kg) category. Catch by commercial category was converted to catch at age by applying age–length keys to the length distributions by commercial category and season. At Hondarribia, each category was sampled monthly at the market to obtain a length distribution. The average number of samples per month and category throughout the study period was 4.9. At Getaria, sampling was by baitboat, but the frequency was similar, namely 5.6. Length was measured as fork length (FL) to the nearest centimetre below. Measurements of 86 332 bluefin tuna were used, representing an annual average of 4.4% of the total number used in standardization.
Seasonal age–length keys were applied to length distributions. This method was used because catch at age estimated using age–length keys based on reading of spines was equivalent to that obtained by length frequency analysis (Rodríguez-Marín et al., 2001). The procedure for reading spine sections was that described by Cort (1991). Seasonal age–length keys by 5-cm length class for each year were used. The mean seasonal age–length key for the period 1985–2000 was used for each of the years 1975–1984, because systematic spine sampling had not been carried out for those years. The number of spines, the mean FL, and the standard deviation at age by season is summarized in Table 1.
Number of spines, mean fork length (FL, cm), and the standard deviation (s.d.) at age by season.
| . | Value at age . | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parameter . | 1 . | 2 . | 3 . | 4 . | 5 . | 6 . | 7 . | 8 . | 9 . | All ages . |
| Spring | ||||||||||
| Total number | 52 | 178 | 103 | 21 | 15 | 11 | 5 | 1 | 1 | 387 |
| Mean FL (cm) | 58.3 | 77.8 | 96.7 | 121.2 | 144.5 | 162.0 | 168.0 | 182 | 192 | |
| s.d. | 2.2 | 4.1 | 6.4 | 10.7 | 7.9 | 8.8 | 9.7 | |||
| Summer | ||||||||||
| Total number | 650 | 980 | 884 | 708 | 465 | 198 | 81 | 28 | 17 | 4011 |
| Mean FL (cm) | 61.3 | 80.4 | 100.6 | 122.5 | 144.7 | 160.1 | 170.7 | 181.8 | 191.7 | |
| s.d. | 4.5 | 6.8 | 8.0 | 10.0 | 9.0 | 10.0 | 9.4 | 6.8 | 6.7 | |
| Autumn | ||||||||||
| Total number | 533 | 499 | 376 | 200 | 64 | 3 | 1 | 1 | 0 | 1677 |
| Mean FL (cm) | 67.4 | 86.9 | 107.8 | 130.3 | 148.1 | 169.2 | 172 | 202 | ||
| s.d. | 4.1 | 8.6 | 8.0 | 11.0 | 8.8 | 8.3 | ||||
| . | Value at age . | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parameter . | 1 . | 2 . | 3 . | 4 . | 5 . | 6 . | 7 . | 8 . | 9 . | All ages . |
| Spring | ||||||||||
| Total number | 52 | 178 | 103 | 21 | 15 | 11 | 5 | 1 | 1 | 387 |
| Mean FL (cm) | 58.3 | 77.8 | 96.7 | 121.2 | 144.5 | 162.0 | 168.0 | 182 | 192 | |
| s.d. | 2.2 | 4.1 | 6.4 | 10.7 | 7.9 | 8.8 | 9.7 | |||
| Summer | ||||||||||
| Total number | 650 | 980 | 884 | 708 | 465 | 198 | 81 | 28 | 17 | 4011 |
| Mean FL (cm) | 61.3 | 80.4 | 100.6 | 122.5 | 144.7 | 160.1 | 170.7 | 181.8 | 191.7 | |
| s.d. | 4.5 | 6.8 | 8.0 | 10.0 | 9.0 | 10.0 | 9.4 | 6.8 | 6.7 | |
| Autumn | ||||||||||
| Total number | 533 | 499 | 376 | 200 | 64 | 3 | 1 | 1 | 0 | 1677 |
| Mean FL (cm) | 67.4 | 86.9 | 107.8 | 130.3 | 148.1 | 169.2 | 172 | 202 | ||
| s.d. | 4.1 | 8.6 | 8.0 | 11.0 | 8.8 | 8.3 | ||||
Number of spines, mean fork length (FL, cm), and the standard deviation (s.d.) at age by season.
| . | Value at age . | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parameter . | 1 . | 2 . | 3 . | 4 . | 5 . | 6 . | 7 . | 8 . | 9 . | All ages . |
| Spring | ||||||||||
| Total number | 52 | 178 | 103 | 21 | 15 | 11 | 5 | 1 | 1 | 387 |
| Mean FL (cm) | 58.3 | 77.8 | 96.7 | 121.2 | 144.5 | 162.0 | 168.0 | 182 | 192 | |
| s.d. | 2.2 | 4.1 | 6.4 | 10.7 | 7.9 | 8.8 | 9.7 | |||
| Summer | ||||||||||
| Total number | 650 | 980 | 884 | 708 | 465 | 198 | 81 | 28 | 17 | 4011 |
| Mean FL (cm) | 61.3 | 80.4 | 100.6 | 122.5 | 144.7 | 160.1 | 170.7 | 181.8 | 191.7 | |
| s.d. | 4.5 | 6.8 | 8.0 | 10.0 | 9.0 | 10.0 | 9.4 | 6.8 | 6.7 | |
| Autumn | ||||||||||
| Total number | 533 | 499 | 376 | 200 | 64 | 3 | 1 | 1 | 0 | 1677 |
| Mean FL (cm) | 67.4 | 86.9 | 107.8 | 130.3 | 148.1 | 169.2 | 172 | 202 | ||
| s.d. | 4.1 | 8.6 | 8.0 | 11.0 | 8.8 | 8.3 | ||||
| . | Value at age . | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parameter . | 1 . | 2 . | 3 . | 4 . | 5 . | 6 . | 7 . | 8 . | 9 . | All ages . |
| Spring | ||||||||||
| Total number | 52 | 178 | 103 | 21 | 15 | 11 | 5 | 1 | 1 | 387 |
| Mean FL (cm) | 58.3 | 77.8 | 96.7 | 121.2 | 144.5 | 162.0 | 168.0 | 182 | 192 | |
| s.d. | 2.2 | 4.1 | 6.4 | 10.7 | 7.9 | 8.8 | 9.7 | |||
| Summer | ||||||||||
| Total number | 650 | 980 | 884 | 708 | 465 | 198 | 81 | 28 | 17 | 4011 |
| Mean FL (cm) | 61.3 | 80.4 | 100.6 | 122.5 | 144.7 | 160.1 | 170.7 | 181.8 | 191.7 | |
| s.d. | 4.5 | 6.8 | 8.0 | 10.0 | 9.0 | 10.0 | 9.4 | 6.8 | 6.7 | |
| Autumn | ||||||||||
| Total number | 533 | 499 | 376 | 200 | 64 | 3 | 1 | 1 | 0 | 1677 |
| Mean FL (cm) | 67.4 | 86.9 | 107.8 | 130.3 | 148.1 | 169.2 | 172 | 202 | ||
| s.d. | 4.1 | 8.6 | 8.0 | 11.0 | 8.8 | 8.3 | ||||
Catch at age of the baitboat fishery for the period 1975–2000 included ages 1–9. Age determination of tuna more than 5 years old is difficult (Cort, 1991), but this did not represent a serious problem because the bulk of the catch was aged 1–4, 2-year-old tuna dominating the total catch. In terms of the catch at age through a fishing season, i.e. by month (Figure 3), age 1 tuna were more abundant in the Bay of Biscay at the end of the fishing season, from September to November, whereas catches of 2-year-olds were more abundant from June to August. Tuna aged 3 years were uniformly available throughout the year, but older tuna were caught mainly in summer.
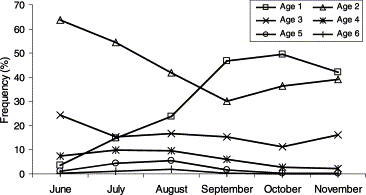
Mean proportion of the baitboat catch of bluefin tuna by age and month.
Vessel characteristics
The annual number of vessels operating throughout the study period remained constant at around 25, except between 1996 and 1998, when boats from Getaria entered the fishery. The fleet file was assembled from information derived from official fleet directories and two personal interviews with skippers, one in 1977 and another in 2001, which were aimed at updating major changes in vessel characteristics and use of instrumentation that could potentially modify catch rates. Information on the date of introduction of different technological improvements in the fleet was also collected from the companies offering such devices. As a generalization, monochrome sonar was introduced at the end of the 1970s, and technological advances were introduced almost simultaneously to the whole fleet throughout the study period.
The information by boat, for each year or fishing season, includes the name of the vessel, its home port, the year it was built, its horsepower (HP), its gross registered tonnage (GRT), its length, construction material, crew number (Crew), and number of bait tanks (Tank), the name of the skipper, the presence or absence of “gonio” (radio direction finder), and the number of the following devices: navigation radar, GPS, plotter, colour echo-sounder, monochrome sonar, and colour sonar. In order to include the different devices in a combined index in such a manner that they could be integrated in the GLM analysis as a single variable, three types of index were developed, each differing in the way that further devices of the same kind installed on each boat were evaluated. These combined indices are referred to as “improvement” indices (Rodríguez-Marín et al., 2002). Overall, the improvement index revealed that the baitboat fleet targeting bluefin tuna was homogeneous in terms of fishing instrumentation or electronics. However, there were differences in the technology of the fleet over the years, especially from 1978 onwards, when the number of technological devices increased progressively.
In order to categorize vessels into homogeneous groups that could account for differences in fishing power within the fleet, and in order to reduce the number of variables related to type of vessel to be included in the standardization model, two analyses were performed for data reduction purposes. Through principal components analysis, the variables that accounted for the highest percentage of the total variance for the main axis were identified for use later in cluster analysis. The variables GRT, HP, Length, Crew, and Tank were chosen to segment the fleet. A hierarchical cluster procedure was carried out using Euclidean metric distance (Sokal and Rohlf, 1962) as an index of similarity, and the aggregation algorithm unweighted pair-group average (Sneath and Sokal, 1973) was applied. From the baitboat fleet, a set of three clusters or boat types was selected (Table 2); they are described by Rodríguez-Marín et al. (2002). The variables GRT, HP, and Length defined three types of vessel. As the variables Crew (number) and Tanks (number of bait tanks) do not contribute many parameters to be estimated by the model, they were included in the standardization process without any grouping.
Mean and standard deviation (s.d.) of gross registered tonnage (GRT), horsepower (HP) and vessel length (m) for each cluster. The same values were calculated for the variables Crew (number of fishers) and Tank (number of bait tanks) for each cluster.
| . | GRT . | HP . | Length (m) . | Crew . | Tank . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Cluster . | Mean . | s.d. . | Mean . | s.d. . | Mean . | s.d. . | Mean . | s.d. . | Mean . | s.d. . |
| 1 | 155.1 | 38.5 | 1175.4 | 91.7 | 32.0 | 3.5 | 16 | 0.8 | 10 | 1.4 |
| 3 | 125.7 | 17.4 | 643.3 | 199.5 | 25.6 | 2.7 | 16 | 1.2 | 7 | 2.0 |
| 2 | 53.5 | 17.9 | 326.5 | 120.5 | 18.1 | 2.1 | 12 | 2.5 | 5 | 0.6 |
| . | GRT . | HP . | Length (m) . | Crew . | Tank . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Cluster . | Mean . | s.d. . | Mean . | s.d. . | Mean . | s.d. . | Mean . | s.d. . | Mean . | s.d. . |
| 1 | 155.1 | 38.5 | 1175.4 | 91.7 | 32.0 | 3.5 | 16 | 0.8 | 10 | 1.4 |
| 3 | 125.7 | 17.4 | 643.3 | 199.5 | 25.6 | 2.7 | 16 | 1.2 | 7 | 2.0 |
| 2 | 53.5 | 17.9 | 326.5 | 120.5 | 18.1 | 2.1 | 12 | 2.5 | 5 | 0.6 |
Mean and standard deviation (s.d.) of gross registered tonnage (GRT), horsepower (HP) and vessel length (m) for each cluster. The same values were calculated for the variables Crew (number of fishers) and Tank (number of bait tanks) for each cluster.
| . | GRT . | HP . | Length (m) . | Crew . | Tank . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Cluster . | Mean . | s.d. . | Mean . | s.d. . | Mean . | s.d. . | Mean . | s.d. . | Mean . | s.d. . |
| 1 | 155.1 | 38.5 | 1175.4 | 91.7 | 32.0 | 3.5 | 16 | 0.8 | 10 | 1.4 |
| 3 | 125.7 | 17.4 | 643.3 | 199.5 | 25.6 | 2.7 | 16 | 1.2 | 7 | 2.0 |
| 2 | 53.5 | 17.9 | 326.5 | 120.5 | 18.1 | 2.1 | 12 | 2.5 | 5 | 0.6 |
| . | GRT . | HP . | Length (m) . | Crew . | Tank . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Cluster . | Mean . | s.d. . | Mean . | s.d. . | Mean . | s.d. . | Mean . | s.d. . | Mean . | s.d. . |
| 1 | 155.1 | 38.5 | 1175.4 | 91.7 | 32.0 | 3.5 | 16 | 0.8 | 10 | 1.4 |
| 3 | 125.7 | 17.4 | 643.3 | 199.5 | 25.6 | 2.7 | 16 | 1.2 | 7 | 2.0 |
| 2 | 53.5 | 17.9 | 326.5 | 120.5 | 18.1 | 2.1 | 12 | 2.5 | 5 | 0.6 |
Analysis of catch rate
Relative abundance indices for bluefin tuna by age class were estimated using generalized linear mixed models (GLMM). Age class was included as a fixed factor within the model specification, with the Year×Age interaction as a fixed factor component, in order to obtain annual indices by age. This model specification was selected against standardization models for each age class independently, because the fishery operates on all available stock fractions, and age determination of the tuna landings is done after removal of the catch.
Trip database
For standardization analyses, nominal cpue was calculated as the number of fish of an age class caught per day of fishing. Nominal cpue distributions by age show typically highly skewed distributions, with a high proportion of low or zero cpues and very few high values. The proportion of positive cpues to the total number of trips (grouped by year, age, and month) was high for ages 1–5, but decreased rapidly for older fish (Figure 4). Ages 5–9 were therefore combined into a single age class (5+) to obtain a standardized cpue, because ages greater than 5 years contribute generally fewer than 1% of the catch by number. Given these data characteristics, we evaluated two distribution models that permit zero observations to be dealt with directly; delta and Poisson model distributions (Lo et al., 1992; Punt et al., 2000).
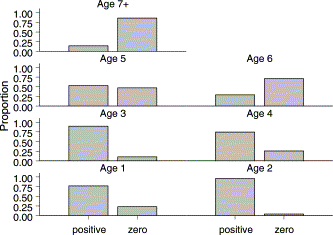
Proportion of zero and positive baitboat trips for bluefin tuna by age.
In the delta model, zero values are treated separately and non-zero catch rates are modelled using a lognormal distribution. The standardized index is the product of these two model-estimated components. Lognormal transformed frequency distributions of positive trips for each age class of bluefin tuna are shown in Figure 5. The estimated proportion of successful trips per stratum is assumed to be the result of consecutive Bernoulli-type realizations, which follow a binomial distribution. The logit function was used as a link between the linear factor component and the binomial error. For trips with bluefin tuna catches, estimated cpue was assumed to follow a lognormal error distribution of a linear function of fixed factors and random effect interactions, particularly when the year effect was within the interaction.
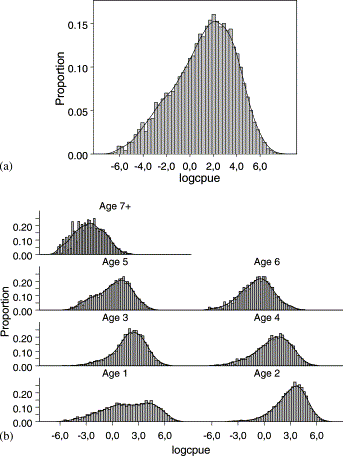
(a) Observed log cpue distribution of all ages of bluefin tuna combined, and (b) by age class.
Relative indices from the delta model formulations were calculated as the product of the Year×Age effect least square means (LSmeans) from the binomial and lognormal model components. The lognormal estimates of LSmeans used a weighted factor proportional to the number of observations in the input data to account for the unbalanced characteristics of the data. In addition, a bias correction was applied to the lognormal estimates, using the algorithm described by Lo et al. (1992). Analysis and model formulations for the delta model were done using the Glimmix and Mixed procedures from the SAS® statistical software package (SAS Institute Inc., 1997). In general, model evaluation and diagnosis was carried out through residual analysis (McCullagh and Nelder, 1989). For the delta models, diagnostic plots are presented for each model component. For the lognormal and binomial components, QQ-plots and Chi-squared residuals against year are presented for each age class, respectively.
A stepwise regression procedure was used to determine the set of systematic factors and interactions that significantly explained the observed variability in each model. A Chi-squared test was used to evaluate the statistical significance of an additional factor (McCullagh and Nelder, 1989). Further, the corresponding percentage of deviance explained by each factor relative to the maximum model was estimated to obtain a profile of the most important explanatory factors in the model. A statistically significant variable may, in some instances, be omitted from the model if the amount of variation explained by the variable is small in relation to the complexity that it adds (Stefánsson, 1996).
A preliminary analysis of deviance was performed on the aggregated data without the age classification, in order to derive a better understanding of the factors that significantly explained the observed variability prior to introducing the Year×Age interaction parameters. The final model included the Year, Age, and Year×Age fixed factors, plus a selection of other explanatory factors that explained at least 5% of the deviance percentage in the aggregated model. Once a set of fixed factors was specified, possible interactions were evaluated, in particular interactions between the Year effect and other factors. All Year interactions besides the Year×Age factor were considered as random. The significance of random interactions was evaluated using the Akaike information criterion (AIC), the Schwarz Bayesian criterion, and the Chi-squared test of the difference of the −2 log-likelihood statistic between successive nested model formulations (Littell et al., 1996).
Changes in fishing power of the fleet may lead to changes in catch rate, and therefore should be incorporated in the process of standardization (Hilborn and Walters, 1992; Salthaug and Godo, 2001). Cluster analysis for vessel characteristic and instrumentation, or combined indices of technological improvements, permitted this information to be introduced in the standardization of nominal cpue. These options required detailed information on vessel features/changes during the whole period. Another useful approach, particularly when vessel changes/modifications data are unavailable, is to remove the variability within each subject (i.e. vessel) from the overall variance in the model. It is common for the same vessel or vessel/skipper unit to have “similar” catch rates from year to year, so in-vessel variability may be considered random. In this case, nominal cpue series may be considered as repeated measures by the same sampling unit or subject (i.e. the vessel or vessel/skipper unit) as a function of consecutive years. In a typical repeated measures experiment, two measurements taken at adjacent times are normally better correlated than two measurements taken several time points apart (Littell et al., 1996). This type of analysis is possible using a specific parametric structure on the covariance matrices. A covariance structure for which correlations of nearby times are higher than far-apart times is the autoregressive of order 1 (AR1). It specifies that the covariance between two measurements w time apart is σ2ρw, where the parameter σ2 stands for the variance of an observation, and ρ for the correlation between adjacent observations on the same subject/sampling unit. As a sensitivity run, the autoregressive covariance (AR1) model was applied to the positive trips dataset component in the delta-lognormal model, using each vessel level as subject, and with repetitive measurements throughout the time-series. In terms of specification, the AR1 model did not include the Year×Month random interaction because it did not converge to a solution, as did the random delta-lognormal model.
In the case of the Poisson model, the dependent variable was the number of fish caught at age (rounded to the nearest integer), and fishing effort (days fishing) was used as an offset term in the model specification. The Poisson model failed to converge if the Year×Month random interaction was included, so only fixed model formulations were evaluated. Poisson analysis was done using the Genmod procedure (SAS Institute Inc., 1997).
Bearing in mind the above considerations and preliminary analyses, different exploratory runs were performed to investigate the sensitivity of the results to various choices of data to be used, and modelling options. The model runs defined were as follows.
Base case
Error model: delta lognormal
Ages 1–4, and 5+
Model factors for positives: cpue∼Year+Age+Year×Age+Month+Crew+Tank
Model factors for proportion of positives: cpue∼Year+Age+Year×Age+Month
Case 1
As for the base case, but only with the catches of vessels that had 5 or more years in the fishery.
Case 1R
As for case 1, but with the random interaction Year×Month.
Case 2
As for case 1, but with an autoregressive covariance model for vessels in time (no Year×Month interaction).
Case 3
Error model: Poisson
Model factors cpue∼Year+Age+Year×Age+Month+Crew+Tank
Logbook database
The information from trip and logbook data represents the same fleet and fishing area. Of particular interest in the logbook data was whether it would be possible to find spatial patterns or trends in catch rates of bluefin tuna. Maps of effort (number of fishing days) and cpue (number of fish by fishing day) were drawn, grouped by year and month to observe annual and seasonal patterns. The information from the two ports was also differentiated on the maps to investigate whether there was a different geographical distribution of catches according to base port.
In considering continuous variables such as latitude and longitude, general additive models (GAMs) have been used to analyse the relative influence of such variables on nominal catch rates (Kleiber and Bartoo, 1998; Bigelow et al., 1999). GAMs are non-parametric generalizations of multiple linear regressions, and are less restrictive in assumptions about the underlying statistical distribution of the data (Hastie and Tibshirani, 1990). For the logbook data, GAMs were used to analyse the relative influence of continuous latitude or longitude information on observed catch rates of bluefin tuna (logcpue). Non-linear effects were fitted using a locally weighted polynomial scatterplot smoother (Loess smoother).
To deal with the geographical distribution of catches as a factor of the standardization model, latitude and longitude were grouped into rectangles of 0.5°×0.5°. Type of bait was also included as a factor, to check whether horse mackerel is indeed the best bait for tuna >10 kg (2 years), and anchovy and sardine for smaller fish, as fishers maintain.
Standardization of logbook nominal cpue was done using the same protocols and model 1R as the standardization of trip data.
Results
Trip database standardization
Preliminary analysis of aggregated data at age indicated that year, month (June–November), number of bait tanks, and number of fishers were the most significant factors explaining the variability observed. Vessel characteristic and fishing-related instrumentation (sonar, radar, GPS, plotter, “Gonio”, and technological improvement index) have a relatively minor explanatory effect on the catch rates. This preliminary analysis also examined the skipper factor which, although it explained a significant percentage of the total variability (6.3%), was not taken into account because of the high number of degrees of freedom it added to the model (d.f.=74). Nor was the interaction Skipper×Boat type significant in explaining the variability observed.
Case 1 was preferred to the base case because vessels with 5 or more years of bluefin tuna catch history represent more consistent sampling units for the standardization of catch rates, although standardized indices and coefficients of variation (CVs) of both models are similar. The standardized cpue at age of the cases based on the delta model (cases 1, 1R, and 2) were similar, but the Poisson model, case 3, generated different estimates and trends. CVs for cases 1 and 2 were also similar and, although they were lower than those of case 1R, they showed the same variability within each age. CVs of the Poisson model were much larger.
Random effects of case 1R were tested for significance. Table 3 shows the results from the random components analyses used for final model selection. In the case of the positive catch component, inclusion of the Year×Month interaction represented an improvement over a model without this interaction.
Analysis of case 1R delta-lognormal mixed model formulations for positive bluefin tuna catch rates in the Bay of Biscay baitboat fishery.
| Model formulation . | n . | Residual log-likelihood . | Akaike's information criterion . | Schwartz's Bayesian criterion . | Likelihood ratio test∗ . | |
|---|---|---|---|---|---|---|
| Year+Age+Month+Crew+Tank+Year×Age | 31 919 | −65336.4 | −65337.4 | −65341.6 | ||
| Year+Age+Month+Crew+Tank+Year×Age+Year×Month | 31 919 | −64836.2 | −64838.2 | −64841.1 | 500.5 | 0.0000 |
| Model formulation . | n . | Residual log-likelihood . | Akaike's information criterion . | Schwartz's Bayesian criterion . | Likelihood ratio test∗ . | |
|---|---|---|---|---|---|---|
| Year+Age+Month+Crew+Tank+Year×Age | 31 919 | −65336.4 | −65337.4 | −65341.6 | ||
| Year+Age+Month+Crew+Tank+Year×Age+Year×Month | 31 919 | −64836.2 | −64838.2 | −64841.1 | 500.5 | 0.0000 |
The likelihood ratio tests the difference of residual log-likelihood between two nested models.
Analysis of case 1R delta-lognormal mixed model formulations for positive bluefin tuna catch rates in the Bay of Biscay baitboat fishery.
| Model formulation . | n . | Residual log-likelihood . | Akaike's information criterion . | Schwartz's Bayesian criterion . | Likelihood ratio test∗ . | |
|---|---|---|---|---|---|---|
| Year+Age+Month+Crew+Tank+Year×Age | 31 919 | −65336.4 | −65337.4 | −65341.6 | ||
| Year+Age+Month+Crew+Tank+Year×Age+Year×Month | 31 919 | −64836.2 | −64838.2 | −64841.1 | 500.5 | 0.0000 |
| Model formulation . | n . | Residual log-likelihood . | Akaike's information criterion . | Schwartz's Bayesian criterion . | Likelihood ratio test∗ . | |
|---|---|---|---|---|---|---|
| Year+Age+Month+Crew+Tank+Year×Age | 31 919 | −65336.4 | −65337.4 | −65341.6 | ||
| Year+Age+Month+Crew+Tank+Year×Age+Year×Month | 31 919 | −64836.2 | −64838.2 | −64841.1 | 500.5 | 0.0000 |
The likelihood ratio tests the difference of residual log-likelihood between two nested models.
Selected model
The results of deviance analysis for case 1R are shown in Table 4. Year, Age, and Year×Age are clearly the main explanatory factors, but the Year×Month interaction was also significant. For the proportion of positive trips, the main explanatory factors were again Year, Age, and Month. The selected final model included the following explanatory factors: Year, Age, Year×Age, Month, Crew (number), Tank (number of bait tanks), with the Year×Month interaction as a random component.
Case 1R deviance table for bluefin tuna catch rates of positive trips and proportion of positive/total trips from the baitboat fishery. Crew = number of fishers; Tank = number of live bait tanks; Colour echo-sounder, Sonar, Gonio, Radar, GPS, Plotter = vessel instrumentation; Port = Port of operation. Explanatory factors are emboldened.
| Model formulation . | d.f. . | Residual deviance . | Change in deviance . | Percentage of total deviance . | P . |
|---|---|---|---|---|---|
| Catch rate of positive trips | |||||
| 1 | 1 | 217 376.3 | |||
| Factor | |||||
| Year | 25 | 205 256.6 | 12 119.7 | 10.9 | <0.001 |
| +Age | 4 | 135 722.0 | 69 534.6 | 62.4 | <0.001 |
| +Month | 5 | 134 487.2 | 1234.8 | 1.1 | <0.001 |
| +Crew | 8 | 133 683.6 | 803.6 | 0.7 | <0.001 |
| +Tank | 8 | 133 482.6 | 210.1 | 0.2 | <0.001 |
| +Colour echo-sounder | 2 | 133 462.8 | 19.8 | 0.0 | <0.001 |
| +Monochrome sonar | 2 | 133 458.1 | 4.7 | 0.0 | 0.095 |
| +Colour sonar | 2 | 133 418.5 | 39.6 | 0.0 | <0.001 |
| +Gonio | 1 | 133 364.4 | 54.1 | 0.0 | <0.001 |
| +Navigation radar | 2 | 133 324.4 | 40.0 | 0.0 | <0.001 |
| +GPS | 2 | 133 309.0 | 15.4 | 0.0 | <0.001 |
| +Plotter | 2 | 133 257.3 | 51.7 | 0.0 | <0.001 |
| +Port | 1 | 133 254.8 | 2.5 | 0.0 | 0.114 |
| +Boat type | 2 | 133 250.4 | 4.4 | 0.0 | 0.036 |
| Interaction | |||||
| +Year × Age | 100 | 110 529.0 | 22 721.4 | 20.4 | <0.001 |
| +Year × Month | 102 | 105 884.7 | 4644.3 | 4.2 | <0.001 |
| Proportion of positive/total trips | |||||
| 1 | 1 | 86 221.8 | |||
| Factor | |||||
| Year | 25 | 84 268.8 | 1953.0 | 5.2 | <0.001 |
| +Age | 4 | 57 911.0 | 26 357.8 | 70.1 | <0.001 |
| +Month | 5 | 54 511.8 | 3399.3 | 9.0 | <0.001 |
| +Crew | 8 | 54 494.7 | 17.1 | 0.0 | <0.001 |
| +Tank | 8 | 54 428.2 | 66.5 | 0.2 | <0.001 |
| +Colour echo-sounder | 2 | 54 422.3 | 5.9 | 0.0 | 0.053 |
| +Monochrome sonar | 2 | 54 419.0 | 3.3 | 0.0 | 0.193 |
| +Colour sonar | 2 | 54 418.5 | 0.6 | 0.0 | 0.756 |
| +Gonio | 1 | 54 416.4 | 2.1 | 0.0 | 0.151 |
| +Navigation radar | 2 | 54 394.1 | 22.3 | 0.1 | <0.001 |
| +GPS | 2 | 54 387.8 | 6.3 | 0.0 | 0.043 |
| +Plotter | 2 | 54 369.8 | 18.0 | 0.0 | <0.001 |
| +Port | 1 | 54 368.5 | 1.3 | 0.0 | 0.260 |
| Interaction | |||||
| Year × Age | 100 | 48 600.6 | 5767.9 | 15.3 | <0.001 |
| Model formulation . | d.f. . | Residual deviance . | Change in deviance . | Percentage of total deviance . | P . |
|---|---|---|---|---|---|
| Catch rate of positive trips | |||||
| 1 | 1 | 217 376.3 | |||
| Factor | |||||
| Year | 25 | 205 256.6 | 12 119.7 | 10.9 | <0.001 |
| +Age | 4 | 135 722.0 | 69 534.6 | 62.4 | <0.001 |
| +Month | 5 | 134 487.2 | 1234.8 | 1.1 | <0.001 |
| +Crew | 8 | 133 683.6 | 803.6 | 0.7 | <0.001 |
| +Tank | 8 | 133 482.6 | 210.1 | 0.2 | <0.001 |
| +Colour echo-sounder | 2 | 133 462.8 | 19.8 | 0.0 | <0.001 |
| +Monochrome sonar | 2 | 133 458.1 | 4.7 | 0.0 | 0.095 |
| +Colour sonar | 2 | 133 418.5 | 39.6 | 0.0 | <0.001 |
| +Gonio | 1 | 133 364.4 | 54.1 | 0.0 | <0.001 |
| +Navigation radar | 2 | 133 324.4 | 40.0 | 0.0 | <0.001 |
| +GPS | 2 | 133 309.0 | 15.4 | 0.0 | <0.001 |
| +Plotter | 2 | 133 257.3 | 51.7 | 0.0 | <0.001 |
| +Port | 1 | 133 254.8 | 2.5 | 0.0 | 0.114 |
| +Boat type | 2 | 133 250.4 | 4.4 | 0.0 | 0.036 |
| Interaction | |||||
| +Year × Age | 100 | 110 529.0 | 22 721.4 | 20.4 | <0.001 |
| +Year × Month | 102 | 105 884.7 | 4644.3 | 4.2 | <0.001 |
| Proportion of positive/total trips | |||||
| 1 | 1 | 86 221.8 | |||
| Factor | |||||
| Year | 25 | 84 268.8 | 1953.0 | 5.2 | <0.001 |
| +Age | 4 | 57 911.0 | 26 357.8 | 70.1 | <0.001 |
| +Month | 5 | 54 511.8 | 3399.3 | 9.0 | <0.001 |
| +Crew | 8 | 54 494.7 | 17.1 | 0.0 | <0.001 |
| +Tank | 8 | 54 428.2 | 66.5 | 0.2 | <0.001 |
| +Colour echo-sounder | 2 | 54 422.3 | 5.9 | 0.0 | 0.053 |
| +Monochrome sonar | 2 | 54 419.0 | 3.3 | 0.0 | 0.193 |
| +Colour sonar | 2 | 54 418.5 | 0.6 | 0.0 | 0.756 |
| +Gonio | 1 | 54 416.4 | 2.1 | 0.0 | 0.151 |
| +Navigation radar | 2 | 54 394.1 | 22.3 | 0.1 | <0.001 |
| +GPS | 2 | 54 387.8 | 6.3 | 0.0 | 0.043 |
| +Plotter | 2 | 54 369.8 | 18.0 | 0.0 | <0.001 |
| +Port | 1 | 54 368.5 | 1.3 | 0.0 | 0.260 |
| Interaction | |||||
| Year × Age | 100 | 48 600.6 | 5767.9 | 15.3 | <0.001 |
Case 1R deviance table for bluefin tuna catch rates of positive trips and proportion of positive/total trips from the baitboat fishery. Crew = number of fishers; Tank = number of live bait tanks; Colour echo-sounder, Sonar, Gonio, Radar, GPS, Plotter = vessel instrumentation; Port = Port of operation. Explanatory factors are emboldened.
| Model formulation . | d.f. . | Residual deviance . | Change in deviance . | Percentage of total deviance . | P . |
|---|---|---|---|---|---|
| Catch rate of positive trips | |||||
| 1 | 1 | 217 376.3 | |||
| Factor | |||||
| Year | 25 | 205 256.6 | 12 119.7 | 10.9 | <0.001 |
| +Age | 4 | 135 722.0 | 69 534.6 | 62.4 | <0.001 |
| +Month | 5 | 134 487.2 | 1234.8 | 1.1 | <0.001 |
| +Crew | 8 | 133 683.6 | 803.6 | 0.7 | <0.001 |
| +Tank | 8 | 133 482.6 | 210.1 | 0.2 | <0.001 |
| +Colour echo-sounder | 2 | 133 462.8 | 19.8 | 0.0 | <0.001 |
| +Monochrome sonar | 2 | 133 458.1 | 4.7 | 0.0 | 0.095 |
| +Colour sonar | 2 | 133 418.5 | 39.6 | 0.0 | <0.001 |
| +Gonio | 1 | 133 364.4 | 54.1 | 0.0 | <0.001 |
| +Navigation radar | 2 | 133 324.4 | 40.0 | 0.0 | <0.001 |
| +GPS | 2 | 133 309.0 | 15.4 | 0.0 | <0.001 |
| +Plotter | 2 | 133 257.3 | 51.7 | 0.0 | <0.001 |
| +Port | 1 | 133 254.8 | 2.5 | 0.0 | 0.114 |
| +Boat type | 2 | 133 250.4 | 4.4 | 0.0 | 0.036 |
| Interaction | |||||
| +Year × Age | 100 | 110 529.0 | 22 721.4 | 20.4 | <0.001 |
| +Year × Month | 102 | 105 884.7 | 4644.3 | 4.2 | <0.001 |
| Proportion of positive/total trips | |||||
| 1 | 1 | 86 221.8 | |||
| Factor | |||||
| Year | 25 | 84 268.8 | 1953.0 | 5.2 | <0.001 |
| +Age | 4 | 57 911.0 | 26 357.8 | 70.1 | <0.001 |
| +Month | 5 | 54 511.8 | 3399.3 | 9.0 | <0.001 |
| +Crew | 8 | 54 494.7 | 17.1 | 0.0 | <0.001 |
| +Tank | 8 | 54 428.2 | 66.5 | 0.2 | <0.001 |
| +Colour echo-sounder | 2 | 54 422.3 | 5.9 | 0.0 | 0.053 |
| +Monochrome sonar | 2 | 54 419.0 | 3.3 | 0.0 | 0.193 |
| +Colour sonar | 2 | 54 418.5 | 0.6 | 0.0 | 0.756 |
| +Gonio | 1 | 54 416.4 | 2.1 | 0.0 | 0.151 |
| +Navigation radar | 2 | 54 394.1 | 22.3 | 0.1 | <0.001 |
| +GPS | 2 | 54 387.8 | 6.3 | 0.0 | 0.043 |
| +Plotter | 2 | 54 369.8 | 18.0 | 0.0 | <0.001 |
| +Port | 1 | 54 368.5 | 1.3 | 0.0 | 0.260 |
| Interaction | |||||
| Year × Age | 100 | 48 600.6 | 5767.9 | 15.3 | <0.001 |
| Model formulation . | d.f. . | Residual deviance . | Change in deviance . | Percentage of total deviance . | P . |
|---|---|---|---|---|---|
| Catch rate of positive trips | |||||
| 1 | 1 | 217 376.3 | |||
| Factor | |||||
| Year | 25 | 205 256.6 | 12 119.7 | 10.9 | <0.001 |
| +Age | 4 | 135 722.0 | 69 534.6 | 62.4 | <0.001 |
| +Month | 5 | 134 487.2 | 1234.8 | 1.1 | <0.001 |
| +Crew | 8 | 133 683.6 | 803.6 | 0.7 | <0.001 |
| +Tank | 8 | 133 482.6 | 210.1 | 0.2 | <0.001 |
| +Colour echo-sounder | 2 | 133 462.8 | 19.8 | 0.0 | <0.001 |
| +Monochrome sonar | 2 | 133 458.1 | 4.7 | 0.0 | 0.095 |
| +Colour sonar | 2 | 133 418.5 | 39.6 | 0.0 | <0.001 |
| +Gonio | 1 | 133 364.4 | 54.1 | 0.0 | <0.001 |
| +Navigation radar | 2 | 133 324.4 | 40.0 | 0.0 | <0.001 |
| +GPS | 2 | 133 309.0 | 15.4 | 0.0 | <0.001 |
| +Plotter | 2 | 133 257.3 | 51.7 | 0.0 | <0.001 |
| +Port | 1 | 133 254.8 | 2.5 | 0.0 | 0.114 |
| +Boat type | 2 | 133 250.4 | 4.4 | 0.0 | 0.036 |
| Interaction | |||||
| +Year × Age | 100 | 110 529.0 | 22 721.4 | 20.4 | <0.001 |
| +Year × Month | 102 | 105 884.7 | 4644.3 | 4.2 | <0.001 |
| Proportion of positive/total trips | |||||
| 1 | 1 | 86 221.8 | |||
| Factor | |||||
| Year | 25 | 84 268.8 | 1953.0 | 5.2 | <0.001 |
| +Age | 4 | 57 911.0 | 26 357.8 | 70.1 | <0.001 |
| +Month | 5 | 54 511.8 | 3399.3 | 9.0 | <0.001 |
| +Crew | 8 | 54 494.7 | 17.1 | 0.0 | <0.001 |
| +Tank | 8 | 54 428.2 | 66.5 | 0.2 | <0.001 |
| +Colour echo-sounder | 2 | 54 422.3 | 5.9 | 0.0 | 0.053 |
| +Monochrome sonar | 2 | 54 419.0 | 3.3 | 0.0 | 0.193 |
| +Colour sonar | 2 | 54 418.5 | 0.6 | 0.0 | 0.756 |
| +Gonio | 1 | 54 416.4 | 2.1 | 0.0 | 0.151 |
| +Navigation radar | 2 | 54 394.1 | 22.3 | 0.1 | <0.001 |
| +GPS | 2 | 54 387.8 | 6.3 | 0.0 | 0.043 |
| +Plotter | 2 | 54 369.8 | 18.0 | 0.0 | <0.001 |
| +Port | 1 | 54 368.5 | 1.3 | 0.0 | 0.260 |
| Interaction | |||||
| Year × Age | 100 | 48 600.6 | 5767.9 | 15.3 | <0.001 |
Observed and standardized scaled cpue series by age class are shown in Figure 6. The two series have similar trends, and nominal values are within the confidence interval of the standardized ones. There were no statistical differences between the historical nominal cpue at age 2 (Anon., 1999) and the nominal one in the present study (r2=0.78, n=24, p<0.001). The lowest cpue indices for age 2 are for 1979 and 1999, agreeing for all series (historical, and the present study nominal and standardized series), with the exception of the historical series ending in 1998. The standardized series shows that some cohorts can be followed through the years in the baitboat fishery. The 1994 cohort is clear at all ages, whereas the 1982 and 1987 cohorts are easily detected at ages 1–3 (Figure 6).
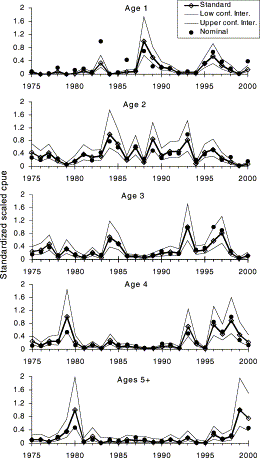
Standardized scaled cpue of baitboat-caught bluefin tuna for case 1R (with the random interaction Year×Month).
Figure 7 shows standardized indices and corresponding CVs for case 1R; there are no residual patterns. Overall CVs were on average about 30% for ages 2, 3, and 4, and about 60% for ages 1 and 5+ (Figure 7, right panel). Fitting diagnoses are shown in Figures 8 and 9 for the positive trips model and the binomial model, respectively, for each age class. The residuals follow the expected linear pattern for the positive catch rates in the QQ-plots (Figure 8), and the residuals plot for the proportion of positives shows no trend (Figure 9).
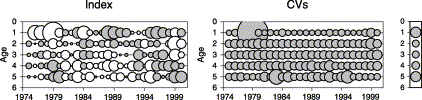
Standardized indices and corresponding CVs for case 1R. The indices and CVs have been scaled within an age to allow patterns in the series to be more easily seen, and the average magnitudes by age of the CVs are shown in the panel on the right. Indices less than average are shown in white and those greater than average are shaded.
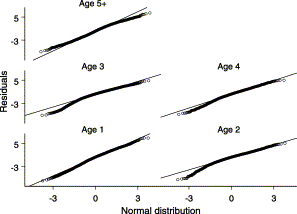
QQ-plots for the final model selected for positive catch rates of bluefin tuna in the trip database.
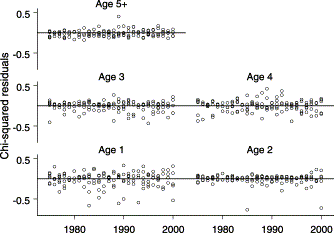
Residuals plot for the final model selected for the proportion of positive catch rates of bluefin tuna in the trip database.
Logbook database standardization
Figure 1 shows the overall distribution of catch locations deduced from fishing logbooks for the period 1987–2000. There are no patterns of annual and monthly distribution of effort and cpue. Getaria vessels fish in the same areas as those of Hondarribia. The GAM results indicate that longitude has no relationship with catch rate of bluefin tuna (p=0.1039). Most observations are from 2 to 4°W, with very few offshore of 4°W. In a latitudinal direction, the deviance table indicates a statistically significant relationship between catch rate and latitude (p=0.0011), but by evaluating the Loess plot between 43.5 and 45.5°N, where 90% of the catch is made, the relationship is flat. Only from 45.5 to 47°N does there appear to be a negative correlation with increasing latitude.
A preliminary deviance analysis with aggregated data by age indicates that the geographical distribution factor, represented by rectangles of 0.5°×0.5°, had no explanatory effect on the observed catch rates, nor did the type of bait. Consequently, it was decided not to include either area factor or type of bait in the standardization analysis. The final model selected included the same explanatory factors as for the standardization of the trips database, i.e. case 1R. Comparing both series of standardized cpue at age is satisfactory because, although the historical series of fishing logbook data is much shorter, the predicted indices for both databases coincide both in estimates and in CVs for all ages (Figure 10). Both series therefore reflect the same trends in bluefin tuna abundance in the Bay of Biscay.
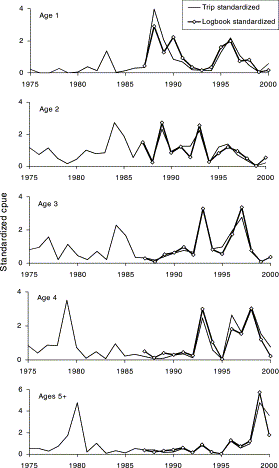
Comparison between the logbook- and trip-standardized cpue bluefin tuna catch series for ages 1, 2, 3, 4, and 5+. Both series have been scaled within each age.
Discussion
The study has provided cpue indices for all well-represented age classes in the bluefin tuna baitboat fishery. The CVs of the indices for ages 2–4 are small, whereas those of ages 1 and 5+ are high. Kell et al. (2002) report that the cpue for ages 1 and 4+ are not good indicators of relative abundance, given that 1-year-old bluefin tuna are not fully recruited, and that few fish older than 4 years are caught. Both the different migratory patterns by age and the state of sexual maturity may be influencing the CVs (Mather et al., 1995). For age 1 tuna, the variability is likely because not all fish join the migration to feeding areas at such a young age. For bluefin tuna aged 5+, the high CVs represent their scarcity in the area as a result of changes in migratory behaviour after the age of 4 years. At that age, bluefin tuna attain sexual maturity and, instead of migrating to the feeding grounds in the Bay of Biscay, they move to the spawning grounds in the Mediterranean (Cort, 1990; Mather et al., 1995).
There is another source of variability at age 1, in that such fish are caught mainly at the end of the fishing season, when inclement weather is more common. Depending on whether the winter storms appear earlier or later, catches of that age of tuna vary from year to year. Following storms at the end of the fishing season, age 1 tuna are no longer found in the Bay. Despite this, and even though the year-on-year presence of age 1 tuna is variable, years of high abundance still reflect year classes identified as strong at an early age. ICCAT regulations on size limits do not appear to influence the catches of 1-year-old bluefin tuna, and although a decreasing trend should be expected, the opposite occurs. The poor influence of this regulation may be due to the fact that most catches of 1-year-olds are made at the end of summer and in autumn, when the largest number of tuna of that age have attained the minimum size limit.
Age is the factor that explains most of the variability in the final model selected for use in standardization. Splitting of the catches into age classes introduces a large number of zero values in the data, perhaps because not all ages are equally accessible in every location, or perhaps because these zero values may be indicative of small stock size. Therefore, models need to be selected where the zero values automatically influence the biomass indices in the correct way (Stefánsson, 1996). Delta-lognormal models are often used to model processes that generate more zero observations than might be expected on the basis of distributional assumptions (Lambert, 1992). In a delta-lognormal distribution, zero values are treated separately, and positive values are assumed to follow a lognormal distribution (Lo et al., 1992). Such methodology has allowed us to obtain age-disaggregated indices for juvenile bluefin tuna, unlike most of the relative abundance indices available for the Eastern Atlantic and Mediterranean bluefin tuna stock, which are estimated for groups of ages. Our results seem promising, because the cpue of the 1994 cohort can be followed throughout the ages, occasionally standing out as an exceptionally large age class. Nevertheless, there are some high catch rates that appear in the same year in consecutive ages, as in 1984 for ages 2 and 3. This suggests that baitboat catchability for different ages may vary in tune with other, e.g. environmental factors. Although preliminary analyses did not reveal any association between environmental parameters and bluefin cpue in the area (Arrizabalaga et al., 2002), vertical migration patterns of bluefin tuna could affect catchability in this surface fishery. Further investigations relating horizontal and vertical behaviour to cpue may therefore improve the usefulness of this cpue series as an abundance index for the Eastern Atlantic bluefin tuna stock (see Brill and Lutcavage, 2001 for a general discussion).
The appearance and abundance of the different ages varies throughout a fishing season in the study area, with a clear annual pattern. The variations justify Month as an explanatory factor in the standardization model. The higher proportion of 2-year-old tuna in catches made between June and August stands out, as do 1-year-olds in the Bay of Biscay at the end of the fishing season. Age 3 fish are caught virtually throughout the year, with a slightly declining trend, whereas ages 4+ are caught mainly in summer. It is again possible that the different migratory behaviour of different ages (Cort, 1990; Mather et al., 1995) determines their temporary appearance in the Bay of Biscay. Different behaviour at age would also be evident in the different composition of schools, because bluefin tuna shoals are age-specific or only partially mixed. In a study of fishing operations aboard fishing vessels, Cort (1990) recorded most 1-year-old bluefin tuna in discrete schools (92%), 2-year-olds similarly but in lesser magnitude (68%), because they were also found in association with 3-year-olds, and 3-year-olds generally in association with 2-year-olds (33%) and 4- and 5-year-olds (53%). Cort's 4-year-old tuna were mostly associated with 3- and 5-year-olds, and his 5-year-old tuna were with ages 4 and older. The age composition of bluefin tuna schools in the Western Atlantic is similar (Baglin, 1978), and indeed such aggregation behaviour by age is common in tuna schools (Sharp, 2001).
The other two significant factors, crew number and number of bait tanks, also reflect their importance on catches as a consequence of the fishing system itself. For crew number, the use of rods that can be handled by 1–5 fishers, depending on the size of the tuna, elevates its importance. Indeed, in the first units of effort applied to this fishery, crew number was included in the measurement of effort (Bard and Cort, 1979). On the other hand, the number of bait tanks determines the quantity of bait available, both to attract fish and to bait hooks, which in turn influences the time spent fishing before the vessel has to break away and go in search of bait. Bait tank volume, which varies between 10 and 100 m3, is a more exact measurement of the capacity of bait storage and may be a more useful explanatory factor than the number of bait tanks. Unfortunately, this information was not available for the entire period analysed.
In general, the standardization procedure showed that vessel characteristic and the presence of fishing-related instrumentation (sonar, GPS, technological improvement index, etc.) have a relatively minor explanatory effect on the catch rates of bluefin tuna in the baitboat fishery. With respect to vessel type, the small size of the fishing area and its close proximity to the base ports results in vessel size and power not playing an important role. In terms of technological advances, the results should be interpreted with caution, because there are several possible underlying effects. In general, technological improvements in fishing gear and electronics increase fishing power. However, they can influence both catch and effort (catch rates of target species) and the overall profitability of the operation, i.e. by reducing the cost of the operation, which may not be reflected in catch rates per se. Another important consideration concerning gear modifications/improvements is that changes are normally implemented rapidly by the entire fleet in a relatively short time (2–3 years), leading to very little or no contrast between annual trends in catch and effort data. This latter consideration is the most plausible, because analysing the evolution of technological advances in the fleet revealed that introductions were made almost simultaneously throughout the fleet during the study period (Rodríguez-Marín et al., 2002). As shown also by Robins et al. (1998), technological innovation can spread quickly in a fleet of vessels competing for a common resource. Whatever the case, differences in the technology of the bluefin tuna baitboat fleet over the years are not shown by the model to be significant, nor are they interpreted as time- (year-) induced variability.
The introduction of monochrome sonar was a great technological advance owing to its importance in detecting bluefin tuna, and its use became widespread by the end of the 1970s. Its influence on fishing power was shown by Cort and Bard (1980), and it led to the division of the nominal cpue of 2-year-old tuna into two series, before and after 1978, to take into account its use (Anon., 1997). As our standardization study spans the years 1975–2000, this variable does not really influence the overall trend, because it only affects the first 2–3 years of the series.
The models selected for standardizing the two databases, trips and logbooks, include the same explanatory factors. Overall, year trends and CVs by age class were similar in the two datasets, which validate both standardizations, given the different nature of the data. Analysis of the standardized database of logbooks reveals that the factor's geographical distribution and type of bait had no explanatory effect on the catch rates observed, although according to information supplied by skippers, there are differences in the size of tuna caught over the continental shelf and in the deep ocean, and small tuna prefer a different bait from larger tuna. The concentration of catches in such a small area (90% were made in the area 2–4°W, 43.5–45.5°N) does not permit discrimination of the geographical variable. Discrimination of the effect of type of bait is also not possible, because horse mackerel is the main bait used.
Despite the limitations of cpue as an abundance index (Richards and Schnute, 1986; Hilborn and Walters, 1992), our study provides useful information on juvenile Eastern Atlantic bluefin tuna, because the analysis covers a long time-series of the baitboat fishery in the Bay of Biscay. During the series, no important changes took place in the exploitation pattern, except for technological advances; in other words, the fishing method remained the same throughout the study period. Future studies incorporating environmental factors may shed light on other factors that may contribute to explain the variability in abundance, fidelity, permanence (availability of food), and even catchability of juvenile bluefin tuna in this feeding area.
The study was supported by the European Commission (DG XIV, Study 00/024), as well as by the employers of all authors, namely IEO, AZTI, the University of the Azores, and CEFAS. We also thank J. L. Cort, J. Santiago, M. Picabea, I. Artetxe, L. A. Martín, and V. Susperregui, for their contribution to data collection and for sharing their knowledge of the bluefin tuna baitboat fishery, and the Fishermen's Association of Hondarribia and Getaria for their cooperation. Finally, Drs J-M. Fromentin and D. Die provided valuable reviews of an early version of the manuscript, and the editor (Dr A. I. L. Payne) helped extensively with the English of the final version.



