-
PDF
- Split View
-
Views
-
Cite
Cite
Francisco J Sánchez-Sesma, Richard L Weaver, Marcela Baena-Rivera, Alejandra Arciniega-Ceballos, Diana A Rodríguez-Zosayas, Mathieu Perton, Modelling noise H/V spectral ratio in a laterally inhomogeneous layered medium, Geophysical Journal International, Volume 240, Issue 3, March 2025, Pages 1652–1666, https://doi.org/10.1093/gji/ggaf009
Close - Share Icon Share
SUMMARY
Central to the task of seismic hazard assessment is the evaluation of potential amplifications due to site effects. The horizontal-to-vertical spectral ratio (HVSR) of ambient seismic noise (ASN) is a widespread measurement to assess the predominant soil frequency of a given site and estimate the wave velocities of the subsoil stratigraphy using inversion schemes. In practice, the inversions are currently made, assuming flat layers. In fact, HVSR measurements may show significant lateral and azimuthal changes due to the spatial variations of local geology, which can introduce uncertainties into the characterization of a site. This suggests the importance of considering detailed measurements of lateral and angular variations in layered settings. Inversion of soil properties at depth for horizontally layered media has become feasible assuming that ASN constitutes a diffuse field, that is, produced by equi-partitioned uniform illumination and/or by random sources and the ensuing multiple scattering by heterogeneities. Under the diffuse field assumption (DFA), the HVSR have been modelled by calculating the imaginary parts of the Green's function (IMGs) when source and observer coincide at the same point. In this work we use the 3-D indirect boundary element method (IBEM) to model the HVSR for each independent horizontal direction referred to here as directional-HVSR for layered media with lateral inhomogeneity. The IMGs at the source required to get HVSR have locality properties that depend on frequency and may imply significant economies in the calculation. For simple models we modelled the IMGs approximately using an adaptive meshing scheme that accounts both for the locality of the problem and the diffraction properties of waves at low and high frequencies. The obtained directional-HVSR displays variations in both frequency and azimuth. The results also show that layer interface variations can lead to ‘spots’ of higher wave excitation associated to local resonant modes. This shows the importance of HVSR in forecasting earthquake response and suggests the need for denser field measurements to study lateral and azimuthal variability. In order to show the reality of directional-HVSR, field data from Chalco, a soft soil site at the southern part of the Valley of Mexico, have been preliminarily analysed.
1. INTRODUCTION
The main goal in earthquake resistant design is to obtain design spectra of structures such that they withstand strong earthquakes. A crucial ingredient in this task is to evaluate the site effects through seismic characterization of the site. This complex issue needs to be simplified in order that practical measures could be at the reach of practitioners such as the predominant soil frequencies and the wave velocities of the soil profile to compute amplification factors.
In Japan, the tradition of studying microtremors dates back to the first half of the 20th century. Microtremors originate by the interaction of the ocean waves and the solid earth, by wind and by human activity as well. Here we call them ambient seismic noise (ASN). Kanai (1983) measurements in the 30s displayed the predominant frequency or period of a site by counting zero crossings in his smoked glass recordings. Nogoshi & Igarashi (1971) first computed the horizontal-to-vertical spectral ratio (HVSR or
On the other hand, the early 21st century has experienced a boom in passive seismology based on the formalization of the pioneering studies of Aki (1957) and the discoveries of Weaver (1982, 1985), which produced spectacular results in experimental (Weaver & Lobkis 2001) and field (Hennino et al. 2001; Campillo & Paul 2003) studies, in regional tomography (Shapiro et al., 2005) and exploration seismology (Schuster 2009). ASN is crucial to construct virtual sources in exploration seismology. In some circumstances, when the field is not completely diffuse, weighting approaches may enhance the diffuse field characteristics (Weaver & Yoritomo 2018; Piña-Flores et al. 2021).
Weaver (1982, 1985) formulated, four decades ago, the diffuse field theory in dynamic elasticity. This theory asserts that, within a diffuse field the average of cross-correlation is proportional to the imaginary part of the Green's function (IMGs) (Sánchez-Sesma & Campillo 2006; Sánchez-Sesma et al. 2008). In the same way, the average autocorrelations are proportional to the IMGs when source and receiver coincide. This fact is associated with the partitions of energy among states or modes (Perton et al. 2009) and exact deterministic results (Miller & Pursey 1955; Sánchez-Sesma et al. 2011a). Under the diffuse field assumption, Sánchez-Sesma et al. (2011b) modelled the HVSR of ASN for horizontally layered medium in terms of the IMGs when source and receiver coincide at the point of interest, and its inversion allowed to retrieve vertical profiles of mechanical properties (see García-Jerez et al. 2016; Piña-Flores et al. 2017, 2024) even for borehole recordings and for offshore and lake sites with an uppermost water layer (see Lontsi et al. 2015, 2019). Molnar et al. (2022) give a complete account of HVSR.
Additionally, the horizontal ASN may show azimuthal variations which may influence HVSR results, these polarizations have been attributed to fault-induced cracking, topographical effects and even anisotropy (see Pischiutta et al. 2017). Matsushima et al. (2014, 2017) explored the HVSR of a varying layer profile at Uji, Kyoto, Japan and Onahama, Tohoku, Japan, respectively, where several measured points allowed detecting significant differences in the HVSRs for independent horizontal components. In those cases, the spectral element method (SEM) was used to compute the response in time domain and the IMGs were computed by Fourier analysis of data close to the loading point. The exercises were not formal inversions, but the numerical modelling showed significant improvement in the matching of calculations with observations when the known structure was accounted for. Similarly, Perton et al. (2017) modelled the lateral variations at the Ijen volcano, Indonesia, taking advantage of the exposed layers at the crater rim.
Looking to understand and model these cases, we studied a flat layer over a half-space using the 3-D indirect boundary element method (IBEM) adapting the formulation by Sánchez-Sesma & Luzón (1995) and Perton & Sánchez-Sesma (2015) to compute the system IMGs directly in frequency domain. The IBEM in 3-D is not too restrictive regarding absorbing boundary conditions. In fact, we left open the layer sides and the underlying half-space was modelled only by a finite flat surface. The HVSR for a single layer is obtained almost as fast as the analytical modelling in cylindrical coordinates. Results reveal the crucial role of diffraction at low frequencies and the asymptotic ray behaviour at high ones. They also show the strong local behaviour of the IMGs ;at a point.
Furthermore, we studied two cases of a layer over a half-space with smooth lateral variations of the interface. The localized behaviour close to the observation point also exists in these varying profiles (the number of equations to solve is no longer constant, but it shows small variations). Our strategy is to compute the system IMGs at a single point implementing an adaptive mesh whose element sizes diminish with frequency as required for wavelength resolution. In this sense, we use large elements and lateral extent for low frequencies; those sizes contract around the observation point as the frequency increases. The number of equations thus remains almost constant for all the frequencies leading to greatly reduced computational burden.
We obtained the HVSR for the horizontal directions and called it directional-HVSR. The computed profiles show the changes in amplitude and localization of the frequency peaks and the apparent polarizations for varying directions and frequencies. The directional-HVSR variations in amplitude make it clear that inverting the spatial distribution of mechanical properties from HVSR requires a novel approach that includes measurements in dense arrays and perhaps attempting a kind of full-wave inversion.
From these numerical exercises we identified simple configurations which, according to the results and theory, can be interpreted as dominance of either energy scattering or energy trapping with also intermediate or mixed behaviours as well. The corresponding HVSR, even if they are relatively simple and are not transfer functions, offer a glimpse of phenomena that may appear in reality.
2. PROBLEM'S FORMULATION
In order to establish the formulation for our study, we will first introduce the concept of energy tensor,
where
Under the DFA, we associate
where
For transversely isotropic medium these tensors are diagonal. In fact, Arai & Tokimatsu (2004) expressed the HVSR of horizontal layers in terms of the power spectra of the two orthogonal horizontal motions over the one of vertical motion. This can be, referring to eq. (1), written as follows:
Sánchez-Sesma et al. (2008) called the spectral energy density of each direction as directional energy densities (DEDs or D), then
Expressing eq. (3) in terms of DEDs and considering the eq. (2), we have:
The expression at the right end introduces the imaginary parts of Green's tensor which are intrinsic properties of a layered system model. Therefore, eq. (4) is suited for inversion as discussed by Sánchez-Sesma et al. (2011b), Sánchez-Sesma (2017) and Lontsi et al. (2015, 2019).
In this communication, we explore a relatively simple case which can be seen as a slight departure of the transverse isotropy case. We are considering smooth lateral variations of the interface between a soft layer and the underlying half-space. In this case,
are indeed generalizations of HVSR and could be compared with the system Green's function counterpart ratios.
3. DIRECTIONAL-HVSR
The directional-HVSR describes the ratio of rotated horizontal energy spectral densities in a given direction
which describes how the recorded HVSR varies with horizontal direction. Regarding the modelling, the directional effects in a horizontal direction
The modelling of HVSR is then transformed into a quest for the 3-D Green's function. To get the system Green's functions we have to simulate the elastic field for unit forces at the observation points. As the lateral inhomogeneities considered here are smooth and restricted to the interface, the description given suffices to analyse and display results. Eq. (7) can be displayed in contours by plotting
A proper generalization of spectral ratios from flat layering to non-flat structure requires reporting the eigenvalue ratios and the eigenvectors of tensors
4. COMPUTATION OF SYSTEM GREEN'S FUNCTION
The system Green's function is computed using the 3-D IBEM (Sánchez-Sesma & Luzón 1995; Perton & Sánchez-Sesma 2015), which is based on first principles and is formulated directly in frequency domain. The 3-D IBEM allows modelling complicated geometries with moderate effort. It is closely related with the Somigliana identity (see Sánchez Sesma & Campillo 1991). The elastic wavefield within a given region is constructed as the superposition of the effects of 3-D unknown point forces distributed on the surfaces that will be boundaries of the region once the boundary conditions are fulfilled. In other words, the displacements and tractions in each region are given by integral representations in terms of the Green's function of full space (Stokes 1849) with the properties of the region.
To fix ideas, consider an elastic layer R of varying thickness,
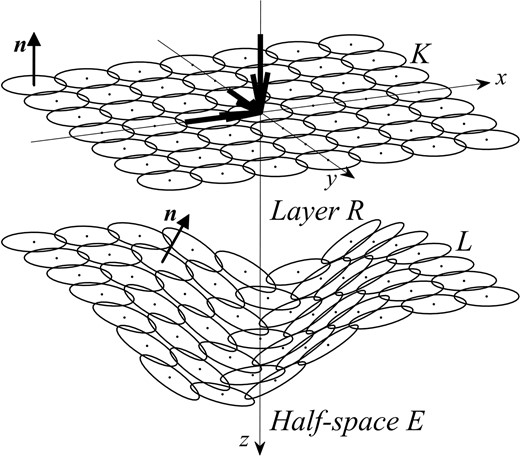
3-D model of a layer R over a half-space E bounded by finite surfaces K and L. The last one is the smooth interface with half-space E. Their normal vectors n are shown. The black arrows at the origin of coordinates indicate vertical and horizontal unit harmonic loads.
The displacement field in the layer R in direction i at a point
where
The traction vector in the layer R in direction i at a point
In the middle section of eq. (9), the first term of the equality is the contribution of force density when
For the half-space E the displacement field is given by:
Here,
These expressions have to be discretized along the surfaces K and L for the components x, y and z corresponding to directions
Surfaces K and L are discretized and force densities are assumed constant within the element. We call
The tractions boundary conditions at surface K and the continuity of both tractions and displacements at L, give a system of
where
The force densities in each element are assumed to be constant. They appear in the unknown vector. Therefore, the various entries in the matrix represent each a block of discretized tractions or displacements after integration in the source elements considering their centres as collocation points. For example, the block
is a matrix of
The same applies for the force densities. For example,
is a vector with the three components of force densities along surface K.
Regarding the loading points, we consider each component as an independent load vector, so we have three vectors for the loads. We assumed the load point at centre of surface K.
The solutions of eq. (12) for the three load components may allow us to compute the system Green's function. In the layer R, using the meshes K and L and a discretized version of eq. (8), we can define
5. ADAPTIVE MESHES
We require to evaluate the system IMGs at the source,
In low frequencies (long wavelengths), the reflections include significant amounts of non-specular waves that are precisely diffracted waves. They cancel the source up to a cut-off frequency. Therefore, non-geometric reflections may be engendered at distant points. Then, the lateral extension of the L mesh may be large to allow for the diffracted waves reaching the source point. In high frequencies (short wavelengths), the diffraction is less important, and the reflections are mainly specular and well described by rays, the clearly geometric waves require collimated reflections. Then, the lateral extent of the L mesh may be small. Fig. 2 presents a sketch of the adaptive meshes in a flat layer model.
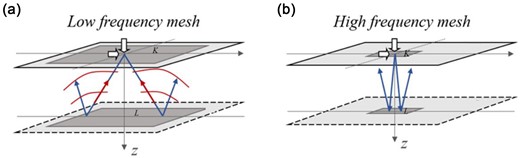
3-D sketch of the adaptive meshes approach of a flat layer R over a half-space E bounded by the K mesh for the surface and the L mesh for the interface (indicated with dark grey squares): (a) for low frequencies (long wavelengths), non-geometric reflections may be engendered at distant points and the mesh extent of K and L is large; and (b) for high frequencies (short wavelengths), the reflections are specular and well described by rays and the mesh extent of K and L is small. The arrows on the surface indicate the applied loads. The light grey squares indicated the extent of the study area.
After a series of tests with small and large meshes and sundry considerations on the size of elements (uniformly located along the surface), we establish a discretization criterion: the minimum wavelength of layer R,
where
where the first factor is less than one (here it runs from 0.75 to 0.15 in the frequency range) for fine-tuning the size of elements and the extension of the mesh. We assumed a square initial mesh K with
As for the L interface mesh, its characteristics are the same if the boundary is flat. For cylindrical profile of slope or channel type the distribution of surface elements is made essentially in 2-D and the y direction follows suite. The number of elements of L may vary with frequency. For more general surfaces, good meshing is critical. However, for smooth mesh L, the surface K provides convenient support.
6. NUMERICAL RESULTS
Using the IBEM in this endeavour allows us to deal with lateral inhomogeneity at the expense of more complex calculations. This critical problem can be simplified with the development of appropriate tools to handle the geometry. Our aim is to obtain meaningful solutions that give insight into the use and limitations of the spectral ratios of ASN and their modelling using IBEM.
It is possible to have a fixed mesh which has to be computed for the maximum frequency, that is, for the shortest wavelengths, to simultaneously introduce various observation-load points and have results for all of them in the same run. This would imply having three independent load vectors and three solutions of force densities for each selected point, that is, each new observation-load point would imply three new vectors in both the independent terms and unknowns. For such a system the number of collocation points would be extremely large, scaling approximately as the square of the maximum frequency. Further scrutiny is required to assess the advantages and limitations of a fixed mesh.
Instead, we propose that our shrinking 3-D meshes scheme become local for a given observation-load point. Then, we can handle both a global and local meshes. At each observation point its local mesh shrinks as frequency grows.
This drastically reduces the computational burden if other stations have to be considered in a global array. This strategy of keeping the number of equations to solve approximately fixed, attempts to keep the problem relatively small and within the reach of diverse practitioners.
Let us describe this idea in detail. In our 3-D IBEM implementation there are two independent meshes: the global and the local. The global mesh describes the surface and the geometry of the interface. On the surface global mesh, a set of observation points are located. The local meshes are generated for each observation point and centred on it in order to calculate its response. Thus, local meshes are those to which the adaptive mesh scheme is applied and move over the global ones. At certain points such as the edges they can even exceed the latter. For the calculation at all frequencies, they have essentially the same number of points, but as the frequency increases the only point that prevails is the observation one. In fact, the separation between the collocation points decreases and then the side length of each mesh will be smaller. This frequency-dependent decrease is obtained by applying the
In this section we present numerical results in which we model HVSR at the free-surface for three cases: (1) a single flat layer overlying a half-space; (2) a layer with a channel-like interface and (3) a layer with a smoothly varying interface making both anticlinal and synclinal shapes. These 3-D models are symmetrical with respect to the x-axis, the system Green's tensor is no longer diagonal. The current results display symmetries as well. Fortunately, the cross-term
In the following, the local meshes K and L for the first calculation frequency of each example will be called initial mesh, and those corresponding to the last calculation frequency of each example will be called final mesh.
The physical properties of interest are the layer thickness h, the vertical and lateral extent of interface perturbation, if any, the mass density
6.1 Example 1
In order to illustrate our approach, we first study the case of a flat layer over a half-space. The flat surface L is at a depth
A calculation from
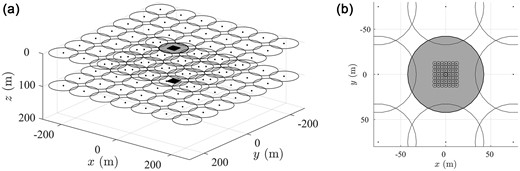
3-D model of an infinite layer of thickness
Regarding numerical results, Figs. 4(a) and (b) depict the analytical reference results for
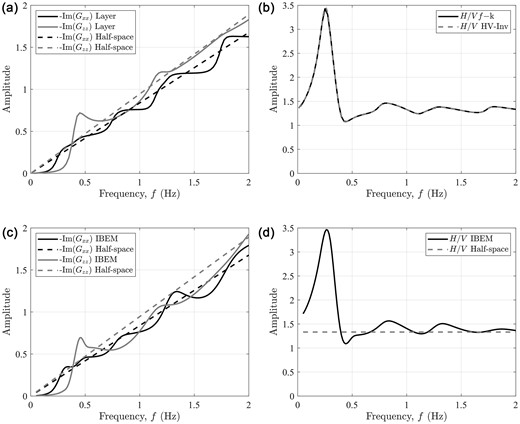
HVSR of the 3-D model of a flat layer over a half-space shown in Fig. 3. (a) and (c) Imaginary parts of Green's function,
6.2 Example 2
The second example corresponds to a layer with a cylindrical channel-type interface over a half-space model. The channel looks like an inverted Gaussian. The mesh L is made along the generator in 2-D and the surface elements along the y direction are uniform following the extension of surface mesh K. Thus, the number of elements of mesh L will vary with frequency and may increase or decrease slightly. At the extremes of surface L,
Fig. 5(a) depicts the initial and final meshes K and L for the observation point at the origin coinciding with the centre of interface topography. Mesh K is flat and conserves
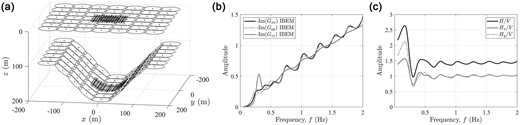
3-D model of an infinite layer with a flat surface over a half-space with a cylindrical channel-type interface. The layer thickness varies from
The theoretical frequency of a uniform layer of thickness
Fig. 5(b) displays some peaks in higher frequencies that reveal trapped waves that we are currently studying. It is of interest at this point to display the azimuthal variation of results. This variation is already shown in Fig. 5(c), but a more suggestive description can be achieved projecting the results according to eq. (7).
The contours of the
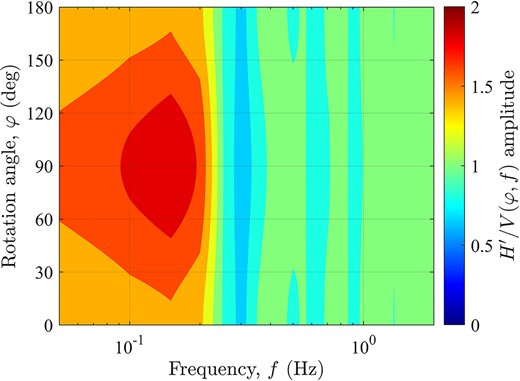
Contour plots of directional HVSR (
6.3 Example 3
The third example corresponds to an infinite layer with a flat surface over a half-space with an interface formed by a syncline-shape and an anticlinal-shape. This analytical shape is given by
Fig. 7(a) shows the global mesh of the interface geometry; the syncline shape is centred at
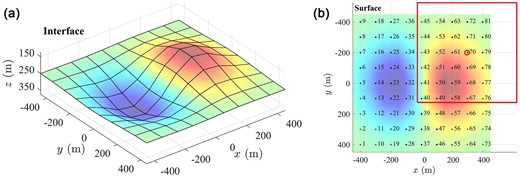
3-D model of an infinite layer with a flat surface over a half-space with an interface formed by a syncline-shape and an anticlinal-shape. (a) Global mesh of the interface; the syncline-shape is centred at
In a relatively straightforward manner, the results are obtained for all global mesh points in about a minute for each one using a common laptop.
In Figs 8(a), (c) and (d) display the results for an observation point located above the topography L at the maximum thickness
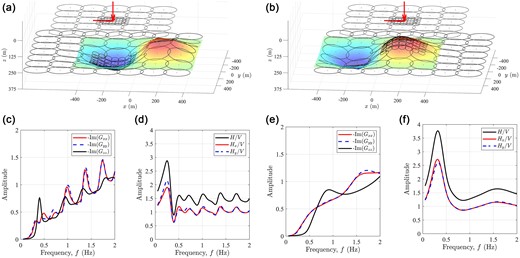
HVSR for the 3-D model of an infinite layer with a flat surface over a half-space with an interface formed by a syncline-shape and an anticlinal-shape shown in Fig. 7. (a) Adaptive initial (big circles) and final (small circles) local meshes for surface K and interface L, for the observation point at the surface at
Figs 8(b), (e) and (f) display the results for a surface observation point (at
As in the channel-like example in this anticlinal–synclinal shape somehow larger meshes were employed and results are stable. The HVSR results depend on the position of the observer. The simplicity of the horizontally layered case is lost. Now we have positional and directional effects. For the ‘bump’ anticlinal shape of Fig. 8(b) the
Fig. 9 displays the spatial location of peak amplitude values and associated frequencies for the
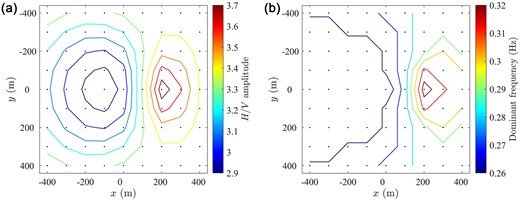
HVSR main peak contours of (a) amplitude and (b) fundamental frequency of the
In this example, there are
This directional measure averages in the frequency range between
Fig. 10 displays at the
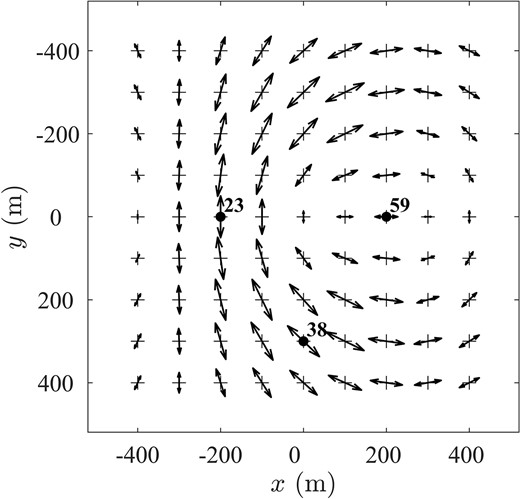
Direction and modulus of the maximum directionally dependent coefficient (
Three stations 23, 38 and 59 (Fig. 10) were selected to display the directional-HVSR against azimuth and frequency, and the
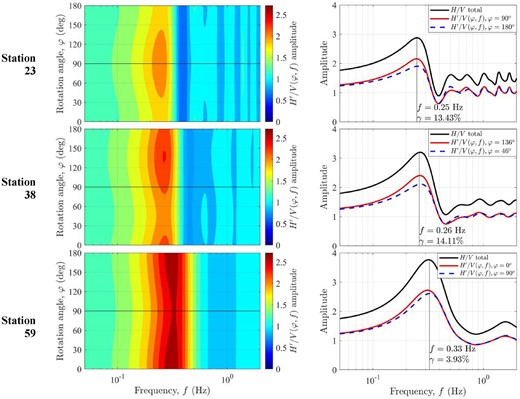
Directional-HVSR (
Station 23 is at the centre of the synclinal zone; the
7. OBSERVED DIRECTIONAL-HVSR AT CHALCO, VALLEY OF MEXICO
At the southern part of the Valley of Mexico, in the Chalco region were used to be a lake (Fig. 12). ASN measurements (
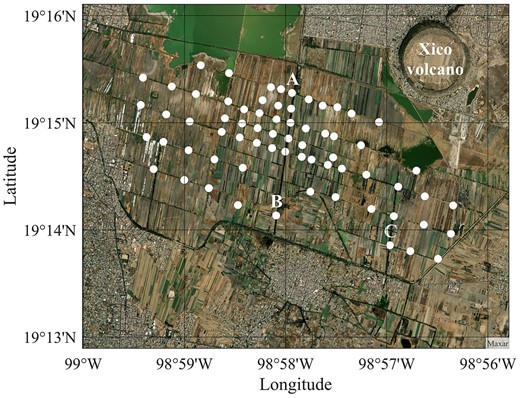
Satellite image with location of the Chalco array at the southern part of the Valley of Mexico (Mapping Toolbox—MATLAB), with the measured points georeferenced in white. Stations marked with A, B and C were selected for discussion in Section 7.
The total
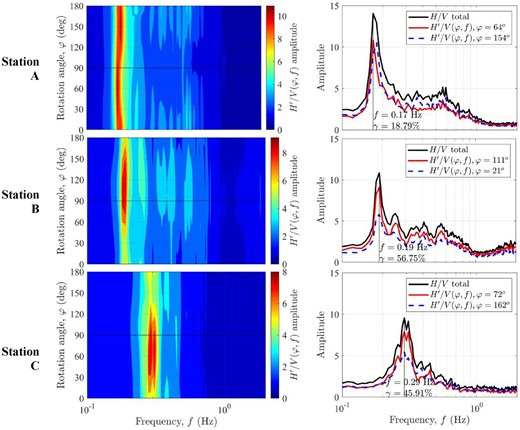
Measurements of directional-HVSR at three sites in Chalco array, Valley of Mexico. Left column, directional-HVSR,
Station A shows a minimum
8. CONCLUSIONS
For a single layer with varying interface, we model the system IMGs using 3-D IBEM. This approach allows the analyst to use the principle of superposition and construct the fields as summations of contributions of unknown force densities, after fulfillment of boundary conditions. This model allowed us to point out the complexity of the problem and opens the door to the numerical modelling based on the diffuse field assumption. Certainly, the exercise could be facilitated if trustworthy information of the system configuration is available (e.g. Matsushima et al. 2017; Perton et al. 2017). The numerical solution of 3-D realistic cases can be very demanding of computer resources. In the design of our simple one-layer model with smooth varying interface, we tried to keep the problem with a reasonable small size and devise adaptive meshes that change size with frequency. Our strategy is based on the properties of diffracted waves which display distinct behaviour at low and high frequencies. This is based upon our preferred interpretation of the cut-off frequencies that appear in the system IMGs spectra. We tested the adaptive mesh concept for the flat layer case with reasonable qualitative results. The concept of locality employed in the modelling can be extended along the lines of reasoning pioneered more than three decades ago by Rial et al. (1992) using local modes and by Kanai (1983) at the beginning of the 20th century.
For a layer over a half-space with a laterally varying interface, we obtained the directional-HVSR detecting both changes in peak frequency and amplitudes for varying azimuth. From these results, it is far from realistic to invert the total HVSR to estimate the vertical velocity model using flat layers.
The full directional-HVSR reveals a more complex problem like the opening of Pandora's box. Fortunately, the 3-D IBEM is a powerful method formulated in the frequency domain. The SEM has also been used for modelling HVSR with success for a known configuration (Matsushima et al. 2017). Here we focused on smooth interface variations and the results are consistent but require further scrutiny to clarify the advantages and limitations of the technique and the simplifications we propose herein. We believe it is too early to foresee the inversion of the structure using one or a few measuring points. The potential variations of possible substructures greatly exceed any information present in a single HVSR measurement. Recorded data in Chalco, at the southern part of the Valley of Mexico, reinforces this idea (Baena-Rivera et al. 2024). One must supplement measurements with extra geophysical information, possibly non-seismic.
A growing number of tasks emerges. A new set of approaches, such as gathering data from dense arrays of measurements, more complete parametric analysis and new ideas to interpret polarizations are needed to generate practical recommendations. The calculation of pseudo-reflection seismograms (PRS) as discussed in Scherbaum (1987) and Sánchez-Sesma et al. (2016) is a pending task. The PRS and the polarization results in the directional-HVSR could be useful to establish the nature of local modes. The measurements themselves have to be used extensively as an output of an analogue computer to foresee possible responses in case of earthquakes.
Acknowledgements
Many thanks are given to R. Avila-Carrera, M. Campillo, E. de Mejía, J.G. González, L.F. Kallivokas, O.I. López-Sugahara, J.C. Pardo-Dañino, J. H. Spurlin, F. Storey and L. Rivera for their comments and suggestions. Particular thanks to I.R. Valverde-Guerrero for his multifarious help. C. Carreón-Otañez participated in early stages of this research. The careful and insightful reviews of S. Matsushima, Y. Zheng and H. Chauris contributed to greatly improve the manuscript. J.E. Plata and M.G. Sánchez of USI-IINGEN, UNAM (Universidad Nacional Autónoma de México), helped locating useful references. This work was partially supported by the UNAM-University of Illinois Research Partnership Program 2023 and by UNAM's DGAPA (Dirección General de Asuntos del Personal Académico) under projects PAPIIT IN105523 and IN104823.
Author contributions: FJS-S and RLW conceived the study and drew the general layout, interpreted the results and wrote the manuscript. MB-R, MP, DAR-Z and FJS-S wrote the codes and performed numerical computations. AA-C organized Chalco, Valley of Mexico, experiment collected the seismograms and interpreted results. MB-R and AA-C analysed the Chalco data, made the numerical models and computed the directional-HVSR and polarization information. MB-R and DAR-Z generated numerical meshes. All authors contributed with discussions and improvements of the manuscript.
DATA AVAILABILITY
The seismograms used in this study were collected by AA-C. Data are available upon request to the corresponding author. The synthetic seismograms used in this study were computed by means of computer codes wrote by the authors and are available upon request to FJS-S.
References
APPENDIX. GREEN'S FUNCTION FOR A FULL SPACE
For the sake of completeness, we give here the expression of the Green's function (see Stokes 1849; Sánchez-Sesma & Luzón 1995) in an unbounded space E:
where
and
which have the constants 1 and (1 +
The corresponding Green's tractions are given by,
Further details can be found in Sánchez-Sesma & Luzón (1995).




