Spectral models for seismological source parameters, path attenuation and site-effects in Alborz region of northern Iran

Davatgari Fami Tafreshi, Mehran; Bora, Sanjay Singh; Mirzaei, Noorbakhsh; Ghofrani, Hadi; Kazemian, Javad

doi:10.1093/gji/ggab227

SUMMARY

We analysed 478 three-component strong ground motion time-series from 65 events in the moment magnitude (M_w) 3–6.5 range recorded at 111 stations at distances up to 150 km from 1997 to 2019 in the Alborz region. Non-parametric spectral functions for seismological source, path and site-effects were derived from Fourier amplitude spectra of observed acceleration time-histories using the generalized inversion technique (GIT) for the Alborz region of Iran. To characterize the spectral models in terms of the anelastic attenuation (Q), geometrical spreading, magnitude and stress parameter (Δσ), we fitted non-parametric attenuation and source functions (resulted from inversion) with the standard parametric models. The frequency-dependent non-parametric attenuation function shows a rapid decay at close distances (<60 km) and decreases monotonically at larger distances. The frequency-independent geometrical spreading follows a bilinear hinged model with a crossover distance at 70 km. For hypocentral distances R_hypo < 70 km, the geometrical spreading is |${R^{ - 1.01}}$|⁠, and for R_hypo > 70 km it is |${R^{ - 1.37}}$|⁠. The corresponding quality factor is |$Q\ ( f ) = \ 146{f^{0.91}}$|⁠. The non-parametric source spectra were found in a good agreement with Brune's ω-squared model. The stress-parameter (Δσ) values were found to exhibit large variability from 0.36 to 86.7 MPa with no significant magnitude-dependence. The average Δσ was found to be 8.6 MPa. The mean value of the estimated near-surface attenuation (κ₀) from high-frequency part of non-parametric source function is 0.032 s (±0.01 s). In general, there is a good agreement between subsoil resonance frequencies and amplification levels estimated from GIT and HVSR (horizontal to vertical spectral ratio). The results of this study provide updated values of seismological source, attenuation and site properties in the Alborz region of northern Iran, which are expected to improve regional seismic hazard analysis studies in the region.

Fourier analysis, Earthquake ground motions, Earthquake source observations, Seismic attenuation, Site effects, Wave propagation

INTRODUCTION

The Alborz mountain range, that forms a part of northern margin of the Alpine–Himalayan collision zone in western Asia, is an active fold-and-thrust belt of approximately 100 km wide and 600 km long in the north of Iran, along the southern margin of the Caspian Sea. Alborz is bounded by Talesh Mountains in the east, Kopeh Dagh-Binalud Mountains in the west and grades to the Central Iran in the south (Mirzaei et al. 1998). The Alborz region is one of the most seismically active regions of Iran and it has been rocked by some of the devastating earthquakes in historical and instrumental time period namely, the Qumis earthquake of 22 December 1856 with surface wave magnitude M_s 7.9 (Ambraseys & Melville 1982) in eastern Alborz, and the Rubdar-Manjil earthquake of 20 June 1990 with moment magnitude M_w 7.3 (Berberian & Walker 2010) in western Alborz. In the recent past, the occurrence of several major earthquakes such as, 1997 M_w 6.5 Garmkhan, 2002 M_w 6.4 Changureh-Avaj, 2004 M_w 6.2 Baladeh (Kojour) earthquakes confirm the high seismicity in the Alborz belt of northern Iran. A pair of earthquakes on 11 August 2012 with M_w 6.4 and 6.2 shook the Varzaghan–Ahar region in northwest Iran. These two damaging earthquakes occurred in a region where there was no major mapped fault or any well-documented historical seismicity (Ghods et al. 2015). The foci of most earthquakes in Alborz are concentrated in the crust at depths less than 30 km. In terms of damage and loss of lives, the Rudbar earthquake is one of the largest, and deadliest, earthquakes in Iran. It affected both urban and rural regions, killed 13 000–40 000 people, and made a further 500 000 homeless (Berberian & Walker 2010). The M_w 6.4 Changureh-Avaj earthquake that occurred in northwest Iran (Qazvin province) killed 261 people and caused 1300 people injured and resulted in widespread damage, in spite of the low population density in this region. Similarly, the M_w 6.2 Baladeh earthquake of 28 May 2004 occurred near Baladeh (70 km north of Tehran) in the Alborz Mountains of northern Iran. Despite the moderate size of this earthquake, it was very significant. It was the first earthquake in the instrumental time periods to occur near Tehran (the capital city of Iran) that caused strong shaking within the city and the first large event to occur in the central Alborz Mountains since the M_s 6.8 28 July 1957 earthquake (Tatar et al. 2007). Evidently, the high seismic activity in this region poses significant seismic threat to Tehran with a population of around 13 million in the city and 23 million in the larger metropolitan area of greater Tehran along with some other major cities situated in this region. Thus, such high seismic activity demands better understanding of seismic hazard in the region thereby better potential risk estimation and disaster preparedness.

Estimation of potential ground motion is an essential element of any seismic hazard study (Cornell 1968; Reiter 1990). In engineering applications this is typically achieved by using, (1) empirically derived ground motion prediction equations (GMPEs) and (2) stochastic simulation method (Boore 1983, 2003). GMPEs are usually calibrated using recordings from past earthquakes and reliability of these empirical equations strongly depends on the quality and the quantity of the utilized database. For this reason, well-constrained GMPEs are often available only for well-monitored active regions such as California, Japan, southern Europe and the Mediterranean. The major issue with regional GMPEs derived in the recent past is the paucity of recorded data in the magnitude and distance range of engineering interest. The Iranian data set is sparse in the near distance range for earthquakes with M > 6.5 (Zolfaghari & Darzi 2019; Farajpour et al. 2019). GMPEs developed for Alborz region (e.g. Soghrat & Ziyaeifar 2016) suffer from lack of near-source data for large-magnitude earthquakes.

The stochastic simulation technique (Boore 1983, 2003) provides an efficient and reliable tool for generating synthetic ground motions of engineering interest. The stochastically simulated ground motions can be used either to develop GMPEs directly or to augment the existing recorded database (e.g. Atkinson & Boore 1995, 2006; Toro et al. 1997; Atkinson & Silva 2000; Raghu-Kanth & Iyenger 2007; Rietbrock et al. 2013). The seismological model used in the stochastic simulation is simple yet powerful enough to capture the essential scaling of ground motion with magnitude and distance. Typically, the stochastic (amplitude) model is characterized in terms of magnitude and stress-parameter (⁠|$\Delta \sigma $|⁠) as being the source parameters; the geometrical spreading and anelastic attenuation (Q) of seismic wave describe the path effects. The site effects are modelled in terms of crustal amplification (Boore & Joyner 1997; Joyner & Boore 1981; Boore 2003) and site-related attenuation parameter (⁠|${\kappa _0}$|⁠). Thus, a prior estimate of stochastic model parameters such as seismic moment |$({M_0})$|⁠, |$\Delta \sigma $|⁠, geometrical spreading, attenuation parameters Q and |${\kappa _0}$| is crucial for forward modelling of ground motions. Estimation of stochastic model parameters essentially involves separation of the source, path and site parameters from Fourier spectra of empirical recordings (Edwards et al. 2008; Drouet et al. 2010; Oth et al. 2011; Poggi et al. 2011; Edwards & Fäh 2013; Rietbrock et al. 2013; Pacor et al. 2016; Bora et al. 2017). Usually, two approaches namely parametric and non-parametric inversion schemes are adopted for estimating the stochastic model parameters from the recorded waveforms. The prominent studies that follow the parametric inversion scheme are Edwards et al. (2008), Drouet et al. (2010), Poggi et al. (2011), Edwards & Fäh (2013), Bora et al. (2015, 2017), while non-parametric inversion studies involve Parolai et al. (2000), Bindi et al. (2006), Oth et al. (2008), Bindi et al. (2009), Drouet et al. (2011) and Pacor et al. (2016). Initially, Castro et al. (1990) used generalized inversion technique (GIT) to find source spectra, S-wave quality factor and site response using records of nine moderate earthquakes (4 < M_w < 7) in a Guerrero, Mexico, subduction environment.

In the north of Iran, a limited number of studies have been carried out to investigate region-specific seismic source, path and site effects for the major seismotectonic provinces in recent years (e.g. Motazedian 2006; Zafarani et al. 2012; Ahmadzadeh et al. 2019). Motazedian (2006) used 259 three-component strong-motion accelerograms recorded within northern Iran from 22 events with M_w range 4.9–7.4 to examine the propagation characteristics of shear waves, including geometric spreading, Q, and κ₀, and the local site amplification using horizontal-to-vertical spectral ratio (HVSR) method. Stochastic point-source and finite-source ground motion simulations were used to estimate the average stress parameter. Zafarani et al. (2012) used the generalized inversion of the S-wave amplitude spectra to estimate simultaneously source parameters, site response and S-wave attenuation (Q_s). They considered 228 records from 29 earthquakes that were recorded at 81 strong-motion stations, with magnitudes (m_b, M_s and M_w) in the range from 4 to 7.4, at focal depths from 5 to 32 km, and hypocentral distances ranging from 10 to 185 km. Ahmadzadeh et al. (2019) analysed 1117 seismograms from 312 crustal earthquakes recorded at the Iranian National Broadband Seismic Network in the Alborz region between 2005 and 2017 with M_L 3–5.6 in the frequency range 0.3–20 Hz. They used S-wave spectral amplitudes and applied non-parametric GIT method to determine source parameters, path attenuation and site amplification functions.

In this paper, we estimated earthquake ground motion parameters by using an updated strong-motion database of recordings in the Alborz region of northern Iran. We used a non-parametric inversion technique to determine source, path and site effects. Estimation of source parameters involves determining M₀ and |$\Delta \sigma $| for all the selected events. We estimated the geometrical spreading model and anelastic attenuation factor for the Alborz region. Furthermore, we presented empirical site amplification factors for some of the selected stations in the study region. All the seismological parameters estimated in this study are constrained by the (broadband) Fourier amplitude spectra (FAS) of the strong-motion accelerograms recorded in the study region. In addition to the use in simulation of ground motion, the seismological parameters in this study are expected to facilitate better understanding of source properties of earthquakes such as variations of |$\Delta \sigma $| in the Alborz region. Moreover, the derived anelastic attenuation function can provide additional insights regarding the path properties in the region. The estimated site amplification functions will be useful for applications such as site classifications and can play an important role for determining site-specific seismic hazard.

DATA SET SPECIFICATIONS

For this study, we used 478 three-component strong ground motion records from 65 events from 1997 to 2019 and 111 stations (Fig. 1) that were recorded by the Building and Housing Research Center (BHRC) of Iran (http://www.bhrc.ac.ir/). BHRC uses three kinds of instruments (SMA-1 analogue, SSA-2 digital and Guralp CMG-5TD digital) for recording strong ground motions. The sampling rate for majority of the instruments was 200 Hz while some of the instruments had sampling rate of 100 Hz. The selected data set consists of recordings from earthquakes in the magnitude range M_w 3–6.5 at distances up to 150 km (Table 1). The magnitude–distance distribution of the selected data set is depicted in Fig. 2(a). We only used crustal events with hypocentral depth up to 40 km. The magnitude–depth distribution of events is shown in Fig. 2(b). Out of 111 stations in the selected data set, there are only 43 stations for which measured V_S30 (time-averaged shear wave velocity in the upper 30 m of the soil column beneath the station) are available. The site characterization information for the remaining 68 stations was not available. Fig. 2(c) shows distribution of V_S30 values in the selected data set. It is evident from Fig. 2(c) that majority of the stations belong to stiff soil (180–360 m s^–1) to very dense soil and soft rock (360–760 m s^–1) condition based on NEHRP site classification. Also, in the compiled data set we have 52 stations which have recorded at least four events, and 65 events were recorded by at least three stations.

Figure 1.

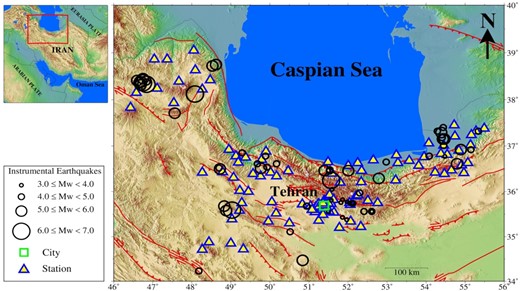
Map of Alborz region and adjacent area, epicenters of the considered earthquakes (circles) occurred during 1997–2019 and selected recording stations (triangles). Green square shows the location of Tehran.

Open in new tab Download slide

Figure 2.

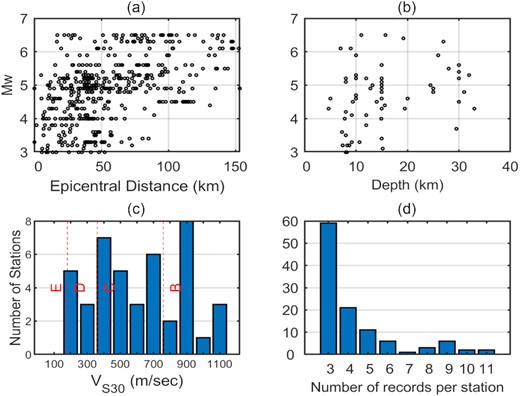
Plots showing, (a) magnitude–distance distribution of records in the data set, (b) magnitude–depth distribution of events, (c) distribution of station V_S30 values and (d) number of stations against number of records per station. Vertical red dashed lines depict the limits of National Earthquake Hazard Reduction Program (NEHRP) site classes (E: soft soil; D: stiff soil; C: very dense soil and soft rock; B: rock).

Open in new tab Download slide

Table 1.

Open in new tab

The event-specific inverted moment magnitude (M_w) and stress parameter (⁠|$\Delta {\rm{\sigma }}$|⁠) values.

Date	Earthquake ID	Lat. (N°)	Lon. (E°)	Magnitude				Inverted M_w	Δσ (MPa)	\|${\kappa _0}$\| (s)	N *
				M_w	M_N	M_b	M_L
2019/11/07	201 901	37.71	47.56	5.9				5.8	4.32	0.016	4
2019/09/16	201 902	36.53	49.92	4.6				4.6	2.1	0.03	3
2018/02/09	201 801	35.43	51.86		3.6			3.8	1.9	0.036	9
2018/04/01	201 802	35.56	52.41		4.2			44	2.22	0.047	4
2018/09/22	201 803	36.65	52.98		3.3			4.8	5.35	0.033	6
2017/02/01	201 701	35.38	51.97	3.2				3.5	0.36	0.027	3
2017/04/28	201 702	35.76	51.82		3.4			3.5	4.42	0.01	18
2017/11/30	201 703	35.74	52.12	4.0				4.3	0.83	0.04	9
2017/12/20	201 704	35.68	50.95	4.9				5.1	8.59	0.043	34
2017/12/26	201 705	35.68	50.94	4.0				4.1	4.1	0.044	22
2016/02/01	201 601	35.81	51.57		3.1			3.4	7.69	0.022	5
2016/03/11	201 602	35.82	51.86		3.2			3.3	2.35	0.014	3
2016/04/17	201 603	35.75	52.04		3.4			3.6	0.67	0.025	6
2016/10/22	201 604	35.75	52.12	3.5				4.2	0.39	0.031	7
2015/05/10	201 501	36.78	49.89	4.3				4.5	1.67	0.033	3
2015/08/02	201 502	36.05	51.59		3.1			3.2	3.26	0.03	6
2015/08/25	201 503	35.56	52.59	4.5				4.8	3.91	0.03	21
2015/08/25	201 504	35.56	52.61		3.2			3.5	5.06	0.018	3
2015/09/15	201 505	37.32	54.29	4.3				4.9	11.62	0.029	4
2015/09/21	201 506	35.77	51.98		3.2			3.5	6.59	0.014	3
2014/08/16	201 401	35.97	52.3	4.1				4.8	1.5	0.044	3
2012/01/11	201 201	36.29	52.79	5.0				4.9	3.56	0.038	6
2012/08/11	201 202	38.33	46.84	6.5				6.0	5.57	0.023	7
2012/08/11	201 203	38.36	46.75	6.4				6.0	9.94	0.021	8
2012/08/11	201 204	38.26	46.76	3.4				3.6	1.62	0.026	5
2012/08/11	201 205	38.38	46.85	4.8				4.7	1.61	0.015	4
2012/08/11	201 206	38.32	46.69	5.2				4.9	1. 9	0.029	4
2012/08/11	201 207	38.36	46.66	5.2				5.1	3.36	0.022	4
2012/08/14	201 208	38.45	46.75	5.1				5.2	2.68	0.018	6
2012/08/14	201 209	38.38	46.7	5.0				5.1	1.73	0.025	4
2012/11/07	201 210	38.41	46.6	5.6				5.7	2.28	0.027	4
2011/08/11	201 101	36.61	54.79		4.9			5.1	8.08	0.046	4
2009/10/17	200 901	35.56	51.5	3.8				4.1	3.4	0.031	9
2008/05/27	200 801	36.5	48.72	5.0				4.9	10.38	0.034	7
2007/02/09	200 701	36.77	54.48	3.7				3.8	4.18	0.031	3
2007/05/11	200 702	36.85	49.29	4.3				4.3	0.86	0.03	3
2007/06/18	200 703	34.47	50.84		5.9			5.7	22.99	0.044	8
2007/07/11	200 704	38.75	48.62	5.2				5.0	2.71	0.005	3
2006/03/31	200 601	33.54	48.78	6.1				5.9	6.19	0.041	4
2005/01/10	200 501	37.15	54.47	5.3				5.5	45.71	0.035	22
2005/11/29	200 502	37.4	54.44					5.0	25.23	0.046	6
2004/03/27	200 401	36.92	55.15	4.7				4.9	2.82	0.044	3
2004/05/28	200 402	36.25	51.57	6.3				6.1	14.00	0.035	24
2004/05/29	200 403	36.46	51.4	5.1				5.2	5.62	0.034	4
2004/05/30	200 404	36.45	51.53	4.2				4.7	2.45	0.038	3
2004/05/30	200 405	36.48	51.53	4.6				5.3	2.67	0.033	3
2004/10/07	200 406	37.15	54.43	5.6				5.7	86.7	0.037	22
2004/10/08	200 407	37.18	54.41	4.8				5.0	16.08	0.032	7
2003/09/12	200 301	37.32	55.32	4.6				5.0	12.6	0.037	3
2003/12/24	200 302	35.11	50.52	4.9				4.7	8.5	0.036	4
2002/04/08	200 201	36.46	52.01		4.6			5.2	2.27	0.036	5
2002/04/19	200 202	36.51	49.77			5.2		5.2	6.7	0.034	12
2002/04/19	200 203	36.61	49.68				4.4	4.5	1.55	0.039	5
2002/06/22	200 204	35.59	49.03	6.5				6.1	7.82	0.046	20
2002/06/22	200 205	35.58	48.88				5.0	5.2	1.53	0.043	4
2002/09/02	200 206	35.68	4.83				5.3	5.4	1.97	0.044	4
2000/08/16	200 001	37.01	54.45	4.9				5.1	14.35	0.036	8
1999/03/26	199 901	36.61	50.17	4.3				4.2	1.08	0.037	3
1999/11/19	199 902	37.29	54.39	5.5				5.5	64.92	0.038	12
1999/11/26	199 903	36.92	54.89	5.3				5.3	23.33	0.033	5
1998/07/09	199 801	38.72	48.53	5.9				6.0	7.22	0.019	7
1998/08/21	199 802	34.23	48.18	4.9				5.0	4.04	0.037	4
1998/09/28	199 803	36.52	48.7	4.6				4.6	5.39	0.039	5
1997/02/28	199 701	38.12	48.08	6.1				5.9	5.24	0.018	11
1997/09/16	199 702	36.78	54.08			4.8		5.0	20.42	0.031	3

Date	Earthquake ID	Lat. (N°)	Lon. (E°)	Magnitude				Inverted M_w	Δσ (MPa)	\|${\kappa _0}$\| (s)	N *
				M_w	M_N	M_b	M_L
2019/11/07	201 901	37.71	47.56	5.9				5.8	4.32	0.016	4
2019/09/16	201 902	36.53	49.92	4.6				4.6	2.1	0.03	3
2018/02/09	201 801	35.43	51.86		3.6			3.8	1.9	0.036	9
2018/04/01	201 802	35.56	52.41		4.2			44	2.22	0.047	4
2018/09/22	201 803	36.65	52.98		3.3			4.8	5.35	0.033	6
2017/02/01	201 701	35.38	51.97	3.2				3.5	0.36	0.027	3
2017/04/28	201 702	35.76	51.82		3.4			3.5	4.42	0.01	18
2017/11/30	201 703	35.74	52.12	4.0				4.3	0.83	0.04	9
2017/12/20	201 704	35.68	50.95	4.9				5.1	8.59	0.043	34
2017/12/26	201 705	35.68	50.94	4.0				4.1	4.1	0.044	22
2016/02/01	201 601	35.81	51.57		3.1			3.4	7.69	0.022	5
2016/03/11	201 602	35.82	51.86		3.2			3.3	2.35	0.014	3
2016/04/17	201 603	35.75	52.04		3.4			3.6	0.67	0.025	6
2016/10/22	201 604	35.75	52.12	3.5				4.2	0.39	0.031	7
2015/05/10	201 501	36.78	49.89	4.3				4.5	1.67	0.033	3
2015/08/02	201 502	36.05	51.59		3.1			3.2	3.26	0.03	6
2015/08/25	201 503	35.56	52.59	4.5				4.8	3.91	0.03	21
2015/08/25	201 504	35.56	52.61		3.2			3.5	5.06	0.018	3
2015/09/15	201 505	37.32	54.29	4.3				4.9	11.62	0.029	4
2015/09/21	201 506	35.77	51.98		3.2			3.5	6.59	0.014	3
2014/08/16	201 401	35.97	52.3	4.1				4.8	1.5	0.044	3
2012/01/11	201 201	36.29	52.79	5.0				4.9	3.56	0.038	6
2012/08/11	201 202	38.33	46.84	6.5				6.0	5.57	0.023	7
2012/08/11	201 203	38.36	46.75	6.4				6.0	9.94	0.021	8
2012/08/11	201 204	38.26	46.76	3.4				3.6	1.62	0.026	5
2012/08/11	201 205	38.38	46.85	4.8				4.7	1.61	0.015	4
2012/08/11	201 206	38.32	46.69	5.2				4.9	1. 9	0.029	4
2012/08/11	201 207	38.36	46.66	5.2				5.1	3.36	0.022	4
2012/08/14	201 208	38.45	46.75	5.1				5.2	2.68	0.018	6
2012/08/14	201 209	38.38	46.7	5.0				5.1	1.73	0.025	4
2012/11/07	201 210	38.41	46.6	5.6				5.7	2.28	0.027	4
2011/08/11	201 101	36.61	54.79		4.9			5.1	8.08	0.046	4
2009/10/17	200 901	35.56	51.5	3.8				4.1	3.4	0.031	9
2008/05/27	200 801	36.5	48.72	5.0				4.9	10.38	0.034	7
2007/02/09	200 701	36.77	54.48	3.7				3.8	4.18	0.031	3
2007/05/11	200 702	36.85	49.29	4.3				4.3	0.86	0.03	3
2007/06/18	200 703	34.47	50.84		5.9			5.7	22.99	0.044	8
2007/07/11	200 704	38.75	48.62	5.2				5.0	2.71	0.005	3
2006/03/31	200 601	33.54	48.78	6.1				5.9	6.19	0.041	4
2005/01/10	200 501	37.15	54.47	5.3				5.5	45.71	0.035	22
2005/11/29	200 502	37.4	54.44					5.0	25.23	0.046	6
2004/03/27	200 401	36.92	55.15	4.7				4.9	2.82	0.044	3
2004/05/28	200 402	36.25	51.57	6.3				6.1	14.00	0.035	24
2004/05/29	200 403	36.46	51.4	5.1				5.2	5.62	0.034	4
2004/05/30	200 404	36.45	51.53	4.2				4.7	2.45	0.038	3
2004/05/30	200 405	36.48	51.53	4.6				5.3	2.67	0.033	3
2004/10/07	200 406	37.15	54.43	5.6				5.7	86.7	0.037	22
2004/10/08	200 407	37.18	54.41	4.8				5.0	16.08	0.032	7
2003/09/12	200 301	37.32	55.32	4.6				5.0	12.6	0.037	3
2003/12/24	200 302	35.11	50.52	4.9				4.7	8.5	0.036	4
2002/04/08	200 201	36.46	52.01		4.6			5.2	2.27	0.036	5
2002/04/19	200 202	36.51	49.77			5.2		5.2	6.7	0.034	12
2002/04/19	200 203	36.61	49.68				4.4	4.5	1.55	0.039	5
2002/06/22	200 204	35.59	49.03	6.5				6.1	7.82	0.046	20
2002/06/22	200 205	35.58	48.88				5.0	5.2	1.53	0.043	4
2002/09/02	200 206	35.68	4.83				5.3	5.4	1.97	0.044	4
2000/08/16	200 001	37.01	54.45	4.9				5.1	14.35	0.036	8
1999/03/26	199 901	36.61	50.17	4.3				4.2	1.08	0.037	3
1999/11/19	199 902	37.29	54.39	5.5				5.5	64.92	0.038	12
1999/11/26	199 903	36.92	54.89	5.3				5.3	23.33	0.033	5
1998/07/09	199 801	38.72	48.53	5.9				6.0	7.22	0.019	7
1998/08/21	199 802	34.23	48.18	4.9				5.0	4.04	0.037	4
1998/09/28	199 803	36.52	48.7	4.6				4.6	5.39	0.039	5
1997/02/28	199 701	38.12	48.08	6.1				5.9	5.24	0.018	11
1997/09/16	199 702	36.78	54.08			4.8		5.0	20.42	0.031	3

*

N is the number of records.

Table 1.

Open in new tab

The event-specific inverted moment magnitude (M_w) and stress parameter (⁠|$\Delta {\rm{\sigma }}$|⁠) values.

Date	Earthquake ID	Lat. (N°)	Lon. (E°)	Magnitude				Inverted M_w	Δσ (MPa)	\|${\kappa _0}$\| (s)	N *
				M_w	M_N	M_b	M_L
2019/11/07	201 901	37.71	47.56	5.9				5.8	4.32	0.016	4
2019/09/16	201 902	36.53	49.92	4.6				4.6	2.1	0.03	3
2018/02/09	201 801	35.43	51.86		3.6			3.8	1.9	0.036	9
2018/04/01	201 802	35.56	52.41		4.2			44	2.22	0.047	4
2018/09/22	201 803	36.65	52.98		3.3			4.8	5.35	0.033	6
2017/02/01	201 701	35.38	51.97	3.2				3.5	0.36	0.027	3
2017/04/28	201 702	35.76	51.82		3.4			3.5	4.42	0.01	18
2017/11/30	201 703	35.74	52.12	4.0				4.3	0.83	0.04	9
2017/12/20	201 704	35.68	50.95	4.9				5.1	8.59	0.043	34
2017/12/26	201 705	35.68	50.94	4.0				4.1	4.1	0.044	22
2016/02/01	201 601	35.81	51.57		3.1			3.4	7.69	0.022	5
2016/03/11	201 602	35.82	51.86		3.2			3.3	2.35	0.014	3
2016/04/17	201 603	35.75	52.04		3.4			3.6	0.67	0.025	6
2016/10/22	201 604	35.75	52.12	3.5				4.2	0.39	0.031	7
2015/05/10	201 501	36.78	49.89	4.3				4.5	1.67	0.033	3
2015/08/02	201 502	36.05	51.59		3.1			3.2	3.26	0.03	6
2015/08/25	201 503	35.56	52.59	4.5				4.8	3.91	0.03	21
2015/08/25	201 504	35.56	52.61		3.2			3.5	5.06	0.018	3
2015/09/15	201 505	37.32	54.29	4.3				4.9	11.62	0.029	4
2015/09/21	201 506	35.77	51.98		3.2			3.5	6.59	0.014	3
2014/08/16	201 401	35.97	52.3	4.1				4.8	1.5	0.044	3
2012/01/11	201 201	36.29	52.79	5.0				4.9	3.56	0.038	6
2012/08/11	201 202	38.33	46.84	6.5				6.0	5.57	0.023	7
2012/08/11	201 203	38.36	46.75	6.4				6.0	9.94	0.021	8
2012/08/11	201 204	38.26	46.76	3.4				3.6	1.62	0.026	5
2012/08/11	201 205	38.38	46.85	4.8				4.7	1.61	0.015	4
2012/08/11	201 206	38.32	46.69	5.2				4.9	1. 9	0.029	4
2012/08/11	201 207	38.36	46.66	5.2				5.1	3.36	0.022	4
2012/08/14	201 208	38.45	46.75	5.1				5.2	2.68	0.018	6
2012/08/14	201 209	38.38	46.7	5.0				5.1	1.73	0.025	4
2012/11/07	201 210	38.41	46.6	5.6				5.7	2.28	0.027	4
2011/08/11	201 101	36.61	54.79		4.9			5.1	8.08	0.046	4
2009/10/17	200 901	35.56	51.5	3.8				4.1	3.4	0.031	9
2008/05/27	200 801	36.5	48.72	5.0				4.9	10.38	0.034	7
2007/02/09	200 701	36.77	54.48	3.7				3.8	4.18	0.031	3
2007/05/11	200 702	36.85	49.29	4.3				4.3	0.86	0.03	3
2007/06/18	200 703	34.47	50.84		5.9			5.7	22.99	0.044	8
2007/07/11	200 704	38.75	48.62	5.2				5.0	2.71	0.005	3
2006/03/31	200 601	33.54	48.78	6.1				5.9	6.19	0.041	4
2005/01/10	200 501	37.15	54.47	5.3				5.5	45.71	0.035	22
2005/11/29	200 502	37.4	54.44					5.0	25.23	0.046	6
2004/03/27	200 401	36.92	55.15	4.7				4.9	2.82	0.044	3
2004/05/28	200 402	36.25	51.57	6.3				6.1	14.00	0.035	24
2004/05/29	200 403	36.46	51.4	5.1				5.2	5.62	0.034	4
2004/05/30	200 404	36.45	51.53	4.2				4.7	2.45	0.038	3
2004/05/30	200 405	36.48	51.53	4.6				5.3	2.67	0.033	3
2004/10/07	200 406	37.15	54.43	5.6				5.7	86.7	0.037	22
2004/10/08	200 407	37.18	54.41	4.8				5.0	16.08	0.032	7
2003/09/12	200 301	37.32	55.32	4.6				5.0	12.6	0.037	3
2003/12/24	200 302	35.11	50.52	4.9				4.7	8.5	0.036	4
2002/04/08	200 201	36.46	52.01		4.6			5.2	2.27	0.036	5
2002/04/19	200 202	36.51	49.77			5.2		5.2	6.7	0.034	12
2002/04/19	200 203	36.61	49.68				4.4	4.5	1.55	0.039	5
2002/06/22	200 204	35.59	49.03	6.5				6.1	7.82	0.046	20
2002/06/22	200 205	35.58	48.88				5.0	5.2	1.53	0.043	4
2002/09/02	200 206	35.68	4.83				5.3	5.4	1.97	0.044	4
2000/08/16	200 001	37.01	54.45	4.9				5.1	14.35	0.036	8
1999/03/26	199 901	36.61	50.17	4.3				4.2	1.08	0.037	3
1999/11/19	199 902	37.29	54.39	5.5				5.5	64.92	0.038	12
1999/11/26	199 903	36.92	54.89	5.3				5.3	23.33	0.033	5
1998/07/09	199 801	38.72	48.53	5.9				6.0	7.22	0.019	7
1998/08/21	199 802	34.23	48.18	4.9				5.0	4.04	0.037	4
1998/09/28	199 803	36.52	48.7	4.6				4.6	5.39	0.039	5
1997/02/28	199 701	38.12	48.08	6.1				5.9	5.24	0.018	11
1997/09/16	199 702	36.78	54.08			4.8		5.0	20.42	0.031	3

Date	Earthquake ID	Lat. (N°)	Lon. (E°)	Magnitude				Inverted M_w	Δσ (MPa)	\|${\kappa _0}$\| (s)	N *
				M_w	M_N	M_b	M_L
2019/11/07	201 901	37.71	47.56	5.9				5.8	4.32	0.016	4
2019/09/16	201 902	36.53	49.92	4.6				4.6	2.1	0.03	3
2018/02/09	201 801	35.43	51.86		3.6			3.8	1.9	0.036	9
2018/04/01	201 802	35.56	52.41		4.2			44	2.22	0.047	4
2018/09/22	201 803	36.65	52.98		3.3			4.8	5.35	0.033	6
2017/02/01	201 701	35.38	51.97	3.2				3.5	0.36	0.027	3
2017/04/28	201 702	35.76	51.82		3.4			3.5	4.42	0.01	18
2017/11/30	201 703	35.74	52.12	4.0				4.3	0.83	0.04	9
2017/12/20	201 704	35.68	50.95	4.9				5.1	8.59	0.043	34
2017/12/26	201 705	35.68	50.94	4.0				4.1	4.1	0.044	22
2016/02/01	201 601	35.81	51.57		3.1			3.4	7.69	0.022	5
2016/03/11	201 602	35.82	51.86		3.2			3.3	2.35	0.014	3
2016/04/17	201 603	35.75	52.04		3.4			3.6	0.67	0.025	6
2016/10/22	201 604	35.75	52.12	3.5				4.2	0.39	0.031	7
2015/05/10	201 501	36.78	49.89	4.3				4.5	1.67	0.033	3
2015/08/02	201 502	36.05	51.59		3.1			3.2	3.26	0.03	6
2015/08/25	201 503	35.56	52.59	4.5				4.8	3.91	0.03	21
2015/08/25	201 504	35.56	52.61		3.2			3.5	5.06	0.018	3
2015/09/15	201 505	37.32	54.29	4.3				4.9	11.62	0.029	4
2015/09/21	201 506	35.77	51.98		3.2			3.5	6.59	0.014	3
2014/08/16	201 401	35.97	52.3	4.1				4.8	1.5	0.044	3
2012/01/11	201 201	36.29	52.79	5.0				4.9	3.56	0.038	6
2012/08/11	201 202	38.33	46.84	6.5				6.0	5.57	0.023	7
2012/08/11	201 203	38.36	46.75	6.4				6.0	9.94	0.021	8
2012/08/11	201 204	38.26	46.76	3.4				3.6	1.62	0.026	5
2012/08/11	201 205	38.38	46.85	4.8				4.7	1.61	0.015	4
2012/08/11	201 206	38.32	46.69	5.2				4.9	1. 9	0.029	4
2012/08/11	201 207	38.36	46.66	5.2				5.1	3.36	0.022	4
2012/08/14	201 208	38.45	46.75	5.1				5.2	2.68	0.018	6
2012/08/14	201 209	38.38	46.7	5.0				5.1	1.73	0.025	4
2012/11/07	201 210	38.41	46.6	5.6				5.7	2.28	0.027	4
2011/08/11	201 101	36.61	54.79		4.9			5.1	8.08	0.046	4
2009/10/17	200 901	35.56	51.5	3.8				4.1	3.4	0.031	9
2008/05/27	200 801	36.5	48.72	5.0				4.9	10.38	0.034	7
2007/02/09	200 701	36.77	54.48	3.7				3.8	4.18	0.031	3
2007/05/11	200 702	36.85	49.29	4.3				4.3	0.86	0.03	3
2007/06/18	200 703	34.47	50.84		5.9			5.7	22.99	0.044	8
2007/07/11	200 704	38.75	48.62	5.2				5.0	2.71	0.005	3
2006/03/31	200 601	33.54	48.78	6.1				5.9	6.19	0.041	4
2005/01/10	200 501	37.15	54.47	5.3				5.5	45.71	0.035	22
2005/11/29	200 502	37.4	54.44					5.0	25.23	0.046	6
2004/03/27	200 401	36.92	55.15	4.7				4.9	2.82	0.044	3
2004/05/28	200 402	36.25	51.57	6.3				6.1	14.00	0.035	24
2004/05/29	200 403	36.46	51.4	5.1				5.2	5.62	0.034	4
2004/05/30	200 404	36.45	51.53	4.2				4.7	2.45	0.038	3
2004/05/30	200 405	36.48	51.53	4.6				5.3	2.67	0.033	3
2004/10/07	200 406	37.15	54.43	5.6				5.7	86.7	0.037	22
2004/10/08	200 407	37.18	54.41	4.8				5.0	16.08	0.032	7
2003/09/12	200 301	37.32	55.32	4.6				5.0	12.6	0.037	3
2003/12/24	200 302	35.11	50.52	4.9				4.7	8.5	0.036	4
2002/04/08	200 201	36.46	52.01		4.6			5.2	2.27	0.036	5
2002/04/19	200 202	36.51	49.77			5.2		5.2	6.7	0.034	12
2002/04/19	200 203	36.61	49.68				4.4	4.5	1.55	0.039	5
2002/06/22	200 204	35.59	49.03	6.5				6.1	7.82	0.046	20
2002/06/22	200 205	35.58	48.88				5.0	5.2	1.53	0.043	4
2002/09/02	200 206	35.68	4.83				5.3	5.4	1.97	0.044	4
2000/08/16	200 001	37.01	54.45	4.9				5.1	14.35	0.036	8
1999/03/26	199 901	36.61	50.17	4.3				4.2	1.08	0.037	3
1999/11/19	199 902	37.29	54.39	5.5				5.5	64.92	0.038	12
1999/11/26	199 903	36.92	54.89	5.3				5.3	23.33	0.033	5
1998/07/09	199 801	38.72	48.53	5.9				6.0	7.22	0.019	7
1998/08/21	199 802	34.23	48.18	4.9				5.0	4.04	0.037	4
1998/09/28	199 803	36.52	48.7	4.6				4.6	5.39	0.039	5
1997/02/28	199 701	38.12	48.08	6.1				5.9	5.24	0.018	11
1997/09/16	199 702	36.78	54.08			4.8		5.0	20.42	0.031	3

*

N is the number of records.

In our data set, the event magnitude scale is not homogenous and some of the events are reported with M_N (Nuttli magnitude scales), local magnitude scale (M_L) and body-wave magnitude scale (m_b). Although a uniform magnitude scale is not required for inversion of the seismological parameters, we converted different magnitude types to a uniform M_w scale (Palmer & Atkinson 2020). This conversion is mainly performed to facilitate an easy comparison of the reported earthquakes magnitudes with the inverted M_w values. The magnitude scale conversion is performed using the empirical relationships developed by Mousavi-Bafrouei et al. (2014) for the study region as follows:

$$\begin{eqnarray*} {M_{\rm w}} = \ 0.922\left( { \pm 0.044} \right){M_{\rm N}} + 0.494\left( { \pm 0.226} \right) \end{eqnarray*}$$

(1)

$$\begin{eqnarray*} {M_{\rm w}} = \ 0.81\left( { \pm 0.045} \right){M_{\rm L}} + 1.098\left( { \pm 0.22} \right) \end{eqnarray*}$$

(2)

$$\begin{eqnarray*} {M_{\rm w}} = \ 1.332\left( { \pm 0.048} \right){m_{\rm b}} - 1.474\left( {0.246} \right). \end{eqnarray*}$$

(3)

PROCESSING OF STRONG MOTION RECORDS

We rotated longitudinal and transverse components to obtain the two orthogonal horizontal components northeast (H1) and east–west (H2) components. We also performed the base line correction that includes removing the mean and detrending any linear trend in the raw acceleration records. In order to identify the noise floor mainly at low frequency end of the spectrum, we performed signal-to-noise ratio (SNR) check for each record. The noise was extracted from the pre-event and post-event portion of the recorded time-history. The computed SNR estimates were then subsequently used to select the corner frequencies of filters used in the subsequent processing stage. We selected the high-pass filter corner frequency as the one for which the SNR becomes equal or larger than 3 (Boore & Bommer 2005). For majority of the recordings pre- and post-event noise was available; however, if for a record the selected noise window was smaller than 5 seconds then we chose a filter cut-off of 0.3 Hz. The low-pass filter corner frequency was computed for each component individually. The subsequent processing steps involve tapering of the time-series with a cosine taper to ensure zero levels on either ends of the time-history. We kept the taper window length 5 per cent (on each side) of the total signal length (Dawood et al. 2016). According to Boore (2005) to reduce the effect of the filter response, time-series are extended symmetrically at both ends with zero padding. Finally, we used two passes of Butterworth filter in the time domain with zero phase shift (Boore & Akkar 2003).

Fourier amplitude spectrum (FAS)

We computed FAS of both horizontal and vertical components. The FAS was computed for the entire frequency range up to the Nyquist frequency; however, we restricted the upper limit of the frequency range as 30 Hz. This is mainly to avoid the high-frequency noise. For computing FAS from the recorded data, we considered only the S-wave window of the recorded time-series. The S-wave window was selected using an automated procedure following the approach of Boore & Thompson (2014, Fig. 3). For that purpose, we computed the cumulative sum of squared acceleration values, which is often referred as Arias intensity (Arias 1970). The time corresponding to 3 per cent level of the maximum Arias intensity was considered as the onset of the S-wave window and the 80 per cent level of the maximum value was chosen as the end of the S-wave window (Fig. 3). The FAS obtained from each record were smoothed using the scheme suggested by Konno & Ohmachi (1998), with the bandwidth parameter b = 40 for the smoothening window over a logarithmically spaced frequency range 0.3–30 Hz (40 frequency points). We used an average rotation independent FAS for further analysis (Bayless & Thompson 2019):

$$\begin{eqnarray*} {\rm FAS}\ = \sqrt {\frac{1}{2}\left[ {{\rm FAS}_{H1}^2 + {\rm FAS}_{H2}^2} \right]} , \end{eqnarray*}$$

(4)

where FAS_H1 and FAS_H2 represent the corresponding smoothed FAS for the two horizontal components, respectively.

Figure 3.

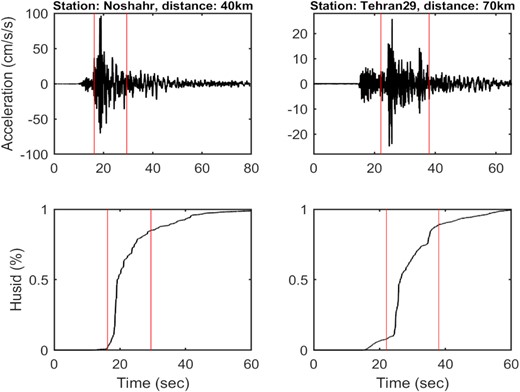
Plots showing the selection of the S-wave window from the acceleration time-series (horizontal components) of the 2004 M_w 6.2 Baladeh (Kojour) earthquake. Upper panels depict the selected S-wave window based on the time interval between the 3 and 80 per cent levels of the normalized Arias intensity (Arias 1970) (bottom panels).

Open in new tab Download slide

METHODOLOGY

Estimation of seismological parameters that characterize the seismic source, path and site effects such as seismic moment (M₀), stress drop (parameter), geometrical spreading, anelastic attenuation and the soil response from recorded earthquake data remains a major challenge. Several approaches have been followed in literature to invert for these model parameters. However, the basic model that represents the FAS of the observed ground motion remains the same and is expressed (Boore 2003) as follows:

$$\begin{eqnarray*} {Y_{ij}}\ \left( {{M_i},\ {R_{ij}},\ f} \right) = {S_i}\ \left( {{M_i},\ f} \right)A\left( {{R_{ij}},\ f} \right){G_j}\left( f \right), \end{eqnarray*}$$

(5)

where Y represents the observed FAS of the ground motion at frequency f, while S, A and G represent seismological source, path and site functions, respectively. R is the distance from the earthquake source to the site (i.e. hypocentral distance).

There are two different approaches for estimating the seismological parameters, one is parametric inversion and the other is non-parametric inversion scheme. In the parametric inversion approach (Kawase 2006; Tsuda et al. 2006, 2010; Edwards et al. 2008; Drouet et al. 2008, 2010, 2011; Poggi et al. 2011; Edwards & Fäh 2013; Bora et al. 2015, 2017; Grendas et al. 2018) a priorifunctional forms are assumed to represent the source, and path functions such as Brune's single corner source model (Brune 1970, 1971) with a specific attenuation function. In the non-parametric approach (Castro et al. 1990; Parolai et al. 2000, 2004; Oth et al. 2008, 2011; Bindi et al. 2009; Pacor et al. 2016; Bindi et al. 2017; Picozzi et al. 2019), the spectra are inverted using GIT, which is essentially a matrix inversion technique. In GIT, a priori functional forms for source and path functions are not required. Instead, source, path and site terms are separated directly from the data. In this study, we adopted GIT approach for estimating the seismological parameters for Alborz region. After taking the logarithm on both sides of eq. (5), we can write a linear equation as:

$$\begin{eqnarray*} {\log_{10}}{Y_{ij}}\ \left( {{M_i},\ {R_{ij}},\ f} \right) &=& {\log_{10}}{S_i}\left( {{M_i},\ f} \right) + {\log_{10}}\ A\left( {{R_{ij}},\ f} \right)\nonumber \\ && + \, {\log_{10}}{G_j}\left( f \right), \end{eqnarray*}$$

(6)

where |${Y_{ij}}( {{M_i},\ {R_{ij}},\ f} )$| is the observed amplitude of the FAS at jth station resulting from the ith earthquake with magnitude M, |${S_i}( {{M_i},\ f} )$| is the source spectrum of the ith earthquake, |$A( {{R_{ij}},\ f} )$| is the attenuation function and |${G_j}( f )$| represents the site response function of the jth station. Note that the FAS here refers to the rotation-independent FAS computed by the two horizontal component using eq. (4).

The inversion was performed in a single step (Oth et al. 2011) using the smoothed and rotational-independent average FAS of the ground motion over 40 frequencies from 0.3 to 30 Hz. The distance range is discretized into 73 bins of width 2 km. This discretization will allow us to estimate the frequency-dependent attenuation function in each distance bin. We used GIT to solve the system of linear equations, written in matrix form as |$Am\ = \ d$|⁠, where d is data vector (i.e. logarithmic FAS), m is the model parameters vector, and A is a data kernel matrix. The overdetermined least square solution is given as, |${m^{est}} = {[ {{A^T}A} ]^{ - 1}}\ {A^T}d$|⁠, where A^–^g =(A^TA)^–¹ is the generalized inverse of A. The system of linear equations is solved in a least-squares sense (Paige & Saunders 1982) and we performed 200 bootstrap analyses (to evaluate the stability of the inversion) at each frequency point (Efron 1979; Parolai et al. 2000, 2004) and estimated the mean and standard deviation from these iterations (Jeong et al. 2020).

At each frequency, we have two unresolved degrees of freedom, that is, attenuation and the site. To address this issue, we need to add constraints in the inversion scheme. Two constrains were imposed in our inversion: (1) we fixed the attenuation term at a reference distance of 15 km, that is A(f,15) = 1 at each frequency. Consequently, the source functions will be representing earthquake source amplitudes at the selected reference distance; (2) to eliminate the trade-off between source and site amplification, we constrained the logarithm of the site amplification of the reference station (generally a rock site) to 0, irrespective of frequency. For selecting an appropriate reference station, we performed a preliminary inversion and also computed the HVSR to examine site transfer functions at all the stations. Our criteria for selecting the reference site were: (1) the inverted site amplification function should be close to 1 over the entire frequency range and (2) for that station the HVSR curve should also be flat over the entire frequency range and must not exhibit any significant peak (i.e. amplification >2). For the selected reference station (Hassan-Abad) that satisfies both of the above-mentioned criteria, the plots of site amplification function from preliminary inversion and HVSR curve are depicted in Fig. 4.

Figure 4.

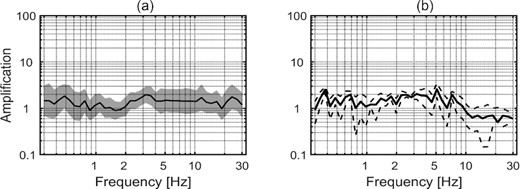
Site amplification for Hassan-Abad chosen as the reference station. (a) Amplification from a preliminary GIT inversion (solid black line and grey shaded area indicate bootstrap mean and ±1 bootstrap standard deviation of the estimated non-parametric site amplification functions from the GIT inversion technique, respectively) and (b) Amplification from HVSR analysis method (solid black line and thin dashed lines indicate mean and ±1 standard deviation).

Open in new tab Download slide

RESULTS

Attenuation function

The non-parametric empirical attenuation functions obtained from inversions are depicted in Fig. 5 corresponding to different frequencies against hypocentral distance.

Figure 5.

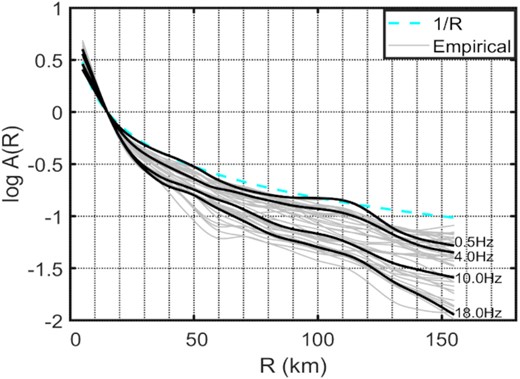
Variation of non-parametric (empirical) attenuation functions with distance in the Alborz region at all frequencies (solid light grey lines). Solid dark-grey lines indicate attenuation function at select frequencies (0.5, 4, 10 and 18 Hz) and the dashed line indicates 1/R amplitude decay.

Open in new tab Download slide

It can be easily noted that the non-parametric attenuation function is frequency-dependent and exhibits rapid decrease up to the distances 40–50 km and followed by a rather slow decay with distance beyond 50 km. The non-parametric attenuation function is expected to capturing the effects from geometrical spreading of body waves and surface waves in the near and far distance range, respectively. Furthermore, it captures frequency-dependent anelastic attenuation function. To separate anelastic attenuation and geometrical spreading from non-parametric attenuation function, we used the following parametric model to fit the observed data:

$$\begin{eqnarray*} A\ \left( {f,\ R} \right) = \frac{{{R_0}}}{{{R^n}}}{\rm{\ exp}}\left[ { - \frac{{\pi f\left( {R - {R_0}} \right)}}{{Q\left( f \right){v_s}}}} \right], \end{eqnarray*}$$

(7)

where |$A( {f,\ R} )$| represents the non-parametric attenuation function obtained from one-step GIT inversion, while n, R₀, Q and |${v_s}$| are the geometrical spreading exponent, reference distance, frequency-dependent apparent quality factor and shear wave velocity, respectively.

Taking the logarithm of both sides of eq. (7), the frequency-dependent apparent quality factor represents the slope of a linear relationship between |$A( {f,\ R} )$| and distance at a selected frequency. However, as can be noted from eq. (7) estimation of |$Q( f )$| is closely tied with the geometrical spreading function and, it is difficult to have simultaneous and unique estimate of both parameters using eq. (7). To avoid the trade-off between geometrical spreading and |$Q( f ),$| we first estimated the geometrical spreading function independent of |$Q( f )\ $|and fixed it in the subsequent estimation of |$Q( f )$|⁠. Thus, the estimated |$Q( f )$| is tied to the adopted geometrical spreading function. We considered the empirical non-parametric functions around 1 Hz (0.8–1.2 Hz), assuming the effect of anelastic attenuation minimum, and fitted them to a bilinear geometrical spreading function. Also, often, 1 Hz is chosen as the reference frequency in attenuation studies (Bora et al. 2015; Pacor et al. 2016; Bindi & Kotha 2020). The choice of the transition distance of the bilinear function was based on our preliminary regressions and, we selected (from a set of transition distances between 30 and 100 km) the cross-over distance resulting in least variance of the residuals. The best non-linear least-squares solution (with minimum residuals) determined as:

$$\begin{eqnarray*} G\ \left( R \right) = \left\{ \begin{array}{@{}*{1}{c}@{}} {{{\left( {\frac{{{R_0}}}{R}} \right)}^{1.01}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ R < 70\ {\rm km}}\\\!\! {{{\left( {\frac{{{R_0}}}{{70}}} \right)}^{1.01}}{{\left( {\frac{{70}}{R}} \right)}^{1.37}}.\!\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 70\ {\rm km} \le R \le 150\ {\rm km}} \end{array} \right.\ \end{eqnarray*}$$

(8)

For the same study region, Motazedian (2006) proposed a tri-linear geometrical spreading model for northern Iran as follows:

$$\begin{eqnarray*} G\ \left( R \right) = \left\{ \begin{array}{@{}*{1}{c}@{}} {{R^{ - 1}}\ \ \ \ \ R < 70\,\,{\rm km}}\\ {{R^{0 \cdot 2}}\ \ \ 70\,\,{\rm km} \le R \le 150\,\,{\rm km}}\\ {{R^{ - 0 \cdot 1}}\ \ \ \ \ \ \ R >150\,\,{\rm km}} \end{array}\right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,. \end{eqnarray*}$$

(9)

In Fig. 6, the estimated geometrical spreading function determined from this study, a theoretical distance decay of |${\raise0.7ex\hbox{$1$} \!{/ {\vphantom {1 R}}} \!\lower0.7ex\hbox{$R$}}$| and, the Motazedian (2006) model are plotted with the empirical non-parametric functions (at different frequencies) to facilitate a graphical comparison. With such comparisons, we aim to evaluate the efficacy of derived geometrical spreading in capturing the apparent attenuation over a broad range of frequencies. We can clearly observe from Fig. 6 that the geometrical spreading function (eq. 8) derived from this study and that of Motazedian (2006) perform similar at near distances, while they are different at larger distances. As expected the match between geometrical spreading functions and the apparent attenuation functions is poorer towards higher frequencies, which can be attributed to frequency-dependent anelastic attenuation. Moreover, the high geometrical spreading rate at large distances obtained in this study is similar to the other studies for this region (Ahmadzadeh et al. 2019). Similar observations were made in southern Australia (Allen et al. 2007) where the apparent high geometrical spreading was attributed to the well-established velocity gradient in the region (Collins et al. 2003) that allows loss of Lg-wave energy into the mantle (e.g. Bowman & Kennett 1991; Atkinson & Mereu 1992).

Figure 6.

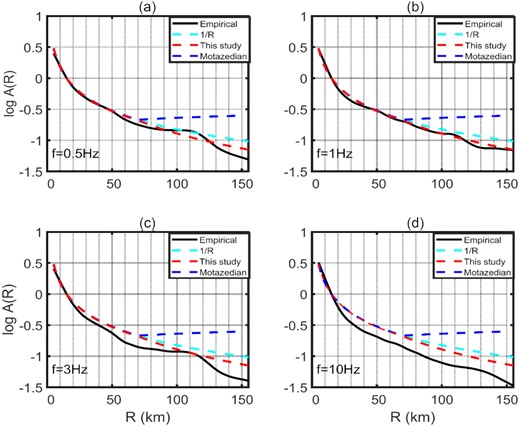
Comparison of the observed non-parametric attenuation functions with different distance decay models at frequencies (a) 0.5 Hz, (b) 1.0 Hz, (c) 3.0 Hz and (d) 10 .0 Hz.

Open in new tab Download slide

Once, the geometrical spreading function is determined we keep it fixed for estimating the |$Q( f )$|⁠. However, as mentioned earlier the geometrical spreading function and the anelastic attenuation functions are tied because of the way they enter into the model formulation (eq. 7). Thus, the estimation of |$Q( f )$| from the empirical attenuation functions is always dependent on the adopted geometrical spreading function. Therefore, in this study, we have estimated |$Q( f )$| by considering three cases of geometrical spreading function. We consider the theoretical geometrical spreading function for Swaves (1/R), bilinear (from this study) and the tri-linear hinged (Motazedian 2006) geometrical spreading model to correct the empirical (non-parametric) attenuation functions. To avoid the numerical instabilities (negative Q values) the fitting was performed in the distance range 21–100 km. The Q was determined at each frequency from the slope of least-squares regression line using |$Q( f )\ = {Q_0}\ {f^N}$| function, where Q₀ and N are the regression coefficients. Fig. 7 depicts the fitting procedure and estimation of Q₀ and N for the two cases: (i) the theoretical geometrical spreading function of |${\raise0.7ex\hbox{$1$} \!{/ {\vphantom {1 R}}} \!\lower0.7ex\hbox{$R$}}$| and (ii) the bilinear geometrical spreading function determined in this study. Final estimate of quality factor has been derived as |$Q\ ( f ) = {\rm{\ }}168{f^{0 \cdot 89}}$| (Fig. 7a) for the single decay geometrical spreading model and |$Q\ ( f ) = {\rm{\ }}146{f^{0 \cdot 91}}$| for the bilinear geometrical spreading model (Fig. 7b). For comparison purpose, we also used Motazedian (2006) geometrical spreading model and obtained the corresponding Q model as |$Q\ ( f ) = {\rm{\ }}93{f^{1 \cdot 02}}$|⁠. From this analysis it is clear that the derived (average) Q model is strongly coupled with the adopted geometrical spreading function. Nevertheless, the derived quality factor values are not very different (statistically) given the uncertainty involved in their determination (Fig. 7).

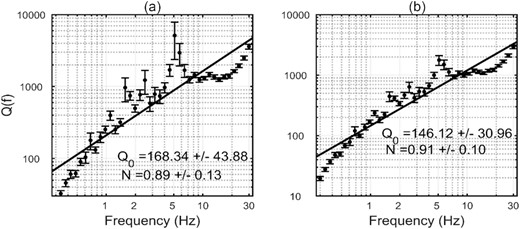
Q(f) model resulting from non-parametric attenuation function after fitting a frequency-dependent Q model along with the Q0 and N parameters, (a) for the 1/R geometrical spreading model and (b) for the bilinear geometrical model obtained from this study for Alborz region.

Figure 7.

Q(f) model resulting from non-parametric attenuation function after fitting a frequency-dependent Q model along with the Q₀ and N parameters, (a) for the 1/R geometrical spreading model and (b) for the bilinear geometrical model obtained from this study for Alborz region.

Open in new tab Download slide

Table 2 presents a comparison of the derived Q models for Alborz region along with the Q-model derived in this study. The adopted geometrical spreading functions are also given along with the derived Qmodels in Table 2. Motazedian (2006) used 259 three-component strong-motion accelerograms recorded within northern Iran from 22 events in the magnitude range 4.9–7.4 and derived the quality factor as |$Q\ ( f ) = {\rm{\ }}87{f^{1 \cdot 46}}$|⁠; this is similar to our estimated Q values using their geometrical spreading model. Zafarani et al. (2012) evaluated the quality factor as |$Q\ ( f ) = {\rm{\ }}101{f^{0 \cdot 8}}$| using the generalized inversion of the S-wave amplitude spectra from the strong-motion data in the Alborz region. Motaghi & Ghods (2012) used 136 earthquakes recorded at stations of the Institute of Geophysics of the University of Tehran during 1996–2007 in central Alborz mountains and reported a quality factor as |$Q\ ( f ) = {\rm{\ }}109{f^{0 \cdot 73{\rm{\ }}}}$|⁠. Farrokhi & Hamzehloo (2017) by using the extended coda normalization method for 380 local earthquakes within frequency band 0.4–24 Hz, estimated the quality factors |$Q\ ( f ) = {\rm{\ }}83{f^{0 \cdot 99{\rm{\ }}}}$| and |$Q\ ( f ) = {\rm{\ }}68{f^{0 \cdot 96{\rm{\ }}}}$| for Alborz region and North Central Iran, respectively. Ahmadzadeh et al. (2019) used 312 crustal earthquakes recorded (1117 seismograms with M_L 3–5.6) in the Alborz region between 2005 and 2017. They applied non-parametric spectral modelling of S-wave spectral amplitudes and estimated a quality factor model as|$\ Q\ ( f ) = {\rm{\ }}162{f^{0 \cdot 61{\rm{\ }}}}$| for a single decay model and |$Q\ ( f ) = {\rm{\ }}135{f^{0 \cdot 76{\rm{\ }}}}$| for a bilinear geometrical spreading model. The Q-model derived from this study is found to be similar to the models derived by Ahmadzadeh et al. (2019) and also, it is not very different from the models of Zafarani et al. (2012) and Motaghi & Ghods (2012). The Q-models determined by Motazedian (2006) and Farrokhi & Hamzehloo (2017) are different from the models derived in this study, which can be attributed to the difference in the underlying data set (Motazedian 2006) and to that the Farrokhi & Hamzehloo (2017) perform their analysis on the coda part of the records, while in the present study the S-wave window is used. Out of 65 events only 4 events are common between our study and the Motazedian (2006) (maximum 50 records).

Table 2.

Open in new tab

Attenuation models for Alborz region.

Reference	Q(f)	Geometrical spreading	Frequency range (Hz)
Motazedian (2006)	\|$Q\ ( f ) = {\rm{\ }}87{f^{1 \cdot 46}}$\|	$\left\{ \begin{array}{@{}*{1}{c}@{}} {{R^{ - 1}}\ \ \ \ \ R < 70}\\ {{R^{0 \cdot 2}}\ \ \ 70 \le R \le 150}\\ {{R^{ - 0 \cdot 1}}\ \ \ \ \ \ \ R >150} \end{array} \right. $	\|$1 < f \le 10$\|
Zafarani et al. (2012)	\|$Q\ ( f ) = {\rm{\ }}101{f^{0 \cdot 8}}$\|	$\left\{ \begin{array}{@{}*{1}{c}@{}} {{R^{ - 1}}\ \ \ \ \ R < 70}\\ {{R^{0 \cdot 2}}\ \ \ 70 \le R \le 150}\\ {{R^{ - 0 \cdot 1}}\ \ \ \ \ \ \ R >150} \end{array} \right. $	\|$0.4 < f \le 15$\|
Motaghi & Ghods (2012)	\|$Q\ ( f ) = {\rm{\ }}109{f^{0 \cdot 73{\rm{\ }}}}$\|⁠.	$\left\{ \begin{array}{@{}*{1}{c}@{}} {{R^{ - 1.15}}\ \ \ \ \ R < 80}\\ {{R^{0 \cdot 09}}\ \ \ 80 \le R \le 160}\\ {{R^{ - 0 \cdot 5}}\ \ \ \ \ \ \ R >160} \end{array} \right. $	\|$0.6 \le f \le 12$\|
Farrokhi & Hamzehloo (2017)	\|$Q\ ( f ) = {\rm{\ }}83{f^{0 \cdot 99{\rm{\ }}}}$\|	$\left\{ \begin{array}{@{}*{1}{c}@{}} {{R^{ - 1}}\ \ \ \ \ R < 90}\\ {{{( {90R} )}^{ - 0 \cdot 5}}\ \ \ \ \ \ \ R \ge 90} \end{array} \right. $	\|$0.4 < f \le 24$\|
Ahmadzadeh et al. (2019)	Q \|$( f ) = {\rm{\ }}162{f^{0 \cdot 61{\rm{\ }}}}$\|	\|${( {\frac{{{R_0}}}{R}} )^1}$\|	\|$0.3 < f \le 20$\|
	\|$Q\ ( f ) = {\rm{\ }}135{f^{0 \cdot 76{\rm{\ }}}}$\|	$\begin{array}{@{}*{1}{c}@{}} {{{( {\frac{{{R_0}}}{R}} )}^1}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ R < 70\ }\\ {{{( {\frac{{{R_0}}}{{60}}} )}^1}{{( {\frac{{60}}{R}} )}^{1.4}}.\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 70\ \le R \le 100\ } \end{array}$
This study	Q \|$( f ) = {\rm{\ }}168{f^{0 \cdot 89{\rm{\ }}}}$\|	\|${( {\frac{{{R_0}}}{R}} )^1}$\|	\|$0.3 \le f \le 30$\|
	Q \|$( f ) = {\rm{\ }}146{f^{0 \cdot 91{\rm{\ }}}}$\|	$\begin{array}{@{}*{1}{c}@{}} {{{( {\frac{{{R_0}}}{R}} )}^{1.01}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ R < 70\ }\\ {{{( {\frac{{{R_0}}}{{70}}} )}^{1.01}}{{( {\frac{{70}}{R}} )}^{1.37}}.\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 70\ \le R \le 150\ } \end{array}$

Reference	Q(f)	Geometrical spreading	Frequency range (Hz)
Motazedian (2006)	\|$Q\ ( f ) = {\rm{\ }}87{f^{1 \cdot 46}}$\|	$\left\{ \begin{array}{@{}*{1}{c}@{}} {{R^{ - 1}}\ \ \ \ \ R < 70}\\ {{R^{0 \cdot 2}}\ \ \ 70 \le R \le 150}\\ {{R^{ - 0 \cdot 1}}\ \ \ \ \ \ \ R >150} \end{array} \right. $	\|$1 < f \le 10$\|
Zafarani et al. (2012)	\|$Q\ ( f ) = {\rm{\ }}101{f^{0 \cdot 8}}$\|	$\left\{ \begin{array}{@{}*{1}{c}@{}} {{R^{ - 1}}\ \ \ \ \ R < 70}\\ {{R^{0 \cdot 2}}\ \ \ 70 \le R \le 150}\\ {{R^{ - 0 \cdot 1}}\ \ \ \ \ \ \ R >150} \end{array} \right. $	\|$0.4 < f \le 15$\|
Motaghi & Ghods (2012)	\|$Q\ ( f ) = {\rm{\ }}109{f^{0 \cdot 73{\rm{\ }}}}$\|⁠.	$\left\{ \begin{array}{@{}*{1}{c}@{}} {{R^{ - 1.15}}\ \ \ \ \ R < 80}\\ {{R^{0 \cdot 09}}\ \ \ 80 \le R \le 160}\\ {{R^{ - 0 \cdot 5}}\ \ \ \ \ \ \ R >160} \end{array} \right. $	\|$0.6 \le f \le 12$\|
Farrokhi & Hamzehloo (2017)	\|$Q\ ( f ) = {\rm{\ }}83{f^{0 \cdot 99{\rm{\ }}}}$\|	$\left\{ \begin{array}{@{}*{1}{c}@{}} {{R^{ - 1}}\ \ \ \ \ R < 90}\\ {{{( {90R} )}^{ - 0 \cdot 5}}\ \ \ \ \ \ \ R \ge 90} \end{array} \right. $	\|$0.4 < f \le 24$\|
Ahmadzadeh et al. (2019)	Q \|$( f ) = {\rm{\ }}162{f^{0 \cdot 61{\rm{\ }}}}$\|	\|${( {\frac{{{R_0}}}{R}} )^1}$\|	\|$0.3 < f \le 20$\|
	\|$Q\ ( f ) = {\rm{\ }}135{f^{0 \cdot 76{\rm{\ }}}}$\|	$\begin{array}{@{}*{1}{c}@{}} {{{( {\frac{{{R_0}}}{R}} )}^1}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ R < 70\ }\\ {{{( {\frac{{{R_0}}}{{60}}} )}^1}{{( {\frac{{60}}{R}} )}^{1.4}}.\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 70\ \le R \le 100\ } \end{array}$
This study	Q \|$( f ) = {\rm{\ }}168{f^{0 \cdot 89{\rm{\ }}}}$\|	\|${( {\frac{{{R_0}}}{R}} )^1}$\|	\|$0.3 \le f \le 30$\|
	Q \|$( f ) = {\rm{\ }}146{f^{0 \cdot 91{\rm{\ }}}}$\|	$\begin{array}{@{}*{1}{c}@{}} {{{( {\frac{{{R_0}}}{R}} )}^{1.01}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ R < 70\ }\\ {{{( {\frac{{{R_0}}}{{70}}} )}^{1.01}}{{( {\frac{{70}}{R}} )}^{1.37}}.\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 70\ \le R \le 150\ } \end{array}$

Table 2.

Open in new tab

Attenuation models for Alborz region.

Reference	Q(f)	Geometrical spreading	Frequency range (Hz)
Motazedian (2006)	\|$Q\ ( f ) = {\rm{\ }}87{f^{1 \cdot 46}}$\|	$\left\{ \begin{array}{@{}*{1}{c}@{}} {{R^{ - 1}}\ \ \ \ \ R < 70}\\ {{R^{0 \cdot 2}}\ \ \ 70 \le R \le 150}\\ {{R^{ - 0 \cdot 1}}\ \ \ \ \ \ \ R >150} \end{array} \right. $	\|$1 < f \le 10$\|
Zafarani et al. (2012)	\|$Q\ ( f ) = {\rm{\ }}101{f^{0 \cdot 8}}$\|	$\left\{ \begin{array}{@{}*{1}{c}@{}} {{R^{ - 1}}\ \ \ \ \ R < 70}\\ {{R^{0 \cdot 2}}\ \ \ 70 \le R \le 150}\\ {{R^{ - 0 \cdot 1}}\ \ \ \ \ \ \ R >150} \end{array} \right. $	\|$0.4 < f \le 15$\|
Motaghi & Ghods (2012)	\|$Q\ ( f ) = {\rm{\ }}109{f^{0 \cdot 73{\rm{\ }}}}$\|⁠.	$\left\{ \begin{array}{@{}*{1}{c}@{}} {{R^{ - 1.15}}\ \ \ \ \ R < 80}\\ {{R^{0 \cdot 09}}\ \ \ 80 \le R \le 160}\\ {{R^{ - 0 \cdot 5}}\ \ \ \ \ \ \ R >160} \end{array} \right. $	\|$0.6 \le f \le 12$\|
Farrokhi & Hamzehloo (2017)	\|$Q\ ( f ) = {\rm{\ }}83{f^{0 \cdot 99{\rm{\ }}}}$\|	$\left\{ \begin{array}{@{}*{1}{c}@{}} {{R^{ - 1}}\ \ \ \ \ R < 90}\\ {{{( {90R} )}^{ - 0 \cdot 5}}\ \ \ \ \ \ \ R \ge 90} \end{array} \right. $	\|$0.4 < f \le 24$\|
Ahmadzadeh et al. (2019)	Q \|$( f ) = {\rm{\ }}162{f^{0 \cdot 61{\rm{\ }}}}$\|	\|${( {\frac{{{R_0}}}{R}} )^1}$\|	\|$0.3 < f \le 20$\|
	\|$Q\ ( f ) = {\rm{\ }}135{f^{0 \cdot 76{\rm{\ }}}}$\|	$\begin{array}{@{}*{1}{c}@{}} {{{( {\frac{{{R_0}}}{R}} )}^1}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ R < 70\ }\\ {{{( {\frac{{{R_0}}}{{60}}} )}^1}{{( {\frac{{60}}{R}} )}^{1.4}}.\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 70\ \le R \le 100\ } \end{array}$
This study	Q \|$( f ) = {\rm{\ }}168{f^{0 \cdot 89{\rm{\ }}}}$\|	\|${( {\frac{{{R_0}}}{R}} )^1}$\|	\|$0.3 \le f \le 30$\|
	Q \|$( f ) = {\rm{\ }}146{f^{0 \cdot 91{\rm{\ }}}}$\|	$\begin{array}{@{}*{1}{c}@{}} {{{( {\frac{{{R_0}}}{R}} )}^{1.01}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ R < 70\ }\\ {{{( {\frac{{{R_0}}}{{70}}} )}^{1.01}}{{( {\frac{{70}}{R}} )}^{1.37}}.\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 70\ \le R \le 150\ } \end{array}$

Reference	Q(f)	Geometrical spreading	Frequency range (Hz)
Motazedian (2006)	\|$Q\ ( f ) = {\rm{\ }}87{f^{1 \cdot 46}}$\|	$\left\{ \begin{array}{@{}*{1}{c}@{}} {{R^{ - 1}}\ \ \ \ \ R < 70}\\ {{R^{0 \cdot 2}}\ \ \ 70 \le R \le 150}\\ {{R^{ - 0 \cdot 1}}\ \ \ \ \ \ \ R >150} \end{array} \right. $	\|$1 < f \le 10$\|
Zafarani et al. (2012)	\|$Q\ ( f ) = {\rm{\ }}101{f^{0 \cdot 8}}$\|	$\left\{ \begin{array}{@{}*{1}{c}@{}} {{R^{ - 1}}\ \ \ \ \ R < 70}\\ {{R^{0 \cdot 2}}\ \ \ 70 \le R \le 150}\\ {{R^{ - 0 \cdot 1}}\ \ \ \ \ \ \ R >150} \end{array} \right. $	\|$0.4 < f \le 15$\|
Motaghi & Ghods (2012)	\|$Q\ ( f ) = {\rm{\ }}109{f^{0 \cdot 73{\rm{\ }}}}$\|⁠.	$\left\{ \begin{array}{@{}*{1}{c}@{}} {{R^{ - 1.15}}\ \ \ \ \ R < 80}\\ {{R^{0 \cdot 09}}\ \ \ 80 \le R \le 160}\\ {{R^{ - 0 \cdot 5}}\ \ \ \ \ \ \ R >160} \end{array} \right. $	\|$0.6 \le f \le 12$\|
Farrokhi & Hamzehloo (2017)	\|$Q\ ( f ) = {\rm{\ }}83{f^{0 \cdot 99{\rm{\ }}}}$\|	$\left\{ \begin{array}{@{}*{1}{c}@{}} {{R^{ - 1}}\ \ \ \ \ R < 90}\\ {{{( {90R} )}^{ - 0 \cdot 5}}\ \ \ \ \ \ \ R \ge 90} \end{array} \right. $	\|$0.4 < f \le 24$\|
Ahmadzadeh et al. (2019)	Q \|$( f ) = {\rm{\ }}162{f^{0 \cdot 61{\rm{\ }}}}$\|	\|${( {\frac{{{R_0}}}{R}} )^1}$\|	\|$0.3 < f \le 20$\|
	\|$Q\ ( f ) = {\rm{\ }}135{f^{0 \cdot 76{\rm{\ }}}}$\|	$\begin{array}{@{}*{1}{c}@{}} {{{( {\frac{{{R_0}}}{R}} )}^1}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ R < 70\ }\\ {{{( {\frac{{{R_0}}}{{60}}} )}^1}{{( {\frac{{60}}{R}} )}^{1.4}}.\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 70\ \le R \le 100\ } \end{array}$
This study	Q \|$( f ) = {\rm{\ }}168{f^{0 \cdot 89{\rm{\ }}}}$\|	\|${( {\frac{{{R_0}}}{R}} )^1}$\|	\|$0.3 \le f \le 30$\|
	Q \|$( f ) = {\rm{\ }}146{f^{0 \cdot 91{\rm{\ }}}}$\|	$\begin{array}{@{}*{1}{c}@{}} {{{( {\frac{{{R_0}}}{R}} )}^{1.01}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ R < 70\ }\\ {{{( {\frac{{{R_0}}}{{70}}} )}^{1.01}}{{( {\frac{{70}}{R}} )}^{1.37}}.\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 70\ \le R \le 150\ } \end{array}$

Source spectra

The non-parametric source spectra obtained from the GIT inversion were used to estimate the parametric source functions. The non-parametric source spectra are constrained at the reference distance of 15 km. The shape of the empirical non-parametric source spectra exhibited an exponential decay at frequencies beyond 6–8 Hz. We attributed this decay at high-frequencies in the source spectra to a high-frequency attenuation parameter |${\kappa _0}$| (Anderson & Hough 1984; Oth et al. 2008, 2011; Ktenidou et al. 2014; Ji et al. 2020). Although in our analysis |${\kappa _0}$| is determined from the source spectra, the exact physical origin of this parameter is not yet clear (Ktenidou et al. 2014, 2015; Edwards et al. 2015). Originally, |${\kappa _0}$| was attributed to the site-related attenuation by Anderson & Hough (1984). However, some studies have also argued that it may also have a component that can be related to the near source attenuation (Papageorgiou & Aki 1983; Oth et al. 2011; Kilb et al. 2012; Bindi et al. 2017; Ji et al. 2020). Discussing the exact physical origin of |${\kappa _0}$| is beyond the scope of this paper, and it is difficult to associate any physical meaning to |${\kappa _0}$| without imposing additional constraints in the current modelling framework. In this study, we estimated |${\kappa _0}$| from the high-frequency portion of the empirical source spectra so as to have a flat spectrum above the corner-frequency |$({f_c})$|⁠. The |${\kappa _0}$| is obtained by fitting the logarithm of non-parametric (source) spectral amplitudes to the following equation:

$$\begin{eqnarray*} \log{_{10}}{S_i}\ \left( {f > {f_E}} \right) = {S_{0.i}}\ - \log{_{10}}{\rm{exp}}\left( {\pi {\kappa _0}_if} \right). \end{eqnarray*}$$

(10)

In eq. (10) |${S_i}$| is the non-parametric source spectrum for ith event while |${\kappa _{0i}}$| is the corresponding |${\kappa _0}$| value and, |${f_E}$| is the lower limit of the frequency used for this fitting (i.e. frequency above which the decay is approximately linear on a plot of log Fourier amplitude versus linear frequency; Van Houtte et al. 2014). For our analysis |${f_E}$| was chosen either 10 or 15 Hz by visually inspecting each source spectrum. Subsequently, the estimated |${\kappa _0}$| was used to correct the high-frequency decay of the non-parametric source spectra. Fig. 8(a) shows an example of an uncorrected and |${\kappa _0}$|-corrected non-parametric source spectrum. Fig. 8(b) depicts distribution of |${\kappa _0}$| determined from each non-parametric source spectrum. The average |${\kappa _0}\ $| was found to be 0.032 s with the standard deviation of 0.01 s. Motazedian (2006) computed κ₀ (represents the attenuation in the near-surface geology) for horizontal and vertical components equal to 0.05 and 0.03 s, respectively. Zafarani et al. (2012) estimated κ₀ = 0.05 s for the horizontal and 0.02 s for the vertical components, respectively.

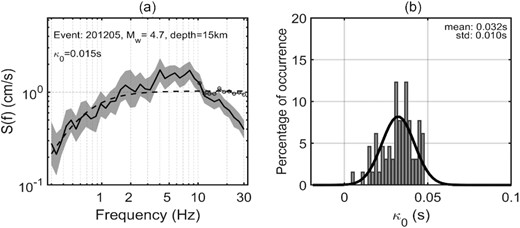
$(a) Bootstrap mean (solid black line) and bootstrap standard deviation (grey shaded portion) of non-parametric source spectrum obtained from GIT inversion. The thin circled-line indicates the source spectrum after ${\kappa _0}$ correction applied on the frequencies beyond 10 Hz. (b) Distribution of ${\kappa _0}$ values obtained from the empirical non-parametric source spectra.$

Figure 8.

(a) Bootstrap mean (solid black line) and bootstrap standard deviation (grey shaded portion) of non-parametric source spectrum obtained from GIT inversion. The thin circled-line indicates the source spectrum after |${\kappa _0}$| correction applied on the frequencies beyond 10 Hz. (b) Distribution of |${\kappa _0}$| values obtained from the empirical non-parametric source spectra.

Open in new tab Download slide

The |${\kappa _0}$|-corrected source spectra are shown for few selected events in Figs 9(a), 9(b) and 9(c), while Fig. 9(d) depicts source spectra for all the events in the data set. We can clearly observe that the |${\kappa _0}$| corrected source spectra are relatively flat at the high-frequency end. The |${\kappa _0}$|-corrected source spectra are modelled by assuming an ω-square Brune model (Aki 1967; Brune 1970, 1971). The single corner Brune's source model is mainly described in terms of the corner frequency, |${f_c}$|⁠, and the asymptotic low-frequency amplitude that is proportional to the seismic moment (⁠|${M_0}$|⁠). We determined |${f_c}$| and |${M_0}$| for each event by fitting the |${\kappa _0}$|-corrected non-parametric source spectra (horizontal component) to the following equation (Boore 1983):

$$\begin{eqnarray*} S\ \left( f \right) = \ C{M_0}\frac{{{{\left( {2\pi f} \right)}^2}}}{{1 + {{\left( {\frac{f}{{{f_c}}}} \right)}^2}}}, \end{eqnarray*}$$

(11)

where C is a scaling constant expressed as follows:

$$\begin{eqnarray*} C\ = \frac{{{R_{{\rm{\Theta }}\phi }}VF}}{{4\pi \rho {\beta ^3}{R_0}}}, \end{eqnarray*}$$

(12)

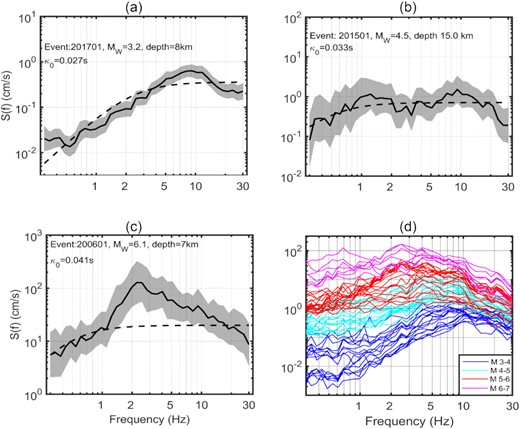
$Panels (a), (b) and (c) represent ${\kappa _0}$ corrected non-parametric source spectrum (solid black line) in comparison with Brune's source model (dashed lines). The grey shaded area is the bootstrap standard deviation corresponding to each source spectrum. (d) Plots of ${\kappa _0}$ corrected non-parametric source spectrum for all events.$

Figure 9.

Panels (a), (b) and (c) represent |${\kappa _0}$| corrected non-parametric source spectrum (solid black line) in comparison with Brune's source model (dashed lines). The grey shaded area is the bootstrap standard deviation corresponding to each source spectrum. (d) Plots of |${\kappa _0}$| corrected non-parametric source spectrum for all events.

Open in new tab Download slide

In eq. (12), |${R_{{\rm{\Theta \varphi }}}}$| is a radiation pattern ( = 0.55 on average for shear waves), V =|$\sqrt 2 \ $| is the partitioning of seismic energy into two horizontal components, F = 2 is the free surface amplification in the vicinity of the source, β = 3.5 km s^–1 is the average shear wave velocity near the source zone and |$\rho \ $|= 2.8 g cm^–3 is the crustal density. The estimated corner frequencies |${f_c}$| are plotted against the estimated |${M_0}$| in Fig. 10(a). A linear trend between logarithms of |${f_c}$| and |${M_0}$| can be easily observed, though towards moderate to larger |${M_0}$| values we observe larger scatter. The relationship between |${f_c}$| and |${M_0}$| can be modelled as:

$$\begin{eqnarray*} {\log _{10}}\left( {{f_c}} \right) = \ 11.1 - 0.293{\log _{10}}({M_0}) \end{eqnarray*}$$

(13)

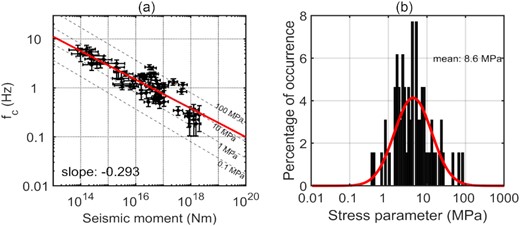
$Plots showing, (a) corner frequency, fc, variations with seismic moment for Alborz earthquakes (constant stress parameter values (dashed lines) and slope of linear fit (solid red line) are also shown) and (b) distribution of stress parameters ($\Delta \sigma $).$

Figure 10.

Plots showing, (a) corner frequency, f_c, variations with seismic moment for Alborz earthquakes (constant stress parameter values (dashed lines) and slope of linear fit (solid red line) are also shown) and (b) distribution of stress parameters (⁠|$\Delta \sigma $|⁠).

Open in new tab Download slide

Eq. (13) and Fig. 10(a) indicate that the slope of the |${f_c}$| and |${M_0}$| fitted line is close to the theoretically expected value of –1/3. This relationship (eq. 13) and the obtained slope indicate that self-similar constant stress-parameter scaling (Aki 1967) holds for the considered data set. The theoretical scaling relationship between |${f_c}$| and |${M_0}$| (Eshelby 1957; Brune 1970, 1971) is as follows:

$$\begin{eqnarray*} {f_c} = \ 4.9 \times {10^6}\beta {\left( {\frac{{{\rm{\Delta }}\sigma }}{{{M_0}}}} \right)^{1/3}}, \end{eqnarray*}$$

(14)

in which |${\rm{\Delta }}\sigma $| is the Brune's stress parameter. As suggested by Atkinson & Beresnev (1997)—‘Don't call it stress drop’—in this study we used the term stress parameter for |${\rm{\Delta }}\sigma .$| In this sense, Δσ describes the high-frequency content of earthquake ground motions (Hanks & McGuire 1981). Using eq. (14) and the event-specific values of |${f_c}$| and |${M_0}$|⁠, we computed |${\rm{\Delta }}\sigma $| for each event. The shear wave velocity near the source is assumed as |$\beta = 3.5\,\, {\rm km\,s}^{-1}$|⁠. Fig. 10(b) depicts the distribution of estimated |${\rm{\Delta }}\sigma $| values ranging from 0.35 to 86.7 MPa. The average |${\rm{\Delta }}\sigma $| is 8.6 MPa. The event-specific |$\Delta \sigma $| values are given in Table 1. The estimated |${M_0}$| values are converted to M_w using the Hanks & Kanamori (1979) relationship defined as follows:

$$\begin{eqnarray*} {M_{\rm w}} = \frac{2}{3}\ \left( {\log {M_0} - 9.05} \right) \end{eqnarray*}$$

(15)

in which |${M_0}$| values are in Nm.

Fig. 11 compares the inverted M_w (computed using source spectral fitting) with the database magnitude values. In Fig. 11(a), the original magnitude values at different scales are shown. Fig. 11(b) compares the inverted M_w values with the converted moment magnitudes using eqs (1), (2) and (3). The magnitude values from spectral fitting of source spectra show a good correlation with the database magnitude values for both cases, with a slight improvement when converting all magnitude scales into M_w. Fig. 12(a) shows the variation of the estimated |${\rm{\Delta }}\sigma $| values against the inverted M_w values. We also show |${\rm{\Delta }}\sigma $| values from Zafarani et al. (2012) for comparison. Clearly, the |${\rm{\Delta }}\sigma $| values exhibit a large scatter over the entire magnitude range and, we observed smaller stress parameter (<5 MPa) towards smaller magnitude (M_w < 4) events, while the |${\rm{\Delta }}\sigma $| values are larger towards larger magnitude. However, we do not prefer to propose a model for magnitude-dependence of |${\rm{\Delta }}\sigma $| owing to the lack of sufficient amount of data from higher magnitude-events (M > 6) in the region. Past studies conducted in this region also reported similar |${\rm{\Delta }}\sigma $| values and variability. Motazedian (2006) have also obtained average stress parameters of 12.5 MPa (Stochastic point-source) and 6.8 MPa (finite-fault modelling based on dynamic corner frequency) for earthquakes in North of Iran. Zafarani et al. (2012) estimated an average stress parameter values of 18.2 and 11.6 MPa, respectively for eastern and western Alborz region. Ahmadzadeh et al. (2019) calculated the stress parameter values range from about 0.02 to 16 MPa with an average of 1.1 MPa. Fig. 12(b) depicts the variation of the estimated |${\rm{\Delta }}\sigma $| values with focal depths. Although the scatter with depth is large, we see that the higher |${\rm{\Delta }}\sigma $| (>10 MPa) values are mainly associated with the deeper events. Owing to the large uncertainties in the reported focal depths, it is difficult to establish a well-constrained model of Δσ as a function of depth.

Figure 11.

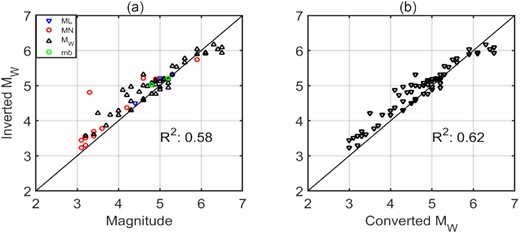
Comparison between the inverted magnitudes and the database magnitudes: (a) the original/reported magnitude values at different scales (b) different magnitudes scales are converted to moment magnitude scale.

Open in new tab Download slide

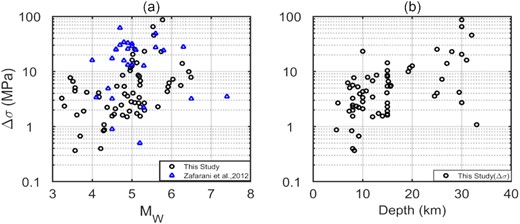
$Stress-parameter ($\Delta \sigma $) values plotted against: (a) the inverted moment magnitude values from this study (black circles) and (b) the focal depth.$

Figure 12.

Stress-parameter (⁠|$\Delta \sigma $|⁠) values plotted against: (a) the inverted moment magnitude values from this study (black circles) and (b) the focal depth.

Open in new tab Download slide

Site amplification functions

Site amplification functions are estimated from the non-parametric inversion. Fig. 13 depicts examples of site amplification functions for some selected stations. Fig. 14 depicts the (station-to-station) variability in the estimated amplification functions. Fig. 14(a) depicts the site-amplification functions determined from GIT, while Fig. 14(b) depicts the HVSR amplification for the same set of stations to facilitate a graphical comparison. Although the site amplification functions at some of the stations may not be well constrained owing to lesser number of recordings, the site amplification functions derived in this study can provide preliminary insights regarding the site effects in the study region. Also, in the absence of site amplification functions from other studies, as is the case for the study region, the site amplification functions derived herein can be potentially useful for further seismological studies. Most of the stations in the data set exhibit amplification factor in the range between 0.2 and 10 (Fig. 14a) and, for some of the stations such as Namin, Vana and Khajeh the resonance peak is clearly visible (Fig. 13). To assess the robustness of the estimated GIT site amplification functions, the site amplification functions are also compared with the empirical transfer functions computed using the HVSR method (Fig. 14b). HVSRs are computed for each record using the following equation:

$$\begin{eqnarray*} {\rm HVSR}\ = \ \frac{{\sqrt {0.5\left( {{\rm FAS}_{H1}^2 + {\rm FAS}_{H2}^2} \right)} }}{{{\rm FAS}{_V}}}, \end{eqnarray*}$$

(16)

where FSA_H1, FAS_H2 and FAS_V are the smoothed FAS values of the two horizontal and vertical components, respectively.

Figure 13.

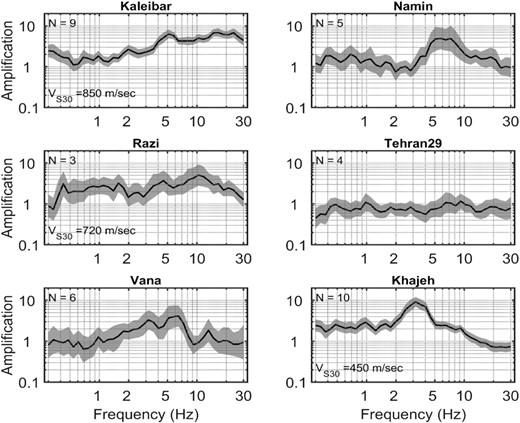
Bootstrap mean (solid black line) and ±1 bootstrap standard deviation (grey shaded area) of the estimated non-parametric site amplification functions at selected stations obtained from the GIT. N represents the number of records analysed at each station.

Open in new tab Download slide

Figure 14.

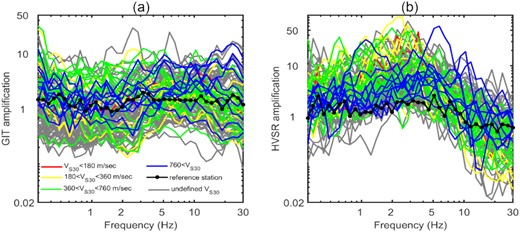
Plots showing: (a) estimated non-parametric site amplification functions at all stations obtained from the GIT inversion technique and (b) site amplification functions at all stations obtained from the HVSR method.

Open in new tab Download slide

We computed the average station-specific HVSR at all the stations with more than three records. As mentioned earlier these station-specific HVSR curves are also used to identify a suitable reference (rock) station. A flat HVSR curve indicates a small or negligible impedance contrast between the sediments and the ‘seismological’ bedrock and thus no amplification of ground motion. In addition to the comparison shown in Fig. 14, Fig. 15 depicts comparison of GIT inverted site amplification functions and HVSR curves for some representative stations individually. At some of the stations such as Abgarm, Arjomand and Mamooniyeh the GIT site amplification curves and HVSR curves exhibit very good match, whereas at stations Eyvanaki1 and Lavasan1 the two curves do not match well. We also checked GIT site amplifications for the vertical components. For the stations where GIT and HVSR site amplification functions were comparable, there was no peak in the GIT site amplification for the vertical component. A similar observation was also made by Pacor et al. (2016) that when the GIT amplification function was flat for vertical component motion, the HVSR amplification function matches well with the GIT derived amplification functions. On the other hand, a non-uniform amplification on the vertical component indicates that two methods have a different shape and HVSR may not be a good indicator of SH site amplification amplitudes.

Figure 15.

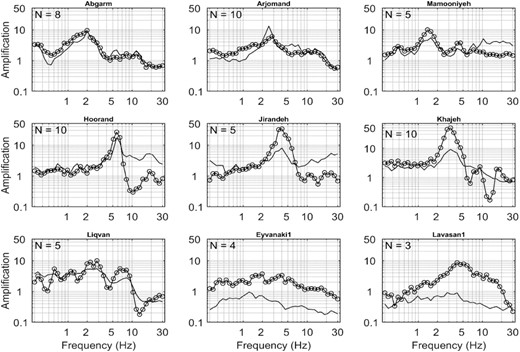
Comparison between GIT (solid line) and HVSR (circled line) site amplification functions for selected stations. N represents the number of records analysed at each station.

Open in new tab Download slide

Furthermore, we compared the peak frequencies and the corresponding peak amplitudes of GIT inverted site amplification functions with those of HVSR curves at each station (Tsuda et al. 2010; Oth et al. 2011). For both the GIT and HVSR amplification functions we picked a global minimum and a global maximum in which the global maximum was accompanied by a local minimum on either side and all other local maxima. The criteria for selecting the peak frequency and the corresponding peak amplitude were: (1) amplitudes of all local maxima should be less than |${\raise0.7ex\hbox{$3$} \!{/ {\vphantom {3 4}}} \!\lower0.7ex\hbox{$4$}}$| of the global maximum, (2) the global minimum is smaller than the global maximum by a factor of five and (3) the amplitude of the global maximum is at least a factor of 2 larger than the amplitudes of the two local minima on either side. Fig. 16 compares peak frequencies and peak amplitudes determined by the two methods for all the stations in the data set. The peak frequencies from the two methods exhibit a better correlation than that for peak amplitudes. Although there is no consensus on whether HVSR amplitude represents the true site response, it is widely accepted that it is being able to adequately capture the resonance peak |${f_0}$| (Fäh et al. 2001).

Figure 16.

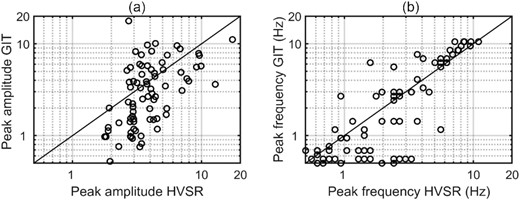
Comparisons between peak amplitudes (a) and peak frequencies (b) determined from GIT and H/V methods.

Open in new tab Download slide

Robustness evaluation of spectral model parameters

The robustness of the spectral model parameters used to parametrize the source spectra |$S( f )$| including stress parameter and inverted moment magnitude, and also the attenuation function |$A( {f,\ r} )$| is evaluated in two ways: (1) visual comparison between the observed and predicted spectra at selected stations and (2) residual analysis. Fig. 17 depicts comparison between the modelled and observed spectra for a selected set of events and station combinations. The source spectra are modelled by assuming an ω-squared model with seismic moments |${M_0}$| estimated from the inversion. The frequency-dependent attenuation function is described by eq. (7), in which the geometrical spreading function is given in eq. (8), and the corresponding quality factor is |$Q\ ( f ) = {\rm{\ }}146{f^{0 \cdot 91}}$|⁠. The forward model predictions were made for two cases of the ω-squared source model, (i) event-specific corner-frequency |${f_c}$| and (ii) |${f_c}$| corresponding to an average stress parameter |$\Delta \sigma \ = \ 8.6$| MPa. In general, the model predicted spectra matched reasonably well with the observed spectra and, as expected the match improves when event-specific |${f_c}$| values are used for the ω-squared source model. However, in practice |$\Delta \sigma $| values of future earthquakes are not known a priori. Hence, it is common practice to use the average stress parameter in such cases. It should also be noted that the forward model predictions shown here are made with an assumption that the source spectrum of an earthquake can be modelled by a single-corner omega-square model.

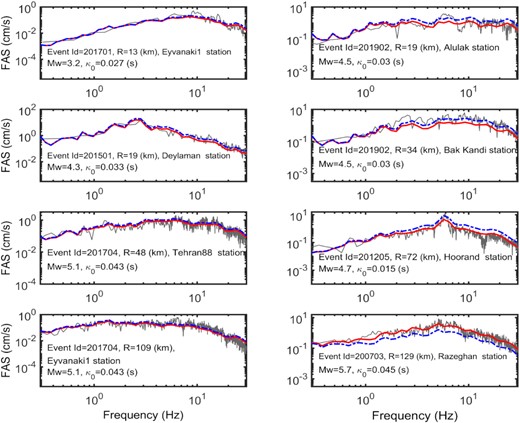
$Comparison between the observed and modelled (using the model parameters derived in this study) FAS. Thin grey curves are showing the observed (average of two horizontal components) spectra at the selected stations. The modelled FAS using the event-specific stress parameter, $\Delta \sigma $, and the average stress parameter $\Delta \sigma = \ 8.6$ MPa, are shown with red thick and blue dashed lines, respectively.$

Figure 17.

Comparison between the observed and modelled (using the model parameters derived in this study) FAS. Thin grey curves are showing the observed (average of two horizontal components) spectra at the selected stations. The modelled FAS using the event-specific stress parameter, |$\Delta \sigma $|⁠, and the average stress parameter |$\Delta \sigma = \ 8.6$| MPa, are shown with red thick and blue dashed lines, respectively.

Open in new tab Download slide

To further evaluate the goodness-of-fit of our non-parametric inverted models, we plotted the residuals against magnitude and distance in Fig. 18 at selected frequencies representing low and high-frequency portion of the spectrum. The residuals are calculated as the difference between the logarithms of the observed spectral amplitudes and the predicted target amplitudes. The predicted values are computed using the non-parametric source, path and site functions. The computed residuals do not show any trend with magnitude and distance and, they are randomly scattered around the center line of zero. It is concluded that, the performed non-parametric inversion provides representative empirical functions for source, path and site effects for the selected data set. The results also indicate robustness of the estimated seismological parameters (e.g.|$\ {M_0}$|⁠, |$\Delta \sigma $|⁠, geometrical spreading function and Q model) from the non-parametric empirical functions.

Figure 18.

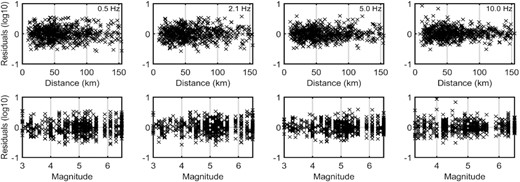
Variation of the residuals with hypocentral distance (top panel) and magnitude (below panel) for 0.5, 2.1, 5.0 and 10.0 frequencies.

Open in new tab Download slide

CONCLUSIONS

In this study, we analysed 478 three-component strong ground motion records from 65 events (M_w 3–6.5) recorded over 111 stations at hypocentral distances |$R \le 150$| km in the Alborz region of northern Iran since 1997. Strong ground motion records are processed following standard protocols, and different magnitude types are converted to a unified moment magnitude to obtain a homogenized catalogue. Fourier spectral amplitudes are computed for the S-wave window of the acceleration time-series. The smoothed Fourier spectral amplitudes at 40 frequencies equally spaced on a log scale are used to estimate non-parametric source, path and site functions using the GIT. Seismological parameters including stress parameter, seismic moment, moment magnitude, geometrical spreading and anelastic attenuation functions are estimated from the non-parametric spectral functions. Major findings from our analysis can be summarized as follows:

The non-parametric empirical attenuation functions were modelled as a combination of frequency-independent geometrical spreading and frequency-dependent anelastic attenuation function. The geometrical spreading function is described by a bilinear piecewise function with a transition distance at 70 km (eq. 8). Motazedian (2006) proposed a trilinear piecewise geometrical spreading function for the same region. The geometrical spreading function derived in this study is simple yet powerful enough to capture the observed trend in the data. Also, the transition distance of 70 km was selected by trial and error method performed over a set of transition distances between 30 and 100 km with an interval of 10 km. The quality factor associated with the bilinear geometrical spreading function was found to be |$Q\ ( f ) = \ 146\ {f^{0.91}}$|⁠. The corresponding quality factor for a theoretical geometrical spreading function of 1/R is |$Q\ ( f ) = \ 168\ {f^{0.89}}$|⁠.
The ω-square single corner source model was found suitable in explaining most of the non-parametric empirical source spectra. The empirical source spectra were first corrected for a high-frequency decay at frequencies beyond 10 Hz. This high-frequency decay was attributed to the |${\kappa _0}$| with an average value (horizontal component) of 0.032 s and standard-deviation of 0.01 s. Although, the exact physical origin of |${\kappa _0}$| is not yet known, we attribute the values determined here with source component of kappa (Papageorgiou & Aki 1983; ; Papageorgiou 1998; Oth et al. 2011; Kilb et al. 2012; Bindi et al. 2017; Ji et al. 2020).
Fitting of an ω-squared source model to |${\kappa _0}$|-corrected empirical source spectra resulted in two source parameters namely seismic moment |${M_0}$| and corner frequency (⁠|${f_c}$|⁠) for each event. The |${M_0}$| values were converted to obtain event-specific moment magnitudes M_w. The inverted M_w were found in good agreement with the magnitude values given in the database. This indicates robustness of the inverted M_w values as well as, that the adequacy of the single-corner ω-squared model to explain the empirical source spectra.
The corner frequency |$( {{f_c}} )$| and the inverted M_w values were used to estimate the Brune's stress parameter (⁠|$\Delta \sigma $|⁠). We observed large variability in |$\Delta \sigma $| but, we did not find a significant dependence of |$\Delta \sigma $| with magnitude. The |$\Delta \sigma $| values in the data set range from 0.36 to 86.7 MPa with an average value of |$\Delta \sigma \ = \ 8.6$| MPa. The |$\Delta \sigma $| values obtained in this study were found comparable with the values obtained from other studies for the study region. Furthermore, the higher |$\Delta \sigma $| values were found to be associated with deeper earthquakes.
The GIT site amplification functions obtained were found to exhibit large station-to-station variability, though we did not observe significant regional pattern in site-amplification functions. We observed a good match between GIT amplification functions and the HVSR curves over some stations. At those stations, a smaller and uniform amplification in the vertical component was found over the entire frequencies range. For stations with high amplification in vertical component, the match between GIT amplification and HVSR curves was found to be poorer.
We tested the robustness of the proposed spectral models herein by comparing the model predicted spectra with the observed spectra for some event and station combinations. Models with event-specific |$\Delta \sigma $| were found to perform better in comparison to an average |$\Delta \sigma $| of 8.6 MPa. From forward prediction perspective, we envisage that the spectral models derived in this study are valid within the magnitude range M_w 3–6.5 and up to a distance of 150 km. Although the models derived in this study are of semi-empirical nature with physics-based ω-squared source model, an extrapolation of the parameters beyond the magnitude and distance range prescribed here must be validated vis-à-vis observed ground motions.

ACKNOWLEDGEMENTS

This work was financially supported by University of Tehran. First author, Mehran Davatgari Fami Tafreshi thanks IIT Gandhinagar for hosting him and providing all the necessary support. The authors also acknowledge the Building and Housing Research Center of Iran for generously providing the data for this work. We also thank Adrien Oth for helping with the technical details related to his GIT code and Saeid Rahimzadeh for his help in preparing Fig. 1. The authors also thank reviewers Daniel Garcia, Carlos Ortiz-Aleman and the editor Prof Victor M. Cruz-Atienza for their constructive comments and feedback, which has helped to improve the paper.

DATA AVAILABILITY

Ground motion records used in this study are accessible at the website of Building and Housing Research Center (BHRC) of Iran (http://www.bhrc.ac.ir/), last accesed February 2020. The derived data generated in this research will be shared on reasonable request to the corresponding author.

REFERENCES

Ahmadzadeh

S.

,

Javan-Doloei

G.

,

Parolai

S.

,

Oth

A.

,

2019

.

Non-parametric spectral modelling of source parameters, path attenuation and site effects from broad-band waveforms of the Alborz earthquakes (2005–2017)

,

Geophys. J. Int.

,

219

,

1514

–

1531

.

Aki

K.

,

1967

.

Scaling law of seismic spectrum

,

J. geophys. Res.

,

72

,

1217

–

1231

.

10.1029/JZ072i004p01217

Ambraseys

N.N.

,

Melville

C.P.

,

1982

.

A History of Persian Earthquakes

,

Cambridge Univ. Press

, p.

219

.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Allen

T.I.

,

Cummins

R.C.

,

Dhu

T.

,

Schneider

J.F.

,

2007

.

Attenuation of ground-motion spectral amplitudes in southeastern Australia

,

Bull. seism. Soc. Am.

,

97

,

1279

–

1292

.

Anderson

J.G.

,

Hough

S.E.

,

1984

.

A model for the shape of the Fourier amplitude spectrum of acceleration at high frequencies

.

Bull. seism. Soc. Am.

,

74

,

1969

–

1993

.

Arias

A.

,

Hansen

R.J.

,

1970

.

A measure of earthquake intensity

, in

Seismic Design for Nuclear Power Plants

, pp.

438

–

483

.,

MIT Press

.

Atkinson

G.M.

,

Mereu

R.

,

1992

.

The shape of ground motion attenuation curves in southeastern Canada

,

Bull. seism. Soc. Am.

,

82

,

2014

–

2031

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Atkinson

G.M.

,

Boore

D.M.

,

1995

.

Ground motion relations for eastern North America

.

Bull. seism. Soc. Am.

,

85

,

17

–

30

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Atkinson

G.M.

,

Beresnev

I.

,

1997

.

Don't call it stress drop

,

Seismol. Res. Lett.

,

68

,

3

–

4

.

Atkinson

G.M.

,

Silva

W.

,

2000

.

Stochastic modeling of California ground motions

,

Bull. seism. Soc. Am.

,

90

,

255

–

274

.

Atkinson

G.M.

,

Boore

D.M.

,

2006

.

Earthquake ground-motion prediction equations for eastern North America

,

Bull. seism. Soc. Am.

,

96

,

2181

–

2205

.

Bayless

B.

,

Thompson

N.A.

,

2019

.

Summary of the BA18 ground-motion model for Fourier amplitude spectra for crustal earthquakes in California

,

Bull. seism. Soc. Am.

,

109

,

2088

–

2105

.

Berberian

M.

,

Walker

R.

,

2010

.

The Rudbar M_w 7.3 earthquake of 1990 June 20; seismotectonics, coseismic and geomorphic displacements, and historic earthquakes of the western ‘High-Alborz’, Iran

,

Geophys. J. Int.

,

182

,

1577

–

1602

.

10.1111/j.1365-246X.2010.04705.x

Bindi

D.

,

Parolai

S.

,

Grosser

H.

,

Milkereit

C.

,

Karakisa

S.

,

2006

.

Crustal attenuation characteristics in northwestern Turkey in the range from 1 to 10 Hz

,

Bull. seism. Soc. Am.

,

96

,

200

–

214

.

Bindi

D.

,

Pacor

F.

,

Luzi

L.

,

Massa

M.

,

Ameri

G.

,

2009

.

The M_w 6.3, 2009 L'Aquila earthquake: source, path and site effects from spectral analysis of strong motion data

,

Geophys. J. Int.

,

179

,

1573

–

1579

.

10.1111/j.1365-246X.2009.04392.x

Bindi

D.

,

Spallarossa

D.

,

Pacor

F.

,

2017

.

Between-event and between station variability observed in the Fourier and response spectra domains: comparison with seismological models

,

Geophys. J. Int.

,

210

,

1092

–

1104

.

Bindi

D.

,

Kotha

S.R.

.,

2020

.

Spectral decomposition of the Engineering Strong Motion (ESM) flat file: regional attenuation, source scaling and Arias stress drop

,

Bull. Eq. Eng.

,

18

,

2581

–

2606

.

10.1007/s10518-020-00796-1

Boore

D.M.

,

1983

.

Stochastic simulation of high-frequency ground motion based on seismological models of the radiated spectra

,

Bull. seism. Soc. Am.

,

73

,

1865

–

1894

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Boore

D.M.

,

Joyner

W.B.

,

1997

.

Site amplifications for generic rock sites

,

Bull. seism. Soc. Am.

,

87

,

327

–

341

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Boore

D.M.

,

2003

.

Simulation of ground motion using the stochastic method

,

Pure appl. Geophys.

,

160

,

635

–

676

.

Boore

D.M.

,

Akkar

S.

,

2003

.

Effect of causal and acausal filters on elastic and inelastic response spectra

,

Earthq. Eng. Struct. Dyn.

,

32

,

1729

–

1748

.

Boore

D.M.

,

2005

.

SMSIM—Fortran programs for simulating ground motions from earthquakes: version 2.3—a revision of OFR 96–80–A, available at:

http://www.daveboore.com/smsim.

Boore

D.M.

,

Bommer

J.J.

,

2005

.

Processing of strong-motion accelerograms: needs, options and consequences

,

Soil Dyn. Earthq. Eng.

,

25

,

93

–

115

.

10.1016/j.soildyn.2004.10.007

Boore

D.M.

,

Thompson

E.M.

,

2014

.

Path durations for use in the stochastic-method simulation of ground motions

,

Bull. seism. Soc. Am.

,

104

,

2541

–

2552

.

Bora

S.S.

,

Scherbaum

F.

,

Kuehn

N.

,

Stafford

P.

,

Edwards

B.

,

2015

.

Development of a response spectral groundmotion prediction equation (GMPE) for seismic-hazard analysis from empirical fourier spectral and duration models

,

Bull. seism. Soc. Am.

,

105

,

2192

–

2218

.

Bora

S.S.

,

Cotton

F.

,

Scherbaum

F.

,

Edwards

B.

,

Traversa

S.

,

2017

.

Stochastic source, path and site attenuation parameters and associated variabilities for shallow crustal European earthquakes

,

Bull. Earthq. Eng.

,

15

,

4531

–

4561

.

10.1007/s10518-017-0167-x

Bowman

J.R.

,

Kennett

B.L.N.

,

1991

.

Propagation of Lg waves in the North Australian craton: influence of crustal velocity gradients

,

Bull. seism. Soc. Am.

,

81

,

592

–

610

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Brune

J.N.

,

1970

.

Tectonic stress and the spectra of seismic shear waves from earthquakes

,

J. geophys. Res.

,

75

,

4997

–

5009

.

10.1029/JB075i026p04997

Brune

J.N.

,

1971

.

Correction

,

J. geophys. Res.

,

76

,

5002

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Building and Housing Research Center (BHRC) of Iran

(http://www.bhrc.ac.ir/).

Castro

R.R.

,

Anderson

J.G.

,

Singh

S.K.

,

1990

.

Site response, attenuation and source spectra of S waves along the Guerrero, Mexico, subduction zone

,

Bull. seism. Soc. Am.

,

80

,

1481

–

1503

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Collins

C.D.N.

,

Drummond

B.J.

,

Nicoll

M.G.

,

2003

.

Moho depth patterns in the Australian continent

, in

The Evolution and Dynamics of the Australian Plate

, Vol.

372

, pp.

121

–

128

., eds

Müller

D.

,

Hillis

R.

,

Geological Society of America

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Cornell

C.A.

,

1968

.

Engineering seismic risk analysis

,

Bull. seism. Soc. Am.

,

58

,

1583

–

1606

.

Dawood

H.

,

Rodriguez-Marek

A.

,

Bayless

J.

,

Goulet

C.

,

Thompson

S.

,

2016

.

A Flatfile for the KiK-net database processed using an automated protocol

,

Earthq. Spectra.

,

32

,

1281

–

1302

.

Drouet

S.

,

Chevrot

S.

,

Cotton

F.

,

Souriau

A.

,

2008

.

Simultaneous inversion of source spectra, attenuation parameters, and site responses: application to the data of the French accelerometric network

,

Bull. seism. Soc. Am.

,

98

,

198

–

219

.

Drouet

S.

,

Cotton

F.

,

Gueguen

P.

,

2010

.

Vs30, kappa, regional attenuation and M-w from accelerograms: application to magnitude 3–5 French earthquakes

,

Geophys. J. Int.

,

182

,

880

–

898

.

10.1111/j.1365-246X.2010.04626.x

Drouet

S.

,

Bouin

M.P.

,

Cotton

F.

,

2011

.

New moment magnitude scale, evidence of stress drop magnitude scaling and stochastic ground motion model for the French West Indies

,

Geophys. J. Int.

,

187

,

1625

–

1644

.

10.1111/j.1365-246X.2011.05219.x

Edwards

B.

,

Rietbrock

A.

,

Bommer

J.J.

,

Baptie

B.

,

2008

.

The acquisition of source, path and site effects from micro-earthquake recordings using Q tomography: application to the United Kingdom

,

Bull. seism. Soc. Am.

,

98

,

1915

–

1935

.

Edwards

B.

,

Fah

D.

,

2013

.

A stochastic ground-motion model for Switzerland

,

Bull. seism. Soc. Am.

,

103

(

1

),

78

–

98

.

Edwards

B.

,

Ktenidou

O.-J.

,

Cotton

F.

,

Abrahamson

N.

,

Van Houtte

Ch.

,

F¨ah

D.

,

2015

.

Epistemic uncertainty and limitations of the κ0 model for near-surface attenuation at hard rock sites

,

Geophys. J. Int.

,

202

,

1627

–

1645

.

Efron

B.

,

1979

.

Bootstrap methods, another look at the jacknife

,

Ann. Stat.

,

7

,

1

–

26

.

10.1214/aos/1176344552

Eshelby

J.D.

,

1957

.

The determination of the elastic field of an ellipsoidal inclusion, and related problems

,

Proc. R. Soc.

,

241

,

376

–

396

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Farajpour

Z.

,

Pezeshk

S.

,

Zare

M.

,

2019

.

A new empirical ground-motion model for Iran

,

Bull. seism. Soc. Am.

,

109

,

732

–

744

.

Farrokhi

M.

,

Hamzehloo

H.

,

2017

.

Body wave attenuation characteristics in the crust of Alborz region and North Central Iran

,

J. Seismol.

,

21

,

631

–

646

.

10.1007/s10950-016-9624-2

Fäh

D.

,

Kind

F.

,

Giardini

D.

,

2001

.

A theoretical investigation of average H/V ratios

,

Geophys. J. Int.

,

145

,

535

–

549

.

10.1046/j.0956-540x.2001.01406.x

Ghods

A.

,

Shabanian

E.

,

Bergman

E.

,

Faridi

M.

,

Donner

S.

,

Mortezanejad

Gh.

,

Aziz-Zanjani

A.

,

2015

.

The Varzaghan–Ahar, Iran, Earthquake Doublet (M_w 6.4, 6.2): implications for the geodynamics of northwest Iran

,

Geophys. J. Int.

,

203

,

522

–

540

.

Grendas

I.

,

Theodoulidis

N.

,

Hatzidimitriou

P.

,

Margaris

B.

,

Drouet

S.

,

2018

.

Determination of source, path and site parameters based on non–linear inversion of accelerometric data in Greece

,

Bull. Earthq. Eng.

,

16

,

5061

–

5094

.

10.1007/s10518-018-0379-8

Hanks

T.C.

,

Kanamori

H.

,

1979

.

A moment-magnitude scale

,

J. geophys. Res.

,

84

,

2348

–

2350

.

10.1029/JB084iB05p02348

Hanks

T.

,

McGuire

T.

,

1981

.

The character of high-frequency strong ground motion

,

Bull. seism. Soc. Am.

,

71

,

2071

–

2095

.

Jeong

S.

,

Stump

B.W.

,

DeShon

H.R.

,

2020

.

Spectral characteristics of ground motion from induced earthquakes in the Fort Worth Basin, Texas, using the generalized inversion technique

,

Bull. seism. Soc. Am.

,

110

,

2058

–

2076

.

Ji

Ch.

,

Cabas

A.

,

Cotton

F.

,

Pilz

M.

,

Bindi

D.

,

2020

.

Within-station variability in kappa: evidence of directionality effects

,

Bull. seism. Soc. Am.

,

110

,

1247

–

1259

.

Joyner

W.

,

Boore

D.

,

1981

.

Peak horizontal acceleration and velocity from strong-motion records including records from the 1979 Imperial Valley, California, earthquake

,

Bull. seism. Soc. Am.

,

71

,

2011

–

2038

.

Kawase

H.

,

2006

.

Site effects derived from spectral inversion method for KNET, KiK-net, and JMA strong-motion network with special reference to soil non linearity in high PGA records

,

Bull. Earthq. Res., Inst. Univ. Tokyo

,

81

,

309

–

315

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Kilb

D.

,

Biasi

G.

,

Anderson

J.G.

,

Brune

J.

,

Peng

Z.

,

Vernon

F.L.

,

2012

.

A comparison of spectral parameter kappa from small and moderate earthquakes using Southern California ANZA Seismic Network Data

,

Bull. seism. Soc. Am.

,

102

,

284

–

300

.

Konno

K.

,

Ohmachi

T.

,

1998

.

Ground-motion characteristics estimated from spectral ratio between horizontal and vertical components of microtremor

,

Bull. seism. Soc. Am.

,

88

(

1

),

228

–

241

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Ktenidou

O.-J.

,

Cotton

F.

,

Abrahamson

N.

,

Anderson

J.G.

,

2014

.

Taxonomy of κ: a review of definitions and estimation approaches targeted to applications

,

Seismol. Res. Lett.

,

85

,

135

–

146

.

Ktenidou

O.-J.

,

Abrahamson

N.A.

,

Drouet

S.

,

Cotton

F.

,

2015

.

Understanding the physics of kappa (κ): insights from a downhole array

,

Geophys. J. Int.

,

203

,

678

–

691

.

Mirzaei

N.

,

Mengtan

G.

,

Yuntai

C.

,

1998

.

Seismic source regionalization for seismic zoning of Iran: major seismotectonic provinces

,

J. Earthq. Pred. Res.

,

7

,

465

–

495

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Motaghi

K.

,

Ghods

A.

,

2012

.

Attenuation of ground-motion spectral amplitudes and its variations across the Central Alborz Mountains

,

Bull. seism. Soc. Am.

,

102

,

1417

–

1428

.

Motazedian

D.

,

2006

.

Region-specific key seismic parameters for earthquakes in northern Iran

,

Bull. seism. Soc. Am.

,

96

,

1383

–

1395

.

Mousavi-Bafrouei

S.H.

,

Mirzaei

N.

,

Shabani

E.

,

2014

.

A declustered earthquake catalog for the Iranian Plateau

,

Ann. Geophys.

,

57

(

6

),

S0653

, doi:

.

Oth

A.

,

Bindi

D.

,

Parolai

S.

,

Wenzel

F.

,

2008

.

S-wave attenuation characteristics beneath the Vrancea region in Romania: new insights from the inversion of ground-motion spectra

,

Bull. seism. Soc. Am.

,

98

,

2482

–

2497

.

Oth

A.

,

Bindi

D.

,

Parolai

S.

,

Di Giacomo

D.

,

2011

.

Spectral analysis of K-NET and KiK-net data in Japan, Part II: on attenuation characteristics, source spectra, and site response of borehole and surface stations

,

Bull. seism. Soc. Am.

,

101

,

667

–

687

.

Pacor

F.

et al. ,

2016

.

Spectral models for ground motion prediction in the L'Aquila region (Central Italy): evidence for stress drop dependence on magnitude and depth

,

Geophys. J. Int.

,

204

,

716

–

737

.

Paige

C.C.

,

Saunders

M.A.

,

1982

.

LSQR: an algorithm for sparse linear equations and sparse least squares

,

ACM Trans. Math. Softw.

,

8

,

195

–

209

.

10.1145/355993.356000

Palmer

S.

,

Atkinson

G.

,

2020

.

The high-frequency decay slope of spectra (kappa) for M ≥ 3:5 earthquakes on rock sites in eastern and Western Canada

,

Bull. seism. Soc. Am.

,

110

,

471

–

488

.

Papageorgiou

A.S.

,

Aki

K.

,

1983

.

A specific barrier model for the quantitative description of inhomogeneous faulting and the prediction of strong ground motion. I. Description of the model

,

Bull. seism. Soc. Am.

,

73

,

693

–

722

.

Papageorgiou

A.S.

,

1998

.

On two characteristic frequencies of acceleration spectra: patch corner frequency and f max

,

Bull. seism. Soc. Am.

,

78

,

509

–

529

.

Parolai

S.

,

Bindi

D.

,

Augliera

P.

,

2000

.

Application of the generalized inversion technique (GIT) to a microzonation study: numerical simulations and comparison with different site-estimation techniques

,

Bull. seism. Soc. Am.

,

90

,

286

–

297

.

Parolai

S.

,

Bindi

D.

,

Baumbach

M.

,

Grosser

H.

,

Milkereit

C.

,

Karakisa

S.

,

Zunbul

S.

,

2004

.

Comparision of different site response estimation techniques using aftershocks of 1999 Izmit earthquake

,

Bull. seism. Soc. Am.

,

94

,

1096

–

1108

.

Picozzi

M.

,

Bindi

D.

,

Spallarossa

D.

,

Oth

A.

,

Di Giacomo

D.

,

Zollo

A.

,

2019

.

Moment and energy magnitudes: diversity of views on earthquake shaking potential and earthquake statistics

,

Geophys. J. Int.

,

216

,

1245

–

1259

.

Poggi

V.

,

Edwards

B.

,

Fah

D.

,

2011

.

Derivation of a reference shear-wave velocity model from empirical site amplification

,

Bull. seism. Soc. Am.

,

101

,

258

–

274

.

Raghu Kanth

S.T.G.

,

Iyengar

R.N.

,

2007

.

Estimation of seismic spectral acceleration in peninsular India

,

J. Earth. System. Sci.

,

116

(

3

),

199

–

214

.

10.1007/s12040-007-0020-8

Reiter

L.

,

1990

.

Earthquake Hazard Analysis: Issues and Insight

,

Columbia Univ. Press

.

Rietbrock

A.

,

Strasser

F.

,

Edwards

B.

,

2013

.

A Stochastic earthquake ground-motion prediction model for the United Kingdom

,

Bull. seism. Soc. Am.

,

103

,

57

–

77

.

Soghrat

M.R.

,

Ziyaeifar

M.

,

2016

.

Ground motion prediction equations for horizontal and vertical components of acceleration in Northern Iran

,

J. Seismol.

,

21

,

99

–

125

.

10.1007/s10950-016-9586-4

Tatar

M.

,

Jackson

J.

,

Hatzfeld

D.

,

Bergman

E.A.

,

2007

.

The 28 May 2004 Baladeh earthquake (M_w 6.2) in the Alborz, Iran: implications for the geology of the south Caspian basin margin and for the seismic hazard of Tehran

,

Geophys J. Int.

,

170

,

249

–

261

.

10.1111/j.1365-246X.2007.03386.x

Toro

G.

,

Abrahamson

A.

,

Schneider

J.

,

1997

.

Model of strong ground motions from earthquakes in the central and eastern North America: best estimates and uncertainties

,

Seismol. Res. Lett.

,

68

,

41

–

57

.

10.1785/gssrl.68.1.41

Tsuda

K.

,

Archuleta

R.J.

,

Koketsu

K.

,

2006

.

Quantifying the spatial distribution of site response by use of the Yokohama high-density strongmotion network

,

Bull. seism. Soc. Am.

,

96

,

926

–

942

.

Tsuda

K.

,

Koketsu

K.

,

Hisada

Y.

,

Hayakawa

T.

,

2010

.

Inversion analysis of site responses in the Kanto Basin using data from a dense strong motion seismograph array

,

Bull. seism. Soc. Am.

,

100

,

1276

–

1287

.

Van Houtte

Ch.

,

Ktenidou

O.-J.

,

Larkin

T.

,

Holden

C.

,

2014

.

Hard-site κ0 (Kappa) calculations for Christchurch, New Zealand, and comparison with local ground-motion prediction models

,

Bull. seism. Soc. Am.

,

104

,

1899

–

1913

.

Zafarani

H.

,

Hassani

B.

,

Ansari

A.

,

2012

.

Estimation of earthquake parameters in the Alborz seismic zone, Iran using generalized inversion method

,

Soil Dyn. Earthq. Eng.

,

42

,

197

–

218

.

10.1016/j.soildyn.2012.05.019

Zolfaghari

M.

,

Darzi

A.

,

2019

.

A prediction model for vertical-to-horizontal ratios of PGA, PGV, and 5%-damped response spectra (0.01–10 s) for Iran

,

J. Seismol.

,

23

,

819

–

837

.

10.1007/s10950-019-09836-z

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Month:	Total Views:
June 2021	36
July 2021	42
August 2021	11
September 2021	22
October 2021	9
November 2021	15
December 2021	6
January 2022	3
March 2022	4
April 2022	10
May 2022	4
June 2022	6
July 2022	5
August 2022	1
September 2022	20
October 2022	1
November 2022	6
December 2022	5
January 2023	9
February 2023	5
March 2023	15
April 2023	1
May 2023	10
June 2023	2
July 2023	12
August 2023	9
September 2023	2
October 2023	3
November 2023	11
December 2023	8
January 2024	18
February 2024	15
March 2024	19
April 2024	9
May 2024	19
June 2024	20
July 2024	45
August 2024	12
September 2024	7
October 2024	7
November 2024	9
December 2024	15
January 2025	12
February 2025	17
March 2025	26
April 2025	11
May 2025	4

Article Contents

Spectral models for seismological source parameters, path attenuation and site-effects in Alborz region of northern Iran

SUMMARY

INTRODUCTION

DATA SET SPECIFICATIONS

PROCESSING OF STRONG MOTION RECORDS

Fourier amplitude spectrum (FAS)

METHODOLOGY

RESULTS

Attenuation function

Source spectra

Site amplification functions

Robustness evaluation of spectral model parameters

CONCLUSIONS

ACKNOWLEDGEMENTS

DATA AVAILABILITY

REFERENCES

Citations

Views

Altmetric

Email alerts

See also

Companion Article

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Spectral models for seismological source parameters, path attenuation and site-effects in Alborz region of northern Iran

SUMMARY

INTRODUCTION

DATA SET SPECIFICATIONS

PROCESSING OF STRONG MOTION RECORDS

Fourier amplitude spectrum (FAS)

METHODOLOGY

RESULTS

Attenuation function

Source spectra

Site amplification functions

Robustness evaluation of spectral model parameters

CONCLUSIONS

ACKNOWLEDGEMENTS

DATA AVAILABILITY

REFERENCES

Citations

Views

Altmetric

Email alerts

See also

Companion Article

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only