Earthquake-origin expansion of the Earth inferred from a spherical-Earth elastic dislocation theory

Xu, Changyi; Sun, Wenke

doi:10.1093/gji/ggu364

Abstract

In this paper, we propose an approach to compute the coseismic Earth's volume change based on a spherical-Earth elastic dislocation theory. We present a general expression of the Earth's volume change for three typical dislocations: the shear, tensile and explosion sources. We conduct a case study for the 2004 Sumatra earthquake (M_w9.3), the 2010 Chile earthquake (M_w8.8), the 2011 Tohoku-Oki earthquake (M_w9.0) and the 2013 Okhotsk Sea earthquake (M_w8.3). The results show that mega-thrust earthquakes make the Earth expand and earthquakes along a normal fault make the Earth contract. We compare the volume changes computed for finite fault models and a point source of the 2011 Tohoku-Oki earthquake (M_w9.0). The big difference of the results indicates that the coseismic changes in the Earth's volume (or the mean radius) are strongly dependent on the earthquakes’ focal mechanism, especially the depth and the dip angle. Then we estimate the cumulative volume changes by historical earthquakes (M_w ≥ 7.0) since 1960, and obtain an Earth mean radius expanding rate about 0.011 mm yr⁻¹.

Numerical solutions, Satellite geodesy, Space geodetic surveys, Seismicity and tectonics

1 INTRODUCTION

The topic of the Earth expanding is a relatively controversial subject in science, and has attracted constant attention. Some researchers support and some oppose the viewpoint. The expanding hypothesis is supported by the palaeontologic, palaeomagnetic, palaeoclimatologic and geologic data (e.g. Wilson 1960; Scalera 2001, 2003). Carey (1976, 1988) concluded that the Earth is expanding within the ocean-floor expansion framework. Chen (2000) reported that the expansion rate of the Earth's radius is about 0.4 mm yr⁻¹ around 4300 Ma, compared with the current rate of 0.1 mm yr⁻¹. Conversely, from the records of historical moment of inertia, Williams (2000) indicate that the Earth is contracting. Scalera (2003) declared that the Earth is presently slowly expanding and the rate may be a few or fractions of millimetres per year. Müller (2010) suggested that the mean radius of Earth is expanding at the rate of 0.6 mm yr⁻¹ under the background of the universe expanding.

With the rapid development of space geodetic techniques [e.g. global positioning system (GPS), very-long baseline interferometry (VLBI), satellite laser raging (SLR), Doppler orbitography and radiopositioning integrated by satellite (DORIS)], variations in the Earth volume (or mean radius) over recent decades can be estimated. Gerasimenko (1993) indicated an increase in the Earth radius of 4.15 ± 0.27 mm yr⁻¹ based on VLBI data. He latterly demonstrated that the expansion rate of the Earth does not exceed 1 mm yr⁻¹ by re-analysing VLBI data Gerasimenko (1996, 1997). Wu et al. (2011) analysed the combined data from SLR, VLBI, GPS and DORIS, and concluded that the Earth mean radius is currently expanding at the rate of 0.1 mm yr⁻¹ with 1σ measurement uncertainty of 0.2 mm yr⁻¹. On the other hand, some research work supports that the Earth is contracting in the shorter period. Lyttleton (1965, 1983) indicated that the radius would have been 370 km greater than the present radius by analysing seismic data. Heki et al. (1989) attempted to measure the Earth mean radius contraction rate using VLBI data. Based on the coordinates’ velocities and the error estimations of the GPS, SLR, and VLBI stations, Huang et al. (2002) and Sun et al. (2006) concluded that the Earth is contracting. Carey (1976) suggested that the Earth expanding hypothesis can be identified adopting the gravity data. Shen et al. (2011) concluded that the Earth is expanding with a rate of 0.2 mm yr⁻¹ from temporal gravity data and space geodetic data analysis. However, the limited spatial distribution of geodetic sites and the presence of other major geophysical processes have reduced the accuracy of detecting the Earth expansion rate.

Some other research work had the similar evidence of the Earth expansion. Lubimova (1958) evaluated the expansion rate of the Earth radius using energy of decay from radioactive elements. Due to the decreasing of gravitational constant (G), Beck (1961) and Birch (1968) concluded that the Earth radius is expanding. Yang & Yang (2011) obtained the expansion rate of Earth radius (0.45 mm yr⁻¹) based on the general theory of relativity.

Regardless of whether the Earth is expanding or contracting, it is interesting to explore possible excitation sources that maintain the process. Various theories and hypotheses of the Earth expanding have been proposed and debated throughout the plate tectonic revolution Carey (1976). Legitimate concerns persist about a possible rate of the Earth radius change on accretionary, geothermal, climate change, cosmological and magmatic data (Mjelde et al. 2010). Post-glacial rebound (PGR) has long been taken as a reasonable candidate in explaining the uplift of the Earth's surface (Lemoine et al. 2006). Shen et al. (2011) estimated the PGR contribution on the Earth expanding issue, and found that the average uplift rate is only 5.69 × 10⁻⁶ ± 1.09 × 10⁻⁴ mm yr⁻¹, because the global integration of the surface uplift rate produced by the PGR effect is almost equal to zero due to the PGR effect of local feature; therefore, the Earth expansion is not significantly attributed to the PGR effect. Another possible excitation source may be earthquakes that not only disturb the global physical field (e.g., gravitational field, displacement, and the stress–strain field), but also change the Earth's shape by perturbing Earth's oblateness (e.g. Chao & Gross 1987; Gross & Chao 2006). Therefore, earthquakes absolutely change the Earth volume (or mean radius), and relate to the Earth expansion or contraction. Based on literature review, volume change and expansion rate due to earthquakes has yet to be computed. Chao & Gross (1987) speculated that earthquakes decrease the Earth's volume via the normal mode method, and attempted to compute the volume change via the normal modes summation. Unfortunately, they found that it's infeasible due to the method's slow convergence.

There is another method to precisely evaluate the effect of earthquakes on the Earth's volume change: the elastic dislocation theory, which is based on the Green's function approach. Earlier dislocation theories were based on the simple earth model, such as the homogeneous model (Smylie & Mansinha 1971) or the half-space model (Okada 1985; Wang et al. 2006). They cannot account for the Earth's layer structure or curvature effect, which lead to inaccuracy when discussing the earthquake-induced Earth expanding issue. Taking the layer structure and the curvature effect into account, Sun & Okubo (1993) derived a new elastic theory based on a more practical earth model.

In this paper, we assume that Earth's mass is conserved before and after earthquakes and no energy escapes into space during earthquakes. we propose a theoretical formula to compute the Earth's volume change based on a spherical-Earth elastic dislocation theory, and we present the general solutions of the Earth volume change for three typical dislocation sources. Then, we choose three large thrust earthquakes and one event occurred along a normal fault since 2004 to conduct the case study. We also evaluate the cumulative volume changes and obtain the rate of the Earth's mean radius change based on the historical earthquakes (M_w ≥ 7.0) catalogue since 1960 with the un-weighted least-square approach.

2 THEORY AND METHOD

2.1 Basic physical principle

The volume change of an arbitrary body lying inside a sphere can be mathematically expressed using the following equation.

\begin{equation} \Delta V = \int _V \bigtriangledown \cdot \mathbf {u} \mathrm{d} V, \end{equation}

(1)

where u is the displacement vector due to the physical field perturbation, the integration is over the entire volume V of the body and Δ indicates the deviation from the reference value. By adopting the Gauss's theorem, we can obtain eq. (1) in the new form:

\begin{equation} \Delta V = \oint _S u_r \text{d} S, \end{equation}

(2)

where |${u}_r$| is the radial displacement produced by the earthquake. |${\rm d} {S} = R^2 \cos \theta \mathrm{d}\theta \mathrm{d}\phi$|⁠, is the surface element. R is the Earth's mean radius.

2.2 The radial displacement in dislocation theory

A SNREI (spherical, non-rotating, elastic, isotropic) earth model, the earth model can be completely characterized by the density (ρ), the bulk modulus (κ) and the shear modulus (μ). The radial displacement caused by an earthquake can be expressed by a spherical-Earth elastic dislocation theory derived by Sun & Okubo (1993).

\begin{equation} u_r(r,\theta ,\phi )= F_{eq} \sum _{i,j} \sum _{n,m} h^{ij}_{n}(r) Y_{nm}(\theta ,\phi ) \cdot v_i n_j, \end{equation}

(3)

where the quantity in the summation is dimensionless, and F_eq = (fault slip * fault area)/R² is a measure of the size of the earthquake in physical dimension of length on the order of millimetre for a large earthquake. |${h}^{ij}_{n}$| is the dislocation Love numbers defined by Sun & Okubo (1993), which is the function of the spherical harmonics degree (n), elastic parameters and the density of the earth model. Y_nm(θ, ϕ) = P_nm(cos θ)e^imϕ is the surface spherical harmonics. The summation indices i, j = 1,2,3 represent only 4 (instead of 9) independent canonical faulting types, appropriate combination of which can represent the geometry of any such faulting (Sun & Okubo 1993). For simplicity and no loss of generality, we shall express the four canonical earthquake source types in an epicentral coordinates, spherical or Cartesian as convenient, by placing the north pole at the epicentre with the |${x}$| axis oriented along the positive strike of the faulting to take advantage of the geometrical symmetry: vertical strike-slip (i, j = 1,2), vertical dip-slip (i, j = 3,2), horizontal tensile (i, j = 2,2) and vertical tensile (i, j = 3,3).Therefore, we can write the radial displacement for the four independent sources in the following:

\begin{eqnarray} u^{12}_r(r,\theta ,\phi )= -2 \sum _{n=2}^N h^{12}_n P_{n2}(\cos \theta ) \sin 2\phi \end{eqnarray}

(4)

\begin{eqnarray} u^{32}_r(r,\theta ,\phi )= -2 \sum _{n=1}^N h^{32}_n P_{n1}(\cos \theta ) \sin \phi \end{eqnarray}

(5)

\begin{eqnarray} u^{22,0}_r(r,\theta ,\phi )= \sum _{n=0}^N h^{22}_n P_{n}(\cos \theta ) \end{eqnarray}

(6)

\begin{eqnarray} u^{22,2}_r(r,\theta ,\phi )= -2 \sum _{n=2}^N h^{12}_n P_{n2}(\cos \theta ) \cos 2\phi \end{eqnarray}

(7)

\begin{eqnarray} u^{33}_r(r,\theta ,\phi )= \sum _{n=0}^N h^{33}_n P_{n}(\cos \theta ). \end{eqnarray}

(8)

Then we can give the general solutions for the three typical dislocation sources—the shear source, the tensile source and the explosion source.

When an earthquake occurs, we can take it as a shear source. Its slip and normal vectors can be defined as:

\begin{eqnarray} \mathbf {v}= \mathbf {e}_1 \cos \lambda + \mathbf {e}_2 \cos \delta \sin \lambda + \mathbf {e}_3 \sin \delta \sin \lambda \end{eqnarray}

(9)

\begin{eqnarray} \mathbf {n}= - \mathbf {e}_2 \sin \delta + \mathbf {e}_3 \cos \delta , \end{eqnarray}

(10)

where λ is the fault slip (rake) angle and δ is the fault dip angle. (e₁,e₂,e₃) is the basic vector. And we can get the co-seismic radial displacement at an arbitrary point:

\begin{eqnarray} u^{S}_r(r,\theta ,\phi ) &=& \left\lbrace \cos \lambda (u^{12}_r \sin \delta - u^{13}_r \cos \delta ) \right. \nonumber\\ &&\left. + \,\sin \lambda \left[\frac{1}{2} \sin 2\delta (u^{33}_r - u^{22}_r) - u^{32}_r \cos 2\delta \right]\right\rbrace \cdot F_{eq}. \nonumber\\ \end{eqnarray}

(11)

If the slip vector is parallel to the normal vector, it becomes the problem of the tensile source, we have:

\begin{equation} \mathbf {v}=\mathbf {n} = -\mathbf {e}_2 \sin \delta + \mathbf {e}_3 \cos \delta . \end{equation}

(12)

We can get the general solution of the radial displacement due to the tensile source:

\begin{equation} u^T_r(r,\theta ,\phi ) = (u^{33}_r \cos ^2 \delta + u^{22}_r \sin ^2 \delta + u^{32}_r \sin 2\delta ) \cdot F_{\text{eq}}. \end{equation}

(13)

When there is an explosion source, such as volcanic eruption or an underground nuclear explosion, the product of its slip vector and normal vector can be expressed:

\begin{equation} \mathbf {v}\mathbf {n} = \mathbf {e}_1 \mathbf {e}_1 + \mathbf {e}_2 \mathbf {e}_2 + \mathbf {e}_3 \mathbf {e}_3 \end{equation}

(14)

and the general solution for the radial displacement of the explosion source is expressed:

\begin{equation} u^E_r(r,\theta ,\phi ) = (u^{33}_r + 2u^{22}_r) \cdot F_{\text{eq}}. \end{equation}

(15)

2.3 Expression of Earth's volume change

Substituting the radial displacements for the four independent sources into eq. (2) and using the orthogonality of the surface spherical harmonics functions, we can get the coseismic Earth's volume change of each component:

\begin{eqnarray} \Delta V^{12}= 0 \end{eqnarray}

(16)

\begin{eqnarray} \Delta V^{32}= 0 \end{eqnarray}

(17)

\begin{eqnarray} \Delta V^{22,2}= 0 \end{eqnarray}

(18)

\begin{eqnarray} \Delta V^{22,0}= 4 \pi R^2\;h^{22}_0 \end{eqnarray}

(19)

\begin{eqnarray} \Delta V^{33}= 4 \pi R^2\;h^{33}_0. \end{eqnarray}

(20)

We refer to the volume changes for the four independent sources as the Green's function of the Earth's volume change. When we get the degree-zero dislocation Love numbers of the radial displacement due to earthquakes, we can evaluate the volume change with the fault's source parameters. The volume changes induced by the earthquakes are in particular dominated by the tensile components (i, j = 3,3 and i, j = 2,2), which can result in the Earth's expansion or contraction. Their values are shown in the Fig. 1, where the PREM model (Dziewonski & Anderson 1981) is adopted in the computation.

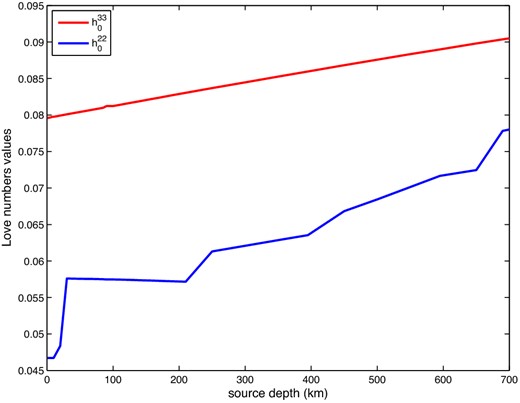
$The values for $h^{33}_0$ and $h^{22}_0$ from 0 to 700 km under the PREM earth model.$

Figure 1.

The values for |$h^{33}_0$| and |$h^{22}_0$| from 0 to 700 km under the PREM earth model.

Open in new tab Download slide

We can get the general solution of volume change for the three dislocation sources:

\begin{eqnarray} \Delta V^S = \frac{1}{2}(\Delta V^{33} - \Delta V^{22,0}) \sin \lambda \sin 2\delta \cdot F_{\text{eq}} \end{eqnarray}

(21)

\begin{eqnarray} \Delta V^T = [\Delta V^{33} \cos ^2 \delta + \Delta V^{22,0} \sin ^2 \delta ] \cdot F_{\text{eq}} \end{eqnarray}

(22)

\begin{eqnarray} \Delta V^E = [\Delta V^{33} + 2\Delta V^{22,0}] \cdot F_{\text{eq}} \end{eqnarray}

(23)

Substituting (19) and (20) into (21), (22) and (23), we can get the final expressions of volume change due to different dislocation sources:

\begin{eqnarray} \Delta V^S = 2\pi R^2(h^{33}_0 - h^{22,0}_0) \sin \lambda \sin 2\delta \cdot F_{\text{eq}} \end{eqnarray}

(24)

\begin{eqnarray} \Delta V^T = 4 \pi R^2 (h^{33}_0 \cos ^2 \delta + h^{22,0}_0 \sin ^2 \delta ) \cdot F_{\text{eq}} \end{eqnarray}

(25)

\begin{eqnarray} \Delta V^E = 4 \pi R^2 (h^{33}_0 + 2h^{22,0}_0) \cdot F_{\text{eq}}. \end{eqnarray}

(26)

Through these theoretical expressions, we conclude that the tensile source and the explosion source always make the Earth expand. The volume change due to the explosion source depends on the source depth and its magnitude. However, for shear sources, volume change must be analysed by three situations including variations to the formulae: (1) for thrust faults (0 < λ < π), the Earth will expand; (2) for normal faults (−π < λ < 0), the Earth will contract and (3) for strike faults, the Earth may expand or contract depending on the fault dip angle.

Furthermore, the volume change can be mathematically expressed as:

\begin{equation} \Delta V = \frac{4}{3} \pi [(R+ \Delta R)^3 -R^3]. \end{equation}

(27)

We need only keep the first-order derivation because ΔR is a small quantity compared to R (ΔR ≪ R), and we can estimate the mean radius variation, assuming that Earth is a rigid body, expressed as.

\begin{equation} \Delta R = \frac{\Delta V}{3V} \cdot R, \end{equation}

(28)

where R = 6371 km, and V = 1.082 × 10¹² km³.

3 RESULTS

3.1 Case study

As an application of the above formula, we conduct case studies of the 2004 Sumatra earthquake (M_w 9.3), the 2010 Chile earthquake (M_w 8.8), the 2011 Tohoku-Oki earthquake (M_w 9.0) and the 2013 Okhotsk Sea earthquake (M_w 8.3). Their focal mechanism solutions are shown in Fig. 2, and these centroid moment tensor (CMT) solutions are from the global CMT solutions (www.globalcmt.org). From these earthquakes, we can see that the first three large earthquakes occurred at the thrust faults, and the fourth one occurred at the normal fault at a depth of approximately 640 km.We first compute degree-zero dislocation Love numbers for the radial displacement at the depth where earthquakes happen. Then we use CMT solutions to get changes in the volume and the radius. The results for four earthquakes are listed in Table 1.

Figure 2.

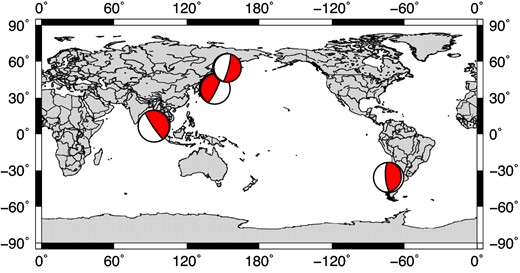
Locations of four recent large earthquakes used in this study, along with their CMT-based seismic source mechanism solutions.

Open in new tab Download slide

Table 1.

Open in new tab

Changes in the Earth's volume and radius induced by four earthquakes.

Event	Depth (km)	\|$h^{33}_0$\|	\|$h^{22}_0$\|	ΔV (km³)	ΔV/V(10⁻¹²)	ΔR (mm)
Sumatra (M_w9.3)	28.6	0.0801	0.0576	26.62	25	0.053
Chile (M_w8.8)	24.1	0.0800	0.0484	45.19	41.76	0.089
Tohoku-Oki (M_w9.0)	20.0	0.0799	0.0484	101.07	93	0.196
Okhotsk Sea (M_w8.3)	640.0	0.0896	0.0723	−11.89	−10.99	−0.023

Event	Depth (km)	\|$h^{33}_0$\|	\|$h^{22}_0$\|	ΔV (km³)	ΔV/V(10⁻¹²)	ΔR (mm)
Sumatra (M_w9.3)	28.6	0.0801	0.0576	26.62	25	0.053
Chile (M_w8.8)	24.1	0.0800	0.0484	45.19	41.76	0.089
Tohoku-Oki (M_w9.0)	20.0	0.0799	0.0484	101.07	93	0.196
Okhotsk Sea (M_w8.3)	640.0	0.0896	0.0723	−11.89	−10.99	−0.023

Table 1.

Open in new tab

Changes in the Earth's volume and radius induced by four earthquakes.

Event	Depth (km)	\|$h^{33}_0$\|	\|$h^{22}_0$\|	ΔV (km³)	ΔV/V(10⁻¹²)	ΔR (mm)
Sumatra (M_w9.3)	28.6	0.0801	0.0576	26.62	25	0.053
Chile (M_w8.8)	24.1	0.0800	0.0484	45.19	41.76	0.089
Tohoku-Oki (M_w9.0)	20.0	0.0799	0.0484	101.07	93	0.196
Okhotsk Sea (M_w8.3)	640.0	0.0896	0.0723	−11.89	−10.99	−0.023

Event	Depth (km)	\|$h^{33}_0$\|	\|$h^{22}_0$\|	ΔV (km³)	ΔV/V(10⁻¹²)	ΔR (mm)
Sumatra (M_w9.3)	28.6	0.0801	0.0576	26.62	25	0.053
Chile (M_w8.8)	24.1	0.0800	0.0484	45.19	41.76	0.089
Tohoku-Oki (M_w9.0)	20.0	0.0799	0.0484	101.07	93	0.196
Okhotsk Sea (M_w8.3)	640.0	0.0896	0.0723	−11.89	−10.99	−0.023

The 2004 Sumatra earthquake (M_w9.3), the 2010 Chile earthquake (M_w8.8) and the 2011 Tohoku-Oki earthquake (M_w9.0) made the Earth expand, but the 2013 Okhotsk Sea earthquake (M_w8.3) made the Earth contract. The 2011 Tohoku-Oki earthquake (M_w9.0) resulted in the greatest change in Earth's radius, about 0.2 mm. These results demonstrate that earthquakes at thrust faults make the Earth expand and earthquakes at normal faults make the Earth contract, and the coseismic Earth's mean radius changes are fractions of millimetres.

We also compute the volume changes for finite fault models to investigate the uncertainty caused by the point source approximation for the large earthquakes. The Tohoku-Oki earthquake (M_w9.0) is taken as an example to conduct the comparison, where three different finite fault models are adopted. These finite fault models are, respectively, derived by Hayes (2011), Shao et al. (2011) and Wei et al. (2011). The results are listed in Table 2.

Table 2.

Open in new tab

Changes in the Earth's volume and radius of the finite fault models for the 2011 Tohoku-Oki earthquakes (M_w9.0).

Finite fault model	ΔV (km³)	ΔV/V(10⁻¹²)	ΔR (mm)
Hayes G.	83.03	76.74	0.163
Shao et al.	111.40	102.96	0.219
Wei et al.	129.10	119.32	0.253

Finite fault model	ΔV (km³)	ΔV/V(10⁻¹²)	ΔR (mm)
Hayes G.	83.03	76.74	0.163
Shao et al.	111.40	102.96	0.219
Wei et al.	129.10	119.32	0.253

Table 2.

Open in new tab

Changes in the Earth's volume and radius of the finite fault models for the 2011 Tohoku-Oki earthquakes (M_w9.0).

Finite fault model	ΔV (km³)	ΔV/V(10⁻¹²)	ΔR (mm)
Hayes G.	83.03	76.74	0.163
Shao et al.	111.40	102.96	0.219
Wei et al.	129.10	119.32	0.253

Finite fault model	ΔV (km³)	ΔV/V(10⁻¹²)	ΔR (mm)
Hayes G.	83.03	76.74	0.163
Shao et al.	111.40	102.96	0.219
Wei et al.	129.10	119.32	0.253

The changes in the Earth's mean radius for the finite fault models are different for the three models. These results are also different from the result of the point source of the 2011 Tohoku-Oki earthquake (M_w9.0), with difference of 17, 12 and 29 per cent, respectively. The reason is that the finite fault model represents the slip pattern and makes the rock rupture at different depth along the fault plane. As a consequence, the coseismic change of the Earth's mean radius is strongly dependent on the depth of the rupture. Therefore, a real fault slip distribution should be taken into account when we compute the coseismic change of the Earth's mean radius.

3.2 Cumulative change

We use the historical earthquakes since 1960 to evaluate the annual rate of Earth expansion. Data required for each earthquake are the focal mechanism based on the CMT solutions, which are available from the International Seismological Centre event catalogue (International Seismological Centre 2012). We select the earthquakes with moment magnitude greater than 7.0 (M_w ≥ 7.0) from the beginning of 1965 to the first quarter of 2014. There are about 410 events (Fig. 3). Most of earthquakes are shallow events (depth <100 km),and only few events occurred at depths exceeding 100 km. Apparently these strong events mainly locate along the circum Pacific seismic belt and the Mediterranean–Himalaya seismic belt. Although there were a large number of small magnitude earthquakes occurring globally, they just contributed very tiny part to the change in Earth's volume or radius. The total released energy of mall magnitude earthquakes was much smaller compared to those large magnitude earthquakes, which can be identified by the Gutenberg–Richter law. We also evaluated the two largest earthquakes—the 1960 Chile earthquake (M_w9.5) and the 1964 Alaska earthquake (M_w9.2). Their source parameters were respectively determined by Kanamori & Cipar (1974) and Kanamori (1970). The computed cumulative volume changes are shown in Fig. 4. We then roughly estimate the annual change rate of the Earth's mean radius by adopting the unweighted least-square approach. The results are shown in Fig. 4.

Figure 3.

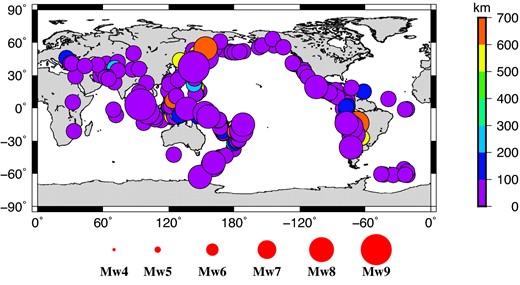
Global historical earthquakes (M_w ≥ 7.0) during the period 1965–2014.

Open in new tab Download slide

Figure 4.

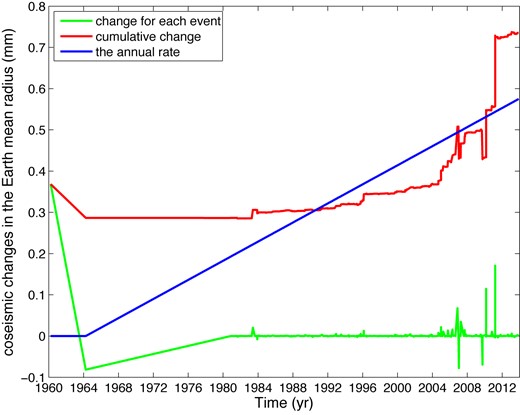
Cumulative change of the Earth mean radius produced by historical earthquakes.

Open in new tab Download slide

The cumulative change of the Earth's radius produced by large earthquakes (red line) since 1960 is on the submillimetre scale. This degree of change is dominated by several large earthquakes—such as the 2004 Sumatra event and the 2011 Tohoku-Oki event. The rate of the Earth's mean radius change estimated using the least-square approach is about 0.011 mm yr⁻¹, which is one magnitude smaller than the observed value (Shen et al. 2011; Wu et al. 2011); however, this demonstrates that earthquakes always make the Earth expand. Due to the uncertainties of source parameters (depth, magnitude), there still exists some errors of evaluating the Earth mean radius change rate.

4 CONCLUSION AND DISCUSSION

In this paper, earthquakes are examined as possible excitation sources that lead to changes in the Earth's volume. Following the basic physical principle, we propose an approach to compute the coseismic Earth's volume changes via the elastic dislocation theory, and derive the general solutions to compute the Earth's volume changes for three typical dislocation sources. Through the theoretical analysis, the Earth will be expanding by tensile source and explosion source excitation. Expansion or contraction of the Earth will depend on the type of earthquakes, which are dominated by the fault slip angle. The coseismic changes in the Earth's volume and the mean radius are strongly dependent on the depth of the earthquake. If we compute the changes in the Earth's volume and the mean radius due to the large earthquakes, we should adopt the finite fault model. Once we get the degree-zero dislocation Love numbers for the radial displacement, and combine the CMT solution, we can compute the coseismic Earth's volume change for the real case.

Because most of global earthquakes occurred at thrust faults or along subduction zones, the Earth tend to expand in most cases. Earthquakes along the normal faults will make the Earth contract over short time period, which was verified in our case studies. As we know, the subduction process is related to the ocean floor spreading due to the mantle convection, which is in fact a cooling process of the earth. Therefore, the coseismic volume increase by subduction earthquakes may be explained as follows: Before each mega subduction event, the oceanic crust has generally experienced a compressive loading process, in which the earth volume might be decreased. The earthquake is then a reverse process causing a part of the decreased volume recovered again. In a whole subduction seismic cycle, the earth radius might be reduced, if it can ever be changed. Based on the cumulative changes induced by historical earthquakes occurring over the last several decades, earthquakes tend to make the Earth expand. The annual change rate of the Earth mean radius was estimated to be about 0.011 mm yr⁻¹, more than an order of magnitude smaller than the observed value of 0.2 mm yr⁻¹ (Shen et al. 2011). Earthquakes only account for a small fraction of the observed rate, which indicate that there is another excitation source.

To compare the results obtained by the dislocation theory, we will try to get the expression of coseismic Earth's volume change via the normal mode method. One limitation of this work was assumption that the Earth's mass and energy were conserved before and after earthquakes. However, some energy may escape into space and some mass may be lost during an earthquake. We only consider the coseismic effect, and ignore the post-seismic effect and the interseismic process (Savage 1983, 1990; Sabadini et al. 1984). In a seismic cycle, the inter-seismic process and the post-seismic effect may play important roles to make the Earth expand or contract. However, we can not consider the interseismic process and post-seismic effect in the current theoretical frame, since the dislocation theory we adopt only concern the coseismic effect. Although the post- and interseismic process cannot be treated by the same dislocation theory, they could be inferred qualitative contributions to the expansion/contraction of the Earth. Based on a recent review by Wang et al. (2012), interseismic deformation is modelled by hypothetical fault dislocation in an opposite sense to the coseismic slip. Such interseismic processes would partly or completely cancel the coseismic expansion of the Earth. The effect of post-seismic on the Earth expansion issue can be obtained based on the viscoelastic dislocation theory (Tanaka et al. 2006). We will evaluate effects of the pose-seismic and interseismic process on the earthquake-induced long -term contribution to the expansion of the Earth in the next step. We use a compressible earth model in the computation which also causes errors when evaluating the coseismic volume change. The earth model's compressibility produces coseismic density changes from the core to the surface by reducing a portion of volume changes while the Earth's mass is conserved during earthquakes. These factors are more complicated to simulate and should contribute to part of the Earth's volume change.

Geothermal activities due to the decays of radioactive elements is a direct factor which can make the Earth expand or contract (Dearnley 1965; Lubimova & Polyck 1969). The gravitational constant (G) decay (Dirac 1937) is also taken as one possible factor to make the Earth expand (Dicke 1957, 1962). Volcanic eruptions, also the result of crustal motion can produce mass migration between Earth's internal solid material and gas. Because volcanic material may cool and accumulate on the Earth's surface, volcanic eruptions will also cause changes in the Earth volume. Further investigation should account for these and many other factors.

Earthquakes not only change the Earth's volume and the mean radius, but also disturb the moment of inertia and the length of day. Chao & Gross (1987) declared that earthquakes tend to decrease the total moment of inertia (sum of the three principal moments of inertia) and the length of day, which means that earthquakes transport the mass toward the centre of the Earth and make the Earth rounder. But they only show the results of the earthquakes during 1977–1985. Our results indicate that earthquakes seem to increase the Earth's volume and the mean radius based on the events in the time period of 1965–2014. The relationship between them should be further investigated.

We appreciate Editor Kosuke Heki, Dr. Wang Rongjiang, and an anonymous reviewer for their constructive and valuable comments, which greatly improved the manuscript. We sincerely thank Wenbin Shen and B. Fong Chao for fruitful discussions. We used the earthquake parameters provided by ISC. This research was financially supported by National Natural Science Foundation of China (Grant No. 41331066, 41174063 and 41474059), the CAS/CAFEA International Partnership Program for Creative Research Teams (No. KZZD-EW-TZ-19) and the SKLGED foundation (No. 2014-1-1-E).

REFERENCES

Beck

A.E.

,

Energy requirements of an expanding Earth

,

J. geophys. Res.

,

1961

, vol.

66

5

(pg.

1485

-

1490

)

Birch

F.

,

On the possibility of large changes in the Earth's volume

,

Phys. Earth planet Inter.

,

1968

, vol.

1

3

(pg.

141

-

147

)

Google Scholar

Crossref

Search ADS

Carey

S.W.

,

The Expanding Earth

,

1976

Elsevier

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Carey

S.W.

,

Theories of the Earth and Universe: A History of Dogma in the Earth Sciences

,

1988

Stanford University Press

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Chao

B.F.

Gross

R.S.

,

Changes in the Earth's rotation and low-degree gravitational field induced by earthquakes

,

Geophys. J. R. astr. Soc.

,

1987

, vol.

91

(pg.

569

-

596

)

Chen

Z.G.

,

The evolution model of the Earth's limited expanding

,

Chinese Sci. Bull.

,

2000

, vol.

45

(pg.

304

-

312

)

Dearnley

D.R.

,

Orogenic fold-belts, convection and expansion of the Earth

,

Nature

,

1965

, vol.

206

4

(pg.

1284

-

1290

)

Dicke

R.H.

,

Principle of equvalence and the weak interactions

,

Rev. Modern Phys.

,

1957

, vol.

29

pg.

355

Dicke

R.H.

,

Implications for cosmology of stellar and galactic evolution rates

,

Rev. Modern Phys.

,

1962

, vol.

34

1

(pg.

110

-

122

)

Dirac

P.

,

The cosmological constants

,

Nature

,

1937

, vol.

139

(pg.

323

-

323

)

Dziewonski

A.M.

Anderson

D.L.

,

Preliminary reference earth model

,

Phys. Earth planet Inter.

,

1981

, vol.

25

(pg.

297

-

356

)

Gerasimenko

M.D.

,

Modeling of the change of Earth dimenssions and deformations from space tracking data

,

Proceedings of the CRCM’93

,

1993

Kobe

J. Geod. Soc. Jap.

(pg.

215

-

217

)

pp.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Gerasimenko

M.D.

,

Very likely that geodesy will soon resolve the main problem of the Earth evolution: a few new facts

,

Proceedings of the 3th International Symposium ‘Regularities of Structure and Evolution of Geospheres’

,

1996

Vladivostok

(pg.

3

-

6

)

pp.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Gerasimenko

M.D.

,

A few geodetic arguments in the favour of hypothesis of expanding Earth

,

Far Eastern Math. Rep.

,

1997

, vol.

3

(pg.

69

-

79

)

Google Scholar

OpenURL Placeholder Text

WorldCat

Gross

R.S.

Chao

B.F.

,

The rotational and gravitational signature of the December 26, 2004 Sumatran earthquakes

,

Surv. Geophys.

,

2006

, vol.

27

(pg.

615

-

632

)

Hayes

G.

,

Finite fault model: updated result of the march 11, 2011 mw9.0 earthquake offshore Honshu, Japan

,

2011

Reston, VA

Tech. rep., U.S. Geol. Surv.

Google Scholar

Heki

K.

Takahashi

Y.

Kondo

T.

,

The baseline length changes of circumpacific VLBI networks and their bearing on global tectonics

,

IEEE Trans. Instrum. Meas.

,

1989

, vol.

38

2

(pg.

680

-

683

)

Huang

L.

Ma

Z.

Zhu

J.

,

The newest observational evidence on asymmetrical deformation of the Earth

,

Acta Seismol. Sin.

,

2002

, vol.

15

(pg.

210

-

213

)

International Seismological Centre

. ,

On-line Bulletin

,

2012

Thatcham, United Kingdom

Int. Seis. Cent.

http://www.isc.ac.uk

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Kanamori

H.

,

The Alaska earthquake of 1964: radiation of long-period surface waves and source mechanism

,

J. geophys. Res.

,

1970

, vol.

75

(pg.

5029

-

5040

)

Kanamori

H.

Cipar

J.

,

Focal process of the great Chilean earthquake may 22, 1960

,

Phys. Earth planet Inter.

,

1974

, vol.

9

(pg.

128

-

136

)

Lemoine

F.G.

Klosko

S.M.

Cox

C.M.

Johnson

T.J.

,

Time-variable gravity from SLR and DORIS tracking

,

Proceedings of the 15th International Workshop on Laser Ranging

,

2006

Canberra

Available at: http://cddis.gsfc.nasa.gov/lw15/docs/papers

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Lubimova

E.A.

Polyck

B.G.

,

Heat flow map of Eurasia

,

Geophys. Monogr. Ser.

,

1969

, vol.

13

(pg.

82

-

88

)

Google Scholar

OpenURL Placeholder Text

WorldCat

Lubimova

H.A.

,

Thermal history of the Earth with consideration of the variable thermal conductivity of its mantle

,

Geophys. J. R. astr. Soc.

,

1958

, vol.

1

2

(pg.

115

-

134

)

Lyttleton

R.A.

,

On the phase-change hypothesis of the structure of the Earth

,

Proc. R. Soc.

,

1965

, vol.

A287

(pg.

471

-

495

)

Lyttleton

R.A.

,

The Earth and its mountains

,

Nature

,

1983

, vol.

305

pg.

672

Mjelde

R.

Wessel

P.

Müller

R.D.

,

Global pulsations of intraplate magmatism through the Cenozoic

,

Lithosphere

,

2010

, vol.

2

5

(pg.

361

-

376

)

Müller

V.

,

Expansion von Erde und Universum

,

2010

http://zeitexpansion/de

Okada

Y.

,

Surface deformation due to shear and tensile faults in a half-space

,

Bull. seism. Soc. Am.

,

1985

, vol.

75

(pg.

1135

-

1154

)

Google Scholar

OpenURL Placeholder Text

WorldCat

Sabadini

R.

Yuen

D.A.

Boschi

E.

,

The effects of post-seismic motions on the moment of inertia of a stratified viscoelastic Earth with an asthenosphere

,

Geophys. J. R. astr. Soc.

,

1984

, vol.

79

(pg.

727

-

745

)

Savage

J.

,

A dislocation model of strain accumulation and release at a subduction zone

,

J. geophys. Res.

,

1983

, vol.

88

(pg.

4984

-

4996

)

Savage

J.

,

Interseismic uplift at the Nankai subduction zone, southwest Japan, 1951–1990

,

J. geophys. Res.

,

1990

, vol.

100

(pg.

6339

-

6350

)

Scalera

G.

,

The global paleogeographical reconstruction of the Triassic in the Earth's dilatation framework and the paleoposition of India

,

Ann. Geofis.

,

2001

, vol.

44

1

(pg.

13

-

32

)

Google Scholar

OpenURL Placeholder Text

WorldCat

Scalera

G.

Scalera

G.

Jacob

K.-H.

,

The expading Earth: a sound idea for the new millennium

,

Why Expanding Earth? A Book in Honour of Ott Christoph Hilgenberg

,

2003

INGV

(pg.

181

-

232

)

pp.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Shao

G.

Li

X.

Li

C.

Maeda

T.

,

Focal mechanism and slip history of the 2011 Mw9.1 off the Pacific coast of Tohoku earthquake, constrained with teleseismic body and surface waves

,

Earth Planet Space

,

2011

, vol.

63

7

(pg.

559

-

564

)

Shen

W.

Sun

R.

Chen

W.

Zhang

Z.

Li

J.

Han

J.

Ding

H.

,

The expanding Earth at present: evidence from temporal gravity field and space-geodetic data

,

Ann. Geophys.

,

2011

, vol.

54

4

(pg.

436

-

453

)

Google Scholar

OpenURL Placeholder Text

WorldCat

Smylie

D.S.

Mansinha

L.

,

The elasticity theory of dislocation in real Earth models and changes in the rotation of the Earth

,

Geophys. J. R. astr. Soc.

,

1971

, vol.

23

(pg.

329

-

354

)

Sun

F.

Zhu

X.

Wang

R.

Li

J.

,

Detection of changes of the earth's volume and geometry by using GPS and VLBI data

,

Chinese J. Geophys.

,

2006

, vol.

49

(pg.

1015

-

1021

)

Sun

W.

Okubo

S.

,

Surface potential and gravity changes due to internal dislocations in a spherical earth -I. Theory for a point dislocation

,

Geophys. J. Int.

,

1993

, vol.

114

(pg.

569

-

592

)

Tanaka

Y.

Okuno

J.

Okubo

S.

,

A new method for the computation of global viscoelastic post-seismic deformation in a realistic earth model (I)vertical displacement and gravity variation

,

Geophys. J. Int.

,

2006

, vol.

164

(pg.

273

-

289

)

Wang

K.

Hu

Y.

He

J.

,

Deformation cycles of subduction earthquakes in a viscoelastic Earth

,

Nature

,

2012

, vol.

484

(pg.

327

-

332

)

Wang

R.

Martin

F.L.

Roth

F.

,

PSGRN/PSCMP—a new code for calculating co- and post-seismic deformation, geoid and gravity changes based on the viscoelastic-gravitational dislocation theory

,

Comput. Geosci.

,

2006

, vol.

32

4

(pg.

527

-

541

)

Wei

S.

Sladen

A.

the ARIA group

. ,

2011

Pasadena

Tech. rep., Calif. Inst. of Technol.

Updated result 3/11/2011 (Mw9.0) Tohoku-Oki, Japan

Williams

G.E.

,

Geological constraints on the Precambrian history of Earth's rotation and the moon's orbit

,

Rev. Geophys.

,

2000

, vol.

38

(pg.

37

-

59

)

Wilson

G.

,

The tectonics of the Great Ice Chasm, Filchner Ice Shelf, Antarctica

,

Proc. Geol. Assoc.

,

1960

, vol.

71

(pg.

130

-

136

)

Wu

X.

Collilieux

X.

Altamimi

Z.

Vermeersen

B.L.A.

Gross

R.S.

Fukumori

I.

,

Accuracy of the International Terretrial Reference Frame origin and Earth expansion

,

Geophys. Res. Lett.

,

2011

, vol.

38

pg.

L13304

doi:10.1029/2011GL047450

Google Scholar

OpenURL Placeholder Text

WorldCat

Yang

J.L.

Yang

M.

,

Improvement of general relativity and cracking of cosmological puzzles

,

J. Vector. Relat.

,

2011

, vol.

6

1

(pg.

117

-

137

)

Google Scholar

OpenURL Placeholder Text

WorldCat

Download all slides

Month:	Total Views:
December 2016	1
February 2017	2
April 2017	1
May 2017	2
June 2017	3
July 2017	2
August 2017	1
September 2017	1
October 2017	6
November 2017	2
December 2017	12
January 2018	15
February 2018	11
March 2018	27
April 2018	27
May 2018	21
June 2018	16
July 2018	19
August 2018	16
September 2018	20
October 2018	6
November 2018	10
December 2018	10
January 2019	11
February 2019	19
March 2019	21
April 2019	13
May 2019	7
June 2019	6
July 2019	14
August 2019	13
September 2019	13
October 2019	13
November 2019	20
December 2019	12
January 2020	36
February 2020	21
March 2020	18
April 2020	15
May 2020	6
June 2020	11
July 2020	14
August 2020	7
September 2020	31
October 2020	40
November 2020	27
December 2020	9
January 2021	17
February 2021	6
March 2021	20
April 2021	32
May 2021	18
June 2021	6
July 2021	9
August 2021	22
September 2021	21
October 2021	19
November 2021	19
December 2021	10
January 2022	16
February 2022	5
March 2022	14
April 2022	19
May 2022	15
June 2022	19
July 2022	27
August 2022	23
September 2022	54
October 2022	18
November 2022	11
December 2022	29
January 2023	14
February 2023	21
March 2023	9
April 2023	16
May 2023	20
June 2023	4
July 2023	19
August 2023	13
September 2023	21
October 2023	9
November 2023	21
December 2023	34
January 2024	20
February 2024	6
March 2024	8
April 2024	12
May 2024	5
June 2024	6
July 2024	23
August 2024	15
September 2024	12
October 2024	9
November 2024	13
December 2024	8
January 2025	15
February 2025	10
March 2025	23
April 2025	24
May 2025	10

Article Contents

Earthquake-origin expansion of the Earth inferred from a spherical-Earth elastic dislocation theory

Abstract

1 INTRODUCTION

2 THEORY AND METHOD

2.1 Basic physical principle

2.2 The radial displacement in dislocation theory

2.3 Expression of Earth's volume change

3 RESULTS

3.1 Case study

3.2 Cumulative change

4 CONCLUSION AND DISCUSSION

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Earthquake-origin expansion of the Earth inferred from a spherical-Earth elastic dislocation theory Free

Abstract

1 INTRODUCTION

2 THEORY AND METHOD

2.1 Basic physical principle

2.2 The radial displacement in dislocation theory

2.3 Expression of Earth's volume change

3 RESULTS

3.1 Case study

3.2 Cumulative change

4 CONCLUSION AND DISCUSSION

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Earthquake-origin expansion of the Earth inferred from a spherical-Earth elastic dislocation theory