-
PDF
- Split View
-
Views
-
Cite
Cite
Stefania Gentili, Gianlorenzo Franceschina, High frequency attenuation of shear waves in the southeastern Alps and northern Dinarides, Geophysical Journal International, Volume 185, Issue 3, June 2011, Pages 1393–1416, https://doi.org/10.1111/j.1365-246X.2011.05016.x
Close - Share Icon Share
Summary
We investigated the high frequency attenuation of S waves in the southeastern Alps and northern External Dinarides using waveforms from 331 earthquakes (3.0 < Mw < 6.5). The spectral decay parameter, k, was computed using 1345 three component high quality records, collected by the Italian Strong Motion Network (RAN) and by the Short-Period Seismometric Network of northeastern Italy (NEI) in the period 1976–2007. Weak motion data from 11 stations of the NEI network and strong motion data collected by five accelerometers of the RAN were analysed. The k parameter was estimated in the 0–250 km distance range, in a frequency band extending from the corner frequency of the event up to 25 or 45 Hz, using the amplitude acceleration Fourier spectra of S waves. The observed record-to-record variability of k was modelled by applying a generalized inversion procedure, using both parametric and non-parametric approaches. Our results evidence that k is independent on earthquake size, while it shows both site and distance dependence. Stations of the NEI network present the same increase of k with epicentral distance, RE, and show values of the zero-distance k parameter, k0(S), between 0.017 and 0.053 s. For the whole region, the k increase with distance can be described through a linear model with slope dk/dRE= (1.4 ± 0.1) × 10−4 s km−1. Assuming an average S-wave velocity,  km s−1 between 5 and 15 km depth, we estimate an average frequency independent quality factor,
km s−1 between 5 and 15 km depth, we estimate an average frequency independent quality factor,  , for the corresponding crustal layer. The non-parametric approach evidences a weak positive concavity of the curve that describes the k increase with RE at about 90 km distance. This result can be approximated through a piecewise linear function with slopes of 1.0 × 10−4 and 1.7 × 10−4 s km−1, in accordance with a three layers model where moving from the intermediate to the bottom layer both
, for the corresponding crustal layer. The non-parametric approach evidences a weak positive concavity of the curve that describes the k increase with RE at about 90 km distance. This result can be approximated through a piecewise linear function with slopes of 1.0 × 10−4 and 1.7 × 10−4 s km−1, in accordance with a three layers model where moving from the intermediate to the bottom layer both  and
and  decrease. Two regional dependences were found: data from earthquakes located westward to the NEI network evidence weaker attenuation properties, probably because of S-wave reflections from different parts of the Moho discontinuity under the eastern Po Plain, at about 25–30 km depth, while earthquakes located eastward (in western Slovenia), where the Moho deepens up to 45–50 km, evidence a higher attenuation. Moreover, the k estimates obtained with data from earthquakes located in the area of the 1998 (Mw = 5.7) and 2004 (Mw = 5.2) Kobarid events are 0.017 s higher than the values predicted for the whole region, probably because of the high level of fracturing that characterizes fault zones. The comparison between measured and theoretical values of k, computed at a few stations with available S-wave velocity profiles, reveals that the major contribution to the total k0(S) is due to the sedimentary column (from surface to 800 m depth). The hard rock section contribution is limited to 0.005 s, in accordance with a maximum contribution of 0.010 s predicted by the non-parametric inversion.
decrease. Two regional dependences were found: data from earthquakes located westward to the NEI network evidence weaker attenuation properties, probably because of S-wave reflections from different parts of the Moho discontinuity under the eastern Po Plain, at about 25–30 km depth, while earthquakes located eastward (in western Slovenia), where the Moho deepens up to 45–50 km, evidence a higher attenuation. Moreover, the k estimates obtained with data from earthquakes located in the area of the 1998 (Mw = 5.7) and 2004 (Mw = 5.2) Kobarid events are 0.017 s higher than the values predicted for the whole region, probably because of the high level of fracturing that characterizes fault zones. The comparison between measured and theoretical values of k, computed at a few stations with available S-wave velocity profiles, reveals that the major contribution to the total k0(S) is due to the sedimentary column (from surface to 800 m depth). The hard rock section contribution is limited to 0.005 s, in accordance with a maximum contribution of 0.010 s predicted by the non-parametric inversion.
1 Introduction
Attenuation of seismic waves, which propagate through the Earth, can strongly influence the ground motion recorded at a site, thus modifying the energy content of the signal radiated from the source. It has long been recognized that body wave attenuation in the crust can be generally ascribed to geometrical spreading, intrinsic anelasticity of materials encountered by waves that propagates along the seismic ray, and scattering from heterogeneities of the lithosphere, randomly distributed along the propagation path. For each seismic phase, the quality factor Q, a dimensionless parameter introduced with the aim to quantify the fractional energy loss per cycle of oscillation as Q= 2πE/ΔE (Knopoff 1964; Lay & Wallace 1995), can be used to describe the spectral decay of the amplitude Fourier spectrum through the factor A∼ exp (–πf t/Q), where f represents the frequency and t is the travel time along the ray path (Aki & Richards 1980). Estimates of Q are often obtained using crustal phases of local earthquakes, after separation of geometrical spreading from the other types of attenuation. Despite of the recognition that scattering from randomly distributed heterogeneities is one of the physical mechanisms responsible of seismic wave attenuation in the crust, the separation of the total quality factor, Q, in terms of scattering and intrinsic absorption contributions according to: Q−1=QS−1+QA−1, still remains a difficult task. Since the paper of Aki (1969), which firstly recognized the coda waves of a seismogram as composed of incoherent scattered seismic waves, many authors inferred attenuation properties from the coda Q parameter, Qc, using different models of scattering (Aki & Chouet 1975; Frankel & Wennerberg 1987; Hoshiba 1991, 1997; Mayeda et al. 1992, Wennerberg 1993; Margerin et al. 1999; Lacombe et al. 2003). Otherwise, as it is often impossible to distinguish between direct and reflected or refracted crustal phases, Q measures from records of local earthquakes are also inferred by analysing both P and S waves with the adoption of time windows which start from the direct phase but probably including also later arrivals and scattered waves (see Bindi et al. 2004, 2006; Castro et al. 2008a; Padhy 2009, among many others). Recently, the separation between intrinsic absorption and scattering has been performed for many regions through the method of Wu (1985) based on the radiative transfer theory (Hoshiba 1991; Fehel et al. 1992; Hoshiba et al. 2001; Bianco et al. 2002). All of the above mentioned estimates of attenuation properties in the crust are inferred from ground motion data recorded with short period or broad-band instruments having frequency bandwidths generally extending up to 20–25 Hz, and using frequency analyses which are performed in logarithmic bins. As a consequence, the high frequency (f > 15 Hz) attenuation of shear waves is often characterized by some degree of uncertainty with observations showing a frequency dependence of Q that weakens or even disappears over some specified frequency (Castro et al. 2004, 2008b). Otherwise, it is notable that reliable characterizations of the S-wave spectral model for high frequencies are necessary both in order to infer earthquake source properties from observed data (Abercrombie 1995; Shi et al. 1998; McGarr et al. 2009) and to perform ground motion simulations from a given source (Ameri et al. 2008; Boore 2009).
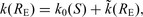
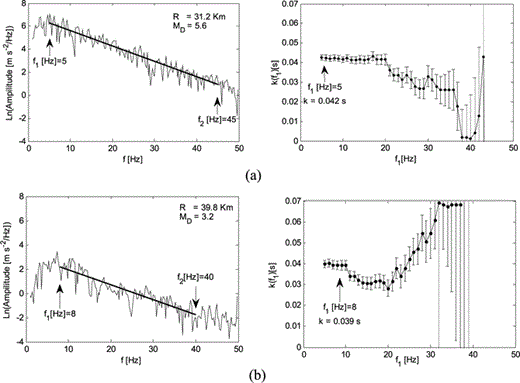
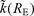 represent the station and the distance dependent contributions (Anderson 1991), respectively. According to this model, data recorded in sufficiently wide ranges of distance show an increase of k with RE and a station dependence of k is also observed when this parameter is measured with data of earthquakes approximately located beneath the recording site [k0(S) ≡k(RE≅ 0)]. The earliest studies interpreted the k0(S) dependence on site in terms of near-surface geological conditions of the considered station and found a general correlation between the k0(S) values estimated with acceleration data and the site classification (Anderson & Hough 1984; Hough & Anderson 1988; Castro et al. 1996); in further papers this dependence was assumed (Gregor et al. 2002; Silva & Costantino 2002; Fernández et al. 2010). Recently, Campbell (2009) recognized that the value of k0(S) depends on the entire geological profile beneath the station site, from the ground surface to a depth corresponding roughly to the earthquake source region (5–10 km). He also hypothesized the separation of k0(S) into two principal components: one due to a sedimentary column with thickness of the order of tens or hundreds of metres and the other one due to the hard-rock section of the geological profile underlying sediments.
represent the station and the distance dependent contributions (Anderson 1991), respectively. According to this model, data recorded in sufficiently wide ranges of distance show an increase of k with RE and a station dependence of k is also observed when this parameter is measured with data of earthquakes approximately located beneath the recording site [k0(S) ≡k(RE≅ 0)]. The earliest studies interpreted the k0(S) dependence on site in terms of near-surface geological conditions of the considered station and found a general correlation between the k0(S) values estimated with acceleration data and the site classification (Anderson & Hough 1984; Hough & Anderson 1988; Castro et al. 1996); in further papers this dependence was assumed (Gregor et al. 2002; Silva & Costantino 2002; Fernández et al. 2010). Recently, Campbell (2009) recognized that the value of k0(S) depends on the entire geological profile beneath the station site, from the ground surface to a depth corresponding roughly to the earthquake source region (5–10 km). He also hypothesized the separation of k0(S) into two principal components: one due to a sedimentary column with thickness of the order of tens or hundreds of metres and the other one due to the hard-rock section of the geological profile underlying sediments.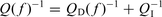
2 Seismicity Distribution and Tectonics of the Area
The southeastern sector of the Alpine chain is one of the most seismic active zones of Italy with seismicity mainly located in the Friuli-Venezia Giulia region, an area sited between the outer front of the southern Alps and the Periadriatic lineament. In the eastern part, the zone of interaction between the southern Alps and External Dinarides is characterized by a more diffuse and less intense seismicity. The main tectonic features of the area are outlined in Fig. 1; Fig. 2 shows historical and instrumental seismicity. According to CPTI04 catalogue (Gruppo di lavoro CPTI 2004), in the last 900 years the southeastern Alps and northern External Dinarides experienced at least nine earthquakes with maximum MCS intensity greater or equal to IX (brown squares in Fig. 2), alternated with periods of minor seismicity. The last destructive event, the 1976 May 6 Mw 6.4 Friuli earthquake, caused 989 fatalities, the destruction of many villages and high economical costs (Slejko et al. 1999). One year later the OGS installed the first permanent stations of the Seismometric Network of Friuli-Venezia Giulia for monitoring the area (Renner 1995; Priolo et al. 2005). The following years, other stations have been placed in the Friuli-Venezia Giulia region and a new network was installed in the Veneto region (for a total number of 12 broad-band and 22 short-period seismic stations). At present, these two networks, forming the Short-Period Seismometric Network of Northeastern Italy (NEI network – http://www.crs.inogs.it/), record the seismicity of the region with high detection capability. According to Gentili et al. (2011), the network has reached a completeness magnitude of 1.5 in 2007 for a large part of Friuli-Venezia Giulia region. In the period 1976–2007, the instrumental seismicity was dominated by earthquakes in the magnitude range [5, 6.4] shown with stars in Fig. 2. The epicentres are mainly located in a belt extending from the northern part of Istria peninsula (Rijeka) to the Asolano area.
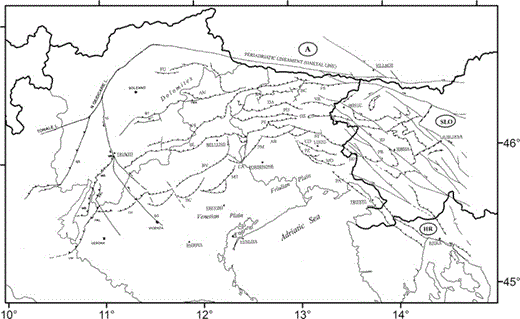
Simplified structural model of NE Italy and W Slovenia (modified from Carulli et al. 1990; Castellarin et al. 2006; Galadini et al. 2005). Legend (structures): MB, M. Baldo-M. Stivo-M. Bondone fault; GS, Giudicarie structural system; VM, Volta Mantovana fault; PAL, M. Pastello-Ala fault; SC, Schio-Vicenza fault; TC, Trento-Cles fault; ST, Stava-Collaccio fault; BC, Bassano-Cornuda fault; BV, Bassano-Valdobbiadene fault; BL, Belluno fault; VS, Valsugana fault; FU, Funes fault; AN, Antelao fault; MT, Montello fault; CA, Cansiglio fault; PM, Polcenigo-Maniago fault; AR, Arba-Ragogna fault; PE, Periadriatic thrust; PU, Pinedo-Uccea fault; DA, Dof-Auda fault; SA, Sauris fault; BC, But-Chiarsò fault; FS, Fella-Sava fault; VR, Val Resia fault; ST, Susans-Tricesimo fault; UD, Udine-Buttrio fault; PZ, Pozzuolo fault; MD, Medea fault; PA, Palmanova fault; ID, Idrija fault; PR, Predjama fault.
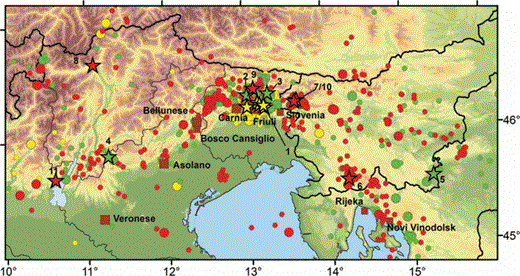
Seismicity in the area. Brown squares: historical seismicity (earthquakes with intensity ≥IX are shown with squares dimensions proportional to earthquake intensity: 1117 January 3, Veronese IMCS = IX–X; 1323 Novu Vinodolsk IMCS = IX; 1348 January 25, Carnia IMCS = IX–X; 1511 March 26, Slovenia IMCS = X;1695 February 25, Asolano IMCS = IX–X; 1721 January 12, Rijeka IMCS = IX; 1873 June 29, Bellunese IMCS = IX–X; 1936 October 18, Bosco del Cansiglio IMCS = IX; 1976 May 6, Friuli IMCS = IX–X). Yellow symbols: seismicity from 1976 to 1977. Green symbols: seismicity from 1977 to 2004. Red symbols: seismicity from 2004 to 2007 (the time period analysed in this paper). Circles: earthquakes with 2.8 ≤ML < 5 (symbol dimensions are proportional to earthquake magnitude). Stars: ML≥ 5 earthquakes (numbers: 1: 1976 swarm; 2: 1977 Trasaghis earthquake; 3: 1979 Lusevera earthquake; 4: 1989 Pasubio earthquake; 5 and 6: 1993 and 1995 Slovenia earthquakes; 7 and 10: 1998 and 2004 Kobarid earthquakes; 8: 2001 Merano Earthquake; 10: 2002 Sernio earthquake; 11: 2004 Salò earthquake).
The investigated region is the northeastern side of the southern Alps and the Dinarides, delimited westward by the Giudicarie line and northward by the Periadriatic line (see Fig. 1) and it is included in a convergent margin zone between the Adria microplate and the Eurasian Plate (see e.g. Castellarin et al. 2006; Burrato et al. 2008). According to Mantovani et al. (1996) the progressive northeastward pushing of African Plate, respect to the Eurasian Plate, generates an anticlockwise rotation of Adria microplate, which causes the present complex tectonic deformation. Several tectonic phases in the region inherited and reactivated the main pre-existing faults and fragmented the crust into different tectonic domains corresponding to different seismotectonic zones (Bressan et al. 2003). The eastern part of the analysed region (in Slovenia and Croatia) is mainly characterized by the Dinaric faults, mainly NW–SE oriented. The western Slovenia, where the Kobarid sequences were located (Bressan et al. 2007; Gentili & Bressan 2008) is characterized by a strike-slip tectonic regime. The tectonic regime is mainly compressive in the central part of Friuli area, with a E–W-trending system of south verging thrust and folds, and a few back thrusts. The western Friuli area and the eastern Veneto region are also characterized by thrust tectonics, with NE–SW-oriented and SE-verging thrust (Bressan et al. 2003). The more external structures NE–SW trending are located in the Montello-Friuli zone (MT in Fig. 1) which were generated by the Messinian-Pliocene compressions. The Venetian sector is dominated by the SE-verging Bassano-Valdobbiadene thrust (Doglioni 1992a, 1992b– BV in Fig. 1), that is displaced by the NW–SE trending Schio-Vicenza strike-slip fault system (SC in Fig. 1). This fault system is interpreted as the Late Miocene-Quaternary kinematic junction between the eastern south alpine chain and the central western southern Alps. The Schio-Vicenza fault system transferred compressive deformations to the Giudicarie belt (Castellarin & Cantelli 2000). The westernmost part of the analysed region is the NNE-trending transpressive Giudicarie belt.
3 Shear Waves Attenuation in Northeastern Italy
In this region, the frequency dependence of S-wave attenuation has been investigated by several authors, who analysed different areas located south to the Periadriatic lineament in the range of latitudes between 45.0° and 46.5°N (Console & Rovelli 1981; Castro et al. 1996; Govoni et al. 1996; Malagnini et al. 2002; Bianco et al. 2005). Console & Rovelli (1981) and Castro et al. (1996) considered the same area, including Veneto and Friuli-Venezia Giulia regions, analysed the 1976–1977 seismic sequences and assumed for the total Q the model Q(f) =Q0 (f/f0)n, with f0= 1 Hz. They inferred the same frequency dependence of the quality factor (n≅ 1.0) but different values of Q0: 80.0 and 20.4 for Console & Rovelli (1981) and Castro et al. (1996), respectively. Actually, although the major events were common to both investigators, they used different global data sets, different approaches in order to take into account site effects and different criteria for the selection of the time window analysis. An area extending eastward respect to the previously investigated regions, covering part of Veneto, Friuli-Venezia Giulia and western Slovenia, was analysed by Malagnini et al. (2002) and by Bianco et al. (2005). The former investigators analysed a large data set of both strong and weak motion records and found a complex dependence of geometrical spreading on distance. In the range of frequencies 0.5–14 Hz, they estimated Q(f) = 260.0 f0.55, up to 200 km hypocentral distance. Bianco et al. (2005) selected 200 three-component waveforms from the same data set and applied the multiple-lapse time window analysis in order to infer intrinsic and scattering attenuation in the region. This kind of analysis allows to infer the relative contributions to the quality factor by estimating the estinction length, Le and the seismic albedo, Bo. These parameters are related to the total Q and to the ratio QS/Q, respectively. Bianco et al. (2005) evaluated the frequency dependence of the total Q with a non-parametric approach for discrete values of frequency ranging from 1 to 16 Hz. They found that both scattering and intrinsic attenuation show similar frequency dependence, and that the intrinsic absorption QA predominates over scattering (QS≈ 2QA). A linear regression of the results obtained for the total Q, for the scattering term and for the intrinsic absorption term, gives Q(f) = 251 f0.7; QS= 794 f0.8 and QA= 398 f0.7, respectively, up to 200 km hypocentral distance.
All of the above considered estimates of the frequency dependence of S-wave attenuation are well established in the lower part of the analysed band of frequencies. At high frequencies (f > 15 Hz), where, according to eq. (2), the frequency independent part of the quality factor predominates, all these estimates are characterized by low resolution and the employed methods seem to be unable to capture an eventual flattening of the frequency dependence. For this reason we considered the total Q measured in these works as an estimate of QD. Since Bianco et al. (2005) selected data that covered a large percentage of the area we analyse, considered a large number of earthquakes in the inversion and applied the more recently developed technique for the quality factor estimation, we choose to apply the frequency dependence established in their work in order to correct the amplitude Fourier spectra of S waves according to eq. (2). The k parameter was inferred from the slope of the amplitude Fourier spectrum of acceleration data after correction for the factor QD(f) = 251 f0.7. Indeed, after correction for QD, all spectra show a high frequency decay compatible with positive values of k, confirming that the total attenuation of S waves measured by Bianco et al. (2005) does not completely take into account of the high frequency (f > 15 Hz) attenuation.
4 Data Set
We selected weak-motion data from the OGS database that includes the time series recorded by the NEI network since 1977 May (http://www.crs.inogs.it/) and strong motion data from the Italian Accelerometric Archive (ITACA database – http://itaca.mi.ingv.it), that collects acceleration data recorded by the Italian Strong Motion Network (RAN), managed by the Italian Department of Civil Protection (DPC, http://www.protezionecivile.it). These two networks adopt different acquisition systems, also depending on the considered time period so that the instrumental data can be roughly divided as follows:
- 1
acceleration data recorded by analogue accelerometers (Kinemetrics SMA-1) operated by the DPC and collected in digital format in the ITACA database, covering the period since 1972 to the present,
- 2
analogue velocity data collected by the OGS from 1977 to 1987, and
- 3
digital data collected by the OGS with two different acquisition systems (Earth Data 9690 from 1988 January to 1994 April and Lennartz Mars 88 from 1994 May to the present).
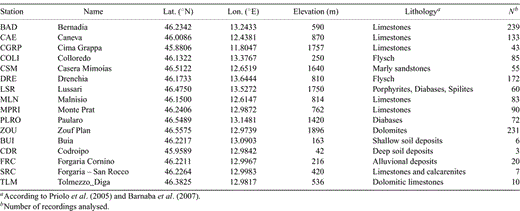
For this area, the ITACA database includes 40 events with ML > 3.0 recorded in the period 1976 May–1989 September. The data set includes all of the strongest events of the 1976 crisis, the main shock of the 1977 September 16 (Mw= 5.3) Trasaghis sequence and the 1989 September 13 (Mw= 5.0) Pasubio earthquake. In order to enhance the reliability of results, in this work we selected acceleration data from stations equipped with instruments having a proper frequency of at least 20 Hz. We also avoided to consider the data from instruments with particular installation conditions (structures monitoring as an example) or data from stations with a small number (N < 3) of recordings. The spectral decay parameter has been estimated at five stations equipped with SMA-1 accelerometers using data characterized by epicentral distances less than 50 km, for a total number of 46 recordings of 29 events with 3.5 < Mw < 6.5. Hypocentres are located in the range 3–16 km depth. Location data are taken from Slejko et al. (1999) and Mw values from Perniola et al. (2004).
The OGS database includes, at present, 39 096 events occurred in the time window 1977 May 6–2007 December 31, 16 496 of which are located events with magnitude assignment (Gentili et al. 2011). The location is routinely performed using the HYPO71 program (Lee & Lahr 1975) with a simple crustal model (three layers, with VP= 5.85, 6.80 and 8.00 km s–1, discontinuities at depths of 22 and 39.5 km, and VP/VS= 1.78); magnitudes are computed from duration data, using the station coefficients as calibrated by Rebez & Renner (1991). In this paper, we used data obtained with the second digital acquisition system adopted by the OGS. Our starting data set was composed by 4442 seismic events recorded from 1994 to 2007 having duration magnitude, MD, between 0.6 and 5.7. For the earthquake location, we used a revised version of the OGS bulletin (Bressan et al. 2009, personal communication) that contains the accurate relocation of the MD > 2.5 earthquakes of the Kobarid seismic sequences (Bressan et al. 2009). According to Bragato & Tento (2005) and Gentili et al. (2011), during this period the duration magnitude MD, calibrated for the analogue period, overestimates the local magnitude, ML, for MD < 3.5. In this paper, to investigate the attenuation of shear waves in the region, we used the information on magnitude only as a threshold to select the records with acceptable values of the S/N. We selected events with MD > 3.0. Indeed, in accordance with Gentili et al. (2011), for this data set, MD≥ 3.0 corresponds to ML≥ 2.8 and, on average, to S/N > 3.4.
We considered earthquakes located south to the Periadriatic lineament in both Alpine and Dinaric domains and east to the Giudicarie arc. To avoid large location errors, only data with epicentral distances less than 200 km were selected. The distance limit was computed with respect to the station of Bernadia (BAD), approximately located at the centre of the network, which recorded the largest number of events. A maximum horizontal location error of 2.5 km (as supplied by the HYPO71 code) was also considered in order to define a data set characterized by reliable locations. More than 75 per cent of the selected data have hypocentres located in the range 5–15 km depth. The studied area, extending in west–east direction from the Schio-Vicenza fault system to the Zagreb area, is depicted in Fig. 3, where epicentres of the selected earthquakes are also shown together with the stations selected for the analysis. Stations characteristics are reported in Table 1. We estimated the spectral attenuation parameter using records of the three component stations of the NEI network. After a visual inspection of results, we decided to exclude from subsequent analyses those stations affected by site effects producing clear amplifications in the high frequency part of the acceleration spectrum (f > 10 Hz) or strong differences between the two horizontal components. We also decided to consider only stations that recorded more than 40 events. Finally, the selection procedure produced 1299 high quality records from 302 events (3.0 < Mw < 5.7), recorded by 11 short-period stations. Seismic traces are mostly from velocimeters, except the case of BAD, where both acceleration and velocity data are available. The signal is generally recorded with acceptable S/N up to about 25 Hz, with the exception of BAD and Zoufplan (ZOU), where high sampling records are available. These stations allowed k estimations from acceleration spectra extending up to 40–50 Hz. Both acceleration and velocity data were base line corrected, deconvolved with the instrumental response and filtered in the frequency domain. A band pass zero-phase eight-poles Butterworth filter with a high-pass frequency of 0.8 Hz was applied. For data recorded with digital instruments, the low pass frequency was set to 31 or 62 Hz depending on the sampling rate (62.5 and 125 Hz, respectively). The data recorded by SMA-1 instruments were low pass filtered up to the proper frequency of accelerometers (ranging from 21.0 to 25.7 Hz). The subsequent analyses were performed with the horizontal components of the 1345 selected acceleration and velocity records. The total number of records used for each station is reported in Table 1.
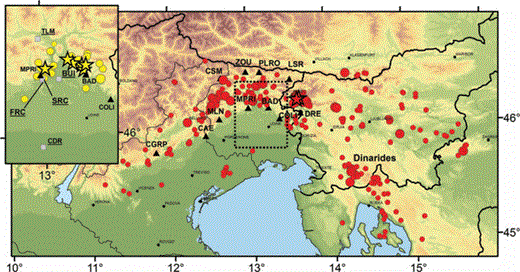
Location of earthquakes and stations used in this study. Red symbols: earthquake epicentres corresponding to digital data collected by the OGS. Yellow symbols (upper left side rectangle – dotted area in the main map): earthquake epicentres corresponding to acceleration data recorded by the RAN and collected in the ITACA database. Symbol dimensions are proportional to earthquake magnitude. Stars indicate the ML≥ 5 events. Black triangles: OGS seismic stations. Grey squares: RAN stations.
5 Method of Analysis
The spectral decay parameter was estimated from the slope of the high frequency part of the acceleration amplitude Fourier spectrum with the model introduced by Anderson & Hough (1984). The horizontal components of the corrected acceleration and velocity time series were used to compute the amplitude spectrum of S waves by selecting time windows starting at the direct S-wave onset and including the significant part of the ground motion. Different crustal phases and also scattered waves are generally included in the windows selected for the analysis, being impossible to identify in the records the seismic phases later than Sg-arrival, due to the seismic waves superposition. The data were windowed using a two-sided 5 per cent cosine taper and padded with zeros before applying the FFT algorithm. Depending on magnitude and distance of the events, variable-length windows with durations ranging from 1.1 to 20.9 s were adopted. In order to reduce the variance of data, a smoothing algorithm was applied to the amplitude Fourier spectrum. Preliminary tests showed that the resulting smoothed amplitudes are mainly dependent on the width of the smoothing function and on the choice between a smoothing function that is symmetric about the central frequency of smoothing, fC, and a smoothing function that is symmetric about the logarithm of fC. With the exception of the box-car, the shape of the smoothing function is not particularly relevant. In order to avoid some possible undesirable effect due to different weightings of low and high frequencies of the spectrum, an fC-symmetric smoothing function was adopted and the amplitude spectra were smoothed by a sliding Hann window (Oppenheim & Schafer 1999) of 0.5 Hz half-width.
5.1 Spectral model
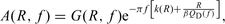
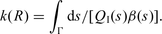
Assuming a negligible dependence of the geometrical spreading on frequency, we estimated the k parameter by correcting the S-wave spectra only for the frequency dependent part of the quality factor. The smoothed S-wave spectra were corrected for QD using the relation QD(f) =Q0fn with Q0= 251 and n= 0.7 correspondingly to the total quality factor estimated for this area by Bianco et al. (2005). Both horizontal components of the smoothed spectra were used to estimate κ through a linear regression of the spectral amplitudes between frequencies f1 and f2. The spectral band adopted for the analysis was determined by selecting the part of the spectrum where a linear decay was clearly evident. In particular, f2 is the frequency at which the noise level starts contaminating the signal and, in the present study, ranged from 20 to 45 Hz. For each record, the first limit of the spectral band was chosen by plotting the k values obtained with different values of f1 with respect to f1 and selecting the k(f1) values in an observed range of stability of this function by a visual inspection of each plot; f1, generally depending on event size, ranged from 5 to 10 Hz. The threshold magnitude adopted in this work ensures the validity of the condition f1 > f0, being f0 the corner frequency of the event. Indeed, according to the scaling of f0 with magnitude, previously assessed for this region (Franceschina et al. 2006), we expect f0≅ 4.5 Hz for ML≅ 3.0. To fit the amplitude spectrum, we used the least absolute residual method. This method minimizes the absolute difference of the residuals rather than the squared differences, thus decreasing the influence of outliers on results. The k values estimated from the two horizontal components of each record were finally averaged by computing the corresponding weighted mean and standard deviation. In order to increase the robustness of the method, the weights were chosen as the inverse of the error of each single fit. Figs 4(a) and (b) shows two examples of spectral decay parameter estimation.
Two examples of spectral decay parameter estimation. Left panels: acceleration spectra and linear regressions used to obtain the single record estimate of the k parameter; right panels: k estimates and corresponding standard deviations as function of the lower limit of the frequency bandwidth adopted for the linear regression, f1. The best estimate of k and the corresponding value of f1 are indicated by an arrow.
5.2 Regional model
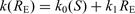
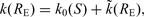
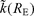 is assumed to be a smooth function of the epicentral distance such that:
is assumed to be a smooth function of the epicentral distance such that: 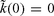 . In principle, this condition could be replaced by
. In principle, this condition could be replaced by 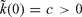 when an a priori average contribution to the k value, due to a predominantly vertical propagation common to all the sites, can be assigned with confidence. Both eqs (5) and (6) can be written in the matrix form:
when an a priori average contribution to the k value, due to a predominantly vertical propagation common to all the sites, can be assigned with confidence. Both eqs (5) and (6) can be written in the matrix form: 
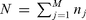 where nj is the number of earthquakes recorded at station j. A is a N× (M+ 1) matrix containing the N corresponding epicentral distances in the last column. In the non-parametric case, the variable RE was discretized into K bins and each of the klj estimations of the spectral decay parameter of earthquake l recorded at station j is assigned to the corresponding distance bin, and then assigned to the data vector b. Now x is a vector containing the M unknown parameters k0(Sj) and the K unknown values of the discretized function
where nj is the number of earthquakes recorded at station j. A is a N× (M+ 1) matrix containing the N corresponding epicentral distances in the last column. In the non-parametric case, the variable RE was discretized into K bins and each of the klj estimations of the spectral decay parameter of earthquake l recorded at station j is assigned to the corresponding distance bin, and then assigned to the data vector b. Now x is a vector containing the M unknown parameters k0(Sj) and the K unknown values of the discretized function 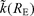 . A is a sparse matrix whose upper lines are defined according to eq. (6). We adopted the approach of Castro et al. (1990) in order to impose both the smoothness and the zero-distance constraints. Following Castro et al. (1990) we quantified the solution roughness by the second derivative of
. A is a sparse matrix whose upper lines are defined according to eq. (6). We adopted the approach of Castro et al. (1990) in order to impose both the smoothness and the zero-distance constraints. Following Castro et al. (1990) we quantified the solution roughness by the second derivative of 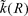 and introduced the constraint at zero-distance and the smoothness constraint with the corresponding weights w1 and w2 through equations
and introduced the constraint at zero-distance and the smoothness constraint with the corresponding weights w1 and w2 through equations 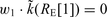
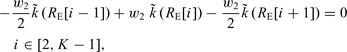
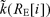 is the value of
is the value of 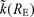 at the central distance RE[i] of the ith bin. K is the number of bins. Eqs (8) and (9) were applied by adding K– 1 lines to the matrix A and K– 1 zero-elements to the data vector b.
at the central distance RE[i] of the ith bin. K is the number of bins. Eqs (8) and (9) were applied by adding K– 1 lines to the matrix A and K– 1 zero-elements to the data vector b.The set of linear equations represented by eq. (7) was solved using a least square inversion scheme. Several preliminary inversions were performed in order to assess how the choice of both weights values and the distance bin-width can influence the result. The solution roughness is controlled by the distance bin-width and by the weight w2. To minimize the number of empty bins, we avoid using small bin-widths. Moreover, the observed dispersion of the k estimates suggests adopting large values of w2 in order to increase the smoothness of the curve  . We adopted bins 10 km wide as a reasonable compromise between smoothness and resolution. The estimated errors, on both the site- and the distance-dependent parameters of the model, change in dependence of the values of w1 and w2. The optimum value for the weights was selected through a grid search having the aim of minimizing the size of the unit covariance matrix of the system (Menke 1984). We used a weights range from 0 to 500 discretized into 50 equal bins. Fig. 5, showing the size of the unit covariance matrix for different values of the weights w1 and w2, evidences that the minimum is reached for w1= 80 and w2= 120. However, it is worth noting that equal variations of the weights around this minimum produce different increments of the matrix size, being this quantity more sensitive to the weight w2.
. We adopted bins 10 km wide as a reasonable compromise between smoothness and resolution. The estimated errors, on both the site- and the distance-dependent parameters of the model, change in dependence of the values of w1 and w2. The optimum value for the weights was selected through a grid search having the aim of minimizing the size of the unit covariance matrix of the system (Menke 1984). We used a weights range from 0 to 500 discretized into 50 equal bins. Fig. 5, showing the size of the unit covariance matrix for different values of the weights w1 and w2, evidences that the minimum is reached for w1= 80 and w2= 120. However, it is worth noting that equal variations of the weights around this minimum produce different increments of the matrix size, being this quantity more sensitive to the weight w2.
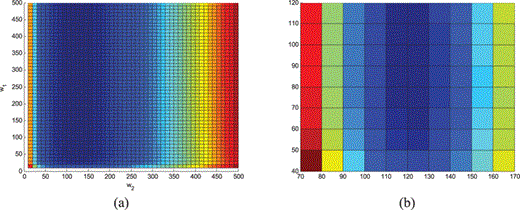
(a) Size of the unit covariance matrix for different values the weights w1 and w2; arbitrary colours: blue is smaller, red is larger. (b) detail of (a); colour scale is stretched.
6 Results
The spectral analyses of weak-motion data of the OGS database and strong motion data of the Italian Accelerometric Archive allowed to estimate 1299 and 46 values, respectively, of the k parameter. The range of epicentral distances extends up to 250 km in the case of weak-motion data and is limited to 50 km for strong motion records. With these two data sets, we obtained k values in the ranges 0.006–0.128 and 0.037–0.075 s, respectively and we employed the former estimates to infer the regional high frequency attenuation model. The first analyses concerned the whole region located south to the Periadriatic lineament and extending in west–east direction from the Schio-Vicenza fault system to the Zagreb area (see Figs 1 and 3). We estimated the high frequency attenuation model using both parametric and non-parametric approaches. Afterwards, we considered two subsets of data by using events located eastward and westward, respectively, to the centre of the NEI network, roughly corresponding to the location of the station BAD. Two models, valid for events located eastward and westward (hereinafter referred to as EAST- and WEST-Dataset, respectively), were inferred with the non-parametric approach. Finally, in order to evaluate the k0(S) values of sites equipped with strong motion instruments, we applied the results concerning the regional attenuation trend obtained for the whole area at epicentral distances less than 50 km, to the estimates of k obtained from strong motion data.
To apply the inversion scheme described in Section 5 we performed a preliminary test on the dependence of k on magnitude. For this purpose we selected the estimates of the k parameter obtained with records of the two main sequences occurred in the region (both in Kobarid on 1998 and on 2004). Indeed, this subset of data consists of 62 earthquakes located within less than 20 km radius (Gentili & Bressan 2008) and show values of magnitude extending over the whole range considered in this study. We investigated the magnitude dependence of the k parameter of these events by neglecting the eventual distance dependence. Figs 6(a)–(d) shows four examples of the dependence of k on magnitude obtained for the stations of the NEI network. A visual inspection of data evidences that k values estimated for these events are approximately independent on magnitude. In the following, we extrapolate this feature to the whole data set employed to infer the regional attenuation model. Preliminary inversions performed on the whole selected catalogue of weak-motion data also showed that the records of earthquakes belonging to the Kobarid seismic sequences generally have higher values of k with respect to the average trend of the function  estimated for the whole area. The k values of these events ranged from 0.011 and 0.109 s with 0.047 s mean and 0.017 s standard deviation. Due to the large number of earthquakes recorded during the Kobarid sequences, the events belonging to this subset of data constitute more than 20 per cent of the whole data set, but cover an area that is less than 2 per cent of the whole analysed region. We decided to separate these data from the other estimates of k in order to infer a general attenuation model valid for the whole area. After having removed these events, we obtained a sufficiently numerous and well distributed sample of data for the assessment of the distance dependence of k. In the following, we show the results obtained by including or not including the Kobarid data. A general discussion of the high frequency attenuation in the Kobarid area is presented in Section 7.
estimated for the whole area. The k values of these events ranged from 0.011 and 0.109 s with 0.047 s mean and 0.017 s standard deviation. Due to the large number of earthquakes recorded during the Kobarid sequences, the events belonging to this subset of data constitute more than 20 per cent of the whole data set, but cover an area that is less than 2 per cent of the whole analysed region. We decided to separate these data from the other estimates of k in order to infer a general attenuation model valid for the whole area. After having removed these events, we obtained a sufficiently numerous and well distributed sample of data for the assessment of the distance dependence of k. In the following, we show the results obtained by including or not including the Kobarid data. A general discussion of the high frequency attenuation in the Kobarid area is presented in Section 7.
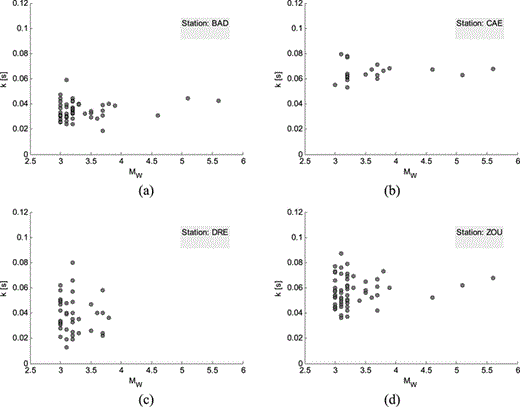
(a–d) k estimates obtained at stations BAD, CAE, DRE and ZOU with data of the Kobarid seismic sequences of 1998 and 2004, as a function of magnitude.
6.1 High frequency attenuation in the southeastern Alps and northern Dinarides
After having removed the events belonging to the Kobarid sequences of 1998 and 2004, we obtained a total number of 996 estimates of k corresponding to 240 earthquakes. Epicentral distances ranged from 0 to 250 km and the selected data have hypocentres mainly located in the range 5–15 km depth. Both parametric and non-parametric approaches were considered. The latter was applied using the weights w1= 80 and w2= 120 (see Section 5). A 10 km bin-width was chosen to discretize the epicentral distance, RE.
The estimated function k(RE) and the corresponding 95 per cent confidence limits, obtained with the non-parametric approach, are shown in Figs 7(a)–(k), for the 11 stations considered of the NEI network. Fig. 7(l) shows the distribution of the k0(S) estimates. The model parameters (mean value and 95 per cent confidence limit) corresponding to the function  and the k0(S) estimates obtained for each station are reported in Table 2 (column 2) and Table 3 (column 2), respectively. Notwithstanding a large spread observed in the data, Figs 7(a)–(k) shows that k generally increases with distance. The non-parametric solution presents a weak positive concavity over the whole range of analysed distances. We roughly approximated the distance dependence with two straight lines having slopes 1.0 × 10−4 and 1.7 × 10−4 s km–1 for RE < 90 and ≥90 km, respectively. The standard deviation, almost independent on both station and epicentral distance, does not exceed 0.005 s. The estimates of k0(S) ranged from 0.019 to 0.053 s (see Table 3 and Fig. 7(l)) and the distribution has 0.037 s mean and 0.010 s standard deviation, coherently with the results of Franceschina et al. (2006), who estimated k0= (0.03 ± 0.01) s for the two stations of the network BAD and ZOU. These values were obtained by a disjoint regression on data recorded at the two abovementioned stations, using a smaller data set (54 events). The stability of this result indicates that stations of the NEI network (all installed on ‘rock-sites’) seems to be characterized by not negligible near-surface attenuation. Moreover, the results listed in Table 3 show that an average contribution to the k value up to about 0.01 s, due to the vertical propagation common to all the sites, can be hypothesized for this area. The model parameters estimated with the parametric approach are reported in Tables 2 (column 3) and 3 (column 3). The value of k1 is (1.4 ± 0.1) × 10−4 s km–1, an intermediate slope respect to the approximated values estimated with the non-parametric model in the ranges of short and large distances, respectively. The values of k0(S) estimated with the parametric model ranged between 0.017 and 0.051 s (see Table 3). We considered negligible the differences obtained between the k0(S) values estimated with the parametric and the non-parametric approaches. Indeed, for each station, the corresponding measures of this parameter are equal at significance levels greater than 25 per cent.
and the k0(S) estimates obtained for each station are reported in Table 2 (column 2) and Table 3 (column 2), respectively. Notwithstanding a large spread observed in the data, Figs 7(a)–(k) shows that k generally increases with distance. The non-parametric solution presents a weak positive concavity over the whole range of analysed distances. We roughly approximated the distance dependence with two straight lines having slopes 1.0 × 10−4 and 1.7 × 10−4 s km–1 for RE < 90 and ≥90 km, respectively. The standard deviation, almost independent on both station and epicentral distance, does not exceed 0.005 s. The estimates of k0(S) ranged from 0.019 to 0.053 s (see Table 3 and Fig. 7(l)) and the distribution has 0.037 s mean and 0.010 s standard deviation, coherently with the results of Franceschina et al. (2006), who estimated k0= (0.03 ± 0.01) s for the two stations of the network BAD and ZOU. These values were obtained by a disjoint regression on data recorded at the two abovementioned stations, using a smaller data set (54 events). The stability of this result indicates that stations of the NEI network (all installed on ‘rock-sites’) seems to be characterized by not negligible near-surface attenuation. Moreover, the results listed in Table 3 show that an average contribution to the k value up to about 0.01 s, due to the vertical propagation common to all the sites, can be hypothesized for this area. The model parameters estimated with the parametric approach are reported in Tables 2 (column 3) and 3 (column 3). The value of k1 is (1.4 ± 0.1) × 10−4 s km–1, an intermediate slope respect to the approximated values estimated with the non-parametric model in the ranges of short and large distances, respectively. The values of k0(S) estimated with the parametric model ranged between 0.017 and 0.051 s (see Table 3). We considered negligible the differences obtained between the k0(S) values estimated with the parametric and the non-parametric approaches. Indeed, for each station, the corresponding measures of this parameter are equal at significance levels greater than 25 per cent.
(a–k) Functions k(RE) with the corresponding 95 per cent confidence limits (solid and dashed lines, respectively), estimated for 11 stations of the NEI network with the non-parametric approach applied to the data set not including Kobarid data. Circles represent the single-record estimates of the k parameter. (l) Distribution of the corresponding station-dependent terms, k0(S).
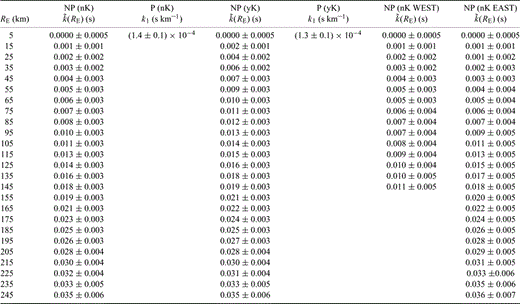
Values of the function  and slope of the straight line obtained with the parametric model, estimated in the range 0–250 km epicentral distance with different data sets. NP (nK): non-parametric method applied to the database not including Kobarid data. P (nK): parametric method applied to the database not including Kobarid data. NP (yK): non-parametric method applied to the database including Kobarid data. P (yK): parametric method applied to the database including Kobarid data. NP (nK WEST): non-parametric method applied to the WEST-Dataset not including Kobarid data. NP (nK EAST): non-parametric method applied to the EAST-Dataset not including Kobarid data.
and slope of the straight line obtained with the parametric model, estimated in the range 0–250 km epicentral distance with different data sets. NP (nK): non-parametric method applied to the database not including Kobarid data. P (nK): parametric method applied to the database not including Kobarid data. NP (yK): non-parametric method applied to the database including Kobarid data. P (yK): parametric method applied to the database including Kobarid data. NP (nK WEST): non-parametric method applied to the WEST-Dataset not including Kobarid data. NP (nK EAST): non-parametric method applied to the EAST-Dataset not including Kobarid data.

Values of k0(S) estimated for 11 stations of the NEI network, using different methods and data sets. NP (nK): non-parametric method applied to the database not including Kobarid data. P (nK): parametric method applied to the database not including Kobarid data. NP (yK): non-parametric method applied to the database including Kobarid data. P (yK): parametric method applied to the database including Kobarid data. NP (nK WEST): non-parametric method applied to the WEST-Dataset not including Kobarid data. NP (nK EAST): non-parametric method applied to the EAST-Dataset not including Kobarid data.
Models (5) and (6) were also applied to the whole data set of weak motion data, composed of 302 earthquakes, 20.5 per cent of which are events belonging to the Kobarid sequences. The estimated model parameters are listed in Tables 2 (column 4) and 3 (column 4) in the case of the non-parametric approach while column 5 of the same tables lists the results obtained with the model (6). Figs 8(a)–(f) shows, for a set of six selected stations, the effect obtained on the results by adding the earthquakes of the Kobarid sequences; k values estimated using the Kobarid data are shown as white circles. As previously mentioned, the records of earthquakes belonging to these sequences generally have higher values of k with respect to the average trend of the whole analysed area. This feature affects the k dependence on distance in the range 35–90 km epicentral distance, modifying the shape of the function .1 or the slope of the linear fit, according to the adopted model. The discrepancies between the  values estimated with the two data sets depend on distance. For epicentral distances less than 35 km or greater than 90 km the corresponding estimates of the model parameters are equal at significance levels greater than 15 per cent. In the range 35–90 km the discrepancies are slightly larger, showing smaller values of significance levels of equality with a minimum level of 4 per cent (corresponding to 2.1 standard deviations). With the inclusion of the Kobarid data, the slope of the linear fit estimated with the parametric approach changes from (1.4 ± 0.1) × 10−4 to (1.3 ± 0.1) × 10−4 s km–1. As far as the station dependent model parameters, k0(S) are concerned (see Table 3), we generally observed limited differences between values obtained including or not including the data of the Kobarid sequences. For the non-parametric approach the corresponding estimates are all equal at significance levels greater than 10 per cent. The parametric inversion, where a deformation of the curve in the range 35–90 km is not allowed, is more sensitive to the inclusion of the Kobarid data. However, also in this case we generally obtained acceptable differences. Except for the station ZOU, the k0(S) values estimated with the two data sets are equal at significance levels greater than 10 per cent.
values estimated with the two data sets depend on distance. For epicentral distances less than 35 km or greater than 90 km the corresponding estimates of the model parameters are equal at significance levels greater than 15 per cent. In the range 35–90 km the discrepancies are slightly larger, showing smaller values of significance levels of equality with a minimum level of 4 per cent (corresponding to 2.1 standard deviations). With the inclusion of the Kobarid data, the slope of the linear fit estimated with the parametric approach changes from (1.4 ± 0.1) × 10−4 to (1.3 ± 0.1) × 10−4 s km–1. As far as the station dependent model parameters, k0(S) are concerned (see Table 3), we generally observed limited differences between values obtained including or not including the data of the Kobarid sequences. For the non-parametric approach the corresponding estimates are all equal at significance levels greater than 10 per cent. The parametric inversion, where a deformation of the curve in the range 35–90 km is not allowed, is more sensitive to the inclusion of the Kobarid data. However, also in this case we generally obtained acceptable differences. Except for the station ZOU, the k0(S) values estimated with the two data sets are equal at significance levels greater than 10 per cent.
(a–f) Functions k(RE) estimated for six stations of the NEI network with different approaches and data sets. Left panels: non-parametric approach; right panels: parametric approach. Black lines: functions k(RE) obtained through parametric (solid lines) and non-parametric (dashed lines) inversions applied to the data set not including Kobarid data. Grey lines: functions k(RE) obtained through parametric (solid lines) and non-parametric (dashed lines) inversions applied to the data set including Kobarid data. Circles represent the single-record estimates of the k parameter. Open circles correspond to the k estimates obtained with Kobarid data.
6.2 Regional dependence
In order to investigate the regional dependence of the function  , previously estimated for the whole area, we applied the non-parametric model. We used the k values obtained from weak motion records. The data of the earthquakes belonging to the Kobarid sequences were not included in the data set. Two subsets of data were defined, according to the azimuth of the events. Azimuths were measured clockwise from north using the location of the station BAD as reference point. Earthquakes with azimuth in the ranges 0–180° (140 events) and 180–360° (100 events) were assigned to the EAST-Dataset and to the WEST-Dataset, respectively. The non-parametric approach has been applied using also in this case the weights w1= 80 and w2= 120 and, due to the paucity of data recorded westward to the NEI network at large distances, for the WEST-Dataset the generalized inversion was limited to 150 km epicentral distance. The estimated function k(RE) and the corresponding 95 per cent confidence limits, obtained with these two data sets are compared in Fig. 9 for a set of six selected stations. Tables 2 and 3 list, in the last two columns, the distance and the station dependent parameters, respectively. As evidenced in Figs 9(a)–(f), k increases with distance both eastward and westward to the NEI network; k values estimated with the two data sets considered here, are generally characterized by comparable levels of dispersion, while different trends with distance are observed in the two areas. The function k(RE) estimated with the EAST-Dataset shows a weak positive concavity with a change of slope at about 90 km epicentral distance. Conversely, the k values of the WEST-Dataset are well fitted by a straight line up to 150 km epicentral distance.
, previously estimated for the whole area, we applied the non-parametric model. We used the k values obtained from weak motion records. The data of the earthquakes belonging to the Kobarid sequences were not included in the data set. Two subsets of data were defined, according to the azimuth of the events. Azimuths were measured clockwise from north using the location of the station BAD as reference point. Earthquakes with azimuth in the ranges 0–180° (140 events) and 180–360° (100 events) were assigned to the EAST-Dataset and to the WEST-Dataset, respectively. The non-parametric approach has been applied using also in this case the weights w1= 80 and w2= 120 and, due to the paucity of data recorded westward to the NEI network at large distances, for the WEST-Dataset the generalized inversion was limited to 150 km epicentral distance. The estimated function k(RE) and the corresponding 95 per cent confidence limits, obtained with these two data sets are compared in Fig. 9 for a set of six selected stations. Tables 2 and 3 list, in the last two columns, the distance and the station dependent parameters, respectively. As evidenced in Figs 9(a)–(f), k increases with distance both eastward and westward to the NEI network; k values estimated with the two data sets considered here, are generally characterized by comparable levels of dispersion, while different trends with distance are observed in the two areas. The function k(RE) estimated with the EAST-Dataset shows a weak positive concavity with a change of slope at about 90 km epicentral distance. Conversely, the k values of the WEST-Dataset are well fitted by a straight line up to 150 km epicentral distance.
(a–f) Functions k(RE) with the corresponding 95 per cent confidence limits (solid and dashed lines, respectively), estimated for 6 stations of the NEI network with the non-parametric approach applied to the WEST-Dataset and to the EAST-Dataset (left and right panels, respectively). Closed circles represent the single-record estimates of the k parameter.
We better investigated the differences observed between these two groups of data by comparing first the corresponding k(RE) values obtained westward and eastward to the NEI network (Table 2, columns 6 and 7, respectively). A linear fit to the estimated values of the distance dependent parameters gives a slope of 0.8 × 10−4 s km–1 both for the WEST-Dataset and for the nearest data of the EAST- Dataset (RE < 90 km). Beyond 90 km, the slope of the best fit line obtained with the WEST-Dataset remains unchanged, while a linear fit through the k(RE) estimates of the EAST-Dataset gives a slope of 1.9 × 10−4 s km–1. The direct comparison between the values of this function obtained westward and eastward to the NEI network up to 90 km epicentral distance shows that the k(RE) estimates are equal with significance levels greater than 52 per cent. Moving toward larger distances, the corresponding estimates gradually become more discordant. In the range 90–150 km the significance levels decrease as much as 4.6 per cent, suggesting that in this range of distances the areas located eastward and westward to the NEI network could be characterized by different attenuation properties. The almost equal trends observed westward and eastward to the NEI network up to 90 km distance were confirmed by the analyses of the station dependent parameters, k0(S) (see Table 3). The significance levels of equality between estimates obtained with the EAST-Dataset and the WEST-Dataset are greater than 5 per cent for eight stations, of the 11 considered. In the other cases (stations CGRP, CSM and DRE), the observed differences are within 2.8 and 3.2 standard deviations. We hypothesize that the discrepancies between the k0(S) values of these stations obtained for the two data sets are due to the non-homogeneous distribution of data in the range 0–30 km epicentral distance (Fig. 9). Finally, we tested if the different trends observed for these two areas are genuine by limiting the inversion of the k values of the EAST-Dataset to the same maximum epicentral distance adopted for the WEST-Dataset. A comparison of the results obtained for the distance dependent parameters, k(RE), using the EAST-Dataset with 250 and 150 km as maximum allowed distances, shows differences limited to 0.6 standard deviations (significance levels greater than 55 per cent).
6.3 High frequency attenuation from strong motion data
The values of k0(S) of the sites equipped with strong motion instruments were estimated using data from 29 events mainly recorded during the 1976–1977 seismic crisis. Due to the small number of available data, and to the fact that the epicentral distance was limited to 50 km, we avoided to estimate the distance dependent parameters of the model. We assumed a linear dependence of the k parameter on distance and applied the parametric approach in the range 0–90 km epicentral distance to the short period data. By excluding the Kobarid events, we obtained a slope of (0.6 ± 0.4) × 10−4 s km–1 for the whole area. This slope was assumed also for strong motion data in order to estimate the values of k0(S) of the stations BUI, CDR, SRC, FRC and TLM. Fig. 10 shows the results and, in particular, Fig. 10(f) shows the distribution of the k0(S) values. Mean values with the corresponding 95 per cent confidence limits are listed in Table 4 (column 2). A comparison between Figs 10(f) and 7(l) evidences that sites equipped with strong motion instruments are characterized by higher attenuation with respect to the sites of the NEI network. Indeed these stations were generally installed on sites with soft soils. The distribution of Fig. 10(f) has 0.056 s mean and 0.007 s standard deviation. Moreover, it is noteworthy that stations SRC and FRC, characterized by an inter-station distance of 600 m have k0 values of 0.067 and 0.054 s, respectively. A general discussion of the high frequency attenuation in this area, also including the station MPRI of the NEI network, located 1.8 km far from SRC, is presented in Section 7.
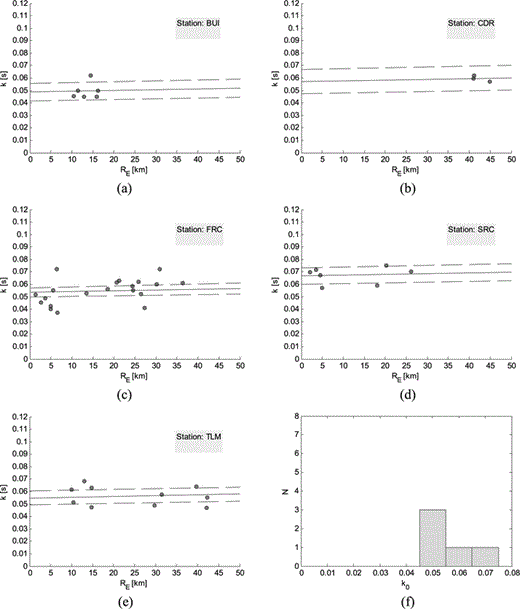
(a–e) Estimates of the spectral decay parameter at the sites equipped with strong motion instruments. A linear dependence with a fixed slope of (0.6 ± 0.4) × 10−4 s km–1 was assumed for the whole area (up to 50 km epicentral distance). 95 per cent confidence limits (dashed lines) are also shown. (f) distribution of the estimated k0(S) values.
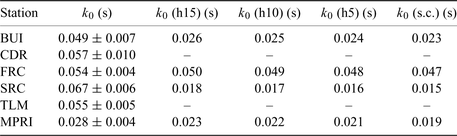
Values of zero-distance k parameter, k0, estimated for the stations equipped with strong motion instruments (BUI, CDR, FRC, SRC, TLM) and comparison between measured and computed values of k0 at the sites BUI, FRC, SRC and MPRI. k0: measured value of the zero-distance k; k0 (h15), k0 (h10), k0 (h5): values of k0 computed with rays coming from 15, 10 and 5 km depth, respectively; k0 (s.c.): sedimentary column contribution.
7 Discussion
7.1 Distance dependence
The spectral decay k is generally interpreted in terms of propagation, considering both the near-surface prevailing vertical propagation beneath the site and the predominantly horizontal propagation of the ray path through deeper crustal layers. This approach, introduced by Anderson & Hough (1984), was applied in several following papers (Hough et al. 1988; Hough & Anderson 1988; Anderson 1991; Humphrey & Anderson 1992; Liu et al. 1994; Castro et al. 1996; Bindi et al. 2004) and some recent works also investigate the magnitude dependence of k (Castro et al. 2000, Purvance & Anderson 2003; Bindi et al. 2006; Fernández et al. 2010). In this work, the preliminary test performed on data belonging to the Kobarid sequences of 1998 and 2004, showed an approximately independence of k on magnitude, confirming that the analysed frequency band is not affected by source effects. We considered these events as representative of the entire data set and hypothesized the independence of the spectral decay parameter on earthquake size for the whole region. A similar independence of k on magnitude was found by Fernández et al. (2010) in the northeastern Sonora (Mexico) and a low correlation was found by Castro et al. (2000) in central Italy. Purvance & Anderson (2003) found a weak magnitude dependence in Guerrero (Mexico), when the k parameter was measured in the frequency bands 10–30 Hz and 10–45 Hz, and do not find any magnitude dependence when k was estimated in the range 25–45 Hz. They explained this result as a source effect. In northwestern Turkey, Bindi et al. (2006) obtained a positive correlation with magnitude of the k parameter using data from 245 aftershocks (2.0 < ML < 4.5) of the 1999 Izmit earthquake, probably due to the trade-off with the corner frequency of the smaller events.
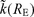 , respectively, can be related to the S-wave velocity, β, and the frequency independent quality factor QI, adopting the following equation:
, respectively, can be related to the S-wave velocity, β, and the frequency independent quality factor QI, adopting the following equation: 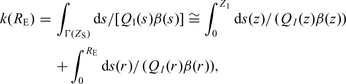
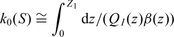
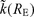 is given by
is given by 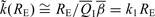
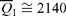 .
.The non-parametric model evidenced a positive concavity of the function  which is also approximated by two linear trends with slopes 1.0 × 10−4 s km–1 and 1.7 × 10−4 s km–1 in the ranges of distance 0–90 and 90–250 km, respectively. Also
which is also approximated by two linear trends with slopes 1.0 × 10−4 s km–1 and 1.7 × 10−4 s km–1 in the ranges of distance 0–90 and 90–250 km, respectively. Also  functions estimated for other regions in the world can be well described by piece-wise linear functions (Anderson 1991; Bindi et al. 2004; Bindi et al. 2006). An increase of slope with distance can be interpreted in terms of a three layers model where moving from the intermediate to the bottom layer, both QI and β values decrease. Seismic rays refracted downward into the low velocity zone, in the bottom layer, can propagate at large distances. So, the observed increase of the slope, dk/dRE, beyond a specified epicentral distance could reflect the strongest attenuation properties of the deeper layers sampled by seismic waves. Hough & Anderson (1988) explained the slope increase observed at about 70 km epicentral distance obtained with data of southern California in terms of QI ranges going from 1000–3000 at 5–12 km depth to 700–1000 at 12 km depth. In the studied area, according to the 1-D model of Bressan et al. (2009), the average S-wave velocity decreases from 3.43 km s–1 at about 7 km depth to 3.28 km s–1 at 11 km depth. Considering these values of velocity as representative of the average S-wave velocities of the intermediate and bottom layers, respectively, we can explain the estimated slopes of the
functions estimated for other regions in the world can be well described by piece-wise linear functions (Anderson 1991; Bindi et al. 2004; Bindi et al. 2006). An increase of slope with distance can be interpreted in terms of a three layers model where moving from the intermediate to the bottom layer, both QI and β values decrease. Seismic rays refracted downward into the low velocity zone, in the bottom layer, can propagate at large distances. So, the observed increase of the slope, dk/dRE, beyond a specified epicentral distance could reflect the strongest attenuation properties of the deeper layers sampled by seismic waves. Hough & Anderson (1988) explained the slope increase observed at about 70 km epicentral distance obtained with data of southern California in terms of QI ranges going from 1000–3000 at 5–12 km depth to 700–1000 at 12 km depth. In the studied area, according to the 1-D model of Bressan et al. (2009), the average S-wave velocity decreases from 3.43 km s–1 at about 7 km depth to 3.28 km s–1 at 11 km depth. Considering these values of velocity as representative of the average S-wave velocities of the intermediate and bottom layers, respectively, we can explain the estimated slopes of the  function in terms of average QI values decreasing with depth from 2915 to 1793. The presence of intermediate layers having weak attenuation properties overlying stronger attenuating materials, has been confirmed by detailed investigations performed with petrophysical data in the central part of the Friuli area (Faccenda et al. 2007).
function in terms of average QI values decreasing with depth from 2915 to 1793. The presence of intermediate layers having weak attenuation properties overlying stronger attenuating materials, has been confirmed by detailed investigations performed with petrophysical data in the central part of the Friuli area (Faccenda et al. 2007).
7.2 Regional dependence
Different trends of the high frequency attenuation were observed eastward and westward to the NEI network, applying the non-parametric model to the k estimates obtained with data selected, based on the azimuth of the events. As previously mentioned, the different properties of the function  estimated with the EAST-Dataset and WEST-Dataset evidenced in Fig. 9, does not depend on the different ranges of distance covered by the two subsets of data. For epicentral distances >90 km, the WEST-Dataset evidences a weaker attenuation with distance with respect to the EAST-Dataset. Similar results were found by Bragato et al. (2009), who analysed the attenuation of PGA with distance using data from weak and moderate earthquakes occurred in the area. They found three different distributions of PGA vs. epicentral distance along the Apennines, in the northern sector of the Po Plain and along the Alps. In particular, the attenuation along the Alps is higher than in the other two regions and they suggested that this effect could be caused by S-wave reflections from the Mohorovicic discontinuity (Moho). Similar amplification effects, generated by focusing and interference of SmS phases reflected by different portions of the Moho, have been already observed in other regions of the world (Burger et al. 1987; Liu & Tsai 2009). In the area investigated in this work, the Moho depth changes from 25–30 km in Veneto to 40–45 km in northern Friuli (Tesauro et al. 2008) and the Veneto region corresponds roughly to the RE > 90 km part of the WEST-Dataset, where data show weaker attenuation properties. It is worth noting that, especially for events recorded at large distances, the time windows employed for the estimation of the k parameter include different seismic phases partially overlapped, a probable result of reflections from different parts of the Moho. Conversely, seismic rays corresponding to the EAST-Dataset, sampling crustal volumes characterized by higher Moho depths (up to 50 km in western Slovenia), do not experience such reflections, thus showing a higher attenuation. Therefore, we hypothesize that the weaker attenuation properties evidenced in the high frequency domain by the data of the WEST-Dataset with respect to the EAST-Dataset, are caused by S-wave reflections from the Moho discontinuity under the eastern Po Plain, at about 25–30 km depth.
estimated with the EAST-Dataset and WEST-Dataset evidenced in Fig. 9, does not depend on the different ranges of distance covered by the two subsets of data. For epicentral distances >90 km, the WEST-Dataset evidences a weaker attenuation with distance with respect to the EAST-Dataset. Similar results were found by Bragato et al. (2009), who analysed the attenuation of PGA with distance using data from weak and moderate earthquakes occurred in the area. They found three different distributions of PGA vs. epicentral distance along the Apennines, in the northern sector of the Po Plain and along the Alps. In particular, the attenuation along the Alps is higher than in the other two regions and they suggested that this effect could be caused by S-wave reflections from the Mohorovicic discontinuity (Moho). Similar amplification effects, generated by focusing and interference of SmS phases reflected by different portions of the Moho, have been already observed in other regions of the world (Burger et al. 1987; Liu & Tsai 2009). In the area investigated in this work, the Moho depth changes from 25–30 km in Veneto to 40–45 km in northern Friuli (Tesauro et al. 2008) and the Veneto region corresponds roughly to the RE > 90 km part of the WEST-Dataset, where data show weaker attenuation properties. It is worth noting that, especially for events recorded at large distances, the time windows employed for the estimation of the k parameter include different seismic phases partially overlapped, a probable result of reflections from different parts of the Moho. Conversely, seismic rays corresponding to the EAST-Dataset, sampling crustal volumes characterized by higher Moho depths (up to 50 km in western Slovenia), do not experience such reflections, thus showing a higher attenuation. Therefore, we hypothesize that the weaker attenuation properties evidenced in the high frequency domain by the data of the WEST-Dataset with respect to the EAST-Dataset, are caused by S-wave reflections from the Moho discontinuity under the eastern Po Plain, at about 25–30 km depth.
Different attenuation properties with respect to the average high frequency attenuation estimated for the whole region were also observed in the Kobarid area. Indeed, the non-parametric approach, more robust in the ability to capture the finest properties of data, evidences a non-negligible increase of attenuation in the 35–90 km distance range. Fig. 8 shows that the k estimates obtained with the events occurred in the Kobarid area are, on average, higher with respect to the k value predicted by the function k(RE). As an example, k values obtained at the station ZOU have 0.057 s mean and 0.011 s standard deviation and, at the corresponding epicentral distance, the non-parametric function gives  s. Therefore, for this station, the mean values of k obtained with the Kobarid data and the k value predicted by the global relationship estimated for the whole area are different at a confidence level exceeding 99.9 per cent. Other stations show similar differences, even if with a minor degree and with a minor level of confidence. Moreover, especially considering that the Kobarid area covers the 2 per cent of the whole region analysed in this study, the k estimates obtained with these data show a large dispersion. Similar attenuation features were observed by Castro et al. (2000) in the Umbria-Marche region analysing 44 small magnitude (M 2.1–4.1) events recorded by the Marchesan Seismograph Network during the 1977 Umbria-Marche sequence; k estimates from events located within 2.5 km radius showed a great variability with differences up to 0.06 s. The result was explained in terms of spatial variation of QI near the source, caused by the high level of fracturing that characterizes the fault zones. In the Kobarid area, the tomographic images of the upper crust show discontinuous blocks marked by sharp lateral variations of P-velocity and P- to S-velocity ratio, suggesting a high level of fracturing (Gentile et al. 2000; Bressan et al. 2003, 2009). We hypothesize that this feature can explain both the high dispersion and the higher mean value of the k estimates obtained with data of the earthquakes occurred in the Kobarid area. Indeed, it has been already observed that fault zones are often characterized by complex rupture pattern that favor both scattering and generation of trapped waves. Low-velocity and low-Q zones (waveguides) have been evidenced along the rupture surface of large earthquakes, with S-wave velocities from 1 to 2.5 km s–1 and Q values from 10 to 60 (Li et al. 2003). Indeed, in the area of the 1998 Kobarid earthquake, variations of P-velocity from 4.8 to 6.8 km s–1 and P- to S-velocity ratio from 1.61 to 1.90 were estimated within 20 km distance in the range 0–8 km depth (Bressan et al. 2009). The observed differences between the mean values of k predicted by the function k(RE) and estimated with Kobarid data recorded at station ZOU could be explained in terms of 10–20 km propagation though low velocity – low QI zones with β≅ 2.5 km s–1 and QI≅ 400. With this purpose, we can observe the different features of the k values distributions obtained at stations ZOU and BAD, approximately located along and perpendicular to the strike of the 1998 Kobarid earthquake, respectively. Seismic waves travelling from the Kobarid area to the station BAD, probably unaffected by the fault-zone waveguides, show, on average, the same attenuation properties of the whole region investigated in this work.
s. Therefore, for this station, the mean values of k obtained with the Kobarid data and the k value predicted by the global relationship estimated for the whole area are different at a confidence level exceeding 99.9 per cent. Other stations show similar differences, even if with a minor degree and with a minor level of confidence. Moreover, especially considering that the Kobarid area covers the 2 per cent of the whole region analysed in this study, the k estimates obtained with these data show a large dispersion. Similar attenuation features were observed by Castro et al. (2000) in the Umbria-Marche region analysing 44 small magnitude (M 2.1–4.1) events recorded by the Marchesan Seismograph Network during the 1977 Umbria-Marche sequence; k estimates from events located within 2.5 km radius showed a great variability with differences up to 0.06 s. The result was explained in terms of spatial variation of QI near the source, caused by the high level of fracturing that characterizes the fault zones. In the Kobarid area, the tomographic images of the upper crust show discontinuous blocks marked by sharp lateral variations of P-velocity and P- to S-velocity ratio, suggesting a high level of fracturing (Gentile et al. 2000; Bressan et al. 2003, 2009). We hypothesize that this feature can explain both the high dispersion and the higher mean value of the k estimates obtained with data of the earthquakes occurred in the Kobarid area. Indeed, it has been already observed that fault zones are often characterized by complex rupture pattern that favor both scattering and generation of trapped waves. Low-velocity and low-Q zones (waveguides) have been evidenced along the rupture surface of large earthquakes, with S-wave velocities from 1 to 2.5 km s–1 and Q values from 10 to 60 (Li et al. 2003). Indeed, in the area of the 1998 Kobarid earthquake, variations of P-velocity from 4.8 to 6.8 km s–1 and P- to S-velocity ratio from 1.61 to 1.90 were estimated within 20 km distance in the range 0–8 km depth (Bressan et al. 2009). The observed differences between the mean values of k predicted by the function k(RE) and estimated with Kobarid data recorded at station ZOU could be explained in terms of 10–20 km propagation though low velocity – low QI zones with β≅ 2.5 km s–1 and QI≅ 400. With this purpose, we can observe the different features of the k values distributions obtained at stations ZOU and BAD, approximately located along and perpendicular to the strike of the 1998 Kobarid earthquake, respectively. Seismic waves travelling from the Kobarid area to the station BAD, probably unaffected by the fault-zone waveguides, show, on average, the same attenuation properties of the whole region investigated in this work.
7.3 Near surface attenuation
In this work we observed high significance levels of equality between the estimates of k0(S) obtained by applying the parametric and the non-parametric inversions, respectively, to the whole data set of records collected by the NEI network. Similar values of k0(S) were obtained with the EAST-Dataset and the WEST-Dataset and very limited differences were also observed between the k0(S) values estimated including or not including the data of the Kobarid sequences. As previously mentioned, the reliability of the estimates of the station dependent part of the k parameter is also confirmed by the results of Franceschina et al. (2006) who estimated k0(S) for the stations ZOU and BAD (Section 6.1). The variations we found in the estimates of k0(S) were obtained only when the parametric fit is used with a large number of earthquakes all belonging to the same area (Section 6.2) or when the data set does not contain earthquakes close to the considered stations (Section 6.3). We consider these differences as due to intrinsic limits of the inversion procedure.
When the spectral decay parameter is estimated at sites where reliable data of the S-wave velocity and quality factor profiles are available, the measured values of k can be compared with the computed ones by means of eq. (11). Unfortunately, velocity profiles of the upper sedimentary column are available only for a limited number of sites and measures of the quality factor are very rare. Moreover the application of eq. (11) requires the knowledge of the entire geological profile from the surface to 5–10 km depth and, at this purpose, the main difficulty consists in joining the upper sedimentary profile, usually measured in great detail for thickness of tens or hundreds of meters, with the deeper hard-rock profile, estimated with different geophysical techniques, and generally known with lower resolution for depths greater than 1–2 km. Finally, the general lack of data concerning the quality factor, often implies the adoption of empirical relationships between this parameter and the S-wave velocity. In this work, we consider, in particular, the RAN stations FRC, SRC and BUI and the station MPRI of the NEI network. Profiles of S-wave velocity were measured for the strong motion stations till 60 m depth (http://itaca.mi.ingv.it) and stations FRC and SRC are particularly relevant for comparison of the measured and computed values of k, respectively, due to their small interstation distance (600 m). Moreover, it is noteworthy that station MPRI is located at about 1.5 km northwest from SRC, on the same geologic unit, made up of limestones and calcarenites, at the western side of the Tagliamento river. In the same area, we consider the station BUI, located in the Tagliamento plain, 3 km far from FRC (see Fig. 3). To compute the k parameter through eq. (11) we defined an S-wave velocity profile for each station considered. The hard-rock section, common to all the stations, was taken from the crustal model of Bressan et al. (2009), using the corresponding VP and VP/VS profiles for depths greater than 800 m. At shallow depths, S-wave velocities were defined according to the velocity profiles measured at sites equipped with the strong motion instruments. For stations SRC, FRC and BUI, measures of the bedrock S-wave velocities give average values of 1400, 800 and 1200 m s–1, respectively. In this simplified modelling, we considered the last two estimates as representative of the S-wave velocity of stations FRC and BUI, respectively, from 50 m below the surface to 800 m depth. For these two stations, we employed the measured VS profiles to define the velocity model of the upper 50 m of the sedimentary column. Due to the relative location of MPRI and SRC, for these stations we assumed the same value of 1400 m s–1 as bedrock S-wave velocity, from 10 m below the surface to 800 m depth. For both stations we hypothesized a surface 10 m layer of weathered rocks with VS= 600 m s–1. Fig. 11 shows the total geological profile (sedimentary column + hard-rock section) adopted for stations SRC, FRC, MPRI and BUI. As far as the quality factor is concerned, we employed the model 3 of Campbell (2009) to estimate the frequency independent QI values of the layers in the sedimentary column (VS < 2000 m s–1). The values of QI in the hard-rock section were assumed in accordance with the results obtained in the present work, concerning the k increase with distance in the region (Sections 7.1 and 7.2).
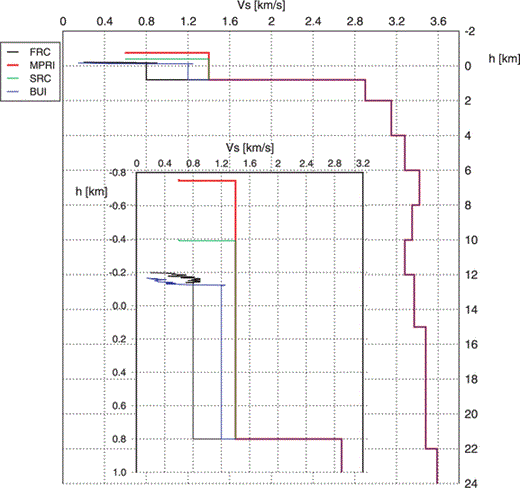
S-wave velocity profile employed in eq. (11) for computation of the zero-distance k parameter, k0, at stations SRC, FRC, MPRI and BUI. Zero depth indicates sea level and negative depths indicate elevations above sea level. The inset shows the corresponding sedimentary columns (from the surface to 800 m depth).
Table 4 compares measured and computed values of k0(S) for stations MPRI, SRC, FRC and BUI. Theoretical values of k were inferred from eq. (11) adopting, for each station, the hypothesized VS geological profile (Fig. 11), together with the abovementioned empirical relation between shear wave velocity and quality factor. Table 4 shows the contribution to the k parameter due to the vertical propagation of seismic rays coming from different depths. As expected, the major contribution is due to the sedimentary column of each profile (from surface to 800 m depth), being the hard-rock contribution to k0(S) of the order of 0.005 s. The high values of both VS and QI, hypothesized for the hard-rock section, produce very limited differences in the k values computed with rays coming from 5, 10 and 15 km depth. For the stations FRC and MPRI, we obtained acceptable differences between theoretical and observed values of k0(S), being the corresponding significance levels of equality greater than 20 per cent. The other stations show higher differences, probably due to the uncertainties that characterize the hypothesized geological profiles at intermediate depths (from a few tens of meters below the surface to 1–2 km depth). Moreover, as recognized by Campbell (2009), also scattering effects due to the small scale heterogeneities of the entire geological profile beneath the recording station, can affect the high frequency attenuation, producing a significant contribution to the final k value. Indeed, the computed values of k underestimate the measured ones in all the cases. On the other side, the results obtained in the present work concerning the station SRC (see Table 4), suggest for this site, the presence of more complex local effects, probably due to the topography.
8 Conclusions
The frequency analysis of 1345 acceleration and velocity data recorded in this region by the NEI network and by strong motion instruments of the RAN allows to estimate the spectral decay parameter k (Anderson & Hough 1984) in the range of distance 0–250 km. The analysed earthquakes, located south to the Periadriatic Lineament in a wide region extending in west–east direction from the Schio-Vicenza fault system to the Zagreb area, have Mw magnitude between 3.0 and 6.5 and hypocentral depth in the range 3–16 km. The high quality of selected records allows to perform a detailed spectral analysis of the high frequency attenuation up to 25 or 45 Hz, according to the sampling rate of data, and to obtain a regional model for the high frequency spectral decay of the acceleration Fourier spectrum of S waves. Several results can be highlighted:
- 1
Both strong and weak motion data show a linear spectral decay above the corner frequency of the recorded event. The linear trend is especially evident on data with a high sampling rate, and it remains significantly different from 0 also after correction of the amplitude spectrum for the frequency dependent part of the quality factor, estimated in recent investigations (Malagnini et al. 2002; Bianco et al. 2005).
- 2
The spectral decay parameter, estimated at 11 stations of the NEI network and 5 stations of the RAN, is confined in the range 0.006–0.128 s and does not show any significant dependence on magnitude. Conversely, the stations of the NEI network present the same increase of k with epicentral distance, RE, and show values of k0≡k (RE= 0) between 0.017 and 0.053 s. Therefore, in this region the record-to-record variability of the k parameter can be modelled in terms of path effect by estimating the distance and the station contributions.
- 3
In the southeastern Alps and northern Dinarides the k increase with distance can be adequately approximated through a linear model with slope dk/dRE = (1.4 ± 0.1) × 10−4 s km–1. Assuming α = 3.34 km s–1 between 5 and 15 km depth (Bressan et al. 2009), an average QI of 2140 can be estimated for the corresponding crustal layer.
- 4
The application of a non-parametric model evidences the presence of a weak positive concavity of the function that describes the k increase with distance. A piecewise linear approximation can be introduced in this case, with slopes of 1.0 × 10−4 and 1.7 × 10−4 s km–1 in the ranges of distance 0–90 km and 90–250 km, respectively. The increase of slope with distance can be now interpreted in terms of a three layers model with average QI of 2915 and 1793 around 7 and 11 km depth, respectively.
- 5
A regional dependence of the k increase with distance can be evidenced by considering the high frequency attenuation in two areas located eastward and westward to the NEI network. Data of the earthquakes located westward show weaker attenuation properties as respect to the average trend of the area, probably because of S-wave reflections from different parts of the Moho discontinuity under the eastern Po Plain, at about 25–30 km depth (Tesauro et al. 2008).
- 6
A regional dependence of k can be inferred from data of the earthquakes occurred in the region of the 1998 and 2004 Kobarid earthquakes. The k estimates obtained with events occurred in this area are, on average, 0.017 s higher than average values predicted for the whole region. Moreover, these data show a large dispersion, especially considering that the recorded earthquakes are located in a small (10 × 20 km2) area. We hypothesize that these effects are both related to the high level of fracturing often characterizing fault zones (Bressan et al. 2009).
- 7
Stations of the NEI network and RAN stations are characterized by different station contributions to the k parameter, with mean k0 values of the corresponding distributions of 0.037 and 0.056 s, respectively. The estimated values of the specific station contributions, k0(S), do not show any significant dependence on both model and data employed in the inversion procedure. The results obtained through the non-parametric inversion indicate that a maximum contribution of 0.010 s to the k value could be due to a predominantly vertical propagation of S waves common to all the sites.
- 8
Available data of S-wave velocity profiles at three stations of the RAN, allowed to compute theoretical values of the station dependent part of the k parameter, k0(S). The comparison between measured and computed values shows that the major contribution to the total k0(S) is due to the sedimentary column of each profile (from surface to 800 m depth), being the hard-rock section term of the order of 0.005 s. Limited differences between measured and computed values were obtained for the stations FRC and MPRI, located on the western side of the Tagliamento river. The other two stations analysed, SRC and BUI, both located in the same area, show higher differences, probably due to uncertainties characterizing the hypothesized geological profile, scattering effects caused by small scale heterogeneities and topographic effects.
Acknowledgments
We would like to thank Gianni Bressan and Pier Luigi Bragato for their valuable discussions and suggestions, Carla Barnaba for supplying the data on mean value of the micro-tremors HVSR and Monica Sugan for the help with ArcGIS program. The management of the Seismometric Network of Friuli-Venezia Giulia is financially supported by the Civil Protection of the Regione Autonoma Friuli-Venezia Giulia. The Seismometric Network of Veneto is owned by the Regione Veneto. We are grateful to all the OGS staff of the Dipartimento Centro Ricerche Sismologiche at Udine for managing the two networks. This research has benefited from funding provided by the Italian Presidenza del Consiglio dei Ministri – Dipartimento della Protezione Civile (DPC). Scientific papers funded by DPC do not represent its official opinion and policies. We would also like to thank Raul Castro and an anonymous reviewer for their appreciable comments and helpful suggestions.
References










