Insights into the lithospheric structure and tectonic setting of the Barents Sea region from isostatic considerations Free

Summary

INTRODUCTION

The continental shelf area of the Barents Sea Region (Fig. 1) and its hydrocarbon potential is the subject of increased scientific and economic interest. Despite the large amounts of industrial data available on the Norwegian part and the easternmost Russian part of the area, only a few regional studies integrating the Eastern and Western Barents Sea have been carried out (e.g. Johansen 1992). Thus, many key questions about the tectonic setting are still disputed. Industrial and academic geophysical studies reveal that the basins have a relatively complete succession of sedimentary strata, but different characteristics in the Western and Eastern Barents Sea (e.g. Fichler 1997; Johansen 1992; Gramberg 2001). Basins in the Western Barents Sea region have a depth of up to 14 km and are generally narrow compared to the broad basins in the Eastern Barents Sea that have a maximum thickness of 20 km (Figs 1 and 2). The Western Barents Sea basins are generally interpreted to be rift basins (e.g. Faleide 1993, 1996), but there is no agreement on the underlying cause of the Eastern Barents Sea basins (e.g. Gramberg 2001; O'Leary 2004; Ritzmann et al. 2006).

Figure 1

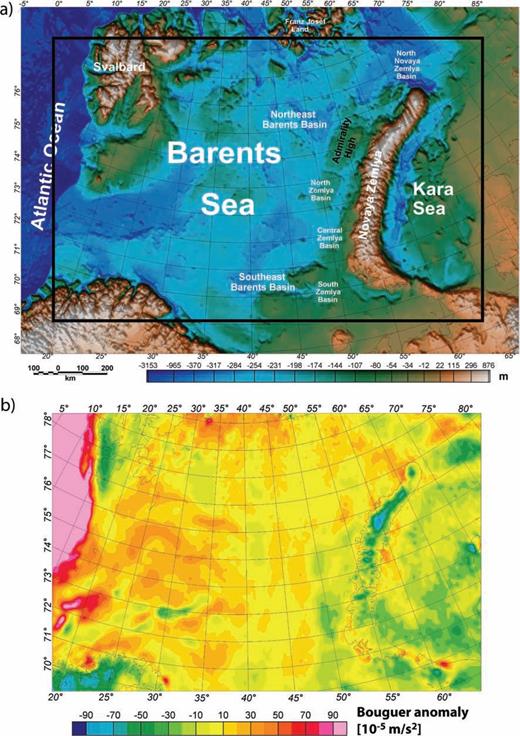
(a) Map showing topography/bathymetry of the greater Barents Sea Region, the location of the study area (black square) and the main structural elements. (b) Bouguer gravity anomaly map based on the gravity data from the Arctic Gravity Project (2002). The Bouguer anomaly is calculated with a complete ice-reduction and a Bouguer density of 2670 kg m⁻³.

Open in new tabDownload slide

Figure 2

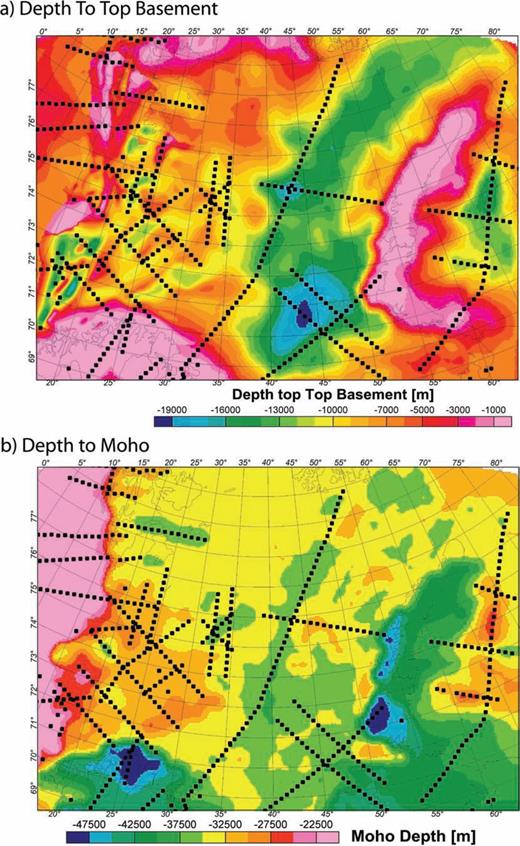
(a) Depth to basement and (b) Moho maps. The maps are adopted from the Barents50 model (Ritzmann 2007) with modifications after Skilbrei (1991, 1995) for the Western Barents Sea. The black dotted lines denote the location of the regional seismic lines used in compiling the Barents50 model.

Open in new tabDownload slide

Despite the large number of studies addressing the tectonic setting and history of the Barents Sea (e.g. Ziegler 1988; Gabrielsen 1990; Johansen 1992; Torsvik & Andersen 2002; Gee 2004; Breivik 2005), some of the key questions have not been resolved. The Paleozoic tectonic history of the southwestern Barents Sea is believed to be influenced by the Caledonian orogeny and the presence of a Caledonian suture (e.g. Fichler 1997; Gudlaugsson 1998; Breivik 2005). However, the location of the supposed suture in the southwestern Barents Sea is widely discussed, as is its continuation into the Eastern Barents Sea (e.g. Gee 2004; Breivik 2005). Another open question is related to the transition from the Western to the Eastern Barents Sea. Johansen (1992) argued for a monocline located within the shallow basement of the transition zone, while other studies regard the area of shallow basement as a suture zone (Gee 2004).

The aim of the present study is to establish differences in the tectonic setting and lithospheric structure within the Barents Sea region by evaluating existing regional geophysical studies and investigating the isostatic state of the lithosphere. The study tries to answer questions related to the transition in the tectonic setting and lithospheric structure of the Western and Eastern Barents Sea, as well as of the adjacent Kara Sea to the east.

GRAVITY DATA AND CONSTRAINING INFORMATION

Gravity field interpretation is the most important tool to analyse the density structure and the isostatic state of the lithosphere of the Barents Sea. A compilation of free-air anomalies offshore and Bouguer anomalies onshore has been prepared within the Arctic Gravity Project (2002). The data from the Arctic Gravity Project take into account the ice cover of Svalbard, but the ice cover in the Eastern Barents Sea has not been considered. Therefore, we digitised the lateral extent of the ice cover on Novaya Zemlya from satellite images and developed a model of ice thickness over the island. The extent of the ice model fits the satellite image and modelling its thickness allows the negative short-wavelength Bouguer anomalies over Novaya Zemlya to be explained. It is important to note that the influence of an incorrect reduction density for the ice cover (rock density 2670 kg m⁻³ instead of ice density 921 kg m⁻³; e.g. Gow 1997) gives a false gravity signal of up to 45 × 10⁻⁵ m s⁻² at most and 30 × 10⁻⁵ m s⁻² on average. Fig. 1(b) shows the ice-corrected Bouguer gravity anomaly of the Barents Sea region.

The ambiguity inherent in the interpretation of potential fields requires the use of constraining data in analysing the gravity field and the isostatic setting. Estimates of the top of basement for the Barents Sea are mainly based on aeromagnetic depth–source estimates (e.g. Skilbrei 1991, 1995) combined with shallow and deep seismic lines (e.g. Johansen 1992; Gramberg 2001; Ritzmann 2007). These studies concentrate either on the Western or Eastern Barents Sea or have only limited resolution along the transition between the two areas. To date, gravity field interpretation has been used only to a minor extent in compiling the depth to basement maps (e.g. Gramberg 2001).

The basement map in Fig. 2(a) combines the recent compilation ‘Barents50’ by Ritzmann (2007) and the compilation by Skilbrei (1991, 1995). The Barents50 model is a seismic-velocity model of the crust in the Barents Sea with a lateral resolution of 50 km. The Barents50 model is based on 2-D wide-angle reflection and refraction lines, passive seismological stations and, to a limited extent, potential field data (Ritzmann et al. 2006). The compilation presented by Skilbrei (1991, 1995) is based on aeromagnetic depth—source estimates combined with a variety of industrial shallow and deep seismic lines. This leads to a high resolution (5 × 5 km), but the data set is only available for the southwestern Barents Sea.

In the Eastern Barents Sea, the compilation of Ritzmann (2007) is in general agreement with studies by Johansen (1992) and Gramberg (2001). While the overall basement shape is similar, the biggest difference is evident in the area of maximum depth to basement in the central eastern Barents Sea. The compilation by Gramberg (2001) features deep basement in the southeast Barents Sea, while the compilation of Johansen (1992) shows the deepest basement in the northeast Barents Sea and thick sediments in the southeast Barents Sea are much less prominent. Differences in the basement depth can be explained by the geophysical interpretation methods and databases used to compile the basement depth estimates.

The depth to basement compilation of Gramberg (2001) is based on the interpretation of a few thousand kilometres of reflection and refraction lines. Interpretation of aeromagnetic surveys and gravity observations were also used to identify the depth to basement. Even if the study by Gramberg (2001) seems to rely on an extensive database, an unambiguous evaluation of the compilations is not possible, as a detailed description is only available in archive data at VNIIOkeangeologia, St Petersburg. Our depth to basement compilation is best constrained along the available 2-D wide-angle lines. Across the transition zone, a composite seismic interpretation (Bungum 2005) and some industry data are available. In general, the accuracy of the depth to basement estimates from the aeromagnetic data is of the order of ±1 km for the deepest part of the basins, but this estimate also depends on the available constraints from seismic data (Skilbrei 1991).

The Barents50 compilation also provides information on the deep structure of the crust, not just basement geometry. For the crust, this compilation includes an intracrustal horizon inferred mainly on the basis of velocity models and 2-D gravity modelling because crustal reflectivity does not allow clear imaging from seismic data alone (e.g. Breivik 2005). The seismic Moho of the Barents50 compilation is generally flat over large parts of the Barents Sea region (Fig. 2b). From the Atlantic continent–ocean boundary in the west to Novaya Zemlya, Moho depth varies only between 32.5 and 37.5 km. In the Western Barents Sea (32.5–35 km) the depth is slightly less than in the Eastern Barents Sea (35–37.5 km). The main changes can be related to the transition to Svalbard and the onshore-offshore transition in the south where the Moho rapidly becomes deeper than 40 km. Novaya Zemlya is associated with a Moho depth of around 45 km in the central part and up to 50 at its western border. This pattern does not correlate with the topographic expression of the island and would be equivalent to a crustal root shifted westwards compared to the topographic expression of the island. However, the location of the single available deep seismic line suggests that this feature is related to interpolation effects in the north and south.

The Moho depth also does not reflect observed changes in the depth to basement (Figs 2a and b). From an isostatic viewpoint and simple models of crustal extension (e.g. McKenzie 1978), a correlation between crustal thickness and Moho geometry would be expected. However, in the Barents Sea the total crustal thickness appears to be generally unaffected by the processes leading to the formation of the thick basins. Only in the Kara Sea is the Moho depth locally less than 30 km, which indicates localised crustal thinning, but here the seismic coverage is only good enough to resolve parts of the area. Therefore, we will evaluate the Moho geometry and its tectonic implications with our isostatic calculations and by gravity modelling.

FORWARD GRAVITY MODELLING

The knowledge of topography, depth to basement and Moho depth allows 3-D forward modelling of the crustal structure of the Barents Sea. We use the programme GMSYS-3D (Popowski 2006) and model against a normal crust reference density model (see Table 1). The ‘geological’ 3-D crustal model consists of a water layer, sediments between water and basement, the intracrustal horizon and Moho geometry from the Barents50 compilation (Ritzmann 2007). For sediment densities, we use a modified density–depth relationship that incorporates a sediment compaction model (e.g. Braitenberg 2006; Wienecke 2006) and assumes equal depth decay parameters (b₁=b₂, see Fig. 3). The function defining the density ρ for the depth d is given by

1

and includes the effect of porosity Φ, fluid density ρ_f= 1030 kg m⁻³, grain density ρ_s= 2700, starting porosity Φ₀= 0.6 and the depth-decay parameters b₁=b₂=−0.9. The values for fluid density, grain density, starting porosity and the depth-decay parameter b of the exponential density–depth relation are all constrained by results from 2-D density modelling in the Eastern Barents Sea (Fichler 1997) and by borehole information in the Western Barents Sea (Tsikalas 1992).

1

Reference parameters for the isostatic and gravity modelling.

Open in new tabDownload slide

Figure 3

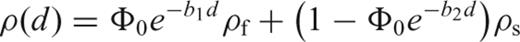
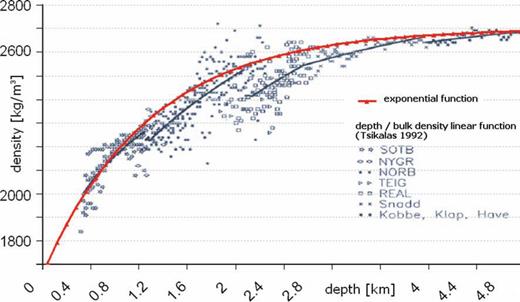
Density–depth function for sediments. We use an exponential function to describe the increased sediment density with depth. This function considers the effect of decreased porosity with depth. The density–depth function is adjusted to borehole measurements from Tsikalas (1992).

Open in new tabDownload slide

The gravity effect of the 3-D model is presented in Fig. 4 and along a profile in Fig. 5. The gravity signature of most continental margins is mainly influenced by the distribution of sediments (short- to intermediate wavelength) and the crust–mantle boundary (long-wavelength). The modelled gravity for this initial model already correlates well with the shape of some observed anomalies, but in general, large differences between the observed and modelled gravity field exist. The most obvious discrepancy is in the level of modelled and observed anomalies: −50 to 0 × 10⁻⁵ m s⁻² in the West Barents Sea, 50 to 100 × 10⁻⁵ m s⁻² in the East Barents Sea, and around −50 × 10⁻⁵ m s⁻² in the Kara Sea (Fig. 4b). These variations mean that the offset between observed and modelled gravity anomalies cannot be adjusted by applying a constant shift value. Furthermore, the large differences between these levels and the fact that the upper-crustal structure is relatively well known, suggests that the masses, needed to remove the offset lie within the lower crust or the mantle. To distinguish between these two possibilities, we study the isostatic state of the model and try to balance our model on a lithospheric scale.

Figure 4

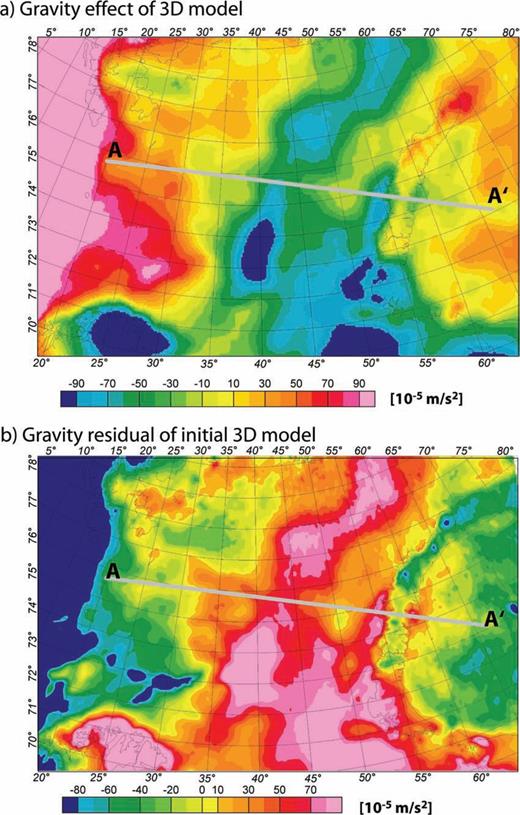
(a) Map showing the gravity effect of the simple 3-D density model based on constant densities for the crust and mantle, the density–depth relation for sediments from Fig. 3 and geometry from Fig. 2. (b) The residual field shows large regional differences between the gravity effect of the 3-D model and the observed Bouguer gravity (Fig. 1b). The profile marked A–A′ is plotted in Fig. 5.

Open in new tabDownload slide

Figure 5

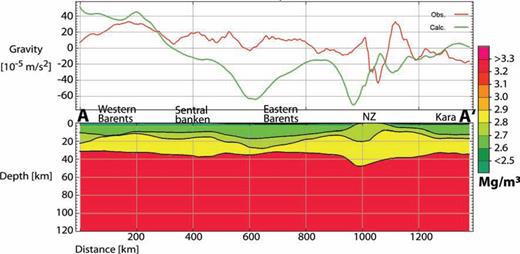
West–east profile through the model from the westernmost border of the Barents Sea to the Kara Sea showing the geometry and density distribution of the initial 3-D density model. The upper panel shows the large differences between the modelled gravity effect (green line) and the observed Bouguer anomaly (red line). For exact profile location and more details see Fig. 4.

Open in new tabDownload slide

ISOSTATIC STATE OF THE BARENTS SEA REGION

Isostatic compensation requires that all topographic masses (loading), and sediments (deloading) must be compensated at lithospheric level. When the loading is zero, the Moho interface has no undulation and is located at the normal crustal depth. In the presence of a crustal load, a flat Moho geometry corresponds either to a very high flexural rigidity, or to compensation in the mantle lithosphere. In a first approach, we consider Airy-type local isostatic compensation adjusted to take into account sediment loading. This loading is calculated using an exponential density-compaction model for the sediments. The resulting isostatic Moho (Fig. 6) is very different from the seismic Moho. For example, the isostatic Moho is 8 km shallower than the seismic Moho in the eastern Barents Sea. Possible explanations for the difference are: (1) the applied sediment densities are too low, (2) there is a compensating surplus mass in the lower crust or/and upper mantle or (3) the seismic Moho is too deep. As we have constraints on the seismic Moho and the applied densities, option (2) is the most likely. Whether isostatic balance is achieved by additional masses in the lower crust and upper mantle can be discussed by considering the gravity signal. Flexural rigidity is a probable cause of deviation from local isostasy. However, accounting for the isostatic balance by flexural rigidity would not explain the observed differences in the level of the gravity field and, furthermore, would not explain the excessively deep Moho. This means that varying densities in the crust or lithospheric mantle is the only way to fit the gravity field and to account for the east–west varying discrepancy between the level of observed and modelled gravity anomalies. In the following, we investigate whether these additional masses are sufficient to achieve local equilibrium at a lithospheric scale.

Figure 6

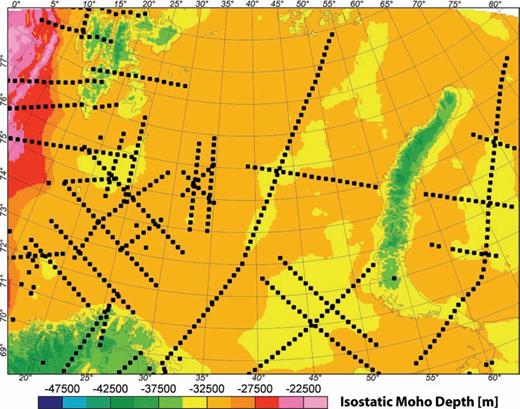
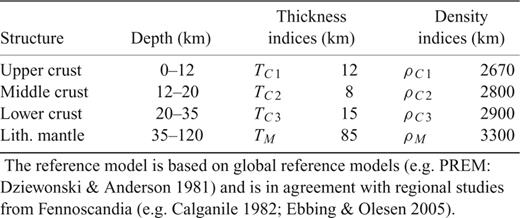
The simple Airy isostatic Moho depth (root) was calculated by taking into account the loading of bathymetry/topography and sediments as well as a density contrast between the lower crust and upper mantle of 400 kg m⁻³ and a relative normal crustal thickness of 35 km (as for the reference model in Table 1).

Open in new tabDownload slide

LITHOSPHERIC ISOSTASY—THEORY

The results of the Airy isostatic analysis show large differences between the ‘geophysical’ and isostatic Moho. We take this into account by applying the concept of lithospheric-scale isostasy, which is more related to the concept of Pratt isostasy. This concept of local isostasy regards the lithosphere–asthenosphere boundary, not the base of the crust, as the compensation depth for balancing the isostatic lithosphere. Hereby, we assume that local isostatic equilibrium exists and we then calculate the balance relative to a reference column. The chosen lithospheric standard column (crust and mantle) has a reference depth of 120 km (as inferred from studies of the adjacent Fennoscandian shield; Calganile 1982) and the density distribution given in Table 1. Isostatic equilibrium is now achieved by density variations in the lower crust or mantle that compensate for topographic and sediment loading. This approach of determining mass excess/deficits in the lithosphere and their associated gravity effect has been shown to be valid for regional investigations (e.g. Roy 2005).

The formula governing the isostatic equilibrium is:

2

In this equation, the subscripts refer to the load of the reference column, and of the ‘geological’ crust and lithospheric mantle, respectively. The load of a general mass column with density ρ and thickness T is Load=ρTg (g= gravity). Assigning a three-layer crust and dividing both sides by g, leads to

3

In this equation, density (ρ_Ci, i= 1, 2, 3) and thickness (T_Ci, i= 1, 2, 3) of the upper, mid and lower reference crust and reference mantle (ρ_M, T_M) are as defined in Table 1. The other parameters in eq. (3) are the density (ρ_cj, j= 1, 2, 3) and thickness of the geologic crust (T_cj, j= 1, 2, 3) and lithospheric mantle (ρ_MIso, T_m), the equivalent topography H_eq, and the seismic Moho depth R_Moho. The equivalent topography H_eq, defined by Braitenberg (2002), helps to simplify the equation, as it represents topography, bathymetry and the depth-dependent density distribution of the sediments using the following equation:

4

In our calculations, the geological model differs from the reference model only by the sediment layer, the topography/bathymetry and the undulations of the Moho geometry as defined by the Barents50 model. The Barents50 model also includes an intracrustal horizon, which is, however, poorly constrained and partly based on gravity modelling. Therefore, to avoid circular use of this gravity-inferred horizon, we only include it in the forward gravity modelling, not in the isostatic calculations.

With ρ_Ci=ρ_cj for i=j= 1, 2, 3 and T_Ci=T_cj for i=j= 1, 2 and solving for mantle density (ρ_MIso), eq. (3) becomes:

5

The mantle density (ρ_MIso) is calculated using eq. (4) in 5 × 5 km vertical columns.

Alternatively, we may consider balancing the upper-crustal loads by density variations in the lower crust. The isostatic lower-crustal density variation between 20 km depth and the Moho (ρ_LC) is given by the following expression:

6

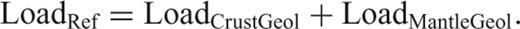
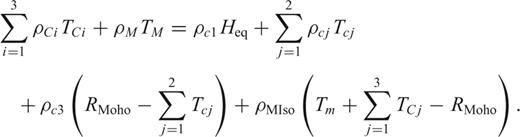
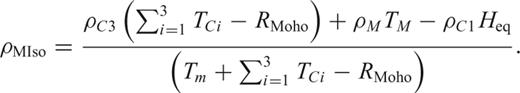
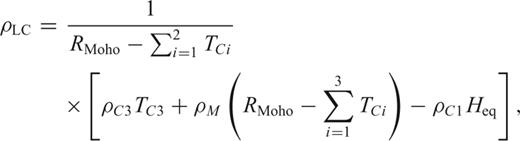
LITHOSPHERIC ISOSTASY—RESULTS

The inversion for lower-crustal density was carried out using the normal density of 2900 kg m⁻³ as a starting density. For the Eastern Barents Sea and Kara Sea, the calculations for the lower-crustal density distribution resulted in values from >2800 kg m⁻³ (Western Barents and Kara Sea) to >3150 kg m⁻³ (entire Eastern Barents Sea) (Fig. 7). Such a large volume of lower-crustal high densities would require that the entire region is underlain by magmatic underplating or eclogites, which should be visible in wide-angle seismic data. In the Barents50 model, some areas have high densities at the base of the crust (Ritzmann 2007), but the extent of these areas is far less than indicated by the isostatic calculation.

Figure 7

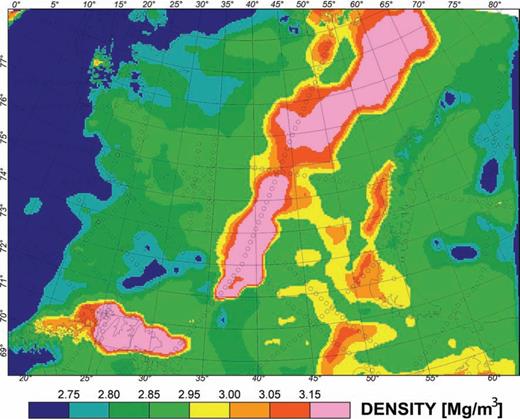
Map showing the distribution of isostatic crustal densities. The lower crustal densities were calculated to isostatically balance the lithosphere without including a variation in mantle densities.

Open in new tabDownload slide

Regional seismic lines crossing the Barents Sea suggest that P-wave velocities for the lower crust are between 6.6 and 6.8 km s⁻¹ (Bungum 2005). In a recent study, Ivanova (2006) also commented on the strong reflectivity of the Moho related to a high contrast in seismic velocities. The observed velocities could be associated with densities below 3000 kg m⁻³, but the area of relatively high lower-crustal velocities is only present in limited parts of the Barents Sea (e.g. Ivanova 2006; Ritzmann 2007). Indications for significant vertical and horizontal heterogeneity in the crust and uppermost mantle are given by Neprochnov (2000), but these are also inconsistent with the calculated density distribution. The geometry of the lower-crustal boundary in the Barents50 model suggests that the lower crust is even thinner than assumed in our isostatic model. Hence, the densities required for isostatic balance would be even higher for parts of the study area. However, as the intracrustal horizon is partly constrained by density modelling along 2-D profiles (Ritzmann 2007), invoking thinner lower crust also relies on circular argumentation. Therefore, we conclude that the scenario in which isostatic compensation is achieved by variations in lower crustal density is unrealistic for the Barents Sea.

The isostatic lithospheric mantle inversion resulted in densities ranging from 3250 to 3375 kg m⁻³ (Figs 8b and 9a). Lower values are only evident for the oceanic lithosphere of the North Atlantic. Generally, the lithospheric mantle densities show a regional division between the Western Barents Sea (3250–3300 kg m⁻³), the Eastern Barents Sea (3300–3350 kg m⁻³) and the Kara Sea (3275–3300 kg m⁻³). Furthermore, the calculated lithospheric mantle densities vary within the range of realistic density values for the upper lithospheric mantle.

Figure 8

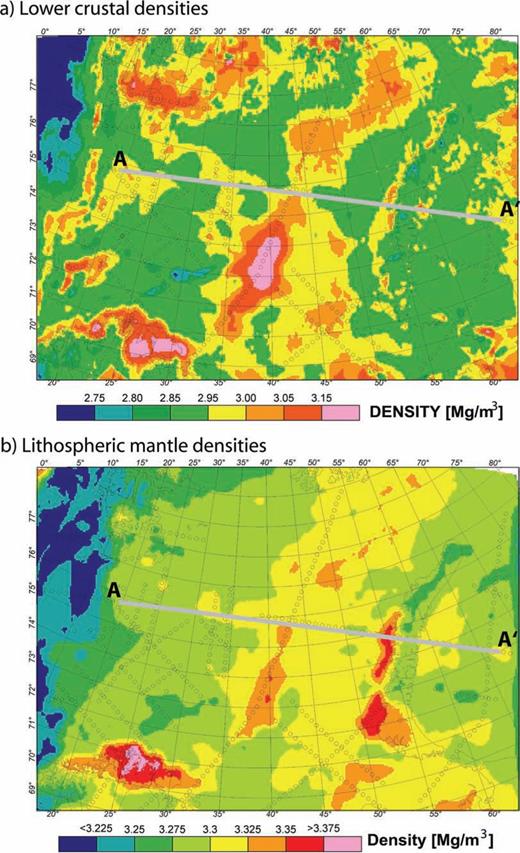
Maps showing (a) lower crustal density and (b) lithospheric mantle density variations. The varying densities allow local isostatic equilibrium to be achieved and give a modelled gravity field that fits the observed gravity to a large degree. The profile marked A–A′ is plotted in Fig. 9. This profile shows the complete crustal structure.

Open in new tabDownload slide

Figure 9

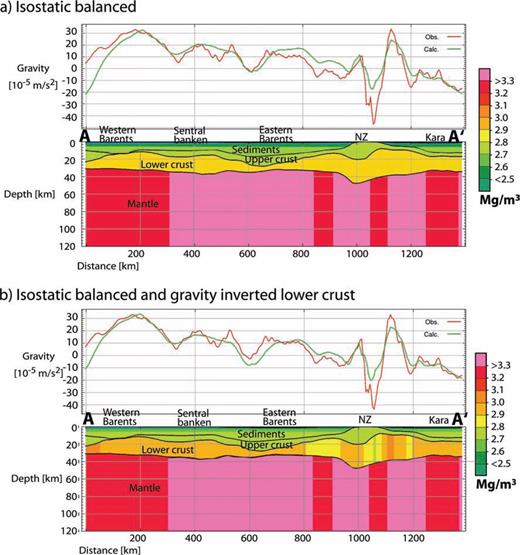
Profiles showing the same geometry as in Fig. 5, but in (a) the densities of the lithospheric mantle are varied to isostatically balance the lithosphere, and in (b) densities in the lower crust are also varied to fit the modelled and observed gravity fields whilst maintaining isostatic balance. The gravity residuals of the entire 3-D model are shown in Figs 10(a) and (b).

Open in new tabDownload slide

Using the variable density distribution calculated for the lithospheric mantle, the large discrepancy between observed and modelled gravity is now greatly reduced (Fig. 10a). However, for short- to intermediate-wavelength anomalies, a substantial misfit remains. To adjust for the intermediate-wavelength anomalies, the configuration of the intracrustal horizon of the Barents50 model is included in the model and the density of the lower crust is allowed to vary between 2800 and 3000 kg m⁻³. This small variation in lower-crustal density only has a minor impact on the isostatic state (Fig. 8a). The changes in lower-crustal density and geometry, in addition to the isostatically calculated mantle densities, lead to an isostatically balanced cross-section, whose structure is shown along the profile AA′ in Fig. 9(b), and to a reduced misfit for intermediate- and short-wavelength gravity anomalies (Fig. 10b).

Figure 10

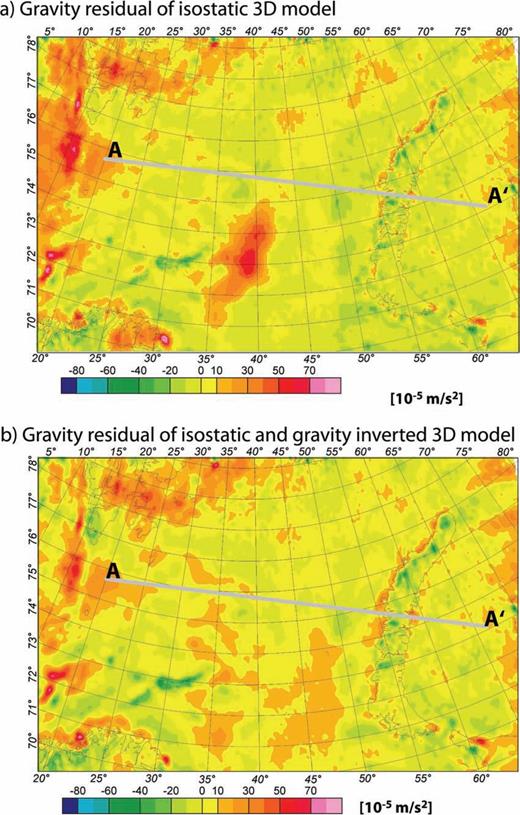
Maps showing residual gravity for the 3-D models. (a) Gravity residual for the model that includes only isostatic mantle densities and the intracrustal horizon in the computation. (b) Gravity residual for the model that also includes small lower-crustal density variations. The profile A–A′ is plotted in Figs 9(a) and (b).

Open in new tabDownload slide

Figs 8–10 show the density distribution for the lower crust and upper mantle from the isostatically balanced model of the greater Barents Sea Region. Despite the good fit between observed and modelled gravity, local differences are evident in the residual gravity anomaly (Fig. 10b). These can be explained by the resolution of the 3-D model, which was intended to explain the regional anomalies. Further adjustment would certainly require detailed modelling of crustal structures constrained by seismic profiles.

DISCUSSION AND CONCLUSION

Gravity forward modelling and isostatic considerations clearly show that the lithospheric mantle below the Barents Sea Region is not homogenous. The regional density distribution in the upper mantle inferred from the isostatically balanced 3-D density model is consistent with the results of a recent seismic tomography study (Faleide 2006). This study detected a high-velocity structure in the lithospheric mantle below the Eastern Barents Sea between Novaya Zemlya and the Eastern-Western Barents Sea transition zone, with its western boundary bending parallel to Novaya Zemlya. In the seismic tomography model, it can be seen that the high-velocity structure deepens below Novaya Zemlya and has the appearance of an old subducting slab. However, a thickness map of this anomaly directly correlates with our isostatic mantle density distribution (Levshin 2007), but the changes in mantle density also correlate with areas of different basin characteristics. The deep and very wide basins of the Eastern Barents Sea correlate with high lithospheric mantle densities, while the narrow (rift) basins of the Western Barents Sea correlate better with low lithospheric mantle densities. This observation suggests a connection between basin formation and underlying large-scale lithospheric processes. In a similar study of the eastern Colorado Plateau and the Rio Grande rift, Roy (2005) showed such a connection between upper mantle structure and tectonic provinces.

Changes in mantle densities may also reflect the presence of different plates and/or different lithospheric ages. A proposed west–east trending Caledonian suture crossing the entire Barents Sea (Gee 2004; Breivik 2005) would fit with this scenario. However, the distribution of lithospheric densities is inconsistent with the presence of a Caledonian suture east of the Central Barents transition because the suture would crosscut the area of high-lithospheric-mantle density. Furthermore, the density distribution in the lower crust shows relatively high densities along the transition between the Western and Eastern Barents Sea as well as a prominent change in the intracrustal horizon (Fig. 9) and the large gravity residuals that remain after including only the isostatic mantle densities in the gravity model (Fig. 10a).

Our observations and the calculated distribution of high-density material in the lower crust and lithospheric mantle suggest a possible relation to the Neoproterozoic Timanide Orogen of Eastern Baltica (e.g. Gee & Pearse 2006). If the mantle densities are related to the Timanide Orogen, the tectonic setting of the Eastern Barents Sea must have been very stable since and less affected by the Caledonian orogen than previously assumed. This would imply that a suture zone exists between the Eastern and Western Barents Sea related to this ancient tectonic process.

The stable setting of the Eastern Barents Sea compared to the Western Barents Sea can also explain the presence of the deep intracratonic basins. The mantle densities may indicate different tectonothermal age of the plates or changes in the gravitational potential stress. One may speculate that the mantle densities are related to the large-scale mantle dynamics that caused a crustal sag by a combination of lithospheric loading and drag at the base of the lithosphere due to downward-moving colder mantle. Hence, rifting processes are only of minor importance for the formation of the Eastern Barents Sea basins.

To understand the basin formation in the Eastern Barents Sea in more detail, one has also to look at the North, Central, and South Zemlya Basins, the flexural foreland basins of Novaya Zemlya, and try to understand their interaction with the Eastern Barents Sea Basin.

Another observation useful in characterising the transition zone is the apparent correlation between the presence of high-density material in the lower crust and the change in upper mantle densities. Comparison between basin geometry and high-density distribution points to the presence of intrusions along the transition zone, a feature often related to suture zones. However, the high-density distribution along the transition zone also coincides with a relatively thin lower crust (Ritzmann 2007) and is the least constrained in our final model. Despite this, the apparent correlation between the high-density feature in the lower crust and an aeromagnetic high along the transition zone points to the presence of intrusions at crustal levels above the lower crust. Here, further modelling is required to validate the interpretation, as our results are certainly limited by the resolution of the Barents50 model (50 × 50 km resolution) and the distribution of deep seismic lines in the Barents Sea (only a few seismic transects that extend from the Eastern to Western Barents Sea are available). Our isostatic analysis helps to link the large-scale structures between the two regions and points to anomalous structures in the crust. However, the precise location of these crustal structures must be the subject of more detailed studies in the future.

The results of our study show that there are differences in the crustal and lithospheric configuration between the Eastern and Western Barents Sea. This is expressed by differences in sediment thickness and basin characteristics, but also by changes in the lithospheric mantle density. Future discussion of the greater Barents Sea Region in a plate tectonic framework has to consider and explain these changes in lithospheric properties. Future work dealing with the tectonic formation of the greater Barents Sea region should be extended to include detailed analysis of the magnetic field. This would help to verify the presence of sutures zones related to the different lithospheric plates. Ongoing cooperation between Norwegian and Russian institutes will certainly allow the development of a more detailed lithospheric model of the Barents Sea and answer some of the open questions regarding the formation of the megascale basins.

ACKNOWLEDGMENTS

We thank Hans Morten Bjørnseth and Christine Fichler from Statoil for the initiation and support of the project. We especially benefited from the experience of and discussions with Jan Reidar Skilbrei. For discussions and the pre-publication release of information on the Barents50 model, we thank Oliver Ritzmann, Jan Inge Faleide, Hilmar Bungum and Nils Maerklin. We also thank Christian Weidle for insights into the seismological studies, David Gee for pointing us towards the Timanides, and Ron Hackney for his constructive comments on the manuscript.

REFERENCES