-
PDF
- Split View
-
Views
-
Cite
Cite
Christopher Kotsakis, A covariance-adaptive approach for regularized inversion in linear models, Geophysical Journal International, Volume 171, Issue 2, November 2007, Pages 509–522, https://doi.org/10.1111/j.1365-246X.2007.03534.x
Close - Share Icon Share
Summary
The optimal inversion of a linear model under the presence of additive random noise in the input data is a typical problem in many geodetic and geophysical applications. Various methods have been developed and applied for the solution of this problem, ranging from the classic principle of least-squares (LS) estimation to other more complex inversion techniques such as the Tikhonov—Philips regularization, truncated singular value decomposition, generalized ridge regression, numerical iterative methods (Landweber, conjugate gradient) and others. In this paper, a new type of optimal parameter estimator for the inversion of a linear model is presented. The proposed methodology is based on a linear transformation of the classic LS estimator and it satisfies two basic criteria. First, it provides a solution for the model parameters that is optimally fitted (in an average quadratic sense) to the classic LS parameter solution. Second, it complies with an external user-dependent constraint that specifies a priori the error covariance (CV) matrix of the estimated model parameters. The formulation of this constrained estimator offers a unified framework for the description of many regularization techniques that are systematically used in geodetic inverse problems, particularly for those methods that correspond to an eigenvalue filtering of the ill-conditioned normal matrix in the underlying linear model. Our study lies on the fact that it adds an alternative perspective on the statistical properties and the regularization mechanism of many inversion techniques commonly used in geodesy and geophysics, by interpreting them as a family of ‘CV-adaptive’ parameter estimators that obey a common optimal criterion and differ only on the pre-selected form of their error CV matrix under a fixed model design.
1 Introduction
A generic estimation problem in many geodetic and geophysical applications is that of determining a set of unknown deterministic parameters which are observed through a known transformation model and corrupted by additive random noise. This type of problem is commonly formulated in terms of a linear system of observation equations  , which needs to be uniquely solved for the unknown parameter vector x given a set of noisy data y (Tarantola 1987; Menke 1989; Dermanis & Rummel 2000). The residual term v describes the effect of random disturbances in the input data, whereas the elements of the matrix A correspond to known coefficients that depend on the conditions of the physical system under study. Note that such problems are inherently ill-posed as they can never have a unique solution due to the existence of the unknown random observation errors. In algebraic terms, we deal with an underdetermined system that has an infinite number of solutions, since for every candidate solution
, which needs to be uniquely solved for the unknown parameter vector x given a set of noisy data y (Tarantola 1987; Menke 1989; Dermanis & Rummel 2000). The residual term v describes the effect of random disturbances in the input data, whereas the elements of the matrix A correspond to known coefficients that depend on the conditions of the physical system under study. Note that such problems are inherently ill-posed as they can never have a unique solution due to the existence of the unknown random observation errors. In algebraic terms, we deal with an underdetermined system that has an infinite number of solutions, since for every candidate solution  for the parameter vector there always exists a corresponding estimate of the unknown data errors,
for the parameter vector there always exists a corresponding estimate of the unknown data errors,  , which satisfies the original system of observation equations.
, which satisfies the original system of observation equations.
Typical examples of such discrete inverse problems arise in several fields of geosciences, including gravity field modelling and satellite geodesy (Schwarz 1979; Rummel 1985; Sanso & Rummel 1989; Xu 1992; Xu & Rummel 1994; Ilk et al. 2002), satellite orbit determination (Engelis & Knudsen 1989; Beutler et al. 1994; Tapley et al. 2004), tectonic plate motions (Chase & Stuart 1972; Minster et al. 1974), satellite altimetry and ocean circulation studies (Wunsch & Minster 1982; Knudsen 1992; Fu & Cazenave 2001), magnetic field modelling (Parker et al. 1987; Backus 1988), atmospheric tomography (Kunitake 1996; Kleijer 2004), seismology and acoustic tomography (Crosson 1976; Aki & Richards 1980; Pavlis & Booker 1980), wave propagation and scattering theory (Bee & Jacobson 1984; Koch 1985) and core and mantle dynamics (Parker 1970; Gire et al. 1986; Nataf et al. 1986).
A fairly common approach for solving parameter estimation problems in linear models is the method of least-squares (LS) which provides an optimal solution  that reproduces as close as possible the given data by minimizing the weighted differences between the original measurements y and the model-induced observables
that reproduces as close as possible the given data by minimizing the weighted differences between the original measurements y and the model-induced observables  . In statistical terms, the LS solution gives an unbiased estimate for the unknown parameters provided that there are no modelling errors or other hidden systematic effects in the data. In addition, it has the minimum mean squared estimation error (MSEE) among all linear unbiased estimators if the chosen weight matrix for the input data is equal to the inverse covariance (CV) matrix of their random observation errors; for more details, see Menke (1989), Koch (1999) and Rao & Toutenburg (1999).
. In statistical terms, the LS solution gives an unbiased estimate for the unknown parameters provided that there are no modelling errors or other hidden systematic effects in the data. In addition, it has the minimum mean squared estimation error (MSEE) among all linear unbiased estimators if the chosen weight matrix for the input data is equal to the inverse covariance (CV) matrix of their random observation errors; for more details, see Menke (1989), Koch (1999) and Rao & Toutenburg (1999).
Within the context of geodetic and geophysical applications, the LS methodology has been used not only as an optimal algorithm for estimating a set of unknown parameters from noisy measurements in a given linear model, but also as a trend analysis tool for identifying the main features of partially known physical systems through the fitting of simple analytic models to complex data records. In any case, the accuracy of LS inversion results may not be satisfactory in practice if the underlying linear model that relates the available data and the unknown parameters is ill-conditioned. In such cases, one or more eigenvalues of the corresponding normal matrix are close to zero, thus causing a large statistical uncertainty in the LS solution even for very precise data sets (Hoerl & Kennard 1970; Sen & Srivastava 1990). In this category belong many geodetic estimation problems that can be expressed in the linear form y = Ax+v, including the downward continuation of gravity field measurements from satellite or aerial altitude to the surface of the earth, the inversion of altimetric data for marine gravity determination, and the computation of gravity gradients from gravity anomaly data. For a general overview of ill-posed inverse problems in geodesy, see Neyman (1985) and Ilk (1991).
Various alternative techniques to the classic LS method have been developed in order to improve the parameter estimation accuracy in linear model inversion. Despite their differences and (sometimes) conflicting interpretations, most of these regularization techniques seem to follow a common rationale which points to the fact that a successful solution to a discrete inverse problem should not be solely determined by the quality of the fit between the data and the corresponding observables obtained from the estimated model parameters (i.e. the typical ‘LS logic’), but it requires also some quality control for the estimated parameters themselves. As an example, we can mention the method of Tikhonov—Philips regularization (Tikhonov & Arsenin 1977) which has been used extensively for the stable inversion of ill-conditioned linear models based on a hybrid optimal criterion that takes into account both the data-model fitting aspect and the size or smoothness of the actual model parameters (Schwarz 1979; Schaffrin 1980; Ilk et al. 2002; Kusche & Klees 2002; Ditmar et al. 2003). Other perspectives of the Tikhonov—Philips inversion scheme have also been considered by many researchers, including its implementation from a biased estimation or ridge regression viewpoint (Xu 1992; Xu & Rummel 1994; Bouman & Koop 1997), and its Bayesian interpretation which involves a priori parameter weighting (Xu & Rummel 1994) and variance component estimation procedures (Koch & Kusche 2002). Alternative regularization approaches that have been followed for the optimal inversion of linear models include the truncated singular value decomposition (TSVD) or bandpass filtering (Xu 1998), stochastic regularization techniques (Schaffrin 1985, 1989), LS collocation (Rummel et al. 1976, 1979) and numerical iterative methods (Landweber algorithm, conjugate gradient algorithm). A detailed comparison of regularization techniques for geodetic inverse problems has been given in Bouman (1998), where a unified framework for the spectral behaviour of several regularized estimators was presented; see also Gerstl & Rummel (1981).
The objective of this paper is to present a new parameter estimator  for linear models y = Ax+v, which unifies under a common statistical framework all regularization methods that are systematically used in geodetic inverse problems. Our study lies on the fact that it adds an alternative perspective on the optimal statistical properties and the regularization mechanism of many inversion techniques commonly used in geodesy and geophysics, including Tikhonov—Philips regularization, generalized ridge regression (GRR) and TSVD estimation. The structure of the paper is organized as follows. In Section 2, the formulation and the properties of the new parameter estimator are presented along with the derivation of its analytic form. Additional topics of study in this section include the MSEE performance and the inherent bias characteristics of the new estimator, as well as the admissible range for the signal-to-noise ratio (SNR) of an arbitrary linear model that guarantees better MSEE performance when using the new estimator over the classic LS solution. Some particular regularization aspects associated with the new parameter estimator are discussed in Section 3, where it is shown that all regularized inversion techniques corresponding to an eigenvalue filtering of the normal matrix of the underlying linear model y = Ax+v are essentially special cases of the general estimation framework presented herein. An example for the numerical solution of a typical ill-conditioned problem in physical geodesy, namely the downward continuation of satellite gradiometry data for the determination of a gravity anomaly grid on the surface of the Earth, is given in Section 4 to demonstrate the practical implementation and the usefulness of the new estimator in geodetic inverse problems. Finally, some concluding remarks are given at the end of the paper.
for linear models y = Ax+v, which unifies under a common statistical framework all regularization methods that are systematically used in geodetic inverse problems. Our study lies on the fact that it adds an alternative perspective on the optimal statistical properties and the regularization mechanism of many inversion techniques commonly used in geodesy and geophysics, including Tikhonov—Philips regularization, generalized ridge regression (GRR) and TSVD estimation. The structure of the paper is organized as follows. In Section 2, the formulation and the properties of the new parameter estimator are presented along with the derivation of its analytic form. Additional topics of study in this section include the MSEE performance and the inherent bias characteristics of the new estimator, as well as the admissible range for the signal-to-noise ratio (SNR) of an arbitrary linear model that guarantees better MSEE performance when using the new estimator over the classic LS solution. Some particular regularization aspects associated with the new parameter estimator are discussed in Section 3, where it is shown that all regularized inversion techniques corresponding to an eigenvalue filtering of the normal matrix of the underlying linear model y = Ax+v are essentially special cases of the general estimation framework presented herein. An example for the numerical solution of a typical ill-conditioned problem in physical geodesy, namely the downward continuation of satellite gradiometry data for the determination of a gravity anomaly grid on the surface of the Earth, is given in Section 4 to demonstrate the practical implementation and the usefulness of the new estimator in geodetic inverse problems. Finally, some concluding remarks are given at the end of the paper.
2 CV-Adaptive Parameter Estimation in Linear Models
2.1 Problem formulation
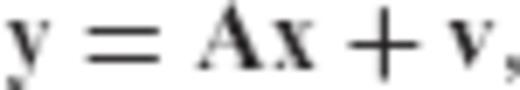
The optimal inversion of eq. (1) will be based on a tailoring methodology, according to which a known reference estimator of x is modified in such a way that it produces an improved solution for the unknown model parameters. This kind of constructive reasoning has actually shaped the development of several parameter estimators in statistics theory (Bibby & Toutenburg 1977). Following Rao (1973), an improved estimator may be heuristically described as one which is derived in the following manner: starting with some prescribed solution, say  , having known statistical properties of bias, variance, etc., we try to adapt it in some way so that a newly generated estimator
, having known statistical properties of bias, variance, etc., we try to adapt it in some way so that a newly generated estimator  (based on
(based on  ) is better in terms of some chosen criterion function. For instance, if the criterion function is the MSEE, then we should say that
) is better in terms of some chosen criterion function. For instance, if the criterion function is the MSEE, then we should say that  is better than
is better than  if
if  is smaller than
is smaller than  (for more details, see Bibby & Toutenburg 1977).
(for more details, see Bibby & Toutenburg 1977).
 for the parameter vector x in a linear model y = Ax+v based on a linear transformation of the classic LS solution (or equivalently, the minimum-variance linear unbiased solution). Thus, we have the following general scheme
for the parameter vector x in a linear model y = Ax+v based on a linear transformation of the classic LS solution (or equivalently, the minimum-variance linear unbiased solution). Thus, we have the following general scheme 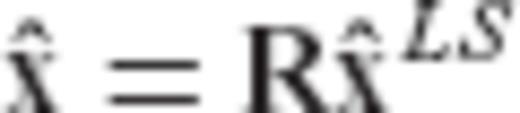
 denoting the usual LS estimator
denoting the usual LS estimator 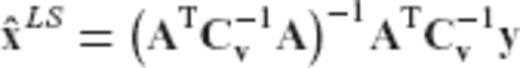
 .
.Despite its optimal statistical properties, the LS solution in eq. (3) gives poor results when the original linear model is ill-conditioned. The effect of the matrix R in eq. (2) should thus be understood in a ‘regularization’ context as an attempt to correct the LS solution by adjusting it closer to the true vector x. In fact, many well-known regularization techniques are known to produce parameter estimators that can take the form of eq. (2) for specific expressions of the matrix R, including Tikhonov—Philips regularization, GRR, shrunken LS estimation, TSVD estimation and principal component estimation (Marquardt 1970; Mayer & Willke 1973). Note that the numerical implementation of the modified estimator  does not necessarily require the prior computation of the entire LS solution (which is actually problematic in the case of ill-conditioned problems), provided that the matrix product R (ATC−1vA)−1 can be separately evaluated in a numerically stable and efficient manner (more details given in Section 3).
does not necessarily require the prior computation of the entire LS solution (which is actually problematic in the case of ill-conditioned problems), provided that the matrix product R (ATC−1vA)−1 can be separately evaluated in a numerically stable and efficient manner (more details given in Section 3).
Our aim is to determine a general form for the regularization matrix R by combining (i) a ‘global’ optimal criterion that minimizes the weighted difference between the original LS solution and the transformed LS solution obtained from eq. (2) and (ii) a constraint that sets the error CV matrix of the modified estimator  equal to an a priori, user-specified form.
equal to an a priori, user-specified form.
As it will be shown in later sections, all existing regularization methods for discrete inverse problems that correspond to an eigenvalue filtering of the ill-conditioned normal matrix N = ATC−1vA can be formulated as special cases of the aforementioned framework. This kind of unification adds an interesting perspective on the statistical properties and the regularization mechanism of many inversion techniques that are currently used in geodesy and geophysics, by interpreting them as a collection of ‘CV-adaptive’ parameter estimators that obey the same optimal criterion and differ only on the pre-selected form of their error CV matrix under a fixed model design.
2.2 CV-adaptive inversion methodology and optimal regularization matrix
A fundamental characteristic of the LS solution is its unbiasedness,  under the absence of any modelling errors. From the Gaussian viewpoint of LS estimation theory, the property of unbiasedness is essentially a constraint that is a priori imposed on the first moment of a linear estimator in conjunction with the minimum MSEE principle.
under the absence of any modelling errors. From the Gaussian viewpoint of LS estimation theory, the property of unbiasedness is essentially a constraint that is a priori imposed on the first moment of a linear estimator in conjunction with the minimum MSEE principle.
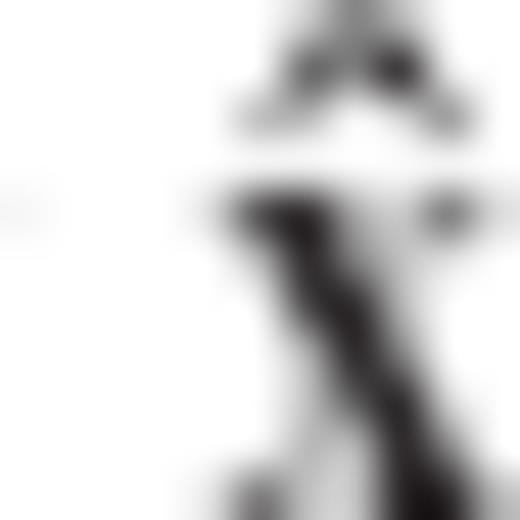 by imposing an a priori constraint on its second (centred) moment
by imposing an a priori constraint on its second (centred) moment 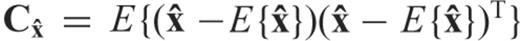 . Since the general form of
. Since the general form of  is taken as a linear transform of the LS solution according to eq. (2), a constraint on its second centred moment can be formulated in terms of the matrix equation
is taken as a linear transform of the LS solution according to eq. (2), a constraint on its second centred moment can be formulated in terms of the matrix equation 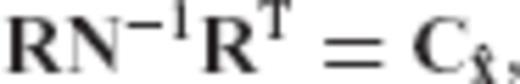
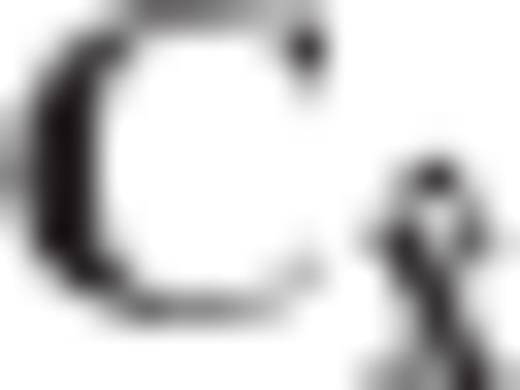 is the user-specified CV matrix of the estimated parameters, N = ATC−1vA is the normal matrix of the underlying linear model, and R is the required transformation matrix.
is the user-specified CV matrix of the estimated parameters, N = ATC−1vA is the normal matrix of the underlying linear model, and R is the required transformation matrix.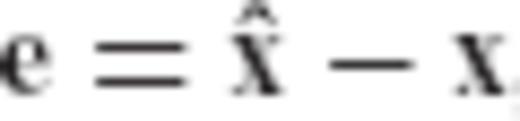 , since
, since 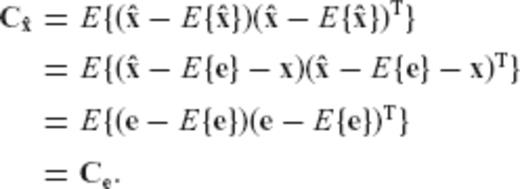
 in terms of the principle
in terms of the principle 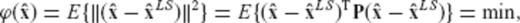
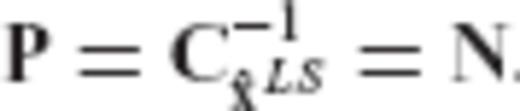 .
.The parameter estimator  is thus characterized by two basic statistical properties.
is thus characterized by two basic statistical properties.
- 1
It adheres to a minimization criterion that provides an optimal weighted fit with the LS solution according to eq. (5). The particular choice of the weight matrix P as the inverse CV matrix of
 ensures that the information about the parameter estimation accuracy in the original LS solution is assimilated into the new estimator by adjusting the elements of
ensures that the information about the parameter estimation accuracy in the original LS solution is assimilated into the new estimator by adjusting the elements of  according to the dispersion of the corresponding elements of
according to the dispersion of the corresponding elements of  .
. - 2
It complies with a user-dependent constraint that specifies the variance and the correlation structure of the parameter estimation errors through an a priori selected CV matrix
 . Particular strategies and further discussion pertaining to the choice of
. Particular strategies and further discussion pertaining to the choice of  will be given in Section 3.
will be given in Section 3.
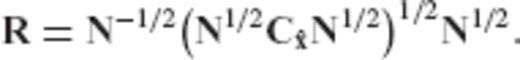
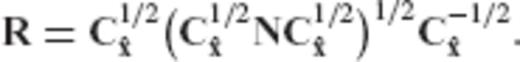
Remark 1: The square root of a symmetric non-negative definite matrix C is a unique matrix which is determined through the square roots of its eigenvalues. In particular, if C = UΛUT is the orthonormalized eigenvalue decomposition of C, then we have that C1/2 = UΛ1/2UT, where the diagonal matrix Λ1/2 contains the square roots of the eigenvalues of C. Also, the inverse square root of a symmetric positive definite matrix is defined as
of a symmetric non-negative definite matrix C is a unique matrix which is determined through the square roots of its eigenvalues. In particular, if C = UΛUT is the orthonormalized eigenvalue decomposition of C, then we have that C1/2 = UΛ1/2UT, where the diagonal matrix Λ1/2 contains the square roots of the eigenvalues of C. Also, the inverse square root of a symmetric positive definite matrix is defined as  (for more details see Rao & Toutenburg 1999, pp. 362–363).
(for more details see Rao & Toutenburg 1999, pp. 362–363).
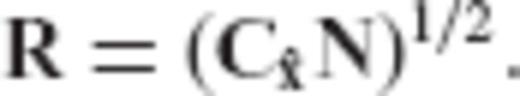
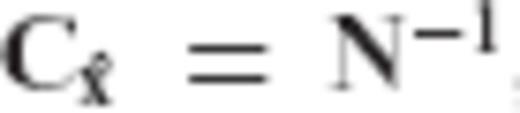 , the regularization matrix becomes identity (R = I) and our inversion scheme simply reproduces the LS solution, as it should be expected.
, the regularization matrix becomes identity (R = I) and our inversion scheme simply reproduces the LS solution, as it should be expected.2.3 Bias of the CV-adaptive estimator
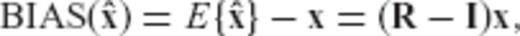
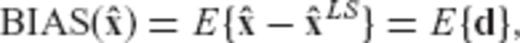
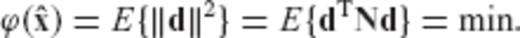

 can be expressed as
can be expressed as 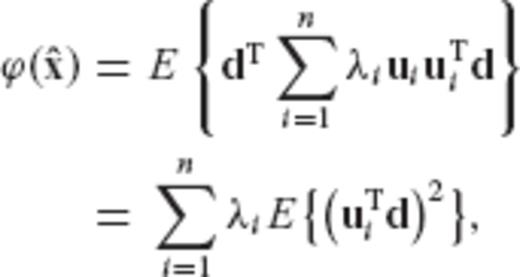
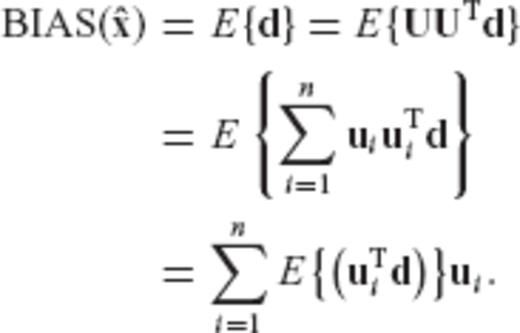
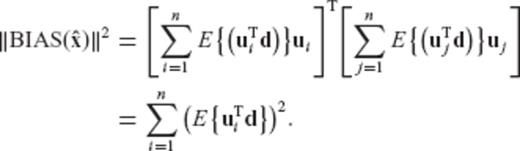
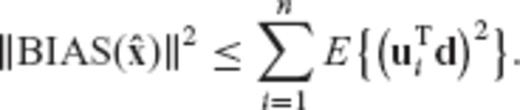
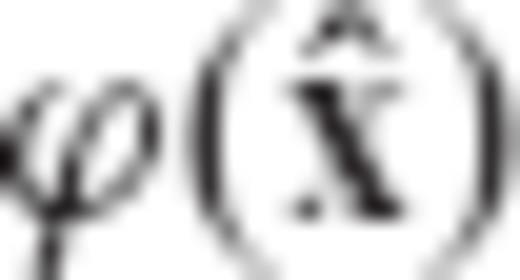 is equivalent to a weighted minimization of the maximum bias' Euclidean spectral components, with respect to the orthonormal basis formed by the eigenvectors of the normal matrix N.
is equivalent to a weighted minimization of the maximum bias' Euclidean spectral components, with respect to the orthonormal basis formed by the eigenvectors of the normal matrix N.Remark 3: The fact that the CV-adaptive estimator is optimized through a fitting to the classic LS solution may be perceived as a ‘weak’ point, due to the problems associated with the LS solution in ill-conditioned problems. However, a closer look at the formulation of the minimization principle in eq. (5) reveals that the fitting does not take place with a particular LS solution, but rather it takes place over the entire ensemble of possible solutions that we would obtain if we repeat the data collection and the LS inversion process an infinite number of times. Moreover, as seen from the previous analysis, the optimality of the CV-adaptive estimator in terms of achieving a best average quadratic fit with the LS estimator is essentially a means to control its inherent bias.
2.4 MSEE performance and admissible SNR range
 requires the analysis of its MSEE matrix
requires the analysis of its MSEE matrix 
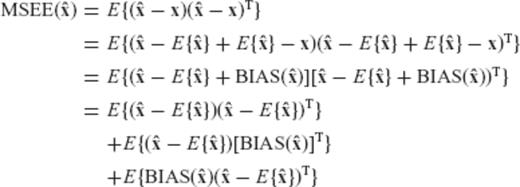
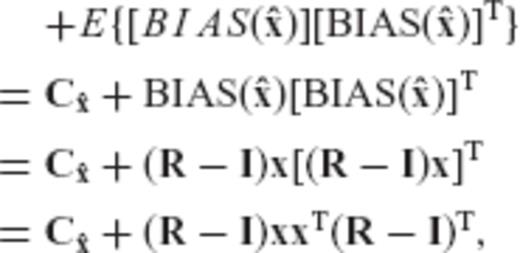
 is the a priori chosen CV matrix of
is the a priori chosen CV matrix of  , and R is the associated regularization matrix obtained from eq. (6) or (7).
, and R is the associated regularization matrix obtained from eq. (6) or (7). , namely the trace of its MSEE matrix
, namely the trace of its MSEE matrix 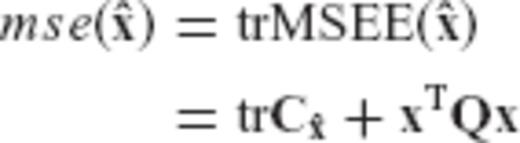
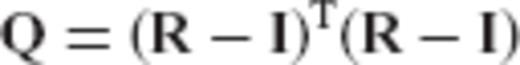
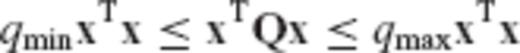
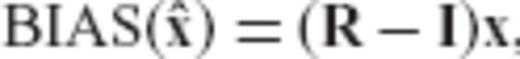 , and thus qmax quantifies the maximum relative bias effect in the parameter solution
, and thus qmax quantifies the maximum relative bias effect in the parameter solution  .
.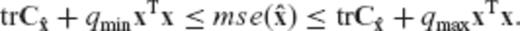
 and the classic LS estimator
and the classic LS estimator 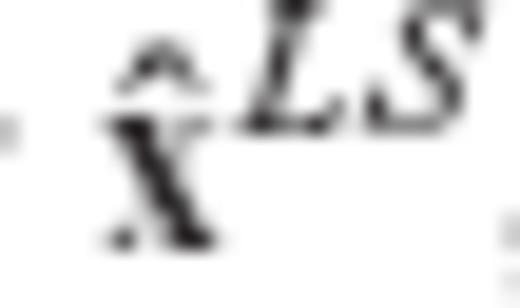 , in terms of their MSEE performance. Due to its unbiasedness property, the MSEE matrix of the LS estimator is equal to its CV matrix
, in terms of their MSEE performance. Due to its unbiasedness property, the MSEE matrix of the LS estimator is equal to its CV matrix 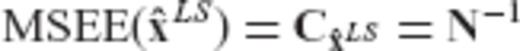
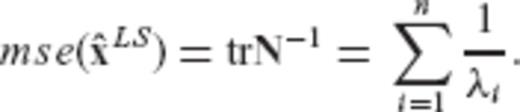
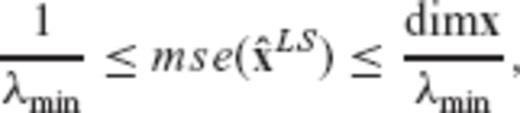
By comparing eqs (22) and (25), we see that the MSEE of the LS estimator has an upper bound that is completely independent of the magnitude of the unknown model parameters, whereas the MSEE of the CV-adaptive estimator has an upper bound that depends directly on the Euclidean length of the parameter vector. Such a result indicates the potential of the biased estimator  to produce better results (with significantly smaller MSEE compared to the classic LS solution) in inverse problems with sufficiently low SNR. In fact, an admissible SNR range for an arbitrary linear model can be derived, within which the CV-adaptive estimator is guaranteed to outperform the LS estimator in the MSEE sense.
to produce better results (with significantly smaller MSEE compared to the classic LS solution) in inverse problems with sufficiently low SNR. In fact, an admissible SNR range for an arbitrary linear model can be derived, within which the CV-adaptive estimator is guaranteed to outperform the LS estimator in the MSEE sense.
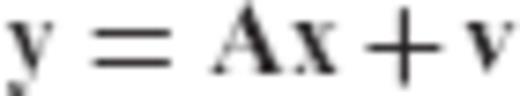 in terms of the ratio
in terms of the ratio 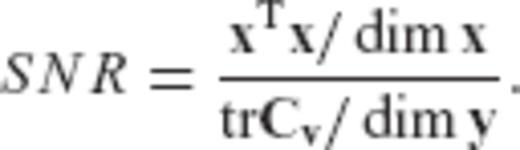
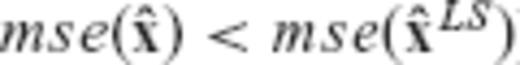 ]
]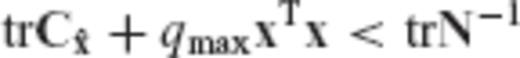
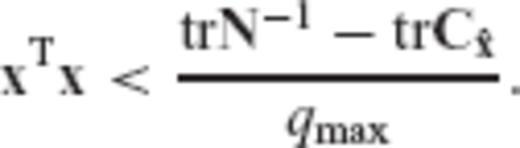
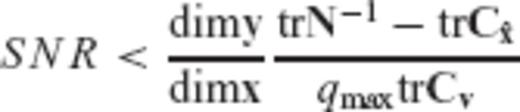
 . The smaller the SNR value of a particular model y = Ax+v with respect to the upper bound given in eq. (29), the greater will be the reduction of the MSEE of
. The smaller the SNR value of a particular model y = Ax+v with respect to the upper bound given in eq. (29), the greater will be the reduction of the MSEE of  .
.Note that the quantities dim x, dim y, trN−1 and trCv are model- and data-dependent, whereas the terms qmax and  are controlled by the a priori choice of the CV matrix for the estimated parameters.
are controlled by the a priori choice of the CV matrix for the estimated parameters.
As a final comment, we should mention that in every linear model there will always exist an admissible SNR range for applying the CV-adaptive biased estimator, provided that the latter is set to have smaller total error variance than the LS solution. Indeed, in such a case we have that  and the right side of the inequality condition (29) will always give a positive upper bound for the admissible SNR of the underlying linear model.
and the right side of the inequality condition (29) will always give a positive upper bound for the admissible SNR of the underlying linear model.
3 Choice of ![graphic]() —Regularization Aspects
—Regularization Aspects
3.1 General remarks
The a priori choice of the error CV matrix for the estimated parameters is a key issue for the implementation of the CV-adaptive estimator  . Although it may seem perplexing to formulate an inversion scheme which conforms to a user-specified error CV structure for the estimated model parameters, the introduction of an external constraint for
. Although it may seem perplexing to formulate an inversion scheme which conforms to a user-specified error CV structure for the estimated model parameters, the introduction of an external constraint for  should be seen as a prospective regularization tool that gives us the flexibility to obtain and compare different solutions for the model parameters with particular statistical quality characteristics.
should be seen as a prospective regularization tool that gives us the flexibility to obtain and compare different solutions for the model parameters with particular statistical quality characteristics.
A relevant example is the case where the CV-adaptive estimator is designed to give a fully decorrelated solution with uniform precision for the model parameters,  . This particular choice (which is actually equivalent to a special implementation of GRR, as it will be explained later on) can be beneficial in inverse problems y = Ax+v with a large number of unknown parameters that will be subsequently used for the determination of other quantities of interest z = f(x). The existence of a diagonal-scalar CV matrix
. This particular choice (which is actually equivalent to a special implementation of GRR, as it will be explained later on) can be beneficial in inverse problems y = Ax+v with a large number of unknown parameters that will be subsequently used for the determination of other quantities of interest z = f(x). The existence of a diagonal-scalar CV matrix  simplifies to a large extent the accuracy assessment of
simplifies to a large extent the accuracy assessment of  , at least with respect to the rigorous propagation of random-related errors.
, at least with respect to the rigorous propagation of random-related errors.
 can be represented through the orthogonal expansion
can be represented through the orthogonal expansion 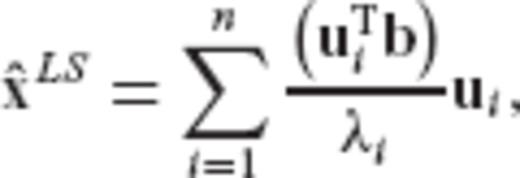
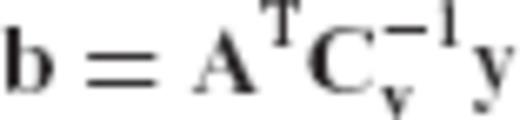
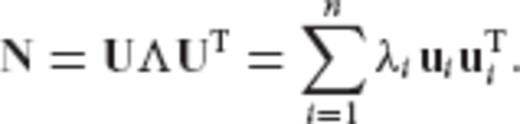
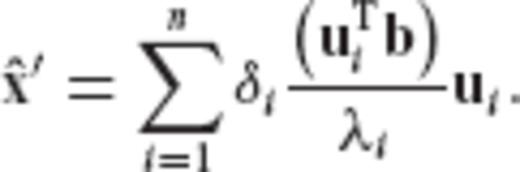
In the next section, it is shown that the CV-adaptive estimator from Section 2 corresponds to an eigenvalue filtering of the type given in eq. (33) for a particular ‘restrictive’ choice of the error CV matrix  for the model parameters.
for the model parameters.
3.2 CV-adaptive regularization in the LS-based eigenvector basis
 can be simplified if the choice of
can be simplified if the choice of  is restricted to an a priori general form. Specifically, we adopt the following scheme:
is restricted to an a priori general form. Specifically, we adopt the following scheme: 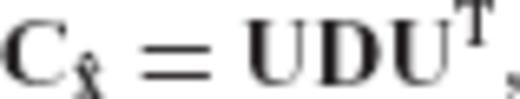
 is constrained to have the same eigenvectors as the normal matrix of the underlying linear model, and its a priori selection is reduced into a problem of specifying only its eigenvalues.
is constrained to have the same eigenvectors as the normal matrix of the underlying linear model, and its a priori selection is reduced into a problem of specifying only its eigenvalues.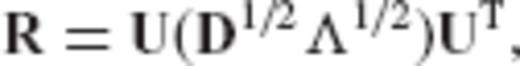
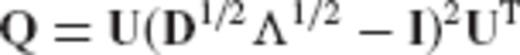
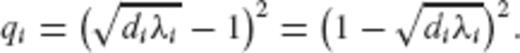
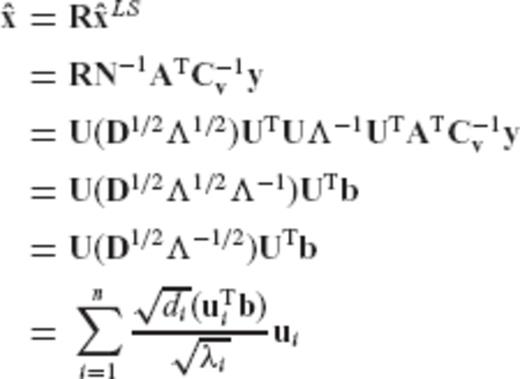
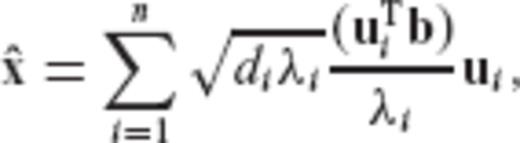
It is seen that the general choice of eq. (34) leads to a CV-adaptive estimator which is equivalent to an eigenvalue filtering of the normal matrix in the underlying linear model. As such, it can cover all regularization techniques that are based on the spectral expansion of eq. (33).
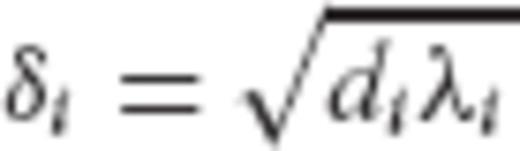
 .
.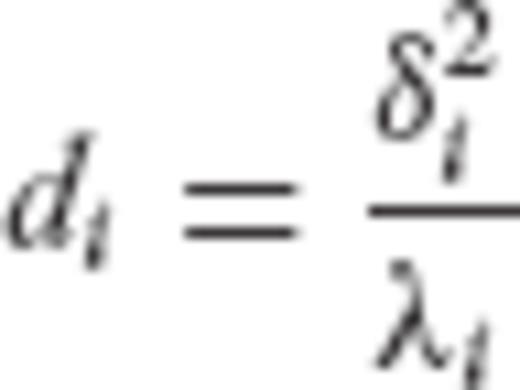
 (‘whitening’ of the parameter estimation errors) and it results in a decorrelated solution with uniform precision for the model parameters. It is actually interesting that this type of solution can be equivalently obtained through the well-known method of GRR by properly selecting its built-in regularization parameters. In general, the filter factors associated with the GRR method are given by the formula (Bouman 1998)
(‘whitening’ of the parameter estimation errors) and it results in a decorrelated solution with uniform precision for the model parameters. It is actually interesting that this type of solution can be equivalently obtained through the well-known method of GRR by properly selecting its built-in regularization parameters. In general, the filter factors associated with the GRR method are given by the formula (Bouman 1998) 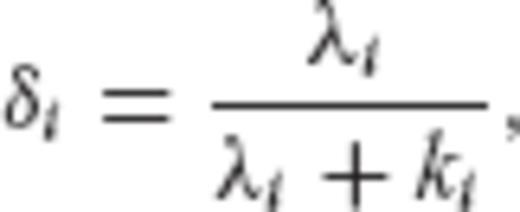
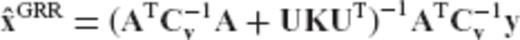
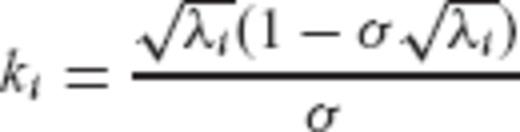
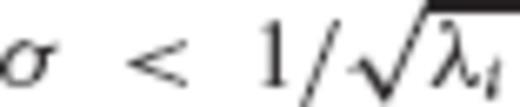 for every eigenvalue λi of the normal matrix N, then the GRR filter factors from eq. (42) become
for every eigenvalue λi of the normal matrix N, then the GRR filter factors from eq. (42) become 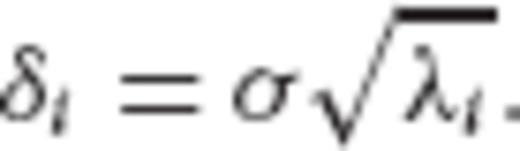
 , according to eqs (39) and (40), requires that the eigenvalues {di} of
, according to eqs (39) and (40), requires that the eigenvalues {di} of  should be chosen as
should be chosen as 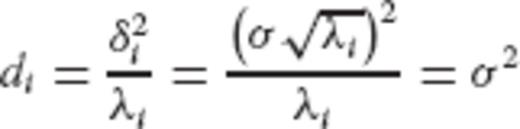
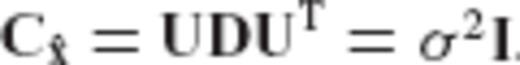 .
.In Table 1, the analytic forms of the filter factors {δi}, the corresponding eigenvalues {di} of the CV matrix  , and the maximum eigenvalue qmax of the auxiliary matrix Q, are provided for some known regularization methods (see also Bouman 1998). Note that all regularized estimators shown in Table 1 can be considered as special cases of the CV-adaptive estimator
, and the maximum eigenvalue qmax of the auxiliary matrix Q, are provided for some known regularization methods (see also Bouman 1998). Note that all regularized estimators shown in Table 1 can be considered as special cases of the CV-adaptive estimator  , for a particular a priori constraint on the CV matrix of the estimated parameters drawn from the general choice
, for a particular a priori constraint on the CV matrix of the estimated parameters drawn from the general choice  .
.

The analytic forms of the filter factors, the eigenvalues of the CV matrix for the estimated model parameters and the maximum eigenvalue of the auxiliary matrix Q, for some common regularization techniques in linear model inversion.
Remark 4: A more general regularization scheme can emerge from the use of the CV-adaptive estimator if the chosen eigenvectors of  are different from the eigenvectors of the normal matrix N = ATC−1vA. In this case, the optimal approximation of the unknown parameter vector is performed in a different orthogonal basis than the one used in traditional regularization schemes which rely on the eigenvalue filtering with respect to the eigenvector basis associated with the normal matrix N (see Section 3.1). In the context of the present paper, the use of such a different ‘regularization basis’ should be linked to the ability of the CV-adaptive estimator to impose an arbitrary structure on the error variances and covariances of the inversion results. As an example, we can mention the choice
are different from the eigenvectors of the normal matrix N = ATC−1vA. In this case, the optimal approximation of the unknown parameter vector is performed in a different orthogonal basis than the one used in traditional regularization schemes which rely on the eigenvalue filtering with respect to the eigenvector basis associated with the normal matrix N (see Section 3.1). In the context of the present paper, the use of such a different ‘regularization basis’ should be linked to the ability of the CV-adaptive estimator to impose an arbitrary structure on the error variances and covariances of the inversion results. As an example, we can mention the choice  with
with  , which gives a decorrelated solution with different error variances for the estimated parameters.
, which gives a decorrelated solution with different error variances for the estimated parameters.
4 Numerical Example
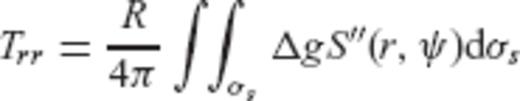
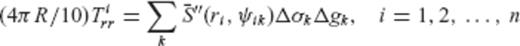
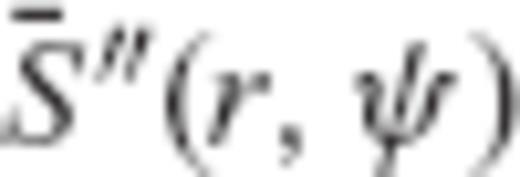 are given by
are given by 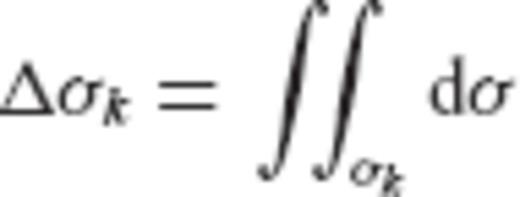
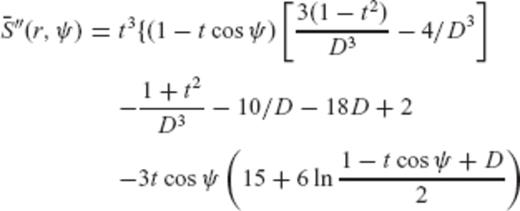
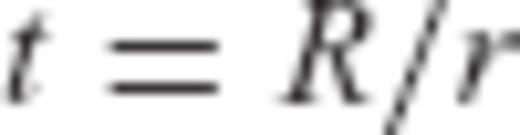
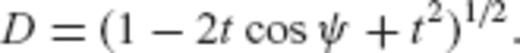
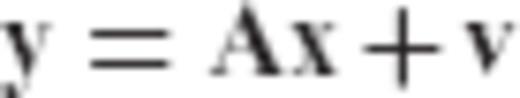 can be formed, where y is the data vector with elements
can be formed, where y is the data vector with elements 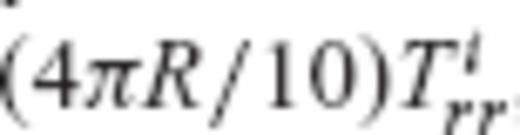 , A is the design matrix whose elements correspond to the products
, A is the design matrix whose elements correspond to the products 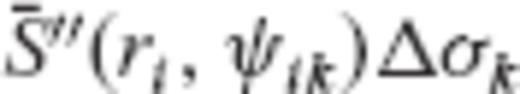 , x is the unknown vector of surface block-mean gravity anomalies Δgk, and v is the data noise vector.
, x is the unknown vector of surface block-mean gravity anomalies Δgk, and v is the data noise vector.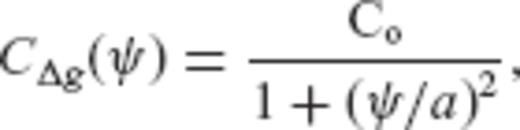
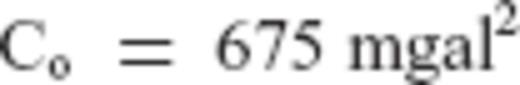 , and the parameter a has been selected such that the correlation length of the gravity anomaly field is
, and the parameter a has been selected such that the correlation length of the gravity anomaly field is  = 15.5 km. The number of satellite gradiometric observables Tirr is 400, taken on an 30′× 30′ grid that is located directly above the area of interest at a constant altitude of
= 15.5 km. The number of satellite gradiometric observables Tirr is 400, taken on an 30′× 30′ grid that is located directly above the area of interest at a constant altitude of  . The accuracy of Tirr is set to 0.01 E(1 E = 10 −9 s−2), which was also employed in similar simulations by Koop (1993), Xu & Rummel (1995) and Xu (1998). The random errors v for the determination of the synthetic observations from the simulated gravity anomalies are generated according to (4πR/10) N(Tirr), where N(Tirr) is a Gaussian random number generator with mean zero and variance 10−4E2.
. The accuracy of Tirr is set to 0.01 E(1 E = 10 −9 s−2), which was also employed in similar simulations by Koop (1993), Xu & Rummel (1995) and Xu (1998). The random errors v for the determination of the synthetic observations from the simulated gravity anomalies are generated according to (4πR/10) N(Tirr), where N(Tirr) is a Gaussian random number generator with mean zero and variance 10−4E2.We shall compare two different estimators for the downward continuation of the gradiometric data and the determination of the surface gravity anomaly grid. First, the inversion of the gradiometric measurements is performed using the standard LS methodology, without applying any special regularization tool. The condition number of the normal matrix is 1.93×106, and its eigenvalues range from 1.58×10−5 to 30.57. As expected, the accuracy of the LS inversion results is considerably poor, giving an average error standard deviation of ±50 mgal in the estimated gravity anomaly values. The detailed statistics of the LS estimation errors are shown in Table 3, where it is seen that extreme errors of more than ±120 mgal occur during the downward continuation of the gradiometric data. In Table 2, we see the statistics of the estimated Δg values which exhibit much stronger variability than the original true values, thus indicating the numerical instability of the downward continuation process through a simple LS inversion algorithm.
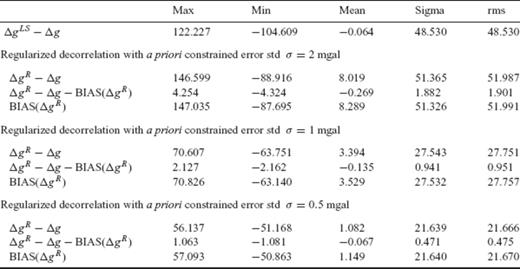
Statistics of the estimation errors in the block-mean gravity anomalies obtained from (i) standard LS inversion of the gradiometric data and (ii) regularized decorrelation for varying values of the a priori constrained error variance. The statistics of the estimation bias in the downward continuation results that are obtained from the regularized decorrelation inversion scheme are also shown. Note that the bias vector for the whole set of the block-mean gravity anomalies is determined as  , where x contains the true (simulated) values and R corresponds to the optimal regularization matrix for each a priori choice of σ2 (all values in mgal).
, where x contains the true (simulated) values and R corresponds to the optimal regularization matrix for each a priori choice of σ2 (all values in mgal).

Statistics of the true (simulated) block-mean gravity anomalies Δg, in comparison with the statistics of the estimated block-mean gravity anomalies obtained from: (i) standard LS inversion (ΔgLS) and (ii) regularized decorrelation  for varying values of the a priori constrained error variance (all values in mgal).
for varying values of the a priori constrained error variance (all values in mgal).
Alternatively, the inversion of the gradiometric data Tirr is performed using the CV-adaptive regularization scheme by constraining the CV matrix of the estimated gravity anomalies to a specific a priori model. In particular, we examine three different constraint choices all of which correspond to a diagonal matrix of the general form  . In this way, it is ensured that the parameter estimation errors during the downward continuation process become uncorrelated (i.e. ‘whitening’ of the estimated gravity anomalies) and they have a common user-dependent variance. The value of σ has been set equal to 2, 1 and 0.5 mgal, respectively. The results obtained from this CV-adaptive decorrelating inversion scheme are presented in Tables 2 and 3.
. In this way, it is ensured that the parameter estimation errors during the downward continuation process become uncorrelated (i.e. ‘whitening’ of the estimated gravity anomalies) and they have a common user-dependent variance. The value of σ has been set equal to 2, 1 and 0.5 mgal, respectively. The results obtained from this CV-adaptive decorrelating inversion scheme are presented in Tables 2 and 3.
From the error statistics shown in Table 3, we see that there is a clear improvement in the downward continuation results when using the CV-adaptive regularized estimator. By setting the error standard deviation in the estimated gravity anomalies σ = 1 mgal, for example, the rms error drops from 48.53 mgal (standard LS inversion) to 27.75 mgal. There is of course a remaining bias in the estimated gravity anomalies that amounts to about 3.4 mgal on average, which is nevertheless well below the statistical uncertainty of the results. It must be noted that, as the value of the a priori constrained error variance σ2 becomes smaller, the corresponding bias in the results of downward continuation decreases considerably (see Table 3). In this way, when we set σ = 0.5 mgal, then the rms estimation error is reduced to 21.67 mgal and the average bias drops to approximately 1 mgal. However, the trade-off in this case lies on the oversmoothing that takes place in the resulting grid of block-mean gravity anomalies, as seen in the values of Table 2.
5 Summary and Conclusions
A new approach for constructing optimal parameter estimators for the inversion of linear models has been presented in this paper. Our methodology is based on a linear transformation of the classic LS estimator and it adheres to two basic criteria. First, it provides a solution that is optimally fitted (in an average quadratic sense) to the classic LS parameter solution. Secondly, it complies with an external constraint that specifies a priori the error CV matrix for the estimated model parameters. The MSEE performance of the new estimator, as well as its optimality with respect to the maximum size of its inherent bias, have been explained and analysed. Furthermore, an expression for the admissible SNR range of the underlying linear model has been derived, within which the new estimator always outperforms (in the MSEE sense) the usual LS solution.
The paper does not claim the development of an autonomous regularization method that competes against other well-known inversion techniques, such as Tikhonov—Philips regularization, GRR or TSVD estimation. The aim of the paper was to present a certain theoretical formulation, based purely on statistical concepts and criteria, for the optimal inversion of linear models that leads to a general CV-adaptive biased estimator. It has been shown that the spectral representation of this parameter estimator offers a unified treatment for existing regularization methods in ill-posed inverse problems, particularly for those techniques that are based on the eigenvalue filtering of the inverse normal matrix. Our study provides an alternative viewpoint on the optimal statistical properties and the regularization mechanism of many inversion techniques commonly used in geodesy, by interpreting them as a family of ‘CV-adaptive’ parameter estimators that obey the same optimal criterion (i.e. optimal fitting with the LS solution in the mean squared sense) and differ only on the pre-selected form of their error CV matrix under a fixed model design.
Further studies and experimentation is obviously needed for the assessment of the practical potential associated with our proposed theoretical methodology in linear model inversion. The results obtained from a simulation experiment that was presented in this study certainly provide some encouragement for exploring new innovative strategies in ill-posed geodetic inverse problems (e.g. regularized decorrelation or optimal ‘whitening’ of the estimated model parameters).
Acknowledgments
The author would like to acknowledge the valuable suggestions and comments on the original manuscript by two anonymous reviewers, which led to an improved revised version of this paper.
References
Appendix A: Determination of the Optimal Regularization Matrix
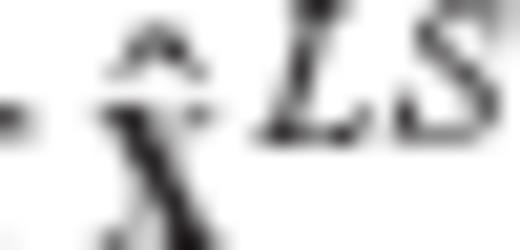 and its associated CV matrix
and its associated CV matrix 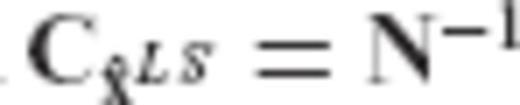 for an unknown parameter vector x in the linear model
for an unknown parameter vector x in the linear model 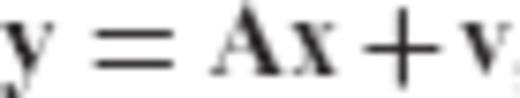 , we seek an optimal regularization matrix R such that the biased estimator
, we seek an optimal regularization matrix R such that the biased estimator 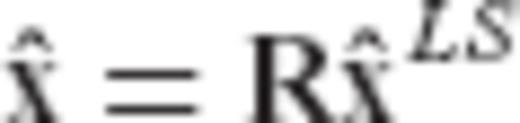
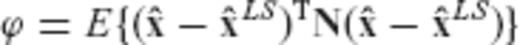
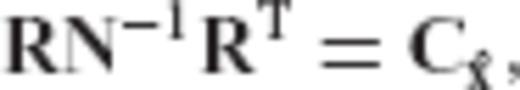
 is a given symmetric positive-definite matrix. To a large extent, the proof that follows adheres to a similar derivation given in Eldar & Oppenheim (2003).
is a given symmetric positive-definite matrix. To a large extent, the proof that follows adheres to a similar derivation given in Eldar & Oppenheim (2003). and
and  , as follows
, as follows 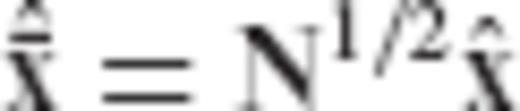
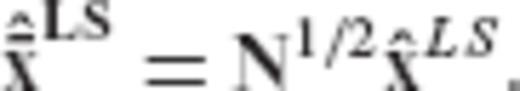
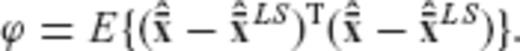
 and
and 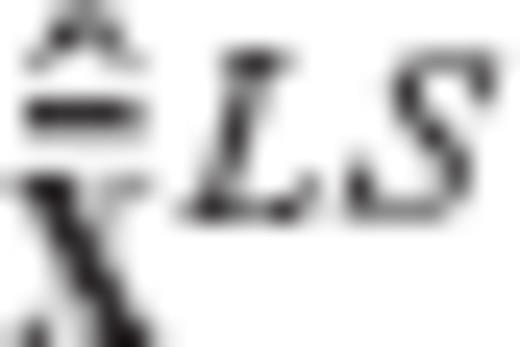 will be given by the equations
will be given by the equations 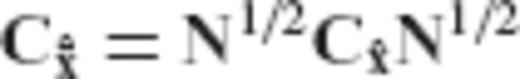
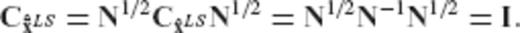
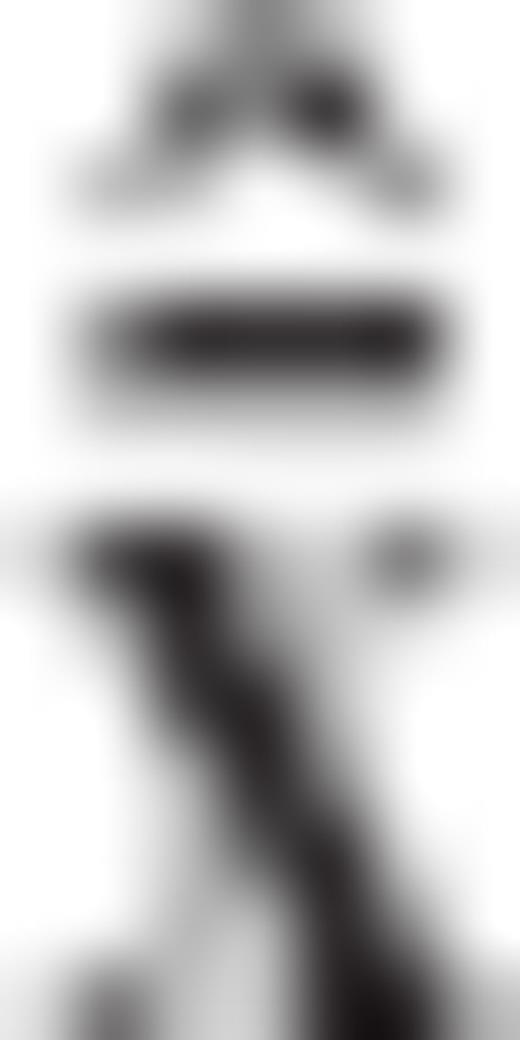 and
and 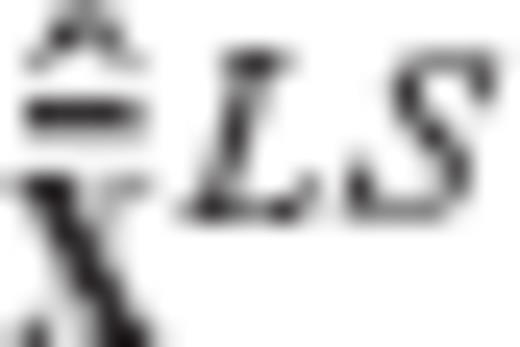 is expressed in terms of the linear equation
is expressed in terms of the linear equation 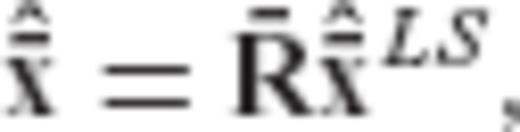
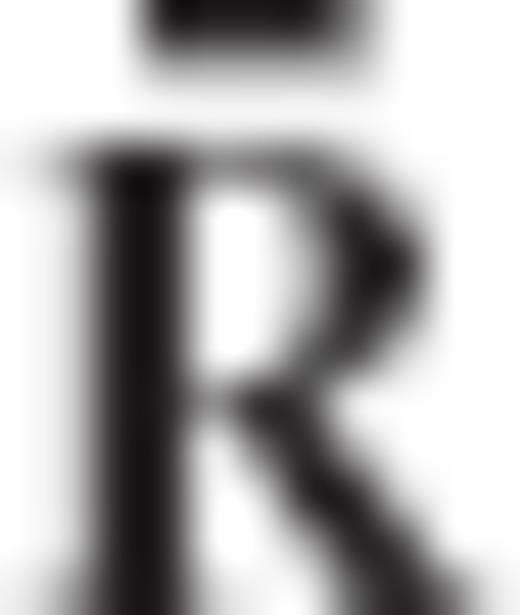 is related to the original regularization matrix R in terms of the transformation formula
is related to the original regularization matrix R in terms of the transformation formula 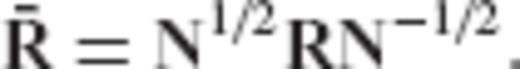
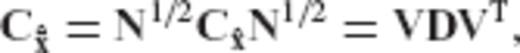
 , and D is a diagonal matrix that contains the eigenvalues of
, and D is a diagonal matrix that contains the eigenvalues of 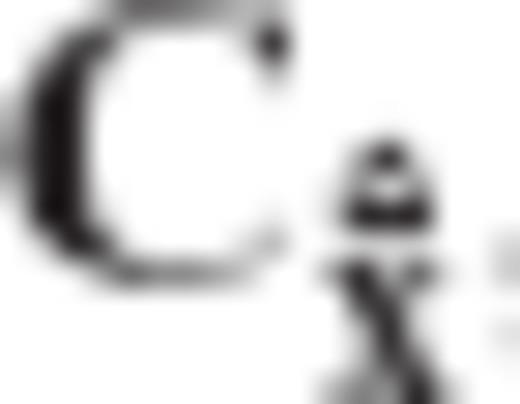 .
.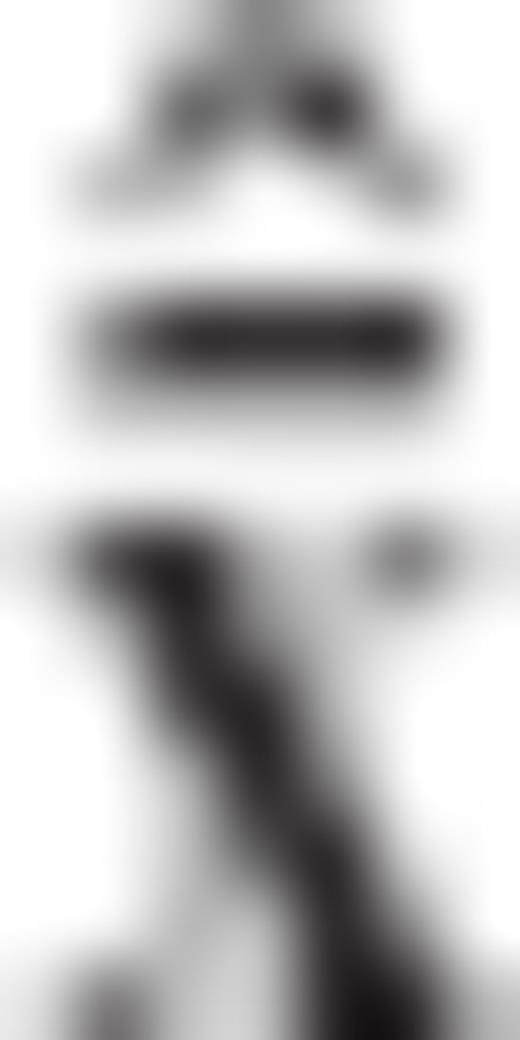 and
and 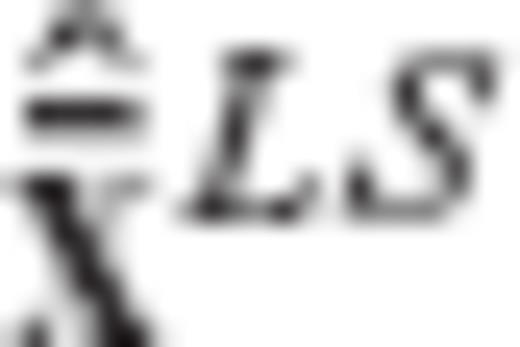 , as follows
, as follows 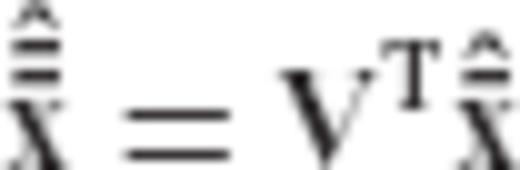
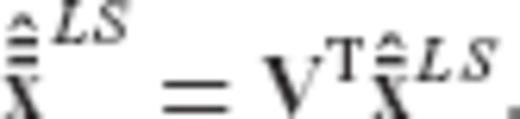
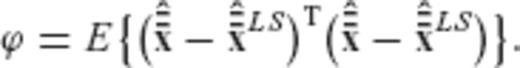
 and
and 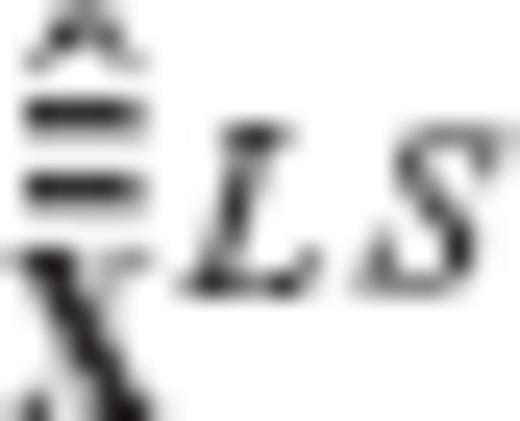 are now diagonal, since
are now diagonal, since 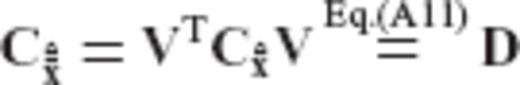
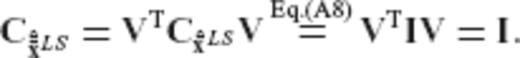
 and
and  is given by the linear formula
is given by the linear formula 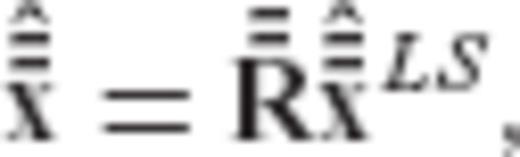
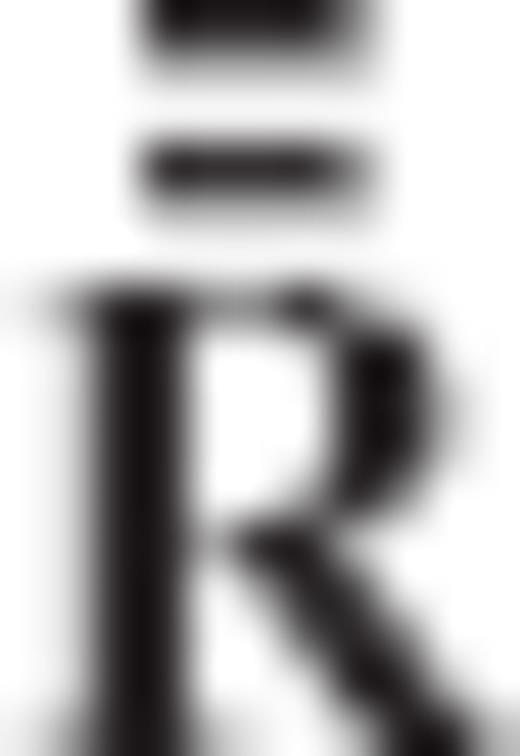 is related to the previous transformation matrix
is related to the previous transformation matrix 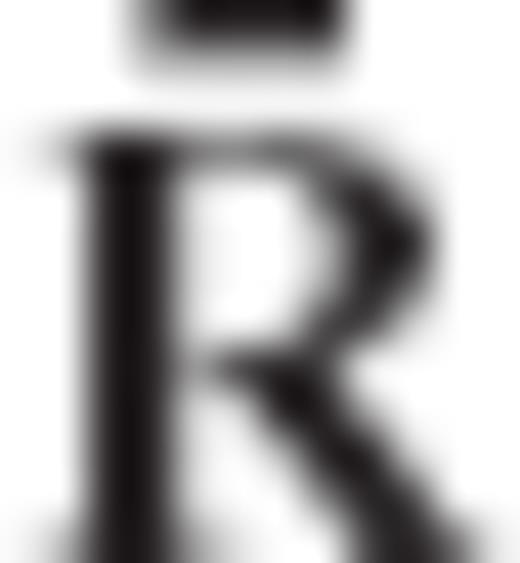 via the equation
via the equation 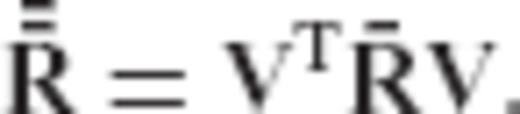
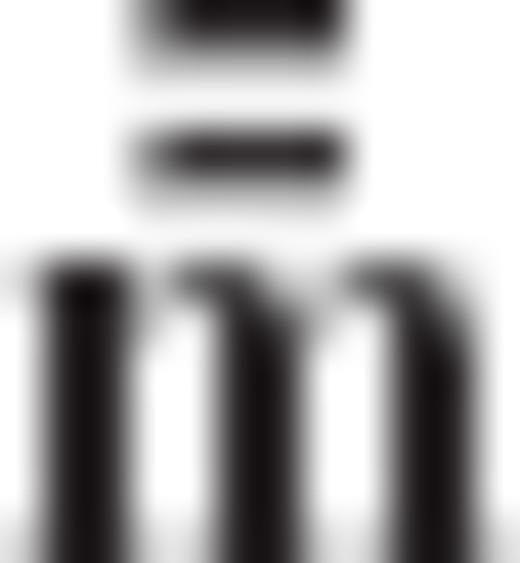 and
and 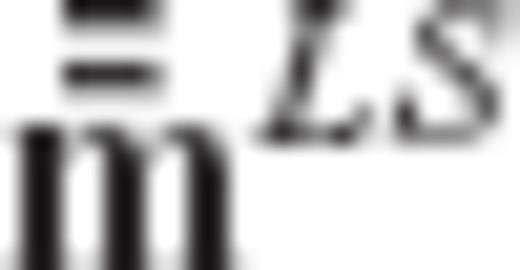 the expectation vectors of
the expectation vectors of  and
and 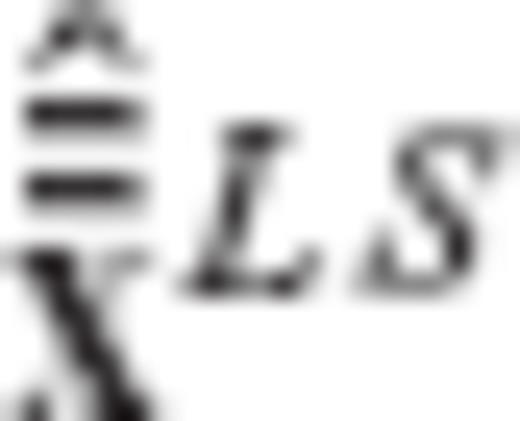 , respectively
, respectively 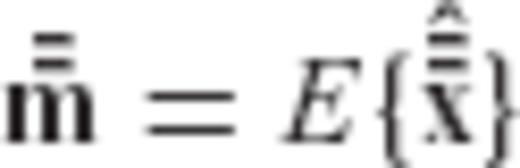
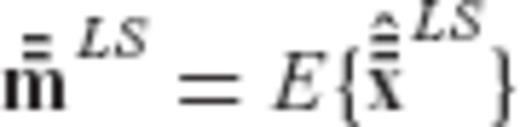
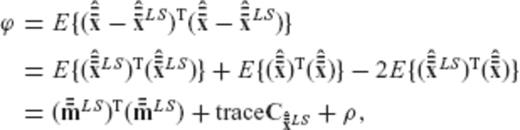
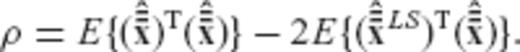
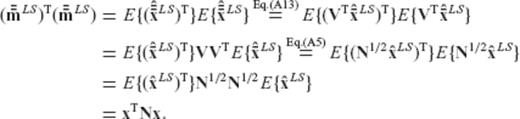
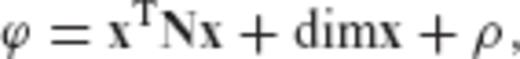
The first two terms in the above equation do not depend on the required regularization matrix R (or on any of its transformed versions  and
and  ), and thus the minimization of ϕ is equivalent to the minimization of the third term ρ which was defined in eq. (A22).
), and thus the minimization of ϕ is equivalent to the minimization of the third term ρ which was defined in eq. (A22).
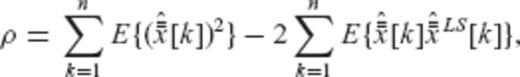
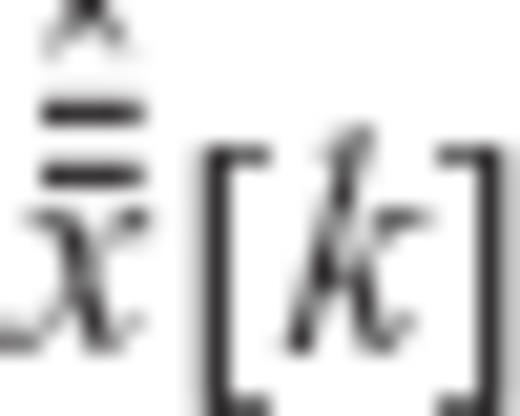 and
and 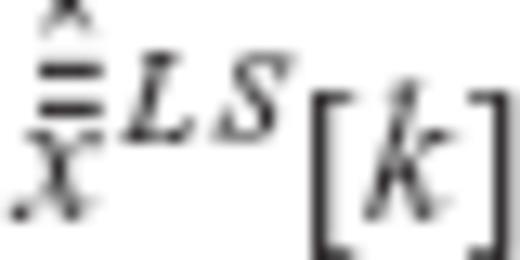 denote the kth elements of the vectors
denote the kth elements of the vectors  and
and  , respectively. Since the auxiliary vector
, respectively. Since the auxiliary vector 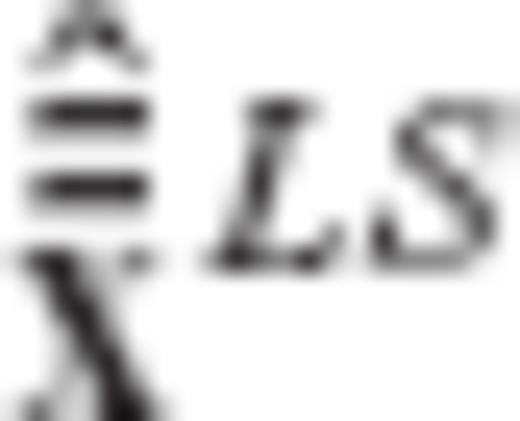 also does not depend on the regularization matrix R (or on any of its transformed versions
also does not depend on the regularization matrix R (or on any of its transformed versions 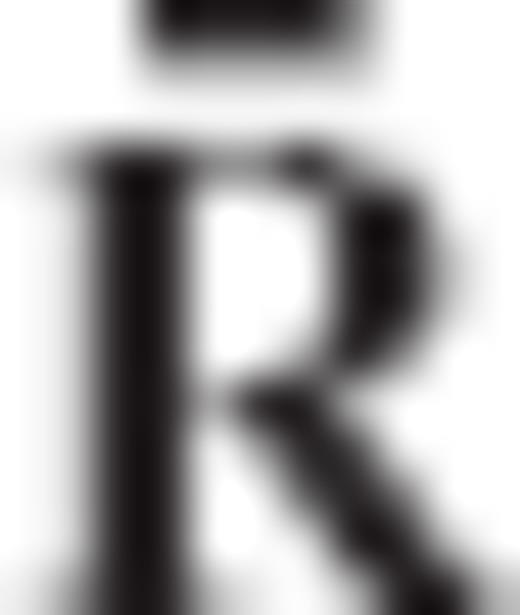 and
and 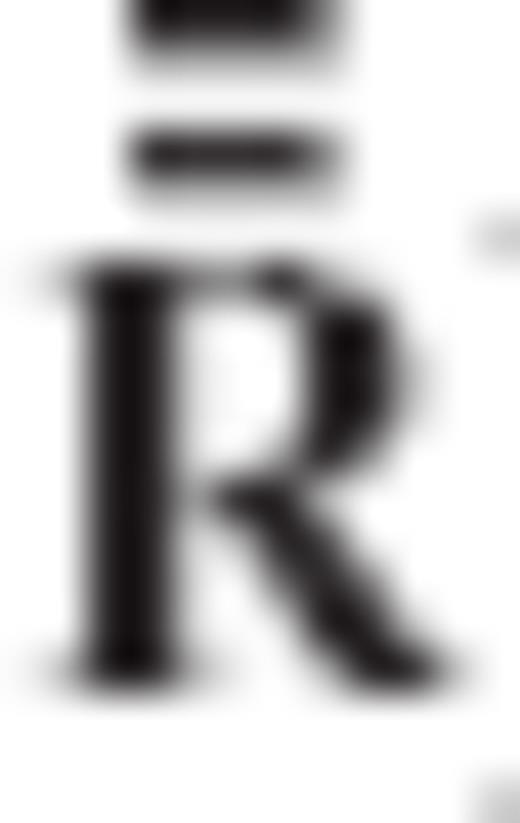 ), the minimization of ϕ is thus reduced in finding the elements
), the minimization of ϕ is thus reduced in finding the elements 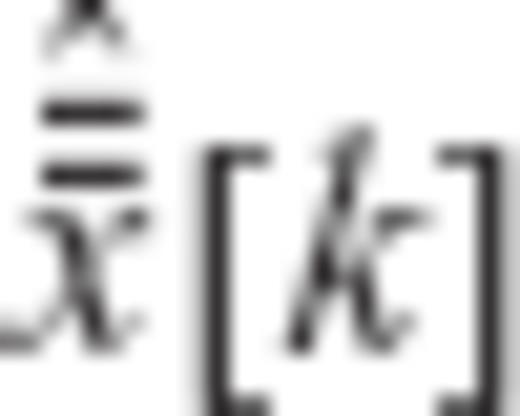 that minimize the value of ρ as given in eq. (A25).
that minimize the value of ρ as given in eq. (A25).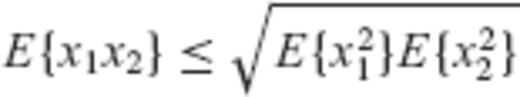
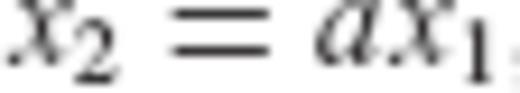 , where a is an arbitrary real scalar.
, where a is an arbitrary real scalar.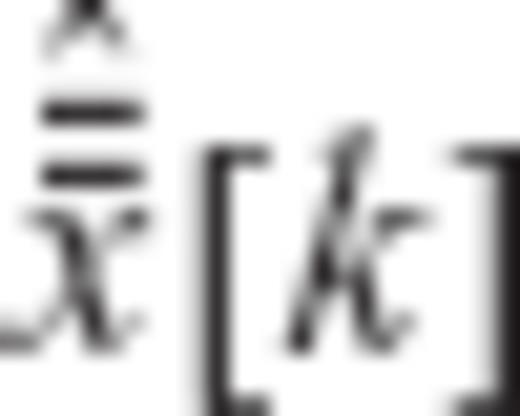 and
and 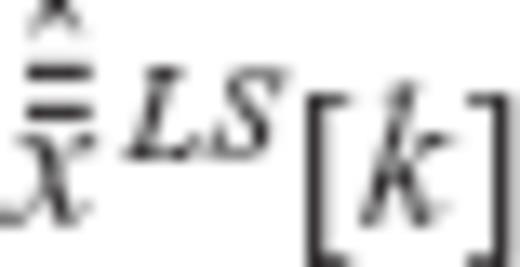 in place of the arbitrary random variables x1 and x2, the cosine inequality of eq. (A26) yields
in place of the arbitrary random variables x1 and x2, the cosine inequality of eq. (A26) yields 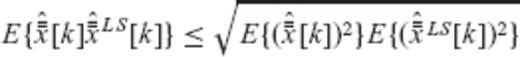

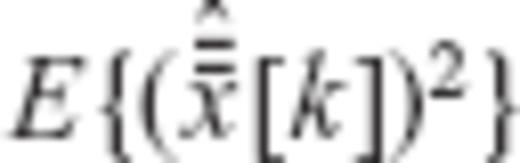 to both sides of the above inequality, we get
to both sides of the above inequality, we get 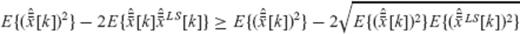
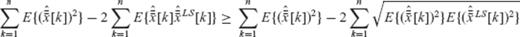
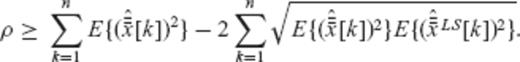
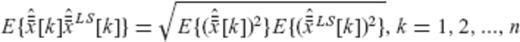
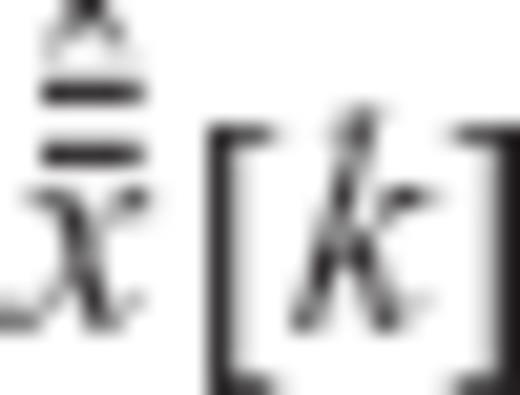 and
and 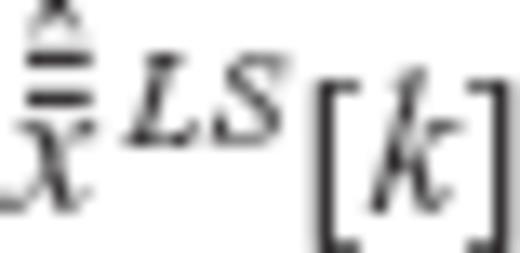 are linearly related
are linearly related 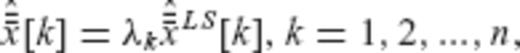
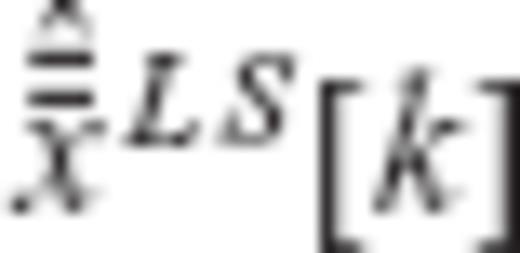 are uncorrelated with each other with variances equal to one
are uncorrelated with each other with variances equal to one 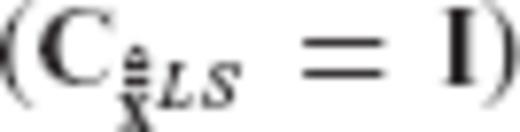 . The elements
. The elements 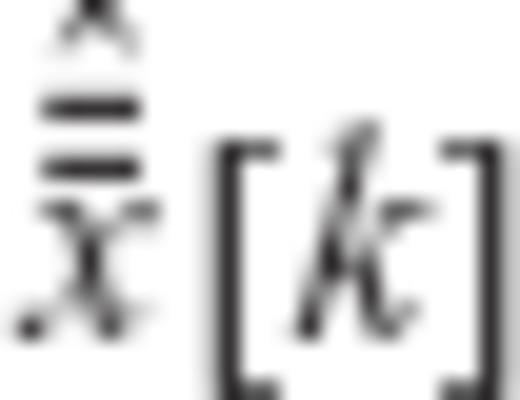 are also uncorrelated with each other, with variances specified by a given diagonal matrix
are also uncorrelated with each other, with variances specified by a given diagonal matrix 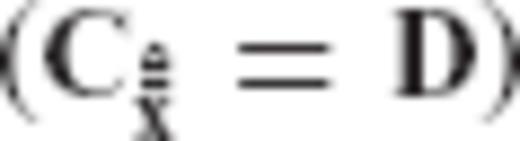 which depends on the a priori choice of the constrained CV matrix
which depends on the a priori choice of the constrained CV matrix 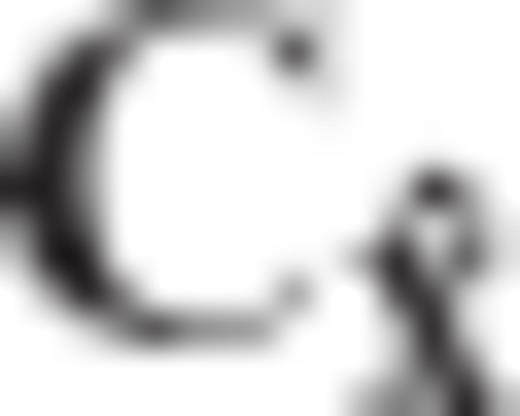 for the original estimated parameters; see eqs (A11), (A15) and (A16). In this way, the proportionality constants λk in (A32) can be uniquely specified. Using vector notation, we have that
for the original estimated parameters; see eqs (A11), (A15) and (A16). In this way, the proportionality constants λk in (A32) can be uniquely specified. Using vector notation, we have that  and
and 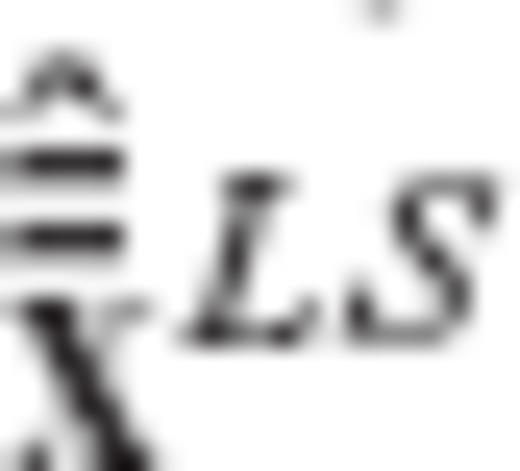 should be related through a diagonal matrix
should be related through a diagonal matrix 
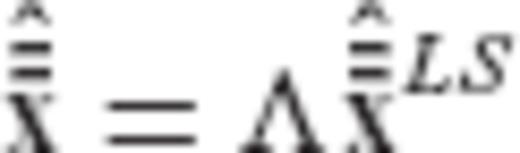
 .
. becomes
becomes 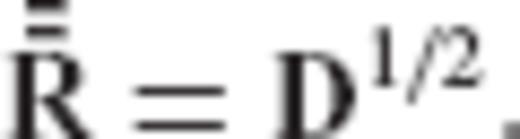
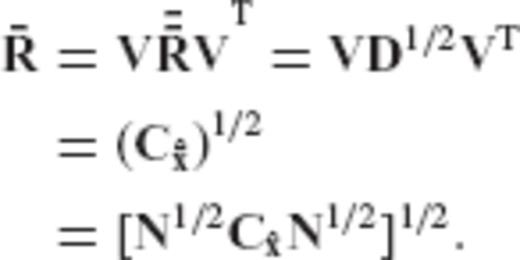

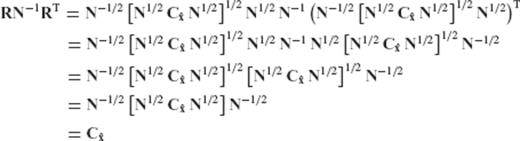
The auxiliary matrices D and Λ which have been used in the previous derivations are not related to the diagonal eigenvalue matrices D and Λ that were introduced in the main body of the paper. In particular, the symbol D in the main paper corresponds to a diagonal matrix containing the eigenvalues of the a priori constrained CV matrix of the estimated parameters  ; see (34). The same symbol, however, is also used in Appendix A to denote an auxiliary matrix that plays a supporting role in the presentation of the proof. Similarly, the symbol Λ in the main paper corresponds to a diagonal matrix containing the eigenvalues of the normal matrix N (see (12)), whereas in Appendix A the symbol Λ is employed to denote an auxiliary matrix that plays a supporting role in the presentation of the proof.
; see (34). The same symbol, however, is also used in Appendix A to denote an auxiliary matrix that plays a supporting role in the presentation of the proof. Similarly, the symbol Λ in the main paper corresponds to a diagonal matrix containing the eigenvalues of the normal matrix N (see (12)), whereas in Appendix A the symbol Λ is employed to denote an auxiliary matrix that plays a supporting role in the presentation of the proof.
Appendix B: An Alternative Formula for the Optimal Regularization Matrix
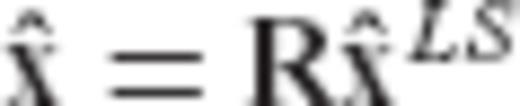 is given by the equation
is given by the equation 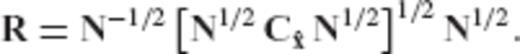
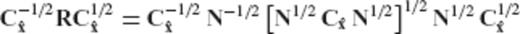
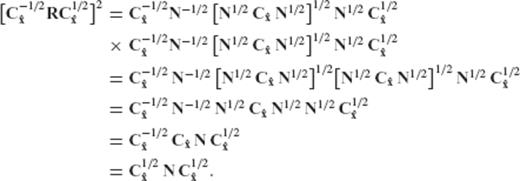
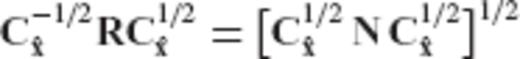
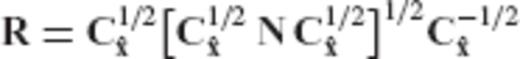




 —Regularization Aspects
—Regularization Aspects