Use of multifractal seismic waveform parameters to characterize the hydraulic properties of fractured media: numerical experiments Free

Summary

Introduction

Most surface and subsurface crustal rocks exhibit some degree of natural fracturing that varies in intensity and scale. Fractures are important in engineering, geotechnical and hydrogeological practice as they play an important role in the storage and migration of geological fluids, water, oil and gas through the Earth’s crust. The permeability and distribution of pore fluids in crystalline rocks are determined primarily by the density and distribution of fractures (Brace 1980). Special methods for increasing the extent of underground reservoirs with fracture systems have been developed to allow for effective transport of petroleum and gas. In the mining, geothermal and petroleum industry, the geometry of fractures is quite important as the vast majority of targeted natural resources are found in fractured rocks (Chernyshev & Dearman 1991). Fractures are also thought to play an important role in predicting earthquakes (Crampin 1984).

Research relating quantifiable seismic information to hydraulic properties of fractured rockmass is limited. Recently, several investigators have attempted to characterize and predict the hydraulic properties of fractured rockmass from geological information and geophysical measurements such as seismic velocity (Myer 1991; Pyrak-Nolte 1995; Boadu 1997a,b). Evidence of direct relationships between hydraulic and seismic waveform properties is presently lacking. However, Boadu (1997a) has recently obtained promising relationships between permeability and seismic attributes (i.e. instantaneous frequency, amplitude and bandwidth).

Seismic waves propagating through a single fracture or a set of fractures are scattered and diffracted at the fracture boundaries and these scattered waves may interfere constructively or destructively. The non-linear constructive and destructive interferences or interactions of scattered and diffracted wavefields result in irregular waveforms for which the amplitude distributions exhibit a chaotic behaviour and hence a fractal phenomenon (Feder 1988; Zosimov & Lyamshev 1995). Such amplitude distributions can be uniquely characterized using a particular parameter, the fractal dimension. If we can conceive that the very geometric properties of the fractures that affect the irregular characteristics of the seismic waveforms do indeed affect the hydraulic properties, then we should expect some relationships among parameters that quantify the waveforms and the hydraulic properties.

In this study, I investigate the possibility of estimating the hydraulic properties of fractured rockmass using information obtained from the fractal properties of seismic waveforms. The investigation is based on the analysis of reflected waveforms from fractured zones in geological media using multifractal measures. Seismic waveforms have been utilized in delineating saturated porous zones (Boadu 2000) and in studying wedge models (Robertson & Nagomi 1984). However, to the best of the knowledge of the author, the rich information inherent in these attributes has not been exploited in fracture characterization. Using the modified displacement discontinuity (MDD) model developed in Boadu & Long (1996) and Boadu (1997a,b), I designed numerical experiments to further explore the relationships between characteristic fractal properties of seismic waveforms after propagation through a fractured zone and representative parameters quantifying the hydraulic or transport properties of the zone.

The Modified Displacement Discontinuity and Seismic Wave Propagation in Fractured Media

In describing the MDD fracture model, we consider two half-spaces bounded by surfaces that may be partly in contact with one another in the x–y (horizontal) plane with a vertically incident wave in the y–z plane (vertical). Regarding the boundary between the two half-spaces as one of a non-welded contact, the boundary conditions for an incident elastic wave have been described by Boadu & Long (1996) as

1

where τ_p and τ_s are the respective normal and tangential stresses, ɛ_p and ɛ_s are normal and tangential strains, and r is the radius vector determining the plane of the fracture in (x, y, z) space. The basic premise of this model is that when a seismic wave propagates across a fracture, the associated stresses are continuous while the displacements are in general discontinuous. The magnitude of the ‘jump’ in the discontinuity of the displacement is determined by the fracture impedance Z_m (Z_p is the longitudinal impedance and Z_s is the transverse impedance).

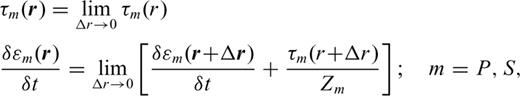
The fracture impedance is obtained by exploiting the well-established analogies between mechanical and electrical quantities (e.g. Anderson 1985). Relations between equations for acoustic wave motion and electric transmission lines allow us to treat the fracture as a transmission line for the passage of seismic waves. When there is no rigid contact between the surfaces (non-welded contact), the transmission of the seismic wave at the fracture takes place in the form of a blow with some inertia, which results in the delay of the transmission of the waves. The corresponding equations of motion have been developed and solved for the transmission and reflection coefficients for an incident P or S wave (Boadu & Long 1996) and will only be summarized here.

The expressions for the fracture impedances for a seismic wave propagating with frequency ω have been derived in detail by Boadu & Long (1996) and are given as

2

where E and μ are the Young’s modulus and shear modulus of the intact rock, respectively; f is the fractional area of the fracture surface in contact; l is the length of the open fracture; h is the region of influence (the ratio of the square of the fracture length to the wavelength of the incident wave); z_cp and z_cs are the characteristic impedances, γ_p and γ_s are the propagation constants. The subscripts p and s denote compressional and shear waves, respectively. For example, the characteristic impedance and the propagation constant for the case of an incident compressional wave on a fracture are given as

3

where η is the dynamic viscosity of the fluid filling the fracture and ρ is the density of the intact rock in which the fracture is embedded. The influence of the fracture on the propagation of the elastic wavefield can be assessed using a dimensionless quantity given by the ratio of the acoustic impedance of the intact medium W_p to the fracture impedance Z_p (Boadu & Long 1996). This ratio, termed the inhomogeneity factor, ξ_p, is a function of the fracture length, the aperture, the viscosity of the infilling fluid, the fractional area of opposing fracture surfaces (f) and the frequency of the propagating waves, and is given by

4

For a compressional wave of unit amplitude incident at an angle θ to the plane of the fracture, the complex frequency-dependent reflection and transmission coefficients are given as

5

where A_PP, A_PS, ϕ_PP and ϕ_PS are all functions of the angle of incidence and the Poisson ratio of the intact material, where R_PS represents incident P and reflected S. For example, the function A_pp is expressed as

6

with d being given by the expression

7

where σ is Poisson’s ratio, V_P and V_S are, respectively, the compressional and shear wave velocity of the intact rock.

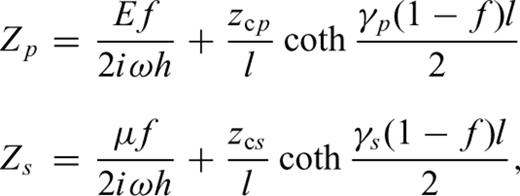
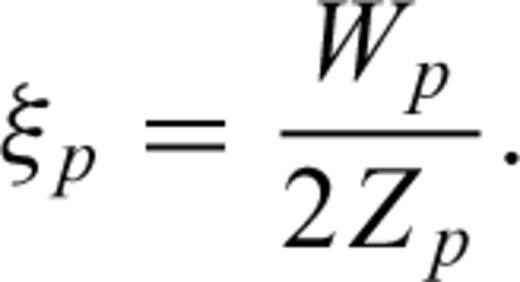
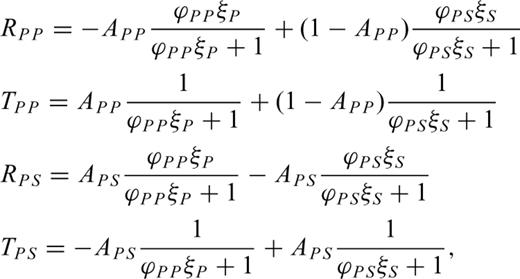
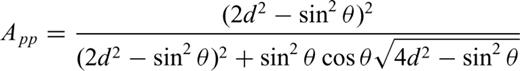
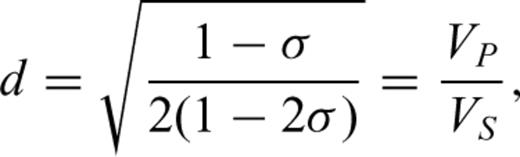
The method described in Boadu (1997a,b) is used to obtain synthetic seismograms for a series of geological layers where one of the layers is fractured (fractured zone). The fractures in this zone are assumed to be horizontal and planar or subplanar fractures (see Fig. 1) and can exhibit varying distributions of length, spacing and aperture. For a propagating wave, we postulate two types of reflections: (1) reflections from the interface of two unfractured geological layers and (2) reflections from the fractures themselves. A recursive scheme is used to compute global reflection and transmission coefficients for these two types of interfaces and synthetic seismograms are then computed using the reflectivity method.

Figure 1

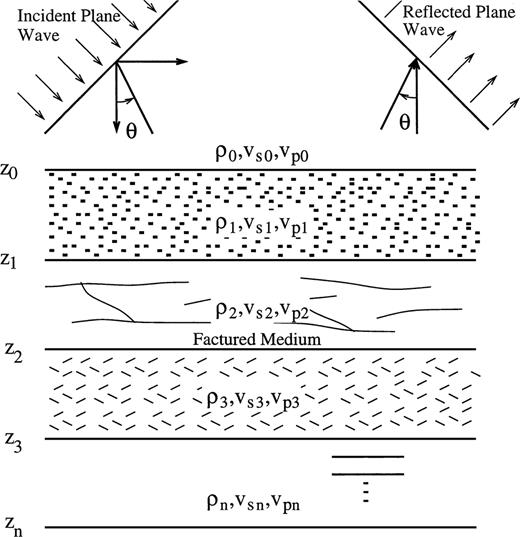
A simple model describing a series of geological layers where one of the layers is fractured (fractured zone).

Open in new tabDownload slide

The spectral responses of the horizontal and vertical displacements at the surface (z= 0) have been derived (see Boadu 1997a; Fuchs & Müller 1971, for a full derivation) and is given below. The vertical displacement for an angle of incidence θ is given by Fuchs & Müller (1971) as

8

and the horizontal displacement is given as

9

The functions t(θ), g(θ) and s(θ) are

(9a)

(9b)

(9c)

(9d)

(9e)

(9f)

(9g)

(9h)

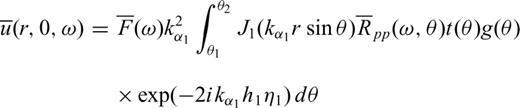
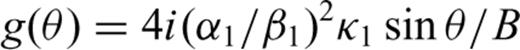
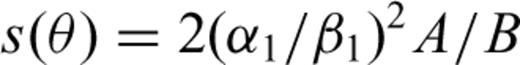
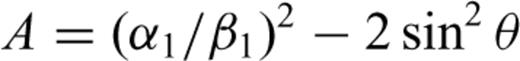
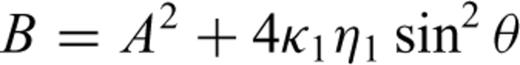
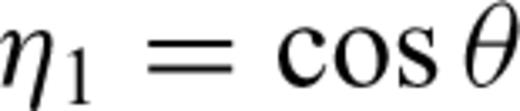
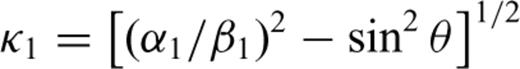
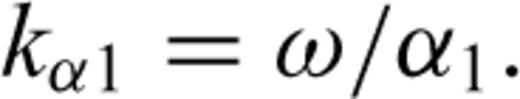
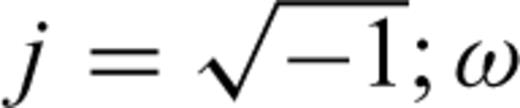F(ω) is the Fourier transform of the source excitation function f(t); J₀ and J₁ are Bessel functions of the first kind and of order zero and one, respectively; v_i and v′_i are the vertical wavenumbers for P and S waves in layer i; k is the horizontal wavenumber; is the angular frequency; h_i is the thickness of layer i, Γ_pp and Γ_ps are the P–P and P–S reflection coefficients of the free surface, and R_pp is the complex global reflectivity function for the stack of layers.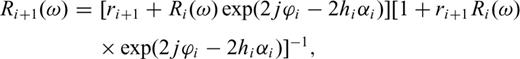

For a series of reflections (from both geological contacts and individual fractures), the generalized frequency-dependent complex reflectivity function is computed using a recursive algorithm as given by Boadu (1997a),

10

where φ_i=ωh_icos θ/v_i is the phase change across the intact rock section with P-wave velocity v_i and attenuation coefficient α_i that lies above the ith reflector with reflection coefficient r_i. In the model described, stresses and displacements associated with a propagating waveform will be continuous across the contact between two geological layers. However, when the waveform encounters a fracture, the stresses will be continuous while the displacements will be discontinuous. When a seismic wave strikes either of these boundaries, there will be reflected and transmitted P and S waves in general. The reflected waves that arrive at the surface are the superposition of all the reflections from the two types of boundaries. The local reflection coefficients for the welded geological interfaces were computed using the computational procedure described by Kind (1976), taking into account wave-type conversions (P to S). For local reflections from the fractures, the expressions in eq. (5) for the reflection coefficients were used. A combination of the local reflection responses from the welded interfaces and those from the fractures is used in a recursive algorithm (eq. 10) to give the frequency-dependent global reflectivity function (frequency response) for the whole half-space (geological section). Synthetic seismograms are obtained from inverse Fourier transformations of eqs (8) and (9).

Numerical results

I provide illustrative examples of numerical experiments which involve a stack of geological layers over a half-space, one of the layers being embedded with horizontal fractures. Such a geological setting is typical of environments for exploration of oil and geothermal energy (van Golf-Racht 1982; Chernyshev & Dearman 1991). The seismic parameters characterizing the individual layers are shown in Table 1.

1

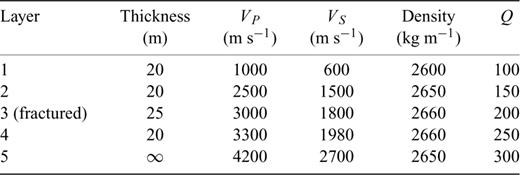
Layer parameters for the model used in the experiment. An illustration of the parameters of the intact rock of each layers used in the computation of the synthetic seismograms. The permeability of the intact rock units in the fractured layer (layer 3) is assumed to be 10⁻¹² m s⁻¹.

Open in new tabDownload slide

Ten discrete planar fractures are embedded in the fractured layer or zone. A seismic source (Ricker wavelet) located at the surface with a peak frequency of 400 Hz and a maximum frequency of 1200 Hz is used in the reflection experiment. Fig. 2 is a generated synthetic seismogram for a vertically incident wave using the procedure described earlier in the text. Normally incident waves are analysed here to illustrate the effect of the fractures on the seismic waveform although the computational methodology is generalized for all incidence angles. As expected based on the model in Table 1, we observe a clean reflected signal at a time of 0.04 s followed by a dispersed waveform. This waveform represents constructive and destructive interference of wave reflections from the fractured zone (windowed and shown in the inset). The dispersive characteristics of the windowed wave train contain useful information concerning the fractured zone and this information will be extracted using a multifractal analysis.

Figure 2

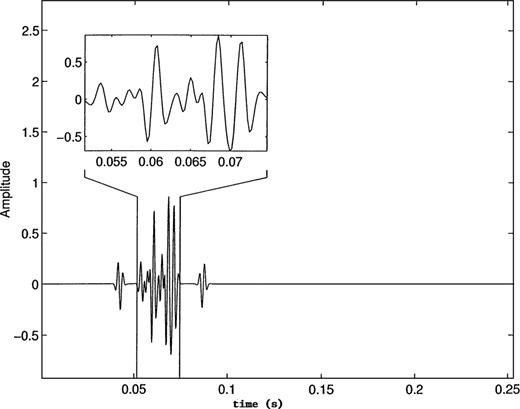
Synthetic seismogram (vertical incidence) for a stack of geological layers with one of the layers containing fractures. The time zone known to contain composite reflections from fractures is shown and is windowed for multifractal analysis.

Open in new tabDownload slide

Fractal Analysis of Waveforms from Fractured Media

Fractals are mathematical constructs that can have a high degree of geometrical complexity and repeat at different scales (Feder 1988). A very important characteristic of fractals useful for their description and classification is their fractal dimension, D, which measures the degree of their irregularity over multiple scales. As the waves propagate through the fractured medium, the distribution of the scattered wave energy associated with the fractures becomes irregular and non-uniform and can be subjected to fractal analysis. Given the complex nature of the seismic waveforms from the fractured media, it is insufficient to characterize the dynamic behaviour of waveforms by a single value of their fractal dimension. Multifractal analysis is the recourse, as it will allow us to characterize the distributional properties of the amplitudes of the waveforms in greater detail.

In this study, the sample values of the waveforms, herein termed amplitudes, are considered as variables and their distributions in time are subjected to multifractal analysis to determine the multifractal attributes. The multifractal attributes provide detailed information concerning the concentration of waveform amplitudes in a given time window and the statistical properties of such measures are characterized by a continuous spectrum of fractal dimensions.

The scheme developed by Boadu & Long (1994b) for multifractal analysis of fracture spacings is modified and used in this study for the multifractal analysis of seismic waveforms and is described below. Consider a signal S(t) containing N sample points or amplitude values. First, the signal is transformed to emphasize significant time variations in the amplitude values and to eliminate background noise. The transformation of the original signal S(t) to S_ω(t) is as follows:

11

where ω > 0 and ρ is the lag. The transformed signal, S_ω(t), is positive, a necessary requirement for multifractal analysis. The parameter ω controls the degree of variability of S_ω(t): decreasing ω causes S_ω(t) to become smoother. The amplitudes of the transformed waveforms are then normalized to the range (0, N). A cell (time window) containing N_k sample points of size δ is considered where the δ-axis is in the units of the sampled data. The probability of finding a sample value δ in a cell number k (k= 1, …, M(δ)) is defined as p_k. The multifractal properties of the signal are then described in terms of the generalized dimension function D(q):

12

where the moment order q is any number in the range −∞ to +∞ and the function D(q) is a spectrum of fractal dimensions characterizing the signal. The generalized dimensions D(q) serve to introduce higher-order fractal dimensions to make up for lack of information that cannot be described by the fractal dimension alone. Values of D(q) for q= 0, 1, 2, … are of physical interest (Boadu & Long 1994b) and will be examined for each waveform from a fractured medium. I investigate the diagnostic and distinguishing characteristics of D(q) values and their potential relationship to the fracture parameters and hence the hydraulic properties of the fractured medium. Details of the computational procedure for D(q) using least-squares regression analysis have been tested successfully for known fractal functions by Boadu & Long (1994b) and will not be repeated here.

For q→ 0 we obtain from eq. (12),

13

The above expression is exactly the definition of the Hausdorff–Besicovitch dimension (also termed box-counting or similarity dimension) of a fractal measure (Grassberger & Procaccia 1983).

As q→ 1 the application of L’Hospital’s rule to eq. (12) yields

14

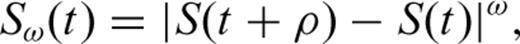
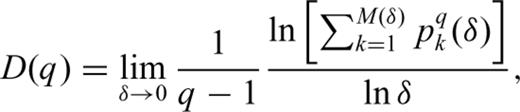
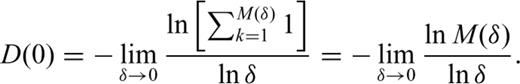
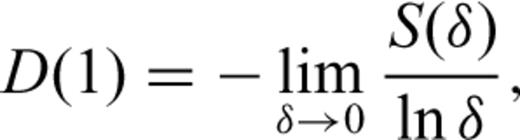
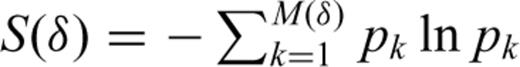where . S(δ) is a familiar expression from information theory that describes the amount of information associated with the distribution of p_k values and thus D(1) is known as the information dimension (Grassberger & Procaccia 1983). The information dimension D(1) quantifies the gain in information as δ→ 0.

In the case where q→ 2eq. (7) yields

15

where D(2) is termed the correlation dimension and D(2) ≤D. Also, eq. (10) reduces to the correlation integral introduced by Grassberger & Procaccia (1983), which measures the probability that two sample values lie within a cell of size or length δ. The correlation dimension thus estimates the probability that two points in the sample space are separated by a distance smaller than δ, a measure that is important in assessing the amplitude distribution of the waveforms from the fractured medium. In general, since the summation term in eq. (7) is, for q > 1, the total probability that q points of the waveform in the sample space are within one cell, the spectrum of D(q) is a measure of the correlation between different sample points in the fractal waveform. It is thus useful in characterizing the heterogeneous distribution of amplitudes in the waveforms.

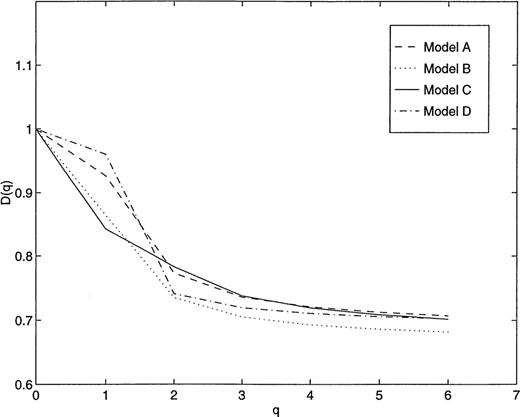
Fig. 3 illustrates the behaviour of D(q) versus q. The values of D(q) are computed from generated waveforms from the fractured zone. An example of such a waveform is shown as an inset in Fig. 2. The fractures in the fractured zone possess exponential distributions of fracture parameters (length, spacing and aperture) with different mean values as shown in Table 2. It is seen that different combinations of fracture parameters, that is, length, spacing and aperture, give a different behaviour of D(q). When the relationship D(0) ≥D(1) ≥D(2) ≥⋯≥D(∞) holds, the distribution of amplitudes is heterogeneous and bears multifractal characteristics. The equality D(0) =D(1) =D(2) =⋯=D(∞) holds for homogeneous distributions that exhibit monofractal behaviour. An interesting and important dimension is D(∞), which sets a lower limit on the fractal dimension. It gives information concerning the extent to which the sample values are clustered in the waveform. The value of D(q) for some theoretically defined fractal systems, for example the Cantor set, has been established analytically (Feder 1988). However, in practice one can compute several values of D(q) and establish D(∞) as the asymptotic value of D(q).

4

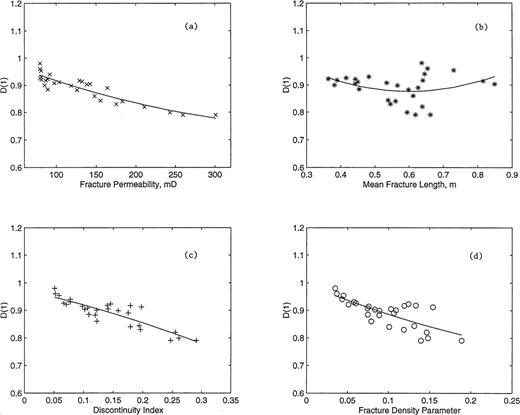
Cross-plots and corresponding least-squares fits of information dimension D(1) versus (a) fracture permeability, (b) mean fracture length, (c) discontinuity index and (d) fracture density parameter. Parameters are extracted from windowed waveforms such as in Fig. 2 for various simulations.

Open in new tabDownload slide

3

A schematic illustration of the spectrum of D(q) versus q for different fracture parameters (models) listed in Table 2. For example, Model C in Table 2 is a fractured medium consisting of planar fractures with exponential distributions of fracture length, aperture and spacing with mean values of 0.68 m, 50 μm and 0.36 m, respectively.

Open in new tabDownload slide

2

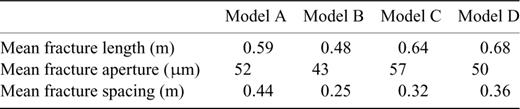
Mean values of the distribution of fracture parameters used for experimental illustration of the behaviour of D(q) versus q.

Open in new tabDownload slide

Representations of Generalized Dimensions

The generalized dimensions characterizing the multifractal properties of the waveforms are conveniently simplified using quantifiable parameters. This is achieved by specifying four parameters obtained from the function D(q): the information dimension D(1) or homogeneity index, the correlation dimension D(2), the curvature index, α, and the range index γ. The curvature and range indices are defined as

16

The α parameter is a contrast index and measures multifractality. A low value of α signifies persistently small or large signal values, while a high value is an indication of a broad range of values around a mean value. In effect, α controls the width of the distribution around α=D(1). The range index parameter, γ, is a measure of the clustering of signal amplitudes. A value of γ= 1 implies a homogeneous distribution (weak clustering) and a value γ≫ 1 is associated with intense clustering. The value of D(5) is taken to be approximately equal to D(∞).

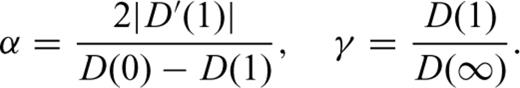
Fracture Parameters and Hydraulic Properties of Fractured Rockmass

The hydraulic properties of a fractured rockmass can be described by its permeability and quantifiable fracture parameters, such as the fracture density parameter, C and the discontinuity index, I_d. Another useful parameter is the linear fracture density, Γ (the number of fractures per unit length), usually measured normal to the average strike of the fractures along a scanline under field conditions.

The fracture density parameter has a strong correlation with the transmissivities of fractured geothermal reservoirs and Watanabe & Takahashi (1995) suggest using it in the prediction of hydraulic properties of fractured reservoirs. The fracture density parameter, C, is defined as

17

where θ_i is the orientation of the ith set of fractures relative to the flow direction, 〈·〉 represents an average and r_min is the smallest fracture length.

The discontinuity index, I_d, is used as an indicator of whether or not a fractured rockmass is permeable (Wei 1995). This index is defined based on the permeability threshold of a jointed rockmass for a representative volume using percolation theory. For an average or mean fracture length L in a given distribution, the discontinuity index is defined as

18

The average fracture spacing is by definition the inverse of the linear fracture density. Thus, fractured rockmasses with shorter and higher fracture density will have lower permeability than those with longer fractures and lower density. A fractured rockmass will tend to be more permeable if I_d≥ 1, and hence the permeability increases with an increase in I_d.

As a generalization of a fractured medium, consider a matrix block with fractures of varying lengths, orientations and thicknesses. When a fracture is parallel to the flow direction, the flow rate through the fracture is given by

19

where b is the mean fracture aperture, W is the width of the fracture, ΔP is the pressure difference across the block and μ is the viscosity of the fluid. The intrinsic fracture permeability, k_f, based on Darcy’s law is given as b²/12. For an inclined fracture at an angle α_n with respect to the hydraulic gradient direction, with finite length L_f, width W_f and thickness b_n, its contribution to the discharge across a section containing a suite of fractures is given by Chernyshev & Dearman (1991) as

20

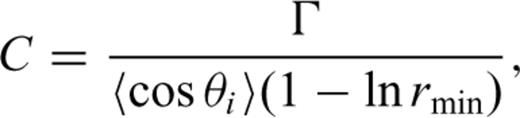
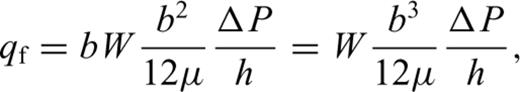
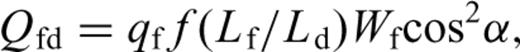
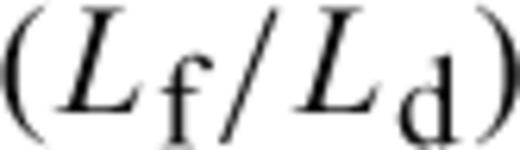where c_f is the hydraulic discharge through a continuous fracture per unit width and under unit hydraulic gradient. The function f(L_f/L_d), is taken as L_f/L_d or as e (Boadu 1997a), where L_d is related to the thickness of the block or section, h, by L_d=h/cos α. The sum of contributions to the discharge from R fractures divided by the section area gives the effective fracture permeability, K_a (Chernyshev & Dearman 1991),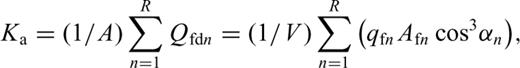

21

where V is the volume of the section and A_fn is the area of the nth fracture. Experimental and field measurements have reasonably substantiated eqs (15) and (16) for known fracture systems (Hossain 1992). The total permeability of the fracture-intact rock system, K_t, may be represented as the sum of the intact rock permeability K_m and the effective fracture permeability K_a.

The hydro-properties of the fractured rock described above, I_d, C and K_a, can be used to characterize its hydraulic conditions. These representative properties will be related to the representations of the generalized dimensions quantifying the seismic waveforms.

Seismic Fractal Attributes and Fracture Hydro-Properties: Numerical Experiments

An important objective of this paper is to investigate, through numerical experiments, the possibility of the existence of relations between seismic waveform parameters and hydro-properties of a fractured rockmass. An exponential distribution of fracture lengths with mean values ranging between 0.2 and 1.0 m were used in the numerical experiments. The minimum and maximum fracture lengths for all simulations were 0.05 and 2 m, respectively. The distribution of the fracture spacings follows the Weibull distribution as described by Boadu & Long (1994a) with the mean varying between 0.1 and 2 m. Fracture apertures are of exponential distribution with a chosen average value of 4 μm. This value is reasonably representative of aperture values found in some sedimentary and igneous rocks (Chernyshev & Dearman 1991; van Golf-Racht 1982).

Figs 4(a)–(d) show cross-plots and least-squares (LS) polynomial fits of information dimension D(1) versus fracture permeability, mean fracture length, discontinuity index and fracture density parameter, respectively. The information dimension is obtained from the multifractal analysis of the wave train from the fractured layer (see Figs 1 and 2) for each numerical experiment where the distribution of the fracture parameters is known. We see a correlation between the information dimension and the fracture permeability, that is, D(1) is sensitive to fracture permeability and decreases with an increase in fracture permeability. The coefficient of determination for the LS fit, R², is 0.89, indicating a reasonable relationship between D(1) and permeability. Both the discontinuity index and the fracture density parameter correlate reasonably with D(1), with R² being 0.78 and 0.63, respectively. The mean fracture length as a fracture parameter, bears a very weak correlation with D(1).

Cross-plots and corresponding LS fits of correlation dimension, D(2), with fracture permeability, mean fracture length, discontinuity index and fracture density parameter are shown in Figs 5(a)–(d), respectively. The correlation dimension increases with an increase in fracture permeability, discontinuity index and fracture density parameter with respective R² values of 0.86, 0.77 and 0.60. Fractures with relatively greater length, greater apertures and closer spacing will produce distinct signal values that would probably interfere constructively and be correlated. The nature of these fractures is such that they would also produce a higher permeability and discontinuity index. Hence the correlation dimension will increase with an increase in fracture permeability and discontinuity index.

Figure 5

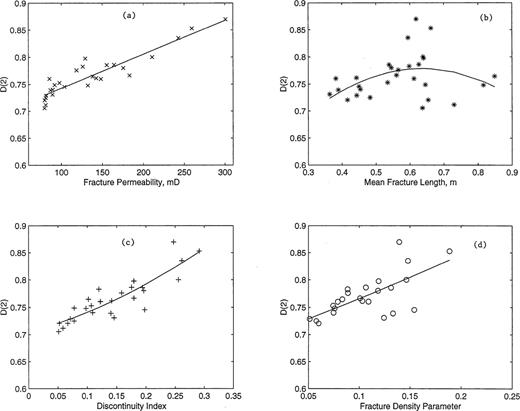
Cross-plots and corresponding least-squares fits of correlation dimension D(2) versus (a) fracture permeability, (b) mean fracture length, (c) discontinuity index and (d) fracture density parameter.

Open in new tabDownload slide

Figs 6(a)–(d) show cross-plots and corresponding LS fits of the curvature index with fracture permeability, mean fracture length, discontinuity index and fracture density parameter, respectively. There are discernible relationships between the curvature index and the fracture permeability, discontinuity index and fracture density parameter with respective R² values of 0.85, 0.79 and 0.55. However, there is a weak correlation of the index with the mean fracture length with a low R² value of 0.17.

Figure 6

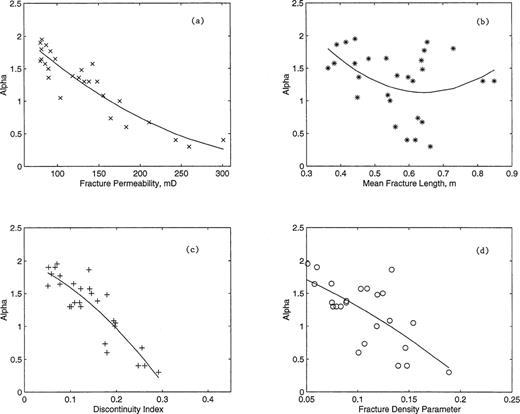
Cross-plots and corresponding least-squares fits of curvature index (α) versus (a) fracture permeability, (b) mean fracture length, (c) discontinuity index and (d) fracture density parameter.

Open in new tabDownload slide

The range index (γ), and its relationship with fracture permeability, mean fracture length, discontinuity index and fracture density parameter are shown in Figs 7(a)–(d), respectively. Again, the fracture permeability, discontinuity index and fracture density parameter show reasonable correlations with γ, with R² values of 0.9, 0.81 and 0.58, respectively. As the permeability and discontinuity index increase, the γ index values decrease. The mean fracture length, however, shows quite a weak correlation with γ(R²= 0.2). Regularity in amplitude distribution (γ→ 1) implies persistence in fracture aperture, spacing and length distributions and hence an increase in the transmissive potential of the fractured rockmass.

Figure 7

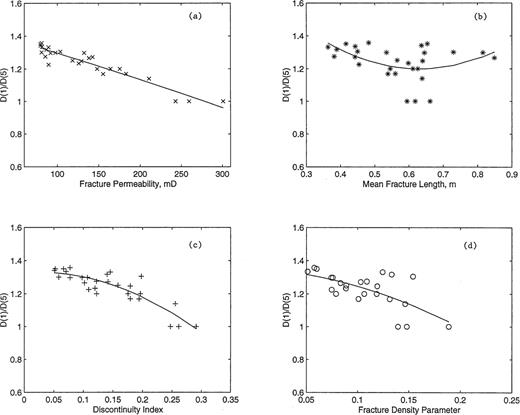
Cross-plots and corresponding least-squares fits of range index (γ) versus (a) fracture permeability, (b) mean fracture length, (c) discontinuity index and (d) fracture density parameter.

Open in new tabDownload slide

Summary and Conclusions

The identification, location and characterization of fractured media is important in engineering, geotechnical, hydrogeological and geoscience applications. In this paper, multifractal analyses of seismic waveforms obtained by numerical reflection experiments in fractured media have been performed to extract quantifiable representative waveform parameters. Based on numerical experiments and analyses, reasonable correlations between the extracted waveform parameters and the hydro-properties characterizing the fractured media have been established.

The results presented here are interesting and important and provide a wealth of information that warrant further investigation involving either a laboratory or field study. The seismic waveform parameters can be reasonably estimated from real seismic data obtained from fractured terrain with a good signal-to-noise ratio. More research work in this direction may lead to innovative and useful ways of assessing the hydraulic properties of fractured rockmass remotely from seismic information. For example, based on these results, one may infer that with estimates of the correlation dimension and the α parameter of waveforms from two fracture zones, the zone with relatively greater value of correlation dimension and smaller value of curvature index, may possess greater storage and transmission potential.

The sensitivity of the fracture permeability and the discontinuity index to these waveform parameters may be due to the fact that, for a given frequency range of the propagating waveform, the amplitude distribution in waveforms is more sensitive to fracture spacing and aperture, which also control the permeability and discontinuity index than the length. The mean fracture length may not be representative as it is possible that a few long fractures may dominantly influence the fracture permeability, an observation that has been established by Cheng-Haw & Farmer (1993). Although the models used in the numerical experiments are quite simple, the insight gained is valuable for possible use as quantifiable criteria for assessing the hydraulic properties of a fractured rockmass.

Acknowledgments

This research work was supported by the National Science Foundation (NSF) under grant no CMS 02-17318 and by Texaco Inc. The author would like to thank the two reviewers for their useful comments and suggestions.

References