-
PDF
- Split View
-
Views
-
Cite
Cite
Neil D. Selby, David Bowers, Peter D. Marshall, Alan Douglas, Empirical path and station corrections for surface-wave magnitude, Ms, using a global network, Geophysical Journal International, Volume 155, Issue 2, November 2003, Pages 379–390, https://doi.org/10.1046/j.1365-246X.2003.02024.x
Close - Share Icon Share
Summary
One of the most commonly used methods of estimating the size of shallow earthquakes is the surface-wave magnitude scale, Ms. It has been known since the inception of the scale that the Ms of a seismic disturbance recorded at different stations can vary due to path propagation and station terms, but it has been difficult to quantify these variations on a global basis because, until recently, there has been no attempt to record Ms in a uniform way on a worldwide network.
Here we use Ms measurements within the Reviewed Event Bulletin (REB) of the International Data Centre (IDC) which is produced to help monitor compliance with the Comprehensive Nuclear Test Ban Treaty (CTBT). The IDC collects waveforms from the as yet incomplete seismological network of the International Monitoring System (IMS) and Ms is then measured using an automatic algorithm, providing a unique set of surface-wave observations.
In this paper we show that the Ms values reported in the REB show distinct geographic variations. We present preliminary attempts to model these observations in terms of a set of station corrections and a 2-D model which can be used to predict path corrections for Ms. The model shows a striking correlation with the known tectonic regions of the Earth, suggesting that this type of data set may provide a valuable tool for investigating shallow Earth structure.
After modelling, the residuals show some systematic patterns which cannot be explained using the model basis we have used. These residuals are presumably due either to source radiation patterns or to complicated propagation effects not allowed for in the model, such as refraction at ocean-continent boundaries.
From the CTBT monitoring viewpoint, Ms station and path corrections are valuable because they should improve the effectiveness of event screening using mb: Ms. However, we recommend that implementation of such corrections should wait until the full seismological network of the IMS is in place, and until a fuller understanding of path effects on Ms is available. In particular, it is vital that path propagation effects do not distort station corrections, and that earthquake radiation patterns should not influence corrections which may be applied to surface-waves from suspected explosions.
1 Introduction
Surface-wave magnitude, Ms, is one of several magnitude scales commonly used in seismology. Ms is of particular interest for two reasons. First, it is perhaps the most useful scale for determining the size of shallow earthquakes. It is believed that the correlation between the Ms and the logarithm of the seismic moment, log10M0, of a seismic disturbance is higher than for any other magnitude scale (Kanamori 1977; Ekström & Dziewonski 1988). Since M0 can only be measured directly for large, recent events, Ms can be of use in studies where the energy release of an earthquake is of interest; for example, seismic risk assessments and regional tectonics. Second, the ratio of body-wave magnitude to surface-wave magnitude, mb: Ms, is one of the most robust methods used in ‘event-screening’, that is, the identification of definite earthquakes in a population of seismic disturbances of unknown origin. Hence the accurate measurement of Ms is vital for monitoring compliance with Comprehensive Nuclear Test Ban Treaty (CTBT).
The use of the Ms magnitude scale makes the implicit assumption that the amplitude of a surface-wave at a particular recording station is related directly to the size of the seismic disturbance which generated the wave. When several stations record an Ms for the same event, there is generally some scatter and the network average  , is used as the magnitude. Here we discuss the possible causes for the scatter in Ms, and present experiments to calculate empirical path and station corrections for Ms on a global basis using observations from the partially-completed seismological network of the International Monitoring System (IMS) currently being established to monitor compliance with the CTBT. We make use of the surface-wave measurements included in the Reviewed Event Bulletin (REB) of the prototype International Data Centre (pIDC) and the International Data Centre (IDC) during the period 1997 January–2002 December inclusive. The REB is invaluable for such a study since it is the only example of routine measurement of Ms, using an automatic algorithm, from centrally-collected waveforms recorded by a global network of seismometers.
, is used as the magnitude. Here we discuss the possible causes for the scatter in Ms, and present experiments to calculate empirical path and station corrections for Ms on a global basis using observations from the partially-completed seismological network of the International Monitoring System (IMS) currently being established to monitor compliance with the CTBT. We make use of the surface-wave measurements included in the Reviewed Event Bulletin (REB) of the prototype International Data Centre (pIDC) and the International Data Centre (IDC) during the period 1997 January–2002 December inclusive. The REB is invaluable for such a study since it is the only example of routine measurement of Ms, using an automatic algorithm, from centrally-collected waveforms recorded by a global network of seismometers.
We then discuss the implications of our results, both for event-screening using the mb: Ms criterion, and the possible relationship between Ms path corrections and Earth structure.
1.1 Surface-wave magnitude, Ms
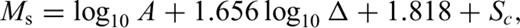
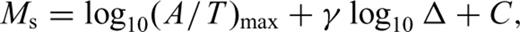
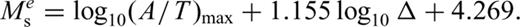
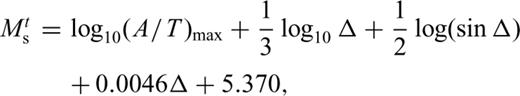
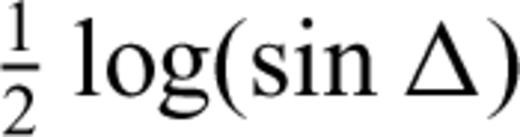 accounts for geometric spreading and the term
accounts for geometric spreading and the term 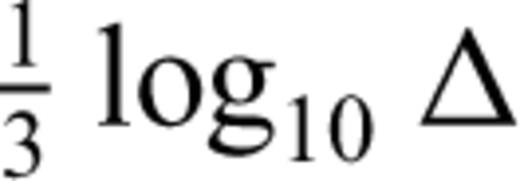 is intended to account for the effect of dispersion of the Rayleigh wave Airy phase (Ewing 1957, p. 165). The residual distance term can then be related to intrinsic Rayleigh attenuation, QR.
is intended to account for the effect of dispersion of the Rayleigh wave Airy phase (Ewing 1957, p. 165). The residual distance term can then be related to intrinsic Rayleigh attenuation, QR.1.2 Scatter in Ms
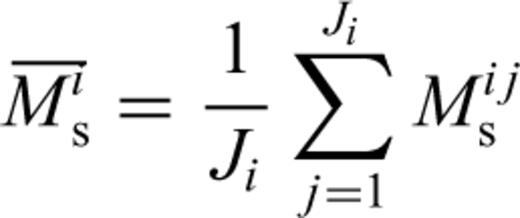
This variation in Mijs may be due to one or more of the following.
1.2.1 Path effects
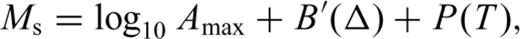
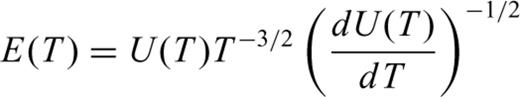
While it is usually assumed that path effects on Ms are mainly due to variations in the group-speed curve, Rayleigh wave amplitudes around 20s are presumably also affected by attenuation, and indeed recent studies at longer periods show large lateral variations in Rayleigh attenuation (Selby & Woodhouse 2000; Billien 2000). However, the average path lengths used for Ms measurements are relatively short, and it may be that large variations in attenuation exist mainly in the asthenosphere (apart from exceptional regions such as mid ocean ridges) and so are too deep to affect 20s Rayleigh waves greatly.
1.2.2 Station terms
Here we use the phrase ‘station term’ to refer to a constant offset in the values of Ms recorded at a particular station, regardless of the location of the seismic disturbance or the path travelled by the surface wave. This is rather different to the usage of the same phrase by other authors such as Thomas (1978) where the station term includes path effects to some extent. Here the station term must be due to the immediate structure at the station or to differences in instrumentation from station to station. That local structure may influence station amplitudes is evident from the variation with station of Rayleigh ellipticity (Sexton 1977; Boore & Toksöz 1969).
Correct estimation of station terms is particularly important when Ms is used for event screening. Station terms would normally be calculated by averaging large numbers of Ms residuals at a particular station. However, these residuals would be based on observation of earthquakes, which have a specific geographic distribution. Hence it is possible that Ms observations at a station may be dominated by measurements from surface waves travelling along similar paths. An explosion could occur at any azimuth and distance from that station and the path travelled by the surface wave from the explosion could be completely different from the paths travelled from earthquakes, so the calculated station term could be inappropriate. Therefore it is essential that path effects on Ms are removed before station terms are calculated, or preferably both should be calculated together.
1.2.3 Radiation pattern
The concept of Ms and other magnitude scales carries the implicit assumption that the size of an earthquake can be determined from the amplitude of a seismic wave without reference to the radiation pattern. Intuitively, however, we would expect that the scatter in Mijs about Mis would be strongly affected by the radiation pattern. At regional distances (less than about 2000 km from the epicentre) several studies have shown that the amplitude of surface waves around 20s period can be related to the radiation pattern. Bowers (1997) successfully models Rayleigh and Love wave amplitudes to a maximum distance of 12.8° using the radiation pattern predicted from a source mechanism constrained using teleseismic body-wave observations and finds a maximum range of Ms of 1.15 m.u. In a theoretical study, von Seggern (1970) discusses the effect of radiation pattern on magnitude estimates, and demonstrates that magnitudes can be incorrect by more than one magnitude unit due to radiation pattern. von Seggern (1970) shows that theoretical variation in Ms due to radiation pattern is strongly dependent on the type of source mechanism, with 45° dip-slip earthquakes showing very little scatter. As Bowers & McCormack (1997) point out, compressional dip-slip mechanisms predominate in moment-tensor catalogues and presumably also in the Earth, which may limit the effect of radiation pattern on Ms. von Seggern (1970) also points out that mb:Ms plots show less scatter for known explosions than for earthquakes, although of course some of this scatter will be due to the effect of radiation pattern on mb, which can be significant (Bowers & Douglas 1998).
Our experience is that for surface waves at periods near 20s path effects usually dominate over radiation pattern at distances Δ > 20°, which is perhaps surprising.
2 Data
The Ms observations reported in the REB differ from those of other bulletins in that the measurements are made using an automated process on centrally collected waveforms. This means that the method of Ms calculation is invariant, so that systematic variation in residuals, should, subject to a number of provisos, reflect real variations in Ms. Stevens & McLaughlin (2001) describe the method of Ms measurement. Rayleigh waves are detected automatically and associated with known epicentres on the basis of a dispersion test. The algorithm then selects the cycle in the period range 18–22s and the amplitude is measured. Ms is calculated using MtS of RP98 (eq. 4 in this paper). Rayleigh waves are reported in the distance range 0° < Δ≤ 100°. The REB reports the instrument-corrected amplitude and period at which the amplitude is measured, together with the magnitude.
2.1 Data editing
Before beginning to interpret the Ms residuals in the bulletin we embark on a thorough process of data editing. This is necessary because we know, as reported in Stevens & McLaughlin (2001), that there have been calibration problems with a number of stations in the IMS network during the period of this study. As an example, Fig. 1 shows data from station CMAR in Thailand. CMAR is one of five long-period arrays in the current IMS network. The top panel of the figure shows log10(A/T) against time. The bottom panel shows the Ms residuals after data editing, with a number of time gaps where data has been excluded. According to Stevens & McLaughlin (2001), all Rayleigh amplitudes in the REB recorded between 1997 April 3 and 1997 June 24 should be considered unreliable. We have therefore omitted all data from this period from the study. Additionally, CMAR underwent a change of instrumentation during the study period which resulted in a period between 1998 October 1 and 1999 May 25 for which the station calibration was incorrect. Stevens & McLaughlin (2001) suggest a correction for CMAR during this time, but after applying the correction we were unhappy with the resulting residuals and so have chosen to omit these data. In fact, the plot of log(A/T) (Fig. 1, top panel) seems to show a trend during this period. The remaining Ms residuals appear to show a definite shift in mean after the change of instrumentation (bottom panel, Fig. 1). We therefore considered these two periods as different stations during the subsequent modelling process. Similar decisions were made for stations ARCES, BGCA, DBIC, ESDC, KBZ, KSAR, NORES, PDAR and TXAR. Table 1 lists the stations used in the study together with the time periods from which data were available at each station. Fig. 2 shows the distribution of these stations. As well as the stations discussed above, two other sets of stations are co-located but cover different time periods (MNV/NVAR and NORES/NOA). Fig. 3 shows the number of observations used at each station. In Fig. 4 we show the distribution of earthquake epicentres used. It can be seen clearly that the small number of stations in the southern hemisphere, together with the restriction of path lengths to less than 100° results in a strong bias in the data set in favour of the northern hemisphere.
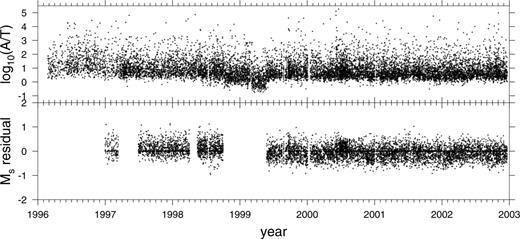
Representation of the data-editing process for station CMAR, Thailand. The top panel shows log10(A/T) plotted against date for the study period. The bottom panel shows the Ms residual (Ms measured at CMAR minus the mean Ms for each event) after unwanted data has been removed.
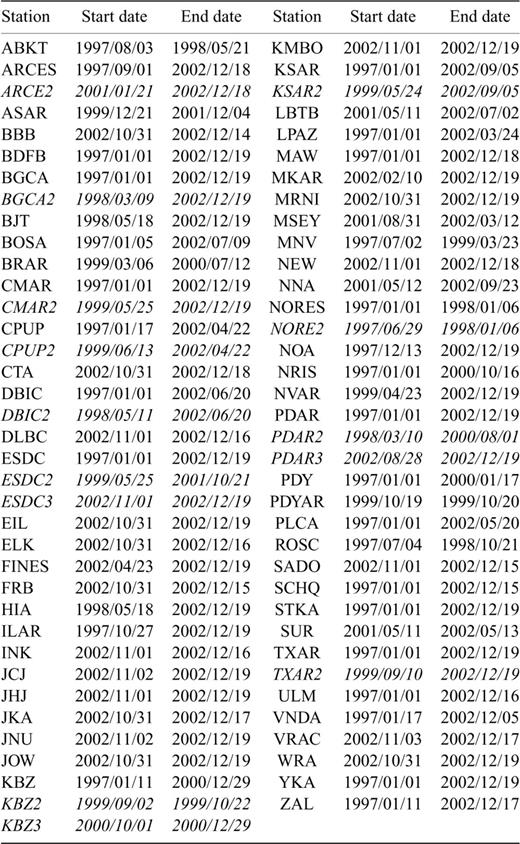
Earliest and latest date for which data are considered for each station utilized in this study. Stations may not be continually operable throughout the period listed. Some stations (including CMAR, ESDC and KSAR) were given alternate names during part of the period; these dates are shown in italics.

Distribution of stations used, which form part of the seismological network of the IMS. Note the co-location of some of the stations.

Number of observations of Ms at each station considered at the beginning of the modelling process. Note that for many stations the number of observations is small.
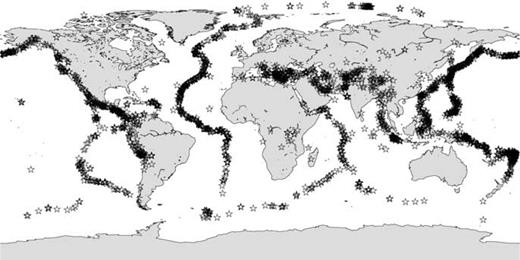
Distribution of epicentres of events used. To be included, there must be at least ten observations of Ms from the event, resulting in a sharp reduction of available events in the southern hemisphere.
In addition to problems with instrument calibration we found a number of discrepancies in the REB where Ms appeared to be calculated from more observations than were listed in the bulletin. We chose to exclude these events from subsequent analysis as the cause of these discrepancies is not immediately apparent.
After the data editing process outlined above we then recalculate all the Mijs and Misj for the remaining observations. At this point we restrict subsequent analysis to events with Ji≥ 10. This is to ensure that the modelling process begins with a reasonable value for  and hence a good estimate of the ‘true’ surface wave magnitude of the event i,
and hence a good estimate of the ‘true’ surface wave magnitude of the event i,  .
.
3 Interpretation
3.1 Observed Ms residuals
Fig. 5 shows the pattern of Ms residuals observed at station ESDC in Spain. The residuals are plotted at the epicentre of the earthquake from which they arise. The size of the symbol is proportional to the size of the residual, with grey circles denoting negative residuals  and black crosses positive residuals. It is obvious that there is a systematic pattern, with, for example, negative residuals from events in the Mediterranean, Middle East, India and the Indian Ocean, and positive residuals in Japan and North America. In fact, the negative residuals seen by ESDC from events in south-west Eurasia are some of the largest in the entire data set. Similar plots for other stations also show systematic patterns. However, some stations, such as BJT, show residuals predominantly of one sign, suggesting that all observations at that station are systematically biased. The pattern of residuals in Fig. 5 is presumably due to either path effects or due to a systematic orientation of earthquake mechanisms, which we might expect within the framework of plate tectonics. To examine the extent to which these residuals are consistent from station to station we attempt to model the residuals in terms of a global correction surface for Ms.
and black crosses positive residuals. It is obvious that there is a systematic pattern, with, for example, negative residuals from events in the Mediterranean, Middle East, India and the Indian Ocean, and positive residuals in Japan and North America. In fact, the negative residuals seen by ESDC from events in south-west Eurasia are some of the largest in the entire data set. Similar plots for other stations also show systematic patterns. However, some stations, such as BJT, show residuals predominantly of one sign, suggesting that all observations at that station are systematically biased. The pattern of residuals in Fig. 5 is presumably due to either path effects or due to a systematic orientation of earthquake mechanisms, which we might expect within the framework of plate tectonics. To examine the extent to which these residuals are consistent from station to station we attempt to model the residuals in terms of a global correction surface for Ms.
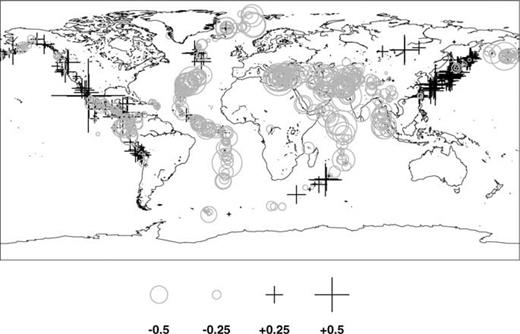
Ms residuals observed at station ESDC (Spain). The residuals are plotted at the epicentre of each event. Negative (grey circle) residuals indicate that the Ms observed at ESDC is below the mean Ms for the event.
3.2 Problem formulation

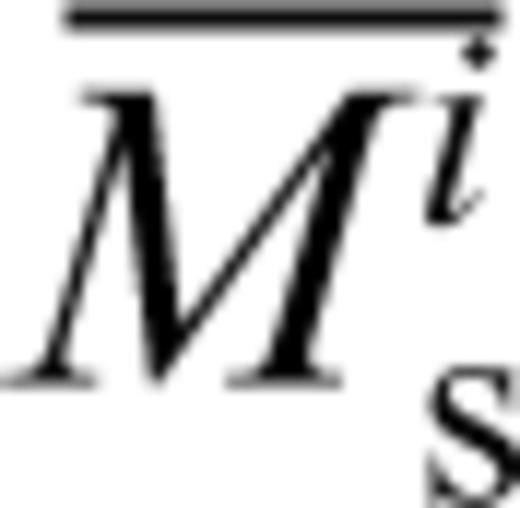 is clearly then
is clearly then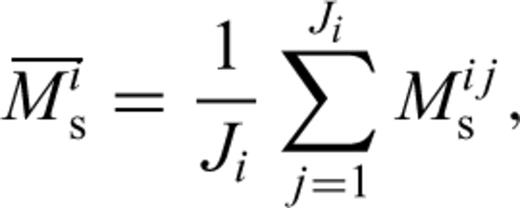
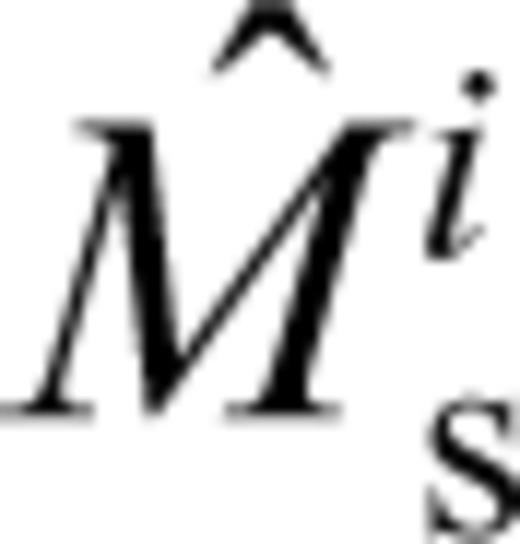 , which is approximately equal to
, which is approximately equal to 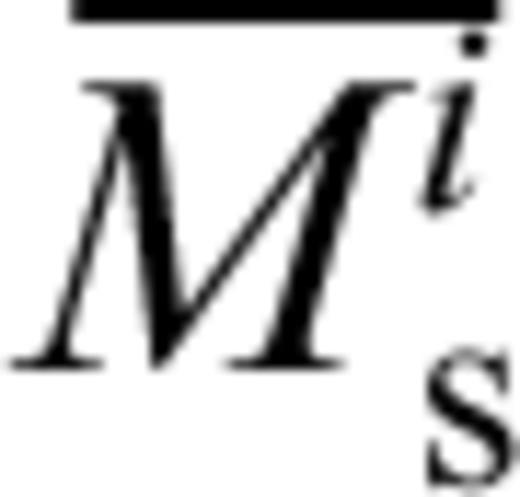 for large Ji. The scatter of Mijs about
for large Ji. The scatter of Mijs about 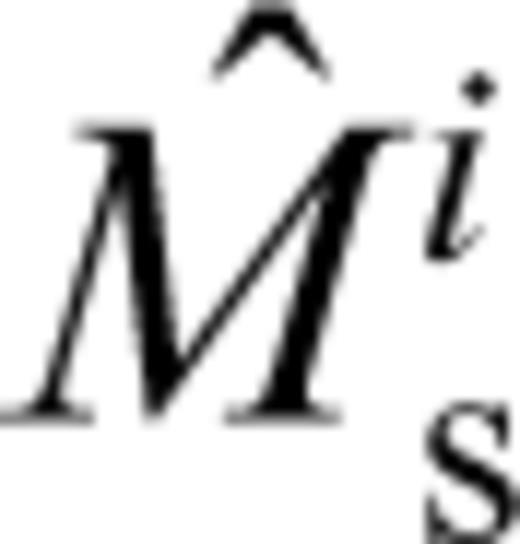 is then assumed to be due to: (1) path-dependent variation in the constant γ (i.e. variations in the effect of dispersion and attenuation); (2) variations with period, T; and (3) a station term. So we can write:
is then assumed to be due to: (1) path-dependent variation in the constant γ (i.e. variations in the effect of dispersion and attenuation); (2) variations with period, T; and (3) a station term. So we can write: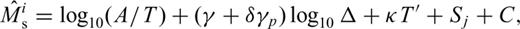
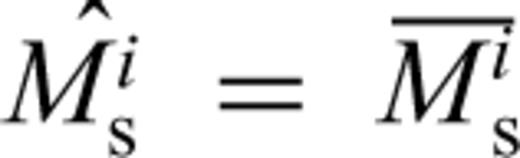 , the residual, dij for each event-station pair is given by
, the residual, dij for each event-station pair is given by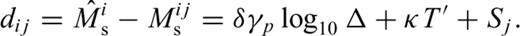
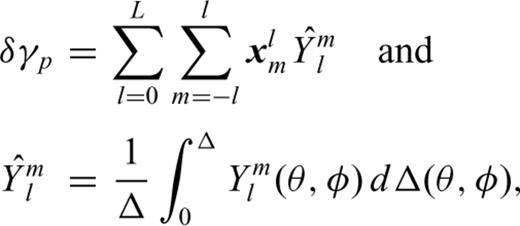
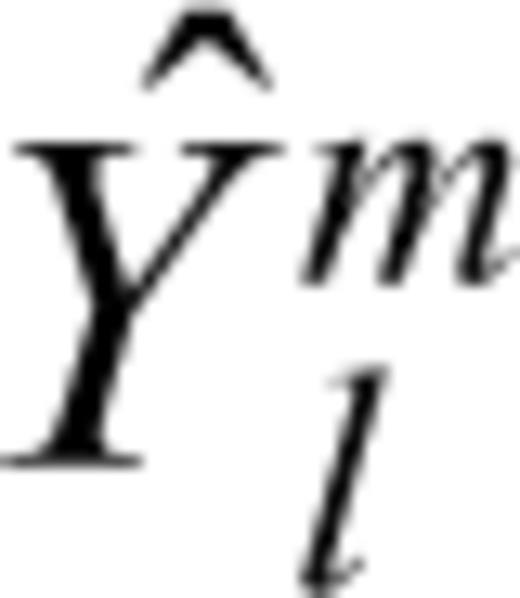 is the path-average of spherical harmonics along path p. We then have a set of equations of the form
is the path-average of spherical harmonics along path p. We then have a set of equations of the form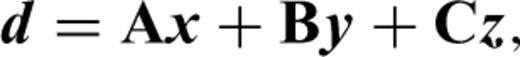
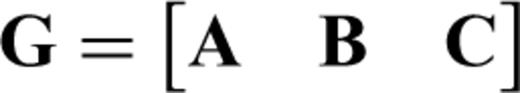
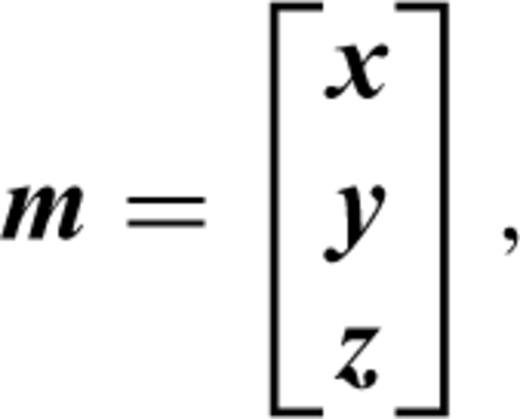
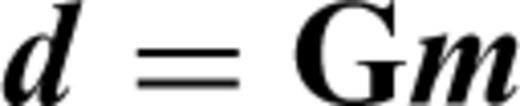
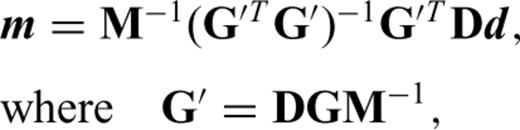
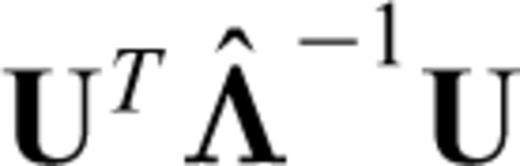 where
where 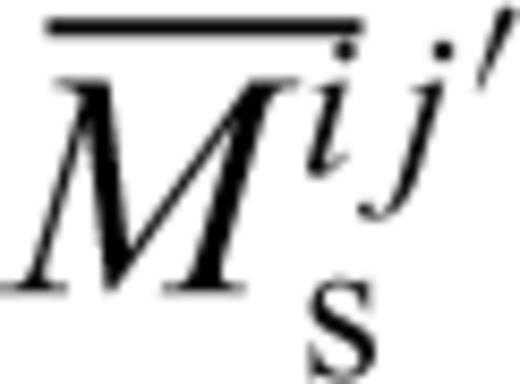 and Λ are the set of eigenvectors and eigenvalues of (G′TG′)−1 respectively, and λn is the nth eigenvalue in order of size where n is chosen as a compromise between model size and variance reduction achieved.
and Λ are the set of eigenvectors and eigenvalues of (G′TG′)−1 respectively, and λn is the nth eigenvalue in order of size where n is chosen as a compromise between model size and variance reduction achieved.3.3 Data weighting
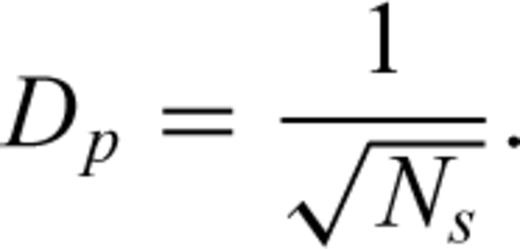
3.4 Model weighting
Model weighting is an important issue in this type of study. First, we impose the condition that each of the three parts of the model [δγ(θ, φ) distribution, period dependence and set of station corrections] is weighted equally. Second, we apply a smoothness constraint to the spherical harmonic expansion of δγ(θ, φ) where each degree, l, of the expansion is weighted by 1/[l(l+ 1)]2 (Trampert & Woodhouse 1995). This weighting reduces the contribution of the shorter-wavelength model components, resulting in a smoother model. However, there is the danger that in areas of poor data-coverage and resolution the amplitude of long-wavelength structure may be exaggerated.
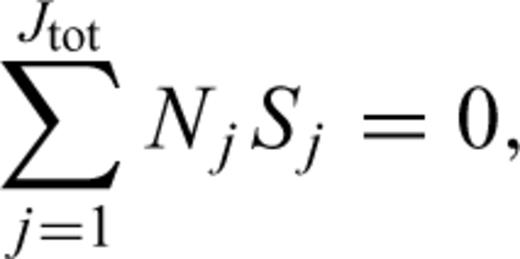
3.5 Modelling procedure
An initial inversion is carried out to degree 10 spherical harmonic expansion of δγ(θ, φ) together with a set of station terms and a term for period-dependence. We then calculate the misfit between observation and model prediction for each path. Paths whose absolute misfit is greater than 2.5σ are excluded at this point.
- 20A second inversion is carried out to degree 20. We then calculate the model prediction for each path (station term, period term and path term) and correct each observation. This allows us to produce a recalculated mean for each event,
 , where:This step allows for any bias in the original mean due to the path and station corrections, i.e. we assume that20
, where:This step allows for any bias in the original mean due to the path and station corrections, i.e. we assume that20
 is closer to
is closer to  than
than  .
. - 21We then recalculate residuals relative to the new mean:and use these values in a second iteration for a degree 20 inversion.21

3.6 Results
The resulting δγ(θ, φ) model is shown in Fig. 6(a). Paths through blue areas give an increased value for Ms whereas paths through orange areas give decreased Ms. There is a clear correlation with tectonic patterns, with continents and ocean basins generally enhancing Rayleigh amplitudes and regions near plate boundaries decreasing amplitudes. The regions of strongest negative δγ(θ, φ) occur in the Mediterranean, Indonesia and the northern Atlantic/Arctic Ocean, and regions of strong positive δγ(θ, φ) are found in continental regions and the central Pacific. However, resolution in the southern hemisphere (particularly in the southern Atlantic and Indian Ocean) and much of the Pacific is poor due to the scarcity of stations, the requirement of at least ten observations of each event, and the limit of 100° on path length.
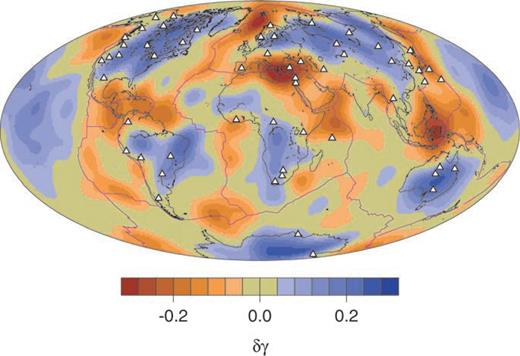
Distribution of δγ(θ, φ). Stations used are shown as white triangles and plate boundaries as purple lines.
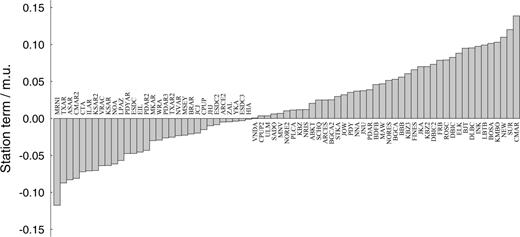
The set of station terms range from about −0.1 to 0.15 m.u. (Fig. 7). Stations with relatively few observations are likely to have large residuals (cf. Fig. 3) so these should be treated with caution. However, BOSA, BJT and DBIC each show large positive station terms and NOA and ILAR show significant negative values. Stations CMAR, KSAR and ESDC each have multiple station terms (see Section 2) which can vary greatly (note in particular CMAR and CMAR2). This suggests that changes in instrumentation (or perhaps changes to the total network over time) can lead to large changes in station term, which may mean that relating station terms to local Earth structure is difficult.
Finally, we find κ=−0.05, which indicates that there is a systematic trend of measured Ms with T, with measurements made at 22s being on average 0.05 m.u. lower than those made at 18s. However, we also find that measurements made on continental paths are likely to be at shorter periods than those made elsewhere, so this value may not be independent of the δγ(θ, φ) distribution.
Table 2 lists the variance reductions achieved for each stage of the modelling process and the variance reduction due to each part of the model. Note that since the model parameters are not orthogonal, there is no requirement that Vtotal=Vpath+Vstation+Vperiod. In Table 3 we list the equivalent variance reductions for an alternate set of models where we included no data weighting. The variance reductions achieved are similar.
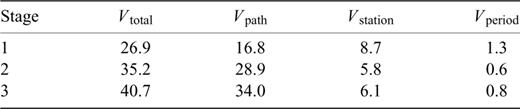
Variance reductions achieved for the Ms correction model. Vtotal is the variance reduction achieved for the total model, and Vpath, Vstation and Vperiod the variance reduction achieved by the δγ(θ, φ) distribution, station corrections, and period correction respectively.
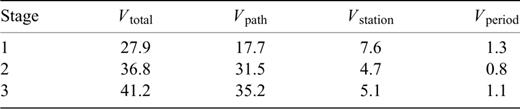
Variance reductions achieved for an alternate model in which data weights were not included, see text for details. Column headings as for Table 2.
4 Discussion
Currently the IMS network is probably insufficient to recover a fully accurate model for Ms corrections. The sparse station network in the southern hemisphere and Pacific region together with the restriction of path length Δ≤ 100° and the requirement for at least 10 stations to record each event mean that data coverage is poor in many areas of the globe, both in absolute and azimuthal terms, which are equally important in this kind of study.
The uneven data coverage means that the model space is not evenly sampled, which will lead to a posteriori correlations between the spherical harmonic parameters. This means that ‘underdamping’ of the inversion could lead to spurious perturbations in the retrieved model. Although we have attempted to minimize the effect of this problem, a more spatially complete data set is required to completely eliminate it. In addition, it is inevitable that some of the station terms will be correlated with each other and with the spherical harmonic coefficients. This again increases the sensitivity of the model to correlated errors in the data.
However, in regions where coverage and resolution is good (North America, the north Atlantic and Arctic and much of Eurasia) the models retrieved appear to be robust and revealing. If variations in Ms are due to the effects of dispersion and attenuation, then we would expect to see amplitudes reduced in areas of thick sediment or tectonic complexity. Rayleigh amplitudes should be enhanced in stable areas such as old continents and oceans. It is important to remember at this point that Ms is effectively a measurement of the envelope of a seismogram convolved with a particular instrument response or filter. Ms is therefore sensitive to a range of periods around the measurement period determined by the dispersion (group speed curve), amplitude spectrum and filter or instrument response. We should not necessarily expect the resulting model to correlate with existing studies of phase-speed or attenuation.
4.1 Regional biases in Ms
Using our model of path, station and period corrections it is now possible to investigate whether there are systematic regional biases in the estimation of Ms. To test this we use the set of events reported during 1999 which are given an Ms value in the REB, subject to the same data-editing as described above. The model described was constructed using only events for which Ji≥ 10 where Ji is the number of stations observing event i. However, this is only a small sub-set of the events with surface wave magnitude given in the REB. Fig. 8 shows the distribution of Ji for 1999. More than 25 per cent of the events with an Ms have that magnitude calculated from only one observation.
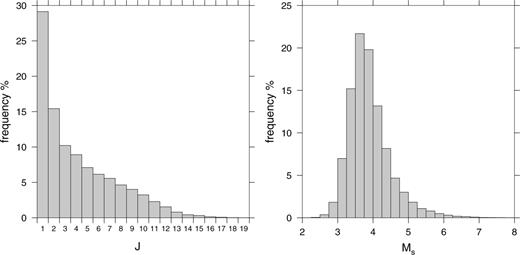
Left: Histogram showing the number of observations used to calculate Ms for events in the REB. For example, around 25 per cent of the events in the REB given an Ms, have that Ms calculated from one observation. Right: Histogram showing the distribution of mean Ms for events used in this study. Note that the majority of the events have mean Ms below 4.0.
We calculate the Ms correction for each observation in the REB and then recalculate  for all i. Fig. 9 shows the difference between the original and updated mean Ms (negative values indicate that the original
for all i. Fig. 9 shows the difference between the original and updated mean Ms (negative values indicate that the original  is an underestimate). Most of these differences are between ±0.2.
is an underestimate). Most of these differences are between ±0.2.
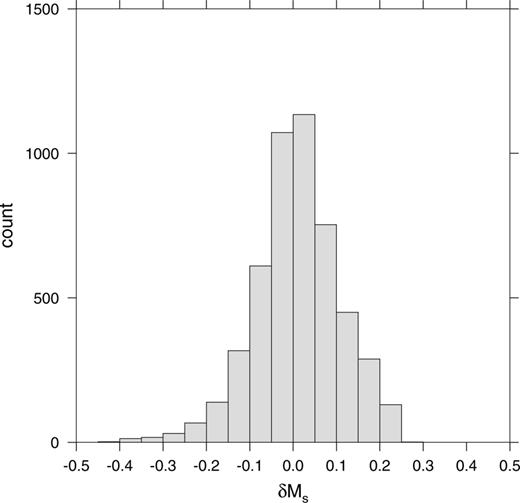
Histogram showing the effect of the model on mean Ms for all events given an Ms during 1999.
We then investigate the geographic distribution of Ms bias. In Fig. 10 we show the distribution of events for which the  . Black crosses indicate events for which the revised magnitude is smaller than the original. We see that the original Ms was overestimated in regions such as central Asia, the western margin of North and South America, Japan and the Tonga-Kermadec trench region. The grey circles show that events in the eastern Mediterranean and Middle East as well as those in Indonesia are underestimated if the corrections are not used.
. Black crosses indicate events for which the revised magnitude is smaller than the original. We see that the original Ms was overestimated in regions such as central Asia, the western margin of North and South America, Japan and the Tonga-Kermadec trench region. The grey circles show that events in the eastern Mediterranean and Middle East as well as those in Indonesia are underestimated if the corrections are not used.
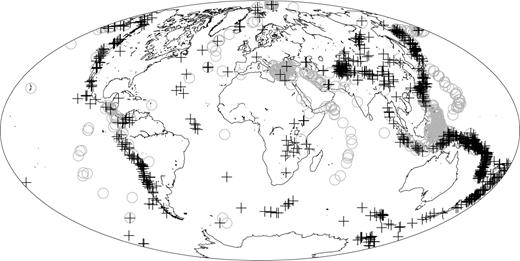
The change in  for events during 1999. Black crosses indicate events for which the model decreases
for events during 1999. Black crosses indicate events for which the model decreases  , i.e. the raw data overestimates
, i.e. the raw data overestimates  . Grey circles indicate events for which the modelling process increases
. Grey circles indicate events for which the modelling process increases  .
.
4.2 Possible effect of data censoring
Surface wave observations are required to pass a dispersion test before Ms can be reported in the REB (Stevens & McLaughlin 2001). This means that any surface waves which deviate greatly from the model group speed predictions will not be included. If, as we assume, Ms residuals are at least partly related to the shape of the group-speed curve for a path, then the observations of amplitude are not independent of the group-speed model, i.e. amplitudes will not be measured for paths which do not fit the group-speed model, producing a data-censoring effect. However, we feel that this is a weak effect since the time window used in association with the group-speed curves is wide enough to allow any genuine surface wave to be detected. The censoring effect is certainly not comparable to that in any study which utilizes a waveform-fitting technique of surface-wave measurement.
4.3 Remaining residuals
The modelling process above accounts for around 40 per cent of the variance of the observations, and so a large part of the observations are not explained by the model. In Fig. 11 we show the effect of the modelling on the observed station residuals. The top panel shows the observed residuals for station NOA in southern Norway, plotted in the same way as Fig. 5. In the middle panel are the model predictions. Although the general pattern of the predictions matches the observations, the size of the residuals is generally smaller. This is presumably because of the trade-off with observations at other stations. The bottom panel shows what remains of the observations after modelling. there are still distinct patterns of residuals, particularly in the western Pacific and Atlantic regions. These residuals are not explainable within the framework outlined above. We surmise that these residuals are due either to path effects which cannot be predicted by our model—for instance, there may be systematic effects on amplitude dependent on the angle of intersection between the path and an ocean/continent boundary—or to the effects of source radiation pattern. However, preliminary attempts to match radiation patterns from earthquakes with known mechanisms to either the initial observations or the residuals after modelling have proved inconclusive, so this question remains to be resolved.
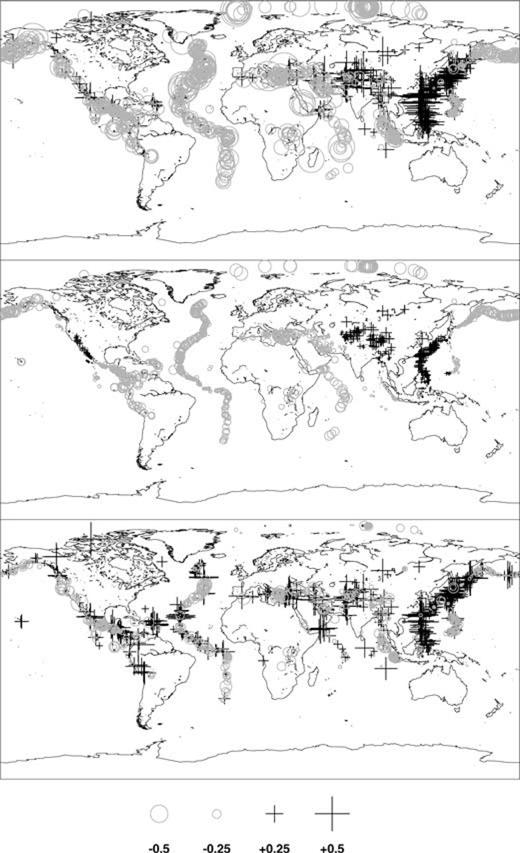
The effect of the modelling process on Ms residuals observed at station NOA, Norway. Top: Observed Ms residuals. Middle: Model predicted residuals. Bottom: Difference between observed and predicted residuals. Distinct clusters of positive and negative residuals are still visible.
5 Conclusions
Ms residuals show systematic patterns which can, at least in part, be attributed to lateral variations in Earth structure. Determining reliable Ms path corrections is potentially vital since event screening and discrimination can depend critically on the use of the mb: Ms criterion. If the number of Ms observations is very low, which is likely to be so for small explosions, then path and station dependent effects can potentially bias the observed Ms of a seismic disturbance. However, it is critical that any postulated Ms corrections are not contaminated by earthquake radiation pattern effects since these would not be applicable to explosions. Hence, using the raw data, ‘source-station specific’ type corrections will probably be contaminated more by radiation pattern effects than this type of model. Also, station corrections for Ms need to be de-sensitized to the effects of path-dependent variations in Ms, so that they can be applied with equal validity to events happening in any region of the Earth. A joint inversion such as is described here can go some way to achieving this.
The type of results presented here are potentially beneficial in studies of Earth structure, and complementary to group-speed studies using Rayleigh waves of similar periods (see, for example Ritzwoller & Levshin 1998; Vdovin 1999). As the IMS network grows, and if, as has been suggested, greater efforts are made to retrieve long-period data from IMS auxiliary stations, our understanding of Ms residual distribution across the Earth can only improve.
This paper does not discuss the relationship between Ms and M0, which has been discussed elsewhere (e.g. Ekström & Dziewonski 1988; Herak 2001). We also do not discuss the relationship between Ms and the yield of explosions (e.g. Marshall 1971; Stevens & Murphy 2001). However, the results presented here suggest further work which may improve our understanding of these relationships.
A final word of caution is that the results in this study can only be guaranteed to apply to Ms measurements made using the methodology of Stevens & McLaughlin (2001) described above. Surface waves generated from small, shallow explosions have a different character to earthquake data (having a much higher frequency content) and so may require a more appropriate method of Ms measurement (such as that described by Marshall & Basham 1972) which would require frequency-dependent path and station corrections.
Acknowledgments
The figures in this paper were produced using GMT (Wessel & Smith 1998). The authors would like to thank the staff of the pIDC, IDC and IMS responsible for producing the data utilized here.
References
Footnotes
More information about the CTBT can be obtained from the website: .




