A seismic hazard scenario for the main cities of Crete island, Greece Free

Summary

1 Introduction

It is well recognized that seismic hazard assessment, namely the computation of long-term probabilities of occurrence of earthquakes of a specified size in a given area during a given time interval, is a prerequisite for seismic risk reduction and urban planning. Greece is one of the most seismically active regions in the world (e.g. Tsapanos & Burton 1991). The seismic hazard in Greece has therefore been widely studied using a number of different techniques and seismic measures. Site-specific hazard analyses have been conducted among others by Papazachos (1995), who investigated the seismic hazard in the city of Heraklion on the Island of Crete. Papaioannou & Papazachos (2000) assessed time-independent and time-dependent seismic hazard for 144 broad sites (cities, towns, villages) of Greece in terms of expected macroseismic intensities at each of these sites, and Lyubushin (2002) estimated the seismic hazard in terms of maximum values of peak ground acceleration for six sites (Griva, Konitsa, Kozani, Aeghio, Killini and Kalamata) using a Bayesian procedure.

This study focuses on the cities of Chania, Rethymno and Heraklion and their neighbouring areas, because these cities are sited in the area of the subduction of Eurasia and Africa's lithosphere. All of them have suffered from the consequences of moderate-to-strong magnitude earthquakes. The event of 365 AD had an estimated magnitude of M_w= 8.3, which is the largest in the seismological record of Greece, and occurred in the vicinity of Crete (Papazachos & Papazachou 1997), where the number of towns destroyed exceeded 100 (Guidoboni 1994). The worst effects of the earthquake of 1303 August 8, one of the largest seismic events in the Mediterranean area, were felt in Crete, where the maximum macroseismic intensity has been estimated at I_max= XI on the MCS scale (Guidoboni & Comastri 1997). Heraklion was badly devastated by this earthquake and the related tsunami.

The purpose of the present study is to assess the level of seismic hazard for the cities of Chania, Rethymno and Heraklion in terms of the probabilities of exceedance of a specified peak ground acceleration (PGA) value, during a given time interval and the maximum possible peak ground acceleration at the site of each city. The methodology for probabilistic seismic hazard assessment (PSHA) developed by Kijko & Graham (1998, 1999) is applied. This approach has been specially developed for PSHA at a specified site and it allows the incorporation of different types of information. Either incomplete (historical) or instrumental earthquake records with varying threshold magnitudes for completeness, or a combination of both, can be taken into account. The technique does not rely on the definition of seismic source zones, which is advantageous for regions where the interpretation of earthquake observations in terms of faults and geological structure may be difficult (Mantyniemi 2001). Site-specific analyses of seismic hazard require knowledge of the attenuation of the chosen ground-motion descriptor as a function of distance. The attenuation law, recently derived for shallow earthquakes in Greece by Margaris (2001), is used and the effect of soil conditions (rock, intermediate, soft) was assessed as well. Only shallow (h≤ 60 km) seismicity is considered. The estimation of the maximum possible magnitude m_max is necessary for the broad areas surrounding the cities and was determined (Tsapanos 2001) using a recently derived formalism (Kijko & Graham 1998). The site-specific results are expressed as probabilities that a given peak ground acceleration value will be exceeded during time intervals of 1, 5, 25 and 50 yr at the sites of interest.

2 Earthquake Data

The earthquake data were taken from the data archive of the Geophysical Laboratory, University of Thessaloniki (Papazachos 2000). Abundant information on Greek earthquakes is available in this data bank, starting from 550 BC. For the purpose of the present study, foreshocks, aftershocks and earthquake swarms were removed from the initial data using a relationship derived by Papazachos & Papazachou (1997), in which the duration of the aftershock sequence depends on the magnitude of the main shock.

The whole catalogue of shallow earthquakes for the area is considered complete for the following time periods: after 550 BC for M≥ 8.0, after 1501 for M≥ 7.3, after 1845 for M≥ 6.0, after 1911 for M≥5.0, after 1950 for M≥ 4.5, after 1964 for M≥ 4.3 and after 1981 for M≥ 4.0 (Papazachos 2000). In the historical data, between 550 BC and 1910, the uncertainty of epicentre and magnitude is less than 30 km and 0.4 magnitude units, respectively (Papazachos & Papazachou 1997). Also Papazachos (2000) claimed that the errors in the data recorded instrumentally since 1911 have been assessed at less than 20 km for epicentres and 0.25 units for magnitudes. The implication of constant epicentre uncertainty since 1911 is not sensible, because these uncertainties are somehow time-dependent owing to the improvement of the instruments and to the installation of more seismological stations all over Greece since 1911. So these error estimates were used as guidelines when determining magnitude uncertainties during different time periods and dividing the five instrumental catalogues into subcatalogues with each one having a minimum threshold of magnitude.

3 Some Theoretical Considerations

The parametric—historic procedure developed by Kijko & Graham (1998, 1999) was applied in the present study to quantify the level of seismic hazard at given sites. This methodology for PSHA has been classified as parametric—historic because it combines several components of the deductive (Cornell 1968) and historical (Veneziano 1984) procedures, which constitute two main categories of PSHA methods (McGuire 1993).

From a computational point of view, the parametric—historic method includes both area-specific and site-specific parts. First, the area specific parameters; maximum possible, magnitude m_max, mean seismic activity rate, λ_A, and the b-value of the Gutenberg—Richter magnitude—frequency relation (or β=b ln 10) are calculated for an area surrounding the site for which seismic hazard analysis is needed. The three parameters are determined simultaneously using an iterative scheme (Kijko & Sellevoll 1992). The estimation of λ_A and β assumes the validity of a Poisson distribution of earthquake occurrence with activity rate, λ_A, and the doubly truncated Gutenberg—Richter relationship. The maximum-likelihood method is used (for details see Kijko & Sellevoll 1989). The maximum possible magnitude, m_max, can be evaluated following different parametric procedures, which are specified by Kijko & Graham (1998).

In the present study, the maximum possible magnitude, m_max, was estimated for the three cities by using the Bayesian extension of the Kijko—Sellevoll estimator, which has been obtained for the doubly truncated Gutenberg—Richter relationship (Cosentino 1977). Its Bayesian extension (abbreviated to KSB) was derived by Kijko & Graham (1998).

The site-specific computations require knowledge of the attenuation of the selected ground-motion parameter, a, as a function of distance. In this work the new PGA attenuation law for shallow earthquakes in Greece recently derived by Margaris (2001) is used:

(1)

where a is PGA, R is the epicentral distance (in km), h₀= 7 km and values of coefficients are c₀= 3.52, c₁= 0.70, c₂=−1.14 and c₃= 0.12, and the standard deviation of ln(PGA) is c₄= 0.70, while S describes soil classification by taking values of 0, 1 or 2 corresponding to rock (hard), intermediate and alluvium (soft) conditions, respectively. The attenuation law of eq. (1) provides acceleration values in units of cm s⁻².

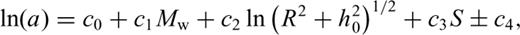
The approach based on the concept of the ‘design’ earthquake, is used to derive the maximum PGA at the examined sites. This approach can be seen as a variation of the technique known as ‘scenario’ earthquakes (Ishikawa & Kameda 1993). According to this procedure, a_max is the value of PGA computed from attenuation laws by assuming the occurrence of the strongest possible earthquakes (m_max) at a very short distance.

Tinti & Mulargia (1985a,b) suggested that an earthquake of magnitude M is determined with an error that is normally distributed and has a mean of zero and a standard deviation of σ_M. The same assumption is made concerning the error in the determination of the epicentral distance R where the standard deviation of R is σ_R. For an earthquake with an apparent magnitude M, and located at a distance R, the value of ln(PGA) is approximately normally distributed (Benjamin & Cornell 1970) with the mean given by the right-hand side of eq. (1) and the standard deviation being similar to that derived by Kijko & Graham (1999):

(2)

where σ_total is the uncertainty, which includes the standard deviations of the PGA, of the apparent magnitude M and of the epicentral distance R.

For an earthquake of apparent magnitude m located at a distance r from a site, the probability that this earthquake will cause a PGA equal to or greater than a is given by

(3)

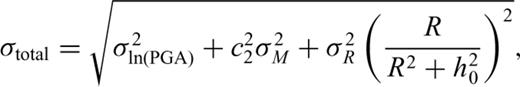
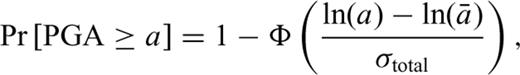
where Φ (·) is the normal probability integral, (Abramowitz & Stegun 1970), and 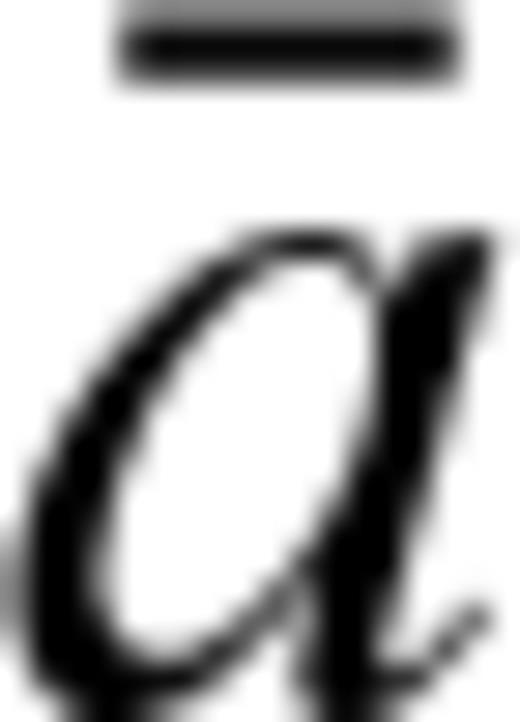is the median value of acceleration, with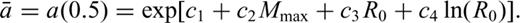

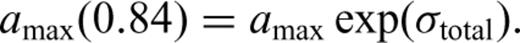
(4)

The value of the maximum PGA plus one standard deviation, a_max (0.84), takes the form

(5)

The maximum possible magnitude is estimated through the KSB estimator, which is used to derive the maximum credible PGA at the sites of the three cities of Crete, as well as when assuming critical epicentral distances R₀= 10, 20 and 30 km (with σ_R=±5 km).

4 Results of the Site-Specific Psha and Discussion

Figs 123 describes the seismic hazard for the cities considered: Chania, Rethymno and Heraklion, respectively. The seismic hazard is expressed as the probability of exceedance of a specified value of PGA at least once during a given time interval of 1, 5, 25 and 50 yr.

Figure 1

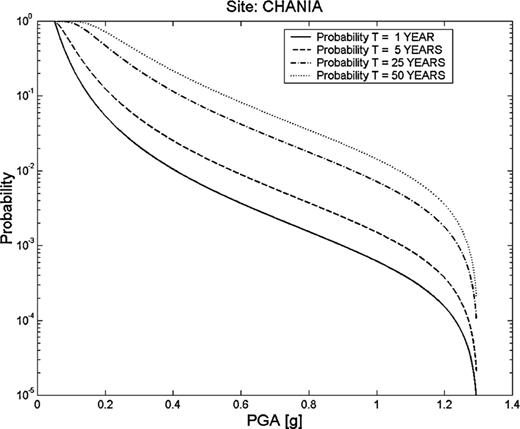
Seismic hazard in the city of Chania, expressed as the probability that a given PGA value will be exceeded at least once during a time period of 1, 5, 25 and 50 yr.

Open in new tabDownload slide

Figure 2

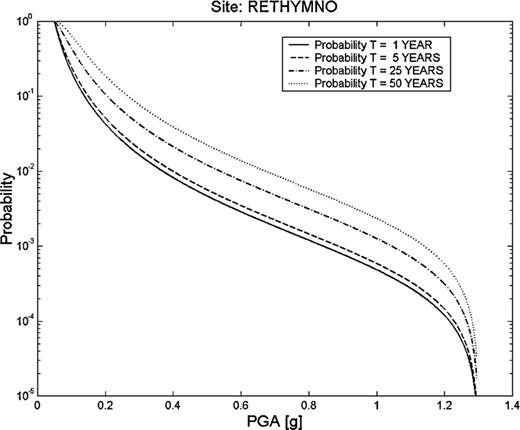
Seismic hazard in the city of Rethymno, expressed as the probability that a given PGA value will be exceeded at least once during a time period of 1, 5, 25 and 50 yr.

Open in new tabDownload slide

Figure 3

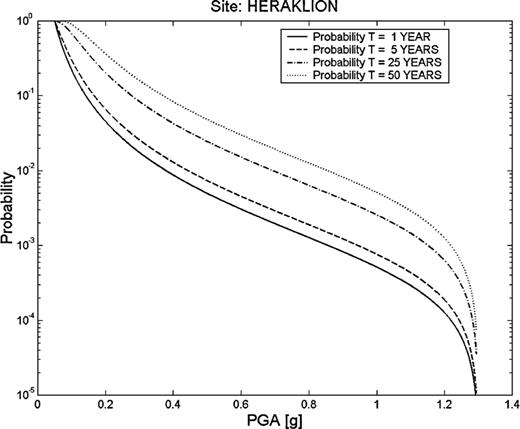
Seismic hazard in the city of Heraklion, expressed as the probability that a given PGA value will be exceeded at least once during a time period of 1, 5, 25 and 50 yr.

Open in new tabDownload slide

The maximum observed magnitudes for the three cities occurred during the historical era. Chania is located about 70 km from the largest known earthquake in Greece with magnitude 8.3 generated in 365 AD, Rethymno is within a distance of about 95 km from the epicentre of the earthquake of 1629 of magnitude 7.3, while Heraklion is situated at a distance of about 60 km from the epicentre of the event of 1508 of magnitude 7.5. Details for the effect of these earthquakes on the island of Crete can be found in Papazachos & Papazachou (1997). Papazachos (1995) specified seismic hazard in Heraklion in terms of expected values of horizontal PGAs for different time return periods. The obtained values were about 85 cm s⁻²≈ 0.087g and 121 cm s⁻²≈ 0.123g for return intervals of 50 and 100 yr, respectively. Previous studies also comprise assessments of the expected ground-motion in terms of PGA. Makropoulos & Burton (1985) presented values that have a 70 per cent probability of not being exceeded in a given time interval. Over T= 50 and 100 yr, these values are 64 cm s⁻²≈ 0.065g and 72 cm s⁻²≈ 0.073g, respectively, for Heraklion. Horizontal PGA values of 46 cm s⁻² (≈0.047g) and 45 cm s⁻² (≈0.046g) were recorded in Heraklion and Chania, respectively, at corresponding epicentral distances of 45 and 65 km, following the 1994 May 23 earthquake of magnitude M_s= 5.8 and focal depth of h= 79 km (Margaris 1995). The same authors found that the site effect in Herraklion caused an increase of about 2 units in the intensity of the earthquakes. This earthquake caused damage at Heraklion and Chania (Papazachos & Papazachou 1997). In a detailed study Tsapanos (2001) estimated the earthquake hazard parameters (m_max, λ and β) in cells of 0.4 × 0.4 deg², in which Crete island and the adjacent area was divided. Based on these parameters he assessed seismic hazard as the annual probability of exceedance of a specified value of magnitude and the mean return periods (in years) that are expected for a given magnitude. These maximum possible magnitude m_max values are adopted for the present study and are listed in Tables 1 and 2.

Table 1

Median a_max(0.5) and upper 84 per cent confidence limit a_max(0.84) of maximum credible PGA (in units of g) at the sites of the three cities. The strongest possible magnitude, m_max (Tsapanos 2001), which is considered as the ‘design’ earthquake and is obtained by the application by the KSB estimator, with epicentre at the site of the city.

Open in new tabDownload slide

Table 2

Median a_max(0.5) and upper 84 per cent confidence limit a_max(0.84) of maximum credible PGA (in units of g) at critical epicentral distances of 10, 20 and 30 (±5) km of the three cities. The strongest possible magnitude, m_max (Tsapanos 2001), which is considered as the ‘design’ earthquake is obtained by the application of the KSB estimator.

Open in new tabDownload slide

Papazachos (1995) estimated the seismic hazard for the city of Heraklion. Margaris (1995) derived an attenuation law for the territory of the south Aegean area where all the examined cities are located. This ‘local’ attenuation law, as well as the new Greek attenuation law (Margaris 2001) are depicted in Fig. 4, for magnitudes M= 5.0 (Fig. 4a) and M= 6.0 (Fig. 4b), respectively. One can observe that the values obtained by the ‘local’ attenuation law are overestimated in comparison with the new Greek attenuation law. According to Margaris (1995) this is mainly owing to the lack of sufficient strong motion records in the Hellenic trough system during the operation of the Greek network (accelerographs) 1972–1986. When they (Margaris 2001) derived the new Greek law they used 474 strong motion recordings from earthquakes over the whole Greek area, and the new attenuation law is based on 744 records of horizontal and 338 vertical components. So the new Greek attenuation law is considered to be more reliable than the older or the ‘local’ ones and for this reason it is used through the present study.

Figure 4

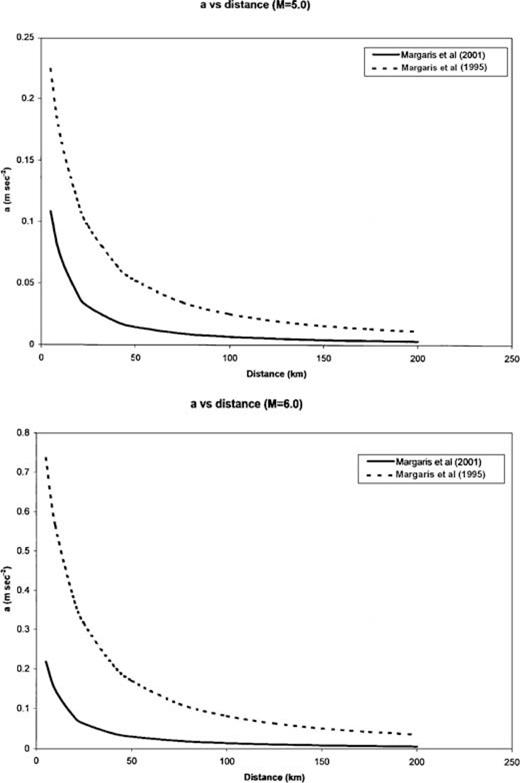
Attenuation law (in m s⁻²) as derived from: (a) Margaris (1995) for the south Aegean region, illustrated by the dashed line and (b) Margaris (2001) which is expressed by the new Greek law depicted by a solid line.

Open in new tabDownload slide

The concept of the ‘design’ earthquake describes the worst scenario at a site for which we assume the genesis for a maximum possible earthquake at very short distances, e.g. 10 km. The approach should therefore provide more conservative results. Based on this concept an effort is made to evaluate the seismic hazard ‘scenario’ for the three examined cities.

The results obtained through the application of the methodology are illustrated in Table 1. The maximum possible PGA at the sites of the three cities on Crete island were estimated. The median a_max(0.5) and the upper 84 per cent confidence limit a_max(0.84) are shown at the site of each city (e.g. by considering the city itself as the epicentre, R₀= 0 km, of the maximum possible magnitude m_max). This shock is considered as the ‘design’ event and consequently, the calculated PGA values deduced by this event are demonstrated as the ‘design’ PGA. Calculated values of PGA for critical epicentral distances of R₀= 10, 20 and 30 km (with σ_R=±5 km) are listed in Table 2. It is easy to observe that in all cases the obtained results of a_max(0.84) are about double compared with results from a_max(0.5). In Table 1 we observe that for the city of Heraklion a_max(0.84) = 1.91, which is about the double the acceleration due to gravity, and this is caused by the attenuation formula used, which seems to be so sensitive and does not fit well with the epicentral distance R₀= 0. This is a good paradigm of how careful we have to be in the interpretation of the calculated PGA at very short distances. In order to obtain reliable results Kijko & Graham (1999) suggested these distances should be greater than or equal to 10 km as we did in Table 2. As previously stated the new Greek attenuation law takes into account the factor of the soil conditions. All the presently investigated sites (cities) are located on the seashore. Therefore, alluvium is the dominant soil type for which the soil classified factor, S, is 2. It is well known (Papazachos & Papazachou 1997) that earthquakes in Greece cause damage when the peak ground acceleration exceeds 90 cm s⁻² (≈0.09g) but because of the different types of soil conditions in the affected areas this value is not valid.

5 Conclusions

The seismic hazard site-specific results for the three cities on the island of Crete (Chania, Rethymno and Heraklion) are assessed. The maximum possible earthquake magnitude m_max was estimated for the areas surrounding the three cities using a recently derived equation (1). The hazard parameter of PGA at the given sites was calculated and the results were expressed as: (1) probabilities that a given PGA value will be exceeded at least once during a time interval of 1, 5, 25 and 50 yr at the sites of the cities and (2) the maximum possible peak ground acceleration at each of these sites (Figs 123). The graphs that depicted the variation of the probabilities with the PGA values for given time spans are very useful not only from a theoretical but also from a practical point of view.

Also the concept of the ‘design’ earthquake is applied to derive the maximum PGA at the three sites. The effect of soil conditions was also taken into account. The earthquakes in Greece cause damage when the peak ground acceleration exceeds 90 cm s⁻² (≈0.09g) and because of the type of soil conditions in which the examined cites are situated (alluvium), the danger of heavy damage increases. It is known that all of these cities experienced such damage from previous earthquake events.

The estimated values of PGA are very useful, if the civil engineers were to take them into account when building, for instance, multifloor structures in Crete. The PGA estimated at sites contributes significantly to the determination of the national seismic codes, according to which buildings of different importance (ordinary, hospitals, plants, etc.) must be constructed and it conditions the priority of intervention for existing buildings. The estimated ‘design’ PGA values offer a seismic hazard scenario and is considered as a tool for engineers, regulators and planners to mitigate adverse social or economic effects of an earthquake and allows them to plan earthquake-resistant designs.

Acknowledgments

The author would like to express his sincere thanks to both reviewers for their constructive criticism of the paper.

References