-
PDF
- Split View
-
Views
-
Cite
Cite
Anthony J. Day, Christine Peirce, Martin C. Sinha, Three‐dimensional crustal structure and magma chamber geometry at the intermediate‐spreading, back‐arc Valu Fa Ridge, Lau Basin—results of a wide‐angle seismic tomographic inversion, Geophysical Journal International, Volume 146, Issue 1, July 2001, Pages 31–52, https://doi.org/10.1046/j.0956-540x.2001.01446.x
Close - Share Icon Share
Summary
In this paper the results of a tomographic analysis of a 3‐D wide‐angle seismic refraction data set acquired at the Valu Fa Ridge (VFR) in 1995 are presented. The VFR is an intermediate‐spreading ridge located in the southern Lau back‐arc basin in the southwest Pacific. The ridge comprises three morphological segments, the Southern, Central and Northern Valu Fa Ridges, separated by overlapping spreading centres (OSCs). Previous seismic experiments have identified a robust axial magmatic system beneath the central segment (CVFR) and the OSC with the northern segment (NVFR). The experiment described in this paper aimed to resolve details of the structure of this magma chamber and the adjacent post‐rift crust.
A regularized inversion scheme that minimizes model roughness was applied to the first‐arrival traveltime picks made from the wide‐angle data. A quantitative approach for determining data uncertainties is described based on the signal‐to‐noise ratio of the arrivals. Several initial model assumptions were tested, including one with a thin melt lens, representing a seismic reflector identified in previous studies, explicitly included in the initial model. The inversion results suggest that crustal layer 2 exhibits northward thickening, which mirrors a similar northward thickening of the whole crust. In addition, local thinning of layer 2 is identified in the vicinity of the boundary between pre‐ and post‐rift crust, which is thought to represent thinning of the crust prior to the onset of rifting. Axial low‐velocity anomalies are identified in layer 2B/C and layer 3. The models are consistent with a continuous ∼ 6 km wide negative velocity anomaly in layer 3 with an amplitude of ∼ 0.7–0.9 km s−1 relative to off‐axis post‐rift crust. This anomaly is consistent with the presence of an axial mush zone comprising a small percentage (< 1 per cent) of partial melt. The negative velocity anomaly in layer 2B/C is modelled with its largest amplitude (∼0.5 km s−1) beneath the northern OSC. Possible origins for this anomaly include locally thicker crust or locally higher porosity near the OSC, or a high‐temperature anomaly associated with the axial magmatic system.
1 Introduction
The global mid‐ocean ridge system is the site of oceanic crustal accretion, and geophysical investigations have played an important part in developing our understanding of how these accretionary processes work. Numerous seismic studies have revealed details of the 2‐D structure of spreading centres, including seismic low‐velocity zones and reflection events that have revealed regions of partial melt in the middle and lower crust beneath the ridge axis. Much of the evidence for the existence of these features is derived from experiments conducted at the fast‐spreading East Pacific Rise (EPR, e.g. Harding . 1989; Vera . 1990; Kent . 1990), although similar features have also been identified at the intermediate‐spreading Valu Fa (Collier & Sinha 1990, 1992; Turner . 1999) and Juan de Fuca Ridges (Rohr . 1988; Christeson . 1993), and the slow‐spreading Reykjanes Ridge (Navin . 1998). However, many ridges exhibit segmentation in their morphology (Macdonald . 1988), geochemistry (Langmuir . 1986) and gravity field (Kuo & Forsyth 1988; Lin . 1990), indicating that crustal structure at mid‐ocean ridges (MORs) is 3‐D. Direct imaging of the 3‐D seismic velocity structure of the oceanic crust requires a tomographic approach, and this technique has been successfully applied to a number of oceanic crustal studies (e.g. Toomey . 1990, 1994; Sohn . 1997; Barclay . 1998; Magde . 2000; Dunn . 2000).
One such experiment was undertaken at the intermediate‐spreading Valu Fa Ridge (VFR) (full spreading rate 60 mm yr−1; Taylor . 1996) in 1995. The VFR is situated on the eastern edge of the Lau Basin, a back‐arc basin in the southwest Pacific located between the volcanically active Tonga Ridge and the inactive Lau Ridge (Fig. 1). The VFR is subdivided into three distinct morphological segments, referred to as the Northern, Central and Southern Valu Fa Ridges (NVFR, CVFR and SVFR, respectively), each separated by overlapping spreading centres (OSCs) (von Stackelberg 1988; Wiedicke & Collier 1993). The Lau Basin is believed to have opened by southward propagation of the spreading axis, and the southernmost end of the SVFR represents the current location of the propagating rift tip (Wiedicke & Collier 1993). Normal‐incidence seismic studies of this ridge system have observed a robust, reversed‐polarity intracrustal reflection event along the entire length of the CVFR and its overlap with the NVFR, which has been interpreted as a reflection from the top of a thin, sill‐like axial melt lens (Morton & Sleep 1985; Collier & Sinha 1992). This paper is concerned with determining the 3‐D crustal structure above and below this feature.
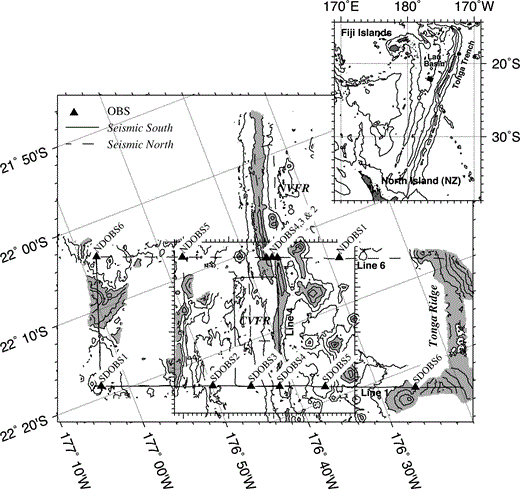
The Valu Fa Ridge seismic study (after Peirce . 1996; Turner . 1999). The seismic experimental configuration overlying the bathymetry of the study area is shown. Profile lines are shown by solid (Seismic South) and dashed (Seismic North) lines, and the main 2‐D seismic profiles are annotated. Bathymetric contours at 250 m intervals have been plotted, and seabed depths shallower than 2000 m have been shaded to show the locations of the Central and Northern Valu Fa Ridges and the Tonga Arc. OBS deployment positions are shown by triangles. Seismic data from the region enclosed by the box are discussed in this paper. The box is graduated at 1 km intervals. The inset shows the location of the work area in the Southern Lau Basin.
The controlled‐source wide‐angle seismic data interpreted in this paper were collected as part of a multidisciplinary geophysical experiment conducted aboard the R/V Maurice Ewing (EW9512) ( Peirce . 1996 ). The acquisition geometry shown in Fig. 1 may be divided into a number of across‐axis and axis‐parallel 2‐D profiles. Forward modelling of the wide‐angle and coincident normal‐incidence seismic data acquired along lines 1, 4 and 6 ( Fig. 1) is described by Turner . (1999) . The most prominent features of their models are a thin, sill‐like axial low‐velocity body underlain by a broader low‐velocity zone where seismic velocities are depressed by up to 0.4 km s−1 relative to the off‐axis crust. The sill‐like body has a first‐order upper boundary identified from reflections in the normal‐incidence and wide‐angle data, and corresponds to the negative‐polarity axial reflection identified in previous normal‐incidence seismic studies ( Morton & Sleep 1985; Collier & Sinha 1992). These features are interpreted as representing a thin sill‐like melt lens containing a continuously connected melt fraction overlying a broader mostly crystalline region containing a small melt fraction (< 1 per cent).
The acquisition geometry ( Fig. 1) also provides 3‐D ray coverage of the axial region of the CVFR in the area located between the two across‐axis model profiles. This paper considers this subset of shot–receiver pairs to determine the 3‐D crustal velocity structure beneath and to the west of the CVFR using a tomographic approach. This method allows the nature of any along‐axis variation in crustal structure, which cannot be properly evaluated from isolated 2‐D profiles alone, to be investigated.
2 Experiment description
In addition to the wide‐angle seismic experiment shown in Fig. 1, normal‐incidence seismic profiles, controlled‐source electromagnetic and underway bathymetry, gravity and magnetic data were also acquired during cruise EW9512 ( Peirce . 1996 ). Interpretation of the gravity data is described by Turner . (1999) and in greater detail by Peirce . (2000) . Full details of the wide‐angle seismic experimental configuration are given by Turner . (1999) and hence only a brief overview is provided here.
Wide‐angle seismic data were recorded using six ocean bottom seismographs (OBSs), each comprising a hydrophone and gimballed three‐component geophone package as sensors. The instruments were successively deployed along line 1 (Seismic South) and line 6 (Seismic North) (see Fig. 1). The seismic source was an ∼ 8500 in3 (140 l) airgun array tuned to a dominant frequency of ∼7–8 Hz. Normal‐incidence and wide‐angle data were acquired contemporaneously with shots fired along the profiles indicated in Fig. 1 at 40 s intervals for the normal‐incidence acquisition. For the wide‐angle acquisition the OBSs were programmed to record traces comprising 20 s of data (at a 5 ms sample interval) every 80 s, i.e. alternate shots. This recording strategy resulted in an effective shot spacing for the wide‐angle experiment of ∼200 m and a shot interval for the normal‐incidence data acquisition adequate to identify prominent intracrustal reflection events.
3 Tomographic method
3.1 Regularized inversion
Tomographic inversions were performed using a regularized inversion algorithm described in full by Zelt & Barton (1998). An initial velocity model is parametrized on a uniform linear grid of nodes and the predicted first‐arrival traveltimes and ray paths for each shot–receiver pair are calculated using a finite difference method ( Vidale 1990; Hole & Zelt 1995; Zelt & Barton 1998). The shot and receiver positions were transformed from a geographical coordinate system onto a linear grid using an oblique transverse Mercator projection centred at 176°40′W, 22°20′S and with an equator azimuth of 111°, chosen such that the y‐axis approximately parallels the ridge crest. The inversion step calculates the best‐fitting velocity perturbation field to minimize the traveltime residuals, in other words the difference between the observed and calculated first‐arrival traveltimes. This inverse problem is usually underdetermined, so the inversion is regularized by applying additional constraints. The regularization scheme of Zelt & Barton (1998) minimizes model roughness, as measured by the second spatial derivative. The objective function Θ minimized at each step is
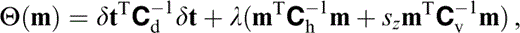
where m and δt are the model and traveltime residual vectors, respectively, Cd is the data covariance matrix, and Ch and Cv the horizontal and vertical roughening matrices containing the 2‐D and 1‐D finite difference second‐derivative operators, respectively. The sz parameter controls the relative importance of maintaining vertical versus horizontal smoothness, and λ is the trade‐off parameter controlling the relative importance of minimizing data misfit versus model roughness ( Zelt & Barton 1998).
The velocity perturbation is added to the initial model to create a new model, and the process repeated until a model is produced with a normalized (χ2) misfit of 1.0, indicating that the model satisfies the observed traveltime data within predetermined error bounds. At each iteration, up to five progressively decreasing values of λ are tested until a local minimum in normalized misfit is found. The resulting model and value of λ are carried forward to the next iteration. Large values of λ imply a high degree of smoothing, so by this method the longest‐wavelength perturbations are defined by the earliest iterations. The model is refined by the addition of shorter‐wavelength perturbations by later iterations as the value of λ becomes smaller.
3.2 First‐arrival traveltime data
First‐arrival traveltimes were picked from the vertical‐component geophone record sections wherever possible since this channel generally showed highest signal‐to‐noise ratio (SNR). As there are 2124 individual seismograms, picking was performed with the aid of an automatic picking tool that picks the traveltimes of arrivals for all seismograms between two bracketing seismograms for which the arrival position has been defined by the user. The method is based on a cross‐correlation process using a reference seismogram that is a distance‐weighted average of the two bracketing seismograms. Data quality is generally good as exemplified by the record sections in Turner . (1999) . Example seismograms recorded by NDOBS5 and the associated first‐arrival traveltime picks are shown in Fig. 2 for reference.
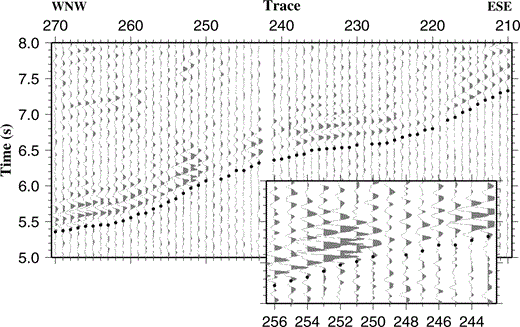
Example seismograms recorded by the vertical‐component geophone of NDOBS5 showing first‐arrival traveltime picks (centres of the black dots). The seismograms have been plotted at true amplitude with a 20 Hz low‐pass filter applied to remove high‐frequency noise. No topographic correction or reduction velocity has been applied. The seismograms correspond to shots at offsets of approximately 15–28 km along line 6 (see Fig. 1). The inset shows detail of low‐amplitude arrivals associated with rays that have passed through the axial magmatic system.
The tomographic method assumes that the predicted first‐arrival ray paths are a close representation of the path actually taken by energy in the subsurface. In the presence of large velocity contrasts such as those associated with an axial magmatic system, complex propagation paths may be encountered. In particular, Wilcock . (1993) demonstrated that sharp velocity contrasts associated with an axial melt lens similar to that modelled at the VFR give rise to diffracted arrivals with unstable ray paths. In particular they modelled an abrupt change in the first‐arrival ray path from a diffracted arrival travelling above the melt lens to one travelling below, leading to the possibility that the first‐arrival ray paths predicted by the forward modelling method may be in error. Thus when picking first‐arrival traveltimes care must always be taken with phase identification. For the VFR data set, Turner . (1999) noted amplitude reductions associated with rays passing through the axial low‐velocity zone (LVZ) that they attribute to increased attenuation, although scattering at the edges of the axial melt lens may also contribute to the amplitude reduction. According to the models of Turner . (1999) the predicted first‐arrival ray paths for the low‐amplitude arrivals between traces 245 and 249 in Fig. 2 pass through the LVZ. Inspection of these traces reveals no clear‐cut evidence for diffracted arrivals in the VFR data set. The apparent absence of diffracted arrivals may reflect a more gradual velocity change at the edge of the melt lens rather than a sharp discontinuity as modelled by Wilcock . (1993) . Alternatively, diffracted arrivals may be present but are of such low amplitude that they are indiscernible above the background noise.
In the example section shown in Fig. 2, the waveform appears to be of a similar shape across the section, including the regions of reduced amplitude, and first‐arrival traveltime picks for low‐amplitude arrivals were made on this basis. All of these observations suggest that all the first‐arrival traveltime picks included in the inversion represent refracted arrivals for which the forward modelling method reliably determines predicted traveltimes and ray paths.
3.3 Initial model
As the inversion method is only capable of reliably determining relatively small perturbations in the velocity field, it is important that the initial velocity model be a good representation of the gross structure being modelled. A number of initial models were considered, and these are described in detail in Section 4. The method used to create the simplest initial model is described below.
Turner . (1999) considered 2‐D subsets of the entire seismic data set acquired during cruise EW9512, and used a forward modelling approach to derive velocity models for those lines. This work indicated that the crust may be divided into three layers, each with distinct velocity gradients, separated by second‐order interfaces corresponding to crustal layers equivalent to layers 2A, 2B/C and 3 as described by Houtz & Ewing (1976) and Bratt & Purdy (1984). Whilst the thicknesses of these layers showed some variation, the layer boundaries were found to approximately parallel the seafloor. Hence the initial model was constructed with seafloor‐parallel layer boundaries, with slight modifications as outlined below.
A 1‐D crustal velocity structure was derived by taking a 1‐D average of the velocity structure determined by Turner . (1999) for lines 1 and 6, shown in Fig. 3(a). These lines were used as they were modelled using the maximum in‐line ray coverage and thus provide the most reliable estimate of the gross crustal structure. Only those parts of the 2‐D lines that fall within the 3‐D study area were averaged. When a first‐order boundary corresponding to the Moho was included in the initial model, some rays were predicted to travel through the mantle layer. There is no indication in the 3‐D subset of the observed seismic data that suggests that arrivals from the mantle have been recorded, as all the shot–receiver offsets in this subset are less than the offset at which the triplication point between crustal diving rays, mantle diving rays and the Moho reflection is observed. Hence these predicted ray paths must be in error. To avoid this problem, the mantle layer was removed and the layer 3 velocity gradient extrapolated to the base of the 3‐D model at 12 km below sea level as shown in Fig. 3(a). The water column velocity structure was determined using a sound velocity dip meter deployed at 176°36′W, 22°26′S ( Peirce . 1996 ) and may be approximated by four layers with horizontal boundaries as shown in Fig. 3(b). Throughout the inversion, the water column velocity structure was not allowed to vary.
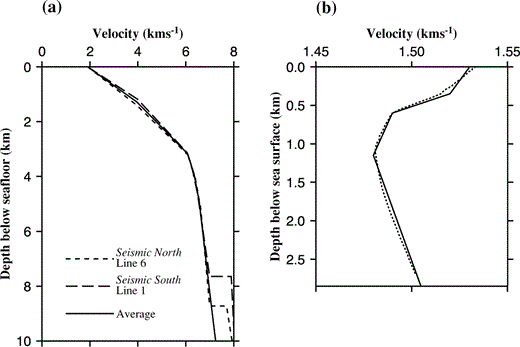
(a) 1‐D average velocity profiles derived from the 2‐D across‐axis models of Turner . (1999). See text for details. The average of these two models forms the basis of the initial model used for 3‐D inversion. (b) Water column velocity structure. The dashed line shows the profile measured using a sound‐velocity dip meter. The solid line is the approximation to this profile used in the initial model.
The seafloor was determined from swath bathymetry data collected during cruise EW9512, and was projected onto a linear grid as outlined in Section 3.1. As swath bathymetry data coverage within the 3‐D study area was incomplete (see Fig. 1), gaps were filled by sampling a best‐fitting surface fit to the gridded bathymetry data. A 1 km square averaging filter was applied to smooth artefacts in the bathymetry data arising from the gridding algorithm and to remove effectively small‐scale features to which the seismic data are insensitive. The filter parameters were chosen to reflect the approximate diameter of the footprint of the wave front at the seafloor for the average water depth in the study area, where the footprint is defined as the area over which seismic energy propagating across the seafloor interferes constructively based on Fresnel zone considerations. The resulting smoothed bathymetry still contained a number of small‐scale irregularities associated with seamounts and the ridge system itself. As this scale of feature is unlikely to be present at greater depths, further smoothing was applied to create the intracrustal layer interfaces of the initial model. Thus a 1.5 km square averaging filter was applied at the layer 2A−2B/C interface, and a 2 km square averaging filter was applied at the layer 2B/C−3 interface and all deeper interfaces. The choice of these averaging filters is subjective, based on the necessity to generate a smooth initial model. Such models are desirable for achieving stable inversions, and better represent the resolution that can be achieved at depth. An example cross‐section through the resulting initial model is shown in Fig. 4.
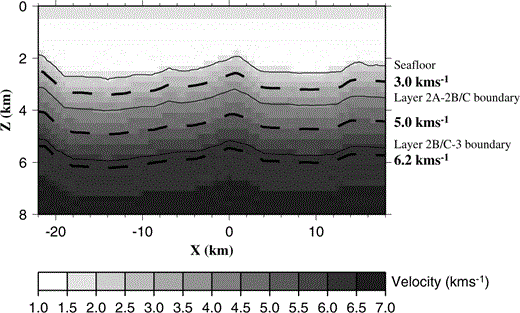
Typical cross‐section through the 1‐D initial model at y = 0 km showing the principal layer boundaries and the positions of the 3.0, 5.0 and 6.2 km s−1 constant‐velocity planes. Vertical exaggeration: × 3. Axes are annotated in model dimensions. z: depth; x: across‐model offset; y: along‐model offset.
3.4 Choice of inversion parameters
For inversion the node spacing of the forward grid should be sufficiently small to allow first‐arrival traveltimes to be calculated to appropriate accuracy, reflected by the traveltime residual uncertainties, which in this case lie in the range 22–76 ms. The traveltime residual uncertainties will be discussed fully in Section 3.5 and are summarized in Table 1. To determine the appropriate node spacing for this data set synthetic tests were performed in which rays were traced through simple 1‐D models. The velocity functions were of the form

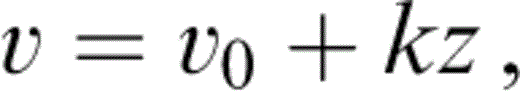
where v = velocity at depth z below the datum level, v0 = velocity at the datum level, and k = vertical velocity gradient. For a shot–receiver pair at the datum level separated by a distance x, the first‐arrival traveltime, t, may be expressed analytically ( Sheriff & Geldart 1995) as
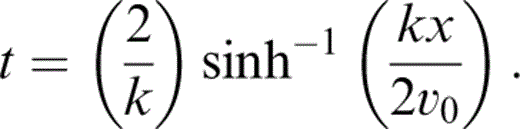
Hence, the accuracy of the forward modelling step may be assessed by comparing the arrival time predicted by the finite difference method with the theoretical time defined by eq. (3). For the synthetic tests, 50 × 50 × 12 km 1‐D velocity models were constructed, with a single source offset from the centre of the model by three‐quarters of a node spacing in both the x‐ and y‐directions, and a regular grid of receivers separated by one node spacing in the x‐ and y‐directions directions, but offset from model nodes by a quarter of a node spacing in both the x‐ and y‐directions. All sources and receivers were placed at half a node spacing below the top of the model. This asymmetry was introduced to avoid placing shots and receivers on model nodes, thus negating any bias that may be introduced by doing so and better simulating the geometry of the real experiment, where sources and receivers are unlikely to lie exactly on model nodes. Only receivers within 24 km of the source were considered.
For a constant node spacing, v0 was found to be the most significant parameter determining the accuracy of traveltime prediction; the larger the value of v0, the better the finite difference algorithm performed. For constant v0, low values of the velocity gradient, k, were found to give more accurate results than high values. The lowest velocities and largest velocity gradient encountered in the 1‐D initial model described in Section 3.3, and illustrated in Fig. 3, occur in layer 2A. Hence, in order to determine an appropriate node spacing for the velocity models, a model with the velocity at the depth of the source and receivers set to 2.0 km s−1 and a velocity gradient of 2.0 s−1 was used, both of these being representative of the values modelled in layer 2A.
Several node spacings were tested, and the resulting traveltime errors for 400, 200 and 100 m node spacings are shown in Fig. 5. In this figure, traveltime error is plotted against both shot–receiver offset and shot–receiver azimuth, the latter defined as 000° along the positive y‐axis and 090° along the positive x‐axis. All three models show azimuthal dependence of the accuracy of the finite difference traveltime calculator, which is most accurate when the shot–receiver azimuth parallels one of the coordinate axes and least accurate at ∼45° to these directions. For the observed 3‐D data set, all shot–receiver offsets lie in the range 2.8–36.1 km. Within this range, the 400 m grid produces errors of up to 20 ms, similar in magnitude to the uncertainty in the best traveltime picks, so this node spacing was not felt to be sufficiently accurate. The 100 m grid is most accurate (errors up to 6 ms) and is computationally very much more expensive since reducing the node spacing by a factor of four produces a 64‐fold increase in the number of model nodes. As the improvement in accuracy of the 100 m grid relative to the 200 m grid is small compared to the range of traveltime pick uncertainties (compare Figs 5b and c), a 200 m node spacing was chosen for the forward modelling step as this provides the best compromise between accuracy and computational efficiency, producing errors of no more than 10 ms within the offset range of interest.
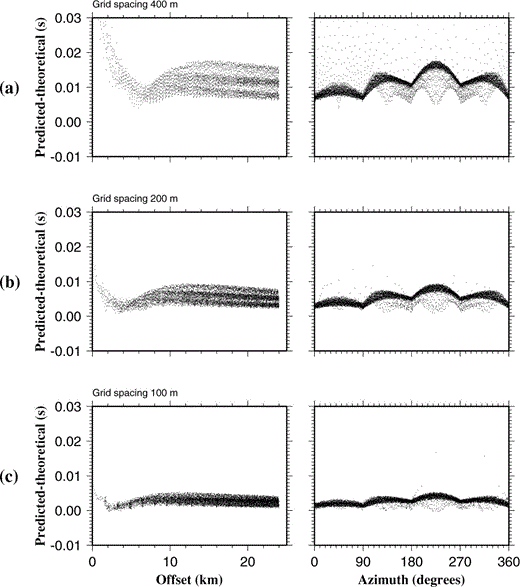
Graphs showing differences between traveltimes predicted by the 3‐D finite difference method and the analytic solution for the 1‐D velocity model, plotted against both shot–receiver offset and shot–receiver azimuth. Shot and receiver geometries are described in the text. All these models show that accuracy has an azimuthal dependence. (a) Forward grid spacing of 400 m. With this grid spacing an error of ∼20 ms is produced, similar in size to those of the actual traveltime picks. (b) Forward grid spacing of 200 m. With this grid spacing an error of ∼ 10 ms is produced, providing the best compromise between accuracy (cf. traveltime picks) and computational efficiency. Only a quarter of the modelled receivers are shown. (c) Forward grid spacing of 100 m. With this grid spacing errors of ∼ 6 ms are produced at the expense of an eightfold increase in computation time over the 200 m grid model. Only 1/16 of the modelled receivers are shown.
Preliminary inversions were performed using the initial model described in Section 3.3 to determine the most appropriate values for inversion parameters. The inversion step is performed using a cell‐based grid, then converted to a node‐based grid by averaging the eight cells surrounding each node to produce a smoothly varying anomaly field. The inversion cells are larger than the velocity model node spacing as the spatial resolution of anomalies that may be determined by the inversion process greatly exceeds 200 m at all depths (see Section 3.6), and they may also be different sizes in the horizontal and vertical directions. Since the largest changes in the velocity structure are expected to occur with depth rather than laterally, and this structure is broadly incorporated in the initial model, a vertical cell size of 400 m was chosen. With larger cell sizes, there is a danger of the inversion smoothing vertical structure, which is known to exist, especially where the velocity gradients are high in layer 2. The degree of vertical smoothing may also be controlled by the sz parameter in eq. (1). However, varying this parameter did not significantly affect the appearance of the final models, so it was set to 1 for simplicity so that vertical smoothing was entirely controlled by the vertical inversion cell size. A horizontal cell size of 1000 × 1000 m was chosen. This cell size results in a number of cells being sampled by only a few rays or no rays at all (see Section 3.6). However, when the horizontal cell size was increased, the resulting best‐fitting anomaly pattern showed similar sized features, but of much larger magnitude. As the smaller cell size did not introduce small‐scale artefacts beyond the resolving power of the inversion method, but produced a smoother final model, the smaller cell size was preferred.
As described in Section 3.1, for each iteration of the inversion, up to five values of the trade‐off parameter λ were tested. The initial value of λ for the first iteration was set to 10, as the value of λ for the final model was always found to be less than 3 and using higher initial values for λ merely increased the number of iterations required for convergence.
3.5 Traveltime residual uncertainties
A reliable estimate of the uncertainty associated with each traveltime residual is required as the inversion weights each traveltime residual according to its uncertainty (see eq. 1), and the criterion by which the model is deemed to have converged is based on the predicted traveltimes matching the observed traveltimes within their uncertainties. There are several errors that combine to produce the overall error associated with each traveltime residual. These will now be discussed in turn.
The most variable contribution to the uncertainty arises from the precision with which the first‐arrival traveltimes are actually picked. Pick position uncertainty is related to the SNR ( Zelt & Forsyth 1994), being worst where the SNR is low. The performance of the automatic picking tool, which was used to pick the majority of first‐arrival traveltimes, was investigated to obtain a relationship between SNR and pick position uncertainty, which could then be applied to each individual arrival to determine the contribution to the total uncertainty arising from uncertainty in the traveltime pick position alone. A reference seismogram was created by stacking a number of adjacent seismograms that showed strong first arrivals, and the SNR of the resulting synthetic first arrival artificially enhanced by multiplying all samples prior to the picked arrival by 0.1. A set of 1000 synthetic seismograms was then created with each one offset by a random amount in the range ± 50 ms (10 samples). Noise was then added with a frequency spectrum derived from a 15 s section of observed data that contained no arrivals and was thus representative of the background noise. The true position of the traveltime pick was inserted for every seventh seismogram, representative of the typical spacing of bracketing picks used when picking the real data, and the automatic picking tool applied to determine the position of the remaining traveltime picks. These were then compared with their known positions to determine the picking error for each individual seismogram. The average SNR and standard deviation of the picking error, the latter defining the pick position uncertainty, for those picks made by the automatic picking tool were then determined. This process was repeated for a number of SNRs, reference traces and noise frequency spectra, resulting in a series of pick position uncertainty versus SNR curves, as illustrated in Fig. 6(a).
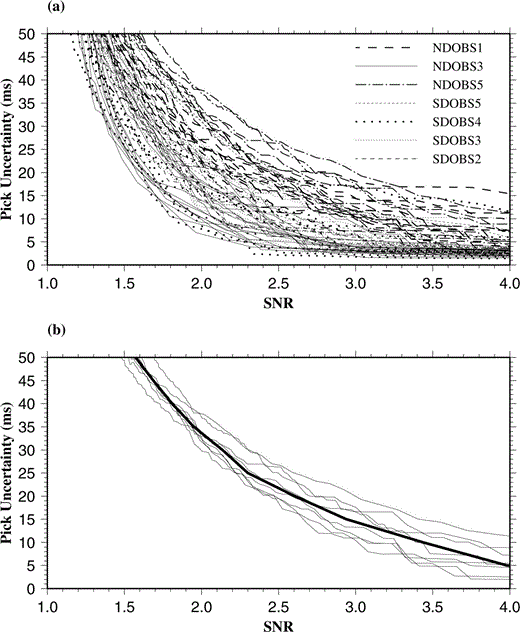
Graphs showing a number of pick position uncertainty versus SNR relationships, showing the general trend of an increase in uncertainty with decrease in SNR. These curves were used to derive relationships for assigning pick position uncertainties based on SNR. (a) Complete set of pick uncertainty versus SNR curves. Several curves are shown for each OBS position. Each curve represents a different reference trace (see text for details). (b) Pick uncertainty versus SNR curves for NDOBS1. The thick line is the median curve, which is used to assign uncertainty to each traveltime pick based on SNR for arrivals recorded by NDOBS1 and the sampling rate of 5 ms. Similar median curves were created for all OBS positions based on the curves shown in (a). See text for details.
It was found that using a time window of 300 ms (60 samples) before and after the pick position for calculating the SNR produced consistent results, except where the reference seismograms contained a strong secondary arrival within this time window after the first‐arrival pick. Careful selection of shorter time windows to calculate the SNR for these picks resolved this problem, and indicated that there was very little variation in the pick uncertainty versus SNR relationships due to differences between reference seismograms. However, the noise frequency spectrum had a strong effect on the shape of the pick uncertainty versus SNR curve. The noise spectra are similar to that of the source signature, having a dominant frequency of ∼ 8 Hz, indicating that noise is mainly derived from reverberations in the water column from earlier shots. However, most of the noise spectra also have a strong secondary peak at ∼12–14 Hz and a significant background component at higher frequencies (> 20 Hz). The strengths of the high‐frequency component and secondary peak relative to the dominant 8 Hz component affect the shape of the pick uncertainty versus SNR curve. Where the frequency spectrum of the background noise is similar to that of the signal, the pick uncertainty for a given SNR is larger than when the signal and noise spectra are distinctly different. The strengths of the background high‐frequency component and the secondary peak are observed to be approximately constant for each OBS position, and are believed to derive from scattering of energy at the seafloor near each instrument. Rough seafloor causes more scattering and results in more background high‐frequency noise and a stronger secondary peak, a phenomenon also observed by Navin (1996) at the Reykjanes Ridge. Hence, a typical noise frequency spectrum was selected for each OBS position when calculating the curves shown in Fig. 6(a). Median pick uncertainty versus SNR curves were obtained for each OBS position, and were applied to determine the uncertainty for each traveltime pick to a precision of 5 ms, the sampling interval. An example is shown in Fig. 6(b). The range of traveltime pick uncertainties determined in this way was 0–50 ms, and any traveltime picks whose SNR was less than the lower limit for the 50 ms interval were discarded.
Some seismograms contain substantial high‐frequency (∼ 60 Hz) noise generated over short periods of time whilst writing data to each instrument's hard disk. A Butterworth bandpass filter with a high‐cut of 40 Hz was applied to allow these traces to be picked. The bandpass filter had a noticeable effect on the noise frequency spectrum, so a further set of pick uncertainty versus SNR curves were created for those picks where the bandpass filter was applied. Also, the frequency response of the hydrophone to background noise and disk spin is different to the response of the vertical geophone. Some picks were made from hydrophone sections wherever it was not possible to use the vertical‐component geophone sections, so bandpass filtered pick uncertainty versus SNR curves for the hydrophone data with a high‐cut of 20 Hz were also constructed to allow pick uncertainties associated with those picks made from hydrophone sections to be assigned.
The inversion algorithm assumes that the positions of shots and receivers within the model space are accurately known. In reality this is not the case, so each traveltime residual uncertainty has a contribution from uncertainty in both shot and receiver positions. The approximate deployment positions are known for each OBS based on GPS satellite fixes when each instrument is deployed from the deck of the survey vessel. However, instrument drift occurs on passage to the seabed. Hence, true OBS positions were determined using direct water wave arrivals recorded by each instrument. For each OBS deployment position, the shot–receiver offset was calculated for each shot for which a direct water wave arrival was observed, and ray tracing through the known water column structure from each OBS position to each shot performed using rayinvr ( Zelt & Smith 1992). The nominal OBS depth was determined from the swath bathymetry data, and a shot depth of 8 m, the nominal tow depth of the airgun array, was assumed. The OBS position was then manually adjusted and the process repeated until the best fit between observed and calculated direct water wave arrival times was obtained. For some OBS positions, the instrument depth was also altered by up to 35 m from the value determined from the swath bathymetry data in order to improve the fit further. The relocated OBS position was used in subsequent inversions. The component of traveltime residual uncertainty arising from uncertainty in the OBS position was determined by multiplying the RMS misfit of the direct water wave arrival times used to calculate the OBS position by the ratio of the velocity at the top of layer 2A to the average water column velocity. This adjustment was necessary because the crustal first arrivals used in the inversion approach the instrument from below. The range in uncertainties was found to be 7–11 ms. Each shot position was GPS navigated, but there is no independent estimate of the GPS accuracy available. Hence, an average RMS misfit of direct water wave arrival times (11 ms) was taken to represent the component of traveltime residual uncertainty arising from uncertainty in shot position on the assumption that this uncertainty is the dominant contributor to the direct water wave arrival time misfit.
A number of other smaller potential sources of uncertainty were also considered. Possible variations in the water column velocity structure were assessed using eight temperature profiles collected elsewhere in the Valu Fa Ridge survey area during cruise EW9512 ( Peirce . 1996 ). Variations were found to be minimal (4.1 × 10−4 km s−1 at 1.90 km depth, giving rise to a timing uncertainty of 0.4 ms). The nominal accuracy of the swath bathymetry data is 10 m, giving a small possible timing error due to the difference in velocity between the water column and the top of the crust (1.5 ms). The uncertainty due to inaccuracy of the finite difference traveltime calculator, described in full in Section 3.4, was estimated as 2 ms. A summary of the contributions to the uncertainty associated with each traveltime pick is given in Table 1.
3.6 Resolution analysis
Analysis of the resolution of the approach to modelling and the parameters chosen for that modelling was undertaken using the method of Zelt (1998), in which a number of checkerboard tests were performed to assess the scale of features that may be resolved at a given point in the model. The approach involved creating a synthetic model with a known anomaly distribution relative to a typical initial model (for this study the initial model described in Section 3.3 was used) and performing ray tracing through this model to generate synthetic traveltimes for first arrivals that would be observed for the shot–receiver pairs considered in the real inversion experiment. Noise was then added to the synthetic first‐arrival traveltime data according to the traveltime residual uncertainty associated with the equivalent traveltime picks for the real data, and an inversion performed. The semblance between the recovered and known anomaly fields was then determined for each point in the model using a planar, circular semblance operator of radius 2.5 km. Anomaly fields that vary sinusoidally in both x and y, with amplitude equal to 5 per cent of the background velocity, were used to create smooth velocity models for which the ray tracer is well behaved. An example of a synthetic model, the anomaly field recovered by the inversion, and the semblance between the synthetic and recovered models is shown in Fig. 7. In this figure, anomalies relative to the initial model along the 3.0, 5.0 and 6.2 km s−1 constant‐velocity planes of the initial model are shown (cf.Fig. 4). These planes correspond to approximate depths of 0.7, 2.2 and 3.5 km beneath the seafloor, and represent the middles of crustal layers 2A and 2B/C and the upper part of layer 3, respectively. Those nodes for which the semblance exceeds 0.7, depicted by the area enclosed by the solid white contour in Fig. 7(c), are deemed to be well resolved ( Zelt 1998). Inspection of Fig. 7 indicates that within the area where the semblance exceeds 0.7, the true positions of the positive and negative anomalies have been recovered, but their amplitudes have generally been underestimated. For those areas for which the semblance exceeds 0.9, enclosed by the dotted white contour in Fig. 7(c), the recovered amplitudes are much better estimates of the true values.
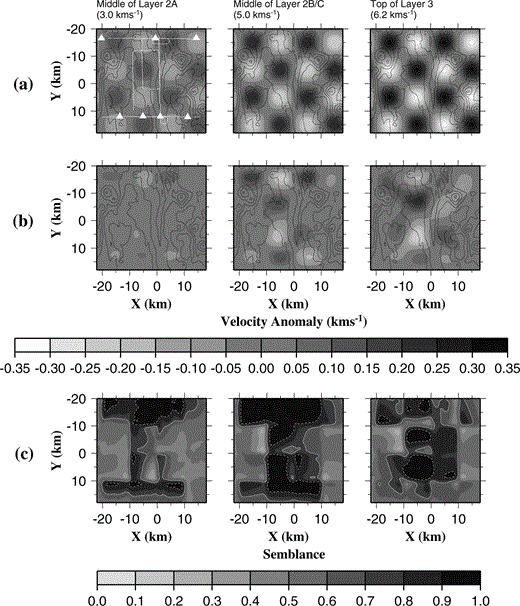
Checkerboard tests of model resolution. (a) Example of the simplest checkerboard model with 10 km checkerboard size. The anomaly field relative to the background model is plotted for the layer 2A, layer 2B and layer 3 planes as described in the text and indicated in Fig. 4. Bathymetric contours at intervals of 250 m are plotted. OBS positions (white triangles) and ship tracks (white lines) are shown on the layer 2A plot for reference. (b) Velocity anomaly recovered by inversion of synthetic data traced through the model shown in (a). (c) Semblance between the synthetic and recovered models shown in (a) and (b), respectively. The solid and dashed contours are at semblance values of 0.7 and 0.9, respectively. For areas where a semblance of 0.7 has been exceeded, the true positions of both positive and negative anomalies have been recovered, but their amplitudes have been underestimated. For areas where a semblance of 0.9 has been exceeded, recovered amplitudes are better estimates of true amplitudes.
There is a clear correlation between the position of the anomaly shown in Fig. 7(a) and those areas that are well resolved shown in Fig. 7(c). To eliminate this effect, a number of different types of checkerboard were tested, as described by Zelt (1998), where the checkerboard pattern shown in Fig. 7(a) was altered by reversing its polarity, offsetting the anomaly pattern by a quarter of the period in x and y, rotating the anomaly pattern through 45°, and all possible combinations of these variations to obtain eight distinct checkerboards. The semblances between the recovered and known anomaly fields for each checkerboard are then averaged. This process is performed for several checkerboard sizes, which are defined as half the wavelength of the sinusoid. For this study, the average semblance was calculated for checkerboard sizes of 4, 5, 6, 8, 10 and 15 km. For a given point in the model, the checkerboard size for which the average semblance equals a given threshold is defined as the horizontal resolution of the model at that point. The horizontal resolution at various depths in the model derived using semblance thresholds of 0.7 and 0.9 are shown in Figs 8(b) and (c), respectively.
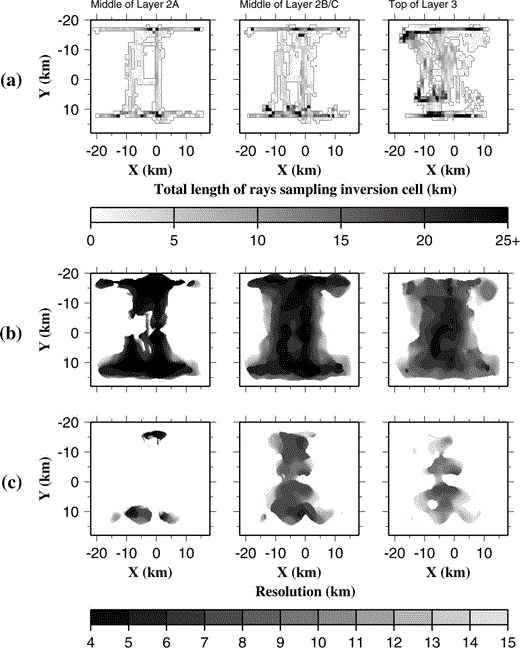
(a) The cumulative ray path length sampling each inversion cell for the planes shown in Fig. 4. The density of ray coverage is greatest in layer 3. (b), (c) Model resolution determined by the method described in Section 3.6 with semblance thresholds of 0.7 and 0.9, respectively. Model resolution is shown to be better in Layer 2B than in layer 3, and of the order of ∼ 6 km or better. For a semblance threshold of 0.7, (b) shows that small‐scale anomalies in layer 2 may be detected but their amplitudes are likely to be underestimated. For a semblance threshold of 0.9, resolution is poor in layer 2A, except in a few areas related to OBS locations.
The checkerboard method described above provides a better estimate of model resolution than the path length distribution shown in Fig. 8(a), since it takes account of variations in the azimuthal coverage between cells and the differences in traveltime residual uncertainty between shot–receiver pairs. Traveltime residual uncertainty generally increases with shot–receiver offset, so deeper parts of the model tend to be sampled by rays with larger traveltime residual uncertainties than shallower parts. Hence although Fig. 8(a) shows generally higher ray coverage in layer 3 than in layer 2B/C, Figs 8(b) and (c) show that the model resolution is generally better in layer 2B/C than in layer 3. At the target depths of the VFR experiment (layer 2B/C and layer 3), Fig. 8(b) shows that the model resolution is generally 6 km or better, which represents the scale of features whose positions may be determined by the inversion. Fig. 8(c) represents the scale of features whose amplitude may also be determined with reasonable accuracy. It can be seen that, for this survey, amplitude resolution is generally 10 km or smaller at the target depths, although areas of good resolution are much more disjointed by this criterion. The largest discrepancies in apparent resolution between the two semblance criteria occur in layer 2A. Using a threshold of 0.7 ( Fig. 8b) the model appears to have very good resolution in layer 2A, whereas using a threshold of 0.9 ( Fig. 8c) implies very poor resolution (generally worse than 15 km) except in a few isolated regions near OBS deployment sites. This observation suggests that small‐scale anomalies in layer 2A may be detected, but their amplitudes are likely to be greatly underestimated except in the few isolated areas shown in Fig. 8(c).
3.7 Modelling strategy
The inversion parameters were set up as described in Section 3.4, and uncertainties associated with each traveltime residual assigned according to the scheme outlined in Section 3.5 and summarized in Table 1. These parameters remained invariant for all inversions. A normalized misfit threshold of 1.01 was chosen to indicate satisfactory convergence, which required two iterations of the inversion. It was found that very many more iterations were required to achieve a model with a normalized misfit of 1.00, and the extra computational expense and introduction of minimal additional structure to obtain such a small improvement in misfit was not felt to be justified. The simplest initial model was constructed as described in Section 3.3.
The inversion process requires that the initial model be close to the true structure in order for the linearization assumption on which it is based to be valid. Hence it was necessary to refine the initial model in order to represent the known velocity structure better and identify and eliminate model artefacts. The aim was to generate an initial model that contained sufficient structure that any velocity anomalies identified by the inversion routine may confidently be ascribed to a geological cause. These modifications are described in detail in Section 4.
4 Inversion results
4.1 1‐D initial model
The normalized misfit for the initial model described in Section 3.3 is 17.788. The anomalies relative to this model, resolved by the inversion to achieve a normalized misfit of less than 1.01, are illustrated in Fig. 9(a). The reduction in misfit indicates that the final model is believed to be a significantly better representation of the true velocity structure than the initial model. However, the anomalies shown in Fig. 9(a) are dominantly negative in the north of the study area and dominantly positive in the south for layers 2A and 2B/C. Further inversions were carried out in which the velocity in layer 2 was increased and decreased whilst retaining a constant velocity structure in layer 3, but no layer 2 velocity structure could be found which resolved this problem. Furthermore, altering the layer 2 velocity structure produced significant variations in the anomalies resolved in layer 3 where all the initial models were kept identical. In layer 2, anomalies were resolved in only a few, well‐sampled areas, a phenomenon which is thought to result from the generally poorer data coverage and hence resolution in the upper part of layer 2 described in Section 3.6. These observations confirm that velocity anomalies in the more poorly sampled parts of layer 2, which in itself is likely to show considerable lateral variability due to its mode of origin, cannot be resolved by the inversion process alone.
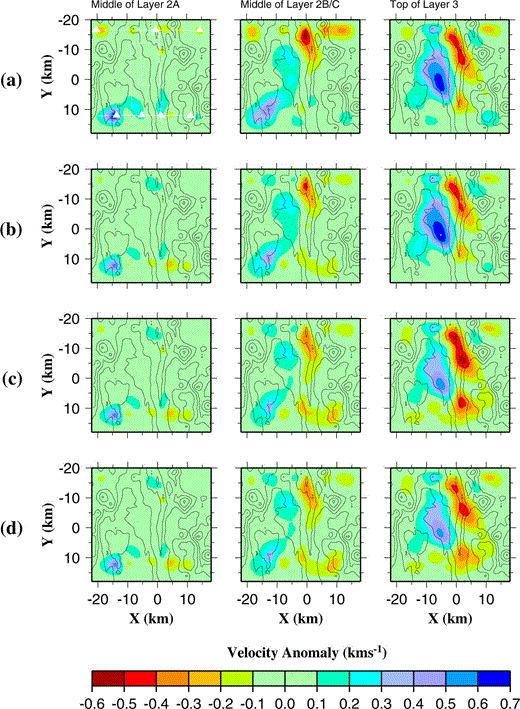
Velocity anomalies recovered by the inversion routine for each of the initial models considered: (a) 1‐D; (b) 2‐D; (c) unbiased 2‐D; and (d) unbiased 2‐D with melt lens explicitly included. Bathymetric contours at 250 m intervals have been overlain on each plot. The OBS positions (white triangles) and ship tracks (white lines) are shown in (a) only but apply to all plots. Anomalies are shown relative to the 3.0, 5.0 and 6.2 km s−1 velocity planes in the 1‐D initial model as shown in Fig. 4. Plots are shown for the same spatial planes for all initial models to allow direct comparison of the anomaly plots. However, for the 2‐D and unbiased 2‐D initial models, these planes are not constant‐velocity planes (see text for details of modifications).
The dependence of the size of anomalies resolved in layer 3 on the velocity structure in layer 2 outlined above illustrates the importance of using an initial model for which the velocity structure in the relatively poorly sampled parts is represented as accurately as possible in order to allow the anomalies in the well‐sampled parts to be interpreted. Moreover, it appears that a 1‐D model is inadequate for representing layer 2, so a 2‐D initial model was investigated.
4.2 2‐D initial model
Fig. 3 shows that the 1‐D average velocity profiles for Seismic North (line 6) and Seismic South (line 1) derived from the across‐axis 2‐D seismic profiles of Turner . (1999) differ from each other. In particular, the velocity at a given depth beneath the seafloor is generally slightly lower for Seismic North than for Seismic South. The same observation can be made from the inversion results for a 1‐D initial model outlined in Section 4.1 and shown in Fig. 9(a). Hence, a 2‐D initial model was constructed with approximately seafloor‐parallel layer boundaries using the method described in Section 3.3, incorporating a north–south‐varying velocity structure between the 1‐D average of the Seismic South across‐axis 2‐D profile at model offset y = 12 km and the 1‐D average of the Seismic North profile at y = − 17 km. The velocity profile at all other y positions was linearly interpolated between these two end‐members. The mantle layer was not included for reasons described in Section 3.3.
The normalized misfit for this initial model is 11.621, which is less than that for the 1‐D initial model. This improvement is to be expected since all of the receivers and a large number of shots are located along y = 12 km and y = − 17 km, and the 2‐D initial model better represents the structure determined by Turner . (1999) at these two end‐member positions. However, when a subset of the data is considered that has shots located within 2.5 km of the y = 12 km and y = − 17 km lines removed, normalized misfits of 24.462 for the 1‐D initial model and 18.151 for the 2‐D initial model were obtained. The reduction in misfit observed for this subset of the data implies that the reduction in misfit observed for the whole data set is not solely a result of the large proportion of in‐line shots, and indicates that the 2‐D initial model is a better representation of the true shallow crustal velocity structure for all y positions.
Fig. 9(b) shows the velocity anomalies relative to the 2‐D initial model resolved by the inversion routines on the same surfaces as in Fig. 9(a) for the 1‐D initial model. It should be noted that, for the 2‐D initial model, due to the introduction of the 2‐D velocity variation described above the surfaces are no longer planes of constant velocity. Comparison of Figs 9(a) and (b) shows that the magnitudes of the anomalies in layer 2 are smaller for the 2‐D initial model than for the 1‐D initial model, and the prevalence of negative anomalies in the north and positive anomalies in the south is less pronounced. These observations imply that the 2‐D initial model is a better representation of the shallow crustal structure than the 1‐D initial model. The implications will be discussed more fully in Section 6.
4.3 Unbiased 2‐D initial model
In order to obtain the optimal results, the initial model should ideally be an average of the true velocity structure such that the overall average anomaly is zero, since for such a model the linearization assumption will be most valid ( Zelt & Barton 1998). The average anomalies for inversions performed using the 1‐D and 2‐D initial models are 0.0498 km s−1 and 0.0575 km s−1, respectively. Inspection of Figs 9(a) and (b) shows that the anomalies are dominantly positive in layer 3, implying that the initial model is generally too slow at this depth. This might be expected as the initial model was created by averaging the 2‐D models of Turner . (1999) , which contain a low‐velocity zone in layer 3 associated with the axial magmatic system. Fig. 8(a) indicates that in layer 3 ray coverage is most dense west of y = 0 km, which marks the approximate position of the ridge axis, and incomplete along‐axis. Considering those parts of the 3‐D model that are sampled by rays at layer 3 depths, the proportion corresponding to the region of depressed velocity in the axial region is likely to be lower than that for the 2‐D models of Turner . (1999) from which the 1‐D and 2‐D initial models are derived, hence resulting in the observed apparent bias.
In order to create a 2‐D initial model that is not significantly biased at any depth, the following method was employed. The anomaly determined using the 2‐D initial model was averaged along planes parallel to the smoothed seafloor derived using the 2 km square averaging filter with a separation of 200 m between planes. Only inversion cells that were sampled by rays were considered, and where the average path length within inversion cells was less than 1 km for a given layer, the average anomaly was set to zero. The 1‐D average anomaly versus depth relationship derived by this method may be added to the initial model to create an unbiased initial model. However, since the initial model from which the anomaly field was derived is 2‐D, a 2‐D anomaly field was found to give better results. The 2‐D anomaly field was obtained by dividing the model into northern and southern parts at the y = − 1 km position and averaging each part separately by the method described above. The two anomaly profiles thus derived, shown in Fig. 10, were then applied at the y = – 9.5 km and y = 8.5 km positions, with the anomaly profile elsewhere being derived by linear interpolation between these two end‐members. The resulting 2‐D average anomaly field was added to the 2‐D initial model to create the unbiased 2‐D initial model.
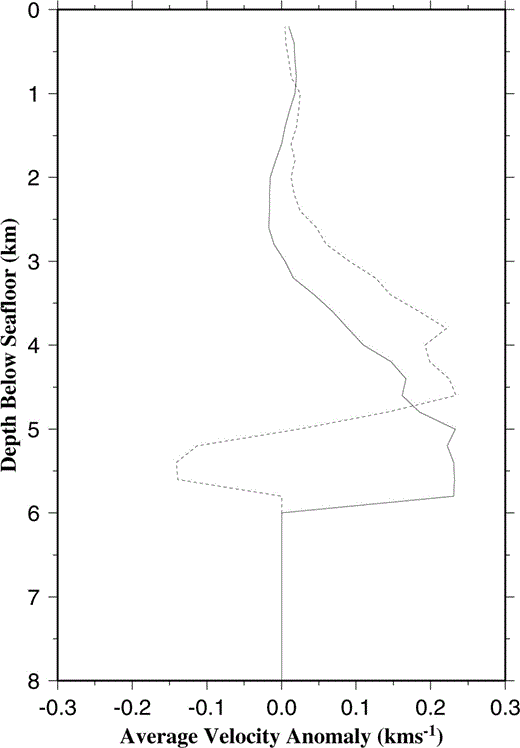
Average velocity–depth anomaly profiles beneath the seafloor, as shown in Fig. 9(b), for those parts of the study area north (solid line) and south (dashed line) of y = − 1 km. These profiles were used to create the unbiased 2‐D initial model (see text for details). The negative average anomalies deeper than 5 km below the seafloor arise from averaging poorly sampled cells located much deeper than the regions of interest.
The normalized misfit for the unbiased 2‐D initial model is 9.351, which is lower than that for the 2‐D and 1‐D initial models. Fig. 9(c) shows the anomaly field obtained from inversion with this initial model. This model has an average anomaly of −0.007 km s−1, which is much smaller than for models derived from the 1‐D and 2‐D initial models. Comparison with the anomaly field produced from the simple 2‐D initial model in Fig. 9(b) shows little difference at shallow crustal levels where the two initial models are almost identical, but in layer 2B/C and particularly in layer 3, the bias in the anomaly field is much less pronounced.
4.4 Effect of a melt lens
Seismic reflection data have indicated the presence of a melt lens containing high degrees of melt at an approximately constant depth of 4.8 km below sea level beneath the entire length of the CVFR ( Collier 1990; Collier & Sinha 1992). This melt lens has been modelled with a seismic velocity of 3.0 km s−1 to be consistent with laboratory measurements of the velocity of an andesite melt ( Murase & McBirney 1973). The melt lens is modelled with a width varying from 0.6 to 4.0 km ( Collier & Sinha 1992), and the presence of diffraction tails observed at the ends of the reflector is interpreted as signifying abrupt lateral termination. Its vertical extent is believed to be very limited; modelling by Turner . (1999) indicates that the velocity must rise to at least ∼5.5 km s−1 250 m below the reflector. The inversion method is unable to resolve such small features and abrupt changes in velocity so these must be included in the initial model, otherwise the assumption that ray paths for first arrivals traced through the initial model are close approximations to the true ray paths may not be valid.
The melt lens was incorporated in the initial model by determining its lateral extent for each of the across‐axis seismic reflection lines modelled by Collier (1990). Interpolating between lines provided the position of the western and eastern edges of the melt lens in model coordinates at 200 m intervals in the y‐direction (the node spacing of the forward grid). Nodes between these limits at a depth of 4.8 km were then set to 3.0 km s−1, the remainder of the nodes being identical to the unbiased 2‐D initial model. For simplicity, the melt lens was modelled as a single body at all positions. However, the smoothing operator acts to remove abrupt changes in velocity, so when an inversion was performed using an initial model containing the melt lens, it becomes laterally and vertically smoothed. To resolve this problem, the nodes corresponding to the melt lens were set to 3.0 km s−1 during the forward modelling stage so that the predicted first‐arrival traveltimes and ray paths were calculated based on the assumption that a melt lens was present, and reset to the value in the background model for the inverse step so that it is performed on a smoothly varying model. This approach is valid because the melt lens is very small relative to the scale of features that may be resolved by the inversion at this depth.
The normalized misfit for the unbiased 2‐D initial model with melt lens is 9.027, slightly lower than without the melt lens included. Fig. 9(d) shows the final anomaly field resulting from inversion with the melt lens included. Comparison with Fig. 9(c) shows that explicit inclusion of the melt lens results in few changes in the final anomaly field. However, the magnitude of the negative anomaly in layer 3 in the axial region is reduced. This difference is believed to arise because the presence of the melt lens causes ray paths travelling close to it to be deflected to deeper levels. Therefore, the predicted first‐arrival traveltime for those rays sampling the low‐velocity zone beneath the axis will be increased, and the magnitude of the traveltime residuals reduced. Hence the magnitude of the anomaly required to resolve those positive residuals is also reduced.
5 Interpretation
The initial model described in Sections 4.3 and 4.4 is believed to be the best 2‐D representation of the known structure, so any anomalies relative to this model, shown in Fig. 9(d), are likely to be derived from geological features. Fig. 11 illustrates that the normalized error, defined as the traveltime residual divided by traveltime residual uncertainty, has been reduced at all offsets, which indicates that the final model is a significantly better representation of the true velocity structure than the initial model at all sampled depths. The main features of the anomaly field are common to the anomaly fields derived from all initial models (see Figs 9a–c), which further suggests that they have a geological origin rather than being simply artefacts arising from deficiencies in these initial models. These anomalies are interpreted in the following sections for each layer, where further tests are also described that are designed to establish which features are geologically real and required to fit the observed data, and which are artefacts of the modelling process. For all tests, the unbiased 2‐D initial model was used as this best represents the known structure, but the melt lens was not explicitly included as this has a small impact on the recovered model. The broader geological implications are considered in Sections 6 and 7.
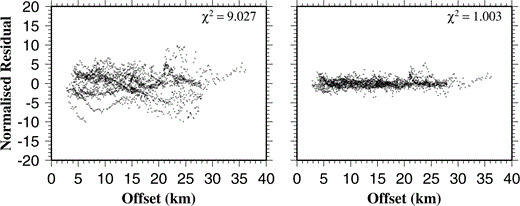
Plots of normalized residual versus offset for the unbiased 2‐D initial model (left) and the final model produced by inversion using this initial model (right). Normalized residual is defined as the traveltime residual divided by its associated uncertainty and is plotted for every arrival used in the inversion. The χ2 value shown for each plot is the mean square normalized residual.
5.1 Layer 3
The most prominent anomalies in layer 3 in Fig. 9 are a ∼ 6 km wide, elongate, negative anomaly lying approximately beneath the ridge axis, and a positive anomaly west of the ridge axis. The negative anomaly corresponds to the region of depressed velocities identified by Turner . (1999) when modelling the 2‐D across‐axis profiles (line 1 and line 6 in Fig. 1) and is interpreted as representing a mush zone containing a very low percentage of partial melt. This interpretation is favoured due to the observation that rays that have travelled through layer 3 in the axial region give rise to much lower‐amplitude first arrivals than rays that have travelled through layer 3 away from the axis for comparable shot–receiver offsets, which implies a highly attenuating on‐axis structure ( Turner . 1999 ). The tomographic results suggest that the causative feature is essentially continuous along‐axis, which is consistent with the continuity of the observed reflection from the top of the melt lens above the zone of partial melt described by Collier & Sinha (1992) and Turner . (1999) .
However, an apparent gap in the negative anomaly is observed between y = 2 km and y = 5 km in Figs 9(c) and (d). This discontinuity may represent a real thinning of the magma chamber towards the segment centre. This feature would be consistent with Turner .'s (1999) conclusion that the overlapping spreading centre between the CVFR and NVFR is currently the site of enhanced magmatism, contrary to many current models of melt supply and accretionary processes at mid‐ocean ridge segments. Alternatively, the discontinuity may arise from the irregular ray path distribution, illustrated in Fig. 8(a), which shows that, in the axial region, ray coverage in layer 3 between y = 2 km and y = 10 km is generally more sparse than elsewhere. To investigate these possibilities, a 2‐D synthetic model was constructed based approximately on the 2‐D average of the structure shown in Fig. 9(c) with layer 2 identical to the unbiased 2‐D initial model. Synthetic data were created by the method described in Section 3.6 for the resolution tests, and inverted using the unbiased 2‐D initial model. Fig. 12 shows the anomaly relative to the unbiased 2‐D initial model for the synthetic and recovered models. Comparison of Figs 12(a) and (b) shows that the negative along‐axis anomaly is only recovered north of y = 0 km, and there its magnitude is much lower than for the synthetic model. These findings are consistent with those of the checkerboard tests illustrated in Fig. 7, which show that the magnitude of anomalies is generally underestimated. The model resolution plots in Figs 8(b) and (c) show that resolution is generally poor east of x = 0 km compared to west of x = 0 km, especially so for Fig. 8(c), which shows those areas within which anomaly amplitudes may be accurately determined. Furthermore, comparison of Figs 9(c) and 12(b) shows that those areas where the negative anomaly is recovered in the synthetic test approximately correspond to the areas where the magnitude of the negative anomaly recovered when inverting the real data is maximum. These results suggest that whilst the presence of a negative anomaly in the axial region can be established, the relatively poor resolution east of x = 0 km does not allow its magnitude or along‐axis continuity to be assessed with absolute confidence. This problem will be discussed further in Section 6.
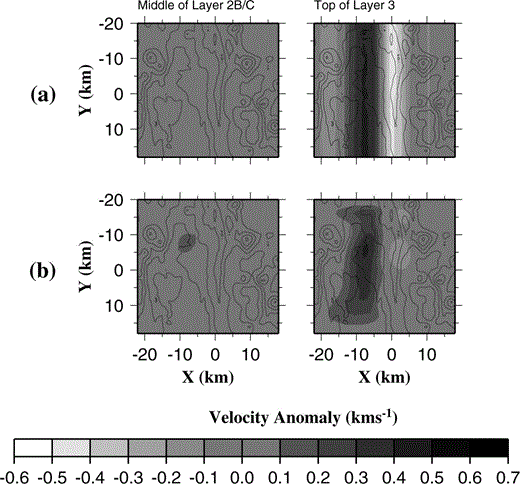
(a) Velocity anomaly relative to the unbiased 2‐D initial model for the 2‐D synthetic model containing anomalies in layer 3 only (see text for details). (b) Velocity anomaly recovered by the inversion from synthetic data produced from the model in (a). Comparison of (a) and (b) shows that the negative along‐axis anomaly is only recovered north of y = 0 km and its magnitude is reduced.
The centre of the negative anomaly is also seen to be offset to the east of the ridge axis south of about y = − 5 km, contrasting with the findings of Collier & Sinha (1992), who observed that the melt lens reflector is generally offset to the west relative to the ridge crest in the south of the area. However, the underlying low‐velocity zone is a much broader feature than the melt lens and the current position of the melt lens need not necessarily represent the geometric centre of the broad low‐velocity zone beneath it.
The positive anomaly seen west of the axial region for all initial models shown in Fig. 9 probably represents normal off‐axis crust in this area. The positive anomaly arises because the initial model is derived from an average of 2‐D models containing a low‐velocity zone and so is slower than the velocity of off‐axis crust. The magnitude of the positive anomaly is highest near y = 2 km, and is generally smaller in the north and south of the area (for the unbiased 2‐D initial model a negative anomaly is required in the south). However, Figs 8(b) and (c) show that model resolution is generally worst in the north and south of the area at these depths. In addition, the synthetic test shown in Fig. 12 indicates that, for a 2‐D anomaly invariant in the y‐direction, smaller amplitudes are recovered at the northern and southern extremities of the model. Hence it is likely that the north–south variations in the magnitude of the positive anomaly are dominantly model artefacts and the maximum values around y = 2 km are more representative of the true velocity. This observation will be discussed further in Section 6.
To the east of the ridge axis, no positive anomaly is observed, although there is a small negative anomaly east of the axis in the south of the area. This latter anomaly may reflect the general thickening of crustal layers east of the axis as modelled in 2‐D by Turner . (1999) as the transition to island‐arc‐generated crust is approached, in which case an initial model with layers of constant thickness will underestimate the true velocity at a given depth. However, a similar small negative anomaly is observed east of the ridge axis near y = 10 km in Fig. 12(b). This anomaly was recovered by inverting synthetic data created from the model in Fig. 12(a) where the negative anomaly is further west. Few ray paths sample layer 3 east of the axis and model resolution is generally very poor here (see Figs 8b and c). Hence the crustal structure east of the ridge axis is poorly constrained and any anomalies present could simply be model artefacts.
5.2 Layer 2B/C
The anomaly pattern in layer 2B/C shown in Fig. 9(d) shows some similarities with that seen in layer 3. A negative anomaly is observed in the axial region, and is particularly prominent in the north, with a corresponding positive anomaly to the west of the ridge axis. This correlation suggests that these features may be model artefacts arising from vertical smoothing of anomalies in layer 3 by the regularization. However, inversion of the synthetic model (see Fig. 12 and Section 5.1), which has anomalies in layer 3 only, shows almost no anomalies recovered in layer 2. This result suggests that if there were anomalies in the axial region in layer 3 but none in layer 2, the large anomaly seen in layer 2B/C when inverting the real data would not be present.
A further test was conducted using the real data. Rays were traced through the model recovered by inversion using the unbiased 2‐D initial model, and arrivals removed that resulted from rays travelling in layer 3. The remaining arrivals, which travel solely in the water column and layer 2, were inverted using the unbiased 2‐D initial model. The recovered model is shown in Fig. 13. Comparison of Fig. 13 with Fig. 9(c) shows a similar anomaly pattern in layer 2B/C, and this suggests that the anomalies recovered from inversion of the full data set are required by rays that do not pass into layer 3. The anomalies in layer 3 in Fig. 13 must be an artefact of the regularization since there is no ray coverage at that depth.
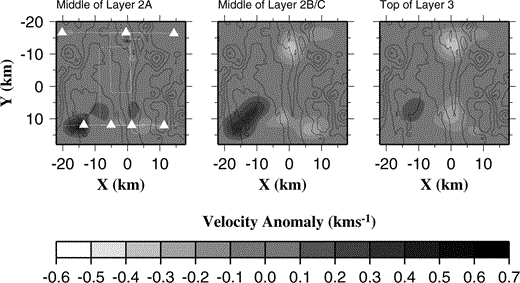
Velocity anomaly relative to the unbiased 2‐D initial model produced by inverting only those rays that pass above the layer 2B/C−3 boundary (see text for details). Comparison with Fig. 9(c) shows a similar anomaly pattern in layer 2B/C, which suggests that the anomalies recovered from the full data set are required by rays that do not pass into layer 3. The anomalies shown in layer 3 must be an artefact of the regularization as rays travelling at this depth have been removed.
The results of these tests indicate that the negative anomalies observed in layer 2B/C are required by the data and are not model artefacts. Depressed velocities in the axial region in layer 2B/C are also consistent with the modelling of line 6 by Turner . (1999) . There are a number of possible causes of these low velocities. If the crustal layers were locally thicker than predicted by the initial model, the velocity at any given depth would be overestimated and a negative anomaly required to resolve this. Alternatively, an increase in porosity could also cause the required reduction in velocity. A third alternative is the presence of a subsolidus high‐temperature anomaly, which has been used to explain a similar feature observed by Toomey . (1994) at the East Pacific Rise (EPR). These possibilities are discussed fully in Section 6. The positive anomaly west of the axis is interpreted as representing typical off‐axis crustal velocities since the initial model contains some bias towards the lower velocities modelled by Turner . (1999) towards the north of the area.
5.3 Layer 2A
Although the structure of layer 2A is generally poorly resolved, there is good resolution in a few isolated areas (see Fig. 8). The adjustments that it was necessary to make to the initial model in order to better represent those parts of layer 2A that are well resolved in themselves yield information about the gross structure. The introduction of along‐axis variation in structure such that the thickness of layer 2A increases from south to north markedly improved the normalized misfit for the initial model. This indicates that the layer 2A thickness varies in a similar manner to the thickness of the whole crust, which has also been shown to exhibit northward thickening based on modelling of the gravity field ( Sinha 1995; Turner . 1999 ; Peirce . 2001 ).
Of the few anomalies that are resolvable in layer 2A, the most striking feature is the large‐magnitude positive anomaly towards the southwest of the study area, which also extends into layer 2B/C (see Fig. 9d). This feature arises because almost all the traveltime residuals for arrivals recorded on the instrument in the southwest corner of the study area (SDOBS2) are negative, implying an anomaly near the OBS. A positive anomaly throughout layer 2 suggests that the initial model velocity is too slow at all depths, implying that here the crust is thinner. A similar feature was observed by Turner . (1999) when modelling the 2‐D across‐axis line 1. This feature was interpreted as representing thinner crust generated at the onset of rifting due to the proximity to the rift‐related pseudo‐fault identified by Wiedicke & Collier (1993), which marks the transition between pre‐ and post‐rift crust. This study thus provides further evidence for the existence and location of this feature.
6 Discussion
The primary aim of the seismic component of the Valu Fa Ridge experiment was to investigate the properties of crustal layer 3 following the identification of a melt lens at the layer 2B/C−3 boundary by previous reflection studies ( Morton & Sleep 1985; Collier & Sinha 1992). Turner . (1999) identified a negative velocity anomaly, with a maximum magnitude of 0.4 km s−1 in the axial region relative to the off‐axis crustal structure, on the two 2‐D profiles considered. This anomaly has a width of ∼ 4 km as defined by the −0.2 km s−1 anomaly contour. This study has identified a negative velocity anomaly in the axial region (see Fig. 9d and in perspective view in Fig. 14), for which the initial model and ray paths are believed to represent the closest approximation to the true velocity structure and ray paths. The average velocity contrast in this region relative to off‐axis crust is approximately −0.7 km s−1, and the low‐velocity region has a width of ∼ 6 km. Moreover, the maximum difference in velocity is approximately 0.9 km s−1. Given that the resolution analysis and synthetic test shown in Fig. 12 suggest that the magnitudes of negative anomalies in the axial region at layer 3 depths are generally underestimated, this maximum value may be more representative. In contrast, the test shown in Fig. 13 indicates that negative anomalies in the axial region in layer 3 may, in part, be a result of vertical smoothing of negative anomalies in layer 2B/C where the resolution is generally better. However, it is unlikely that this effect can account for all of the negative anomaly seen in layer 3, especially since it is generally larger in magnitude than that in layer 2B/C. Even after accounting for this effect, the inversion results imply a larger velocity anomaly than that modelled by Turner . (1999) . All these estimates lie within the range of velocity anomalies (0.5–2.5 km s−1) observed for similar low‐velocity zones at the Mid‐Atlantic Ridge (MAR) and East Pacific Rise (e.g. Navin . 1998 ; Harding . 1989 ; Toomey . 1990 ; Caress . 1992 ; Dunn . 2000 ). The greater apparent width of the anomaly may in part be due to smoothing in the poorly resolved parts of the model east of x = 0 km.
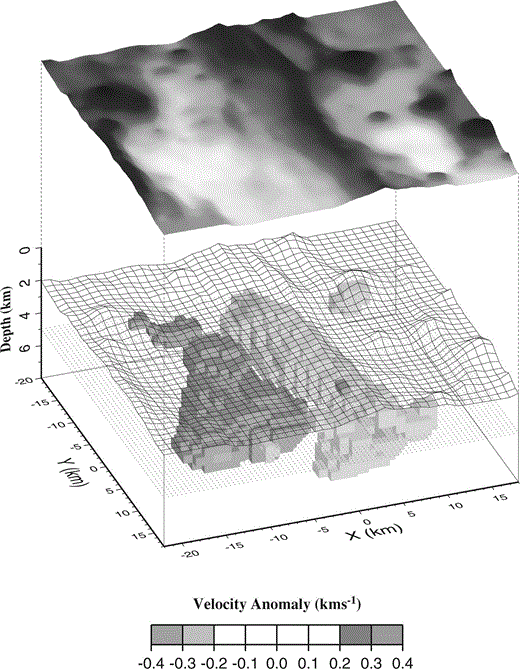
Summary 3‐D perspective view of the velocity anomaly associated with the axial magma chamber beneath the CVFR. The top of this anomaly is consistent with that predicted by Collier & Sinha (1992) and Turner . (1999) from analysis of normal‐incidence reflection events associated with an axial melt lens. Velocity anomalies relative to the 2‐D initial model with melt lens included are shown, together with the 5 km depth plane (dotted), showing anomaly outline shape. The seafloor bathymetry has been included for reference as an open mesh directly above the magma chamber anomaly, and as a grey‐shaded surface to show more clearly the location of the OSC between the CVFR and NVFR segments. Note that whilst this figure may indicate that velocity anomalies are confined to the middle crust, resolution is poor below about 7 km depth. Therefore, the velocity anomalies shown may extend to greater depth but are unresolvable with this data set.
The negative anomaly observed in layer 2B/C in Fig. 9(d) has a magnitude of approximately 0.4 km s−1, and the resolution plot in Fig. 8(c) suggests that this amplitude is likely to be more accurately represented than that of the negative anomaly in layer 3. The possible causes of this negative anomaly (outlined in Section 5.2), namely an increase in extrusive layer thickness, an increase in porosity or a temperature anomaly, will now be considered in turn.
Thickening of layer 2A has been modelled off‐axis at the EPR, associated with relict overlap basins near 17°15′S ( Bazin . 1998 ) and 9°03′Ν ( Bazin . 2001 ). Local thickening of the extrusive layer 2A would cause a negative velocity anomaly because of the higher porosity, and hence lower P‐wave velocity, of extrusive material relative to intruded dykes. Lava samples dredged from two sites on the VFR are highly vesicular and typically have porosities of 10–25 per cent, up to a maximum of 35 per cent by volume ( Vallier . 1991 ). Thickening of the extrusive layer could occur if lava is being supplied from two active ridge systems simultaneously, and the normal‐incidence studies of Collier & Sinha (1992) and Turner . (1999) suggest that melt is present beneath both the northern and central VFR ridges at the OSC. Local thickening of layer 2A associated with the overlap basin would explain the apparent maximum in the magnitude of the negative anomaly beneath it in the north of the study area.
Alternatively, lower P‐wave velocities could occur due to a porosity change associated with deformation rather than a lithological change. A number of studies of the development of oceanic crustal porosity structure (e.g. Shaw 1994; Berge . 1992 ; Wilkens . 1991 ) demonstrate that increasing porosity decreases both P‐ and S‐wave velocity, with the relative effect on P‐ and S‐wave velocity determined by crack aspect ratio. In an OBS study at the EPR between 9° and 10°N, Christeson . (1997) identified one instrument placed in a relict overlap basin for which the modelled P‐wave velocity was depressed at all crustal depths relative to the surrounding area whilst maintaining the same overall layer structure. At the top of layer 3, velocities were 4–5 per cent lower and were modelled as a porosity change of 0.5 per cent in the form of thin cracks (aspect ratio of 0.015) based on the cracking model of Kuster & Toksöz (1974). This is similar in magnitude to the anomaly observed in layer 2B/C in this study. High Poisson's ratios (in excess of 0.39) have been modelled in layer 2A (Day et al. in preparation), which implies that porosity in layer 2A is dominantly in the form of low aspect ratio (thin) cracks ( Shearer 1988) probably associated with rifting. Although no Poisson's ratio estimates are available for layer 2B/C, it is plausible that thin cracks could extend to these depths, and that the overlap basin should be subject to particularly intense deformation, thus giving rise to the observed anomaly pattern.
A low‐velocity anomaly similar in magnitude to that observed at the VFR has been modelled in layer 2B/C on‐axis at the EPR at 9°30′Ν by Toomey . (1994) . An earlier refraction study in the area by Vera . (1990) did not show any reduction in S‐wave velocity, which would be expected if there were a porosity change, so the low P‐wave velocities were attributed to high‐temperature anomalies of the order of 250–450 °C in the sheeted dyke complex in the axial region. Low‐velocity anomalies have also been modelled in the upper crust at the MAR at 35°N ( Magde . 2000 ) and similarly attributed to anomalously high temperatures, possibly associated with a small percentage of partial melt, based on correlation with constructional volcanic features on the seabed and deeper crustal low‐velocity anomalies. A similar explanation might also apply at the VFR. Such a temperature anomaly might occur if there had been a recent phase of dyke injection into layer 2B/C. Modelling of the gravity field ( Sinha 1995; Peirce . 2001 ) suggests that the OSC is currently the site of vigorous magmatism, so a very recent phase of dyke injection here would be consistent with the regional geological trends and the observation of a low‐velocity anomaly centred on the OSC. Subsolidus temperatures are preferred as the presence of very small levels of partial melt would be expected to give rise to significant attenuation, which is not observed in the wide‐angle and normal‐incidence seismic studies of Turner . (1999) and Collier & Sinha (1992).
Since the S‐wave velocity structure of layer 2B/C is unknown, it is difficult to distinguish between these possible causes of the observed P‐wave low‐velocity anomaly. In addition, the along‐axis variability in the magnitude of the low‐velocity anomaly associated with the magma chamber in layer 3 cannot be determined to any degree of certainty, hence it is also not possible to establish whether the anomaly in layer 2B/C correlates with that in layer 3, which might suggest a thermal origin. Similarly, it is possible that the apparent along‐axis variation in the magnitude of the negative anomaly in layer 2B/C is also dominantly a model artefact arising from irregular ray coverage. However, Figs 8(b) and (c) indicate that model resolution is generally better in layer 2B/C than in layer 3. Comparing the two areas on‐axis where Figs 8(b) and (c) indicate that the resolution is best, namely the points where lines 1 and 6 ( Fig. 1) cross the axis, the magnitude of the negative anomaly is seen to be larger in the north than in the south. Also, the negative anomaly in the south is seen to extend into the off‐axis crust, so the velocity contrast between on‐axis and off‐axis crust is greatest in the north. Hence, whilst the variations in model resolution mean the magnitude of the negative anomaly might not be accurately determined along the full length of the ridge, the overall increase in magnitude from south to north is probably real.
For all initial models, the well‐sampled parts of layer 2A (defined in Fig. 8c) near the southern instrument deployment sites (y = ∼ 12 km) exhibit markedly slower anomalies than those well‐sampled parts immediately to the north. The introduction of 2‐D south–north variation in the initial model does not remove this feature. In addition, for the 2‐D initial models, which are felt to represent the structure of layer 2 better, a similar feature is seen in layer 2B/C. At this depth, a broad negative anomaly is required across the whole width of the model at y = 12 km, apart from the positive anomaly in the extreme west that is discussed in Section 5.3. This structure requires an abrupt increase in velocity, which may reflect a decrease in layer thickness, immediately north of the line of the southern instrument deployment sites. Whilst such a velocity structure is viable and satisfies the available traveltime data, it contradicts the overall trend of increasing layer 2 and crustal thickness towards the north. A similar anomaly pattern might be observed in the presence of a small degree of azimuthal anisotropy, which is widely observed in the velocity structure of the upper oceanic crust (e.g. White & Whitmarsh 1984; Caress . 1992 ; Sohn . 1997 ; Barclay . 1998 ) and is usually attributed to preferentially aligned vertical cracks, often perpendicular to the spreading direction. The velocity structure along the y = 12 km line is primarily defined by ray paths travelling perpendicular to the ridge axis. In the presence of the anisotropy described, these rays would encounter the lowest velocities as they travel perpendicular to the presumed preferred crack orientation. Furthermore, the behaviour of P–S mode converted arrivals, believed to arise from mode conversion at the layer 2A−2B/C boundary beneath the receivers, suggests that the S‐wave velocity structure in layer 2A might exhibit such anisotropy as described above (Day et al. in preparation).
7 Implications for ridge segmentation
The results of this and other studies conducted at the Valu Fa Ridge raise important questions about the relationship between morphological segmentation and melt supply at this mid‐ocean ridge and at mid‐ocean ridges in general. The classic ridge segmentation model, where morphological segmentation is ultimately linked with along‐axis variation in melt supply from the mantle, is based primarily on studies conducted at the slow‐spreading MAR. Gravity studies (e.g. Kuo & Forsyth 1988; Lin . 1990 ) have shown negative ‘bull’s eye' mantle Bouguer anomalies associated with segment centres, implying thick crust beneath segment centres and correspondingly thinner crust associated with axial discontinuities at segment ends. Wide‐angle seismic data have confirmed this crustal thickness variation (e.g. Tolstoy . 1993 ). These observations suggest that, at slow‐spreading ridges, segment centres represent the sites of enhanced magma supply, while segment ends have relatively weak magma supply. Therefore, at the slow‐spreading MAR, there is strong evidence that morphological segmentation is closely related to magma supply on a variety of scales.
Intermediate‐ and fast‐spreading ridges exhibit similar morphological segmentation, and the model of Macdonald . (1988) predicts that a similar relationship between ridge segmentation and magma supply should apply. Negative mantle Bouguer anomalies associated with segment centres have been observed in a number of locations (e.g. Wang & Cochran 1993; Cormier . 1995 ; Weiland & Macdonald 1996), although the along‐axis variations in anomaly magnitude are usually much smaller than those observed at the MAR. However, for the faster spreading ridges, many indicators of magma budget do not conform to the pattern that would be predicted from study of the MAR. Indicators of enhanced magma supply include thicker crust, thicker extrusive layer, shallower bathymetric depth to the ridge crest, hydrothermal activity and the presence of a robust axial magmatic system. In a study of an 800 km long section of the southern EPR, Hooft . (1997) found that whilst axial depth and mantle Bouguer gravity anomaly generally showed the predicted strong correlation with ridge segmentation, the axial melt lens characteristics and hydrothermal activity along‐axis were found to be highly variable and exhibited no such correlation. However, Begnaud . (1997) and Van Avendonk . (1998) found normal thickness crust (∼ 5.5 km) beneath the Clipperton transform at 10°10′Ν, a first‐order segment boundary that would, according to the model of Macdonald . (1988) , be expected to be relatively magma starved. Furthermore, Barth & Mutter (1996) identified crustal thinning beneath the centre of a ridge segment at 9°50′Ν and thick crust near 9°10′Ν, immediately north of an OSC at 9°03′Ν on the EPR. These observations directly contradict the expected crustal thickness pattern. In this case, a gravity study at the same ridge segment described by Wang . (1996) demonstrated that, after correcting for the effect of this variable thickness crust, a gravity low was observed beneath the segment centre near 9°50′Ν, which they interpret as indicating the site of mantle upwelling. Therefore, there is evidence for mantle upwelling focused beneath segment centres on the EPR, which is consistent with the model of Macdonald . (1988) , but other, small‐scale indicators of magma supply (e.g. crustal thickness, magma chamber characteristics) do not always conform to the pattern that would be expected based on studies at the MAR. These discrepancies may arise from the generally higher magmatic budget at faster‐spreading ridges coupled with efficient transfer of melt away from the centre of upwelling and the short‐lived nature of some of the magma budget indicators described above.
At the CVFR, this and other studies (e.g. Turner . 1999 ) have shown that layer 2A exhibits south–north thickening. Therefore, the thickest extrusive layer is found associated with the OSC. Modelling of the gravity field implies that crust beneath the OSC is locally thicker than elsewhere at the VFR ( Sinha 1995; Peirce . 2001 ), and the general south–north shallowing of the bathymetry also mirrors the general trend of south–north whole‐crustal thickening. In addition, the widest and largest‐magnitude negative anomalies in layers 2B/C and 3 modelled in this study, and the widest melt lens modelled by Collier (1990) and Collier & Sinha (1992), are found in the north near the OSC. These results suggest that magma supply is most robust beneath the OSC. Furthermore, this study and the modelling of Turner . (1999) suggest that there is probably a single magma chamber beneath the OSC that supplies both ridges. Finally, an active hydrothermal field (the Vai Lili field) was observed near the OSC at 22°13′S and was found to be discharging fluids at temperatures of up to ∼350 °C (Fouquet . 1991, 1993). Therefore all these indicators of magmatic budget suggest that the OSC is currently the site of particularly vigorous magmatism at the VFR, contrary to the model of Macdonald . (1988) and observations at the EPR.
A reconstruction of the evolutionary history of the CVFR–NVFR OSC by Wiedicke & Collier (1993) provides further evidence of anomalous behaviour. They note that this OSC is situated on a broad bathymetric high that extends into pre‐rift crust, and which is associated with a high density of seamounts. These observations support the notion that the OSC is located at a site of enhanced magmatism. Wiedicke & Collier (1993) speculate that the enhanced magmatism may be subduction related since the bathymetric anomaly and high density of seamounts extends into crust that pre‐dates the onset of rifting. At a typical OSC, it is normally observed that one ridge propagates at the expense of the other. The VFR is undergoing southward propagation, and therefore it would be expected that the NVFR would propagate south and that the CVFR would eventually become abandoned. Thus the OSC would also be expected to undergo southward propagation. However, Wiedicke & Collier (1993) demonstrated from analysis of seabed bathymetry data that the OSC has a complex history and that, on occasions, the CVFR tip has propagated north following a phase of southward propagation of the NVFR such that the position of the OSC has remained approximately constant over time. Therefore, far from being a site of attenuated magma supply, the OSC appears to have remained over a site of enhanced magma supply for some considerable time when the regional tectonic trends suggest it should have migrated south. By contrast, Cormier . (1996) demonstrated that, at the EPR between 16° and 19°S, OSCs have migrated away from the magmatically most robust section of the ridge that was previously the site of a large OSC. This behaviour is consistent with the model of Macdonald . (1988) in that the ridge segmentation appears to have responded to changes in magma supply in a manner consistent with that model, unlike the VFR example where a small OSC appears to have remained at the site of vigorous magmatism when regional tectonic trends suggest it should have migrated to the south. Clearly, the relationship between ridge segmentation and melt supply at the VFR is different to that observed at the EPR and that predicted by the model of Macdonald . (1988) .
8 Conclusions
Most of the features resolved by the forward modelling of 2‐D seismic refraction lines by Turner . (1999) are seen in this study. The 3‐D nature of the ray coverage, more rigorous treatment of data uncertainties, and the automated nature of the inversion routine allowing fewer a priori assumptions to be made about the expected final structure mean that in many ways this study is better constrained. The similarity between models produced by the two methods reinforces the conclusions of Turner . (1999) . The features of crustal structure at the CVFR determined by this study are summarized below.
- (i)
A south–north thickening of layer 2A, which mirrors the south to north thickening of the whole crust determined by modelling the gravity field ( Sinha 1995; Peirce . 2001 ).
- (ii)
Evidence of thinning of layer 2 is present in the southwest of the area associated with the pseudo‐fault between pre‐ and post‐rift crust identified by Wiedicke & Collier (1993).
- (iii)
A negative axial velocity anomaly is present in layer 2B/C, with maximum amplitude beneath the OSC. Possible causes include increased porosity associated with increased faulting or thickening of the extrusive layer at the OSC or a high‐temperature anomaly associated with the underlying magmatic system. It is not possible to distinguish between these possibilities with this data set.
- (iv)
A crustal magma body is identified beneath most of the CVFR. The dimensions cannot be determined accurately, but appear to be consistent with other similar magma chambers observed at other mid‐ocean ridge systems. The results of this study are consistent with a continuous broad mush zone centred on the ridge beneath the whole of its length, which mirrors the along‐axis continuity of the melt lens reflector observed by Collier & Sinha (1992). The discontinuity in the negative velocity anomaly between y = 2 km and y = 10 km modelled in this study is believed to be predominantly a model artefact arising from irregular ray coverage. However, it is possible that the discontinuity in part reflects real thinning of the mush zone towards the CVFR segment centre, which would support Turner .'s (1999) conclusion that the overlapping spreading centre between the CVFR and NVFR is currently the site of enhanced magmatism.
Acknowledgments
We would like to thank the officers and crew of the R/V Maurice Ewing and members of the Scientific Party of cruise EW9512, without whom data collection would not have been possible. AJD wishes to thank Colin Zelt of Rice University, Houston, TX for considerable assistance in the early stages of this project. This research was supported by the National Environment Research Council, via research grant (GST/02/1123), ship time and a PhD studentship (AJD GT04/97/71/ES). The Generic Mapping Tool of Wessel & Smith (1995) was used to plot all figures. We acknowledge helpful comments and suggestions from Andrew Barclay and an anonymous reviewer that improved the clarity of this paper. Further information can be found on the University of Durham DOBS www home page ( ), or by emailing any of the authors.
References




