-
PDF
- Split View
-
Views
-
Cite
Cite
Cor B. De Boer, Tom A. T. Mullender, Mark J. Dekkers, Low‐temperature behaviour of haematite: susceptibility and magnetization increase on cycling through the Morin transition, Geophysical Journal International, Volume 146, Issue 1, July 2001, Pages 201–216, https://doi.org/10.1046/j.0956-540x.2001.01443.x
Close - Share Icon Share
Summary
It has been realized previously (e.g. Borradaile 1994) that cycling through the Morin transition (Tm, occurring in ideal α‐Fe2O3 at −10 °C) may have implications for the NRM of some haematite‐bearing rocks. We investigate the behaviour of the low‐field susceptibility (χlf), several magnetizations (in fields of 5, 25, 100 and 1600 mT) and SIRM on cycling through Tm of several well‐characterized haematite types of varying crystallinity and particle shape. Before low‐temperature treatment, χlf of the haematites varied between ∼ 40 and ∼ 235 × 10−8 m3 kg−1. Below Tm, where only haematite's defect moment resides, χlf was much more uniform at ∼ 19 to ∼ 28×10−8 m3 kg−1. After return to room temperature, increases in χlf of up to ∼ 50 per cent were observed (when cycling in the Earth's magnetic field as well as in a field‐free space), inferred to be a function of the domain state of the haematite. This was shown for one of the haematites (LH2 which occurs as small platelets and is particularly well crystalline) where a relation y = (8.60 ± 1.01) ln(x)−2.98 was obtained, where x is the grain size (µm) and y is the percentage susceptibility increase. We suggest that transdomain changes induce the change in χlf. The nucleation of (additional) domain walls in ‘metastable’ single‐domain (SD) to pseudo‐single‐domain (PSD) grains is made possible by the low anisotropy at the Morin transition. In view of this mechanism, small stable SD haematite particles would not be affected and the grain size corresponding to y = 0 (∼ 1.5 µm for LH2) would represent the ‘real’ SD threshold size. Thermal cycling to over the Curie temperature (680 °C) is needed to return to the original domain state before the LT treatment, as expressed by a return to the original χlf values. Measuring χlf between alternating field (AF) demagnetization steps shows that AF demagnetization gradually removes the χlf increase, which appears to be soft; 30 mT is sufficient to erase 90 per cent. Thermal cycling in a 5 mT field between temperatures above Tm showed that irreversible changes in domain structure are noticeable before the isotropic point is passed. After cycling, magnetization is added to PSD and multidomain (MD) grains that intriguingly appears to be remanence, probably induced by the broadening and subsequent irreversible displacement of loosely pinned domain walls. Complete cycling through the isotropic point considerably enhances the new remanence component in ‘metastable’ SD to MD particles by an increase in the number of domains. If this behaviour can be extrapolated to the intensity of the Earth's magnetic field, this would imply that large ‘metastable’ SD to MD specularite crystals with a well‐developed Morin transition are susceptible to acquiring geologically irrelevant remanence components when subjected to low ambient temperatures. Fine‐grained haematite pigment, on the other hand, would not be affected. Thermal demagnetization alone would not be able to separate these two remanences as the new domain structure persists up to close to the Curie temperature. Our findings indicate that a cleaning procedure consisting of an initial AF step followed by stepwise thermal demagnetization is preferable in order to isolate the original remanence component properly in haematite‐bearing rocks.
1 Introduction
Hematite (α‐Fe2O3) is an important carrier of natural remanent magnetization (NRM), mostly in sedimentary rocks, but certain metamorphic and igneous rocks may also contain haematite. NRMs residing in haematite can be very stable, mainly because at ambient temperature the coercivity of fine‐grained haematite is commonly of the order of several hundred milliteslas (e.g. Dankers 1978; Hartstra 1982). The so‐called Morin transition (Tm; Morin 1950), which is equivalent to the isotropic point of haematite, probably represents its most prominent property. This characteristic low‐temperature transition typically occurs at ∼−10 °C for pure samples. At temperatures above Tm haematite is a spin‐canted antiferromagnet, while below Tm only the isotropic defect remanence survives ( Morrish 1994; Dunlop & Özdemir 1997). For reasons unresolved to date, the spin‐canted remanence remembers its original direction on reheating through Tm in zero field. The original intensity of an isothermal remanent magnetization (IRM) induced at room temperature is partly recovered (e.g. Haigh 1957). Gallon (1968), however, showed that the memory of the spin‐canted (or intrinsic) moment decreases when the defect moment is partially annealed out. Apparently, both moments are not entirely independent, and a defect moment seems to be necessary to renucleate the spin‐canted moment during reheating (cf.Dunlop & Özdemir 1997). Therefore, cycling through the Morin transition is not recommended as a method of low‐temperature cleaning because it enhances the defect moment at the expense of the probably more reliable intrinsic moment ( Borradaile 1994; Dunlop & Özdemir 1997).
In nature, however, it is not unlikely that surface rocks have been repeatedly cycled through the Morin transition, especially haematite‐bearing rocks occurring at high latitudes and altitudes. This process will not only partly erase the pre‐existing remanence, but it may even introduce a secondary magnetization in the rock because cycling occurs in the Earth's magnetic field. Borradaile (1994) showed that stress effects caused by pore ice expanding on melting could reduce the memory of remanence on rewarming through Tm even further. Close to the isotropic point when the magnetocrystalline anisotropy becomes small, demagnetization could result from broadening, unpinning and/or complete reorganization of domain walls (e.g. Ozima . 1964 ). In magnetite the isotropic point is close to the Verwey transition. Halgedahl & Jarrard (1995) showed that pseudo‐single‐domain (PSD) to multidomain (MD) magnetite particles might lose part of their remanent magnetization in the temperature range before the actual isotropic point. For haematite, this would mean that part of the NRM may be lost at common ambient Earth surface temperatures. Therefore, more insight into the physical mechanism by which the low‐temperature transition of haematite occurs is necessary to understand better how this process may influence the NRM.
Here we report on the effect of cycling through a range of temperatures straddling Tm on the domain configuration of haematite, as deduced from changes in mineral‐magnetic parameters. The results are derived from a set of well‐characterized, relatively pure haematites, spanning the single‐domain (SD) to MD range. We measured the low‐field mass susceptibility (χlf) before and after cycling through Tm. Any irreversible change in the domain configuration caused by cooling and warming through Tm may be reflected in a change of the χlf value. Test runs showed that χlf increases up to ∼ 50 per cent for coarse‐grained MD haematites. The stability of the new domain configuration is tested against alternating field (AF) demagnetization and to temperatures up to 700 °C, i.e. just above the Curie point. In addition, we checked for a possible field dependence of the irreversible change in domain configuration by monitoring cooling and warming runs of magnetization induced in various saturating and nonsaturating magnetic fields ranging from 5 to 1600 mT.
2 Relevant rock‐magnetic data
The magnetic structure of haematite is basically antiferromagnetic, with a magnetic disordering temperature or Néel point (Tn) of ∼ 680 °C. The canting of the spins vanishes at the same temperature as the long‐range antiferromagnetic ordering does (e.g. De Boer & Dekkers 1998), that is, for haematite the Curie (Tc) and Néel points are identical. Neutron diffraction studies at room temperature (e.g. Shull . 1951 ) showed that the antiferromagnetically coupled sublattice magnetizations are confined to the basal plane of the crystal, orthogonal to the hexagonal c‐axis. The weak ferromagnetic moment (spontaneous magnetization of ∼ 0.4 A m2 kg−1) is caused by a slight canting of the spin axes out of exact antiparallelism in the basal plane ( Dzyaloshinsky 1958) due to anisotropic superexchange interaction in haematite ( Moriya 1960). Hence, it is an intrinsic property of haematite and the moment is referred to as the canted moment (also known as the intrinsic, fundamental, anisotropic or magnetocrystalline moment).
In addition, haematite may have another, more variable, magnetic moment that is believed to reside in an ordered structure of chemical and/or lattice defects, which cause an imbalance between the antiferromagnetically coupled sublattices. This moment is referred to as the defect moment (also known as the isotropic moment) and is held responsible for the highly variable magnetic properties of haematite. The magnetization vector for the defect moment is parallel to the sublattice magnetizations and thus nearly perpendicular to the magnetization vector for the canted moment. Because of its origin, the defect moment can be structure‐sensitive and thus susceptible to applied stress or annealing, e.g. through the mobility of dislocations.
2.1 Sources of anisotropy
The sources of anisotropy in haematite are briefly recapitulated because at the Morin transition the principal anisotropy constant changes sign. When dealing with haematite, for Tm < T< Tc, the magnetocrystalline anisotropy can be expressed in terms of a first‐order uniaxial constant (K1) that determines the anisotropy between the ‘hard’c‐axis and the ‘easy’ basal plane (0001), and a triaxial constant (Kb) that determines the in‐plane anisotropy (cf.Hunt . 1995 and references therein). However, to fit all experimental results, a second‐order anisotropy constant (K2) is often added (cf.Morrish 1994). It is expected that K1 ≫ K2 ≫ Kb (cf.Morrish 1994). The constants vary as a function of chemical composition, crystal structure, temperature and pressure, but are independent of grain size. Flanders & Schuele (1964) found a relation (between 20 and 500 °C) Kb(T) ∝ σsm(T), with m = 10 ± 1, in one of their crystals. The sources of K1 are the magnetic dipole anisotropy and the magnetocrystalline anisotropy of the Fe3+ ion ( Artman . 1965 ), while the origin of K2 is solely a single‐ion contribution (cf.Morrish 1994). The two microscopic origins of K1 have opposite signs and different temperature dependences. Above Tm, the negative magnetic dipole term dominates the positive single‐ion term. Resonance measurements (e.g. Anderson . 1954 ; Kumagai . 1955 ) indicated the anisotropy field between the c‐axis and the ‘easy’ plane to be 3–4 T. Dunlop & Özdemir (1997, p. 51) reported a K1 of −1.2 × 106 J m−3. As a consequence of the high value of the main magnetocrystalline anisotropy, the magnetization process under the action of the Earth's magnetic field (remanence acquisition) or of common laboratory fields is restricted to the basal plane.
The triaxial magnetocrystalline anisotropy within the basal plane, however, is weak. Reported values are variable and range between < 1 and 400 J m−3 (cf.Dunlop 1971; Banerjee 1971). They are, however, not sufficiently large to account on their own for the observed high coercivities in haematite. Shape anisotropy cannot be the origin of the required energy barriers in the basal plane of haematite since it is proportional to σs. Dunlop (1971) showed that uniaxial magnetoelastic anisotropy due to internal stress is the most likely candidate responsible for the high basal plane anisotropy observed in fine‐grained haematite. He calculated that a polycrystalline magnetostriction constant λs of ∼ 8 × 10−6 ( Urquhart & Goldman 1956) can produce a coercivity of ∼ 500 mT for an internal stress of 100 MPa. Porath (1968) has argued that internal stress becomes more important in fine grains.
2.2 Low‐field and high‐field susceptibility
At room temperature, the low‐field mass susceptibility of natural haematite samples is in the range (10–750) × 10−8 m3 kg−1 ( Hunt . 1995 ). χlf values increase with increasing grain size (e.g. Dankers 1978; Collinson 1983). They also show a strong dependence on crystallographic orientation, with χlf values being higher when measured in the ‘easy’ plane. For SD haematite grains, the in‐plane or ferromagnetic susceptibility arises from the rotation of the spontaneous magnetization in the basal plane. It only exists between Tm and Tc, and its value depends on the type of basal plane anisotropy, i.e. the number of ‘easy’ axes ( Dunlop 1971). If the basal plane anisotropy is uniaxial, the susceptibility is inversely related to the coercive force Hc ( Stacey & Banerjee 1974). The intrinsic initial susceptibility in large MD particles, however, is controlled primarily by reversible domain wall displacements. The high‐field mass susceptibility (χhf) or antiferromagnetic susceptibility is due to the rotation of the spins by a field against the exchange forces. Above Tm it is almost isotropic, has a value of ∼ 25 × 10−8 m3 kg−1 and shows only a slight temperature dependence (e.g. Chevallier 1951; Néel & Pauthenet 1952; Pastrana & Hopstock 1977). In being an intrinsic property, it is independent of grain size and virtually constant for different haematite samples.
2.3 Morin transition
In pure, well‐crystalline haematite the Morin transition shows up as an abrupt drop in values for magnetic parameters around −10 °C [susceptibility: Morin (1950); (saturation) magnetization: Néel & Pauthenet (1952) and Flanders & Remeika (1965); various remanent magnetizations: Haigh (1957) and Gallon (1968)]. The Morin transition was also extensively studied using other techniques such as Mössbauer spectroscopy (e.g. Kündig . 1966 ; Van der Woude 1966; Nininger & Schroeer 1978; De Grave . 1982 ) and neutron diffraction (e.g. Shull . 1951 ; Besser . 1967 ; Sváb & Krén 1979).
It is now well known that the Morin transition is actually haematite's magnetic isotropic point and does not represent a crystallographic change, like the Verwey transition of magnetite. At the isotropic point the first hexagonal magnetocrystalline anisotropy constant (K1) of haematite changes sign, being negative above Tm and positive below it (e.g. Morrish 1994). As a consequence, the easy directions of magnetization change as well, resulting in a reorientation of the antiferromagnetically coupled atomic spins from the basal plane for T> Tm to the hexagonal c‐axis for T< Tm (e.g. Shull . 1951 ; Besser . 1967 ). Artman . (1965) showed that the spin rotation is driven by the competition between the two main origins of K1, which each have a different temperature dependence. Below Tm, the antiparallel spin alignment is perfect; any canting would violate the magnetic symmetry ( Dzyaloshinsky 1958; Moriya 1960). Hence, the intrinsic canted moment is susceptible to the Morin transition, but the defect moment is not. Consequently, below Tm only the defect moment persists.
The parameters related to the Morin transition, however, are affected in a significant way by small changes in the haematite lattice. Impurity cations and small grain sizes are reported to shift Tm to lower temperatures and tend to smear the reorientation of the magnetic spins over a larger temperature range (cf.Morrish 1994 and references therein). The transition becomes completely suppressed in pure haematite grains less than ∼ 0.02–0.03 µm (e.g. Bando . 1965 ; Kündig . 1966 ) or due to the incorporation of critical quantities of impurity cations in the haematite lattice (e.g. Morin 1950; Flanders & Remeika 1965). Consequently, the weakly ferromagnetic phase persists in these haematites over the whole temperature range down to 4 K. Vacancies or defects, morphology, degree of crystallinity and structurally bound water may also alter Tm and the range of temperatures over which the transition occurs (cf. Morrish 1994). Nininger & Schroeer (1978) and De Grave . (1982) showed that during a smeared transition both the antiferromagnetic phase and the weakly ferromagnetic phase coexist over a considerable temperature range.
The Morin transition is not only temperature‐induced but also magnetic field or pressure driven (cf.Morrish 1994). The three variables are interdependent. By application of an external field the transition occurs at lower temperatures; the critical field required to induce the transition is dependent on the temperature and the angle between the field and the crystal axis (e.g. Morrish 1994).
The high‐field susceptibility becomes isotropic on cooling below Tm (e.g. Néel & Pauthenet 1952; Creer 1967). The susceptibility parallel to the c‐axis decreases sharply from a fairly uniform value of ∼ 25 × 10−8 m3 kg−1 to ∼ (1–2.5) × 10−8 m3 kg−1. The susceptibility in the basal plane, however, shows no appreciable change except for a small increase (to ∼ 30 × 10−8 m3 kg−1) around Tm. Consequently, below Tm a sample of randomly oriented particles, with a third of the grains having their c‐axes parallel to the applied field, has a χhf around ∼ 17 × 10−8 m3 kg−1. The low‐field susceptibility below Tm consists only of the antiferromagnetic susceptibility and a superimposed susceptibility in the direction of the c‐axis arising from defects in the haematite lattice. Below the Morin transition, no or a small amount of domain walls are observed (cf.Morrish 1994), thus displacement of domain walls in formerly PSD and MD grains no longer contributes to the low‐field susceptibility below Tm. So far, no data are available on the change of χlf values of PSD and MD haematite particles on cooling and rewarming through Tm.
3 Samples, methods and equipment
3.1 Samples
Seven well‐characterized natural haematite samples and one sample of synthetic origin were used for the experiments. The synthetic sample was prepared by heating analytical grade iron(III)‐nitrate [Fe(NO3)3·9H2O] to 800 °C in an oven. The material obtained consists of fine‐grained (< 1 µm) dark‐red particles.
The natural samples comprise one haematite‐bearing rock sample (a so‐called red bed) and six samples obtained by crushing macroscopic haematite crystals. They were all used in previous palaeomagnetic and/or rock‐magnetic studies on haematite. The red beds from Dôme de Barrot (France) were the subject of the PhD thesis by Van den Ende (1977), and some samples were also used in a rock‐magnetic study by Dekkers & Linssen (1989). These Permian sediments consist of fine‐grained dark red mudstones that are calcified or silicified, and are believed to originate from rhyolitic volcanic material. Dankers (1978, 1981) studied the haematite samples labelled LH2 (Kimberley, South Africa) and LH3 (Vosges, France), while those labelled LH4 (origin unknown), LH6 (Gellivara, Lapland) and LHC (origin unknown) were investigated by Hartstra (1982). The haematite material from the Kadaň locality in the Czech republic was previously studied by Hejda . (1992) and Petrovský. (1994, 1996).
The crushed natural haematite samples were characterized by the aforementioned authors using microprobe analyses (chemical composition), X‐ray diffraction (unit‐cell parameters and crystallinity) and optical microscopy (shape and lamellar twinning). Their findings are summarized in Table 1. Unfortunately, only from some of Dankers' and Hartstra's coarse‐grained fractions was enough sample material (> 0.5 g) left to measure reliably changes in χlf on cycling through Tm. Consequently, identical grain‐size fractions of each haematite type were not available. In Table 1 the particular grain‐size fraction used in the present study is given together with some rock‐magnetic parameters obtained by the aforementioned authors. Dankers' and Hartstra's results from various rock‐magnetic experiments indicate that the particles of the grain‐size fractions mentioned in Table 1 are PSD or MD. For instance, remanent coercivities measured by Dankers and Hartstra for grain‐size fractions ranging from < 5 µm to 150–250 µm do not show a peak diagnostic for the SD to PSD change, but decrease with increasing grain size over the whole range. The results from Hejda . (1992) , however, might indicate that the Kadaň haematite is still SD for acicular particles between 75 and 100 µm.
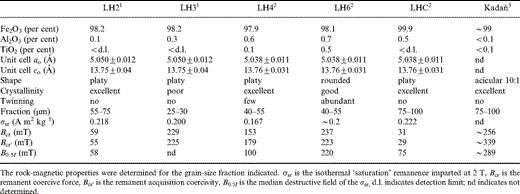
Some chemical and physical properties of the crushed natural haematite samples used in this study as determined by 1Dankers (1978, 1981), 2Hartstra (1982) and 3Hejda . (1992) .
In order to measure the grain‐size dependence of changes in χlf on cycling through Tm and to obtain a suite of haematite particles spanning the SD to MD range, we prepared new fine‐grained fractions from the 40–55 µm particles of sample LH2. The 30–40, 25–30, 20–25, 15–20, 10–15, 5–10 and < 5 µm fractions were obtained by gently crushing the 40–55 µm grains followed by ultrasonic microsieving in propanon. The < 5 µm fraction was further separated into two fractions by stirring the grains in propanon and decanting the particles remaining in suspension. This fraction consists of ultrafine red‐coloured particles (pigment) that are all < ∼ 1 µm, while the grey‐coloured bottom material consists of particles ranging roughly between 1 and 5 µm, checked with reflected light microscopy. LH2 haematite was chosen not only because enough material was available to crush new fractions, but also because the grains of this haematite type clearly consist of only one or a few layers of non‐twinned well‐crystalline plates according to the basal plane and are not complex intergrowths of several particles as is often the case when grain‐size fractions are obtained by crushing compact masses of haematite ore. Furthermore, Dankers' results on this haematite type showed clear grain‐size‐dependent trends for various rock‐magnetic parameters. Table 2 summarizes the hysteresis parameters of sample LH2 obtained from some of Dankers' original fractions and from the newly prepared fractions.
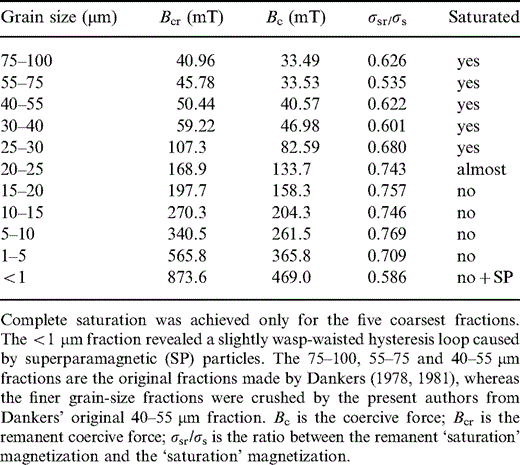
Rock‐magnetic properties of various grain‐size fractions for haematite sample LH2 determined at room temperature by measurements on an alternating gradient magnetometer. The maximum field used was 1.6 T.
3.2 Experimental methods and instrumentation
3.2.1 Low‐field magnetic susceptibility measurements
A CS‐2 furnace apparatus and low‐temperature unit connected to a low‐field KLY‐2 susceptibility bridge (all AGICO, Brno, Czech Republic) was used to record the temperature variation of χlf between −196 °C and + 700 °C. Operating conditions of the instrument are a measuring frequency of 720 Hz with an rms field strength of 0.377 mT (corresponding to a peak field strength of ∼ 0.5 mT). Demagnetizing fields are negligible in haematite, and thus it is the intrinsic initial susceptibility that is measured ( Collinson 1983). Between high‐ (HT) and low‐temperature (LT) measurements, switching of furnace type and temperature sensor is necessary. Unfortunately, only the warming run from −196 °C back to room temperature can be monitored during the LT experiment. Typically 0.5–0.8 g was inserted in the quartz glass sample tube.
The following measuring procedure was used to obtain the χlf–T curves plotted in Figs 1 and 2. First the sample was cycled between room temperature and + 150 °C at a rate of ∼ 5 °C min−1 to determine whether mild heating causes any change in χlf. Then the sample was cooled to liquid nitrogen temperature and χlf was monitored on warming back to 0 °C or room temperature. Afterwards, the sample was again cycled between room temperature and + 150 °C to study how the possibly changed domain structure (as deduced from changes in χlf) reacts to mild heating.
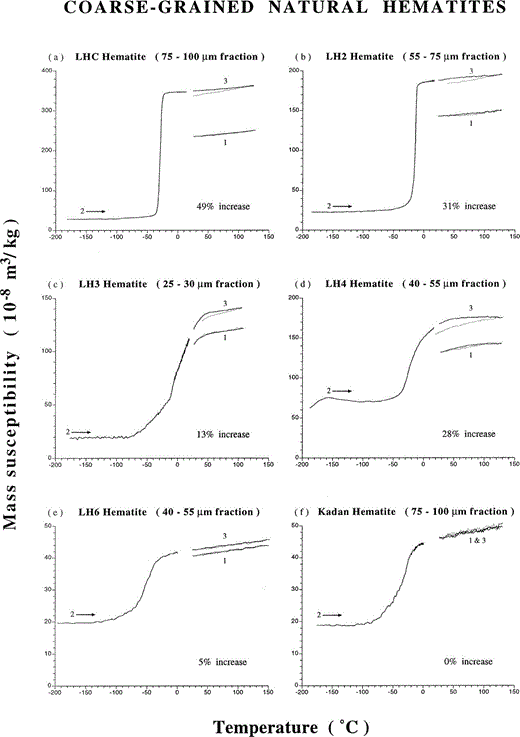
Low‐field susceptibility versus temperature runs for various coarse‐grained natural haematites. 1 and 3 refer to cycles between room temperature and 150 °C, while 2 is a warming run from −196 °C to room temperature. Cycle 3 is measured after run 2. An increase in χlf after cycling through the Morin transition (i.e. isotropic point) is observed for platy (LHC, LH2, LH3, LH4) and rounded (LH6) particles but not for acicular Kadaň haematite. Solid and dotted lines denote heating and cooling runs, respectively.
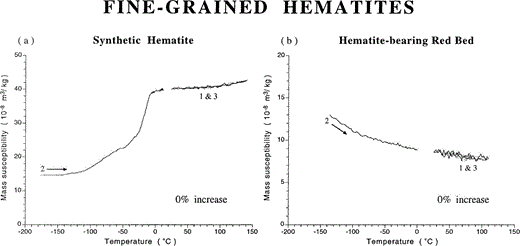
Low‐field susceptibility versus temperature runs for fine‐grained haematites; curve numbering as in Fig. 1. (a) Synthetic haematite prepared by thermal decomposition of hydrated ferric nitrate salt at 800 °C, and (b) haematite‐bearing red bed from Dôme de Barrot (France). No difference in χlf is obtained before and after a low‐temperature run.
Two haematite samples (LH2 and LHC) were also cycled to 700 °C at a rate of ∼ 10 °C min−1 to determine the effect of high temperatures and cycling through Tc (∼ 680 °C) on the new magnetic state. These two samples were chosen because they have the highest susceptibility and revealed the highest change in χlf on cycling through Tm. Furthermore, test runs to 700 °C with a non‐treated LH2 sample showed identical heating and cooling curves. The complete recovery of the initial magnetic state on cooling implies that no heating‐induced chemical or physical changes (e.g. grain growth or reordering of the lattice) occur in this haematite type when heated up to 700 °C. This means that for LT‐treated LH2 haematite any irreversible behaviour between the heating and cooling curves can be interpreted as a heating‐induced change in the new magnetic state as obtained after cycling through Tm. Non‐treated LHC haematite, on the other hand, does show a slight susceptibility increase after cycling to 700 °C. This haematite type was used to determine whether heating‐induced chemical or physical changes affect the χlf increase obtained on cycling through Tm.
The magnetic properties of haematite show a strong directional dependence; χlf measured in the basal plane will be much higher than in the direction of the hexagonal c‐axis (cf. Section 2.2). Therefore, some degree of magnetic anisotropy may exist in our samples, that is, the particles are not likely to be oriented fully randomly in the sample tube. As a result, the measured absolute χlf values will in essence only be representative of that particular orientation of the grains. Moreover, the orientation of the particles may possibly also affect the χlf change obtained after cycling through Tm. Furthermore, it was recognized that the orientation of the grains might have changed during the experiment because of the required change in sample set‐up between HT and LT runs. This could also affect the difference obtained in χlf measured before and after cycling through Tm, and might be misinterpreted as a change in domain configuration.
We checked in several ways whether or not these orientational effects seriously affect our results. First, the absolute χlf values measured initially at room temperature for LHC and LH2 haematite indeed depend on the orientation of the grains in a particular batch. Absolute differences in χlf up to ∼ 50 × 10−8 m3 kg−1 due to stirring or ultrasonic vibrating of the grains in the sample tube could be included in LHC and LH2 haematite, respectively. Differences in the other haematite samples, however, appeared to be marginal, possibly due to their finer grain size or different shape. LH4 haematite, for instance, consists just like LHC and LH2 of well‐crystallized plates, but the former grains are thicker, being comprised of a larger number of plates.
Second, the change in χlf was also determined without monitoring the low‐temperature warming run on the KLY‐2/CS‐2 device, that is, no change of sample set‐up was required in this way. For this purpose the quartz glass sample tube with the connected temperature sensor was taken out of the furnace of the susceptibility bridge after an initial measurement at room temperature. The sample was then placed in liquid nitrogen and measured again after warming to room temperature. In this way possible movement of the haematite particles was minimized to barely noticeable proportions. χlf increases were still measured after LT treatment, implying that changes in particle orientation are not responsible for the effects observed. It also appears that absolute χlf increases after an LT treatment might depend on the orientation of the grains in the sample tube (for example, depending on the grain size and the thickness of the platy grains), whereas the χlf increases normalized to their initial value measured at room temperature were independent of the particle orientation within a particular batch. Normalization thus provides an orientation‐independent parameter. The aforementioned procedure without changing the sample set‐up was used to measure the grain‐size dependence of the normalized χlf change for sample LH2 (see Fig. 3). During the course of the measurements it also became possible to carry out a cooling and warming cycle in a field‐free space by placing the sample tube in a set of Helmholtz coils. Warming through the Morin transition of haematite in the Earth's magnetic field or in a field‐free space appears not to affect the χlf increase obtained.
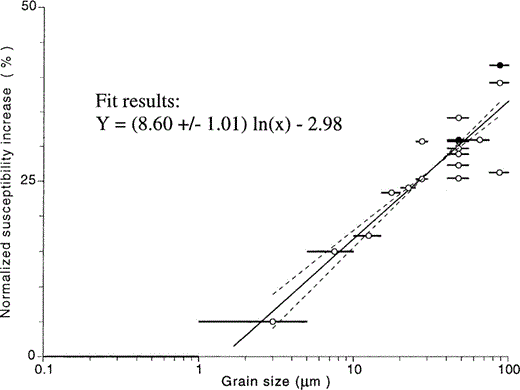
Percentage susceptibility increase after cycling through the Morin transition for various grain‐size fractions of well crystalline, platy LH2 haematite. Open and solid circles denote measurements in the Earth's magnetic field and in a field‐free space, respectively. Solid lines through the circles denotes the grain‐size fraction used.
Third, the anisotropy of magnetic susceptibility (AMS) was measured on a KLY‐3 kappabridge (AGICO, Brno) before and after a complete cooling and warming cycle through the Morin transition. Any significant change in AMS would imply that the χlf is changed preferentially in a specific direction. The AMS measurement was carried out on a standard size cylindrical artificial sample consisting of five thin layers of highly aligned haematite particles in an epoxy resin matrix (Araldit D with hardener HY 956, Ciba‐Geigy). The thin haematite platelets of the 40–55 µm grain‐size fraction of sample LH2 were positioned in such a way that they had a preferred orientation in the basal plane of the sample. No significant changes in the AMS ellipsoid orientation (directions of the three principal susceptibility axes) were detected. The extremely high anisotropy factors F (k2/k3) and P (k1/k3) change from 3.10 and 3.12 to 3.58 and 3.60 before and after the LT treatment, respectively. The measurements were corrected for the isotropic diamagnetic moment of the matrix. Furthermore, the normalized χlf increase (26 per cent) obtained for these highly oriented grains falls within the range (24–33 per cent) obtained during experiments on the same grain‐size fraction using the powders (see Fig. 3). This experiment also indicates that a possible (slight) movement of the grains between the high‐ and low‐temperature measurements does not cause the observed gain in χlf. Furthermore, it can be concluded that χlf becomes higher irrespective of the orientation of the grains and no relation exists between the orientation of the haematite grains in the sample and the changes found in bulk susceptibility normalized to its initial value.
Measurements on a similar non‐treated sample showed that changes in bulk susceptibility due to AF demagnetization (300 mT) of the initial state are negligible (< 1 per cent). Warming this sample from −196 °C to room temperature in a field‐free space again yields similar increases in normalized bulk susceptibility (31 per cent) compared to warming in the Earth's magnetic field. Afterwards, the stability of the new magnetic state against increasing AF demagnetizing fields was tested on this sample. This experiment resulted in a full recovery of the original mean susceptibility value (see Section 4.1 and Fig. 5).
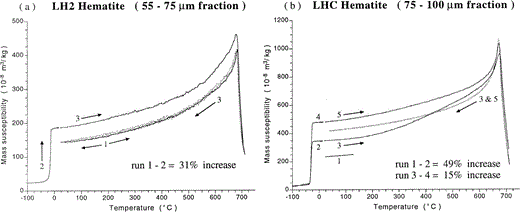
Measurements of χlf between AF demagnetization steps of sample LH2 after being cycled through Tm showing the gradual neutralization of the χlf increase. The difference between χlf values before and after cycling and before AF treatment, i.e. the susceptibility increase, is normalized to 100 per cent. Therefore, zero is equivalent to the χlf value before cycling through Tm.
3.2.2 MicroMag measurements
A Princeton alternating gradient magnetometer (MicroMag 2900) equipped with a helium (or nitrogen) flow‐through cryostat was used to monitor low‐temperature cooling (+ 80 to −100 °C) and warming (− 100 to + 80 °C) runs of induced magnetic moments (σ in various fields and σrs), and to measure hysteresis loops at various temperatures between + 80 °C and −170 °C. This specific temperature range was chosen because + 80 °C lies fully above the onset of the Morin transition, whereas −100 °C is fully below Tm. Cooling and warming rates were ∼ 3 °C min−1. All measurements were made on the same sample, which was demagnetized between the different experiments by the MicroMag routine using a 5 per cent decrement in magnetization per iteration starting at 300 mT. The sample consisted of 2.85 mg of the 75–100 µm grain‐size fraction of LHC haematite. This particular haematite type was used because it yielded the highest χlf increase on cycling through Tm and also showed the most pronounced and abrupt Morin transition with the largest difference between the magnetic states above and below Tm. The grains were stuck to a small quartz glass platelet by using double‐sided tape and subsequently fixed with transparent lacquer spray. Repeating the hysteresis loop measurements under identical conditions showed that no particle movement had taken place because the loops could be duplicated. A slight preferred orientation of the basal plane of haematite parallel to the applied field might exist as a consequence of this sample preparation procedure. However, by sticking the glass platelet with the sample perpendicular to the probe and using the room temperature X‐probe of the MicroMag, the three loops obtained (Z‐probe, X‐probe‐parallel and X‐probe‐perpendicular) were essentially the same, so preferred orientation of basal planes is not significant. Note that the loops obtained are not very different from loops measured for large (100 µm and ∼1 mm) single haematite platelets with the basal plane parallel to the field direction ( Halgedahl 1998). All results were afterwards corrected by subtracting the values obtained by measuring a blank (quartz glass platelet with tape and lacquer spray only).
The low‐temperature σ–T cycles were recorded in various applied magnetic fields (5, 25, 100 and 1600 mT) to determine the field dependence of the magnetization increase on cycling through the Morin transition. The highest applied field appears to be sufficient to saturate LHC haematite completely. Hysteresis loops were measured at various temperatures to follow its change in shape by cooling through the Morin transition. The saturation remanence (1.6 T) obtained at + 80 °C was also cycled through Tm to determine its memory.
Repeated cooling and warming cycles to increasingly lower temperatures were recorded in a 5 mT field to determine the onset of the irreversible change in magnetization (i.e. domain configuration) related to Tm. After each cycle the field was momentarily turned off to determine which part of the magnetization increase could be considered as being remanence.
Minor hysteresis loops (5 mT) were measured at various temperatures to determine the change in shape of the loops obtained in a non‐saturating applied field. A first minor loop was obtained at + 80 °C starting from a demagnetized state. The sample was then cooled to −30 °C within a 5 mT field and two subsequent minor loops were measured at this temperature. Next, the sample was warmed back to + 80 °C, demagnetized at this temperature and then cycled between + 80 °C and −100 °C in a 5 mT field before measuring the two subsequent minor loops at + 80 °C. Additional runs were carried out to obtain the Bcr values at the aforementioned temperatures.
4 Experimental results
4.1 Low‐field susceptibility measurements
4.1.1 Coarse‐grained haematites
The χlf–T behaviour between + 150 °C and −196 °C is shown in Fig. 1 for six coarse‐grained haematites, LHC, LH2, LH3, LH4, LH6 and Kadaň. The χlf values initially measured at room temperature (starting point of cycle 1) differ widely between the various haematite types, ranging between 40 and 235 × 10−8 m3 kg−1. They fall within the range reported in the literature (see Section 2.2). Platy‐developed haematite particles (LHC, LH2, LH4 and LH3) appear to have the highest χlf values, while the rounded (LH6) and acicular (Kadaň) haematite grains show the lowest values, irrespective of orientational effects and differences in grain size.
A first heating to 150 °C (solid line of cycle 1) results in all cases in a slight gradual increase in χlf, probably caused by a small decrease in coercivity. The break in slope at ∼ 50 °C and ∼ 100 °C for sample LH3 and LH4, respectively, represents the high‐temperature onset of the Morin transition for these haematites (cf.Hartstra 1982; De Boer & Dekkers 1998). The cooling curves of these first cycles (dotted lines) are reversible with respect to the heating curve, indicating that the initial magnetic state is recovered on cooling to room temperature. This part of the experiment thus shows that mild heating neither changes the initial magnetic state of the coarse‐grained haematites nor causes any chemical and/or physical changes.
After cooling to liquid nitrogen temperature, the χlf recorded at the beginning of the warming curve (run 2) is almost identical for all haematite samples and ranges between 19 and 28 × 10−8 m3 kg−1, except for sample LH4, which has a value of ∼ 65 × 10−8 m3 kg−1. The former χlf values are only slightly higher than that reported for randomly oriented haematite particles. Here, the susceptibility below Tm consists only of the antiferromagnetic susceptibility (∼ 16.6 × 10−8 m3 kg−1, see Section 2.3). This indicates that the superimposed susceptibility due to ordered defects is not very significant in our haematite samples. The higher value of sample LH4 can be explained by a minute magnetite contamination (cf.De Boer & Dekkers 1998). The increase in χlf on warming from −196 °C and the characteristic local maximum around −160 °C are typical of the Verwey transition and the magnetic isotropic point of slightly oxidized or substituted magnetite.
All coarse‐grained haematites show a well‐developed Morin transition. These haematites can be divided into three groups (I, II and III) on the basis of the shape of the Morin transition. Group I haematites (LHC and LH2) are characterized by a sharp (< 10°) transition with hardly any tail at the low‐temperature end. The switch of the ‘easy’ axis of magnetization, resulting in the change between the antiferromagnetic and the weak ferromagnetic state, must be very abrupt. The complete Morin transition may lie within the range of Earth surface temperatures, especially during colder geological periods. Group II haematites (LH3 and LH4) have, apart from the effect caused by the magnetite contamination (LH4), a more smeared transition (> 50 °C) with its high‐temperature onset above room temperature. The rotation of the magnetic spins is thus more gradual, but starts (far) above normal Earth surface temperatures. Group III haematites (LH6 and Kadaň) also have a smeared transition (> 50 °C), but with its high‐temperature onset below 0 °C and with a relatively large low‐temperature tail. For this type of haematite, the rotation of the magnetic spins will not be fully completed within an extreme range of Earth surface temperatures.
All coarse‐grained haematites, which are PSD or MD according to previous rock‐magnetic studies (cf.Dankers 1978, 1981; Hartstra 1982), show a distinct increase in χlf when comparing the values measured at room temperature before and after cycling through Tm. The absolute χlf increase ranges between 2 × 10−8 and 115 × 10−8 m3 kg−1, and between 5 and 49 per cent when normalized to its initial value. Samples with comparable grain sizes (LHC and Kadaň, and LH4 and LH6) show different percentages of susceptibility increase. Evidently, the increase in susceptibility is dependent on the haematite type under investigation. The acicular Kadaň sample, which despite its coarse grain size is most probably SD (cf.Hejda . 1992 ), shows no increase in χlf on cycling through Tm. The existence of a Morin transition is apparently necessary to have a χlf increase, but does not automatically imply an increase. Repeating the low‐temperature experiment several times before the second high‐temperature cycle to 150 °C, yields similar shaped warming curves and thus identical χlf increases.
The heating curve of the second χlf–T cycle to 150 °C (cycle 3, solid lines) has a similar shape and inclination to the heating curve of the first run. On cooling back to room temperature, however, some cooling curves now become irreversible with respect to the heating curve. This indicates that mild heating is able to neutralize a portion of total χlf increase gained on cycling through Tm. This portion is ∼ 15 per cent for samples LHC and LH2, ∼ 35 per cent for samples LH3 and LH4, and ∼ 0 per cent for haematite LH6, although this latter value cannot be determined very accurately. The relatively high losses obtained for samples LH3 and LH4 are because these haematites pass the high‐temperature onset of their Morin transition on cooling back to room temperature.
4.1.2 Fine‐grained haematites
The χlf–T curves obtained for the fine‐grained synthetic haematite and the red bed sample are shown in Figs 2(a) and (b), respectively. Both haematites, which are most probably SD, do not show any χlf increase after the LT treatment. The warming curve of the synthetic haematite from −196 °C back to room temperature (run 2) reveals a more or less two‐step Morin transition, probably indicating the presence of two distinct grain‐size distributions. In this view, the steep part of the warming curve between ∼−30 °C and −10 °C represents the relatively coarse, well‐crystalline fraction with grains up to ∼ 1 µm, whereas the smeared low‐temperature tail of the curve represents the ultrafine, possibly less crystalline particles of the sample. The high‐temperature onset of the Morin transition at ∼−10 °C indicates that the particles consist of pure α‐Fe2O3.
On warming from −196 °C, the red bed sample does not show the characteristic increase in susceptibility related to a switch of ‘easy’ axes of magnetization, but rather shows a hyperbolic temperature dependence of χlf. This specific χlf–T behaviour can be caused either by ultrafine haematite grains being superparamagnetic over the whole temperature range or by the paramagnetic minerals of the sediment. A rock‐magnetic study by Dekkers & Linssen (1989) on samples from the same locality, however, showed that the first possibility is highly unlikely because their isothermal remanent magnetization (IRM) was not viscous. LT cycling of their induced IRM also did not reveal a clear Morin transition. In view of the volcanic origin of the haematite, the persistence of the weak ferromagnetic phase down to −196 °C can be explained by a small amount of incorporated Ti ( Kruiver . 2000 ).
4.1.3 Grain‐size dependence of the χlf increase caused by cycling through Tm
The percentage χlf increase caused by cycling through Tm is plotted in Fig. 3 for several grain‐size fractions of LH2 haematite. The χlf increase (y), normalized to its initial value, clearly increases with the logarithm of grain size (x). A linear fit results in y = (8.60 ± 1.01) ln(x) − 2.98 with R2 = 0.82, implying that for this particular haematite no increase in χlf can be observed in grains smaller than ∼ 1.5 µm (± 0.5 µm). The results plotted in this figure also illustrate that normalized χlf increases obtained in a field‐free space (indicated with solid dots) fall in the same range as those obtained on identical grain‐size fractions in the Earth's magnetic field.
4.1.4 High‐temperature and AF stability of the new magnetic state
Figs 4(a) and (b) show the HT behaviour of the initial magnetic state and the new magnetic state as obtained by cycling through Tm for LH2 and LHC haematite, respectively. For LH2 haematite, a high‐temperature χlf–T cycle to 700 °C starting from the initial state revealed complete reversible behaviour ( Fig. 4a, cycle 1). No heating‐induced changes in χlf caused by irreversible chemical and/or physical changes were detected after cycling. Next, the new magnetic state, characterized by the higher χlf value, is obtained by cooling to −196 °C and subsequent warming to room temperature (run 2). Subsequent heating to 700 °C (cycle 3) shows that the heating curve of the new magnetic state resembles that of the initial magnetic state in shape, but lies entirely above it until the Curie point is reached at ∼ 685 °C, indicating that the new magnetic state remains up to Tc. The cooling curve of cycle 3, on the other hand, is irreversible with respect to the heating curve, but perfectly matches the curves obtained during cycle 1, indicating that after cycling through Tc the initial magnetic state is recovered. A subsequent LT treatment (not shown here) yielded a warming curve similar to run 2.
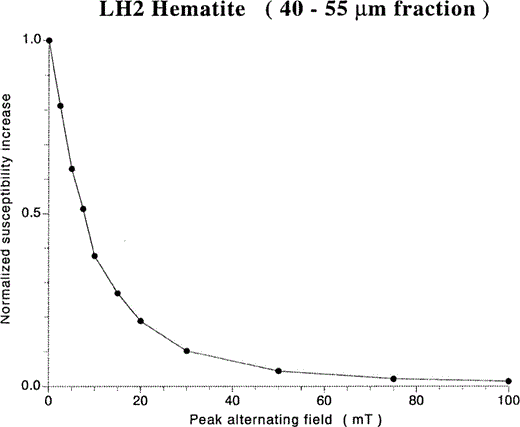
Low‐field susceptibility versus temperature runs for coarse‐grained (a) LH2 and (b) LHC haematite. Cooling curves are dotted. See text for explanation of curve numbers. The susceptibility increase obtained after cycling through the Morin transition is fully neutralized after heating above the Curie point, recovering the initial magnetic state.
Unlike the procedure followed for LH2 haematite, the treatment on LHC haematite was not started with an initial cycle to 700 °C. Instead, cycle 1 and warming run 2 shown in Fig. 4(b) are identical to those plotted in Fig. 1(a), and represent the initial magnetic state and the new magnetic state obtained after cycling through the Morin transition, respectively. A subsequent HT cycle to 700 °C does not recover the initial magnetic state on cooling but produces a further increase in susceptibility. Preceding test runs on an untreated sample (see Section 3.2.1) revealed that this increase in susceptibility is most probably caused by a heating‐induced structural change of the haematite (e.g. recrystallization). A subsequent test cycle to 700 °C showed no further irreversible χlf changes and the heating and cooling curves were identical. From this perspective, the magnetic state of the annealed haematite can be regarded as a new ‘initial’ state. A low‐temperature treatment (run 4) on this structurally improved haematite increases its χlf value by ∼ 15 per cent. Cycling to 700 °C (cycle 5) fully neutralizes this increase and recovers the ‘initial’ state of the annealed haematite, i.e. that after cycle 3.
Fig. 5 shows that the increase in bulk susceptibility obtained on cycling through Tm can also be neutralized to its initial value before the LT experiment by AF demagnetization. This involves measurement of χlf between subsequent AF steps. For the 40–55 µm fraction of LH2 haematite, 50 per cent of the increase is lost in an AF demagnetizing field of 7.5 mT, while peak fields up to ∼ 100 mT are required for a full recovery of the initial bulk susceptibility.
4.2 MicroMag measurements
Fig. 6 shows the changing shape of the hysteresis loops obtained in a 1.6 T field when passing through the Morin transition. The 75–100 µm grain‐size fraction of sample LHC appears to be fully saturated at temperatures above Tm. At temperatures during and below the Morin transition, however, the 1.6 T field is no longer sufficient to saturate the sample. Below Tm, some hysteresis can still be seen, indicating the presence of a small defect moment. Hysteresis parameters measured at + 20 °C are σs = 0.316 A m2 kg−1, σrs = 0.218 A m2 kg−1, Bc = 23.4 mT and Bcr = 28.9 mT. The high‐field susceptibility at 20 °C deduced from the hysteresis loop is 26.76 × 10−8 m3 kg−1. This is in good agreement with published data on χhf. Using 26.76 × 10−8 m3 kg−1 would yield a χhf value of ∼ 18.5 × 10−8 m3 kg−1 below Tm for randomly oriented particles with a third of the grains having their c‐axes parallel to the applied field (see Section 2.3). A high‐field susceptibility of 22.8 × 10−8 m3 kg−1 at −170 °C was measured, which is on the high side and could indicate that the grains have a slightly preferred orientation in our sample, with their basal planes parallel to the applied field, something that can hardly be avoided due to the sample holder, although strong‐field (1.6 T) hysteresis loops, made at room temperature, are essentially the same, regardless of sample orientation.
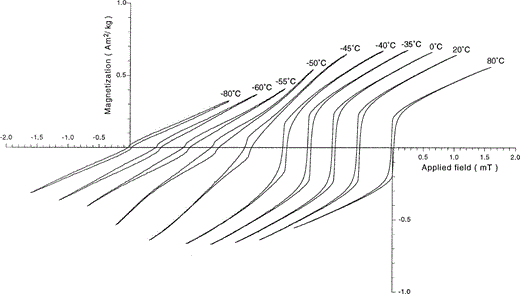
Hysteresis loops (maximum applied field 1.6 T) measured at various temperatures for LHC haematite (75–100 µm) showing the changing shape on passing through the Morin transition.
The hysteresis values obtained at 20 °C, together with the shape of the curve, are diagnostic of multidomain haematite. The slight wasp‐waisted shape of the hysteresis loops might be explained by the difference in coercivity between the canted and defect moment. Canting would be soft and the defect moment harder in coarse haematite grains ( Fuller 1970). In fine grains the reverse seems to be true ( Dunlop 1971); why this is the case remains enigmatic to date. Halgedahl (1998) argues for spatially localized defects (not randomly distributed throughout the grain) to explain observed leaps of domain walls through the haematite associated with measured Barkhausen jumps on hysteresis loops. The existence of SP grains or a magnetic contaminant are less likely explanations because no adhering ultrafine haematite particles were observed under an optical microscope (grains down to ∼1 µm would be detectable, also no colouring of propanon occurs when putting the grains in an ultrasonic bath) and other magnetic measurements (e.g. χlf–T curves) revealed no indication of a magnetic impurity. Similar hysteresis loops are obtained by Flanders & Schuele (1964) and Halgedahl (1998) on a large natural haematite crystal.
A low‐temperature cycle of the saturation remanence imparted at + 80 °C (σrs = 0.183 A m2 kg−1) is shown in Fig. 7(a). Apart from effects due to the preferred orientation of the grains, it should be realized that LT cycling of σrs using a MicroMag without applying a magnetic field is not completely identical to LT cycling in zero field. First, no correction for the vertical component of the Earth's magnetic field is possible. Second, the edges of the sample sense an AF peak field of ∼ 1 mT with the measuring resonance frequency, typically c. 300 Hz.
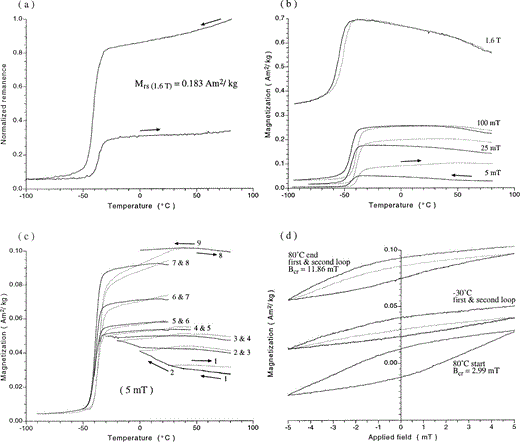
Various low‐temperature MicroMag measurements obtained on LHC haematite (75–100 µm). (a) LT cycle of the saturation remanence (1.6 T). (b) LT cycles in various applied fields. (c) Repeated in‐field cycling (5 mT) to increasingly lower temperatures. (d) Minor hysteresis loops (5 mT) obtained at different temperatures during an LT cycle through the Morin transition.
Above Tm, the remanence vector lies in the ‘easy’ basal plane of haematite, and thus along the measuring direction for most of the grains. During cooling to the high‐temperature onset of the actual Morin transition at −30 °C, ∼ 18 per cent of the initial remanence is destroyed. At −100 °C, well below Tm, only ∼ 6 per cent of the original remanence is left, which resides in haematite's defect moment. For temperatures below Tm, the remanence vector of this moment lies orthogonal to the basal plane and thus also orthogonal to the measurement direction for the largest fraction of the grains. For these oriented grains the remanence measured below Tm will thus be lower than that of randomly oriented grains. Hartstra (1982) reported that c. 33 per cent of an initial σrs (2 T) imparted at 0 °C was left after cooling to −150 °C for randomly oriented samples of LHC haematite, whereas c. 75 per cent of the initial remanence was recovered after rewarming. Rewarming our sample to + 80 °C recovered only ∼ 33 per cent of the initial remanence. The discrepancy may be caused by the influence of the vertical component of the Earth's magnetic field. On warming through the Morin transition, part of the domains will orient themselves along this component, which lies in the basal plane but orthogonal to the measuring direction. Only the most strongly pinned domains can recover their initial direction. In the warming curve a slight break in slope is recognizable at c. + 40 °C. Warming above this temperature tends to recover the remanence faster than during the temperature range between Tm and + 40 °C. For the cooling curve a similar break in slope at the same temperature may be recognized.
Fig. 7(b) shows low‐temperature σ–T runs measured in various applied magnetic fields (5, 25, 100 and 1600 mT). Cycling in a 1.6 T field, which is a saturating field down to the high‐temperature onset of the Morin transition, results in reversible cooling and heating curves except for some temperature hysteresis observed in the temperature range in which the actual switch of axis occurs. An increase in magnetization, however, is observed on cycling through the Morin transition in the other three, non‐saturating fields. The relative gain in magnetization decreases with increasing field strength; it is 200, 25 and 5 per cent for 5, 25 and 100 mT fields, respectively. Fig. 7(b) also illustrates that the Morin transition is shifted to slightly lower temperatures with increasing field strength. By applying a magnetic field in the direction of the basal plane, the rotation of the magnetic spins from this plane to the hexagonal c‐axis is hampered (see Section 2.3). For all applied fields, a break in slope around + 40 °C is again visible in both the cooling and the warming curves.
The characteristic break in slope at c. + 40 °C is even more visible in Fig. 7(c). This figure shows repeated cooling and warming cycles to increasingly lower temperatures in a 5 mT field. The warming curves (dotted lines) are already irreversible compared with the corresponding cooling curves (solid lines) long before the actual Morin transition starts. Cycling between + 80 °C and + 25 °C results in a ∼ 15 per cent increase in magnetization measured at + 80 °C. After this first cycle, the sample was demagnetized using the MicroMag routine with a starting field of 30 mT. This procedure resulted in the full recovery of the initial demagnetized state, and an identical magnetization was obtained when reapplying the 5 mT field. Between subsequent cycles, the sample was not demagnetized. The magnetic field, however, was switched off before the next run was started. Only small differences in magnetization were observed, implying that the increase in magnetization caused by thermal cycling is for the greater part a remanent magnetization. The remanent magnetization values are not plotted in this figure but are clearly illustrated in Fig. 7(d) for three different temperatures. The small discrepancies observed between the starting point of the cooling curve and the endpoint of the warming curve of the previous run ( Fig. 7c) can be explained as follows. When the magnetic field is switched off, a small negative field overshoot occurs that slightly demagnetizes the remanent magnetization gained. When reapplying the field, the original value is not fully recovered due to this effect. Differences between the remanent magnetization values obtained and the starting points of the new cooling curve are marginal, not exceeding 2 per cent (the points are not shown because they are beyond plotting resolution). Between the last cycle (no. 8) and the partial cooling run to 0 °C (no. 9) the field was not switched off.
Cycling down to −30 °C (cycle 1–4), i.e. to just before reaching Tm, increases the magnetization to ∼ 95 per cent of the initial value, which is ∼ 35 per cent of the total increase after the entire experiment. By far the largest part of this 95 per cent increase is gained during cycling to temperatures below the break in slope around + 40 °C. Complete cycling through the Morin transition (cycle 8) results in a c. 260 per cent gain in magnetization when compared to the initial value at + 80 °C.
In the temperature range between Tm and + 40 °C, i.e. at the low‐temperature side of the break in slope, the warming curve of a particular cycle differs in shape from the cooling curve of a subsequent cycle, that is, in this particular temperature range, the magnetization increases more rapidly with temperature during warming than it decreases with temperature during the next cooling run. Above the break in slope, however, the warming and subsequent cooling curves are colinear.
Fig. 7(d) shows some minor hysteresis loops obtained in a 5 mT magnetic field at different temperatures during cycling through Tm. Note that the curves shown have the same ordinate axis; they are not displaced with respect to each other. The minor loop of the initial demagnetized state at + 80 °C is closed at both sides. A partial Bc and Bcr of 2 mT and 2.99 mT, respectively, are measured. The minor loop measured at −30 °C, however, is no longer closed at the right‐hand side, indicating that a portion (∼ 50 per cent) of the magnetization gained on cooling is demagnetized by a backfield of only −5 mT. A subsequent minor loop measured at the same temperature is again closed. Before measuring the following minor loop, the sample was warmed back to + 80 °C, demagnetized, and next cycled to the desired temperature. The minor loop measured when the sample is returned to + 80 °C after a complete cycle through the Morin transition (− 100 °C) is not closed either. However, now only ∼ 10 per cent of the magnetization gained is demagnetized by a 5 mT backfield. The partial Bcr value is increased to 11.86 mT.
5 Discussion
5.1 Domain reorganization as deduced from mineral‐magnetic measurements
5.1.1 Low‐field susceptibility measurements
For PSD and MD grains, the number of magnetic domains and the mobility of the domain walls determine the susceptibility, whereas for SD grains it is determined by the elastic simultaneous rotation of the spins. Wall motion usually requires lower fields than domain rotation. Consequently, it may be stated that SD grains have lower susceptibility than MD grains. This holds for antiferromagnetic substances especially because wall displacements are not limited by any demagnetizing field, as is the case for ferrimagnetic substances ( Dunlop & Özdemir 1997, p. 139). Irreversible changes in susceptibility caused by a particular treatment that does not chemically or physically (e.g. grain growth) change the material under investigation may thus be interpreted in terms of domain reorganization.
It is known that low‐temperature cycling changes the domain configuration of haematite. The saturation remanence of haematite, for instance, is usually only partly recovered upon cycling. Domain structure observations on haematites in a saturation remanent state ( Eaton & Morrish 1969; Morrish 1994) show that most crystals lose their domain pattern on cooling. Below Tm a single‐domain state is often observed, and if they are warmed to room temperature again, a new pattern is seen. In some crystals, however, the walls, or part of the walls, persist below Tm and act as nucleating centres for the configuration that is achieved upon warming the sample back to room temperature (cf.Fuller 1970). The latter situation can give an almost perfect recovery of the initial domain configuration.
We showed that thermal cycling through haematite's magnetic isotropic point appears to increase the initial low‐field susceptibility of large (at least > 1.5 µm) platy and rounded grains, whereas fine to ultrafine grains and large acicular grains that are likely to be SD do not show this irreversible behaviour. Moreover, the percentage χlf increase obtained on cycling through the Morin transition increases linearly with the logarithm of grain size.
Dankers (1978) showed that the susceptibility of haematites could be changed considerably by the imparting of a saturation remanence. Consequently, the χlf increase observed on cycling through Tm might be caused by the destruction of an old remanence or the development of a new remanence. However, for three reasons this explanation is unlikely. First, our initial state and the magnetic state obtained after AF demagnetization yield identical bulk susceptibilities and thus have comparable domain configurations. Second, χlf increases are independent of the crystallographic orientation of the haematite grains (at least within the basal plane). Third, cycling in the Earth's magnetic field and in a field‐free space yield similar increases.
In our opinion, the results observed must be explained by an increased number of magnetic domains induced by thermal cycling through Tm. The fact that AF demagnetization of the new magnetic state is able to recover the bulk susceptibility value related to the initial magnetic state seems to support this assumption. The transdomain changes ( Moon & Merrill 1984, 1986) invoked as a consequence of temperature variation have been reported for (titano)magnetite above room temperature, although domain observations yield contrasting results. The number of domains on cooling of Fe2.4Ti0.6O4 from its Curie point was found by Metcalf & Fuller (1986, 1987) to increase, whereas Halgedahl (1991) observed denucleation of domain walls during cooling of Al0.1Mg0.1Fe2.2Ti0.6O4. In hydrothermally recrystallized magnetite Heider . (1988) observed that the domain structure was temperature‐dependent below 100 °C, while for natural crystals no major changes occurred up to ∼ 400 °C followed by a gradual decrease up to the Curie temperature ( Ambatiello . 1999 ). Also, in acquisition experiments, patterns of partial TRM suggest temperature dependence of domain structure in MD magnetite ( Muxworthy 2000). Field‐history‐dependent domain structures with a metastable SD state acquired after the saturation of grains in large magnetic fields were observed by Halgedahl & Fuller (1983) for pyrrhotite at room temperature. It is evident that these observations are made at or above room temperature up to temperatures close to the Curie temperature. However, Boyd . (1984) reported that low‐temperature cycling through the Verwey transition also triggers the nucleation of walls in large magnetite particles that initially appear to be saturated at room temperature.
The renucleation of domain walls on warming through Tm obviously happens under different conditions as those at room temperature or above. Near the isotropic point the magnetocrystalline anisotropy constant K1 is almost zero, resulting in a relatively low domain wall energy, γw ≈ (Ktot)1/2 (where Ktot = total anisotropy energy), and nucleation field, 2Ktot/σs ( Dunlop & Özdemir 1997, Chapter 5). According to Halgedahl & Jarrard (1995), the net result is increasing accessibility of equilibrium domain states and the addition of energetically favourable walls in some grains. Consequently, the increase in susceptibility probably reflects the nucleation of (additional) domain walls to reduce the net magnetostatic energy of haematite grains that initially had ‘metastable’ SD or PSD domain configurations. This also suggests that these so‐called transdomain changes could contribute substantially to the observed loss of remanence during zero‐field cycling through Tm, even for originally SD haematite particles.
Transdomain changes will have the biggest effect on susceptibility when a relatively large area of uniform magnetization becomes subdivided by an elastic domain wall. The low spontaneous magnetization of haematite means that even large grains should have only a few broad domains because the equilibrium number and average width of lamellar domains are proportional to (σs2)1/2 and (1/σs2)1/2, respectively ( Dunlop & Özdemir 1997, Chapter 5). Indeed, Halgedahl (1995, 1998) observed only very few domains in ∼ 100 µm sized haematite platelets and reported typical PSD behaviour with low coercivity. This suggests that the coarsest grain‐size fractions consist of an assemblage of relatively soft MD particles and metastable PSD particles with only a few large domains and possibly even a small portion of large metastable SD particles. The relationship obtained between the grain size and the normalized susceptibility increase for sized fractions of LH2 haematite reflects the increasing size of the metastable uniformly magnetized parts of the grains, rather than a fast increase in the number of domains as observed for ferrimagnetic substances such as magnetite, Ti‐magnetite and pyrrhotite ( Dunlop & Özdemir 1997, Figs 5.10 and 6.7). If the suggested mechanism of transdomain changes due to thermal cycling through Tm is correct, then the intercept of the fitted line drawn in Fig. 5 gives the approximate value for the ‘true’ critical SD threshold size d0 for LH2 haematite. Evidently, below a grain size of ∼ 1.5 ± 0.5 µm walls cannot be nucleated, even in the more favourable conditions at the transition, so χlf is unaffected. Above this size, however, nucleation can take place and becomes increasingly easy with increasing grain size (cf.Boyd . 1984 ). The value determined, d0 = ∼ 1.5 µm, is much lower than the value predicted by domain theory (∼ 10–100 µm) and observed by domain observations on well‐crystalline annealed haematites ( Eaton & Morrish 1969, 1971; Halgedahl 1995, 1998), but agrees better with the size range of 0.5–1 µm suggested for d0 by Dekkers & Linssen (1989).
Repeated thermal cycling through Tm of the same sample yielded identical warming curves and χlf values back at room temperature. The reproducibility of the results suggests that only one final domain configuration, i.e. a so‐called local energy minimum (LEM) state, is obtained by cycling. The AF stability of the new magnetic state is not very high; 30 mT is sufficient to erase 90 per cent of the χlf increase, whereas a complete recovery of the initial LEM state is achieved in AF demagnetizing fields up to ∼ 100 mT ( Fig. 5). On the other hand, temperatures up to ∼ 680 °C are necessary before the new LEM state with the higher amount of walls returns to the initial LEM state ( Fig. 4). The magnetic state after AF demagnetization and that after thermal treatment above the Curie temperature have approximately equal susceptibilities, although the thermally treated state is commonly regarded as the absolute or global energy minimum state (e.g. Shcherbakov . 1993 ; Dunlop & Özdemir 1997). The χlf–T heating curves obtained for the new and initial magnetic states are identical in shape almost up to Tc. This agrees with Dunlop & Özdemir (1997, p. 197), who stated that only at temperatures close to the Curie point does the exchange energy drop to such an extent that energy barriers between LEM states can be overcome by thermal energy alone. The fact that the initial magnetic state and those obtained after AF demagnetization and thermal cycling through the Curie point all yield identical values may suggest that these states represent identical LEM states and that only thermal cycling may cause a different LEM state in haematite. The assumption that haematite has far fewer LEM states and that switching between them is much more difficult compared to ferrimagnetic substances possibly results from the fact that even large grains of weakly magnetic haematite can only contain a small number of domains.
5.1.2 MicroMag measurements
The MicroMag measurements show that 75–100 µm haematite particles can gain magnetization when they are thermally cycled through the Morin transition in non‐saturating fields. Lower applied fields appear to induce higher magnetization increases upon cycling. Even more important is the observation that this gain in magnetization appears to be remanence. This is clearly demonstrated by the shift of the minor hysteresis loops obtained at different temperatures during cycling in a non‐saturating 5 mT field. Moreover, for the haematite under investigation, the irreversible displacement of domains started ∼ 70 °C before the actual Morin transition is reached.
The gain in magnetization caused by thermal cycling between 80 °C and temperatures above the high‐temperature onset of the Morin transition could be explained by the transdomain mechanism described previously. In this case both the metastable SD and PSD fractions of the haematite grains could be responsible for the observed behaviour. This explanation, however, is not likely. As mentioned, domain structure observations on haematites report a decrease rather than an increase in the number of domains upon cooling in the vicinity of the Morin transition ( Gustard 1967; Gallon 1968). This phenomenon can possibly be explained as follows. On approaching haematite's isotropic point, the vanishing of K1 will result in a considerable broadening of the domain walls because wall width is proportional to K1−1/2 (cf.Dunlop & Özdemir 1997, Chapter 5). Xu & Merrill (1989) and Moskowitz (1993) showed that broad walls are less effectively pinned by localized defects and eventually escape. They ‘sense’ the defects less because of a lower energy contrast. Domain wall thickness also varies with temperature but this is probably a less important factor in the temperature range mentioned. Consequently, a non‐saturating field that is not sufficiently strong to overcome a certain energy barrier, i.e. to move a particular domain wall, may overcome the lower energy barrier on cooling, resulting in the displacement of a relatively loosely pinned domain wall. As a result of this, more domains can become aligned with the field. Evidently, the unpinned or vanished domain walls do not return to their initial position on rewarming in a non‐saturating field. If this is the correct mechanism then the metastable SD fractions of the haematite grains could not take part in this mechanism, simply because they do not contain a domain wall.
On passing through the isotropic point, all or at least the greater part of the most rigid domain walls will now become unpinned due to the switch of the ‘easy’ axis. On warming back, a number of broad domain walls will instantly nucleate, possibly in part prescribed by the existing antiferromagnetic domain structure below Tm ( Mitsek & Gaidanskii 1971), which when dealing with remanent magnetizations would explain the partial recovery of remanence in its original direction. Mitsek & Gaidanskii (1971) modelled the weakly ferromagnetic domain structure above Tm as being the consequence of 90° domain walls that after nucleation swept through the whole grain with increasing temperature. The considerable increase in magnetization compared to the situation before cycling must be caused by distinct domain reorganization. In our opinion, a substantial part or even the total increase compared to the magnetization achieved just before the actual Morin transition is caused by the nucleation of (additional) domain walls in formerly metastable SD and/or PSD grains. A minor additional increase in magnetization is achieved on further warming. It might be caused by decreasing wall thickness, increasing wall rigidity and/or some repositioning of the domain walls on energetically more favourable positions. Another explanation may be that some tiny nuclei of walls were already formed instantly at the Morin transition but could only escape from the nucleation site and traverse the particle at somewhat higher temperatures (cf.Boyd . 1984 ). Whatever the exact reason may be, the fact is that the behaviour becomes irreversible on subsequent cooling between + 40 °C and the high‐temperature onset of the Morin transition. Cycling above the break in slope at + 40 °C, however, yields reversible cooling and warming behaviour.
What particular role the characteristic break in slope at + 40 °C plays in the whole process is not clear at present. It could represent a change in exchange energy or some sort of critical point below which K1 becomes sufficiently low to be no longer the most important anisotropy constant. Another suggestion is that the canting angle of the atomic spins may change slightly in the vicinity of the isotropic point. No explanation is found in the literature. A similar break in slope, however, is observed in the σs–T curves obtained by Néel & Pauthenet (1952).
5.2 Possible palaeomagnetic implications
Large (> 1 µm) black haematite particles (specularite) are often believed to carry a stable primary DRM or CRM in red sediments, whereas the fine‐grained red pigment carries a secondary CRM. Our LT experiments suggest that the interpretation of remanences residing in specularite in particular should be made with some caution, especially in areas of high altitude or latitude. Variations in Earth surface temperature might possibly induce secondary remanence components in these large haematite grains that may partially or totally overprint the primary remanence. Moreover, our experiments also seem to indicate that separation of an original remanence and the remanence induced by cycling through the Morin transition will be difficult to achieve by means of standard thermal demagnetization. However, stepwise thermal demagnetization in combination with an initial AF demagnetizing step of a few tens of milliteslas might solve this problem: 95 per cent of the χlf increase obtained on cycling through Tm was neutralized in a 50 mT AF field.
Necessary conditions for the induction of such a secondary remanence are that the haematite grains must be at least > 1.5 µm and that they exhibit a well‐pronounced Morin transition with its high‐temperature onset in the range of (extreme) Earth surface temperatures, i.e. not to far below 0 °C. Specularite formed in situ often fulfils these conditions because it usually consists of relatively pure platy‐developed particles. Detrital specularite, on the other hand, is often Ti‐substituted because of its high‐temperature origin (e.g. Dôme de Barrot red beds) and small amounts of Ti successfully shift the Morin transition to lower temperatures.
Although complete passing of the Morin transition on LT cycling is required for relatively large ‘metastable’ SD grains, thermal cycling in the vicinity of the Morin transition may already be sufficient to induce a secondary remanence in PSD and MD grains. It is, however, realized that the in‐field LT runs were recorded in magnetic fields many times that of the Earth, and our experimental results may not be projected unambiguously to the natural situation. On the other hand, χlf–T runs in zero field also showed the susceptibility increase, and the saturation remanence lost part of its intensity on cooling in zero field before the actual high‐temperature onset of the Morin transition was reached.
We plan to test these suggestions on a set of artificial samples with a DRM carried by haematite particles. The samples will be thermally cycled through the Morin transition in various magnetic fields with a direction perpendicular to the original DRM. Afterwards the samples will be AF and thermally demagnetized.
6 Conclusions
The low‐field susceptibility of large (> 1.5 µm) haematite particles can be increased by low‐temperature cycling through their Morin transition. We suggest that transdomain changes are responsible for this irreversible behaviour. The nucleation of additional domain walls in formerly ‘metastable’ SD and PSD grains is triggered on rewarming through the isotropic point when the crystalline anisotropy and thus the nucleation energy is relatively low. The new LEM state with a greater number of domains can only be obtained by cycling through the isotropic point; AF demagnetization and high‐temperature thermal cycling recover the initial LEM state. A ‘true’ critical SD threshold size of ∼ 1.5 µm is obtained for a well‐crystalline platy haematite. Below this grain size walls cannot be nucleated, even in the more favourable conditions at the transition. Because of the same mechanism, a new remanence component can be induced in large SD and PSD haematite grains on cycling through the Morin transition in non‐saturating fields, at least for field strengths as low as 5 mT. Thermal cycling in the vicinity of Tm achieved irreversible changes in the domain configuration of PSD and MD haematite grains when cycling was carried out in a 5 mT field. Consequently, palaeomagnetic results obtained from red beds in which the remanence is dominantly carried by low‐temperature specularite exhibiting a well‐pronounced Morin transition with a high‐temperature onset near −10 °C must be regarded with some caution, all the more so as it seems to be difficult to separate the original and the cycling‐induced remanences by standard thermal demagnetization. A procedure with an initial AF demagnetizing step of a few tens of milliteslas is recommended for cleaning the aforementioned red bed varieties.
Acknowledgments
We gratefully acknowledge the assistance given by Adry van Velzen with the low‐temperature measurements on the MicroMag. Eduard Petrovský kindly made available a high‐purity haematite rock sample of the Kadaň hydrothermal ore deposit. This work was conducted under the programme of the Dutch national research school, the Vening Meinesz Research School of Geodynamics (VMSG).
References




