-
PDF
- Split View
-
Views
-
Cite
Cite
Frank D. Stacey, Donald G. Isaak, Compositional constraints on the equation of state and thermal properties of the lower mantle, Geophysical Journal International, Volume 146, Issue 1, July 2001, Pages 143–154, https://doi.org/10.1046/j.1365-246X.2001.00437.x
Close - Share Icon Share
SUMMARY
By extrapolating the lower mantle equation of state (EoS) to P=0, T=290 K, we determine the EoS parameters that are compatible with a mixture of (Mg, Fe)SiO3 perovskite (with a small admixture of Al2O3), (Mg, Fe)O magnesiowüstite and CaSiO3 perovskite in arbitrary proportions and with arbitrary Fe/(Fe+Mg) ratio. The parameters fitted are density, ρ, adiabatic incompressibility, KS, and its pressure derivative, K′S≡(∂KS/∂P)S. The first stage is adiabatic extrapolation to P=0, T=T0, that is, to the foot of the lower mantle adiabat, at which K′0(T0) is allowed to have any value between 3.8 and 4.6, and 1500 K≤T0≤2000 K. It is important to use an equation for which the lower mantle fitting does not prescribe K′0(T0) and this rules out the third-order Birch theory, which gives a seriously wrong value. The further extrapolation to 290 K at P=0 uses thermodynamic relationships with maximum generality, allowing all of the following thermoelastic parameters to be arbitrary functions of temperature: K;ρ; Grüneisen parameter, γ;q=(∂ ln γ/∂ ln V)T, where V is volume; volume coefficient of thermal expansion, α; adiabatic Anderson–Grüneisen parameter, δS=(1/α) (∂ ln KS/∂T)P; and the mixed P, T derivative (∂K′S/∂T)P. The heat capacity at constant volume, CV, is assumed to follow the Debye function, so α is controlled by that. The temperature dependences of the dimensionless parameters γ, q and δS at P=0 are slight. We find γ to be precisely independent of T at constant V. The parameter dK′0/dT increases strongly with T, as well as with the assumed value of K′0(T0), where K′0 is K′S at P=0. The fitting disallows significant parameter ranges. In particular, we find solutions only if K′0(T0)≥4.2 and the 290 K value of K′0 for Mg perovskite is less than 3.8. Conclusions about composition are less secure, partly because of doubt about individual mineral properties. The volume of magnesiowüstite is found to be between 10 and 25 per cent for respective T0 values of 2000 and 1500 K, but the Ca-perovskite volume is no more than 6 per cent and has little influence on the other conclusions. The resulting overall Fe/(Fe+Mg) ratio is 0.12 to 0.15. Although this ratio is higher than expected for a pyrolite composition, the ratio depends critically on the assumed mineral densities; some adjustment of the mineral mix may need to be considered.
1Introduction
Geochemical and geophysical evidence (Ito & Takahashi 1987; Anderson 1989; Bina 1998) indicates that the composition of Earth's lower mantle is primarily (Mg, Fe)SiO3 perovskite with a little dissolved Al2O3, (Mg, Fe)O magnesiowüstite and a few per cent CaSiO3 perovskite. This composition is just simple enough to make a useful comparison of its properties with seismological data. In making this comparison, we have two aims: to determine the range of equation-of-state parameters that is consistent with the mineralogy and to estimate the proportions of the three minerals and the ratio f=Fe/(Fe+Mg). Although it appears that the quantities we are calculating are seriously underdetermined by the available data, we can impose significant restrictions on both composition and the equation of state.
Jackson (1998) reported a detailed study of this problem, but Stacey & Isaak (2000) objected to his use of the third-order Birch theory of finite strain because it gives a value of K′0=(∂KS/∂P)S at P=0 (K is incompressibility, P is pressure, and subscript S indicates adiabatic values) incompatible with the fitted mineralogy. One of the conclusions of the Stacey & Isaak (2000) analysis was that the value of K′0 is more important to the estimation of thermoelastic properties than the choice of equation of state and that for the lower mantle K′0 is at least 4.2, compared with 3.8 obtained from fitting the third-order Birch theory. The impossibility of estimating K′0 from the PREM lower mantle tabulation (Dziewonski & Anderson 1981) alone was emphasized by Stacey (2000), who compared a plot of K′ for PREM with several equations that are claimed to ‘fit’ PREM. The parametrization of the model gives a variation of K′ with pressure quite unlike any plausible equation of state, so that attempts to fit an equation of state in a manner that determines K′0 are meaningless.
Stacey & Isaak (2000) addressed the K′0 problem by using a quadratic relationship between K′ and the dimensionless ratio P/K for the equation of state. Such an equation can be fitted to the PREM tabulation with an independently fixed value of K′0, allowing a self-consistent calculation in which the value of K′0 used in the equation of state is made equal to the value required by the inferred mineralogy. Stacey (2000) subsequently found that a reciprocal relationship is a better representation,
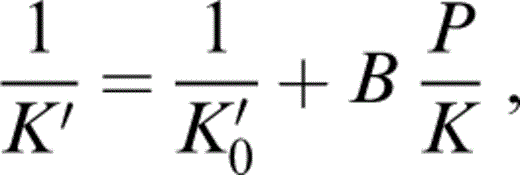
where
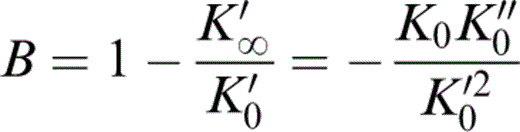
and K′∞=(dK/dP)P→∞ is the same for an isotherm as for an adiabat. The relationships described by eqs (1) and (2) are used here. However, the results obtained by using eq. (1) differ very little from those obtained with the quadratic equation as long as K′0 is constrained to the same value.
Another development in the Stacey & Isaak (2000) approach was to allow K′0 to vary with temperature, so that the match of the equation of state and mineral values of K′0 required a temperature adjustment from the foot of the lower mantle adiabat, or temperature T0, to 290 K. A thermodynamic analysis was used to estimate dK′0/dT from the equation of state. This derivative was assumed to be zero in earlier calculations by Jackson (1998) and Stacey (1998). Stacey & Isaak (2000), however, found that dK′0/dT is not necessarily zero. Their calculations indicate that dK′0/dT is negligible when K′0≈3.8 but is positive and has an increasingly larger magnitude as K′0 increases above 3.8. Such higher-order corrections are here taken to another level by allowing both dK′0/dT and δS=−(1/α) (∂ ln KS/∂T)P to vary arbitrarily with temperature instead of being assumed to be independent of T. It may appear surprising that we can claim significance for these higher-order derivatives, but they are closely coupled and are linked to K′0 in a systematic way so that all of them are necessary for strict internal consistency of the calculations. Allowing all thermodynamic parameters, especially dK′0/dT, to vary arbitrarily with temperature appears to be the single most important improvement in the present calculations relative to Stacey & Isaak (2000). A better approximation than constant dK′0/dT would be the assumption that (1/α)(dK′0/dT) is constant, as assumed by Stacey & Isaak (2000), but even this has no obvious theoretical justification.
The original motivation for the present calculations was to include Ca perovskite, omitted in the earlier work. It was not obvious that we would succeed in introducing another unknown mineral fraction to the problem, especially as the properties of Ca perovskite are only poorly known. Some past investigators have suggested that the density and compressibility of Ca perovskite are such that it is seismically invisible (Wang 1996 ). Recent work has focused on determining the shear properties of Ca perovskite and whether they are elastically visible in the lower mantle. No consensus exists yet. State-of-the-art theoretical calculations (Karki & Crain 1998) obtain a value for the shear modulus μ of CaSiO3 perovskite that is 50 per cent higher than obtained by extrapolating measurements on CaSiO3–CaTiO3 mixtures to end-member CaSiO3 (Sinelnikov 1998a ). Nevertheless, Stacey & Isaak (2000) suggested that their own work was incomplete in excluding CaSiO3 perovskite. Their estimate of an implausibly high lower mantle iron content [Fe/(Fe+Mg)≈0.22] was attributed to its exclusion. It now appears that the improved temperature correction reported here is more important.
For the purpose of the analyses in the following three sections, it is convenient to present with minimal explanation a reference list of definitions and notation used in this paper. Table 1 provides the required listings.

2Equation-of-state fits to the lower mantle
Eq. (1) integrates to expressions for K/K0 and ρ/ρ0 in terms of P/K that are convenient to use in extrapolating lower mantle properties to zero pressure,
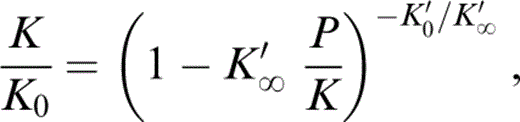

Values of ρ, K and P are tabulated in PREM (Dziewonski & Anderson 1981), so that for the radius range over which the lower mantle is modelled as uniform (3630–5600 km), values of ρ/ρ0 and K/K0 are obtained directly for each tabulated (P/K) for any (assumed) values of K′0 and K′∞.
We do not prejudge the value of K′0(T0) but fix it only after we have compared our calculated properties with those of the inferred mineral composition. We thus start by assuming a range of alternative values, from 3.8 to 4.6, and follow the calculations through for each value. The results in Table 2 are obtained from eq. (3) by taking trial values of K′∞ for each K′0 and for each trial calculating K/K0 at each depth. Using the tabulated (PREM) values of K, this procedure gives the apparent K0 at each depth. K′∞ is then repeatedly adjusted until a linear regression of the calculated K0 versus P gives zero gradient. For each assumed K0, this fixes K′∞ and gives the value of K0 as the intercept of the linear regression. The quoted uncertainty in K0 is the standard deviation of the intercept and is a measure of the misfit of the PREM tabulation to eq. (3).

Extrapolation of lower mantle properties to zero pressure and to infinite pressure for different assumed values of K′0(T0).
The corresponding value of ρ0 is obtained from eq. (4) using the same values of K′0 and K′∞ as for the K0 calculation. The value of ρ/ρ0 is calculated at each depth, and then ρ0 is obtained from the PREM value of ρ. Table 2 gives the average value of ρ0 obtained in this way for each value of K0(T0). The result is marginally different from the intercept of a zero gradient linear regression of ρ0 versus P because the PREM tabulation does not precisely conform to the Adams–Williamson equation (Stacey 1997).
Values of the other equation-of-state parameters in Table 2 follow. K0K″0 is given by eq. (2). The infinite pressure Grüneisen parameter is given by
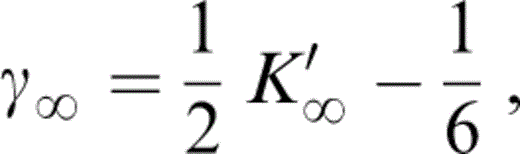
which is the form that all of the familiar equations for γ reduce to in the infinite pressure limit. The linear relationship
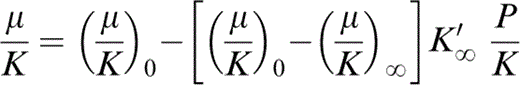
found to give excellent agreement with the PREM lower mantle tabulation, with (μ/K)0 = 0.631 and [(μ/K)0 − (μ/K)∞]K′∞ = 0.899 (Stacey 1992, 2000), gives the values of (μ/K)∞. Eq. (1) differentiates to give
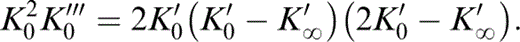
All of the values in Table 2 are obtained by fitting eq. (1) to the PREM lower mantle model with the specified values of K′0. Assuming that the lower mantle has an adiabatic temperature profile, the zero-pressure extrapolations give properties at the potential temperature, T0, that is, the temperature the lower mantle mix would have if its mineral structure survived adiabatic decompression to P=0. The infinite-pressure extrapolations follow from these fits. We do not have a precise value for T0, but none of the parameters in Table 2 depends on this. The three thermodynamic properties listed in Tables 3(a), (b) and (c) and illustrated in Figs 1(a), (b) and (c) are calculated from Table 2, but they depend on what is assumed about T0. Three alternative values, 1500, 1700 and 2000 K, are considered for T0, as in Stacey & Isaak (2000). The near-superposition of the T0=1500, 1700 and 2000 K curves at P=0 in Figs 1(a)–(c) is not an indication of temperature independence of γ, δS and dK′0/dT. These curves are calculated with different assumptions about T0 and therefore use different parameters. They are not curves calculated with the same parameters for different temperatures.
As emphasized in the introduction and by Stacey (2000), K′0 cannot be determined by fitting the lower mantle tabulation to an equation of state. Results obtained by fitting equations such as the third-order Birch theory are artefacts of the equations, not lower mantle properties. We, therefore, follow through our calculations for several assumed values of K′0 in Table 2 and restrict the plausible range only when we are able to compare calculated lower mantle properties with those of a three-mineral mix.
3Thermoelastic properties deduced from the equation of state
Since our aim is to compare properties of the lower mantle, K′0, K0 and ρ0, with those of plausible mineral mixtures, we must relate the Table 2 results at (unknown) temperature T0 to mineral values at laboratory temperature, assumed to be 290 K. In principle, we could do this either by extrapolating laboratory data to high temperatures or by extrapolating the equation-of-state results to low temperature. We argue that the second approach is more reliable because we can calculate temperature variations of lower mantle properties from the equation of state with greater certainty than we know temperature variations of properties of Mg–Fe and Ca perovskites.
The starting point for thermal corrections is the Grüneisen parameter, γ. We use the acoustic formula
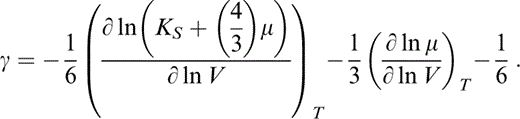
An alternative, the modified free volume formula, is under a new cloud of doubt. It includes a higher anharmonic correction factor (Stacey 1996) that was seriously overestimated and a term to allow for correlations in atomic motions that neglected the effect of bond interactions on these correlations. At least until these problems are resolved, eq. (8) is the best that we have.
As Stacey & Isaak (2000) pointed out, a correct application of Grüneisen's theory requires isothermal derivatives of adiabatic moduli as in eq. (8). Adiabatic derivatives are given by eq. (2), which gives K′≡(∂KS/∂P)S, so that μ′≡(∂μ/∂P)S is obtained by differentiating eq. (6),
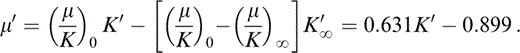
Conversion to isothermal derivatives using the general relationship for any parameter X,

requires the temperature dependences that can be written in terms of L, δS, R and ε by the definitions in Table 1, so that

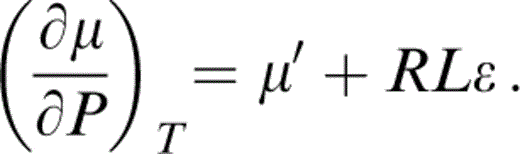
δS is then obtained from the equation of state by thermodynamic relationships that follow. The estimate of ε is less direct, but the prominence of μ in eq. (8) means that ε must be carefully considered.
We appeal to the temperature variation of the ratio R=μ/K, with the lower mantle value at P = 0, T = T0 being R0 (T0)=0.631 as in eq. (6). Stacey (1998) used the elasticity data for Mg perovskite of Yeganeh-Haeri (1994) with a plausible admixture of magnesiowüstite to estimate R0(290 K)=0.7076. This value is assumed here. It allows us to make use of the relationship
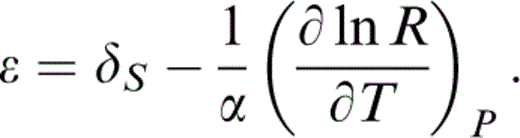
We assume that the temperature variations of μ and KS at P=0 track each other, i.e.
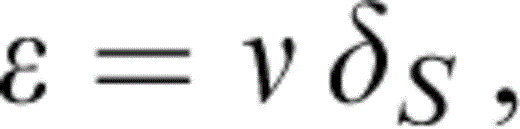
where ν is independent of T. An arbitrary temperature variation of δS is allowed, although it turns out to be constant (at P=0) within our uncertainties. Eqs (13) and (14) give
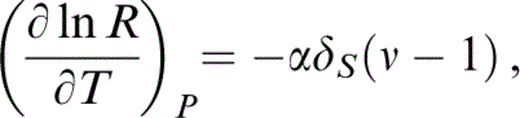
which is integrated over the range T=290 K to T0 with arbitrary temperature variations of δS and K to give
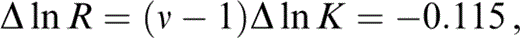
so that
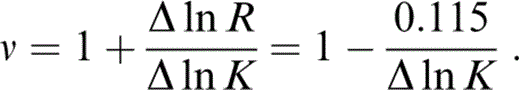
Since Δ ln K is obtained by extrapolating properties at T0 to 290 K, an extrapolation that assumes the solution to our problem, the whole calculation is iterative. We start by guessing ν and updating it when we have calculated Δ ln K. Two iterative loops suffice.
The higher-derivative corrections that we apply require also ε′≡(∂ε/∂P)S. Differentiating eq. (6),

Since eq. (6) is an adiabat,
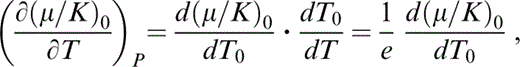
where, for small P,
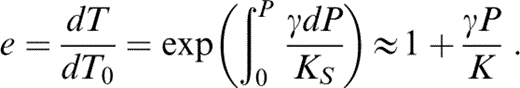
Substituting eqs (19) and (20) into eq. (18), writing (∂K/∂T)P in terms of δS (Table 1), and rearranging,
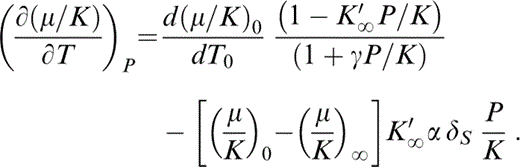
Since we are assuming here that P/K≪1, we can rewrite eq. (21) to make the change in [∂(μ/K)/∂T]P due to the small change in P from 0 to ΔP apparent:
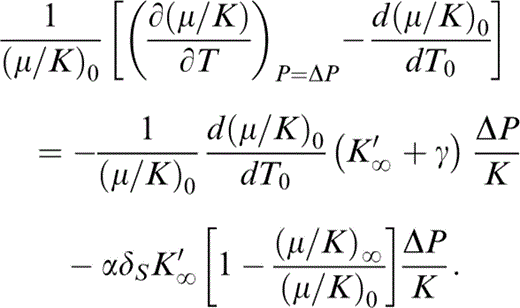
Then, letting ΔP→0,
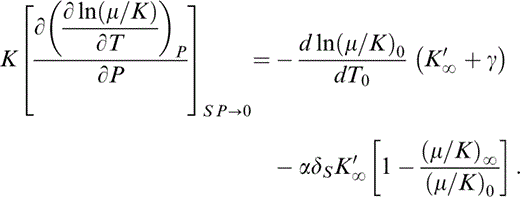
By eq. (13), d ln (μ/K)0/dT0=α0(δS−ε)0, so that
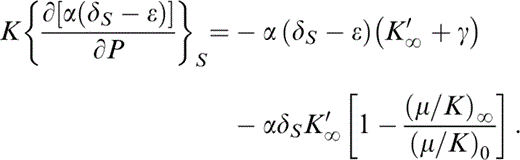
Breaking up the derivative on the left-hand side, representing (∂/∂P)S by a prime and rearranging,
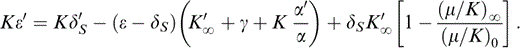
Eqs (13) and (25) give ε and ε′ in terms of δS, δ′S, γ and α′/α, plus equation-of-state parameters listed in Table 2. The parameters δS and ε are needed in the ‘correction’ terms in eqs (11) and (12) for calculating γ by eq. (8). However, δS and α can be obtained thermodynamically from the equation of state only when γ and γ′ are known. Therefore, these quantities must all be determined iteratively. As explained above, the iteration cycle extends to the extrapolation of properties from T0 to 290 K because ΔK is needed for calculation of ν by eq. (17). However, the corrections are small, so the procedure converges rapidly.
We can now rewrite eq. (8):
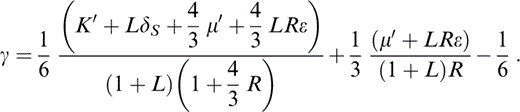
We need also the adiabatic derivative of γ,
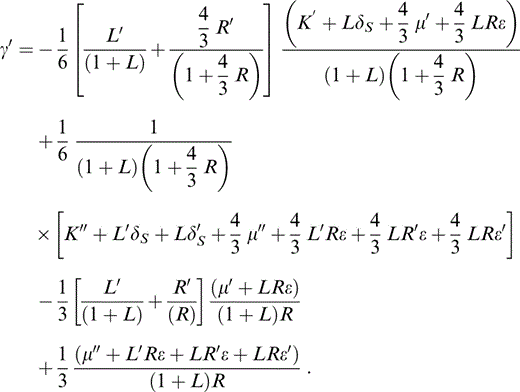
With the definitions of q and CS* (Table 1) we have a thermodynamic identity,
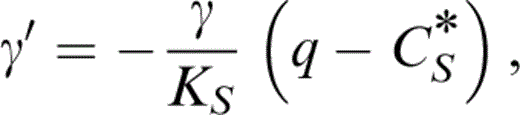
so that eq. (27) gives q, which is needed to obtain δS by another identity,
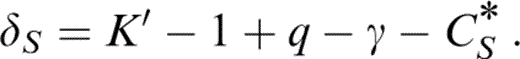
To allow for a temperature dependence of δS, we need the next derivative of γ or q′. A common assumption is that q is constant, but, as Stacey (2000) pointed out, the definition of q (Table 1) requires either γ or q to vanish at P→∞. The idea that γ vanishes is disallowed thermodynamically, so q must vanish. Therefore, a better assumption is a constant value for
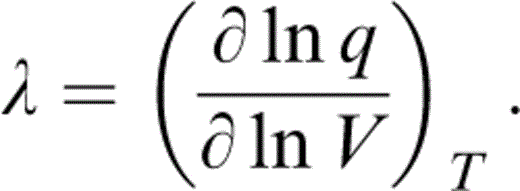
Integrating at constant T,

and
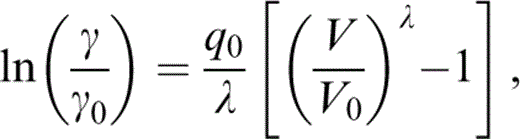
which we use with γ∞ to obtain λ from the equation of state,
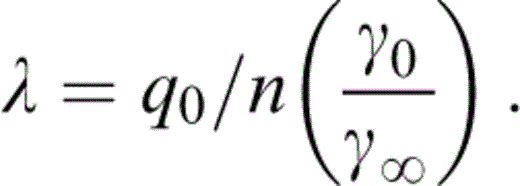
Although we have no fundamental reason for believing that λ defined by eq. (30) is in fact a constant, this is a much better approximation than assuming that q is constant. Furthermore, since terms involving λ are only marginally significant, it is apparent that λ defined by eqs (30) and (33) suffices for our purpose. Note that q is obtained from eq. (28), not eq. (31), but we use eq. (30) for its volume dependence.
For the evaluation of γ as well as extrapolation of properties from T0 to 290 K, we need several pressure and temperature derivatives, not all of which are familiar identities. The pressure derivatives are adiabatic, with primes representing (∂/∂P)S. Eq. (29) differentiates to give
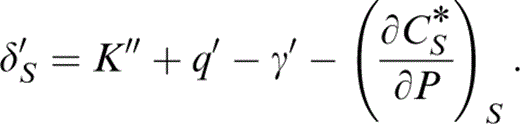
This is readily determined because at zero pressure K0K0″ is given by eq. (2) and listed in Table 2, γ′ is given by eq. (28) and q′ by converting eq. (30) to an adiabatic derivative,
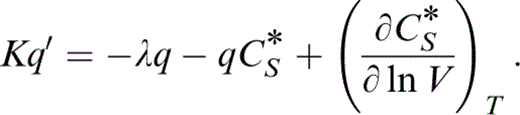
Differentiation of L requires
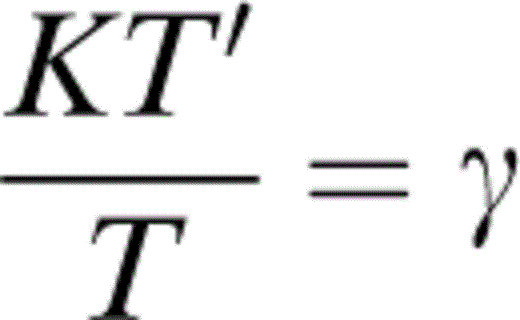
and Kα′/α, which is given in Table 2 and eqs (5), (6) and (7) of Stacey (1995):
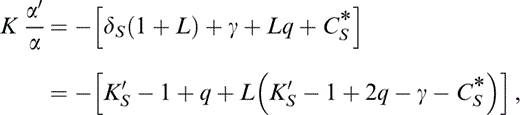
from which
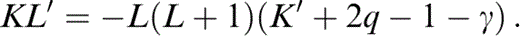
Now consider temperature derivatives. The temperature variations of ρ and KS are simply given by α and δS (Table 1). We allow both α and δS to vary with temperature, although δS turns out to be nearly independent of T (see Fig. 1b). α depends strongly on T below the Debye temperature and is calculated from the thermodynamic definition of γ (Table 1) with the relationship
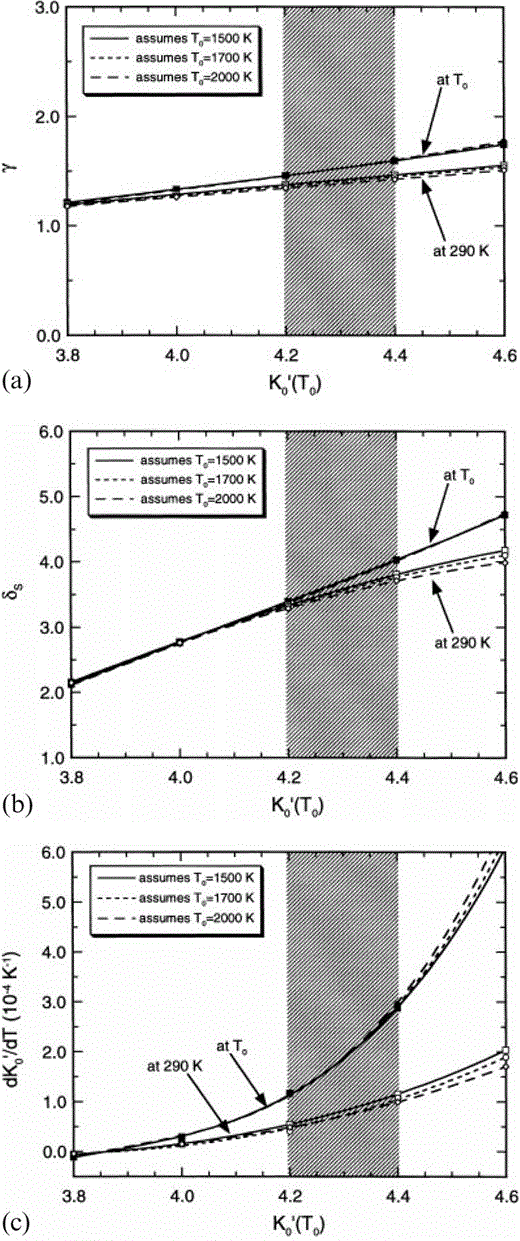
The dependences of (a) the Grüneisen parameter, γ, (b) δS, and (c) (∂K′S/∂T)P on assumed K′0(T0) and T0 for the lower mantle. The set of three lines from closed symbols are at P=0 and T=T0 (Table 3). The set of three lines from open symbols are at P=0 and T=290 K (Table 4). The shaded region represents the preferred K′0(T0) from the present analysis. Note that the temperature dependences are smaller (negligible for γ and δS) at constant volume and that the temperature dependences apparent here are accounted for by thermal expansion.
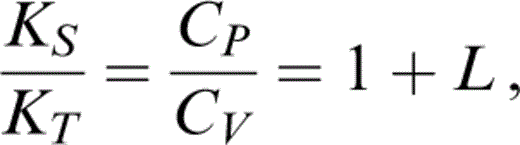
from which
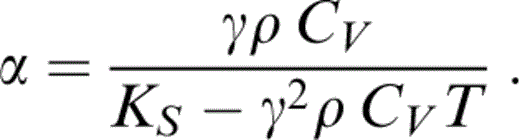
The temperature variations of K, γ and ρ are calculated step by step, as discussed in Section 4, and CV is assumed to follow a Debye function with an effective zero-pressure Debye temperature, ΘD=950 K.
Of particular significance to our approach is the behaviour of K′. It is important to the validity of the calculations that K′(T0) and K′ (290 K) be related without serious approximation. Stacey & Isaak (2000) used the identity
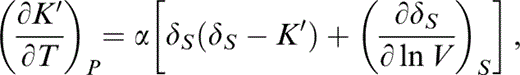
which is evaluated by eqs (31) and (34). This derivative itself varies with T and is followed step by step in the integration from T0 to 290 K.
Differentiation of eq. (29) gives
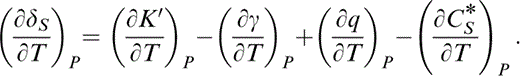
The first term in eq. (42) is given by eq. (41) and the second term by the identity
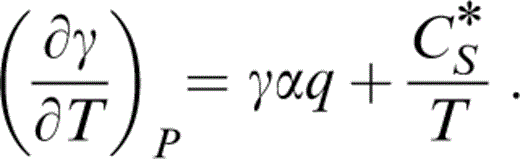
Differentiating the definition of q (Table 1) gives
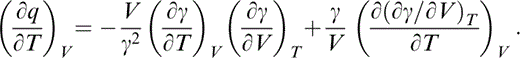
Substituting identities for the derivatives in the first term and reversing the order of differentiation in the second term results in
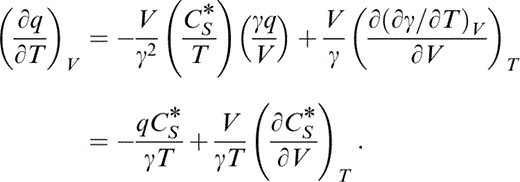
We can now write
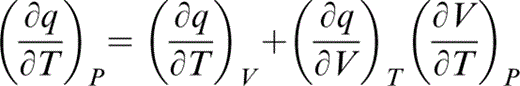
and substitute for the first term by eq. (45) and the second by the definition of λ (eq. 30), so that
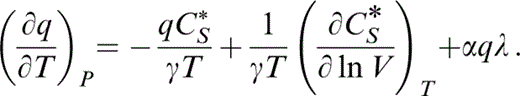
These equations present all of the required derivatives in terms of accessible quantities. In applying them we assume that CS*≡(∂CV/∂ ln V)S is negligible. This is consistent with our use of the Debye formula to calculate CV in the extrapolation to 290 K (Section 4) because, by Debye theory, T/ΘD is constant on an adiabat.
4Extrapolation to 290 K
The results listed in Table 2 are obtained from the equation-of-state fitting to PREM without reference to thermal properties. They give the extrapolation of lower mantle properties to zero pressure with no assumption or inference about the potential temperature, T0, of this extrapolation. However, a value of T0 is required for calculating the thermal properties. The next step is the calculation of the Grüneisen parameter, γ, by eq. (26) and γ′ by eq. (27) and for this we need ε and ε′ from eqs (13) and (25). For this we need Δ ln K=(ln K0(T0)−ln K0(290 K)) to determine ν and hence (∂ ln R/∂T)P by eqs (17) and (15). Since K0(290 K) is an end-product of the extrapolation calculation, the procedure is iterative. We start by assuming values estimated by Stacey & Isaak (2000) and successively refine them. Since ΔK/K0≈0.1, the iteration converges rapidly.
The results listed in Table 3 and illustrated in Fig. 1 are calculated from the values in Table 2 by the equations in Section 3 with only two additional external inputs, the values of T0 and K0(290 K). Since K0(290 K) is obtained from the next stage of the calculation, this means that there are two arbitrary parameters for which trial values are used, K′0 and T0. The maximum plausible range of each is represented in the array of fitted results to avoid pre-judging the comparison with mineral data (Section 5).
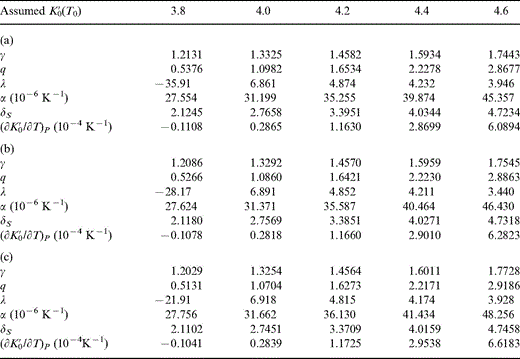
Zero-pressure properties of the lower mantle at potential temperature T0 assuming (a) T0=1500 K, (b) T0=1700 K and (c) T0=2000 K for various assumed values of K′0(T0).
Since the parameters in Tables 3(a), (b) and (c) are inter-related by the equations in Section 3 as well as requiring ΔK0, they are obtained by a two-stage iteration, the second stage being the calculation of parameters at 290 K in Tables 4(a), (b) and (c). This means that the results in corresponding columns of Tables 2, 3(a), (b) and (c) and 4(a), (b) and (c) are a self-consistent set. The calculated parameters at P=0 and for both T=T0 and T=290 K are illustrated in Figs 1 and 2 for the different assumed values of K′0 and T0.
At the high temperatures of the lower mantle adiabat (T/ΘD ≈ 2) CV is assumed to be constant, but in the extrapolation to 290 K we use the Debye function
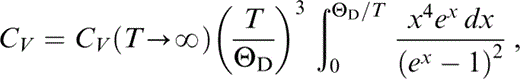
taking ΘD=950 K (at P=0) and CV(T→∞)=1163 J kg−1 K−1. At the three potential temperatures considered, CV/CV(T→∞) has the following values: 0.98046 at 1500 K, 0.98482 at 1700 K and 0.98912 at 2000 K. The extrapolation proceeds in 1° steps from these values at the assumed T0 to 290 K, with CV recalculated at each step by continuing the integral in eq. (48). This is needed in the calculation of α by eq. (40). The other parameters are then recalculated at each step by the equations in Section 3.
For each iterative cycle, λ is assumed to be constant, but is re-estimated each time round by eq. (33) because γ depends on ε, which, in turn, depends on K0(290 K), which is a product of the extrapolation. However, γ∞ and K′∞ are absolute constants specified by Table 2 for each assumed K′0. With fixed λ, q is recalculated at each step by eq. (47) and then an adjustment of γ follows by eq. (43). Similarly, ΔK=−αKδSΔT, ΔK′=(∂K′/∂T)PΔT and Δρ=−αρΔT with ΔT=−1 K. Then, α, δS and (∂K′S/∂T)P are redetermined at each step by the simultaneous solution of eqs (29), (40) and (41). As mentioned, CS* is neglected as insignificant at all stages, but it is included in the equations for completeness.
With reasonable starting conditions, two or three iterations suffice to produce the results in Tables 3 and 4 to the precision indicated. However, all of these results are merely trial solutions and are not properties of the real lower mantle nor even necessarily physically plausible. The negative values of λ for K′0=3.8 are examples of physical implausibility, reinforcing our contention that K′0(T0) cannot be as low as 3.8. The ultimate result that we seek is some interpolated table of values corresponding to the actual T0 and K′0, which, as we have pointed out, cannot be obtained from equations-of-state fitting alone. However, the essential point of the fitting process is that we have sets of mutually compatible values of K′0, K0 and ρ0 at 290 K. How well they can be matched to plausible compositions depends partly on how well we know the properties of candidate minerals.
5Procedure for matching properties of a mineral composite to the lower mantle
We can determine three unknown compositional parameters for any set of K′0, K0 and ρ0 data in Table 4. It is essential that two of the unknowns are the volume fractions x of magnesiowüstite and y of Ca perovskite. We make the third unknown the ratio f=Fe/(Fe+Mg) (atomic fraction) in the Mg–Fe perovskite with the assumptions that its value is 2f in the magnesiowüstite and that no iron enters the Ca perovskite. However, it turns out that our results are insensitive to the partitioning of Fe between minerals, so it is really the ratio f¯ in the composite that we estimate, with no indication of how it is distributed between minerals, so that this assumption has no effect on our conclusions.
We seek combinations of x, y and f (or f¯) that fit the results in Table 4. This could be unambiguous if we had precise values of properties of the component minerals, but, in any case, we have an array of possible solutions for the alternative values of K′0 and T0. However, even acknowledging the doubt about mineral properties, especially of Ca perovskite, the fitting is much less ambiguous than the multiplicity of uncertain parameters suggests.
The ranges of mineral properties that we consider are given in Table 5. We assume the densities to be reasonably well known with the only doubt arising from the partitioning of Fe. The 2:1 ratio in Fe partitioning between magnesiowüstite and Mg perovskite assumes that about 2 per cent (atomic) of Al2O3 in the perovskite reduces the proportion of Fe in the perovskite relative to an Al2O3-free mix (Kesson 1998 ). However, we are matching the total density and this depends on the total Fe and is little affected by the partitioning. The effect of Al itself on the density of pure Mg perovskite would be insignificant if it simply replaced (1/2)(Mg+Si), which has almost the same atomic weight. With the inclusion of Fe, the introduction of Al has a bigger effect. We account for this by reducing the coefficient of f in the expression for Mg–Fe perovskite density in Table 5 relative to values for Al-free perovskite because there is then less Fe present than the f ratio would give for Al-free perovskite.

Mineral properties at P=0, T=290 K used to determine compositions compatible with Table 4. The atomic ratio Fe/(Fe+Mg) is f in Mg–Fe perovskite and 2f in magnesiowüstite.
The values of K and K′0 for MgO (Jackson & Niesler 1982) and FeO (Jackson 1990 ) are well documented. Reichmann (2000) report that the variation in the C11 modulus of magnesiowüstite is not linearly dependent on the iron content. Such non-linear behaviour in elasticity has not yet been observed in the bulk modulus or its pressure derivative. Thus, we assume that K and K′0 vary linearly with the iron content along the MgO–FeO join. The value of K for Mg perovskite has also been measured (Yeganeh-;Haeri 1994), but K′0 for Mg perovskite is not yet well known. Our results confirm a suggestion by Jackson (reported by Stacey & Isaak 2000) that at ambient temperature the generally assumed value, 4.0, is too high and that 3.8 is nearer to correct. Kung (2000) also obtain 3.8 for K′0 from room temperature ultrasonic measurements on polycrystalline ScAlO3, a close structural analogue of Mg perovskite. The range of 3.8 to 4.0 for K′0 of Mg perovskite is used in our data fitting.
The properties of Ca perovskite are much more uncertain. The various estimates, both experimental and theoretical, are summarized in Table 6. Most experimental values listed in Table 6 for K0 are for the isothermal bulk modulus at laboratory temperature. The Sinelnikov (1998a) data are for the adiabatic case. The theoretical values are athermal moduli, although the Chizmeshya (1996) values include an estimated correction from zero to ambient temperature. Athermal moduli represent static lattice properties, that is, properties at 0 K and without including the small effects of the quantum mechanical zero-point energies (see e.g. Isaak 1990 ). Furthermore, the experimental values listed under K′0 are the zero-pressure (∂KT/∂P)T and not (∂KS/∂P)S as K′0 is defined elsewhere in this paper. However, the differences at ambient temperature between KS, KT and athermal K, and between (∂KT/∂P)T and (∂KS/∂P)S are of the order of 1 per cent and do not account for the wide ranges in reported values of K0 and K′0 for Ca perovskite.
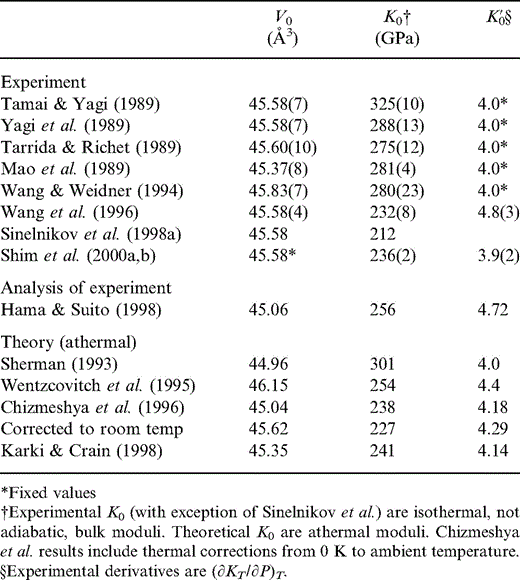
Zero-pressure unit-cell volume V0, bulk modulus K0 and pressure derivative of bulk modulus K′0 for CaSiO3 perovskite from experiment and theory.
As Table 6 indicates, there is no consensus about the values for Ca perovskite. One difficulty is that zero-pressure properties are obtained by extrapolation; this has generally involved use of the third-order Birch equation, which, as we have pointed out (e.g. Stacey 2000), can give quite misleading conclusions. Thus, we admit a wide range of possible values of both K and K′0. Logically, we would expect to identify a low K′0 with high K and vice versa, but we do not impose this constraint on our analysis. For most of our fitting results, the fraction of Ca perovskite (y) is quite small, so these uncertain parameters have limited effect.
The composite density is a weighted sum of the densities in Table 5. Identifying the properties of the three minerals listed in Table 5 with subscripts 1, 2 and 3, we have
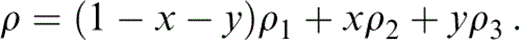
The bulk modulus for the composite is assumed to be the average of Voigt (V) and Reuss (R) limits,

where
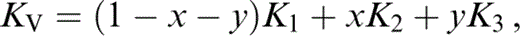
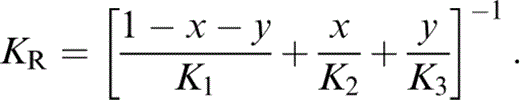
For K′ of the composite, we require an extension to three minerals of the two-mineral analysis by Stacey (1998), which recognizes that not only the individual values of K, but also the volume fractions x and y, vary with pressure. We take the composite K′ to be the average of Voigt and Reuss limits,
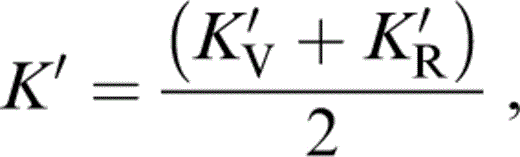
where
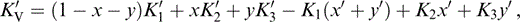
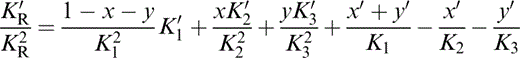
and
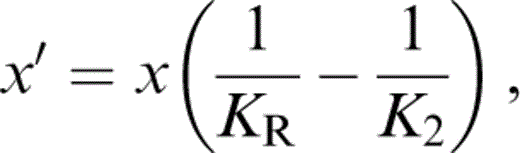
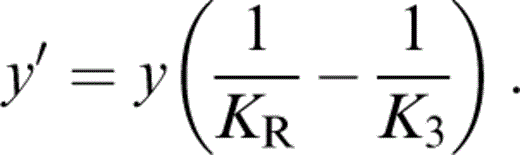
The term KR appears in eqs (56) and (57) because, in matching values to lower mantle properties, we need the fully relaxed (Reuss) adjustment of the volume fractions with pressure.
For each pair of values of K and ρ in Table 4 we guessed a value of f and solved eqs (49) to (52) for x and y. Then x, y and f give K′ by eqs (53) to (57) and f was adjusted until repeat calculations yielded the value of K′ corresponding to K and ρ. This process was repeated with the alternative mineral properties in Table 5.
6Results of mineral comparisons
The range of alternative solutions is not nearly as wide as the choice of parameters to be fitted suggests. For certain parameter ranges no solution at all is possible. In particular, K′0(T0)=3.8, 4.0 or even 4.1 (intermediate between the tabulated values) gives no solution for any T0 or any of the alternative mineral properties. K′0(T0) cannot be less than about 4.2, whatever one believes about T0 or mineral properties. This agrees with our earlier conclusion (Stacey & Isaak 2000) using a different equation of state, and we present it as a robust result.
If we take K′0(T0)=4.2 and K′0(290 K)=3.8 for Mg perovskite, then we obtain the results in Table 7. However, no solution is possible with the Mg perovskite K′0(290 K) in the range 3.85 to 4.0 for any value of T0 and any Ca perovskite properties. If we take K′0(T0)=4.4 for the lower mantle, then there is a narrow window of admissible solutions for the Mg perovskite K′0(290 K)≈3.9 if K′0(290 K)=4.0 for Ca perovskite. If we take K′0(T0)=4.6, then we obtain solutions for the Ca perovskite value of K′0(290 K)=4.7 but not 4.0 and with the Mg perovskite K′0(290 K) not greater than 3.8 (for any value of T0). Thus, a second result, almost as robust as the limit on K′0(T0), is that K′0(290 K) for Mg perovskite is not greater than about 3.8.

The range of solutions for K′0(T0)=4.2, T0=1700 K and K′1(Mg pv)=3.8 with alternative values of K3 and K′3 for Ca pv. There are no solutions for K′1=3.85 to 4.0. x, y are volume fractions of mw and Ca pv. f=Fe/(Fe+Mg) in Mg pv and f¯ is the value for the composite.
High values of T0 and K′0(T0) favour larger values of y (fraction of Ca pv) but this fraction is generally too small to have a material effect on the other parameters, and the sample results in Table 7 are representative. This means that we can throw no new light on Ca pv properties, but, conversely, they have little influence on our other conclusions.
The volume fraction of magnesiowüstite (x) varies with the assumed T0, being 0.25 to 0.26 if T0=1500 K but only 0.09 to 0.11 if T0=2000 K. In spite of this wide range in x, the range of f¯ in all solutions is limited, 0.120 to 0.155.
7Conclusions
In spite of doubts about the properties of lower mantle minerals, especially Ca perovskite, and independently of the assumed temperature, the value of K′0 at the foot of the lower mantle adiabat cannot be less than about 4.2 and could be 4.4. This confirms our earlier conclusion and is a robust result. Equation-of-state fitting using the third-order Birch theory, which gives K′0(T0)≈3.8, is clearly awry. We also strongly favour K′0(290 K)=3.8 for Mg perovskite because higher values cannot be matched to the lower mantle properties.
Useful conclusions emerge independently of the compositional considerations. The adiabatic Anderson–Grüneisen parameter, δS, varies only slightly with temperature and can be treated as constant in a simplified calculation without seriously affecting results. However, dK′0/dT varies strongly with T (see Fig. 1c). Furthermore, (1/α) (dK′0/dT) cannot be assumed to be constant, even though it varies much less with T than does dK′0/dT. Thus the extrapolation of properties between T0 and 290 K must be made with some care. The value of dK′0/dT is also very sensitive to the assumed value of K′0(T0); so much so that, as K′0(T0) is increased, K′0(290 K) passes through a maximum value that is about 4.15 for T0=1500 K but less for higher T0 (see Fig. 2b). This imposes an important restriction on the value of K′ for the dominant mineral, Mg perovskite, and is the essential reason why we conclude that this must be close to 3.8.
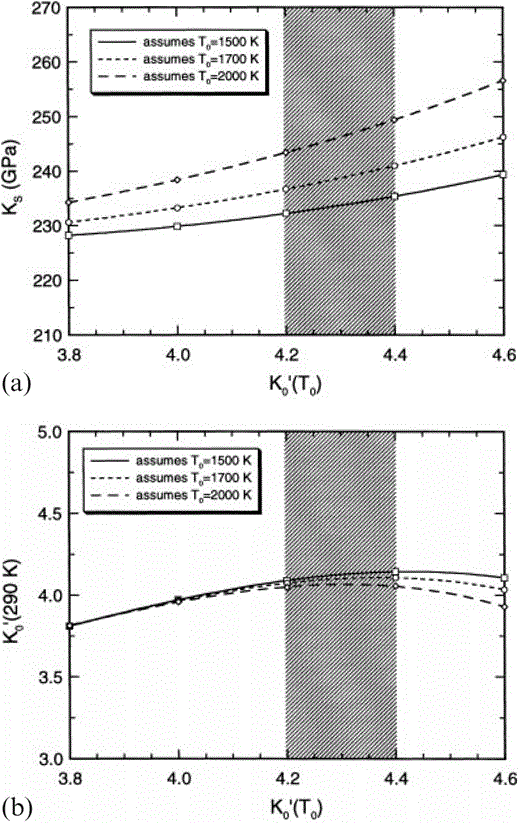
The dependences of (a) KS(290 K) and (b) K′0(290 K) at zero pressure (from Table 4) on assumed K′0(T0) and T0 for the lower mantle. The shaded region represents the preferred K′0(T0) from the present analysis.
Our conclusions about mineralogy are less certain because they depend on finer details of the calculations. Volume fractions of 0.20 magnesiowüstite and up to about 0.05 Ca perovskite appear uncontentious. In fact, the fraction of Ca perovskite is small enough to have little influence on our results, so that its exclusion was not the most important deficiency of the Stacey & Isaak (2000) calculations. Our range of 0.12–0.15 for the f¯=Fe/(Fe+Mg) ratio is consistent with allowable values found in several other studies (Hemley 1992 ; Stixrude 1992 ; Zhao & Anderson 1994; Wang 1994 ), but it is a little higher than 0.10–0.11, obtained from geochemical estimates based on a uniform mantle of pyrolite composition (Bina 1998; Jackson & Rigden 1998). We contemplate the possibility of changes to our model that would bring f¯ down to more conventional values of 0.10 or 0.11. No reasonable adjustment of either the equation of state or the seismological model achieves this. There appear to be only three options: (1) using different mineralogy; (2) a reduction in one or more of the densities in Table 5, perhaps by introducing more Al2O3 or revising laboratory values of elasticities; and (3) a revision of the extrapolation from T0 to 290 K. The third possibility would require the acoustic formula for γ (eq. 8) to be discarded. Although this is our weakest theoretical link, it has, at present, no serious rival.
The central point of our paper is the presentation in Section 3 of a thermodynamic analysis that avoids common assumptions that we find to be unsatisfactory. In particular, the third-order Birch equation, K′0=4 (e.g. Gillet 2000 ), q0=1 (e.g. Anderson 1996 ) and even q independent of V have been convenient approximations that can be abandoned with the sharper focus on derivative properties that is now possible with a properly constrained equation of state. The numerical results concerning composition in Section 6 will inevitably be changed as improved laboratory data for relevant minerals become available. [Even properties of MgO, believed to be secure, may be subject to revision (Sinogeikin & Bass 2000).] However, the methodology in Section 3 is not dependent on such changes. Another development, still to be investigated, is the use of data on rigidity modulus, μ, now available for Mg silicate perovskite (Sinelnikov 1998b ), although we face the limitation that μ is not linked by thermodynamic identities to other thermoelastic properties as is bulk modulus, K.
Mineralogical doubts aside, we conclude that the zero-pressure properties of the lower mantle mineral mix at T0 and 290 K respectively are bracketed by the K′0(T0)=4.2 and 4.4 columns in Tables 3(b) and 4(b).
Acknowledgments
This work was supported in part by the United States Office of Naval Research and NSF EAR-0073989. This is IGPP report 5476. We appreciate careful reviews of this paper by Isabella Bovolo and Philippe Gillet.
References
Primes represent (∂/∂P)S. Subscripts 0 and ∞ in the text represent respective values at zero and infinite pressure limits.
*Fixed values †Experimental K0 (with exception of Sinelnikov et al.) are isothermal, not adiabatic, bulk moduli. Theoretical K0 are athermal moduli. Chizmeshya et al. results include thermal corrections from 0 K to ambient temperature. §Experimental derivatives are (∂KT/∂P)T.





