Haploid Selection Favors Suppressed Recombination Between Sex Chromosomes Despite Causing Biased Sex Ratios

Scott, Michael F; Otto, Sarah P

doi:10.1534/genetics.117.300062

Abstract

To date, research on the evolution of sex chromosomes has focused on sexually antagonistic selection among diploids, which has been shown to be a potent driver of the strata and reduced recombination that characterize many sex chromosomes. However, significant selection can also occur on haploid genotypes during less conspicuous life cycle stages, e.g., competition among sperm/pollen or meiotic drive during gamete/spore production. These haploid selective processes are typically sex-specific, e.g., gametic/gametophytic competition typically occurs among sperm/pollen, and meiotic drive typically occurs during either spermatogenesis or oogenesis. We use models to investigate whether sex-specific selection on haploids could drive the evolution of recombination suppression on the sex chromosomes, as has been demonstrated for sex-specific selection among diploids. A potential complication is that zygotic sex-ratios become biased when haploid selected loci become linked to the sex-determining region because the zygotic sex ratio is determined by the relative number and fitness of X- vs. Y-bearing sperm. Despite causing biased zygotic sex-ratios, we find that a period of sex-specific haploid selection generally favors recombination suppression on the sex chromosomes. Suppressed recombination is favored because it allows associations to build up between haploid-beneficial alleles and the sex that experiences haploid selection most often (e.g., pollen beneficial alleles become strongly associated with the male determining region, Y or Z). Haploid selected loci can favor recombination suppression even in the absence of selective differences between male and female diploids. Overall, we expand our view of the sex-specific life cycle stages that can drive sex chromosome evolution to include gametic competition and meiotic drive. Based on our models, sex chromosomes should become enriched for genes that experience haploid selection, as is expected for genes that experience sexually antagonistic selection. Thus, we generate a number of predictions that can be evaluated in emerging sex chromosome systems.

meiotic drive, sperm competition, pollen competition, sex ratio, sex chromosomes, recombination evolution

IN organisms with diploid genetic sex determination, recombination is typically suppressed between the X and Y chromosomes, or Z and W chromosomes. Suppressed recombination appears to begin near the sex-determining region (SDR) and then expand to include larger segments of each sex chromosome (Bergero et al. 2007; Nam and Ellegren 2008; Lemaitre et al. 2009; Wang et al. 2012; Charlesworth 2013). In the absence of recombination, the sex-limited chromosome (Y or W) accumulates deleterious mutations and rearrangements within the nonrecombining region, and “genetic degeneration” occurs (Rice 1996; Charlesworth and Charlesworth 2000; Bachtrog 2006; Marais et al. 2008). Thus, the selective forces driving reduced recombination on sex chromosomes are fundamental to our understanding of sex chromosome evolution.

Typically, selective differences between males and females have been evoked to explain the suppression of recombination around established sex-determining regions (Fisher 1931; Bull 1983; Rice 1987). Considering species with separate diploid sexes, Charlesworth and Charlesworth (1980) showed that loci where males and females differ in equilibrium allele frequency due to selection (for example, sexually antagonistic selection) should evolve complete linkage with the sex-determining locus via translocations or fusions. Subsequently, Lenormand (2003) demonstrated that sex differences in allele frequencies at equilibrium are not required in order to favor reduced recombination with the SDR. In fact, recombination suppression can evolve around the SDR even if selection favors the same allele in both sexes, as long as that allele is favored more strongly in one sex than the other. Immler and Otto (2015) considered species, such as mosses and liverworts, where sex is determined genetically during the haploid phase (U and V sex chromosomes), finding that fitness differences between haploid sexes can also drive suppressed recombination around the SDR. In essence, these studies have demonstrated that suppressors of recombination can be favored because they strengthen the association between the sex in which an allele is most favored, and the chromosome that is present in that sex more often, e.g., between male beneficial alleles and the Y or Z and between female beneficial alleles and the X or W (Otto et al. 2011).

While differences in selection between the diploid sexes has attracted the most theoretical and empirical attention, the haploid gametes/gametophytes produced by male and female diploids also experience distinct selective environments. Intense competition typically occurs among pollen and sperm (Mulcahy et al. 1996; Bernasconi 2004; Joseph and Kirkpatrick 2004). To the extent that pollen and sperm success reflects differences in their haploid genotypes, competition among these gametes/gametophytes is qualitatively distinct from selection among diploid males (Immler et al. 2012). In plants, selection among haploid male gametophytes is thought to be pervasive (Skogsmyr and Lankinen 2002; Moore and Pannell 2011; Marshall and Evans 2016); in Arabidopsis, 60–70% of all genes are expressed during the haploid phase (Borg et al. 2009), and pollen-expressed genes exhibit stronger signatures of purifying selection and positive selection (Arunkumar et al. 2013; Gossmann et al. 2014). For agricultural breeding, pollen has been exposed to a variety of selection pressures in vivo and in vitro, including temperature (Clarke et al. 2004; Hedhly et al. 2004), herbicides (Frascaroli and Songstad 2001), metals (Searcy and Mulcahy 1985), water stress (Ravikumar et al. 2003), and pathogens (Ravikumar et al. 2012), resulting in an increased frequency of beneficial genotypes among the diploid sporophytic offspring. In animals, expression during the haploid sperm stage is traditionally thought to be suppressed (Hecht 1998), although recent evidence suggests that postmeiotic gene expression occurs (Zheng et al. 2001; Vibranovski et al. 2010), that hundreds of genes are haploid selected (Joseph and Kirkpatrick 2004), and that haploid selection can impact offspring fitness (Immler et al. 2014; Alavioon et al. 2017). Even without postmeiotic gene expression, meiotic drive can cause strong selection on haploid genotypes. As with gamete/gametophyte competition, meiotic drive is usually sex specific (Úbeda and Haig 2005), with biased segregation occurring either during polar body formation in females (Buckler et al. 1999; Fishman and Saunders 2008; Didion et al. 2015) or during male gamete/spore production (Jaenike 2001; Burt and Trivers 2006; Larracuente and Presgraves 2012).

In this study, we include haploid selection in models for the evolution of recombination, assuming separate diploid sexes and genetic sex determination (XY or ZW). Specifically, we include a period of selection among the gametes/gametophytes produced by one sex, for example, competition among sperm but not among eggs, see Figure 1. Thus, we investigate whether sex differences in the haploid selective environment can cause the evolution of suppressed recombination on sex chromosomes, as with sex differences in diploid selection. One reason to rigorously examine this hypothesis is that haploid selection can cause zygotic sex ratios to become biased. For example, sex-chromosome-linked meiotic drivers can alter the relative frequency of X- vs. Y-bearing gametes (Jaenike 2001). Similarly, sex-chromosome-linkage allows alleles with high pollen fitness to become associated with the Y, such that Y-bearing pollen outcompetes X-bearing pollen, and most zygotes will become males, see Figure 1. Sex ratio biases caused by meiotic drive or gametic competition have been found to favor more equal zygotic sex ratios via the evolution of new sex-chromosomes (Kozielska et al. 2010; Úbeda et al. 2015) or modifications to the haploid selective arena (Hough et al. 2013; Otto et al. 2015). Here, we find that meiotic drive or gametic competition typically favors suppressed recombination on the sex chromosomes, despite causing biased zygotic sex ratios.

Figure 1

XY and ZW diploid genetic sex determination systems. In our model, haploid selection occurs during gamete/gametophyte production (meiotic drive) and/or competition (gametic competition) in one sex. In this case, haploid selection occurs in males, as indicated by the dashed circle. In an XY system, male haploid selection causes the zygotic sex ratio to become biased when X- and Y-bearing gametes/gametophytes have different haploid fitnesses.

Open in new tab Download slide

Model Background

Recombination evolution on sex chromosomes is usually modeled by considering a locus under selection, the SDR, and another locus that modifies the recombination rate between them. Recombination modifiers may be inversions, fusions, translocations, hotspot mutations, and changes to genes involved in double-strand breaks and repairs. A general model therefore includes three loci and the recombination rates between them, which is typically too complex to interpret without further simplifying assumptions (Otto and Day 2007). Lenormand (2003) assumed that the recombination rates between these loci are large relative to selection, such that the linkage disequilibria among loci equilibrate on a faster timescale than changes in allele frequencies (a “quasi-linkage equilibrium” approximation). This analysis is most appropriate for selected loci that are far from the SDR on sex chromosomes and when modifiers of recombination are weak and loosely linked (e.g., autosomal modifiers of recombination machinery). Charlesworth and Charlesworth (1980) assumed that the selected locus is initially autosomal and then considered fusions with (or translocations to) the SDR, where their analysis assumed these rearrangements became closely linked to the selected locus. Their model also corresponds to modifications on sex chromosomes (e.g., inversions) that change the recombination rate with the SDR from a very high to a very low level. Finally, Otto (2014) considered modifiers of recombination between the SDR and selected loci when the linkage between them is initially very tight.

Here, we study recombination evolution in a manner akin to Charlesworth and Charlesworth (1980) and Otto (2014), except that we include a period of selection upon haploid genotypes of one sex (gametic competition and/or meiotic drive). The model of Lenormand (2003) is very general and allows a period of gametic competition (assuming weak linkage); he recognizes but does not discuss the potential of such sex-specific gametic competition to favor suppressed recombination on sex chromosomes. The models we develop here, in which haploid selected loci and the SDR can become tightly linked, are particularly significant because strong associations between haploid selected alleles and the SDR (that can build up when linkage is tight) will cause zygotic sex ratios to become strongly biased.

Model

We consider a modifier model in which the recombination rate between a locus under selection (selected locus, A, with alleles A and a) and the SDR depends on the genotype at the modifier locus (M, with alleles M and m). In our model, haploids of one sex experience selection according to their A locus genotype. The appropriate nomenclature for the haploid stage of animals and plants is different. For simplicity, we will use the animal terms “egg,” “sperm,” and “gamete”; in angiosperms, the appropriate terms for these stages would be “embryo sac,” “pollen,” and “gametophyte,” respectively. We assume that the number of eggs fertilized does not depend on the strength of haploid selection (i.e., that there is no sperm limitation). Our model includes both “gametic competition” and “meiotic drive” in one sex; we use the term “haploid selection” to encompass both selective processes. In the case of gametic competition (e.g., sperm competition), all haploids produced by one sex compete before mating. In the case of meiotic drive, after recombination, a fraction α of spores/gametes produced by an $A a$ heterozygote will inherit the A allele, whereas $(1 - α)$ spores/gametes inherit the a allele (overall fertility is assumed to be unaffected). Therefore, the main distinction between meiotic drive and gametic competition in our model is that haploid selection via meiotic drive only occurs among gametes/spores produced by a heterozygote, whereas all gametes/gametophytes compete for fertilization during gametic competition. Under monogamous mating, gametic competition among sperm is equivalent to male meiotic drive because haploid allele frequencies would only change during matings with a heterozygous male.

Zygotes develop as diploid males or females depending on their genotype at the SDR. Diploid genetic sex determination systems are either male heterogametic (females XX and males XY) or female heterogametic (females ZW and males ZZ). There are therefore two important asymmetries in the model, the sex in which haploid selection occurs and the sex that is heterogametic. For simplicity, we primarily describe XY sex determination with male haploid selection (sperm competition or meiotic drive during spermatogenesis), although we also present results for ZW sex determination and male haploid selection. By interchanging “male” and “female” labels, this pair of models covers all four cases of haploid selection in males or females and heterogamety in males or females.

After a period of selection among diploid males and females (Table 1), recombination occurs to produce haploid gametes/gametophytes. Because females are homozygous at the SDR (with XY sex determination), the only recombination event of consequence in females is between the A and M locus, which occurs at rate $R^{♀} .$ In males, recombination similarly occurs between the selected locus A and the modifier locus M at rate $R^{♂} .$ Recombination can also occur between the SDR and the A locus in males; this recombination rate is controlled by the modifier locus, and is given by $r_{i j},$ where $i j$ is the genotype at the M locus (⁠ $M M,$ $M m,$ or $m m$ ⁠), allowing this recombination rate to evolve. Recombination events between the SDR and M locus in males occur at rate ρ. Note that $R^{♂}$ and ρ only impact offspring genotypes in males that are heterozygous at the M locus, so we take their values to be those in $M m$ males in cases where the modifier has broader effects. Because we have three loci and three recombination parameters, any ordering of the loci or type of modifier (genic, inversion, and fusion) can be modeled with appropriate choices of ρ, $r_{i j},$ and $R^{♂},$ see Table A1. We track the frequencies of $M A,$ $M a,$ $m A,$ and $m a$ genotypes among female eggs, male X-bearing sperm, and male Y-bearing sperm separately to allow sex-specific allele frequencies and disequilibria. The recursion equations describing the change in genotype frequencies after a single generation of this life cycle are provided in Appendix A.1.

Sex- and stage-specific selection terms

Table 1

Open in new tab

Sex- and stage-specific selection terms

Diploid Selection	Male Fitness	Female Fitness^a
AA	$w_{A A}^{♂} = 1 + s^{♂}$	$w_{A A}^{♀} = 1 + s^{♀}$
Aa	$w_{A a}^{♂} = 1 + h^{♂} s^{♂}$	$w_{A a}^{♀} = 1 + h^{♀} s^{♀}$
aa	$w_{a a}^{♂} s = 1$	$w_{a a}^{♀} = 1$

Gametic Competition	Male fitness	Female fitness
A	$w_{A}^{♂} = 1 + t^{♂}$	1
a	$w_{a}^{♂} = 1$	1

Transmission During Meiosis	$A a$ Males	$A a$ Females
A	$α^{♂} = 1 / 2 + α_{Δ}^{♂} / 2$	1/2
a	$1 - α^{♂} = 1 / 2 - α_{Δ}^{♂} / 2$	1/2

a

When assuming weak selection, we assume s^⚥, $t^{♂}$ ⁠, and $α_{Δ}^{♂}$ are small.

Table 1

Open in new tab

Sex- and stage-specific selection terms

Diploid Selection	Male Fitness	Female Fitness^a
AA	$w_{A A}^{♂} = 1 + s^{♂}$	$w_{A A}^{♀} = 1 + s^{♀}$
Aa	$w_{A a}^{♂} = 1 + h^{♂} s^{♂}$	$w_{A a}^{♀} = 1 + h^{♀} s^{♀}$
aa	$w_{a a}^{♂} s = 1$	$w_{a a}^{♀} = 1$

Gametic Competition	Male fitness	Female fitness
A	$w_{A}^{♂} = 1 + t^{♂}$	1
a	$w_{a}^{♂} = 1$	1

Transmission During Meiosis	$A a$ Males	$A a$ Females
A	$α^{♂} = 1 / 2 + α_{Δ}^{♂} / 2$	1/2
a	$1 - α^{♂} = 1 / 2 - α_{Δ}^{♂} / 2$	1/2

a

When assuming weak selection, we assume s^⚥, $t^{♂}$ ⁠, and $α_{Δ}^{♂}$ are small.

In our first analysis, we assume that selection is weak relative to the initial recombination rate (⁠ $r_{M M}$ ⁠), such that allele frequency differences between males and females are initially small. We then evaluate the spread of modifiers of recombination (m) that cause recombination rates to become very small (assuming $r_{M m},$ ρ, and $R^{♂}$ are all small). These modifiers could be translocations or fusions from autosomes to sex chromosomes or, if the selected locus (A) begins on the sex chromosome, inversions or expansions of the nonrecombining region. We assume that chromosomes are still able to pair regularly with their homologs during meiosis, and we do not include any direct selection on the modifier (e.g., meiotic drive between acrocentric and metacentric chromosomes following a fusion, Yoshida and Kitano 2012).

Summary of cases considered, simplifying assumptions, and results (⁠ $λ > 1$ indicates invasion by m)

Table 2

Open in new tab

Summary of cases considered, simplifying assumptions, and results (⁠

λ > 1

indicates invasion by m)

Selection Weak Relative to $r_{M M}$ (s^⚥, $t^{♂}$ ⁠, $α_{Δ}^{♂}$ of Order $ϵ^{2}$ ⁠)
Assumptions: $r_{M m} =$ R^⚥ $= ρ = 0$	$λ_{Y A} > 1 & λ_{X a} > 1$ if $D^{♂} - D^{♀} + α_{Δ}^{♂} + t^{♂} > 0$
Assumptions: $r_{M m} =$ R^⚥ $= ρ = 0$	$λ_{Y a} > 1 & λ_{X A} > 1$ if $D^{♂} - D^{♀} + α_{Δ}^{♂} + t^{♂} < 0$
No sex differences in fitness in diploids (⁠ $w_{i j}^{♂} = w_{i j}^{♀}$ ⁠), variation maintained by ploidally antagonistic selection and/or overdominance
Assumptions: $r_{M m} =$ R^⚥ $= ρ = 0,$ $r_{M M} = 1 / 2,$ $α_{Δ}^{♂} = 0$	$λ_{Y A} > 1 & λ_{X a} > 1$ if $t^{♂} > 0$
	$λ_{Y a} > 1 & λ_{X A} > 1$ if $t^{♂} < 0$
SDR-A linkage tight (⁠ $r_{M M}$ and $\| r_{M M} - r_{M m} \|$ of order ε)
Assumptions: $α_{Δ}^{♂} = 0,$ Arbitrarily assume A allele nearly fixed on Y	Typically (but not always) $λ > 1$ if $r_{M m} < r_{M M};$
	Necessary (not sufficient) conditions for $λ > 1$ when $r_{M m} > r_{M M}$ are that $R^{♀} > 0$ and that $w_{A}^{♂} > w_{a}^{♂}$ and/or $w_{A a}^{♂} > w_{A A}^{♂}$

Table 2

Open in new tab

Summary of cases considered, simplifying assumptions, and results (⁠

λ > 1

indicates invasion by m)

Selection Weak Relative to $r_{M M}$ (s^⚥, $t^{♂}$ ⁠, $α_{Δ}^{♂}$ of Order $ϵ^{2}$ ⁠)
Assumptions: $r_{M m} =$ R^⚥ $= ρ = 0$	$λ_{Y A} > 1 & λ_{X a} > 1$ if $D^{♂} - D^{♀} + α_{Δ}^{♂} + t^{♂} > 0$
Assumptions: $r_{M m} =$ R^⚥ $= ρ = 0$	$λ_{Y a} > 1 & λ_{X A} > 1$ if $D^{♂} - D^{♀} + α_{Δ}^{♂} + t^{♂} < 0$
No sex differences in fitness in diploids (⁠ $w_{i j}^{♂} = w_{i j}^{♀}$ ⁠), variation maintained by ploidally antagonistic selection and/or overdominance
Assumptions: $r_{M m} =$ R^⚥ $= ρ = 0,$ $r_{M M} = 1 / 2,$ $α_{Δ}^{♂} = 0$	$λ_{Y A} > 1 & λ_{X a} > 1$ if $t^{♂} > 0$
	$λ_{Y a} > 1 & λ_{X A} > 1$ if $t^{♂} < 0$
SDR-A linkage tight (⁠ $r_{M M}$ and $\| r_{M M} - r_{M m} \|$ of order ε)
Assumptions: $α_{Δ}^{♂} = 0,$ Arbitrarily assume A allele nearly fixed on Y	Typically (but not always) $λ > 1$ if $r_{M m} < r_{M M};$
	Necessary (not sufficient) conditions for $λ > 1$ when $r_{M m} > r_{M M}$ are that $R^{♀} > 0$ and that $w_{A}^{♂} > w_{a}^{♂}$ and/or $w_{A a}^{♂} > w_{A A}^{♂}$

In our second analysis, following Otto (2014), we assume that the A locus begins at equilibrium and in tight linkage with the SDR (⁠ $r_{M M}$ and ρ are on the order of a small term, ε). We then consider whether any modifiers can invade that increase this recombination rate slightly (where the change in recombination rate, $r_{M m} - r_{M M},$ is on the order of ε). The recombination rate between the modifier locus and the selected locus (⁠ $R^{♀}$ and $R^{♂}$ ⁠) is not constrained. This analysis focuses on the final stages of sex chromosome evolution, asking when complete recombination suppression is favored or not. Table 2 summarizes the results of these analyses.

Results

In a population fixed for the M allele, the frequencies of the A allele among X-bearing eggs, X-bearing sperm, and Y-bearing sperm are given by $p_{X}^{♀},$ $p_{X}^{♂},$ and $p_{Y}^{♂},$ respectively. The frequency of Y-bearing sperm among all sperm before gametic competition can deviate from $1 / 2$ due to meiotic drive, and is given by q. The spread of a rare mutant, m, that changes the recombination rate, can be evaluated using the leading eigenvalue, λ, of the system described by Equations (A.1c), (A.1d), (A.2c), (A.2d), (A.3c), and (A.3d). We first consider modifiers that completely suppress recombination. (In Appendix A.2B, we consider cases where carriers of the recombination suppressor have small, but nonzero, recombination rates, such that modifier alleles can recombine onto alternative A allele and SDR backgrounds, which tends to slow their spread.) Finally, we consider arbitrarily linked recombination modifiers and assume close linkage between A and the SDR.

Suppressors of recombination

Complete suppressors of recombination (⁠

r_{M m} = 0

⁠) that are closely linked to the A locus (⁠

R^{♀} = R^{♂} = ρ = 0

⁠) experience the strongest selective force. These modifiers can bring either the A or the a allele into tight linkage with either the X or Y chromosome. Thus, the invasion of these mutants can be evaluated by haplotype, where the spread for haplotype

i j

is given by

λ_{i j},

where

i j

refers to the allele carried at the SDR and A loci, alongside the m allele. Because the A and a alleles are arbitrarily labeled, we will focus on cases where the suppressors that are likely to spread involve YA or Xa, e.g., where A is more strongly favored through males and a through females. The spread of modifiers that create tight linkage and that couple the Y and A allele is given by

λ_{Y A} = {\bar{w}}_{Y A}^{♂} / (2 q {\bar{w}}^{♂}) .

(1)

q is the fraction of male gametes produced that carry the Y, therefore the term

(1 / 2 q)

accounts for the fact that the spread of the YA haplotype depends only on the number of Y-bearing male gametes produced.

{\bar{w}}_{Y A}^{♂}

is the marginal fitness of YA haplotypes in males,

{\bar{w}}^{♂}

is the mean fitness of males, see Table A2. These modifiers will spread if

λ_{Y A} > 1,

which is often true when

{\bar{w}}_{Y A}^{♂} > {\bar{w}}^{♂},

that is, when YA males produce more gametes on average across both haploid and diploid phases of selection.

Invasion of a recombination suppressor that creates a strong association between the X and a allele is determined by the largest solution to the characteristic polynomial (A.5). For such modifiers, the leading eigenvalue

λ_{X a}

is >1 if

{\bar{w}}_{X a}^{m a t, ♀} / {\bar{w}}^{♀} + ({\bar{w}}_{X a}^{m a t, ♂} / (2 (1 - q) {\bar{w}}^{♂})) ({\bar{w}}_{X a}^{p a t, ♀} / {\bar{w}}^{♀}) > 2

(2)

where

{\bar{w}}^{♀}

is the mean fitness of females, and

{\bar{w}}_{X a}^{i, j}

indicates the marginal fitness of Xa haplotypes when inherited from the mother (⁠

i = m a t

⁠) or father (⁠

i = p a t

⁠) and found in offspring of sex j. This condition is the necessary condition for an X-linked haplotype to grow between the points in time that it resides in a particular sex (either male or female). Thus, condition (2) demonstrates that the newly formed sex chromosome is able to invade if its marginal fitness is higher than average once appropriately weighted across carriers of maternal and paternal copies.

Equilibrium allele frequencies:

Equation (1) and inequality (2) depend on the frequency of the A and a alleles. If either allele were fixed, recombination would have no effect, and recombination modifiers would be neutral. Furthermore, because recombination only occurs in double heterozygotes, suppressors of recombination generally have a larger effect when the frequency of heterozygous males is higher (XY– $A a$ heterozygotes common). An allele that is directionally selected will segregate for a relatively brief time, during which a recombination modifier would have to arise and/or experience selection. We therefore focus on longer-lasting polymorphisms at the A locus that are maintained by selection. However, we expect similar results in cases where selection is not balanced. For example, we find below that suppressors of recombination are typically favored when they associate pollen-beneficial alleles (e.g., A) with the Y because the Y experiences pollen competition most often. We would predict that recombination suppressors would be similarly favored while the A allele were spreading to fixation, even if the A and a alleles were neutral during all other life cycle stages.

Here, we give the equilibrium allele frequencies and stability conditions for our model, assuming that selection and meiotic drive are weak relative to recombination. Figure 2 shows the zygotic sex ratio at equilibrium for a range of recombination rates. In Appendix A.2.C, we calculate these equilibria and stability conditions (and the corresponding invasion conditions,

λ_{Y A}

and

λ_{X a}

⁠) without assuming weak selection by assuming that recombination is initially free (⁠

r_{M M} = 1 / 2

⁠), and that there is no sex-specific diploid selection or meiotic drive (⁠

w_{i j}^{♂} = w_{i j}^{♀} = w_{i j},

α^{♂} = 1 / 2

⁠). With weak selection (⁠

s^{♂},

s^{♀},

t^{♂},

α_{Δ}^{♂}

of order

ϵ^{2}

⁠), maintenance of a polymorphism at the A locus requires that

- h^{♀} s^{♀} - h^{♂} s^{♂} < t^{♂} + α_{Δ}^{♂} < - (1 - h^{♀}) s^{♀} - (1 - h^{♂}) s^{♂},

(3)

which indicates that a polymorphism can be stably maintained by a combination of sexually antagonistic selection (⁠

s^{♂} s^{♀} < 0

⁠), ploidally antagonistic selection (⁠

t^{♂} s^{♀} < 0,

t^{♂} s^{♂} < 0,

α_{Δ}^{♂} s^{♀} < 0,

and/or

α_{Δ}^{♂} s^{♂} < 0

⁠), and/or overdominance (⁠

h^{♂} > 1

and/or

h^{♀} > 1,

Immler et al. 2012). If there is haploid selection in favor of an allele and a polymorphic equilibrium allele frequency is reached, the other allele must be favored by selection during another life cycle phase.

With weak selection, the polymorphic equilibrium frequencies of A in each type of gamete are the same to leading order (⁠

{\hat{p}}_{X}^{♀} = {\hat{p}}_{X}^{♂} = {\hat{p}}_{Y}^{♀} = \bar{p}

⁠) and given by

\bar{p} = \frac{h^{♀} s^{♀} + h^{♂} s^{♂} + t^{♂} + α_{Δ}^{♂}}{(2 h^{♀} - 1) s^{♀} + (2 h^{♂} - 1) s^{♂}} + o (1) .

(4)

The evolution of recombination suppressors further depends on differences in frequency between gamete types, which are of the same order as selection (⁠

ϵ^{2}

⁠), and given by

\begin{array}{l} {\hat{p}}_{X}^{♂} - {\hat{p}}_{X}^{♀} = V_{A} (D^{♂} - D^{♀} + α_{Δ}^{♂}) \\ {\hat{p}}_{Y}^{♂} - {\hat{p}}_{X}^{♀} = V_{A} (1 - 2 r_{M M}) (D^{♂} - D^{♀} + α_{Δ}^{♂} + t^{♂}) / 2 r_{M M} \end{array}

,

(5)

where

V_{A} = \bar{p} (1 - \bar{p})

is the variance in the frequency of A, and D^⚥ = (⁠

\bar{p}

s^⚥ + (1−

\bar{p}

⁠) h^⚥ s^⚥)–(⁠

\bar{p}

h^⚥ s^⚥ + (1−

\bar{p}

⁠))corresponds to the difference in fitness between A and a alleles in diploids of sex ⚥

\in {♂, ♀}

(⁠

\bar{p}

is the leading-order probability of mating with an A-bearing gamete from the opposite sex). The frequency of Y among male gametes depends upon the difference in the frequency of the A allele between X- and Y-bearing male gametes and the strength of meiotic drive in favor of the A allele in males,

q = 1 / 2 + α_{Δ}^{♂} ({\hat{p}}_{Y}^{♂} - {\hat{p}}_{X}^{♂}) / 2 + o (ϵ^{4}) .

Invasion conditions:

Assuming that selection is weak relative to the initial recombination rate (⁠

r_{M M}

⁠), as above (⁠

s^{♂},

s^{♀},

t^{♂},

α_{Δ}^{♂}

of order

ϵ^{2}

⁠), the spread of modifiers that create tight linkage and that couple the Y and A allele is governed by

λ_{Y A} = 1 + \frac{1}{2 \bar{p}} (({\hat{p}}_{X}^{♂} - {\hat{p}}_{X}^{♀}) + V_{A} t^{♂}) + o (ϵ^{2}) .

(6)

If there is no haploid selection (⁠

α_{Δ}^{♂} = 0,

t^{♂} = 0

⁠), Equation (6) confirms the expectation from Charlesworth and Charlesworth (1980) that recombination suppressors that bring together the Y and A allele invade (⁠

λ_{Y A} > 1

⁠) when the A allele is favored more in males than in females (⁠

D^{♂} > D^{♀}

⁠).

In addition, Equation (6) shows that recombination suppressors are favored even when polymorphism is not maintained by differences in selection between the diploid sexes (⁠ $s^{♂} = s^{♀}$ and $h^{♂} = h^{♀}$ such that $D^{♂} = D^{♀}$ ⁠). Specifically, recombination suppressors that couple the Y and A allele spread (⁠ $λ_{Y A} > 1$ ⁠) when the A allele is favored during male gametic competition (⁠ $t^{♂} > 0,$ see Equation 6) and/or meiotic drive (see Equations 5 and 6). That is, these recombination suppressors spread when the A allele is favored by haploid selection in males.

Similarly, we can consider the spread of strong recombination suppressors that couple the a allele and the X, assuming that selection is weak,

λ_{X a} = 1 + \frac{1}{6 (1 - \bar{p})} (({\hat{p}}_{X}^{♂} - {\hat{p}}_{X}^{♀}) + V_{A} t^{♂}) + o (ϵ^{2}) .

(7)

As with

λ_{Y A},

λ_{X a}

tends to be >1 when the a allele is favored more in females than in males (⁠

D^{♂} > D^{♀}

⁠) and/or when the a allele is disfavored by haploid selection in males (⁠

α_{Δ}^{♂} > 0

or

t^{♂} > 0

⁠). Therefore, recombination suppressors that couple YA haplotypes and those that couple Xa haplotypes are favored under the same conditions. We assume that strong suppressors of recombination will eventually arise that couple any combination of alleles. Thus, because the labeling of A and a alleles is arbitrary, we conclude that strong suppressors of recombination are favored whenever there are differences in selection between males and females in the diploid phase (⁠

D^{♀} \neq D^{♂}

⁠) and/or sex-specific haploid selection (⁠

α_{Δ}^{♂} \neq 0

or

t^{♂} \neq 0

⁠).

It may not be intuitively obvious why an association between the X and the allele that is less fit during meiotic drive or gametic competition should be favored. This result comes from the fact that the a allele is initially maintained at an equilibrium frequency by selection. At equilibrium, selection against a during meiotic drive or sperm competition in males must be balanced by selection in favor of a in diploids (given the equilibrium exists). The X chromosome experiences meiosis in males and sperm competition less often than an autosomal or loosely linked locus. Thus, linked Xa haplotypes are favored because the a allele experiences haploid selection less often and is beneficial during other life cycle stages. More intuitively, Equation (6) indicates that linkage between the Y, which experiences haploid selection most often, and a haploid beneficial allele is favored.

As with previous analyses (Charlesworth and Charlesworth 1980; Charlesworth and Wall 1999; Lenormand 2003), we find that the strength of selection in favor of recombination modifiers is strongest on Y chromosomes because these are always found in only one sex, whereas the X will sometimes be found in males and sometimes in females. In particular, (6) and (7) differ by a factor of $1 / 3$ once we account for the difference between the probability of linkage arising with the A allele, $\bar{p},$ or the a allele, $(1 - \bar{p}) .$ However, mutations causing linkage with the Y (e.g., fusions) should also arise at a lower rate because there are three times as many X chromosomes as Y chromosomes in the population, such that the overall establishment rate of recombination modifiers is the same on the X and Y, all else being equal (Pennell et al. 2015).

In Figure 3, Figure S3 in File S2, and Figure S4 in File S2, we numerically iterate the recursion Equations A.1–A.3. As expected from the above results, a recombination suppressor spreads and the haploid beneficial allele (A, green and purple curves in Figures) becomes more common on the Y and less common on the X (even without sex-differences in selection among diploids). These numerical simulations and our approximation (Appendix A.2.B) show that incomplete recombination suppressors are also favored by selection. Incomplete recombination suppressors spread less quickly than complete recombination suppressors because associations between loci are disrupted by continuing recombination between the A locus, M locus, and the SDR. Despite the fact that zygotic sex ratios become increasingly biased as recombination declines, recombination suppressors typically spread to fixation and new mutations that further suppress recombination are also favored (e.g., Supplemental Material, Figure S1 in File S2). Below, we consider whether recombination should evolve to become completely suppressed by considering selected loci that are closely linked to the SDR.

ZW sex determination:

We derive equivalent results for ZW sex chromosome systems (where males are ZZ and females are ZW) with a period of haploid selection among male gametes/gametophytes. We again consider invasion of a modifier that creates tight linkage between the A locus and the M locus (⁠

r_{M m} = ρ = R^{♂} = R^{♀} = 0

⁠) and assume that selection is weak relative to

r_{M M} .

Again labeling the A allele as favored across haploid and diploid selection in males, the invasion of strong recombination suppressors that co-occur with Wa and ZA haplotypes are given by

\begin{array}{l} λ_{W a} = 1 + \frac{1}{2 (1 - \bar{p})} (({\hat{p}}_{Z}^{♂} - {\hat{p}}_{Z}^{♀}) + V_{A} t^{♂}) + o (ϵ^{2}) \\ λ_{Z A} = 1 + \frac{1}{6 \bar{p}} (({\hat{p}}_{Z}^{♂} - {\hat{p}}_{Z}^{♀}) + V_{A} t^{♂}) + o (ϵ^{2}), \end{array}

(8)

where

{\hat{p}}_{Z}^{♂} - {\hat{p}}_{Z}^{♀} = V_{A} (D^{♂} - D^{♀} + α_{Δ}^{♂}) .

(9)

Equations (8) show that recombination suppressors that cause linkage between the male Z chromosome and the A allele or linkage between the female-specific W chromosome and the a allele are favored when the A allele is favored by diploid and haploid selection in males (⁠

D^{♀} > D^{♂},

α_{Δ}^{♂} > 0,

t^{♂} > 0

⁠). When these forms of selection conflict, Equation (8) shows that the male-beneficial allele can be defined by that causing

({\hat{p}}_{Z}^{♂} - {\hat{p}}_{Z}^{♀}) + V_{A} t^{♂} > 0.

Even in the absence of differences in selection between diploid sexes, recombination suppression can evolve and allow an association between the chromosome that is present in males most often (Z) and alleles favored during haploid selection in males, i.e., during male meiosis or sperm competition.

Recombination evolution between SDR and closely linked selected loci

Finally, we evaluate the evolution of recombination during the final stages of sex chromosome evolution by considering the evolution of small amounts of recombination around the SDR. As discussed above, linkage allows favorable associations to build up between the SDR and selected loci. Therefore, we generally also expect that recombination rates near the SDR will also evolve to be lower. Considering diploid selection alone, Otto (2014) demonstrated that, while this prediction is usually true, a small amount of recombination around the SDR can be maintained by selection. Otto (2014) showed that certain forms of selection (particularly overdominance in males), combined with the asymmetrical inheritance patterns of sex chromosomes can favor loosely linked modifiers that increase recombination around the SDR. Here, our goal is to evaluate the conditions under which recombination can be selectively maintained when there is also haploid selection and also to confirm whether suppressed recombination generally continues to be favored when linkage is tight. For simplicity, we consider an XY sex determination system and gametic competition (not meiotic drive) among male gametes/gametophytes.

With tight linkage between the SDR and a selected locus, A, the Y chromosome always becomes fixed for one allele or the other (or nearly so if there is some recombination, see Appendix A.3). Without loss of generality, we will assume that selection on the Y favors the A allele, which becomes nearly fixed on the Y. X chromosomes will therefore be paired with a YA haplotype in diploid males; this alters selection experienced by X chromosomes found in diploid males vs. those found in diploid females. For example, the A locus will never be homozygous for the a allele in males but could be in females. When there is a polymorphism maintained, the X can either be fixed for the a allele or be polymorphic (both XA and Xa haplotypes present). In either case, the effect of increasing the recombination rate with the SDR is to produce more Ya and XA haplotypes among sperm. Ya haplotypes always have low fitness given that the Y was originally fixed for the A allele. However, the XA haplotypes produced by recombination can be favored because they are found in male gametes/gametophytes. X-bearing male gametes/gametophytes first experience sperm competition and then necessarily produce females in the next generation (see Figure 1). Thus, the XA haplotypes produced by recombination in males do not experience the same selective environment as X chromosomes from mothers, which do not experience sperm competition and can be inherited by daughters or sons. Interestingly, certain selection regimes favor XA haplotypes in sperm (even if the X is fixed for the a allele), which can counterintuitively favor modifiers that increase recombination around the SDR.

With diploid selection only, increased recombination around the SDR can evolve only if selection in females favors the A allele (which is fixed on the Y) because XA sperm produced by recombination will next be found in a female (Figure 1). For this to occur, selection in males must be overdominant (a necessary, but not sufficient, condition). With overdominance in males, the a allele has the highest fitness on the X chromosome in males because it is always paired with an A allele on the Y. Thus, the a allele can be maintained (or even fixed) on X chromosomes, and yet the A allele can be favored during selection in females. However, with sperm competition, it is possible for increases in recombination to be favored under a wider variety of selective regimes in diploids, including overdominance, underdominance, sexually antagonistic selection and ploidally antagonistic selection. In Appendix A.3, we show that the evolution of increased recombination requires either that the A allele is selected against on the X in males (⁠ $w_{A A}^{♂} < w_{A a}^{♂}$ ⁠), and/or that the A allele is favored during male gametic competition (⁠ $w_{A}^{♂} > w_{a}^{♂}$ ⁠). If the A allele is selected against on X chromosomes in males (⁠ $w_{A A}^{♂} < w_{A a}^{♂}$ ⁠), it is possible for it to be favored on X chromosomes in females and yet still maintain the a allele. In addition, XA haplotypes produced by recombination will be found in sperm and, thus, experience gametic competition before becoming diploid females. Therefore, if gametic competition favors the A allele (⁠ $w_{A}^{♂} > w_{a}^{♂}$ ⁠), XA haplotypes in sperm can have high fitness, easing the conditions under which increased recombination is favored.

Given that XA sperm have an advantage due to male gametic competition and/or high fitness in female diploids, the fitness advantage of XA sperm must outweigh the cost of producing low-fitness Ya sperm. Thus, increased recombination around the SDR only evolves in particular regions of parameter space (Figure A1). In addition, the evolution of increased recombination requires that the modifier is sufficiently loosely linked to the SDR (⁠ $R^{♀}$ and $R^{♂}$ are sufficiently large), e.g., modifiers are autosomal. This allows the modifier to gain the short-term advantage described above while not remaining linked to the selected locus for long (over the long term, an association with XA or Ya is neutral or deleterious when averaged across all backgrounds). Thus, although haploid selection means that overdominance is not required for the selective maintenance of recombination, increased recombination around the SDR still only evolves under a small subset of possible selective regimes. Suppressed recombination is favored in most circumstances (e.g., locally acting recombination suppressors spread, Figure S1 in File S2).

Discussion

Even in predominantly diploid organisms such as animals and angiosperms, there is considerable potential for selection upon haploid genotypes during competition among male gametes (sperm/pollen) and/or meiotic drive. Here, we demonstrate that haploid selection typically favors linkage with the diploid SDR (XY or ZW). Thus, along with selective differences between diploid sexes, selection among haploids could be a potent driver of recombination suppression on sex chromosomes.

In ZW sex determination systems, the zygotic sex ratio is unaffected by haploid selection in males. However, in XY sex determination systems, the number of males and females in each generation depends on the frequency of X and Y gametes after haploid selection in males. Despite this, we find that selection on recombination modifiers is not primarily driven to balance the zygotic sex ratio but to strengthen genetic associations between selected alleles and the SDR when selection differs between males and females in the haploid and/or diploid phase. In fact, the evolution of recombination suppression should lead to zygotic sex ratios becoming biased (typically biased toward males but see Figure 2 and Figure S2 in File S2 for cases where female-bias develops because the allele favored during male haploid selection is even more favored in females).

Figure 2

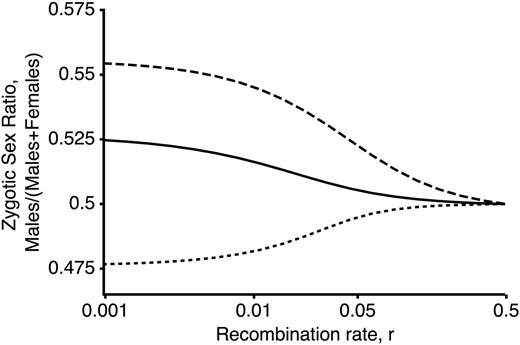
The zygotic sex ratio is biased by linkage between an XY SDR and a locus that experiences competition among male gametes. Here, we plot the zygotic sex ratio at equilibrium assuming that all individuals have the same recombination rate, r (fixed for modifier allele M). Male-biased sex ratios result when the Y becomes associated with alleles conferring high sperm fitness (solid line: $w_{A a} = 0.97,$ $w_{A A} = 0.91,$ $w_{a}^{♂} = 0.9,$ $w_{A}^{♂} = 1,$ dashed line: $w_{A a} = 0.92,$ $w_{A A} = 0.8,$ $w_{a}^{♂} = 1,$ $w_{A}^{♂} = 1.25,$ both with $w_{i j}^{♂} = w_{i j}^{♀} = w_{i j},$ $w_{a a} = 1$ such that selection is ploidally antagonistic). Female-biased sex ratios can, however, arise if the haploid-beneficial allele is also strongly favored in females and becomes associated with the X (dotted line: $w_{a a}^{♂} = 1,$ $w_{A a}^{♂} = 0.94,$ $w_{A A}^{♂} = 0.8,$ $w_{a a}^{♀} = 1,$ $w_{A a}^{♀} = 1.14,$ $w_{A A}^{♀} = 1.2,$ $w_{a}^{♂} = 1,$ $w_{A}^{♂} = 1.1,$ such that selection in diploids is sexually antagonistic).

Open in new tab Download slide

Although potentially caused by sex differences in survival, biased sex ratios at flowering are common among dioecious plants with 76/243 species exhibiting significantly male-biased sex ratios and 45/243 exhibiting female-biased ones (Field et al. 2013). We predict that, in the early stages of sex chromosome evolution, recombination suppression should allow associations between the Y and haploid-beneficial alleles leading to male-biased zygotic sex ratios. However, following recombination suppression, the Y-chromosome is expected to accumulate deleterious mutations and deletions, resulting in heteromorphic sex chromosomes (Charlesworth and Charlesworth 2000; Bachtrog 2013). Following Y-chromosome degeneration, Y-bearing gametophytes should have low haploid fitness, leading instead to female-biased zygotic sex ratios (Lloyd 1974; Stehlik and Barrett 2005). Indeed, plant species with heteromorphic rather than homomorphic sex chromosomes tend to have more female biased flowering sex ratios (Field et al. 2013). For example, in Rumex species with heteromorphic sex chromosomes and female biased flowering sex ratios, more intense pollen competition appears to result in more female biased sex-ratios among the progeny (Conn and Blum 1981; Stehlik and Barrett 2006; Field et al. 2012). Thus, while we predict that the Y should typically be associated with the allele that is beneficial during the male haploid stage when there are functional alleles present on both X and Y chromosomes, the overall fitness of the Y chromosome may become reduced due to degeneration. Therefore, the net effect of experimentally manipulating the intensity of haploid selection may depend on the stage of sex chromosome degeneration, as well as the alleles associated with the Y, where we predict that associations between haploid-beneficial alleles and the Y are favored when haploid selection occurs in males. The increasing availability of sex-linked markers should allow sexes to be identified before reproductive maturity in plants (e.g., McKown et al. 2017), thus allowing changes in the sex ratio to be directly evaluated across haploid and diploid phases in species with differing degrees of Y chromosome degeneration and recombination suppression.

The increasing study of both haploid expression profiles (Joseph and Kirkpatrick 2004; Borg et al. 2009) and a broader array of sex chromosome systems (Ming et al. 2011; Charlesworth 2013, 2015; Bachtrog et al. 2014; Vicoso and Bachtrog 2015) provides an excellent opportunity to evaluate whether sex chromosomes are enriched for genes selected during gametic competition, as predicted by our models. While Crowson et al. (2017) did not find evidence for an over-representation of haploid-expressed genes (as identified in Arabidopsis thaliana) on the sex chromosomes of Rumex rothschildianus, G. Sandler and colleagues (personal communication) recently sequenced the pollen transcriptome in R. rothschildianus and R. hastatulus directly and found that sex-linked genes show significantly higher expression in pollen, relative to autosomal genes, particularly so for Y-linked genes. We predict a stronger signal of association with SDRs should occur among loci explicitly shown to exhibit variation in haploid competitive ability (Travers and Mazer 2001) or loci where mutants affect fitness in both haploid and diploid phases (Muralla et al. 2011). Finally, we predict that the strength of gametic competition partly determines whether, and how fast, recombination suppression evolves. Selection on recombination suppression due to sexually antagonistic selection was recently investigated using populations that differ in the strength of sexually antagonistic selection (Wright et al. 2017); we predict that recombination suppression could be similarly correlated with the strength of haploid selection. Evaluating a related hypothesis, Lenormand and Dutheil (2005) correlate heterochiasmy (differences in autosomal recombination between sexes) with the degree of sex-specific haploid selection across species, using outcrossing rate as a proxy for male haploid selection. We would expect a similar pattern for recombination suppression around SDRs rising with the degree of outbreeding and polygamy.

Haploid expression and selection may occur during sperm competition in animals, particularly when sperm are long-lived (Immler et al. 2014; Alavioon et al. 2017). Genes expressed in the testes appear to accumulate on Y and Z chromosomes via translocations (Arunkumar et al. 2009; Mahajan and Bachtrog 2017), but it is not yet clear what proportion of these genes express their haploid vs. diploid genotype in sperm (Namekawa et al. 2006). Nevertheless, haploid selection in animals might occur via meiotic drive, of which there are many known examples (Jaenike 2001; Helleu et al. 2015; Lindholm et al. 2016). Meiotic drive in animals or plants is usually sex specific, either acting during spermatogenesis in males or polar body formation in females (Úbeda and Haig 2005). In the absence of diploid sex differences in selection, we predict that recombination suppression could evolve if it allows alleles favored by meiotic drive to become associated with the sex in which drive occurs (e.g., a male meiotic drive allele and the Y). This result is reflected in some other studies of meiotic drive. For example, reduced recombination is expected to evolve between an X chromosome that experiences drive and another selected locus (Feldman and Otto 1989; Rydzewski et al. 2016), and new male determining alleles can be favored when they appear in linkage to a locus that experiences drive in males (Úbeda et al. 2015). These studies reinforce the view that sex-specific meiotic drive can affect the evolution of recombination, often in a similar manner to sex-specific diploid selection.

Our model of meiotic drive is simple, involving a single locus with two alleles. However, many meiotic drive systems involve an interaction with another locus at which alleles may confer “susceptibility” or “resistance” to meiotic drive (Burt and Trivers 2006; Lindholm et al. 2016). Thus, the dynamics of meiotic drive alleles can be heavily dependent on the interaction between two loci and the recombination rate between them (Haig and Grafen 1991). After recombination suppression has evolved, sex chromosomes may therefore be more likely to facilitate the spread of new meiotic drive alleles (Hurst and Pomiankowski 1991). In addition, divergence between sex chromosomes may provide a particularly large source of suitable targets for drive, and meiotic drive on sex chromosomes is likely to be particularly easy to detect (Burt and Trivers 2006). Finally, meiotic drive can be strong, causing sex ratios to become extremely biased, which can have demographic consequences, especially where population growth depends predominantly on the number of females. This could mean that population extinction is more likely when meiotic drive alleles are linked to the Y (Hamilton 1967). These considerations should be taken into account when interpreting the genomic distribution of meiotic drive alleles.

As in a previous analysis by Otto (2014), we find that a small amount of recombination can be selectively maintained around the SDR. Otto (2014) considered only diploid selection and found that overdominance in males was required for recombination to be selectively maintained. Here, we include a period of competition among haploids and find that increased recombination can be favored with various forms of selection among diploids, including directional selection, sexually antagonistic selection, and ploidally antagonistic selection (Figure A1), as long as the allele fixed on the Y is favored in male haploids and/or females. However, increased recombination is never favored when modifiers of recombination act locally, such that they are also closely linked to the SDR. In a previous study, Feldman and Otto (1989) considered meiotic drive alleles that target the SDR and included no diploid selection. Numerically, Feldman and Otto (1989) also identified cases where loosely linked modifiers favor increased recombination, which parallels our results under gametic competition. Overall, while these dynamics may influence the maintenance of small amounts of recombination around SDRs when polymorphisms with the right form of selection arise (e.g., within the colored regions in Figure A1), suppressed recombination will be favored in most circumstances. Importantly, our results confirm that locally acting recombination modifiers continue to favor reduced recombination, even in cases where the zygotic sex ratio is initially strongly biased. Indeed, with initially biased zygotic sex ratios, the fact that reduced recombination typically evolves generally drives more extreme sex ratio biases (Figure S1 in File S2).

As well as providing several predictions, our model offers a new perspective on drivers of sex chromosome evolution. Traditionally, sex differences in selection are thought to provide the raw material driving recombination suppression on sex chromosomes. However, even where diploid sexes exhibit very few morphological or ecological differences, selection upon haploid genotypes may be very divergent. We have shown that sex-specific meiotic drive or gamete competition should typically also favor suppressed recombination despite causing the zygotic sex ratio to become biased. Consequently, our view of sex chromosome evolution is expanded to incorporate the degree of sex specific selection in haploids along with that in diploids.

Appendix A

In addition to this appendix, in File S1 we provide a supplementary Mathematica file (Wolfram Research Inc. 2017), which can be used to replicate our analyses.

A.1. Recursion Equations

In each generation, we census the genotype frequencies in male and female haploids before gametic competition. At this stage, the frequencies of X-bearing male and female haploids are given by $X_{i}^{♂}$ and $X_{i}^{♀},$ and the frequency of Y-bearing haploids is given by $Y_{i}^{♂},$ where the index i specifies genotypes $M A,$ $M a,$ $m A,$ and $m a$ and $\sum_{i = 1}^{4} X_{i}^{♂} + Y_{i}^{♂} = \sum_{i = 1}^{4} X_{i}^{♀} = 1.$ Competition then occurs among male haploids according to the A locus allele, k, carried by individuals with genotype i. The genotype frequencies after gametic competition are $X_{i}^{♂, s} = w_{k} X_{i}^{♂} / {\bar{w}}_{H}$ and $Y_{i}^{♂, s} = w_{k} Y_{i}^{♂} / {\bar{w}}_{H},$ where ${\bar{w}}_{H} = \sum_{i = 1}^{4} w_{k} X_{i}^{♂} + w_{k} Y_{i}^{♂}$ is the mean fitness of haploid sperm. Random mating then occurs between gametes to produce diploid females with genotype $i j$ at frequency $x_{i j} = X_{i}^{♀} X_{j}^{♂, s}$ and diploid males at frequency $y_{i j} = X_{i}^{♀} Y_{j}^{♂, s} .$ In females, individuals with genotype $i j$ are equivalent to those with genotype $j i .$ For simplicity we denote the frequency of genotype $i j$ in females to the average of these frequencies, $x_{i j} = (X_{i}^{♀} X_{j}^{♂, s} + X_{j}^{♀} X_{i}^{♂, s}) / 2 .$

Selection among diploids then occurs according to the diploid genotype at the A locus, k, for an individual of type

i j

(see Table 1). The diploid frequencies after selection are given by

x_{i j}^{s} = w_{k}^{♀} x_{i j} / {\bar{w}}^{♀}

in females and

y_{i j}^{s} = w_{k}^{♂} y_{i j} / {\bar{w}}^{♂}

in males, where

{\bar{w}}^{♀} = \sum_{i = 1}^{4} \sum_{j = 1}^{4} w_{k}^{♀} x_{i j}

and

{\bar{w}}^{♂} = \sum_{i = 1}^{4} \sum_{j = 1}^{4} w_{k}^{♂} y_{i j} .

Finally, these diploids undergo meiosis to produce the next generation. The haplotype frequencies in the next generation of eggs is given by:

X_{M A}^{♀'} = (\sum_{j = 1}^{4} x_{1 j}^{s}) - R^{♀} (x_{14}^{s} - x_{23}^{s})

(A.1a)

X_{M a}^{♀'} = (\sum_{j = 1}^{4} x_{2 j}^{s}) + R^{♀} (x_{14}^{s} - x_{23}^{s})

(A.1b)

X_{m A}^{♀'} = (\sum_{j = 1}^{4} x_{3 j}^{s}) + R^{♀} (x_{14}^{s} - x_{23}^{s})

(A.1c)

X_{m a}^{♀'} = (\sum_{j = 1}^{4} x_{4 j}^{s}) - R^{♀} (x_{14}^{s} - x_{23}^{s})

(A.1d)

which only involve the recombination rate between the A locus and the M locus in females (⁠

R^{♀}

⁠). In males, recombination between the SDR and the A locus or the M also affects the frequencies of haplotypes produced. Here, we allow the relative locations of the SDR, A, and M loci to be generic by using three parameters to describe the recombination rates between them.

R^{♂}

is the recombination rate between the A locus and the M locus in males, ρ is the recombination rate between the M locus and the SDR, and

r_{i j}

is the recombination rate between the A locus and the SDR. Table A1 gives substitutions for ρ for defined physical positions of these loci.

The frequencies of haplotypes among X-bearing sperm (before gametic competition) in the next generation are given by

\begin{matrix} X_{M A}^{♂'} = (y_{11}^{s} + y_{13}^{s}) / 2 + (y_{12}^{s} + y_{14}^{s}) α^{♂} \\ - r_{M M} (y_{12}^{s} - y_{21}^{s}) α^{♂} - ρ (y_{13}^{s} - y_{31}^{s}) / 2 \\ + {- (R^{♂} + r_{M m} + ρ) y_{14}^{s} + (r_{M m} + ρ - R^{♂}) y_{41}^{s} \\ + (R^{♂} + r_{M m} - ρ) y_{23}^{s} + (R^{♂} + ρ - r_{M m}) y_{32}^{s}} α^{♂} / 2 \end{matrix}

(A.2a)

\begin{matrix} X_{M a}^{♂'} = (y_{22}^{s} + y_{24}^{s}) / 2 + (y_{21}^{s} + y_{23}^{s}) (1 - α^{♂}) \\ - r_{M M} (y_{21}^{s} - y_{12}^{s}) (1 - α^{♂}) - ρ (y_{24}^{s} - y_{42}^{s}) / 2 \\ + {- (R^{♂} + r_{M m} + ρ) y_{23}^{s} + (r_{M m} + ρ - R^{♂}) y_{32}^{s} \\ + (R^{♂} + r_{M m} - ρ) y_{14}^{s} + (R^{♂} + ρ - r_{M m}) y_{41}^{s}} (1 - α^{♂}) / 2 \end{matrix}

(A.2b)

\begin{matrix} X_{m A}^{♂'} = (y_{33}^{s} + y_{31}^{s}) / 2 + (y_{32}^{s} + y_{34}^{s}) α^{♂} \\ - r_{M M} (y_{34}^{s} - y_{43}^{s}) α^{♂} - ρ (y_{31}^{s} - y_{13}^{s}) / 2 \\ + {- (R^{♂} + r_{M m} + ρ) y_{32}^{s} + (r_{M m} + ρ - R^{♂}) y_{23}^{s} \\ + (R^{♂} + r_{M m} - ρ) y_{41}^{s} + (R^{♂} + ρ - r_{M m}) y_{14}^{s}} α^{♂} / 2 \end{matrix}

(A.2c)

\begin{matrix} X_{m a}^{♂'} = (y_{44}^{s} + y_{42}^{s}) / 2 + (y_{41}^{s} + y_{43}^{s}) (1 - α^{♂}) \\ - r_{M M} (y_{43}^{s} - y_{34}^{s}) (1 - α^{♂}) - ρ (y_{42}^{s} - y_{24}^{s}) / 2 \\ + {- (R^{♂} + r_{M m} + ρ) y_{41}^{s} + (r_{M m} + ρ - R^{♂}) y_{14}^{s} \\ + (R^{♂} + r_{M m} - ρ) y_{32}^{s} + (R^{♂} + ρ - r_{M m}) y_{23}^{s}} (1 - α^{♂}) / 2 \end{matrix}

(A.2d)

and the frequencies of Y-bearing sperm haplotypes (before gametic competition) are given by

\begin{matrix} Y_{M A}^{♂'} = (y_{11}^{s} + y_{31}^{s}) / 2 + (y_{21}^{s} + y_{41}^{s}) α^{♂} \\ - r_{M M} (y_{21}^{s} - y_{12}^{s}) α^{♂} - ρ (y_{31}^{s} - y_{13}^{s}) / 2 \\ + {- (R^{♂} + r_{M m} + ρ) y_{41}^{s} + (r_{M m} + ρ - R^{♂}) y_{14}^{s} \\ + (R^{♂} + r_{M m} - ρ) y_{32}^{s} + (R^{♂} + ρ - r_{M m}) y_{23}^{s}} α^{♂} / 2 \end{matrix}

(A.3a)

\begin{matrix} Y_{M a}^{♂'} = (y_{22}^{s} + y_{42}^{s}) / 2 + (y_{12}^{s} + y_{32}^{s}) (1 - α^{♂}) \\ - r_{M M} (y_{12}^{s} - y_{21}^{s}) (1 - α^{♂}) - ρ (y_{42}^{s} - y_{24}^{s}) / 2 \\ + {- (R^{♂} + r_{M m} + ρ) y_{32}^{s} + (r_{M m} + ρ - R^{♂}) y_{23}^{s} \\ + (R^{♂} + r_{M m} - ρ) y_{41}^{s} + (R^{♂} + ρ - r_{M m}) y_{14}^{s}} (1 - α^{♂}) / 2 \end{matrix}

(A.3b)

\begin{matrix} Y_{m A}^{♂'} = (y_{33}^{s} + y_{13}^{s}) / 2 + (y_{23}^{s} + y_{43}^{s}) α^{♂} \\ - r_{m m} (y_{43}^{s} - y_{34}^{s}) α^{♂} - ρ (y_{13}^{s} - y_{31}^{s}) / 2 \\ + {- (R^{♂} + r_{M m} + ρ) y_{23}^{s} + (r_{M m} + ρ - R^{♂}) y_{32}^{s} \\ + (R^{♂} + r_{M m} - ρ) y_{14}^{s} + (R^{♂} + ρ - r_{M m}) y_{41}^{s}} α^{♂} / 2 \end{matrix}

(A.3c)

\begin{matrix} Y_{m a}^{♂'} = (y_{44}^{s} + y_{24}^{s}) / 2 + (y_{14}^{s} + y_{34}^{s}) (1 - α^{♂}) \\ - r_{m m} (y_{34}^{s} - y_{43}^{s}) (1 - α^{♂}) - ρ (y_{24}^{s} - y_{42}^{s}) / 2 \\ + {- (R^{♂} + r_{M m} + ρ) y_{14}^{s} + (r_{M m} + ρ - R^{♂}) y_{41}^{s} \\ + (R^{♂} + r_{M m} - ρ) y_{23}^{s} + (R^{♂} + ρ - r_{M m}) y_{32}^{s}} (1 - α^{♂}) / 2 \end{matrix}

(A.3d)

where

α^{♂}

defines meiotic drive based on the A locus genotype such that the A allele “drives” if

α^{♂} > 1 / 2 .

A.2. Invasion of Recombination Suppressors

A. General

We can write Equation (1), for the invasion of modifiers that bring the A allele into tight linkage with the Y chromosome, as

λ_{Y A} = 1 + \frac{r_{M M} w_{A a}^{♂} α^{♂}}{{\hat{p}}_{Y}^{♂} {\bar{w}}^{♂} {\bar{w}}_{H}} ({\bar{w}}_{Y} ({\hat{p}}_{Y}^{♂} - {\hat{p}}_{X}^{♀}) + V_{m} (w_{A}^{♂} - w_{a}^{♂})),

(A.4)

where

V_{m} = {\hat{p}}_{Y}^{♂} (1 - {\hat{p}}_{Y}^{♂})

is the variance in allele frequency among Y-bearing sperm,

{\bar{w}}_{Y} = ({\hat{p}}_{Y}^{♂} w_{A}^{♂} + (1 - {\hat{p}}_{Y}^{♂}) w_{a}^{♂})

is the mean fitness of Y-bearing sperm, and

{\bar{w}}_{H}

is the mean fitness of X- or Y-bearing sperm. This is similar to Equation (6), but includes several extra terms because we have not assumed that selection is weak relative to recombination. However, we assume that selection is weak when we derive the equilibrium allele frequencies

({\hat{p}}_{Y}^{♂} - {\hat{p}}_{X}^{♀})

explicitly. Charlesworth and Charlesworth (1980) took a similar approach to that in Equation (A.4) and did not explicitly solve for these equilibrium frequencies.

In general, invasion of modifiers that create strong linkage between the X and a allele is determined by the largest solution to the characteristic polynomial

2 (1 - q) λ_{X a}^{2} - λ_{X a} {\bar{w}}_{X a}^{m a t, ♀} / {\bar{w}}^{♀} - ({\bar{w}}_{X a}^{p a t, ♀} / {\bar{w}}^{♀}) ({\bar{w}}_{X a}^{m a t, ♂} / {\bar{w}}^{♂}) = 0.

(A.5)

Where various marginal fitness definitions are given in Table A2.

B. Incomplete recombination suppression

The case considered above, where a modifier suppresses recombination between itself, the selected locus, and the SDR (e.g., an inversion or a fusion) is the best case scenario for generating selection in favor of recombination suppressors. For a few parameters, Charlesworth and Charlesworth (1980) find numerically that recombination suppressors spread, but at lower rates, if the modifier loci remain loosely linked (⁠

R^{♂}

and

R^{♀}

are larger). Here, we find analytical results by assuming the recombination rates between the A locus, the M locus, and the SDR are small but not negligible (⁠

r_{M m},

ρ,

R^{♂}

and

R^{♀}

of order

ϵ^{3}

⁠). For tractability, we neglect meiotic drive and assume that recombination is initially loose (⁠

r_{M M} = 1 / 2,

α^{♂} = 1 / 2,

such that

p_{Y}^{♂} = p_{X}^{♂}

⁠) and assume that the loci are in the order SDR-M-A (Table A1) with no crossover interference. Neglecting terms of order

ϵ^{4}

and higher, the growth rate of such mutants (⁠

λ \tilde{_{i j}}

⁠) is

λ_{\tilde{Y A}} = \frac{V_{A}}{2 \bar{p}} (D^{♂} - D^{♀} + t^{♂}) - (1 - \bar{p}) R^{♂} - ρ

(A.6a)

λ_{\tilde{X a}} = \frac{1}{3} (\frac{V_{A}}{2 (1 - \bar{p})} (D^{♂} - D^{♀} + t^{♂}) - \bar{p} R^{♀} - ρ) .

(A.6b)

In each case, the first term corresponds to the tight linkage results in (6) and (7), where we also assume that there is no meiotic drive (⁠

α_{Δ}^{♂} = 0

⁠). The additional terms in (A.6) illustrate that the spread of linked haplotypes is slowed when the alternative A allele recombines onto the modifier and SDR background (recombination rate

R^{♂}

or

R^{♀}

⁠), or when the modifier recombines onto the opposite sex chromosome (which occurs at rate ρ in males). In Figure 3, we track the spread of a recombination modifier where

R^{♂}, R^{♀}, ρ, r_{M m} \neq 0,

such that both M alleles and both A alleles can recombine onto both sex chromosomes. As predicted from Equation (A.6), the X and Y chromosomes become associated with the a and A alleles, respectively, which continues to favor the spread of the suppressor allele, m.

Figure 3

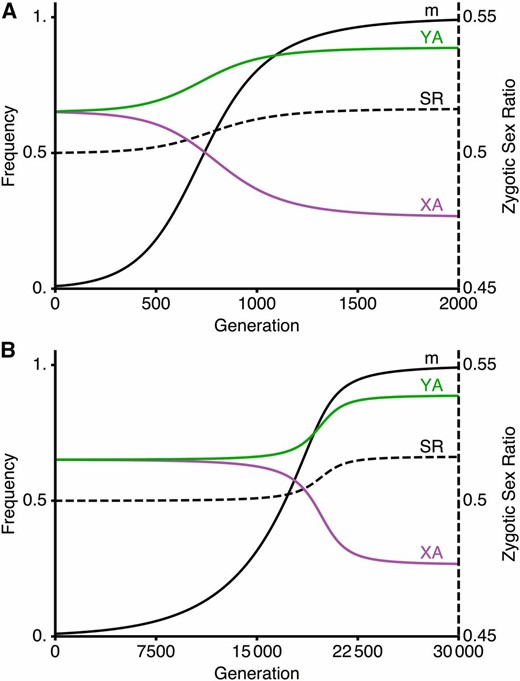
A modifier that reduces the recombination rate between the (A) locus and the SDR can spread to fixation despite causing sex ratios to become biased. We assume that the population initially has loose linkage between the (A) locus and the SDR (⁠ $r_{M M} = 0.5,$ where M is initially fixed), and allow allele frequencies to reach a polymorphic equilibrium. We then introduce a modifier allele m that reduces the recombination rate between (A) locus and the SDR (⁠ $r_{M m} = 0.02,$ $r_{m m} = 0.01$ ⁠); in generation 0, m is at frequency 0.01 and in linkage equilibrium with M. In (A) the M locus lies between the (A) locus and the SDR (e.g., a fusion) with no crossover interference such that $ρ = (r_{M m} - R^{♂}) / (1 - 2 R^{♂}),$ where $R^{♂} = R^{♀} = 0.005.$ In (B), the M locus is autosomal and unlinked to either the SDR or (A) locus: $R^{♂} = R^{♀} = ρ = 1 / 2 .$ The autosomal recombination suppressor spreads more slowly (note change of x-axis scale), but it spreads despite an increasingly biased zygotic sex ratio. Fitness parameters are as in the solid curve in Figure 2. That is, selection is ploidally antagonistic with A favored during gametic competition (see Figure S3 in File S2 and Figure S4 in File S2 for meiotic drive). Curves show the frequencies of the recombination suppression mutant, m, among sperm (black curve), the A allele among Y-bearing sperm (green curve), the A allele among X-bearing sperm (purple curve), and male zygotes (dashed black curve, shown against the scale on the right hand side).

Open in new tab Download slide

C. Ploidally antagonistic selection

In the main text, we predominantly assume that selection is weak relative to recombination to calculate

λ_{Y A}

and

λ_{X a} .

Here, we assume that the selected locus is initially loosely linked to the SDR (⁠

r_{M M} = 1 / 2

⁠), there is no meiotic drive (⁠

α^{♂} = 1 / 2

⁠), and that there are no sex differences in selection (⁠

w_{i j}^{♂} = w_{i j}^{♀} = w_{i j}

⁠). Regardless of the strength of selection, the polymorphic equilibrium frequency of the A allele is then

{\hat{p}}_{X}^{♂} = {\hat{p}}_{Y}^{♂} = {\hat{p}}_{X}^{♀} = \frac{2 w_{a}^{♂} w_{a a} - w_{A a} (w_{A}^{♂} + w_{a}^{♂})}{2 (w_{A}^{♂} (w_{A A} - w_{A a}) + w_{a}^{♂} (w_{a a} - w_{A a}))} .

(A.7)

This equilibrium is valid and stable when

2 w_{a}^{♂} w_{a a} < w_{A a} (w_{A}^{♂} + w_{a}^{♂}) > 2 w_{A}^{♂} w_{A A} .

(A.8)

Therefore, a polymorphism can be maintained either if there is heterozygote advantage in diploids (⁠

w_{A a} > w_{a a}

and

w_{A a} > w_{A A}

⁠), or if there is antagonistic selection between haploids and diploids (e.g.,

w_{A}^{♂} > w_{a}^{♂}

and

w_{a a} > w_{A a} > w_{A A}

⁠), or a combination of both (Immler et al. 2012). After equilibrium (A.7) is reached, the invasion of a modifier that brings the A allele into complete linkage with the Y is given by

λ_{Y A} = 1 + \frac{(w_{A}^{♂} - w_{a}^{♂}) w_{A a} (w_{A}^{♂} + w_{a}^{♂}) (w_{A a} (w_{A}^{♂} + w_{a}^{♂}) - 2 w_{A A} w_{A}^{♂})}{(w_{A}^{♂} + w_{a}^{♂}) (w_{A a}^{2} {(w_{A}^{♂} + w_{a}^{♂})}^{2} - 4 w_{A}^{♂} w_{A A} w_{a}^{♂} w_{a a})},

(A.9)

where

λ_{Y A} > 1

indicates that the modifier increases in frequency. Given that a polymorphism at the A locus is initially stable (conditions A.8 are met), the sign of

λ_{Y A} - 1

depends on the sign of

w_{A}^{♂} - w_{a}^{♂} .

That is, modifiers that bring the allele favored in haploids (e.g., A when

w_{A}^{♂} > w_{a}^{♂}

⁠) into tight linkage with the Y will spread.

Similarly, condition (2) for the invasion of modifiers that bring the a allele into tight linkage with the X chromosome is satisfied if

\frac{(w_{A}^{♂} - w_{a}^{♂}) w_{A a} (w_{A}^{♂} + w_{a}^{♂}) (w_{A a} (w_{A}^{♂} + w_{a}^{♂}) - 2 w_{A A} w_{A}^{♂})}{2 (w_{A}^{♂} + w_{a}^{♂}) (w_{A a} (w_{A}^{♂} + w_{a}^{♂}) - w_{A}^{♂} w_{A A} - w_{a}^{♂} w_{a a})} > 0,

(A.10)

which requires

w_{A}^{♂} > w_{a}^{♂},

given that conditions (A.8) are met. These results indicate that recombination modifiers invade if they bring the X into tight linkage with the allele that is less fit during gametic competition, even without the weak selection assumptions in Equation (7), at least under the assumptions made here of no meiotic drive or sex differences in selection during the diploid phase.

A.3. Invasion of Modifiers that Increase Recombination from an Initially Low Level

We consider a population in which linkage is tight between the A locus and the SDR (⁠

r_{M M}

is of order ε, where the M allele is initially fixed). Furthermore, we focus on haploid selection in the form of gametic competition rather than meiotic drive (⁠

α^{♂} = 1 / 2

⁠). Recombination has no effect if the A locus is fixed for one allele, we therefore focus on the five equilibria that maintain both A and a alleles, of which four are given to leading order by:

\begin{matrix} (A) {\hat{p}}_{Y}^{♂} = 0, {\hat{p}}_{X}^{♀} = \frac{φ}{φ + ψ}, {\hat{p}}_{X}^{♂} = \frac{w_{A a}^{♂} φ}{w_{A a}^{♂} φ + w_{a a}^{♂} ψ} \\ (A^{'}) {\hat{p}}_{Y}^{♂} = 1, {\hat{p}}_{X}^{♀} = 1 - \frac{φ^{'}}{φ^{'} + ψ^{'}}, {\hat{p}}_{X}^{♂} = 1 - \frac{w_{A a}^{♂} φ^{'}}{w_{A a}^{♂} φ^{'} + w_{A A}^{♂} ψ^{'}} \\ (B) {\hat{p}}_{Y}^{♂} = 0, {\hat{p}}_{X}^{♀} = 1, {\hat{p}}_{X}^{♂} = 1 \\ (B^{'}) {\hat{p}}_{Y}^{♂} = 1, {\hat{p}}_{X}^{♀} = 0, {\hat{p}}_{X}^{♂} = 0 \end{matrix}

(A.11)

\begin{array}{l} φ = w_{A a}^{♀} (w_{a a}^{♂} w_{a}^{♂} + w_{A a}^{♂} w_{A}^{♂}) - 2 w_{a a}^{♀} w_{a a}^{♂} w_{a}^{♂} \\ φ^{'} = w_{A a}^{♀} (w_{A A}^{♂} w_{A}^{♂} + w_{A a}^{♂} w_{a}^{♂}) - 2 w_{A A}^{♀} w_{A A}^{♂} w_{A}^{♂} \\ ψ = w_{A a}^{♀} (w_{a a}^{♂} w_{a}^{♂} + w_{A a}^{♂} w_{A}^{♂}) - 2 w_{A A}^{♀} w_{A a}^{♂} w_{A}^{♂} \\ ψ^{'} = w_{A a}^{♀} (w_{A A}^{♂} w_{A}^{♂} + w_{A a}^{♂} w_{a}^{♂}) - 2 w_{a a}^{♀} w_{A a}^{♂} w_{a}^{♂} . \end{array}

A fifth equilibrium

(C)

also exists where A is present at an intermediate frequency on the Y chromosome (⁠

0 < {\hat{p}}_{Y} < 1

⁠). However, equilibrium

(C)

is never locally stable when

r_{M M} \approx 0

and is therefore not considered further (see File S1). Thus, the Y can either be fixed for the a allele (equilibria A and B) or the A allele (equilibria

A^{'}

and

B^{'}

⁠). The X chromosome can then either be polymorphic (equilibria A and

A^{'}

⁠) or fixed for the alternative allele (equilibria B and

B^{'}

⁠). Since equilibria

(A)

and

(B)

are equivalent to equilibria

(A^{'})

and

(B^{'})

with the labelling of A and a alleles interchanged, we discuss only equilibria

(A^{'})

and

(B^{'}),

in which the YA haplotype is favored (as in the previous section), without loss of generality.

We next calculate when $(A^{'})$ and $(B^{'})$ are locally stable for $r_{M M} = 0.$ According to the “small parameter theory” (Karlin and McGregor 1972a,b), these stability properties are unaffected by small amounts of recombination between the SDR and A locus, although equilibrium frequencies may be slightly altered. For the A allele to be stably fixed on the Y requires that ${\bar{w}}_{Y A}^{♂} > {\bar{w}}_{Y a}^{♂},$ where the marginal fitnesses of YA and Ya haplotypes are ${\bar{w}}_{Y A}^{♂}$ (as above, Table A2) and ${\bar{w}}_{Y a}^{♂} = w_{a}^{♂} (p_{X}^{♀} w_{A a}^{♂} + (1 - p_{X}^{♀}) w_{a a}^{♂}) / {\bar{w}}_{H}^{♂},$ respectively. Substituting ${\hat{p}}_{X}^{♀}$ from above, fixation of the A allele on the Y requires that $γ_{i} > 0$ where $γ_{(A^{'})} = w_{A}^{♂} (w_{A a}^{♂} φ^{'} + w_{A A}^{♂} ψ^{'}) - w_{a}^{♂} (w_{a a}^{♂} φ^{'} + w_{A a}^{♂} ψ^{'})$ for equilibrium $(A^{'})$ and $γ_{(B')} = w_{A a}^{♂} w_{A}^{♂} - w_{a a}^{♂} w_{a}^{♂}$ for equilibrium $(B^{'}) .$ Stability of a polymorphism on the X chromosome (equilibrium $A^{'}$ ⁠) further requires that $φ^{'} > 0$ and $ψ^{'} > 0.$ Fixation of the a allele on the X (equilibrium $B^{'}$ ⁠) is mutually exclusive with $(A^{'}),$ and requires that $ψ^{'} < 0$ and that $4 w_{a a}^{♀} > w_{A a}^{♀} .$ We will assume that these conditions are met, such that the population has reached a stable equilibrium at the A locus when considering evolution at the modifier locus.

To consider recombination rate evolution, we evaluate whether a mutant allele, m, can invade if it modifies the recombination rate between A and the SDR by a small amount (⁠

| r_{m m} - r_{M M} |

and

| r_{M m} - r_{M M} |

are of order ε). As above, we use the leading eigenvalue, λ, from a local stability analysis to evaluate the spread of a rare mutant modifier, where now

λ_{i}

determines invasion into a population at equilibrium i. Firstly, because stability of equilibrium

(A^{'})

requires that

φ^{'} > 0

and

ψ^{'} > 0

and all fitnesses must be non-negative, we can define the following series of κ terms, which must be positive when

(A^{'})

is locally stable.

\begin{array}{l} κ_{1} = w_{a a}^{♀} φ^{'} + w_{A a}^{♀} ψ^{'} \\ κ_{2} = w_{A a}^{♀} φ^{'} + w_{A A}^{♀} ψ^{'} \\ κ_{3} = w_{A a}^{♂} φ^{'} + w_{A A}^{♂} ψ^{'} \\ κ_{4} = w_{a a}^{♀} φ^{'} + w_{A A}^{♀} ψ^{'} \\ κ_{5} = w_{A a}^{♂} w_{a}^{♂} + w_{A A}^{♂} w_{A}^{♂} \\ κ_{6} = w_{A a}^{♂} w_{a}^{♂} w_{A A}^{♂} w_{A}^{♂} \\ κ_{7} = w_{a a}^{♀} w_{A a}^{♂} w_{a}^{♂} φ^{'} + w_{A A}^{♀} w_{A A}^{♂} w_{A}^{♂} ψ^{'} \\ κ_{8} = w_{a a}^{♂} φ^{'} φ^{'} + 2 w_{A a}^{♂} φ^{'} ψ^{'} + w_{A A}^{♂} ψ^{'} ψ^{'} \\ κ_{9} = w_{A a}^{♂} w_{a}^{♂} φ^{'} + w_{A A}^{♂} w_{A}^{♂} ψ^{'} \\ κ_{10} = w_{A a}^{♀} κ_{9} + 2 κ_{6} κ_{4} / κ_{5} \end{array}

These are useful in determining the magnitude of

λ_{(A^{'})},

which determines invasion of modifiers, and is given by

λ_{(A^{'})} = 1 + (r_{M m} - r_{M M}) \frac{w_{A a}^{♂} φ^{'} K_{1}}{{γ_{(A')} + w_{a}^{♂} R^{♂} (w_{a a}^{♂} φ^{'} + w_{A a}^{♂} ψ^{'})} K_{2}},

(A.12)

where we neglect terms of order

ϵ^{2}

and higher, and

K_{2}

is strictly positive,

\begin{matrix} K_{2} = R^{♀} 2 w_{A a}^{♀} κ_{3} κ_{5} (φ^{'} + ψ^{'}) κ_{10} + 4 R^{♀} R^{♂} w_{A a}^{♂} w_{A A}^{♂} w_{a}^{♂} w_{A}^{♂} κ_{10} κ_{3} κ_{4} / κ_{5} \\ + R^{♂} (1 - 2 R^{♀}) w_{A a}^{♂} w_{A A}^{♂} & (w_{a}^{♂} ψ^{'} κ_{1} (2 w_{A A}^{♂} w_{A}^{♂} κ_{2} + κ_{10}) + w_{A}^{♂} φ^{'} κ_{2} (2 w_{A a}^{♂} w_{a}^{♂} κ_{1} + κ_{10})), \end{matrix}

such that

λ_{(A')} > 1

if, and only if,

(r_{M m} - r_{M M}) K_{1} > 0,

where

\begin{matrix} K_{1} = - (1 - 2 R^{♀}) R^{♂} γ_{(A^{'})} κ_{1} κ_{2} κ_{6} \\ - R^{♂} R^{♀} γ_{(A^{'})} κ_{4} κ_{6} (κ_{7} / κ_{5} + w_{A a}^{♀} (φ^{'} + ψ^{'}) / 2) \\ - R^{♀} γ_{(A^{'})} w_{A a}^{♀} w_{a}^{♂} κ_{1} κ_{3} κ_{5} \\ + R^{♀} w_{A a}^{♀} w_{A a}^{♂} (γ_{(A^{'})} φ^{'} + R^{♂} w_{a}^{♂} κ_{8}) & ((w_{A a}^{♂} - w_{A A}^{♂}) w_{a}^{♂} w_{A}^{♂} κ_{4} + (w_{A}^{♂} - w_{a}^{♂}) w_{A a}^{♀} κ_{5} (φ^{'} + ψ^{'}) / 2) . \end{matrix}

Modifiers that increase recombination (⁠

r_{M m} - r_{M M} > 0

⁠) therefore only spread if

K_{1} > 0.

Only the last term of

K_{1}

can be positive, and this term can only be positive if either

w_{A a}^{♂} > w_{A A}^{♂}

or

w_{A}^{♂} > w_{a}^{♂} .

Thus, for increased recombination to be favored by selection (⁠

K_{1} > 0

⁠), heterozygous males must be more fit than males homozygous for the allele fixed on the Y, and/or the allele fixed on the Y must be favored during haploid selection. Since the A allele is fixed on the Y,

w_{A a}^{♂} > w_{A A}^{♂}

implies that X chromosomes bearing the a allele are favored during selection in males. If a polymorphism is maintained on the X (equilibrium

A^{'}

⁠), counter-selection must favor the A allele during gametic competition, and/or selection in females when

w_{A a}^{♂} > w_{A A}^{♂} .

In addition, when linkage between the modifier locus and the selected locus is tight (at least in females,

R^{♀} = 0

⁠),

K_{1}

is always negative, and increased recombination is never favored.

We next consider the invasion of a recombination modifier into a population at equilibrium

(B^{'}) .

Local stability of this equilibrium requires that

(- ψ^{'}) > 0

and

γ_{(B^{'})} > 0.

Ignoring terms of order

ϵ^{2}

and higher,

λ_{(B^{'})} = 1 + (r_{M m} - r_{M M}) K_{3} / K_{4}

where

K_{4}

is positive

\begin{matrix} K_{4} = 4 (γ_{(B')} + R^{♂} w_{a a}^{♂} w_{a}^{♂}) & ((- ψ^{'}) + w_{A a}^{♀} (R^{♀} w_{A a}^{♂} w_{a}^{♂} + (R^{♀} + R^{♂} (1 - R^{♀})) w_{A A}^{♂} w_{A}^{♂}) \end{matrix}

Therefore

λ_{(B^{'})} > 1

if and only if

(r_{M m} - r_{M M}) K_{3} > 0,

where

\begin{matrix} K_{3} = - 2 γ_{(B^{'})} (- ψ^{'}) - (2 R^{♀} + R^{♂} (1 - R^{♀})) w_{A a}^{♀} w_{A A}^{♂} w_{A}^{♂} γ_{(B^{'})} & - R^{♂} (- ψ^{'}) w_{a a}^{♂} w_{a}^{♂} \\ + R^{♀} (w_{A}^{♂} - w_{a}^{♂}) w_{A a}^{♀} w_{A a}^{♂} (2 γ_{(B')} + R^{♂} w_{a a}^{♂} w_{a}^{♂}) & + R^{♀} R^{♂} (w_{A a}^{♂} - w_{A A}^{♂}) w_{A a}^{♀} w_{a a}^{♂} w_{a}^{♂} w_{A}^{♂} \end{matrix}

The only terms in

K_{3}

that can be positive involve the factors

(w_{A}^{♂} - w_{a}^{♂})

and

(w_{A a}^{♂} - w_{A A}^{♂}),

such that either

w_{A a}^{♂} > w_{A A}^{♂}

or

w_{a}^{♂} > w_{A}^{♂}

are again necessary (but not sufficient) conditions for the invasion of modifiers that increase recombination.

At equilibrium

(B^{'}),

w_{A a}^{♂} > w_{A A}^{♂}

implies that the a allele is favored during selection on X chromosomes in males. This equilibrium with a fixed on the X (⁠

{\hat{p}}_{X}^{♂} = {\hat{p}}_{X}^{♀} = 0

⁠) can then be stable with either the A or a allele favored during the other life cycle stages. However, we show that the evolution of increased recombination is only consistent with A being favored during gametic competition and/or selection in females by rewriting the condition

K_{3} > 0

to obtain

\begin{matrix} w_{a a}^{♀} < w_{A a}^{♀} + w_{A a}^{♀} (- γ_{(B')} (R^{♀} (2 - R^{♂}) + R^{♂}) & - (w_{A a}^{♂} - w_{A A}^{♂}) K_{5} + (w_{A}^{♂} - w_{a}^{♂}) K_{6}) / K_{7} \end{matrix}

(A.13)

where the following terms are positive

\begin{array}{l} K_{5} = (1 - R^{♀}) (2 γ_{(B^{'})} (1 - R^{♂}) + R^{♂} w_{A a}^{♂} w_{A}^{♂}) / w_{A a}^{♂} \\ K_{6} = {(w_{A A}^{♂} (1 - R^{♀}) + R^{♀} w_{A a}^{♂}) (2 γ_{(B^{'})} (1 - R^{♂}) + w_{A a}^{♂} w_{A}^{♂} R^{♂}) + R^{♀} R^{♂} w_{A}^{♂} {(w_{A a}^{♂})}^{2}} / (w_{A a}^{♂} w_{a}^{♂}) \\ K_{7} = 4 γ_{(B^{'})} + 2 w_{a a}^{♂} w_{a}^{♂} R^{♂} . \end{array}

Thus, if gametic competition favors the A allele (⁠

w_{A}^{♂} > w_{a}^{♂}

⁠), then condition (A.13) can be met whether selection among diploid females favors allele A or a (⁠

w_{a a}^{♀} < w_{A a}^{♀}

or

w_{a a}^{♀} > w_{A a}^{♀}

⁠). However, if gametic competition favors the a allele (⁠

w_{a}^{♂} > w_{A}^{♂}

⁠), Equation (A.13) shows that selection must favor the A allele during selection in females (⁠

w_{a a}^{♀} < w_{A a}^{♀}

⁠) for increased recombination to be favored (in addition to requiring that

w_{A a}^{♂} > w_{A A}^{♂},

see above).

Therefore, increased recombination is only favored if the A allele is favored during selection in females (⁠ $w_{a a}^{♀} < w_{A a}^{♀}$ ⁠) and/or the A allele is favored during gametic competition (⁠ $w_{A}^{♂} > w_{a}^{♂}$ ⁠). Only under these conditions is it possible for recombination between the XA and Ya to produce XA sperm that are favored over the short term (in daughters and/or sperm competition, respectively).

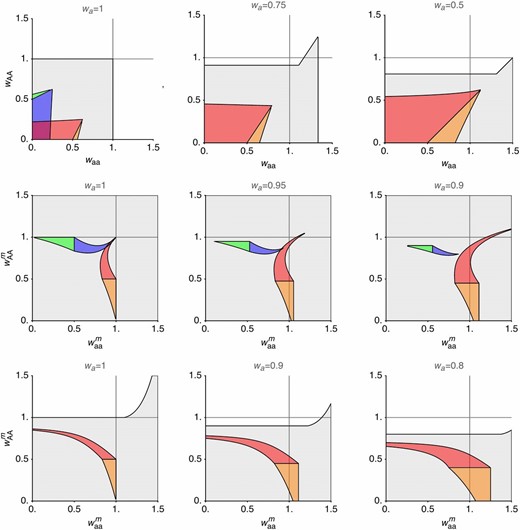
Selection can favor increased recombination between the SDR and a selected locus that is closely linked to the SDR (rij≈0), even when selection in males is not overdominant. The gray regions show where one or more of the polymorphic equilibria are stable, and thus recombination modifiers can affect fitness. Colored regions show where increased recombination is favored in a population at equilibrium (A) in blue, (B) in green, (A′) in red, and (B′) in orange. Since this model is symmetrical, red/orange regions can be exchanged with blue/green regions if the labeling of A and a alleles is switched. Across columns, we vary the fitness of a-bearing haploids relative to the A-bearing haploids (wA♂=1). Gray lines show the fitness of heterozygous diploids wAak=1. In the first row, there are no differences in selection between male and female diploids (wij♀=wij♂=wij), where waa and wAA are varied along the x and y axes, respectively. As haploid selection becomes stronger, increased recombination can evolve with weaker overdominance in diploids, and also with ploidally antagonistic selection (waa>1>wAA). In the second and third rows, we consider sex differences in selection, where waa♂ and wAA♂ are varied along the x and y axes (wAa♂=1). In the second row, where selection in females is overdominant (wAA♀=0.75, wAa♀=1, waa♀=0.75), increased recombination can be favored when selection is directional (or underdominant) in males, and haploid selection is moderately strong. In the third row, selection favors the A allele in females (wAA♀=1.05, wAa♀=1, waa♀=0.75) and increased recombination can be favored with overdominance in males or sexually antagonistic selection (wAA♂<1<waa♂). For this plot, we assume that the modifier of recombination is unlinked (R♀=R♂=1/2).

Figure A1

Selection can favor increased recombination between the SDR and a selected locus that is closely linked to the SDR (⁠ $r_{i j} \approx 0$ ⁠), even when selection in males is not overdominant. The gray regions show where one or more of the polymorphic equilibria are stable, and thus recombination modifiers can affect fitness. Colored regions show where increased recombination is favored in a population at equilibrium $(A)$ in blue, $(B)$ in green, $(A^{'})$ in red, and $(B^{'})$ in orange. Since this model is symmetrical, red/orange regions can be exchanged with blue/green regions if the labeling of A and a alleles is switched. Across columns, we vary the fitness of a-bearing haploids relative to the A-bearing haploids (⁠ $w_{A}^{♂} = 1$ ⁠). Gray lines show the fitness of heterozygous diploids $w_{A a}^{k} = 1.$ In the first row, there are no differences in selection between male and female diploids (⁠ $w_{i j}^{♀} = w_{i j}^{♂} = w_{i j}$ ⁠), where $w_{a a}$ and $w_{A A}$ are varied along the x and y axes, respectively. As haploid selection becomes stronger, increased recombination can evolve with weaker overdominance in diploids, and also with ploidally antagonistic selection (⁠ $w_{a a} > 1 > w_{A A}$ ⁠). In the second and third rows, we consider sex differences in selection, where $w_{a a}^{♂}$ and $w_{A A}^{♂}$ are varied along the x and y axes (⁠ $w_{A a}^{♂} = 1$ ⁠). In the second row, where selection in females is overdominant (⁠ $w_{A A}^{♀} = 0.75,$ $w_{A a}^{♀} = 1,$ $w_{a a}^{♀} = 0.75$ ⁠), increased recombination can be favored when selection is directional (or underdominant) in males, and haploid selection is moderately strong. In the third row, selection favors the A allele in females (⁠ $w_{A A}^{♀} = 1.05,$ $w_{A a}^{♀} = 1,$ $w_{a a}^{♀} = 0.75$ ⁠) and increased recombination can be favored with overdominance in males or sexually antagonistic selection (⁠ $w_{A A}^{♂} < 1 < w_{a a}^{♂}$ ⁠). For this plot, we assume that the modifier of recombination is unlinked (⁠ $R^{♀} = R^{♂} = 1 / 2$ ⁠).

Open in new tab Download slide

ρ substitutions for different physical arrangements of the loci (assuming no crossover interference)

Table A1

Open in new tab

ρ substitutions for different physical arrangements of the loci (assuming no crossover interference)

Order of loci
SDR-A-M	$ρ = R^{♂} (1 - r_{M m}) + r_{M m} (1 - R^{♂})$
SDR-M-A	$ρ = (r_{M m} - R^{♂}) / (1 - 2 R^{♂})$
A-SDR-M	$ρ = (R^{♂} - r_{M m}) / (1 - 2 r_{M m})$

Table A1

Open in new tab

ρ substitutions for different physical arrangements of the loci (assuming no crossover interference)

Order of loci
SDR-A-M	$ρ = R^{♂} (1 - r_{M m}) + r_{M m} (1 - R^{♂})$
SDR-M-A	$ρ = (r_{M m} - R^{♂}) / (1 - 2 R^{♂})$
A-SDR-M	$ρ = (R^{♂} - r_{M m}) / (1 - 2 r_{M m})$

Marginal fitnesses of YA and Xa haplotypes and mean fitnesses in the resident population

Table A2

Open in new tab

Marginal fitnesses of YA and Xa haplotypes and mean fitnesses in the resident population

Marginal Fitnesses of YA and Xa Haplotypes
${\bar{w}}_{Y A}^{♂} = (w_{A}^{♂} (p_{X}^{♀} w_{A A}^{♂} + 2 α^{♂} (1 - p_{X}^{♀}) w_{A a}^{♂})) / {\bar{w}}_{H}^{♂}$
${\bar{w}}_{X a}^{m a t, ♂} = (2 (1 - α^{♂}) p_{Y}^{♂} w_{A}^{♂} w_{A a}^{♂} + (1 - p_{Y}^{♂}) w_{a}^{♂} w_{a a}^{♂}) / {\bar{w}}_{H}^{♂}$
${\bar{w}}_{X a}^{p a t, ♀} = (p_{X}^{♀} w_{a}^{♂} w_{A a}^{♀} + (1 - p_{X}^{♀}) w_{a}^{♂} w_{a a}^{♀}) / {\bar{w}}_{H}^{♂}$
${\bar{w}}_{X a}^{m a t, ♀} = (p_{X}^{♂} w_{A}^{♂} w_{A a}^{♀} + (1 - p_{X}^{♂}) w_{a}^{♂} w_{a a}^{♀}) / {\bar{w}}_{H}^{♂}$
Mean Fitnesses in Resident Population
${\bar{w}}_{H}^{♂} = (1 - q) (p_{X}^{♂} w_{A}^{♂} + (1 - p_{X}^{♂}) w_{a}^{♂}) + q (p_{Y}^{♂} w_{A}^{♂} + (1 - p_{Y}^{♂}) w_{a}^{♂})$
${\bar{w}}^{♂} = \begin{matrix} {p_{X}^{♀} p_{Y}^{♂} w_{A}^{♂} w_{A A}^{♂} + (1 - p_{X}^{♀}) p_{Y}^{♂} w_{A}^{♂} w_{A a}^{♂} + & p_{X}^{♀} (1 - p_{Y}^{♂}) w_{a}^{♂} w_{A a}^{♂} + (1 - p_{X}^{♀}) (1 - p_{Y}^{♂}) w_{a}^{♂} w_{a a}^{♂}} / {\bar{w}}_{H}^{♂} \end{matrix}$
${\bar{w}}^{♀} \begin{matrix} = {p_{X}^{♀} p_{X}^{♂} w_{A}^{♂} w_{A A}^{♂} + (1 - p_{X}^{♀}) p_{X}^{♂} w_{A}^{♂} w_{A a}^{♂} + & p_{X}^{♀} (1 - p_{X}^{♂}) w_{a}^{♂} w_{A a}^{♂} + (1 - p_{X}^{♀}) (1 - p_{X}^{♂}) w_{a}^{♂} w_{a a}^{♂}} / {\bar{w}}_{H}^{♂} \end{matrix}$

Table A2

Open in new tab

Marginal fitnesses of YA and Xa haplotypes and mean fitnesses in the resident population

Marginal Fitnesses of YA and Xa Haplotypes
${\bar{w}}_{Y A}^{♂} = (w_{A}^{♂} (p_{X}^{♀} w_{A A}^{♂} + 2 α^{♂} (1 - p_{X}^{♀}) w_{A a}^{♂})) / {\bar{w}}_{H}^{♂}$
${\bar{w}}_{X a}^{m a t, ♂} = (2 (1 - α^{♂}) p_{Y}^{♂} w_{A}^{♂} w_{A a}^{♂} + (1 - p_{Y}^{♂}) w_{a}^{♂} w_{a a}^{♂}) / {\bar{w}}_{H}^{♂}$
${\bar{w}}_{X a}^{p a t, ♀} = (p_{X}^{♀} w_{a}^{♂} w_{A a}^{♀} + (1 - p_{X}^{♀}) w_{a}^{♂} w_{a a}^{♀}) / {\bar{w}}_{H}^{♂}$
${\bar{w}}_{X a}^{m a t, ♀} = (p_{X}^{♂} w_{A}^{♂} w_{A a}^{♀} + (1 - p_{X}^{♂}) w_{a}^{♂} w_{a a}^{♀}) / {\bar{w}}_{H}^{♂}$
Mean Fitnesses in Resident Population
${\bar{w}}_{H}^{♂} = (1 - q) (p_{X}^{♂} w_{A}^{♂} + (1 - p_{X}^{♂}) w_{a}^{♂}) + q (p_{Y}^{♂} w_{A}^{♂} + (1 - p_{Y}^{♂}) w_{a}^{♂})$
${\bar{w}}^{♂} = \begin{matrix} {p_{X}^{♀} p_{Y}^{♂} w_{A}^{♂} w_{A A}^{♂} + (1 - p_{X}^{♀}) p_{Y}^{♂} w_{A}^{♂} w_{A a}^{♂} + & p_{X}^{♀} (1 - p_{Y}^{♂}) w_{a}^{♂} w_{A a}^{♂} + (1 - p_{X}^{♀}) (1 - p_{Y}^{♂}) w_{a}^{♂} w_{a a}^{♂}} / {\bar{w}}_{H}^{♂} \end{matrix}$
${\bar{w}}^{♀} \begin{matrix} = {p_{X}^{♀} p_{X}^{♂} w_{A}^{♂} w_{A A}^{♂} + (1 - p_{X}^{♀}) p_{X}^{♂} w_{A}^{♂} w_{A a}^{♂} + & p_{X}^{♀} (1 - p_{X}^{♂}) w_{a}^{♂} w_{A a}^{♂} + (1 - p_{X}^{♀}) (1 - p_{X}^{♂}) w_{a}^{♂} w_{a a}^{♂}} / {\bar{w}}_{H}^{♂} \end{matrix}$

Acknowledgments

We thank Jeannette Whitton, Loren Rieseberg, and two anonymous reviewers for helpful comments on this project. This work was supported by Natural Sciences and Engineering Research Council of Canada Discovery grant (RGPIN-2016-03711).

Footnotes

Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.117.300062/-/DC1.

Communicating editor: S. Wright

Literature Cited

Alavioon

G

,

Hotzy

C

,

Nakhro

K

,

Rudolf

S

,

Scofield

D G

et al. ,

2017

Haploid selection within a single ejaculate increases offspring fitness.

Proc. Natl. Acad. Sci. USA

114

:

8053

–

8058

.

Google Scholar

Crossref

Arunkumar

K P

,

Mita

K

,

Nagaraju

J

,

2009

The silkworm Z chromosome is enriched in testis-specific genes.

Genetics

182

:

493

–

501

.

Arunkumar

R

,

Josephs

E B

,

Williamson

R J

,

Wright

S I

,

2013

Pollen-specific, but not sperm-specific, genes show stronger purifying selection and higher rates of positive selection than sporophytic genes in Capsella grandiflora.

Mol. Biol. Evol.

30

:

2475

–

2486

.

Bachtrog

D

,

2006

A dynamic view of sex chromosome evolution.

Curr. Opin. Genet. Dev.

16

:

578

–

585

.

Bachtrog

D

,

2013

Y-chromosome evolution: emerging insights into processes of Y-chromosome degeneration.

Nat. Rev. Genet.

14

:

113

–

124

.

Bachtrog

D

,

Mank

J E

,

Peichel

C L

,

Kirkpatrick

M

,

Otto

S P

et al. ,

2014

Sex determination: why so many ways of doing it?

PLoS Biol.

12

:

e1001899

.

Bergero

R

,

Forrest

A

,

Kamau

E

,

Charlesworth

D

,

2007

Evolutionary strata on the X chromosomes of the dioecious plant Silene latifolia: evidence from new sex-linked genes.

Genetics

175

:

1945

–

1954

.

Bernasconi

G

,

2004

Evolutionary ecology of the prezygotic stage.

Science

303

:

971

–

975

.

Borg

M

,

Brownfield

L

,

Twell

D

,

2009

Male gametophyte development: a molecular perspective.

J. Exp. Bot.

60

:

1465

–

1478

.

Buckler

E S

,

Phelps-Durr

T L

,

Buckler

C S K

,

Dawe

R K

,

Doebley

J F

et al. ,

1999

Meiotic drive of chromosomal knobs reshaped the maize genome.

Genetics

153

:

415

–

426

.

Bull

J J

,

1983

Evolution of Sex Determining Mechanisms

.

The Benjamin Cummings Publishing Company

,

San Francisco

.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Burt

A

,

Trivers

R

,

2006

Genes in Conflict: The Biology of Selfish Genetic Elements

.

Belknap Press

,

Cambridge, MA

.

Charlesworth

B

,

Charlesworth

D

,

2000

The degeneration of Y chromosomes.

Philos. Trans. R. Soc. Lond. B Biol. Sci.

355

:

1563

–

1572

.

Charlesworth

B

,

Wall

J D

,

1999

Inbreeding, heterozygote advantage and the evolution of neo-X and neo-Y sex chromosomes.

Proc. Biol. Sci.

266

:

51

–

56

.

Google Scholar

Crossref

WorldCat

Charlesworth

D

,

2013

Plant sex chromosome evolution.

J. Exp. Bot.

64

:

405

–

420

.

Charlesworth

D

,

2015

Plant contributions to our understanding of sex chromosome evolution.

New Phytol.

208

:

52

–

65

.

Charlesworth

D

,

Charlesworth

B

,

1980

Sex differences in fitness and selection for centric fusions between sex-chromosomes and autosomes.

Genet. Res.

35

:

205

–

214

.

Clarke

H J

,

Khan

T N

,

Siddique

K H M

,

2004

Pollen selection for chilling tolerance at hybridisation leads to improved chickpea cultivars.

Euphytica

139

:

65

–

74

.

Google Scholar

Crossref

WorldCat

Conn

J S

,

Blum

U

,

1981

Sex ratio of Rumex hastatulus: the effect of environmental factors and certation.

Evolution

35

:

1108

–

1116

.

Crowson

D

,

Barrett

S C H

,

Wright

S I

,

2017

Purifying and positive selection influence patterns of gene loss and gene expression in the evolution of a plant sex chromosome system.

Mol. Biol. Evol.

34

:

1140

–

1154

.

Didion

J P

,

Morgan

A P

,

Clayshulte

A M F

,

Mcmullan

R C

,

Yadgary

L

et al. ,

2015

A multi-megabase copy number gain causes maternal transmission ratio distortion on mouse chromosome 2.

PLoS Genet.

11

:

e1004850

.

Feldman

M W

,

Otto

S P

,

1989

More on recombination and selection in the modifier theory of sex-ratio distortion.

Theor. Popul. Biol.

35

:

207

–

225

.

Field

D L

,

Pickup

M

,

Barrett

S C H

,

2012

The influence of pollination intensity on fertilization success, progeny sex ratio, and fitness in a wind-pollinated, dioecious plant.

Int. J. Plant Sci.

173

:

184

–

191

.

Google Scholar

Crossref

WorldCat

Field

D L

,

Pickup

M

,

Barrett

S C H

,

2013

Comparative analyses of sex-ratio variation in dioecious flowering plants.

Evolution

67

:

661

–

672

.

Fisher

R

,

1931

The evolution of dominance.

Biol. Rev. Camb. Philos. Soc.

6

:

363

.

Google Scholar

Crossref

WorldCat

Fishman

L

,

Saunders

A

,

2008

Centromere-associated female meiotic drive entails male fitness costs in monkeyflowers.

Science

322

:

1559

–

1562

.

Frascaroli

E

,

Songstad

D D

,

2001

Pollen genotype selection for a simply inherited qualitative factor determining resistance to chlorsulfuron in maize.

Theor. Appl. Genet.

102

:

342

–

346

.

Google Scholar

Crossref

WorldCat

Gossmann

T I

,

Schmid

M W

,

Grossniklaus

U

,

Schmid

K J

,

2014

Selection-driven evolution of sex-biased genes is consistent with sexual selection in Arabidopsis thaliana.

Mol. Biol. Evol.

31

:

574

–

583

.

Haig

D

,

Grafen

A

,

1991

Genetic scrambling as a defence against meiotic drive.

J. Theor. Biol.

153

:

531

–

558

.

Hamilton

W D

,

1967

Extraordinary sex ratios.

Science

156

:

477

–

488

.

Hecht

N B

,

1998

Molecular mechanisms of male germ cell differentiation.

Bioessays

20

:

555

–

561

.

Hedhly

A

,

Hormaza

J I

,

Herrero

M

,

2004

Effect of temperature on pollen tube kinetics and dynamics in sweet cherry, Prunus avium (Rosaceae).

Am. J. Bot.

91

:

558

–

564

.

Helleu

Q

,

Gérard

P R

,

Montchamp-Moreau

C

,

2015

Sex chromosome drive.

Cold Spring Harb. Perspect. Biol.

7

:

a017616

.

Google Scholar

Crossref

WorldCat

Hough

J

,

Immler

S

,

Barrett

S

,

Otto

S P

,

2013

Evolutionarily stable sex ratios and mutation load.

Evolution

7

:

1915

–

1925

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Hurst

L D

,

Pomiankowski

A

,

1991

Causes of sex ratio bias may account for unisexual sterility in hybrids: a new explanation of Haldane’s rule and related phenomena.

Genetics

128

:

841

–

858

.

Immler

S

,

Otto

S P

,

2015

The evolution of sex chromosomes in organisms with separate haploid sexes.

Evolution

69

:

694

–

708

.

Immler

S

,

Arnqvist

G

,

Otto

S P

,

2012

Ploidally antagonistic selection maintains stable genetic polymorphism.

Evolution

66

:

55

–

65

.

Immler

S

,

Hotzy

C

,

Alavioon

G

,

Petersson

E

,

Arnqvist

G

,

2014

Sperm variation within a single ejaculate affects offspring development in Atlantic salmon.

Biol. Lett.

10

:

20131040

.

Jaenike

J

,

2001

Sex chromosome meiotic drive.

Annu. Rev. Ecol. Syst.

32

:

25

–

49

.

Google Scholar

Crossref

WorldCat

Joseph

S

,

Kirkpatrick

M

,

2004

Haploid selection in animals.

Trends Ecol. Evol.

19

:

592

–

597

.

Google Scholar

Crossref

WorldCat

Karlin

S

,

McGregor

J

,

1972

a

Application of method of small parameters to multi-niche population genetic models.

Theor. Popul. Biol.

3

:

186

–

209

.

Karlin

S

,

McGregor

J

,

1972

b

Polymorphisms for genetic and ecological systems with weak coupling.

Theor. Popul. Biol.

3

:

210

–

238

.

Kozielska

M

,

Weissing

F J

,

Beukeboom

L W

,

Pen

I

,

2010

Segregation distortion and the evolution of sex-determining mechanisms.

Heredity

104

:

100

–

112

.

Larracuente

A M

,

Presgraves

D C

,

2012

The selfish segregation distorter gene complex of Drosophila melanogaster.

Genetics

192

:

33

–

53

.

Lemaitre

C

,

Braga

M D V

,

Gautier

C

,

Sagot

M F

,

Tannier

E

et al. ,

2009

Footprints of inversions at present and past pseudoautosomal boundaries in human sex chromosomes.

Genome Biol. Evol.

1

:

56

–

66

.

Lenormand

T

,

2003

The evolution of sex dimorphism in recombination.

Genetics

163

:

811

–

822

.

Lenormand

T

,

Dutheil

J

,

2005

Recombination difference between sexes: a role for haploid selection.

PLoS Biol.

3

:

e63

.

Lindholm

A K

,

Dyer

K A

,

Firman

R C

,

Fishman

L

,

Forstmeier

W

et al. ,

2016

The ecology and evolutionary dynamics of meiotic drive.

Trends Ecol. Evol.

31

:

315

–

326

.

Lloyd

D G

,

1974

Female-predominant sex ratios in angiosperms.

Heredity

32

:

35

–

44

.

Google Scholar

Crossref

WorldCat

Mahajan

S

,

Bachtrog

D

,

2017

Convergent evolution of Y chromosome gene content in flies.

Nat. Commun.

8

:

785

.

Marais

G A B

,

Nicolas

M

,

Bergero

R

,

Chambrier

P

,

Kejnovsky

E

et al. ,

2008

Evidence for degeneration of the Y chromosome in the dioecious plant Silene latifolia.

Curr. Biol.

18

:

545

–

549

.

Marshall

D L

,

Evans

A S

,

2016

Can selection on a male mating character result in evolutionary change? A selection experiment on California wild radish, Raphanus sativus.

Am. J. Bot.

103

:

553

–

567

.

McKown

A D

,

Klápště

J

,

Guy

R D

,

Soolanayakanahally

R Y

,

La Mantia

J

et al. ,

2017

Sexual homomorphism in dioecious trees: extensive tests fail to detect sexual dimorphism in Populus.

Sci. Rep.

7

:

1831

.

Ming

R

,

Bendahmane

A

,

Renner

S S

,

2011

Sex chromosomes in land plants.

Annu. Rev. Plant Biol.

62

:

485

–

514

.

Moore

J C

,

Pannell

J R

,

2011

Sexual selection in plants.

Curr. Biol.

21

:

R176

–

R182

.

Mulcahy

D L

,

Sari-Gorla

M

,

Mulcahy

G B

,

1996

Pollen selection - past, present and future.

Sex. Plant Reprod.

9

:

353

–

356

.

Google Scholar

Crossref

WorldCat

Muralla

R

,

Lloyd

J

,

Meinke

D

,

2011

Molecular foundations of reproductive lethality in Arabidopsis thaliana.

PLoS One

6

:

e28398

.

Nam

K

,

Ellegren

H

,

2008

The chicken (Gallus gallus) Z chromosome contains at least three nonlinear evolutionary strata.

Genetics

180

:

1131

–

1136

.

Namekawa

S H

,

Park

P J

,

Zhang

L-F

,

Shima

J E

,

McCarrey

J R

et al. ,

2006

Postmeiotic sex chromatin in the male germline of mice.

Curr. Biol.

16

:

660

–

667

.

Otto

S P

,

2014

Selective maintenance of recombination between the sex chromosomes.

J. Evol. Biol.

27

:

1431

–

1442

.

Otto

S P

,

Day

T

,

2007

A Biologist’s Guide to Mathematical Modeling in Ecology and Evolution

.

Princeton University Pres

,

Princeton, NJ

.

Otto

S P

,

Pannell

J R

,

Peichel

C L

,

Ashman

T-L

,

2011

About PAR: the distinct evolutionary dynamics of the pseudoautosomal region.

Trends Genet.

27

:

358

–

367

.

Otto

S P

,

Scott

M F

,

Immler

S

,

2015

Evolution of haploid selection in predominantly diploid organisms.

Proc. Natl. Acad. Sci. USA

112

:

15952

–

15957

.

Google Scholar

Crossref

WorldCat

Pennell

M W

,

Kirkpatrick

M

,

Otto

S P

,

Vamosi

J C

,

Peichel

C L

et al. ,

2015

Y fuse? Sex chromosome fusions in fishes and reptiles.

PLoS Genet.

11

:

e1005237

.

Ravikumar

R L

,

Patil

B S

,

Salimath

P M

,

2003

Drought tolerance in sorghum by pollen selection using osmotic stress.

Euphytica

133

:

371

–

376

.

Google Scholar

Crossref

WorldCat

Ravikumar

R L

,

Chaitra

G N

,

Choukimath

A M

,

Soregaon

C D

,

2012

Gametophytic selection for wilt resistance and its impact on the segregation of wilt resistance alleles in chickpea (Cicer arietinum L.).

Euphytica

189

:

173

–

181

.

Google Scholar

Crossref

WorldCat

Rice

W R

,

1987

The accumulation of sexually antagonistic genes as a selective agent promoting the evolution of reduced recombination between primitive sex chromosomes.

Evolution

41

:

911

.

Rice

W R

,

1996

Evolution of the Y sex chromosome in animals.

Bioscience

46

:

331

–

343

.

Google Scholar

Crossref

WorldCat

Rydzewski

W T

,

Carioscia

S A

,

Liévano

G

,

Lynch

V D

,

Patten

M M

,

2016

Sexual antagonism and meiotic drive cause stable linkage disequilibrium and favour reduced recombination on the X chromosome.

J. Evol. Biol.

29

:

1247

–

1256

.

Searcy

K B

,

Mulcahy

D L

,

1985

Pollen selection and the gametophytic expression of metal tolerance in Silene dioica (Caryophyllaceae) and Mimulus guttatus (Scrophulariaceae).

Am. J. Bot.

72

:

1700

–

1706

.

Google Scholar

Crossref

WorldCat

Skogsmyr

I

,

Lankinen

A

,

2002

Sexual selection: an evolutionary force in plants?

Biol. Rev. Camb. Philos. Soc.

77

:

537

–

562

.

Stehlik

I

,

Barrett

S

,

2005

Mechanisms governing sex-ratio variation in dioecious Rumex nivalis.

Evolution

59

:

814

–

825

.

Google Scholar

PubMed

OpenURL Placeholder Text

WorldCat

Stehlik

I

,

Barrett

S C H

,

2006

Pollination intensity influences sex ratios in dioecious Rumex nivalis, a wind-pollinated plant.

Evolution

60

:

1207

–

1214

.

Travers

S E

,

Mazer

S J

,

2001

Trade-offs between male and female reproduction associated with allozyme variation in phosphoglucoisomerase in an annual plant (Clarkia unguiculata: Onagraceae).

Evolution

55

:

2421

–

2428

.

Úbeda

F

,

Haig

D

,

2005

On the evolutionary stability of Mendelian segregation.

Genetics

170

:

1345

–

1357

.

Úbeda

F

,

Patten

M M

,

Wild

G

,

2015

On the origin of sex chromosomes from meiotic drive.

Proc. Biol. Sci.

282

:

20141932

.

Google Scholar

PubMed

OpenURL Placeholder Text

WorldCat

Vibranovski

M D

,

Chalopin

D S

,

Lopes

H F

,

Long

M

,

Karr

T L

,

2010

Direct evidence for postmeiotic transcription during Drosophila melanogaster spermatogenesis.

Genetics

186

:

431

–

433

.

Vicoso

B

,

Bachtrog

D

,

2015

Numerous transitions of sex chromosomes in Diptera.

PLoS Biol.

13

:

e1002078

.

Wang

J

,

Na

J-K

,

Yu

Q

,

Gschwend

A R

,

Han

J

et al. ,

2012

Sequencing papaya X and Yh chromosomes reveals molecular basis of incipient sex chromosome evolution.

Proc. Natl. Acad. Sci. USA

109

:

13710

–

13715

.

Google Scholar

Crossref

WorldCat

Wolfram Research, Inc., 2017 Mathematica, version 11. Champaign, IL. Available at: http://www.wolfram.com/mathematica/.

Wright

A E

,

Darolti

I

,

Bloch

N I

,

Oostra

V

,

Sandkam

B

et al. ,

2017

Convergent recombination suppression suggests role of sexual selection in guppy sex chromosome formation.

Nat. Commun.

8

:

14251

.

Yoshida

K

,

Kitano

J

,

2012

The contribution of female meiotic drive to the evolution of neo-sex chromosomes.

Evolution

66

:

3198

–

3208

.

Zheng

Y

,

Deng

X

,

Martin-DeLeon

P A

,

2001

Lack of sharing of Spam1 (Ph-20) among mouse spermatids and transmission ratio distortion.

Biol. Reprod.

64

:

1730

–

1738

.

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Month:	Total Views:
January 2021	4
February 2021	6
March 2021	6
April 2021	12
May 2021	7
June 2021	8
July 2021	9
August 2021	6
September 2021	6
October 2021	6
November 2021	23
December 2021	10
January 2022	15
February 2022	10
March 2022	13
April 2022	10
May 2022	12
June 2022	7
July 2022	12
August 2022	13
September 2022	15
October 2022	14
November 2022	7
December 2022	14
January 2023	9
February 2023	10
March 2023	14
April 2023	14
May 2023	1
June 2023	7
July 2023	7
August 2023	24
September 2023	9
October 2023	9
November 2023	10
December 2023	15
January 2024	16
February 2024	11
March 2024	8
April 2024	15
May 2024	21
June 2024	7
July 2024	9
August 2024	8
September 2024	9
October 2024	9
November 2024	13
December 2024	11
January 2025	11
February 2025	5
March 2025	13
April 2025	15
May 2025	5

Article Contents

Haploid Selection Favors Suppressed Recombination Between Sex Chromosomes Despite Causing Biased Sex Ratios

Abstract

Model Background

Model

Sex- and stage-specific selection terms

Summary of cases considered, simplifying assumptions, and results (⁠ $λ > 1$ indicates invasion by m)

Results

Suppressors of recombination

Equilibrium allele frequencies:

Invasion conditions:

ZW sex determination:

Recombination evolution between SDR and closely linked selected loci

Discussion

Appendix A

A.1. Recursion Equations

A.2. Invasion of Recombination Suppressors

A. General

B. Incomplete recombination suppression

C. Ploidally antagonistic selection

A.3. Invasion of Modifiers that Increase Recombination from an Initially Low Level

ρ substitutions for different physical arrangements of the loci (assuming no crossover interference)

Marginal fitnesses of YA and Xa haplotypes and mean fitnesses in the resident population

Acknowledgments

Footnotes

Literature Cited

Supplementary data

Citations

Views

Altmetric

Email alerts

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Haploid Selection Favors Suppressed Recombination Between Sex Chromosomes Despite Causing Biased Sex Ratios Free

Abstract

Model Background

Model

Sex- and stage-specific selection terms

Summary of cases considered, simplifying assumptions, and results (⁠λ>1 indicates invasion by m)

Results

Suppressors of recombination

Equilibrium allele frequencies:

Invasion conditions:

ZW sex determination:

Recombination evolution between SDR and closely linked selected loci

Discussion

Appendix A

A.1. Recursion Equations

A.2. Invasion of Recombination Suppressors

A. General

B. Incomplete recombination suppression

C. Ploidally antagonistic selection

A.3. Invasion of Modifiers that Increase Recombination from an Initially Low Level

ρ substitutions for different physical arrangements of the loci (assuming no crossover interference)

Marginal fitnesses of YA and Xa haplotypes and mean fitnesses in the resident population

Acknowledgments

Footnotes

Literature Cited

Supplementary data

Citations

Views

Altmetric

Email alerts

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Haploid Selection Favors Suppressed Recombination Between Sex Chromosomes Despite Causing Biased Sex Ratios

Summary of cases considered, simplifying assumptions, and results (⁠ $λ > 1$ indicates invasion by m)