Modelling of short QT syndrome in a heterogeneous model of the human ventricular wall Free

Disease	Disease subtype/classification	Gene	Protein	Ion channel type	Molecular defect	Reference
I_Ks disease	LQT1	KCNQ1	KvLQT1	I_Ks channel (α-subunit)	loss of function	[4]
	LQT5	KCNE1	MinK	I_Ks channel (β-subunit)	loss of function	[5]
	FAF	KCNQ1	KvLQT1	I_Ks channel (α-subunit)	gain of function	[6–8]
	SQT2	KCNQ1	KvLQT1	I_Ks channel (α-subunit)	gain of function	[9]
I_Kr disease	LQT2	KCNH2	HERG	I_Kr channel (α-subunit)	loss of function	[10]
	LQT6	KCNE2	MiRP1	I_Kr channel (β-subunit)	loss of function	[11]
	SQT1	KCNH2	HERG	I_Kr channel (α-subunit)	gain of function	[12]
I_Na disease	LQT3	SCN5A	Nav1.5	I_Na channel	gain of function	[13]
	Brugada syndrome	SCN5A	Nav1.5	I_Na channel	loss of function	[14,15]
	FCD	SCN5A	–	I_Na channel	loss of function	[16]
I_K1 disease	Andersen syndrome	KCNJ2	Kir2.1	I_K1 channel	–	[17]
	SQT3	KCNJ2	Kir2.1	I_K1 channel	gain of function	[18]
Ankyrin disease	LQT4	ANK2	Ankyrin B	Ankyrin	–	[19]

Disease	Disease subtype/classification	Gene	Protein	Ion channel type	Molecular defect	Reference
I_Ks disease	LQT1	KCNQ1	KvLQT1	I_Ks channel (α-subunit)	loss of function	[4]
	LQT5	KCNE1	MinK	I_Ks channel (β-subunit)	loss of function	[5]
	FAF	KCNQ1	KvLQT1	I_Ks channel (α-subunit)	gain of function	[6–8]
	SQT2	KCNQ1	KvLQT1	I_Ks channel (α-subunit)	gain of function	[9]
I_Kr disease	LQT2	KCNH2	HERG	I_Kr channel (α-subunit)	loss of function	[10]
	LQT6	KCNE2	MiRP1	I_Kr channel (β-subunit)	loss of function	[11]
	SQT1	KCNH2	HERG	I_Kr channel (α-subunit)	gain of function	[12]
I_Na disease	LQT3	SCN5A	Nav1.5	I_Na channel	gain of function	[13]
	Brugada syndrome	SCN5A	Nav1.5	I_Na channel	loss of function	[14,15]
	FCD	SCN5A	–	I_Na channel	loss of function	[16]
I_K1 disease	Andersen syndrome	KCNJ2	Kir2.1	I_K1 channel	–	[17]
	SQT3	KCNJ2	Kir2.1	I_K1 channel	gain of function	[18]
Ankyrin disease	LQT4	ANK2	Ankyrin B	Ankyrin	–	[19]

Summary of genetic findings in inherited arrhythmogenic diseases. LQT = Long QT syndrome, FAF = familial atrial fibrillation, SQT = short QT syndrome, FCD = familial conduction disease.

Table 1

Disease	Disease subtype/classification	Gene	Protein	Ion channel type	Molecular defect	Reference
I_Ks disease	LQT1	KCNQ1	KvLQT1	I_Ks channel (α-subunit)	loss of function	[4]
	LQT5	KCNE1	MinK	I_Ks channel (β-subunit)	loss of function	[5]
	FAF	KCNQ1	KvLQT1	I_Ks channel (α-subunit)	gain of function	[6–8]
	SQT2	KCNQ1	KvLQT1	I_Ks channel (α-subunit)	gain of function	[9]
I_Kr disease	LQT2	KCNH2	HERG	I_Kr channel (α-subunit)	loss of function	[10]
	LQT6	KCNE2	MiRP1	I_Kr channel (β-subunit)	loss of function	[11]
	SQT1	KCNH2	HERG	I_Kr channel (α-subunit)	gain of function	[12]
I_Na disease	LQT3	SCN5A	Nav1.5	I_Na channel	gain of function	[13]
	Brugada syndrome	SCN5A	Nav1.5	I_Na channel	loss of function	[14,15]
	FCD	SCN5A	–	I_Na channel	loss of function	[16]
I_K1 disease	Andersen syndrome	KCNJ2	Kir2.1	I_K1 channel	–	[17]
	SQT3	KCNJ2	Kir2.1	I_K1 channel	gain of function	[18]
Ankyrin disease	LQT4	ANK2	Ankyrin B	Ankyrin	–	[19]

Disease	Disease subtype/classification	Gene	Protein	Ion channel type	Molecular defect	Reference
I_Ks disease	LQT1	KCNQ1	KvLQT1	I_Ks channel (α-subunit)	loss of function	[4]
	LQT5	KCNE1	MinK	I_Ks channel (β-subunit)	loss of function	[5]
	FAF	KCNQ1	KvLQT1	I_Ks channel (α-subunit)	gain of function	[6–8]
	SQT2	KCNQ1	KvLQT1	I_Ks channel (α-subunit)	gain of function	[9]
I_Kr disease	LQT2	KCNH2	HERG	I_Kr channel (α-subunit)	loss of function	[10]
	LQT6	KCNE2	MiRP1	I_Kr channel (β-subunit)	loss of function	[11]
	SQT1	KCNH2	HERG	I_Kr channel (α-subunit)	gain of function	[12]
I_Na disease	LQT3	SCN5A	Nav1.5	I_Na channel	gain of function	[13]
	Brugada syndrome	SCN5A	Nav1.5	I_Na channel	loss of function	[14,15]
	FCD	SCN5A	–	I_Na channel	loss of function	[16]
I_K1 disease	Andersen syndrome	KCNJ2	Kir2.1	I_K1 channel	–	[17]
	SQT3	KCNJ2	Kir2.1	I_K1 channel	gain of function	[18]
Ankyrin disease	LQT4	ANK2	Ankyrin B	Ankyrin	–	[19]

Summary of genetic findings in inherited arrhythmogenic diseases. LQT = Long QT syndrome, FAF = familial atrial fibrillation, SQT = short QT syndrome, FCD = familial conduction disease.

The first report of the short QT syndrome as a hereditary, clinically relevant entity was provided by Gussak et al.[23]. The familial origin of the syndrome was recently affirmed in five unrelated families [12,,24]. The short QT syndrome is characterized by an abbreviation of the QT interval (QTI) in the ECG without significant dynamic changes in the QTI during heart rate variations. Affected subjects suffer from syncope, high familial incidence of palpitations, high risk of sudden death, paroxysmal atrial fibrillation, and easily inducible ventricular fibrillation in electrophysiological studies in the presence of structurally normal hearts [24] and display short refractory periods and autosomal mode of inheritance. The clinical importance of this recently discovered mutation is high because it occurs often in young and otherwise healthy people. These individuals are at high risk of sudden death.

Gaita et al.[24] supposed that either a factor reducing sodium or calcium inward currents or a factor increasing the potassium outward currents is responsible for short QT intervals. Furthermore, they postulated that the molecular substrate producing the shortened action potential durations (APD) and, therefore, the shortened QT interval in ECG are expressed in atrial as well as in ventricular cardiomyocytes.

Recently, Brugada and colleagues [12] presented a study on the genetic and biophysical basis of the short QT syndrome. They identified a mutation in the rapidly activating delayed rectifier cardiac potassium channel promoting the I_Kr current. In human cardiomyocytes, the human ether-a-go-go-related gene (HERG) forms the α-subunit of the I_Kr channel; the regulatory β-subunit is the MinK-related peptide 1 (MiRP1). MiRP1 ensures the following effects on the HERG channel: increased sensitivity of the channel to I_Kr blockers (E-4031 and clarithromycin), decreased sensitivity to elevation of the extracellular potassium concentration [K⁺]_o, positive shift of the voltage-dependence of activation, and accelerated deactivation [11]. The topology of the HERG channel is similar to other voltage-gated ion channels ^[25–^27]. Each HERG subunit consists of six transmembrane α-helices, with the fourth carrying seven positive charges, and a pore-loop region between the fifth and sixth transmembrane helices (S5-P loop region) that acts as the selective K⁺ filter [28,,29]. Coassembly of HERG encoded by KCNH2 with MiRP1 encoded by KCNE2 reproduced the biophysical and pharmacological properties of the I_Kr channel [11,,30,,31].

In this work, a computer model of human cardiomyocytes is presented that incorporates the modifications in the rapidly activating delayed rectifier potassium current I_Kr due to the short QT mutation reported by Brugada et al.[12]. This modification was obtained by curve fitting the results of computational simulations with measurement data by means of numerical optimization methods [32]. The new model, based on the Priebe–Beuckelmann description of a human ventricular myocyte, was used to reproduce the activation and repolarization in a heterogeneous and anisotropic representation of a human left ventricle. The modified characteristic of the I_Kr channel led to a heterogeneous abbreviation of the APD in the distinctive cardiac cells within the ventricular wall. The consequence of this homogenized repolarization was visible in the transmural ECG: the T wave showed a reduced amplitude compared with the normal physiological case.

Materials and methods

The simulation environment consisted of three components: cellular electrophysiology, excitation propagation and anatomical structure. A detailed biophysical model of the cellular electrophysiology described the behaviour of a single cardiomyocyte with a set of nonlinear-coupled partial differential equations. Modelling of a multi-cellular environment required an anatomical representation of the considered tissue and a method defining the electrical coupling of excitable cells. Both a thin, three-dimensional parallelepiped bidomain model and a three-dimensional whole heart monodomain model were used to study propagation.

Measurement data

Brugada et al. identified and genetically screened three unrelated families with short QT associations [12]. The measurement data revealing the amino acid substitution lysine for asparagines at codon 588 (N588K) in the KCNH2 protein HERG were utilized to adapt an existing mathematical model of a ventricular cardiac cell. It was obtained by analysis of the data from the publication of Brugada et al. with permission from Dr. R. Brugada.

Modelling cellular electrophysiology

A modified Priebe–Beuckelmann (PB) model [33] of a human ventricular cardiomyocyte forms the base of this work. The modification includes an adaptation of the model to measurements on human cardiac myocytes and heterogeneous characteristics of ventricular tissue [34]. The model consists of a set of coupled nonlinear ordinary differential equations describing state variables by Hodgkin–Huxley like formalisms [35]. Furthermore, these equations define the intra- and extra-cellular ion concentrations, ionic currents flowing through membrane proteins, and the transmembrane voltage. The ionic currents are time dependent and interact with the ion concentrations in intra- and extracellular space. The model includes the handling of intracellular calcium by the sarcoplasmic reticulum and takes several calcium buffers such as troponin, calsequestrin, and calmodulin into account. The Euler forward method [36] with a time increment of 20 μs was used to solve the set of differential equations. The temporal variation of the transmembrane voltage V_m was calculated by

\frac{d V_{m}}{d t} = \frac{1}{C_{m}} (l + m e m l) s t i m

with the membrane capacitance C_m, the additionally applied stimulus current I_stim, and the sum of all ion currents I_mem flowing through the sarcolemma.

Special focus was given on the rapidly activating delayed rectifier potassium current I_Kr, since it is the parameter to be modified for reconstructing short QT syndrome in human ventricular myocytes. The definition of I_Kr is given by

l = k r δ_{k r, \max} X r \times r i k (V_{m} - E_{l})

with the constant maximum conductance g_Kr,max of the I_Kr channel, the activation gate Xr, the inward rectification factor rik, and the equilibrium potential E_K for potassium ions. The time-dependent alteration of the Xr gate is calculated by

\frac{d X r}{d t} = \frac{X r_{\infty} - X r}{τ_{X r}}

where the steady-state value

X r_{\infty}

and the time constant τ_Xr are described by the voltage-dependent rate constants α_Xr and β_Xr

\begin{array}{l} X r_{\infty} = \frac{α_{X r}}{α_{X r} + β_{x r}} τ_{x r} = \frac{1}{α_{X r} + β_{x r}} \\ α_{X r} = a_{X r, 1} \exp (a_{X r, 2} (V_{m} + a_{x r, v 0.5})) \\ \times \frac{1}{\begin{array}{l} 1 + \exp (a_{x r, k} (V m + a_{x r} v 0.5)) \end{array}} \\ β_{X r} = b_{X r, 1} \exp (b_{X r, 2} (V_{m} + b_{x r, v 0.5})) \\ \times \frac{1}{\begin{array}{l} 1 + \exp (b_{x r, k} (V m + b_{x r} v 0.5)) \end{array}} \end{array}

The definition of these rate constants consists of an amplifying and a gate-like term described by the constant values a_Xr,1, a_Xr,2, a_Xr,k, a_Xr,V0.5 and b_Xr,1, b_Xr,2, b_Xr,k, b_Xr,V0.5, respectively. The half-activation voltage of the gating term is determined by a_Xr,V0.5 and b_Xr,V0.5, respectively, and the corresponding slope factor by 1/a_Xr,k and 1/b_Xr,k. The specification of rik follows the Boltzmann like equation for inactivation and is given by

r i k = \frac{1}{1 + \exp (} V_{m} - r i k_{v 0.5} r i k_{k})

rik_V0.5 denotes the 50% activation voltage, rik_k the slope factor of rik formulation. The parameter sets of the I_Kr definition for the original Priebe–Beuckelmann model and our heterogeneous adaptation are given in Table 2.

Table 2

Parameter	Original Priebe–Beuckelmann model [33]	Modified wild-type PB model [34]	N588K/KCNE2 mutant model
g_Kr,max	0.015	0.0159	0.02165
a_Xr,1	0.005	0.005	0.015
a_Xr,2	5.266E − 4	4.4761E − 4	4.4761E − 4
a_Xr,k	−0.1262	−0.10727	−0.10727
a_Xr,V0.5	4.067	2.23685	−20.23685
b_Xr,1	0.016	0.016	0.16
b_Xr,2	0.0016	0.00232	0.00232
b_Xr,k	0.0783	0.066555	0.066555
b_Xr,V0.5	65.66	55.811	85.811
rik_V0.5	−26	−29.9	–
rik_k	23	41.818	–
bs_V0.5	–	–	10
bs_k	–	–	1
bs_m	–	–	0.0375
bs_b	–	–	−0.25

Parameter	Original Priebe–Beuckelmann model [33]	Modified wild-type PB model [34]	N588K/KCNE2 mutant model
g_Kr,max	0.015	0.0159	0.02165
a_Xr,1	0.005	0.005	0.015
a_Xr,2	5.266E − 4	4.4761E − 4	4.4761E − 4
a_Xr,k	−0.1262	−0.10727	−0.10727
a_Xr,V0.5	4.067	2.23685	−20.23685
b_Xr,1	0.016	0.016	0.16
b_Xr,2	0.0016	0.00232	0.00232
b_Xr,k	0.0783	0.066555	0.066555
b_Xr,V0.5	65.66	55.811	85.811
rik_V0.5	−26	−29.9	–
rik_k	23	41.818	–
bs_V0.5	–	–	10
bs_k	–	–	1
bs_m	–	–	0.0375
bs_b	–	–	−0.25

Definitions for the modelled I_Kr current. Columns 2 and 3 contain the values of the original as well as our modified wild-type modelling. In the fourth column the values for the presented N588K/KCNE2 mutant model are depicted. To emulate the properties of the short QT mutation the channel description of the wild-type modelling was combined with the N588K/KCNE2 formulation. In this formulation wild-type as well as N588K/KCNE2 channels represent 50% of the I_Kr channel.

Table 2

Parameter	Original Priebe–Beuckelmann model [33]	Modified wild-type PB model [34]	N588K/KCNE2 mutant model
g_Kr,max	0.015	0.0159	0.02165
a_Xr,1	0.005	0.005	0.015
a_Xr,2	5.266E − 4	4.4761E − 4	4.4761E − 4
a_Xr,k	−0.1262	−0.10727	−0.10727
a_Xr,V0.5	4.067	2.23685	−20.23685
b_Xr,1	0.016	0.016	0.16
b_Xr,2	0.0016	0.00232	0.00232
b_Xr,k	0.0783	0.066555	0.066555
b_Xr,V0.5	65.66	55.811	85.811
rik_V0.5	−26	−29.9	–
rik_k	23	41.818	–
bs_V0.5	–	–	10
bs_k	–	–	1
bs_m	–	–	0.0375
bs_b	–	–	−0.25

Parameter	Original Priebe–Beuckelmann model [33]	Modified wild-type PB model [34]	N588K/KCNE2 mutant model
g_Kr,max	0.015	0.0159	0.02165
a_Xr,1	0.005	0.005	0.015
a_Xr,2	5.266E − 4	4.4761E − 4	4.4761E − 4
a_Xr,k	−0.1262	−0.10727	−0.10727
a_Xr,V0.5	4.067	2.23685	−20.23685
b_Xr,1	0.016	0.016	0.16
b_Xr,2	0.0016	0.00232	0.00232
b_Xr,k	0.0783	0.066555	0.066555
b_Xr,V0.5	65.66	55.811	85.811
rik_V0.5	−26	−29.9	–
rik_k	23	41.818	–
bs_V0.5	–	–	10
bs_k	–	–	1
bs_m	–	–	0.0375
bs_b	–	–	−0.25

Definitions for the modelled I_Kr current. Columns 2 and 3 contain the values of the original as well as our modified wild-type modelling. In the fourth column the values for the presented N588K/KCNE2 mutant model are depicted. To emulate the properties of the short QT mutation the channel description of the wild-type modelling was combined with the N588K/KCNE2 formulation. In this formulation wild-type as well as N588K/KCNE2 channels represent 50% of the I_Kr channel.

Model adaptation

To adapt the behaviour of the modelled cardiomyocytes to the measured mutant cells, the single mathematical model of a human cardiac M cell was stimulated. The same environmental conditions as in the patch clamp measurement [12] to elicit the mutant N588K/KNCE2 current were assumed. Intracellular potassium concentration [K⁺]_i was set to 140 mmol/L, extracellular potassium concentration [K⁺]_o to 5 mmol/L, extracellular sodium concentration [Na⁺]_o to 132.8 mmol/L, and extracellular calcium concentration [Ca²⁺]_o to 1.8 mmol/L. Furthermore, the conditions given by the voltage protocol were transferred to the simulation. The temperature for the simulation of the I_Kr behaviour under voltage clamp conditions was set to 296.15 K. A gradient optimization method minimizing the root-mean-square error between computational and experimental data [32] was used to specify the parameters adapting the simulated electrophysiological behaviour to the measurements on mutant cells.

For the subsequent simulations the temperature was raised to 310.15 K to perform simulations at body temperature. A Q10 of three for the kinetics of the channel was assumed [37]. The 14 K increase resulted in an approximately five times reduced time constant τ_Xr. The acceleration of the opening of the activation gate Xr led to an increased repolarizing current I_Kr. To consider a heterozygous expression, the mutant I_Kr channel formulation was combined with the wild-type representation [34]. In this configuration representing the short QT mutation both the N588K/KCNE2 and the wild-type HERG/KCNE2 channel reproduced 50% of the resulting I_Kr current.

Heterogeneity

Cells isolated from different regions within the ventricular wall display a different characteristic response to pharmacological agents, expression of pathology, and their electrophysiological properties [38]. In the heterogeneous ventricular myocardium, three principal cell types with varying ion channel density and kinetics can be distinguished: subendocardial, subepicardial and M cells. The main distinctive feature is the variable action potential shape from endocardium to epicardium. Canine M cells are located in the lateral deep subepicardium to midmyocardium, the anterior deep subendocardium to midmyocardium, and throughout the wall near the outflow tracts. They are characterized by a marked prolongation and steeper frequency-dependence of the APD. Epicardial and M cells display action potentials with a prominent notch. This spike-and-dome morphology vanishes towards the endocardium [38].

Formalisms were integrated in the model to represent this transmural electrophysiological heterogeneity within the ventricle in a preliminary study [34]. Smooth gradients of maximum ion channel conductivity and, therefore, gradients in current densities across the virtual wall affect the distinctive behaviour of the transmurally varying cell types. Changes in four different ionic currents were considered. The involved potassium currents were the transient outward current I_to, the slow delayed rectifier current I_Ks, and the inward rectifier current I_K1[39,,40]. Also, the findings of a study [41] reporting transmural changes of the Na⁺/Ca²⁺ exchange current in canine myocytes with a reduced current density in endocardial cells were included in the cellular model.

In the model of the left ventricular wall the M cells were located relatively near to the endocardium. A realistic upright positive T wave in transmurally computed ECG was obtained with this configuration and the heterogeneous distribution as well as the smooth transition of ion channel density across the ventricular wall [42].

Excitation propagation

A bidomain diffusion model depicting current flow through gap junctions and intracellular as well as extracellular space ensured anisotropic electrical coupling of the cells [43,,44]. An iterative Gauss–Seidel method with a time step of 20 μs was used to solve the Poisson type equations. Assuming that the intra- and extracellular domain have equal anisotropy ratios, the bidomain model can be reduced to the so-called monodomain model and the entire tissue volume is represented as one domain with anisotropic conductivities.

Anatomical model

A detailed three-dimensional anatomical data set of a female left ventricle applying data from the Visible Human Project was created [45]. The photographic images of the transversal cryosections with a resolution of 0.33 mm and a layer thickness of 0.33 mm were preprocessed to obtain a three-dimensional data set. This data set consisting of cubic volume elements (voxel) with a side length of 0.33 mm was segmented and classified with techniques of digital image processing such as thresholding, region growing and interactive deformable contours [46]. The resulting left ventricular model is composed of approximately 16 million elements. More than 6.5 million of these elements describe excitable tissue, the remainder blood and surrounding tissue. A realistic fibre orientation was integrated to allow the assignment of anisotropic electrical properties to the tissue. This orientation was constructed with a rule-based algorithm derived from anatomical studies [47]. Hence, the fibres twist from subendocardial (55°) via midmyocardial (0°) to subepicardial myocytes (−75°) in a three-dimensional way. Fig. 1 shows the anatomical ventricular dataset with a highlighted slice depicting fibre vectors. The cardiac conduction system was constructed manually, since these structures were not visible in the cryosection images. Important for application of the ventricular model was the identification of electrical transition points of the cardiac conduction system to the subendocardial myocardium, i.e. the connection between myocytes and Purkinje fibres. These points were placed semi-automatically. Stimulation was initiated at the subendocardium in voxels modelling myocytes with connections to Purkinje fibres by applying point wise intracellular currents in a specific temporal sequence. The application of currents started at apical points and wandered in a basal direction.

Figure 1

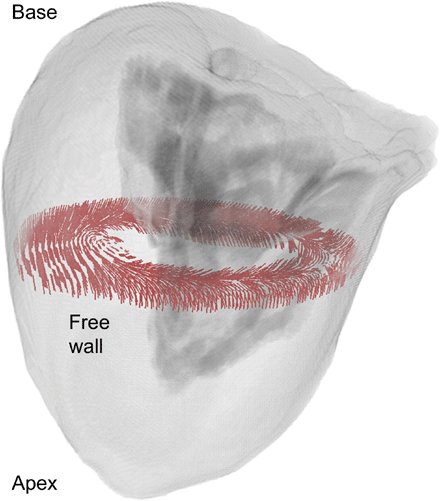
Three-dimensional anatomical model of the human left ventricle obtained from the Visible Female data set in transparent view. An exemplary cross-sectional slice perpendicular to the longitudinal axis depicts the realistic rotating fibre orientation within the wall.

A long and thin three-dimensional parallelepiped domain was used to calculate extracellular potentials in the tissue and the surrounding bath medium. It describes an approximately one-dimensional line from endocardium to epicardium through the ventricular wall and considers transmural heterogeneity of the electrophysiological properties within the tissue in the absence of electrical anisotropy. This thin representation to simulate excitation conduction across the heart wall consists of 96 × 9 × 9 cubic voxels with an edge length of 0.2 mm and is surrounded by a bath with a thickness of 5 voxels in each direction.

Computational environment

The three-dimensional ventricular simulation was performed on 10 Apple XServe G5 dual 2 GHz processor cluster nodes using multiprocessing techniques [48]. This simulation required 2.6 GB of main memory and needed for a 600 ms interval with a temporal increment of 20 μs approximately 7 h of calculation time.

Results

A new description for the rapidly activating delayed rectifier potassium current I_Kr was developed to model the behaviour of a cardiomyocyte affected by the short QT mutation. Because of the homogeneous distribution of the I_Kr current in the ventricular wall [40] the modifications were performed on a wild-type M cell [34] and afterwards adapted to the other ventricular cell types. The characteristics of the voltage-dependent inward-rectifying component rik and the rate constants for the activation gate Xr of I_Kr were altered. The measurement data revealed that the mutant I_Kr channel failed to rectify significantly and the steady-state current continues to increase linearly [12]. Thus, we decided to invert the characteristic of rik and introduced an additional amplifying background substitution component bs, which replaces rik to model this opposite behaviour of the short QT mutation compared with healthy myocytes. The I_Kr equation for the short QT mutant case changed to

l_{k r}, S Q T = δ_{k r, \max} x r \times b s (V_{m} - E_{k})

The condition that bs should only increase but not decrease I_Kr led to the following definition of bs:

b s = 1 + b s_{g} b s_{l}

where bs consists of a term bs_l linearly depending on the transmembrane voltage V_m and a Boltzmann like definition bs_g describing the activation of this term. The mathematical definition of the gate bs_g is given by

b s_{g} = \frac{1}{1 + \exp (} b s_{v 0.5} - V_{m} b s_{k})

with the half-activation voltage bs_V0.5 and the slope factor bs_k. The linear voltage-dependence of the bs_l component is defined by

b s_{l} = b s_{m} V_{m} + b s_{b}

and delineates a straight line with the slope bs_m and a shift along the y-axis by bs_b. Thus, the definition of the additional background component bs is

\begin{array}{l} b s = 1 + \frac{1}{1 + \exp (} b s_{v 0.5} - V_{m} b s_{k}) (b s_{m} V_{m} + b s_{b}) \\ l_{k r}, S Q T = δ_{k r, \max} x r \times b s (V_{m} - E_{k}) \end{array}

Furthermore, the gating parameters α_Xr and β_Xr of the activation gate Xr for the I_Kr current were modulated. The half-activation voltage a_Xr,V0.5 was shifted to negative values and the amplifying factor a_Xr,1 was increased to realize a faster activation and consequently an increased activity of I_Kr. The abolished rectification and accelerated tail current decay were obtained by shifting the half-activation voltage b_Xr,V0.5 to a more positive value and an elevated intensifying factor b_Xr,1.

The measurement of the I_Kr current performed by Brugada et al. was reproduced (Fig. 3 in Ref. [12]). Simulation with our M cell representation of the wild-type modification of the Priebe–Beuckelmann cellular model [34] displayed the behaviour of a healthy cardiomyocyte. The inward rectification factor rik of I_Kr led to a reduction of this ionic current activity within the whole physiological range of potentials. This effect was augmented at voltages above rik_V0.5. A slowly deactivating inward tail current caused by the repolarizing step was generated. The steady-state I_Kr current reached its maximum at nearly 0 mV and decreased at more positive potentials. The mutant definition of I_Kr describing the N588K/KCNE2 channel was integrated in the wild-type M cell model. As in the measurement, the virtual mutation abolished the rectification of the I_Kr channel due to the amplifying background substitution component bs. The current density during depolarization was increased and the tail current elicited by the repolarizing pulse displays accelerated kinetics. The smallest root-mean-square error under environmental conditions corresponding to the measurement and thus the best match between the N588K/KCNE2 emulating mathematical model and the measured N588K/KCNE2 mutant I_Kr channel [12] was found for the parameters of the I_Kr definition shown in the right column of Table 2. Fig. 2 compares the voltage-dependent course of rik for the wild-type and bs for the mutant modelling (left). The influence of the voltage-shifting in the mutant case on the gating-like components of the activation gate Xr is also shown (right). Fig. 3 demonstrates the course of the I_Kr current (top) and the normalized steady-state currents (bottom) for the wild-type (left) and the mutant (right) modelling during penetration with the stimulation protocol described by Brugada et al.[12].

Figure 2

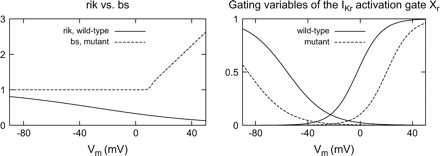
Left: Inward rectification factor rik of the heterogeneous adaptation of the Priebe–Beuckelmann model compared with background substitution factor bs in short QT modification. The factor rik decreased the I_Kr current over the whole range of physiological potentials. The new formulation of bs elevated the activity of the I_Kr channel for positive transmembrane voltages. Right: Gating-like portion of the rate constants of Xr for physiological and mutant modelling. In the mutant case, the half-activation voltage for activation is shifted to the positive, for inactivation it is shifted to negative values.

Figure 3

I_Kr elicited by voltage clamp conditions (top) in wild-type (left) and N588K/KCNE2 mutant (right) M cell modelling. Notice the different scaling. The voltage clamp protocol and the measurement data [12] are shown in the insets. The currents were elicited by 800 ms lasting depolarizing pulses from a holding potential of −80 mV. The amplitude of the pulses was between −50 and 50 mV with increments of 10 mV. To investigate the deactivating inward tail currents, a repolarizing voltage to −100 mV followed. In the mutant ionic model, the amplitude of the potassium current at depolarizing pulses was increased. The repolarizing voltage step generated a small tail current with an accelerated decay. Normalized current–voltage relationships are shown at the bottom. Amplitudes of the steady-state I_Kr currents are normalized to their values at 0 mV. Short QT mutation abolished rectification of I_Kr and induced a linear relationship for positive potentials.

The action potentials at body temperature in consideration of coexpressed wild-type and mutant channels to mimic heterozygous conditions were markedly abbreviated under the influence of the short QT mutation. The differences in APD between the distinctive cardiac cell types were decreased. In wild-type the maximum difference of the APD₉₀ in a homogeneous tissue is 72 ms between epicardium and M cells whereas in the mutant modelling it is reduced to 29 ms. Fig. 4 displays on the top the 30th elicited action potential at a stimulus frequency of 1 Hz for the wild-type (left) and the short QT mutant modelling (right). The altered kinetics of the mutant I_Kr current during an action potential was determined as in the experiment by Brugada et al. (Fig. 3G in Ref. [12]). While the wild-type ionic model showed the hump-like configuration with slow activation kinetics and rapid increase of I_Kr during the repolarization phase, the virtually short QT mutant cell displayed the reported dome-like shape and larger amplitude of I_Kr during the initial phases of the action potential. Fig. 5 shows this behaviour for an M cell modelling.

The electrophysiological heterogeneity was introduced into a parallelepiped domain, replicating a line through the left ventricle from endocardium to epicardium. The two bottom panels in Fig. 4 illustrate the effect of the heterogeneous expression of the ion channels on the electrical activity of the distinctive cell types within the virtual wall. The differences of the action potential shapes and durations are reduced for both the wild-type and mutant case. The short QT mutation barely influenced the activation but resulted in a marked abbreviation of the repolarization time and decreased dispersion of repolarization. The maximum difference of the APD₉₀ decreases from 43 ms in the wild-type to 27 ms in the mutant case, see Fig. 6.

Figure 4

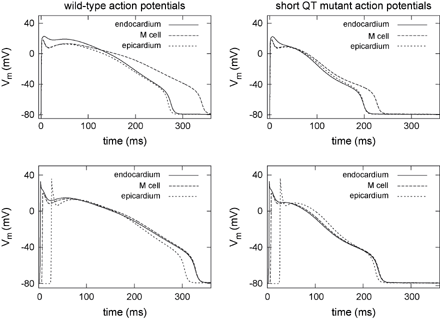
Action potentials generated in homogeneous (top) and heterogeneous (bottom) virtual tissue in wild-type (left) and short QT mutant case (right) at a stimulus frequency of 1 Hz. The results in the homogeneous environment represent the intrinsic behaviour of a single cell. The mutation led to a marked abbreviation of the action potentials and the APD₉₀ differences between the distinctive cells are decreased. The depolarizing wave propagating through the wall led to an activation delay in tissue and, therefore, to a homogenized time to repolarization.

Figure 5

I_Kr during an action potential in an M cell. While the wild-type case displayed the typical hump-like waveform, the mutant case showed the reported dome-like waveform. Measurement data [12] are shown in the inset for comparison.

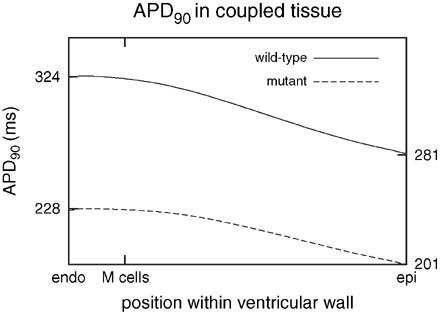
Distribution of APD90 in heterogeneous wild-type and mutant tissue. The mutation reduced the time to repolarization and reduced the dispersion of repolarization within tissue from 43 to 27 ms. Maximum and minimum of APD90 are marked at the left and right axis, respectively.

Figure 6

Distribution of APD₉₀ in heterogeneous wild-type and mutant tissue. The mutation reduced the time to repolarization and reduced the dispersion of repolarization within tissue from 43 to 27 ms. Maximum and minimum of APD₉₀ are marked at the left and right axis, respectively.

To determine the consequences of the short QT mutation in a complex three-dimensional model the transmurally heterogeneous configuration was included in an anisotropic model of the human left ventricle. The colour-coded transmembrane voltages during depolarization, plateau phase and repolarization for the wild-type as well as the mutant case are shown in Figs. 7 and 8, respectively. In both cases, the depolarization started at the apical endocardial site and wandered in a basal epicardial direction. During the plateau phase no significant transmural gradient of V_m was present. In wild-type the final repolarization was located in midmyocardial areas near the M cells. In short QT mutant case the time to repolarization was markedly reduced and homogenized for the distinctive cell types within the ventricular wall. The final repolarization was shifted to the epicardial region.

Figure 7

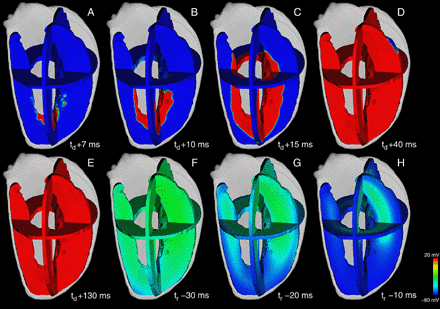
Excitation propagation and repolarization in the Visible Female left ventricle computed with the heterogeneous wild-type model at different time steps. The transmembrane voltage distribution is illustrated in three perpendicular planes. Blue corresponds to resting potential and red depicts activated tissue. The depolarization starts at t = t_d in the apical endocardium (A) and propagates to basal epicardial direction (B–D). After the plateau phase (E) the repolarization starts from apical endocardium (F) and vanished in basal midmyocardium (G,H). The time to full repolarization was t_r = 330 ms.

Figure 8

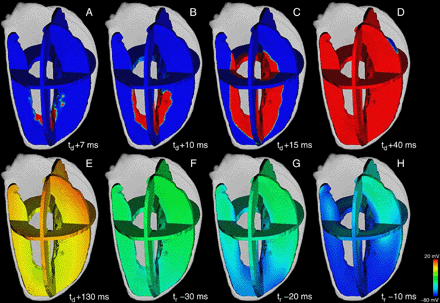
Activation and repolarizing phase in short QT mutant case in the same anatomical and excitation propagation model and at the same relative time steps as in Fig. 7. The mutation had no effect on the activation of the virtual ventricle but led to a marked abbreviation of the repolarization time. Time to full repolarization was decreased to t_r = 253 ms. Final repolarization was homogenized in the transmural direction caused by the reduced dispersion of repolarization within the wall.

An approximate transmural ECG was computed in the parallelepiped bidomain model. The short QT mutation led to an obvious abbreviation of the QT interval caused by the increased outward potassium current I_Kr (Fig. 9). It was reduced from 339 ms in the wild-type to 253 ms in the mutant case. The homogenization of the repolarization in the mutant tissue yielded a T wave with reduced amplitude.

Figure 9

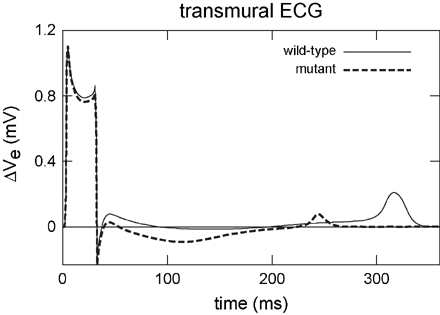
Transmural ECGs computed in a parallelepiped model. Wild-type modelling generated an upright positive T wave. The short QT mutation had no effect on the activation of tissue but reduced the time to repolarization and therefore yielded a shortened QT interval. The reduced amplitude of the T wave originates from a reduced dispersion of repolarization in the mutant case.

Discussion

In this work, our heterogeneous formulation of the Priebe–Beuckelmann electrophysiological model of a human cardiac myocytes [33,,34] was modified to simulate the behaviour of cells related to a recently described short QT syndrome. The formulation of the activating gate of the I_Kr current was changed, a background substitution factor was introduced instead of the inward rectification factor, and the maximum conductance for I_Kr was increased. The simulation results corresponded with the measurements of Brugada et al.[12].

As in the experiment the mutation abolished the rectification of the I_Kr current and caused a linear increase in the I_Kr activity over the range of physiological potentials. The decay of the tail current was significantly accelerated. The I_Kr current elicited during an action potential generated a waveform in the mutant modelling which was clearly distinguishable from the wild-type formulation. The altered characteristic of the mutant rapidly activating rectifier potassium current is consistent with the experimental findings. As in the measurement the short QT mutation led to an increase in this repolarizing ionic current during the early phases of repolarization. This gain of function in I_Kr reduced the repolarization time and produced markedly abbreviated APDs in the mutant compared with the wild-type case.

The impact of the short QT mutation in heterogeneous tissue was investigated in a thin parallelepiped domain as well as in a three-dimensional anatomical model. As shown, the heterogeneous electrophysiology is necessary to obtain an upright positive T wave in the approximate transmural ECG in wild-type case. In the short QT modelling the computed ECG displayed a noticeable decrease in the QT interval caused by shortened action potentials leading to a reduced repolarization time. The decrease in the T wave amplitude representing reduced dispersion of repolarization is in contrast with the assumption of Brugada et al.[12]. They speculated that the heterogeneous distribution of the ion currents in the heart [49] leads to heterogeneous abbreviations of APD in the short QT case. On the assumption that the reduction of the APD is less pronounced in M cells this behaviour would affect an accentuation of repolarization dispersion in coupled heterogeneous tissue visible as increased T_peak−T_end interval and thus, as widened T wave with increased amplitude in the transmural ECG [50,,51]. In the computational simulations, the I_Kr current came to the foreground caused by the increase in its activity in cells emulating the behaviour of short QT affected cells. Thus, the transmurally homogeneous distributed I_Kr depleted the repolarizing effect of the heterogeneous distributed I_Ks[40] and became the main repolarizing part. This homogenization of the repolarizing current reduced the APD differences between the distinctive cell types leading to a more pronounced abbreviation of the action potential in M cells compared with the remaining cardiomyocytes. Thus, the heterogeneous action potential shortening led to a reduced dispersion of repolarization that was visible as a T wave with reduced amplitude in the transmural ECG. A possible explanation for the difference between simulated ECGs and the assumption of the Brugada group is the assumed distribution and characteristics of the currents in the computer model.

Brugada et al. ascertained a reduced affinity of the I_Kr channel to I_Kr blockers caused by the mutation. Gaita et al.[52] administered various antiarrhythmic drugs to patients with short QT affections and only hydroquinidine administration achieved QT prolongation. Although hydroquinidine has the potential to be an effective therapy for these individuals the long-term benefit has yet to be determined. The first-choice therapy so far is the implantable cardioverter defibrillator implantation [53]. In the computational model the maximal I_Kr current was determined by the maximum conductance g_Kr,max of the I_Kr channel. Effects of I_Kr blockers will be estimated by reducing this value. The model is not able to reproduce reduced affinity of I_Kr blockers in the short QT mutation.

The model presented here can be expanded to investigate the effects of the genetic heterogeneity of the short QT syndrome. Bellocq et al.[9] recently linked a G919C substitution in KCNQ1 encoding the cardiac KvLQT1 channel to the short QT syndrome (SQT2). This effects a V307L mutation in KvLQT1. The mutation manifests in a −20 mV shift of the half-activation potential and accelerated activation kinetics of I_Ks and results in a gain of function in the heterogeneous distributed I_Ks channel. Recently, Priori et al.[18] described a novel form of the short QT syndrome (SQT3) due to a G514A substitution in KCNJ2. This results in a D172N amino acid change in Kir2.1, the inwardly rectifying I_K1 channel. The current density of I_K1 was increased and the peak of the current was shifted to a more positive value. By incorporating the three-dimensional heart model into a representation of the torso, simulations can be performed to uncover how changes in the heterogeneity of the short QT mutation affect the standard ECGs measured on the body surface.

References

[1]

Zipes

DP

Wellens

HJ

,

Sudden cardiac death

,

Circulation

,

1998

, vol.

98

(pg.

2334

-

2351

)

[2]

Priori

SG

Barhanin

J

Hauer

RN

et al. ,

Genetic and molecular basis of cardiac arrhythmias: impact on clinical management parts I and II

,

Circulation

,

1999

, vol.

99

(pg.

518

-

528

)

[3]

Priori

SG

Barhanin

J

Hauer

RN

et al. ,

Genetic and molecular basis of cardiac arrhythmias: impact on clinical management part III

,

Circulation

,

1999

, vol.

99

(pg.

674

-

681

)

[4]

Wang

Q

Curran

ME

Splawski

I

et al. ,

Positional cloning of a novel potassium channel gene: KvLQT1 mutations cause cardiac arrhythmias

,

Nat Genet

,

1996

, vol.

12

(pg.

17

-

23

)

[5]

Splawski

I

Tristani-Firouzi

M

Lehmann

MH

Sanguinetti

MC

Keating

MT

,

Mutations in the hminK gene cause long QT syndrome and suppress IKs function

,

Nat Genet

,

1997

, vol.

17

(pg.

338

-

340

)

[6]

Chen

YH

Xu

SJ

Bendahhou

S

et al. ,

KCNQ1 gain-of-function mutation in familial atrial fibrillation

,

Science

,

2003

, vol.

299

(pg.

251

-

254

)

[7]

Brugada

R

Tapscott

T

Czernuszewicz

GZ

et al. ,

Identification of a genetic locus for familial atrial fibrillation

,

N Engl J Med

,

1997

, vol.

336

(pg.

905

-

911

)

[8]

Eckardt

L

Kirchhof

P

Loh

P

et al. ,

Brugada syndrome and supraventricular tachyarrhythmias: a novel association?

,

J Cardiovasc Electrophysiol

,

2001

, vol.

12

(pg.

680

-

685

)

[9]

Bellocq

C

van Ginneken

AC

Bezzina

CR

et al. ,

Mutation in the KCNQ1 gene leading to the short QT-interval syndrome

,

Circulation

,

2004

, vol.

109

(pg.

2394

-

2397

)

[10]

Curran

ME

Splawski

I

Timothy

KW

Vincent

GM

Green

ED

Keating

MT

,

A molecular basis for cardiac arrhythmia: HERG mutations cause long QT syndrome

,

Cell

,

1995

, vol.

80

(pg.

795

-

803

)

[11]

Abbott

GW

Sesti

F

Splawski

I

et al. ,

MiRP1 forms IKr potassium channels with HERG and is associated with cardiac arrhythmia

,

Cell

,

1999

, vol.

97

(pg.

175

-

187

)

[12]

Brugada

R

Hong

K

Dumaine

R

et al. ,

Sudden death associated with short-QT syndrome linked to mutations in HERG

,

Circulation

,

2004

, vol.

109

(pg.

30

-

35

)

[13]

Wang

Q

Shen

J

Splawski

I

et al. ,

SCN5A mutations associated with an inherited cardiac arrhythmia, long QT syndrome

,

Cell

,

1995

, vol.

80

(pg.

805

-

811

)

[14]

Chen

Q

Kirsch

GE

Zhang

D

et al. ,

Genetic basis and molecular mechanism for idiopathic ventricular fibrillation

,

Nature

,

1998

, vol.

392

(pg.

293

-

296

)

[15]

Baroudi

G

Napolitano

C

Priori

SG

Del Bufalo

A

Chahine

M

,

Loss of function associated with novel mutations of the SCN5A gene in patients with Brugada syndrome

,

Can J Cardiol

,

2004

, vol.

20

(pg.

425

-

430

)

[16]

Kyndt

F

Probst

V

Potet

F

et al. ,

Novel SCN5A mutation leading either to isolated cardiac conduction defect or Brugada syndrome in a large French family

,

Circulation

,

2001

, vol.

104

(pg.

3081

-

3086

)

[17]

Plaster

NM

Tawil

R

Tristani-Firouzi

M

et al. ,

Mutations in Kir2.1 cause the developmental and episodic electrical phenotypes of Andersen's syndrome

,

Cell

,

2001

, vol.

105

(pg.

511

-

519

)

[18]

Priori

SG

Pandit

SV

Rivolta

I

et al. ,

A novel form of short QT syndrome (SQT3) is caused by a mutation in the KCNJ2 gene

,

Circ Res

,

2005

, vol.

96

(pg.

800

-

807

)

[19]

Schott

JJ

Charpentier

F

Peltier

S

et al. ,

Mapping of a gene for long QT syndrome to chromosome 4q25–27

,

Am J Hum Genet

,

1995

, vol.

57

(pg.

1114

-

1122

)

[20]

Keating

M

Dunn

C

Atkinson

D

Timothy

K

Vincent

GM

Leppert

M

,

Consistent linkage of the long-QT syndrome to the Harvey ras-1 locus on chromosome 11

,

Am J Hum Genet

,

1991

, vol.

49

(pg.

1335

-

1339

)

[21]

Keating

M

Atkinson

D

Dunn

C

Timothy

K

Vincent

GM

Leppert

M

,

Linkage of a cardiac arrhythmia, the long QT syndrome, and the Harvey ras-1 gene

,

Science

,

1991

, vol.

252

(pg.

704

-

706

)

[22]

Algra

A

Tijssen

JG

Roelandt

JR

Pool

J

Lubsen

J

,

QT interval variables from 24 h electrocardiography and the two year risk of sudden death

,

Br Heart J

,

1993

, vol.

70

(pg.

43

-

48

)

[23]

Gussak

I

Brugada

P

Brugada

J

et al. ,

Idiopathic short QT interval: a new clinical syndrome?

,

Cardiology

,

2000

, vol.

94

(pg.

99

-

102

)

[24]

Gaita

F

Giustetto

C

Bianchi

F

et al. ,

Short QT Syndrome: a familial cause of sudden death

,

Circulation

,

2003

, vol.

108

(pg.

965

-

970

)

[25]

Roden

DM

George

AL

Jr

,

Structure and function of cardiac sodium and potassium channels

,

Am J Physiol

,

1997

, vol.

273

(pg.

H511

-

H525

)

[26]

Guy

HR

Durell

SR

,

Structural models of Na^y, Ca2⁺, and K⁺ channels

,

Soc Gen Physiol Ser

,

1995

, vol.

50

(pg.

1

-

16

)

[27]

Kukuljan

M

Labarca

P

Latorre

R

,

Molecular determinants of ion conduction and inactivation in K⁺ channels

,

Am J Physiol

,

1995

, vol.

268

(pg.

C535

-

C556

)

[28]

Heginbotham

L

Lu

Z

Abramson

T

MacKinnon

R

,

Mutations in the K⁺ channel signature sequence

,

Biophys J

,

1994

, vol.

66

(pg.

1061

-

1067

)

[29]

Doyle

DA

Morais Cabral

J

Pfuetzner

RA

et al. ,

The structure of the potassium channel: molecular basis of K⁺ conduction and selectivity

,

Science

,

1998

, vol.

280

(pg.

69

-

77

)

[30]

Ficker

E

Jarolimek

W

Kiehn

J

Baumann

A

Brown

AM

,

Molecular determinants of dofetilide block of HERG K⁺ channels

,

Circ Res

,

1998

, vol.

82

(pg.

386

-

395

)

[31]

Tseng

GN

,

I(Kr): the hERG channel

,

J Mol Cell Cardiol

,

2001

, vol.

33

(pg.

835

-

849

)

[32]

Sachse

FB

Seemann

G

Chaisaowong

K

Mohr

MB

,

Modeling of electro-mechanics of human cardiac myocytes: parametrization with numerical minimization techniques

,

Proc 25th Conf IEEE EMBS

,

2003

(pg.

2810

-

2813

)

[33]

Priebe

L

Beuckelmann

DJ

,

Simulation study of cellular electric properties in heart failure

,

Circ Res

,

1998

, vol.

82

(pg.

1206

-

1223

)

[34]

Seemann

G

Sachse

FB

Weiss

DL

Dossel

O

,

Quantitative reconstruction of cardiac electromechanics in human myocardium: regional heterogeneity

,

J Cardiovasc Electrophysiol

,

2003

, vol.

14

10 Suppl.

(pg.

S219

-

S228

)

[35]

Hodgkin

AL

Huxley

AF

,

A quantitative description of membrane current and its application to conduction and excitation in nerve

,

J Physiol

,

1952

, vol.

117

(pg.

500

-

544

)

[36]

Press

WH

Teukolsky

SA

Vetterling

WT

Flannery

BP

Press

WH

Teukolsky

SA

Vetterling

WT

Flannery

BP

,

Integration of ordinary differential equations

,

Numerical recipes in C: the art of scientific computing

,

1992

2nd ed.

Cambridge, UK

Cambridge University Press

(pg.

707

-

752

)

[37]

Hille

B

Hille

B

,

Classical biophysics of the squid giant axon

,

Ionic channels of excitable membranes

,

2001

3rd ed.

Sunderland, Mass, USA

Sinauer

(pg.

25

-

60

)

[38]

Antzelevitch

C

Yan

G

Shimizu

W

Burashnikov

A

Zipes

DP

Jalife

J

,

Electrical heterogeneity, the ECG, and cardiac arrhythmics

,

Cardiac electrophysiology. From cell to bedside

,

1999

3rd ed.

W.B. Saunders Company

(pg.

222

-

238

)

[39]

Li

GR

Feng

J

Yue

L

Carrier

M

,

Transmural heterogeneity of action potentials and Ito1 in myocytes isolated from the human right ventricle

,

Am J Physiol

,

1998

, vol.

275

(pg.

H369

-

H377

)

[40]

Liu

DW

Antzelevitch

C

,

Characteristics of the delayed rectifier current (IKr and IKs) in canine ventricular epicardial, midmyocardial, and endocardial myocytes. A weaker IKs contributes to the longer action potential of the M cell

,

Circ Res

,

1995

, vol.

76

(pg.

351

-

365

)

[41]

Zygmunt

AC

Goodrow

RJ

Antzelevitch

C

,

I(NaCa) contributes to electrical heterogeneity within the canine ventricle

,

Am J Physiol Heart Circ Physiol

,

2000

, vol.

278

(pg.

H1671

-

H1678

)

[42]

Weiss

DL

Seemann

G

Dössel

O

,

Conditions for equal polarity of R and T wave in heterogenous human ventricular tissue

,

Proc BMT

,

2004

, vol.

49

(pg.

364

-

365

)

[43]

Henriquez

CS

,

Simulating the electrical behavior of cardiac tissue using the bidomain model

,

Crit Rev Biomed Eng

,

1993

, vol.

21

(pg.

1

-

77

)

[44]

Henriquez

CS

Muzikant

AL

Smoak

CK

,

Anisotropy, fiber curvature, and bath loading effects on activation in thin and thick cardiac tissue preparations: simulations in a three-dimensional bidomain model

,

J Cardiovasc Electrophysiol

,

1996

, vol.

7

(pg.

424

-

444

)

[45]

Visible Human Project, National Library of Medicine, Bethesda, USA: <http://www.nlm.nih.gov/research/visible/visible_human.html>

[46]

Sachse

FB

Werner

CD

Stenroos

MH

Schulte

RF

Zerfass

P

Dössel

O

,

Modeling the anatomy of the human heart using the cryosection images of the Visible Female dataset

,

Proc Third Users Conference of the National Library of Medicine's Visible Human Project

,

2000

[47]

Streeter

DD

,

Gross morphology and fiber geometry of the heart

,

Handbook of physiology. Am Physiol Soc

,

1979

(pg.

61

-

112

)

[48]

The message passing interface (MPI) standard: <http://www-unix.mcs.anl.gov/mpi>

[49]

Antzelevitch

C

Dumaine

R

Page

E

Fozzard

HA

Solaro

RJ

,

Electrical heterogeneity in the heart: physiological, pharmalogical and clinical implications

,

Handbook of physiology: the heart

,

2001

Oxford, UK

Oxford University Press

(pg.

654

-

692

)