Relative conditional survival analysis provides additional insights into the prognosis of heart failure patients Free

Heart failure (HF) entails high mortality rates.¹ Mortality rates presented in the literature are usually based on cumulative probabilities, providing statistical estimates for the entire duration of the follow-up period. Presented this way, aspects of prognosis in HF are missed that may contain important information for the patient or treating physician. Additional insights into prognosis may be gained by using relative and conditional survival analysis, approaches commonly used and proven highly useful in oncology research.² We explored these measures of survival in a large cohort of patients with acute HF.

We used a consecutive single-centre cohort of acute HF patients with long-term follow-up.³ Briefly, 1810 patients admitted with acute HF to Erasmus MC, Rotterdam, the Netherlands, were included in a prospective registry between 1985 and 2008 (baseline characteristics: Supplementary material online, Table S1). We calculated cumulative survival rates for 10 years, stratified by age in four equal groups, using the Kaplan–Meier method (Figure 1A, Supplementary material online, Table S2). As expected, 1- and 10-year survival rates were low (between 56–5% at 1 year and 9–35% at 10 years). Overall, younger patients had better survival than older patients.

Figure 1

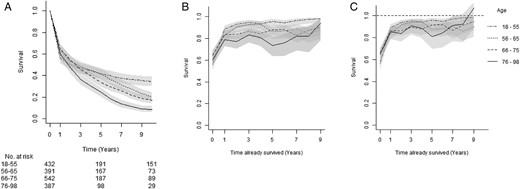
Cumulative, conditional, and relative conditional survival curves. (A) Cumulative survival in years (with 95% confidence intervals) for four age groups and the number of patients still at risk at 0, 5, and 10 years. (B) One-year survival estimates, conditional on surviving the number of years indicated on the x-axis. (C) The 1-year conditional survival relative to the general population. The estimates at Year 0 in (B and C) correspond to (relative) survival estimate at one. The dashed line in (C) indicates survival equal to the general population (relative survival = 1).

Open in new tabDownload slide

The steep decline in survival in the first year attenuated during subsequent follow-up. This became even more evident when 1-year conditional survival rates were calculated, which indicate the probability of surviving 1 year, given that the patient had already survived up to that time, and show how a patient’s estimated survival changes over time (Figure 1B). For example, patients aged 55 or younger had a cumulative survival probability of 56% at 1 year and of 50% at 2 years of follow-up. However, if those patients survived the first year, the survival probability of also surviving the second year increased to 89%. These much higher 1-year survival rates persisted throughout the remainder of the follow-up (Figure 1B). A similar pattern was seen in the other age groups. Younger patients had higher 1-year conditional survival rates than older patients.

How much of the all-cause mortality in this cohort can be attributed to HF is shown by relative or relative conditional survival (RCS). Relative survival directly compares a patient's survival to the survival of a person in the general population with the same age and gender, retrieved from Statistics Netherlands.⁴ Relative conditional survival demonstrates at which point in time the survival of a patient becomes similar to that of the general population (RCS = 1).⁵Figure 1C shows the 1-year RCS estimates. For example, if patients aged 75 or older survive the first year, their survival is 79%, This corresponds to a prognosis that is 85% of the general population. The RCS probability lines never reach the value of one, indicating that during the entire 10-year follow-up period, all patients continue to have an increased mortality rate compared to the general population. Relative survival rates show more overlap for the different patient groups than in the conditional analysis. So, although younger patients have a better prognosis than older patients, compared to their peers survival remains suboptimal and increased HF mortality persists throughout follow-up.

We repeated the analyses stratifying on sex, left ventricular ejection fraction (LVEF), aetiology, diabetes, hypertension, and kidney function (results: Supplementary material online). For patients with a poor LVEF, survival was lower in the first year compared to the other patients. Interestingly, this difference disappeared when patients with poor LVEF survived the first period, as demonstrated by RCS. Patients with severe kidney dysfunction similarly showed lower survival rates. This difference persisted, although less pronounced, when calculating (relative) conditional survival. For the other factors and comorbidities, differences were less evident but in line with previous literature. For every stratifying factor, all patient groups showed excess mortality compared to the general population. A multivariable relative regression model was estimated (details in Supplementary material online). In short, the first follow-up period, age, LVEF, eGFR, diabetes, and hypertension were significantly independently associated with relative excess risk, in line with results of the stratified analyses.

In conclusion, acute HF entails high mortality. (Relative) conditional survival can be used to gain additional insights into the disease course and communicate this more clearly to patients. Using these measures, we found that mortality occurs largely in the first period, and there is substantial improvement thereafter. Thus the first period after hospitalization is crucial. Cardiologists could use conditional survival to update patient prognosis during each visit and show higher survival probabilities to patients once they survive the first year. The RCS estimates however show that, for these acute HF patients, survival never becomes ‘normal’ again. This also holds for younger patients, patients without specific comorbidities, and with ejection fraction ≥ 45%. This notion is particularly important for young patients, who will carry the burden of their disease for the rest of their lives.

Supplementary material

Supplementary material is available at European Journal of Preventive Cardiology online.

Conflict of interest: none declared.

References