-
PDF
- Split View
-
Views
-
Cite
Cite
Lennart Froede, Sebastian Schäfers, Gudrun Wagenpfeil, Alexander Raddatz, Klaus Hoffmann, Hans-Joachim Schäfers, Simplified determination of commissural orientation in bicuspid aortic valves, European Journal of Cardio-Thoracic Surgery, Volume 58, Issue 6, December 2020, Pages 1153–1160, https://doi.org/10.1093/ejcts/ezaa230
Close - Share Icon Share
Abstract
In bicuspid aortic valves (BAV), commissural orientation (CO) varies between 180° and close to 120°. Postoperative CO has a strong effect on repair durability, and different repair approaches have been proposed according to CO; it is thus important for aortic repair. A precise, simple and reproducible determination by preoperative echocardiography would facilitate intraoperative decision-making. We compared 4 different methods of determination of CO in BAV.
Preoperative transoesophageal echocardiograms of 62 patients with BAV were analysed. CO was measured using either the coaptation centre or the geometric centre of the root. The geometric centre of the root was determined through approximation using a circle or an ellipse, or the midpoint of a line between the centre of the non-fused and the fused sinuses.
The 3 different geometric methods led to almost identical results (interclass coefficient 0.98–0.99), with the line segment being the easiest to use. The use of the coaptation centre was associated with the underestimation of commissural angle of up to 30° compared to the geometric centre; the discrepancy was significant and most pronounced for asymmetric BAV (140–160°; P = 0.005).
CO can reproducibly be determined using a line segment between the centre of the non-fused and fused sinuses. The use of the coaptation centre can lead to misleading results, in particular in asymmetric BAVs.
INTRODUCTION
In the past 25 years, repair of regurgitant bicuspid aortic valves (BAVs) has evolved into an increasingly practised alternative to valve replacement [1, 2]. Over time, anatomical characteristics of the BAV have been found to be determinants of repair durability [3]. The anatomy of the BAV is characterized by the fact that there are 2 normal commissures, i.e. with normal height and absence of cusp fusion in the pericommissural area [4, 5]. There is variable degree of fusion; the commissure adjacent to cusp fusion is hypoplastic, i.e. lower than the 2 normal commissures. In some, few instances, it may be absent [4]. Sabet et al. [4] pointed out that there is marked variability in commissural orientation (CO), ranging from 180° to close to 120°. These findings were confirmed by a clinical study [5] analysing morphometric details of BAVs. It confirmed that on one side of the spectrum is the symmetric BAV with 180° CO and complete fusion of 2 cusps. CO, degree of fusion and height of the hypoplastic commissure correlate [5].
CO has been found to have a strong effect on repair durability of the BAV [3]. In addition, it was shown to influence systolic function of the repaired BAV, with symmetric BAVs yielding the best function and durability [3, 6]. This was confirmed by the observation that modifying CO through making it more symmetric as part of the repair led to improved function and durability [7–9]. These observations have become the base for clinical decision-making in repair, i.e. choosing a specific repair approach according to CO of the BAV [3]. In experienced centres, it has now become routine to maintain a symmetric configuration when present preoperatively, or achieve it through configuration of the valve within the graft if root enlargement triggers root replacement. Very asymmetric BAVs are treated in analogy to tricuspid valves. In asymmetric valves, however, CO is made more symmetric, for instance through sinus plication [5, 7]. Thus, determination of CO has become an important part of clinical decision-making, in particular in those whose root size does not require root replacement.
In our previous study, CO was determined retrospectively in print outs of short axis echo images. The geometric centre of the aortic root was determined, and the angle of the 2 sections marked by geometric centre and each of the 2 functional commissures was measured [3, 7]. For clinical application, online measurement of this angle at the time of intraoperative transoesophageal echocardiogram (TOE) has become important. So far, a gold standard for this measurement is lacking.
The long-term performance of a reconstructed valve is influenced by a number of fluid-dynamic properties beyond the point of coaptation of the valve cusps. Based on computer simulation [10], the geometric centre of the root determining the angle has been shown to best represent the centre of valve motion. However, there has been uncertainty how to define the geometric centre of the root; some have measured the angle from the coaptation centre (verbal communications). In addition, it is yet unclear whether CO is best measured in systole or diastole.
For the previous studies [3, 7] the geometric centre of the root was estimated by drawing different lines through the assumed centre and thus approximating the centre. As the next step, we have approximated the short axis view of the root by a circle to facilitate the determination of its centre. Since the short axis view of the root may be elliptical, we have occasionally approximated it through an ellipse.
We intended to develop a measurement that can easily be used in a reproducible fashion on echocardiography machines. The core objective was determination of the geometric centre of the root. This can be achieved through a circle or ellipse, but neither circle nor ellipse is part of the standard programmes on echocardiography machines. We hypothesized that a simple line segment drawn from the rudimentary commissure of the fused cusp (representing the centre of the fused sinuses) to the centre of the non-fused sinus would lead to reliable determination of the root centre.
In a retrospective analysis, we tested this hypothesis and compared the results of determination of CO using circle, ellipse and line segment. In addition, we compared these results to measurement from the coaptation centre.
PATIENTS AND METHODS
The investigation had been approved by the regional ethics committee (Ärztekammer des Saarlandes, 202/19), and the need for patient consent was waived for the analysis of the data in anonymized fashion.
Of patients undergoing BAV repair between September 2016 and May 2017, 122 were initially included. Of these, 60 had relevant root dilatation requiring root replacement and were excluded. The remaining 62 were analysed and represent the study group. Of the 62 patients, 55 were male.
The indication for surgery was aortic regurgitation in all instances, and the maximum root diameter was 43 mm. The patients’ age ranged from 20 to 75 (mean 47 years). The anatomic types according to the recent classification [5] were: 12 symmetric (type A), 40 asymmetric (type B) and 10 very asymmetric (type C).
The visual estimation of CO had been performed at the time of surgery and was retrieved from the patient chart. The intraoperative TOEs had been stored electronically and were retrieved. In all instances, the TOE had been performed by 1 of 2 echocardiographers (A.R., K.H.) with a constant protocol.
Prior to sternotomy, the short axis view was obtained by multiplanar projection, making certain that it was perpendicular to the long axis of the left ventricular outflow tract and root and thus parallel to the annular plane. The short axis plane was then moved cranially from an annular level until the rudimentary commissure just became visible as thickened tissue. Consequently, the 2 functional commissures were higher than the echocardiographic plane and visible as triangles formed by cusp tissue and aortic wall (Fig. 1).
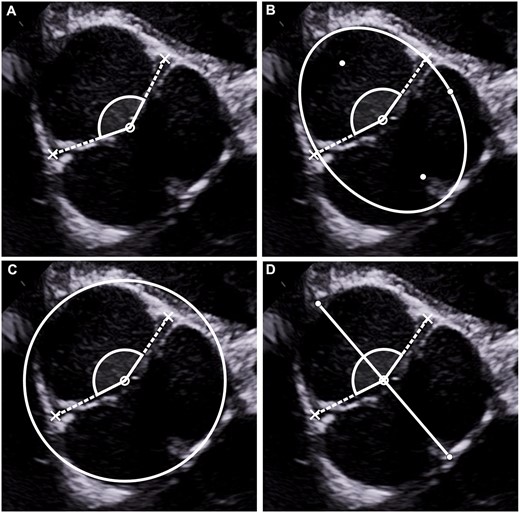
(A) Angle measurement according to coaptation centre. The most central point of the coaptation line is determined; the angle is measured with lines drawn from the coaptation centre through the 2 functional commissures. (B) Angle measurement according to geometric centre determined by the ellipse method. The ellipse is adjusted to accommodate the root shape, yielding the geometric centre of the root. The angle is measured with lines drawn from the geometric centre through the 2 functional commissures. (C) Angle measurement according to geometric centre determined by the circle method. The circle is adjusted to accommodate the root shape. The angle is measured with lines drawn from the centre of the circle through the 2 functional commissures. (D) Angle measurement according to geometric centre determined by the line method. The central line is drawn from the rudimentary commissure to the approximate centre of the non-fused sinus and then cut in half, yielding the geometric centre of the root. The angle is measured with lines drawn from the geometric centre through the 2 functional commissures.
A digital still image of the short axis view in systole and diastole of the TOE was transferred into the geometric analysis programme Geogebra (www.geogebra.org).
Thus, we imported 2 frames from each loop, 1 in mid-systole and 1 in mid-diastole. The geometry software Geogebra (www.geogebra.org) was used for the subsequent geometric measurements. Only for determination of the coaptation centre, a single image of the valve in mid-diastole was analysed further.
Subsequently, the centre of the root was defined by different methods. For each method, the angle was measured by lines from the centre of the root to the 2 functional commissures. We first determined the coaptation centre, and then—using 3 different methods—the geometric centre of the root.
Angle measurement—coaptation centre
For measurement according to the centre of coaptation, the vertex of the measured angle was placed in centre of the coaptation line. This could only be done in diastole; the line of coaptation was marked, and the centre was estimated visually. The distance from the assumed coaptation centre to each of the functional commissures was measured, and the centre then adjusted until both distances were equal (Fig. 1A).
Angle measurement—geometric approach
The geometric angle was determined using either an ellipse, a circle or a line segment.
For measurement according to ellipse (Fig. 1B), an ellipse was determined that approximated the short axis form of the aortic root. To achieve this, a centre line was assumed and 2 points on this line were determined (F1 and F2). All points on the ellipse (Px) are characterized by equality of the sum of the distances |PxF1| and |PxF2| (Fig. 2). The points F1, F2 and 1 Px were adjusted until the ellipse approximated the inner shape of the root. The geometric centre was measured as half of the distance between F1 and F2.
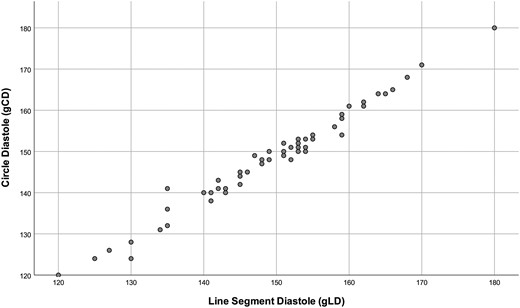
Scatter plot comparing the results of the geometric centre-derived angles, here circle method and line method (diastole). There is a high correlation, and the regression line is y = −0.51 + 0.99x.
For measurement according to the circle method, a circle was placed to approximate the aortic root (Fig. 1C). The geometric centre of the root was approximated by using a circle all points Tx are equidistant from the midpoint C with the radius r. A preliminary circle was drawn within the root. This circle was then adjusted to best accommodate the shape of the root, and the centre of the circle was taken from the geometric calculation.
For the determination of the geometric centre of the root approximated by using a line segment, a line segment was drawn from sinus wall, where the rudimentary commissure is located (almost always the centre of the fused sinuses), to the assumed centre of the non-fused sinus. Subsequently, the line segment was bisected for the determination of the geometric centre (Fig. 1D).
For the measurement of CO, lines were drawn from the determined centre to the 2 functional commissures, and the commissural angle calculated through the geometry software. These measurements were repeated in systole and diastole for the geometric methods of centre determination. For the coaptation centre, it could only be done in diastole. Thus, 7 measurements were made of each patient using 4 different methods.
Visual determination of angle
At the time of surgery the surgeon (H.-J.S.) visually estimated the commissural angle. It was recorded and the echocardiographers were blinded to these data at the time of echocardiographic analysis.
Statistical analysis
The statistical analysis was conducted using SPSS 25 (IBM SPSS Statistics 25, Armonk, NY, USA). Continuous variables were reported as mean ± standard deviation. P-value ˂0.05 was considered as statistically significant. The correlation between the different methods was calculated by intraclass correlation coefficients using a two-way mixed model with consistency type. The 95% confidence intervals were stated. Normal distribution was tested with the Shapiro–Wilk test and visually confirmed with a quantile–quantile plot. After verifying normal distribution, the multi-group comparison of normally distributed variables was performed using univariate analysis of variance. The Bonferroni procedure was used for post hoc analysis. The association between the circle and line segment methods was tested using linear regression. Linearity was ascertained with a residual versus predictor plot. For the analysis of discrepancy between coaptation and geometric methods, individual differences were calculated. In addition, the images were grouped according to the commissural angles based on the geometric determination of centre, using a published classification [5]. A linear regression analysis was performed to analyse a potential systematic difference between coaptation and geometric methods. The raw data were modified, and the ‘minimum distance to extreme’ (MinDist) was calculated as the absolute difference in degrees between the measured angle and the closer extreme: The linear regression was expanded to account for the existing classification [5].
RESULTS
The valve was repaired in all instances, a suture annuloplasty was applied in all. The 10 very asymmetric valves were repaired by separate prolapse correction of the right cusp. The 12 symmetric valves were corrected by plication of the fused cusp, in 4 instances also of the non-fused cusp. In the 40 asymmetric cases, the fused cusp was shortened and, in addition, CO was modified to achieve a symmetric configuration.
The intraoperative visual estimate of the commissural angle was 149° ± 13.4°; it was 166.3° ± 9.8° in symmetric, 149° ± 6.3° in asymmetric and 129° ± 7.8° in the very asymmetric valves.
The mean angle determined according to coaptation centre was 138.2° ± 14.4°. In diastole, the mean angle based on geometric centre was 138.2° ± 14.4° (circle method), 149.0° ± 12.6° (ellipse method) and 149.8° ± 12.4° (line segment method). The mean angle in systole was 148.6° ± 12.7° for the circle method, 149.0° ± 13.1° for the ellipse and 149.7° ± 12.6° for the line segment.
There were high correlations between circle and ellipse [systole: interclass coefficient (ICC) = 0.993, diastole: ICC = 0.992] as well as circle and line segment (systole: ICC = 0.994, diastole: ICC = 0.990; Fig. 2) or ellipse and line segment (systole: ICC = 0.990, diastole: ICC = 0.988) for all different angles, irrespective of whether they were measured in diastole or systole (Table 1). There was also a high correlation (ICC = 0.993) between diastolic and systolic measurements (Table 1). There was a good correlation between the angles determined by visual assessment and the mean of the 3 geometric methods [0.921 (95% CI 0.872–0.951), Fig. 3].
![Scatter plot comparing the results of intraoperative visual estimation of commissural angle by the surgeon with the mean of the echocardiography-derived angles. There is a high correlation [0.921 (95% CI 0.872–0.951)].](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/ejcts/58/6/10.1093_ejcts_ezaa230/1/m_ezaa230f3.jpeg?Expires=1747953391&Signature=m7FDXIscn~JVgWVx8BfYliQp95WCcxfgRmesGH1E8QK9ntn1oykg2bEhl34BBKEOp~kcwXI-sAoqiabRevbYHIMGUVEuQ9W7KEksvD3CiaRB4bnA5UJExLh6mcVPisBSUDdXA4DJ-iyKUblAdkvoPaZmJZf0c4HVNZZevOTZSeovzkbCMBdQZDLS9kbKbtczgCt7V509GOEcUftP46djEBbdy6ehy~jjcwqLJsuyAO-JDm2PaHTb8zxF61RzA5TudQxDfmiw0AeZSLlVmVAany5mQU7NUbJ7nhzNN9h8rTdz~WoynjNzK6I0p1fp7joiM3-biNtXJUbWO3fvUySKsQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Scatter plot comparing the results of intraoperative visual estimation of commissural angle by the surgeon with the mean of the echocardiography-derived angles. There is a high correlation [0.921 (95% CI 0.872–0.951)].
Interclass coefficients for the analysis of the different angle measurements
| Compared methods . | ICC . | 95% CI lower . | 95% CI upper . |
|---|---|---|---|
| gED versus gCD | 0.992 | 0.987 | 0.995 |
| gCD versus gLD | 0.990 | 0.984 | 0.994 |
| gED versus gLD | 0.988 | 0.980 | 0.993 |
| gES versus gCS | 0.993 | 0.988 | 0.996 |
| gCS versus gLS | 0.994 | 0.990 | 0.997 |
| gES versus gLS | 0.990 | 0.983 | 0.994 |
| Mean gES/gCS/gLS versus mean gED/gCD/gLD | 0.993 | 0.988 | 0.996 |
| CL versus mean gED/gCD/gLD | 0.783 | 0.663 | 0.863 |
| Compared methods . | ICC . | 95% CI lower . | 95% CI upper . |
|---|---|---|---|
| gED versus gCD | 0.992 | 0.987 | 0.995 |
| gCD versus gLD | 0.990 | 0.984 | 0.994 |
| gED versus gLD | 0.988 | 0.980 | 0.993 |
| gES versus gCS | 0.993 | 0.988 | 0.996 |
| gCS versus gLS | 0.994 | 0.990 | 0.997 |
| gES versus gLS | 0.990 | 0.983 | 0.994 |
| Mean gES/gCS/gLS versus mean gED/gCD/gLD | 0.993 | 0.988 | 0.996 |
| CL versus mean gED/gCD/gLD | 0.783 | 0.663 | 0.863 |
CI: confidence interval; CL: coaptation line; gCD: geometric circle in diastole; gEC: geometric circle in systole; gED: geometric ellipse in diastole; gES: geometric ellipse in systole; gLD: geometric line in diastole; gLS: geometric line in systole; ICC: interclass coefficient.
Interclass coefficients for the analysis of the different angle measurements
| Compared methods . | ICC . | 95% CI lower . | 95% CI upper . |
|---|---|---|---|
| gED versus gCD | 0.992 | 0.987 | 0.995 |
| gCD versus gLD | 0.990 | 0.984 | 0.994 |
| gED versus gLD | 0.988 | 0.980 | 0.993 |
| gES versus gCS | 0.993 | 0.988 | 0.996 |
| gCS versus gLS | 0.994 | 0.990 | 0.997 |
| gES versus gLS | 0.990 | 0.983 | 0.994 |
| Mean gES/gCS/gLS versus mean gED/gCD/gLD | 0.993 | 0.988 | 0.996 |
| CL versus mean gED/gCD/gLD | 0.783 | 0.663 | 0.863 |
| Compared methods . | ICC . | 95% CI lower . | 95% CI upper . |
|---|---|---|---|
| gED versus gCD | 0.992 | 0.987 | 0.995 |
| gCD versus gLD | 0.990 | 0.984 | 0.994 |
| gED versus gLD | 0.988 | 0.980 | 0.993 |
| gES versus gCS | 0.993 | 0.988 | 0.996 |
| gCS versus gLS | 0.994 | 0.990 | 0.997 |
| gES versus gLS | 0.990 | 0.983 | 0.994 |
| Mean gES/gCS/gLS versus mean gED/gCD/gLD | 0.993 | 0.988 | 0.996 |
| CL versus mean gED/gCD/gLD | 0.783 | 0.663 | 0.863 |
CI: confidence interval; CL: coaptation line; gCD: geometric circle in diastole; gEC: geometric circle in systole; gED: geometric ellipse in diastole; gES: geometric ellipse in systole; gLD: geometric line in diastole; gLS: geometric line in systole; ICC: interclass coefficient.
The correlation between coaptation centre method and the average of the 3 geometric centre methods was less (ICC = 0.783) (Table 1). The commissural angle determined by coaptation centre differed from that determined according to geometric centre in the majority of cases; the discrepancy ranged from −12° to +33° (Fig. 4). Mean values for commissural angles were significantly higher with geometric measurement than using coaptation line approach (P < 0.001). The angle determined by the coaptation method was 10.8° ± 9.0° smaller than the angle determined by the ellipse method, 10.6° ± 8.8° smaller than determined by the circle method and 11.6° ± 9.1° smaller than determined by the line segment method.
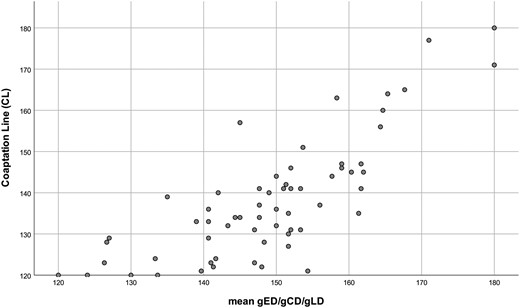
Scatter plot comparing the angles derived through use of the coaptation centre (CL) versus the mean of the 3 geometric methods. CL: coaptation line; gCD: geometric circle diastole; gED: geometric ellipse diastole; gLD: geometric line diastole.
Linear regression showed no significant correlation between the discrepancy and angles determined using geometric methods. Nevertheless, the scatter plot (Fig. 3) indicated potentially relevant discrepancies between the angles 140° and 160°, i.e. in type B [5]. For very asymmetric valves (type C: 120°–139°), the mean discrepancy between coaptation method and the average of the geometric methods was 3.9° ± 5.8°. For asymmetric valves (type B: 140°–159°), it was 13.2° ± 8.5°; for symmetric valves (type A: 160°–180°), it was 9.5° ± 9.5° (Table 2).
Regression coefficients for MinDist in relation to discrepancy in commissural orientation measurements for different categories of valves [5]
| Linear regression coefficientsa . | ||||
|---|---|---|---|---|
| Model . | Standardized coefficients . | T . | Sig. . | |
| Beta . | ||||
| 1 | Constant | −0.035 | 0.972 | |
| MinDist × type A | 0.191 | 1.163 | 0.250 | |
| MinDist × type B | 0.738 | 3.747 | 0 | |
| MinDist × type C | 0.505 | 2.903 | 0.005 | |
| Linear regression coefficientsa . | ||||
|---|---|---|---|---|
| Model . | Standardized coefficients . | T . | Sig. . | |
| Beta . | ||||
| 1 | Constant | −0.035 | 0.972 | |
| MinDist × type A | 0.191 | 1.163 | 0.250 | |
| MinDist × type B | 0.738 | 3.747 | 0 | |
| MinDist × type C | 0.505 | 2.903 | 0.005 | |
Dependent variable: difference mean geometric approach and coaptation line approach.
MinDist: minimum distance to extreme.
Regression coefficients for MinDist in relation to discrepancy in commissural orientation measurements for different categories of valves [5]
| Linear regression coefficientsa . | ||||
|---|---|---|---|---|
| Model . | Standardized coefficients . | T . | Sig. . | |
| Beta . | ||||
| 1 | Constant | −0.035 | 0.972 | |
| MinDist × type A | 0.191 | 1.163 | 0.250 | |
| MinDist × type B | 0.738 | 3.747 | 0 | |
| MinDist × type C | 0.505 | 2.903 | 0.005 | |
| Linear regression coefficientsa . | ||||
|---|---|---|---|---|
| Model . | Standardized coefficients . | T . | Sig. . | |
| Beta . | ||||
| 1 | Constant | −0.035 | 0.972 | |
| MinDist × type A | 0.191 | 1.163 | 0.250 | |
| MinDist × type B | 0.738 | 3.747 | 0 | |
| MinDist × type C | 0.505 | 2.903 | 0.005 | |
Dependent variable: difference mean geometric approach and coaptation line approach.
MinDist: minimum distance to extreme.
A univariate factor analysis indicated a trend to inter-categorical differences (P = 0.008). The post hoc analysis confirms a significant discrepancy between very asymmetric (type C) and asymmetric (type B) valves (P = 0.007). Based on the scatter plot, we hypothesized that at the extremes, i.e. angles of 120° and 180°, the discrepancy would be low. These extremes correspond to the idealized valve geometries, the symmetric BAV (180°) and the seemingly tricuspid BAV (120°). The raw data were modified, and the ‘MinDist’ was calculated as the absolute difference in degrees between the measured angle and the closer extreme: Linear regression analysis of commissural angle discrepancy against MinDist showed a significant, positive coefficient (). In addition, a linear regression was generated, splitting the MinDist variable into the proposed classification [5]. This analysis confirmed the hypothesis based on visual analysis of the scatter plot (Fig. 4). The discrepancy between the geometric and coaptation line approach was significant for BAV of types B and C; it was largest for BAV of type B. The scatter plot analysing MinDist versus the difference between coaptation and geometric angle showed an increasing discrepancy with increasing deviation form 120° or 180° (Fig. 5).
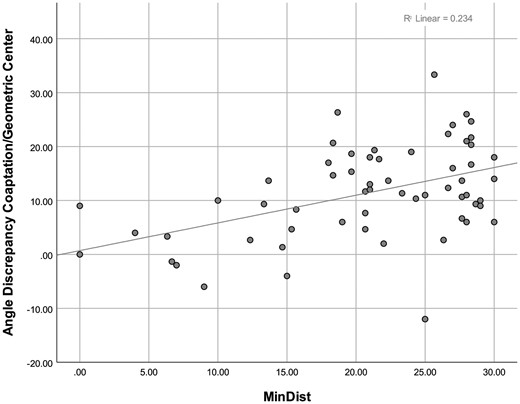
Scatter plot of discrepancy between coaptation angle and geometric angle versus MinDist. The positive correlation (r = 0.435) indicates increasing discrepancy with increasing MinDist, i.e. increasing minimum difference from 120° and 180°, respectively. MinDist: minimum distance to extreme.
DISCUSSION
In the past 2 decades, repair of the BAV has evolved into an increasingly practised alternative to replacement. In particular, the realization that certain anatomic characteristics determine the mid- and long-term results has led to more uniform and reproducible surgical approaches, such as the concepts of effective and geometric height, and in particular annular stabilization [1]. CO has been recognized as one of the important determinants of the functional result of BAV repair [1, 3].
Apart from repair durability, several groups have made the observation that shortening of the fused cusp in asymmetric BAVs will lead to its functional restriction with consecutively increased systolic gradients [7] and turbulent flow [6]. These observations have led to the concept of modifying CO to improve systolic function and repair durability [7]. CO has thus become an important parameter in choosing the best procedure for a given patient [1, 5]. It has become routine to keep a symmetric configuration or achieve it in the case of root replacement through configuration of the graft. Very asymmetric is commonly treated in analogy to the concepts of tricuspid aortic valve repair. The modification in CO is particularly helpful in asymmetric BAVs.A ‘standard’ repair (mainly by adapting the 2 parts of the fused cusp) in both asymmetric and very asymmetric valves will lead to increased postoperative gradients and poor durability [7]. Making the valve more symmetric, e.g. through plicating the fused sinus, results in better mobility of the fused cusp, lower gradients and better durability.
The use of CO as base for operative decision-making requires a quick and reproducible way of measuring it. Since surgical inspection allows at best a rough estimate, echocardiographic determination appears as the best approach. In principle, orientation can be measured easily once the centre of the root has been defined by placing lines through the centre and each of the functional commissures. Modern echocardiographic machines allow for instant determination of such an angle.
Thus, the key to online measurement of CO is precise determination of the centre of the root. Some have done this by simply taking the most central point of the coaptation line (verbal communication). This may be misleading, in particular in the presence of a large non-fused cusp. Our current results confirm that, particularly in asymmetric valves (in whom the precise determination of the angle is especially important), the most discrepant findings between coaptation centre and visual estimate were obtained. We [3, 7] have instead taken the geometric centre of the root. This can be determined through approximating the root shape by a circle or ellipse. The centre of the circle is defined by the crossing point of diametrical lines. This can be done by postprocessing of the echocardiographic image but is difficult to use for online determination. Thus, a method has to be developed that allows for easier determination. In addition, it is yet unclear whether CO is constant throughout the cardiac cycle, i.e. differs between diastole and systole.
To develop an easy determination of the root configuration, we attempted to simplify the ellipse approach. In an ellipse, the centre is the point at which the longest and shortest diameters cross; this is half of either the long diameter or the short diameter, giving 4 points of calibration. We hypothesized that a line segment, representing the longest diameter (with 2 points of calibration), could be used as simple approximation. The line segment is in practice the connecting line between the centres of the fused and non-fused sinuses. In most instances, the rudimentary commissure is visible within the fused part of the root, and the 2 components of the fused cusp are more or less symmetric. Thus, the rudimentary commissure marks the centre of the fused sinuses. The centre of the non-fused sinus is determined by visual estimation. A line is placed connecting the 2 sinus centres, and its length is measured and cut in half. These determinations can easily be done on the screen of currently available echocardiography machines.
We hypothesized that such a determination of the geometric centre by line segment would result in determination with sufficient accuracy and reproducibility. Interestingly, the angles determined by visual inspection were very similar to those obtained through echocardiographic determination if the geometric centre was used. The correlation between circle, ellipse and line segment was so high that they can be considered as equivalent. There was no difference between the angles measured in systole or diastole, so both variants can be used. Commissures may be easier visualized in diastole, so this approach can be expected to yield the more reproducible results.
Interestingly, the coaptation centre approach led to variable differences compared to the geometric methods. The correlation between coaptation centre method and the average of the 3 geometric centre methods was less than ideal (ICC = 0.744). The coaptation centre method underestimates the commissural angle on average by 11° ± 9° compared to the geometric centre methods. The discrepancy varied between the symmetry types of the valves, being highest in asymmetric valves and least in the very asymmetric ones, i.e. those that resemble a tricuspid aortic valve. This is important to consider, since the asymmetric BAVs appear to benefit most from modification in the CO.
Limitations
The limitations of the current analysis are primarily related to the limited number of patients and the possibility source or error of visual estimates. On the other hand, the geometric determinations had a very high correlation and thus consistency, and even a systemic error of ±5° can be considered as clinically irrelevant. An error may be higher if the 2 parts of the fused cusp are asymmetric, i.e. if the rudimentary commissure does not represent the centre of the fused sinus. A further limitation may have been introduced by the fact that the measurements were made by echocardiographers who have been trained in echo analysis prior to repair and working in a centre where repair is part of the routine. The current results will have to be confirmed by others and in a larger patient cohort.
CONCLUSION
In summary, CO can reproducibly be determined in an echocardiographic short axis image. The line segment, connecting the rudimentary commissure with the assumed centre of the non-fused sinus, is a reproducible way of determining the geometric centre of the root andfacilitates intraoperative determination of CO.
Conflict of interest: none declared.
Author contributions
Lennart Froede: Conceptualization; Data curation; Formal analysis; Investigation. Sebatsian Schäfers: Data curation; Formal analysis; Methodology; Validation. Gudrun Wagenpfeil: Data curation; Formal analysis. Alexander Raddatz: Data curation; Writing—review & editing. Klaus Hoffmann: Data curation; Writing—review & editing. Hans-Joachim Schäfers: Conceptualization; Methodology; Project administration; Writing—original draft; Writing—review & editing.
Reviewer information
European Journal of Cardio-Thoracic Surgery thanks Laurent De Kerchove, Alessandro Della Corte and the other, anonymous reviewer(s) for their contribution to the peer review process of this article.
REFERENCES
Abbreviations
- BAV
Bicuspid aortic valve
- CO
Commissural orientation
- ICC
Interclass coefficient
- MinDist
Minimum distance to extreme
- TOE
Transoesophageal echocardiogram





