-
PDF
- Split View
-
Views
-
Cite
Cite
Michael P. Poullis, Richard Warwick, Aung Oo, Robert J. Poole, Ascending aortic curvature as an independent risk factor for type A dissection, and ascending aortic aneurysm formation: a mathematical model, European Journal of Cardio-Thoracic Surgery, Volume 33, Issue 6, June 2008, Pages 995–1001, https://doi.org/10.1016/j.ejcts.2008.02.029
Close - Share Icon Share
Abstract
Objective: To develop a mathematical model to demonstrate that ascending aortic curvature is an independent risk factor for type A dissections, in addition to hypertension, bicuspid aortic valve, aneurysm of ascending aorta, and intrinsic aortic tissue abnormalities, like Marfan’s syndrome. Methods: A steady state one-dimensional flow analysis was performed, utilising Newton’s third law of motion. Five different clinical scenarios were evaluated: (1) effect of aortic curvature; (2) effect of beta-blockers, (3) effect of patient size, (4) forces on a Marfan’s aorta, and (5) site of entry flap in aortic dissection. Results: Aortic curvature increases the forces exerted on the ascending aorta by a factor of over 10-fold. Aortic curvature can cause patients with a systolic blood pressure of 80 mmHg to have greater forces exerted on their aorta despite smaller diameters and lower cardiac outputs, than patients with systolic blood pressures of 120 mmHg. In normal diameter aortas, beta-blockers have minimal effect compared with aortic curvature. Aortic curvature may help to explain why normal diameter aortas can dissect, and also that the point of the entry tear may be potentially predictable. Aortic curvature has major effects on the forces exerted on the aorta in patients with Marfan’s syndrome. Conclusions: Aortic curvature is relatively more important that aortic diameter, blood pressure, cardiac output, beta-blocker use, and patient size with regard to the force acting on the aortic wall. This may explain why some patients with normal diameter ascending aortas with or without Marfan’s syndrome develop type A dissections and aneurysms. Aortic curvature may also help to explain the site of entry tear in acute type A dissection. Further clinical study is needed to validate this study’s finding.
1 Introduction
The imbalance between the forces exerted on the ascending aorta and its biological strength determine its fate, be it a normal ageing process, aneurysmal dilatation or acute dissection.
Risk factors for dissection of the ascending aorta include hypertension, bicuspid aortic valve [1], aneurysm of ascending aorta, and intrinsic aortic tissue abnormalities, like Marfan’s syndrome [2], Loeys–Dietz syndrome [3], or Ehlers–Danlos syndrome [4]. Risk factors for aneurysm formation of the ascending aorta are essentially identical.
Elective surgery of the ascending aorta is solely dictated by its diameter [5] (in the absence of concomitant valvular or coronary disease); however, with the recent widespread introduction of 3D CT reconstruction [6] of the ascending aorta becoming widespread, the degree of curvature of the ascending aorta can now be easily evaluated (Fig. 1 ). Previously invasive investigations like aortography would have been the only investigation available. Cardiac surgeons are well aware of the differing curvatures of patients ascending aorta immediately upon entering the pericardial space.

3D CT reconstructions allow non-invasive assessment of aortic curvature.
Calculating the forces imparted on the aortic wall secondary to blood flow provides a quantitative assessment of the force that the aorta is under due to its 3D geometric shape. The greater the forces exerted on the aorta the more likely it is to dissect or become aneurysmal, due to Laplace’s law.
To determine the possible clinical importance of aortic curvature, five different clinical scenarios were evaluated: (1) effect of aortic curvature and its relative effect compared with (2) beta-blockers; (3) patient size; (4) a Marfan’s aorta; and (5) site of entry flap in aortic dissection.
Due to the large number of variables studied a mathematical model was developed to provide proof of principle (Fig. 2 ).

2 Methods
2.1 Aortic curvature definition
As currently no definition exists of aortic curvature, we define it as the angle between the perpendicular to the plane of the aortic valve, and the perpendicular to the cross section at the origin of the innominate artery (Fig. 2).
2.2 Cardiovascular values utilised in the models
To maintain clinical relevance, for calculation purposes the cardiac output was varied between 3 and 6 l/min, the systolic blood pressure 110–150 mmHg, and ascending aortic diameter 20–40 mm (i.e. non-aneurysmal). Aortic curvature was varied from 10° to 90°. The body’s natural negative intrathoracic pressure was not included in this model. The aortic valve was assumed to be anatomically normal for analysis, with blood ejected at right angles to the plane of the valve.
2.3 Steady state model
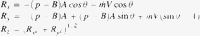
 mass flow rate within lumen of aorta; V, Velocity of flow; Rx, force on aortic wall in x direction; Ry, force on aortic wall in y direction; Rz, resultant force on aortic wall.
mass flow rate within lumen of aorta; V, Velocity of flow; Rx, force on aortic wall in x direction; Ry, force on aortic wall in y direction; Rz, resultant force on aortic wall.2.4 Effect of beta-blockers
Previous work has demonstrated that beta-blockers reduce the peak velocity of blood in the ascending aorta from 130 cm/s to about 80 cm/s [7]. In addition beta-blockers reduce systolic blood pressure and cardiac output. We assumed a 10% reduction in blood pressure (140 mmHg vs 126 mmHg) and cardiac output (5 l/min vs 4.5 l/min) for these calculations. By inserting these values into Eq. (1), the effect of beta-blockade can be modelled. The aortic diameter was 4 cm for all calculations.
2.5 Effect of patient size
To model for the effects of patient size, the effects of aortic curvature was compared in 50, 70, 90, and 110 kg patients. The associated ascending aortic diameters, cardiac outputs, and blood pressures utilised are shown in Table 1 .

Variables utilised in calculating forces acting on ascending aorta for different body sizes.
2.6 Forces on a Marfan’s aorta
Previous work has demonstrated that the elasticity of a Marfan’s aorta has two components separated by a threshold point [8]. Up to the threshold point the elasticity is determined by elastin, and above the threshold it is determined by collagen. The blood pressure determines on which point of the elasticity curve a particular patient is. Typically a pressure of 120 mmHg ensures that the aortic elasticity is due to collagen, and a blood pressure of 80 mmHg ensures the aortic elasticity is due to elastin. The forces in a Marfan’s aorta was thus modelled at 120 and at 80 mmHg, with a cardiac output of 5.0 l/min, and ascending aortic diameters of 4.0 cm (i.e. non-aneurismal).
2.7 Site of aortic dissection
3 Results
3.1 Steady state model
3.1.1 Aortic curvature
As the curvature in the ascending aortic increases (Fig. 3a ) from straight to curved (90°–10°), the force on the aortic wall increases by a factor of over 10, this is despite a normal aortic diameter, normal blood pressure and normal cardiac output.

(a) Effect of aortic curvature on the reaction force acting on the ascending aorta. Model variables: aorta was 3.5 cm in diameter, systolic blood pressure was 140 mmHg, and the cardiac output 5 l/min. (b) Effect of diameter on the reaction force acting on the ascending aorta. Model variables: systolic blood pressure was 140 mmHg, and the cardiac output 5 l/min.
3.1.2 Diameter effects
As would be predicted, as the diameter of the ascending aorta increases so does the reaction force acting on the ascending aorta (Fig. 3b). As the ascending aorta diameter increases in size from 3.5 to 5.5 cm it can be seen that the magnitude of increase in force on the wall increases by about four times. However, the absolute increase in force is greatest the more curved the ascending aorta is, with over 10-fold increase in the total force exerted on the ascending aorta as curvature increases from straight to curved.
3.1.3 Blood pressure
It can be seen from Fig. 4a that as the blood pressure increases so does the reaction force acting on the ascending aorta. As the patient’s systolic blood pressure increases from 110 to 150 mmHg, it can be seen that the increase in force on the wall is 1.3-fold. However, as the curvature increases the force increases to over 10-fold.

(a) Effect of Blood pressure on the reaction force acting on the ascending aorta. Model variables: aortic diameter was 3.5 cm, and the cardiac output 5 l/min. (b) Effect of cardiac output on the reaction force acting on the ascending aorta. Model variables: aortic diameter was 3.5 cm, and the blood pressure 140 mmHg.
3.1.4 Cardiac output
From Fig. 4b it can be seen that as the cardiac output increases from 4 to 7.5 l/min the reaction force acting on the ascending aorta is virtually unchanged. However, as the aortic curvature increases the force acting on the ascending aorta increases to over 10-fold.
3.2 Effect of beta-blockers
Beta-blockers had a relatively small effect, (Fig. 5a ), on reducing the force acting on the ascending aorta by a factor of 1.2. It should be noted that in the calculations for the effect of beta-blockers the blood pressure, cardiac output and aortic blood flow velocity were all reduced appropriately, but despite this, beta-blockers have a relatively small effect compared to aortic curvature. As aortic curvature increased this had greater than 10-fold increase in the force acting on the ascending aorta.

(a) Effect of beta-blockers on the reaction force acting on the ascending aorta. Model variable: aortic diameter was 3.5 cm. (b) Effect of patient size on the reaction force acting on the ascending aorta. Model variables: aortic diameter, blood pressure and cardiac output are detailed in Table 1.
3.3 Effect of patient size
It can be seen, (Fig. 5b), that the larger the patient the greater the forces acting on their aorta for a given aortic curvature. However, patients who are 50 kg can have forces exerted on their aorta that are greater than those experienced in a 110 kg patients, depending on their aortic curvature. A 50 kg patient with an aortic curvature of 10° has the same force on their aortas as a 110 kg patient with a curvature of 65°. This is despite the 110 kg patient having a higher systolic blood pressure (140 mmHg vs 110 mmHg), a larger aortic diameter (4.5 cm vs 3.0 cm), and a higher cardiac output (5.5 l/min vs 4.0 l/min). Patients who are 110 kg only start to have greater forces exerted on their aortas when their aortic curvature is less than 60°.
3.4 Forces on a Marfan’s aorta
It can be seen, (Fig. 6a ), that patients who have a systolic blood pressure of 80 mmHg can have forces exerted on their aorta that are greater than those experienced in a patient with a systolic blood pressure of 120 mmHg. Patients with a systolic blood pressure of 120 mmHg only start to have greater forces exerted on their aortas when their aortic curvature exceeds 45°.

(a) Effect of blood pressure on the reaction force acting on a Marfan’s ascending aorta. Model variables: cardiac output was 5.0 l/min, and ascending aortic diameter of 4.0 cm (i.e. non-aneurismal). (b) Effect of aortic curvature on height of impact above the aortic valve of blood being ejected through the aortic valve.
3.5 Site of aortic dissection
The height above the aortic valve where the aorta receives the greatest impact from blood being ejected through the aortic valve increases the straighter the ascending aorta (Fig. 6b). This calculated variable is independent of blood pressure, cardiac output, beta-blocker therapy, intrinsic aortic tissue abnormality and ascending aortic diameter (Fig. 7 ).

Diagrammatic representation of mathematical model, and the variables utilised.
4 Discussion
We have shown that aortic curvature is, potentially, a more important factor than diameter, blood pressure or cardiac output with regards to the forces on the aortic wall. With the introduction of 3D CT reconstructions the curvature of the ascending aorta can now be easily measured. Conventional 2D CT plane films are not adequate to calculate aortic curvature.
The force exerted on the ascending aorta is dependent on the 3D geometry of the vessel and the pressure and flow within the vessel. Assuming a smooth walled rigid vessel, the tensile physical characteristics of the vessel have no effect on determining this force. However, the vessels’ physical properties determine its fate due to the forces imposed on it.
Aortic rupture and aortic dissection are known adverse effects that occur to patients on surgical waiting lists. The frequency is increased with patients with known aneurysms. Demonstration of the importance of aortic curvature will enable clinicians to prioritise surgical intervention with regard to aortic diameter, extent of aneurysm, and aortic curvature. In the past the aortic diameter was the major risk factor for aortic rupture or dissection. Up to a third of aortic dissections occur in patients with no demonstrable tissue defect and with normal ascending aortic diameters. Aortic curvature may help to explain this.
Beta-blockers are the mainstay of medical management in aortic dissections; however, it can be seen that their effect is only modest compared to the effect of aortic curvature. The cumulative effect of beta-blockers on peak aortic blood flow velocity (130 cm/s vs 80 cm/s), cardiac output (5 l/min vs 4.5 l/min) and systolic blood pressure (140 mmHg vs 126 mmHg) can result in the forces on the ascending aorta being reduced by 1.2-fold. Aortic curvature reduced the force by a factor of over 10-fold.
Patient size is an important consideration with regard to the forces acting on the aortic wall. For any given aortic curvature a 110 kg patient will have greater forces acting on their ascending aorta than a 50 kg patient; however depending on the aortic curvature, the 50 kg patient (aortic curvature between 0° and 10°) may potentially have more than double the forces acting on their aorta than a 110 kg patient (aortic curvature greater then 80°).
Interpretation in the medical literature of the stresses and strains exerted on the ascending aorta in normal and Marfan patients is difficult due to the variable use of the following terms: Young’s modulus, Petersons’s pressure–strain elastic modulus, arterial stiffness constant, stiffness [9], static aortic compliance, compliance [10], elasticity, distensibility, and extensibility, when referring to essentially the same physical property of the aorta. We based our calculations on previously published elastance data [8].
Aortic elasticity is determined by its elastin and collagen content. At higher pressure (>120 mmHg) collagen is relatively inelastic, and consequently increases the stresses experienced by the ascending aorta. The Young’s modulus (the ratio between stress and strain) in a Marfan’s aorta is twice that of a normal aorta. We have shown that the forces exerted in a Marfan’s aorta can be greater with a blood pressure of 80 mmHg, compared to a pressure of 120 mmHg, depending on the aortic curvature. Patients with Marfan’s syndrome can dissect despite normal aortic diameter [11]. To date the only risk factor for this occurrence is familial history of dissection [12]. Aortic curvature may thus help to partially explain dissection in a non-aneurysmal Marfan’s aorta.
The most common site of an entry tear in type A dissection is just above the sinotubular junction. The second most common site is just before the innominate artery. We have shown that the aortic curvature affects the site of impact of the ejected blood. Thus aortic curvature in a non-diseased aorta may help predict the entry site of a future aortic dissection.
Aortic elongation can occur in the absence of dilatation. As the aortic valve position is relatively fixed by the cardiac geometry and the innominate artery is relatively fixed by the head and neck structures, increased aortic curvature is the only possible result. Anecdotally this can be sometimes observed at surgery in Marfan’s patients with isolated root dilation. Patients with Loeys–Dietz syndrome develop elongated tortuous and dilated arteries that are prone to dissection and rupture [13]. Elongation and tortuosity are synonymous with increased curvature.
Aortic stenoses with or without a bicuspid valve are known risk factors for dissection or aneurysm formation in the ascending aorta. Our model could be extended to analyse these scenarios, via modelling the effects of jet flow through the valve, but the same principle of the effects of aortic curvature still holds regardless of angle and direction of jet.
The geometry of the ascending aorta affects the fluid dynamics of the blood flow in the arch. Having demonstrated that the geometry of the ascending aorta is potentially crucial to the development of dissections or aneurysms, the aortic arch now needs to be studied. Aortic arch curvature has recently been shown to be associated with enhanced systolic wave reflection, central aortic stiffness, and increased left ventricular mass [14].
4.1 Clinical implications
Aortic curvature in addition to aortic diameter may need to be considered when deciding on when to operate on the ascending aorta, should this mathematical treatise prove to be correct in humans.
4.2 Study limitations
This study was a mathematical treaty to apply a basic science concept in fluid dynamics to cardiac surgery. The mathematical analysis assumed Newtonian flow in a rigid tube, which was steady state. Future work in a clinical setting is now needed to validate this work.
5 Conclusion
Aortic curvature is relatively more important than aortic diameter, blood pressure, cardiac output, beta-blocker use, and patient size with regard to the force acting on the aortic wall. This may explain why some patients with normal diameter ascending aortas with or without Marfan’s syndrome develop type A dissections, and aneurysms. In addition aortic curvature may help to explain why some patients dissect just above the sinotubular junction, and others just proximal to the innominate artery.
Aortic curvature should now be studied in humans as a possible risk factor for dissection and potentially influencing timing of ascending aortic replacement surgery.
Appendix B
Basic fluid mechanic theory dictates that the force exerted on fluid in aorta due to fluid motion (Fig. 7) (change of momentum) can be calculated from Eq. (3).

Assumptions
Quasi steady flow (peak values)
Two-dimensional
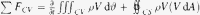
Eq. (3) simplifies to (see Fig. 6), Eq. (4) in x-axis, and Eq. (5) in y-axis

Forces on aorta must be in static equilibrium, Eq. (6)
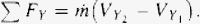
Combining Eq. (4) and (6), yields Eq. (7)

Similarly, combining Eqs. (5) and (6), yields Eq. (8)
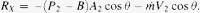
Further assumptions
(a) Pressure loss across aorta is small, therefore p1 ~ p2.
(b) Diameter change along aorta is small, therefore A1 ~ A2. where p – B = systolic blood pressure; A = ascending aorta cross-sectional area;
 (cardiac output) in Kg/s.
(cardiac output) in Kg/s.
Total force (N) acting on aorta, combining Eqs. (7) and (8), yields Eq. (9)
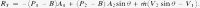
References
Author notes
Presented at the 21st Annual Meeting of the European Association for Cardio-thoracic Surgery, Geneva, Switzerland, September 16–19, 2007.




