Abstract
Objective: To identify pre-operative factors associated with in-hospital mortality following lung resection and to construct a risk model that could be used prospectively to inform decisions and retrospectively to enable fair comparisons of outcomes. Methods: Data were submitted to the European Thoracic Surgery Database from 27 units in 14 countries. We analysed data concerning all patients that had a lung resection. Logistic regression was used with a random sample of 60% of cases to identify pre-operative factors associated with in-hospital mortality and to build a model of risk. The resulting model was tested on the remaining 40% of patients. A second model based on age and ppoFEV1% was developed for risk of in-hospital death amongst tumour resection patients. Results: Of the 3426 adult patients that had a first lung resection for whom mortality data were available, 66 died within the same hospital admission. Within the data used for model development, dyspnoea (according to the Medical Research Council classification), ASA (American Society of Anaesthesiologists) score, class of procedure and age were found to be significantly associated with in-hospital death in a multivariate analysis. The logistic model developed on these data displayed predictive value when tested on the remaining data. Conclusions: Two models of the risk of in-hospital death amongst adult patients undergoing lung resection have been developed. The models show predictive value and can be used to discern between high-risk and low-risk patients. Amongst the test data, the model developed for all diagnoses performed well at low risk, underestimated mortality at medium risk and overestimated mortality at high risk. The second model for resection of lung neoplasms was developed after establishing the performance of the first model and so could not be tested robustly. That said, we were encouraged by its performance over the entire range of estimated risk. The first of these two models could be regarded as an evaluation based on clinically available criteria while the second uses data obtained from objective measurement. We are optimistic that further model development and testing will provide a tool suitable for case mix adjustment.
1 Introduction
The risk of death is one of the major factors to be taken into account when deciding with a patient whether surgery is the best course of action. The considerations vary depending upon whether the operation is being done largely for symptoms or is being undertaken to avert the natural course of a life-threatening disease. Lung cancer falls strongly into the life-saving category [1,2], while more emphasis may be placed on symptom relief in other thoracic operations. Although data on operative risk are available for the patient population as a whole from case series and registry data, there is currently no accepted risk model for thoracic surgery that can be used to estimate the risk of operative death amongst subgroups of patients.
Several scoring systems have previously been developed in order to stratify patients according to risk of complications following lung-resection [3–7]. These models have been developed in relatively small studies. As a result, there has been limited scope within these studies for testing the models developed. Also, due to the low peri-operative mortality rate amongst lung resection patients, there is limited information within these studies as to which factors are related to mortality as opposed to non-fatal complications. This is also the case for models that have been developed in other patient populations and used or adapted for use amongst lung resection patients [8,9].
In addition to providing patients and their surgeons with better quality information upon which to base the clinical decision to operate or not, a robust risk model would allow fairer comparison of mortality data between institutions. This was in fact the original purpose of the cardiac surgical risk model devised by Parsonnet [10]. UK thoracic surgeons are currently obliged to publish mortality data with no such risk adjustment and this is widely recognised as being undesirable [11,12].
This paper describes the development of two models of the risk of in-hospital death following a patient’s first lung resection. The decision to build the second model was made on inspection of the results of the first model building exercise.
2 Patients and methods
Data were collected using a computer database (Filemaker Pro) developed by one of the authors (RGB). Units that applied to join the project via a World Wide Web page linked to both the ESTS and EACTS Internet sites were sent a confidential code. This enabled them to download the database application and instructions for its use from the Internet. The database application was password protected, allowing each unit to have multiple users with their own passwords.
Any sensitive information such as surgeon and patient identification was encrypted such that patient data remained the property of each unit, the central database manager being blind to the encryption key of each unit. Data were exported from within each unit’s database using encryption, automatically attached to an email and sent to the central data repository. Units could submit data whenever they wished, but each case was added to the central database only if more than 95% of appropriate fields were complete and valid.
The data set included information on the type of procedure performed, the stated urgency of the procedure, the date that the procedure was performed and the speciality of the surgeon. Patient characteristics reported included age, sex, diagnosis, ECOG (Eastern Cooperative Oncology Group) performance classification, ASA (American Society of Anaesthesiologists) score, the UK Medical Research Council dyspnoea score, ppoFEV1% (the predicted post-operative FEV1%) and ppoDLCO% (the predicted post-operative DLCO%). For cancer patients, additional information concerning pathological staging and any adjuvant chemotherapy received was reported. A full description of the data collected and the definitions used can be viewed at http://www.ests.org.uk/Archive/Enrollment.htm.
The outcomes reported included post-operative complications, deaths within 30 days and deaths within the same hospital admission. Status at discharge was used as the outcome measure of interest for the risk analysis, as it has become customary in other large data collections for performance monitoring purposes [11].
Data entry was constrained as much as possible by using hierarchical dropdown menus to record procedure and diagnosis. Free text entry was allowed as an extra option. As this resulted in a number of different descriptions for these two factors, mutually exclusive categories of procedure type were defined on inspection of the data, but prior to any analysis of the mortality data. For each patient, the reported type of procedure was matched to one of these categories. The same procedure was followed to define a number of categories of diagnosis.
Records were excluded from the analysis if the procedure described was not judged by one of the surgical authors (TT) as constituting lung resection. Only records representing the first lung resection procedure for a patient were entered into the risk analysis to ensure that the records analysed were independent of each other. Analysis was restricted to patients over 16 for whom mortality data were available.
The data were analysed using the Statistics Package for the Social Sciences (SPSS) version 7.5. The in-hospital mortality rate was calculated for all patients undergoing lung resection and for each sub-category of procedure, along with exact 95% confidence intervals in each case. Of the records, 60% were selected to contribute to model development and the remaining 40% were reserved for model testing.
2.1 Model 1—statistical risk model building for all diagnosis groups
Logistic regression analysis was performed to identify pre-operative clinical characteristics of patients that were significantly associated with in-hospital mortality. For the purposes of the regression analysis, procedures were divided into four groups: wedge and segment resections, lobectomy and extended lobectomy, pneumonectomy and extended pneumonectomy (including extra pleural pneumonectomy), and lung volume reduction. The urgency of the procedure was not considered a candidate within the model building, as such judgements of priority are often influenced by levels of service provision and these vary across the centres and nations involved in the study. One feature of logistic regression analysis is that only cases with data for all of the variables considered are included in the analysis. Based on this regression analysis, a logistic model of risk of in-hospital death was developed using the ‘forward stepwise’ method [13].
To assess the performance of the model amongst the cases used for its development, these were ordered according to increasing predicted risk and the cumulative predicted mortality and the cumulative actual mortality were plotted and compared visually as suggested by Gallivan (Professor S. Gallivan, Director of the Clinical Operational Research Unit, University College London, private communication).
In order to evaluate the performance of the model across the spectrum of predicted risk amongst the test group, a plot of cumulative predicted mortality and cumulative actual mortality was constructed as for the development set.
2.2 Model 2—a model of risk for lung tumour resections based on age and ppoFEV1%
Once the performance of Model 1 amongst the test data had been established and reviewed, the authors decided to construct a separate model for risk amongst patient with a diagnosis involving tumour growth based on the objective measures of age and ppoFEV1%. This second model was built using the ‘enter’ method of logistic regression [13].
3 Results
The data reported here were collected between January 2001 and December 2003. Of 112 Units who requested the database, 27 units in 14 countries compiled data sets that were sufficiently complete to enter the central database. The data consisted of 3517 procedures identified as ‘lung resections’ by the contributors, performed on 3488 patients. Six records were removed as the specific procedure identified was not recognised as a lung resection by the adjudicating surgical author (TT). Selecting the first lung resection for each patient gave 3481 records, amongst which in-hospital mortality data were unavailable in 30 cases (30-day mortality was unavailable in 568 cases). Removing 25 paediatric cases (reported age <16) gave 3426 records available for analysis (see Fig. 1 ).
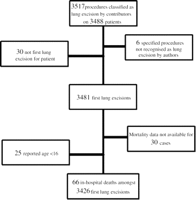
A flow chart summarising how the records used in the analysis were selected from the database.
Of the 3426 patients, 2480 (72.4%) were males and 946 (27.6%) were females. The median age amongst the patients was 62 (interquartile range 53–70). The diagnoses recorded by contributors were divided into 10 groups as given in Table 1 .
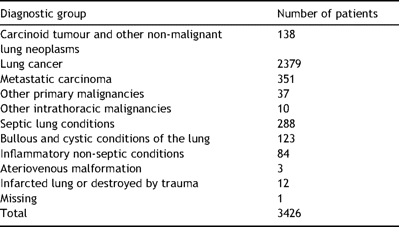
The number of patients in each of 10 diagnostic groups defined retrospectively, but prior to analysis of mortality data
There were 66 deaths amongst the 3426 cases (1.9%, 95% confidence interval 1.5–2.4%). The in-hospital mortality rates for different categories of lung resection procedure are given in Table 2 .
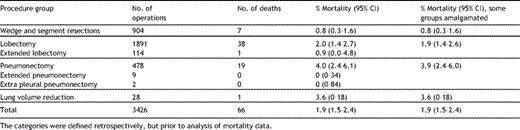
The in-hospital mortality rate (and exact 95% confidence intervals) for different categories of lung resection procedure
Of the records, 2056 were selected at random to comprise the data set used for model development and the remaining 1370 records were retained for testing the resulting model.
3.1 Model 1—all diagnosis groups
For all diagnosis groups, the variables considered for the initial logistic regression model are shown in Table 3 . Also shown is the statistical significance of the univariate association between each factor and in-hospital death. As ppoDLCO% data were missing for a large proportion of cases, this variable was excluded from the analysis. The initial regression analysis identified dyspnoea, ASA score and procedure group as significantly associated with in-hospital mortality.
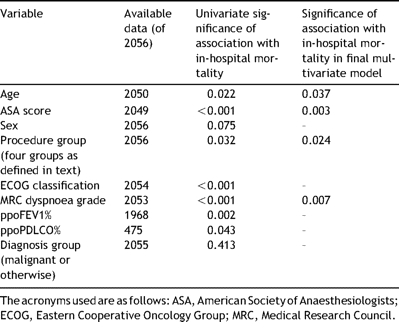
The pre-operative factors entered as candidates for a multiple variable model of risk of in-hospital mortality for patients undergoing lung resection. The statistical significance of any association between a factor and risk of in-hospital death is shown at univariate level and multivariate level
As 88 cases (2 deaths) had missing data concerning ppoFEV1% and this variable was not found to be associated with in-hospital mortality at a multivariate level, a further analysis was performed including these extra cases. This analysis identified dyspnoea, ASA score, procedure group and age as being significantly associated with in-hospital mortality. The statistical significance of the association between each factor that contributed to the resulting model 1 and in-hospital mortality is given in Table 3.
Fig. 2 A shows a comparison of the cumulative predicted and actual mortality amongst the data used for model development, with the cases ordered by increasing predicted risk. The performance of the model displayed in this plot was deemed sufficiently good that no further model development was undertaken for fear of ‘over-fitting’ the data.
Model 1. The cumulative observed mortality and that predicted using model 1 amongst (A) the development set and (B) the test set, with the cases ordered by increasing predicted risk.
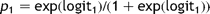
Terms that contribute to model 1 of risk of in-hospital death for all diagnosis groups
For 1361 (99%) of the 1370 cases in the test data set, there was sufficient data to use the model to estimate the risk of in-hospital death. The plot of cumulative predicted mortality and cumulative actual mortality amongst this group is shown in Fig. 2B.
3.2 Model 2—lung tumour resections
Between the development of model 1 and the development of model 2, survival data were obtained for a further 21 patients. Thirteen of these records (60%) selected at random were allocated to the data set used for model development and the remaining eight to the test data set. Selecting those patients in diagnosis groups 1–5 (carcinoid and non-malignant lung neoplasms, lung cancer (SCLC and NSCLC), metastatic carcinoma, other primary malignancies, and other intrathoracic malignancies) gave 1753 patients (34 deaths) within the development set and 1166 (23 deaths) in the test set.
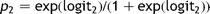
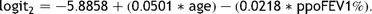
Amongst the remaining 1166 cases, there were sufficient data to use model 2 to calculate the predicted risk in 1128 (97%). Fig. 3 shows the comparison of cumulative predicted and actual mortality within these, with the cases ordered by increasing predicted risk.
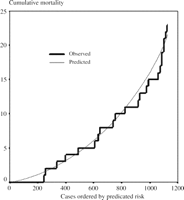
Model 2. The cumulative observed mortality and that predicted using model 2 with cases ordered by increasing predicted risk.
4 Discussion
The rate of accrual of data was slower than expected. Data were collected on all thoracic surgical procedures, not just lung excision so that an overview of thoracic surgical practice in Europe could be obtained (Fig. 4 ). This was unattractive to many units that wanted to submit only data on lung resections. It should be noted that there is no mechanism for independent validation of the completeness or accuracy of each centre’s data.
The European Thoracic Surgery Database.
In many units, 30-day mortality is not collected routinely. It was not made a mandatory field in this first version of the database, but it will be a mandatory field in subsequent versions.
The overall in-hospital mortality rate was calculated as 1.9% (95% CI 1.5–2.4). The factors identified as being associated with increased risk were MRC dyspnoea and ASA scores, class of procedure, and age. These factors have clinical face validity. One counterintuitive feature of the model is that patients with ASA=4 (incapacitating systemic disease, constant threat to life) have lower predicted risk than patients with ASA=3 (severe systemic disease, not incapacitating). Subsequent investigation of these data has revealed that in a cluster of cases there was a high use of the ASA=4 category, which was so prevalent that it might have amounted to ‘gaming’. That is to say that criteria based on clinical judgements are over stated with the effect that the risk-adjusted mortality is artificially lowered. To have removed these data and repeat the analysis would have been scientifically improper. It should be stated that in-hospital death is an imperfect surrogate for the risk of death attributable to surgery.
It is perhaps surprising that ppoFEV1% was not found to be associated with outcome. However, dyspnoea score reflects the patient’s overall cardiorespiratory status more completely than ppoFEV1%. The equation used in the database for calculating predicted post-operative values simply scaled the pre-operative value by the proportion of segments remaining. This is slightly different from the equation by Nakahara [14]. Data concerning ppoDCLO%, which has been shown to be associated with mortality [15], were available for only a quarter of patients; this is a limitation of the study.
It should be remembered that if some apparently obvious risk factor does not appear in a logistic model, one cannot infer that this is irrelevant to outcome. Failure to show that, for instance, ppoFEV1% is associated with outcome is by no means the same as establishing that it is not associated with outcome. Although the number of cases appears large, the small number of deaths precludes such inference.
When tested on 1370 cases that did not contribute to development, model 1 could be used to generate an estimate of risk in 1361 (>99%) cases. The similar shape of the curves of predicted and actual cumulative mortality in Fig. 2B indicates that model 1 is a useful tool for discerning between different groups of patient in terms of the risk of in-hospital death following surgery. Within the test data set, model 1 performed well for patients at low risk, underestimated mortality at medium risk and overestimated mortality at high risk. The relatively small size of the data set precludes more general statements on the model’s performance.
On viewing the results of the regression analysis and the performance of Model 1, the authors noted that some objective measures (for example ppoFEV1) were excluded and the model appeared to be dominated by subjective assessments. The authors decided at this point of the analysis that while this was a useful clinically based model and propose that it be referred to as the European Society Subjective Score (ESSS.01), a model based on objective measures would be preferable. It was also considered at this stage that the patient group used for the development of Model 1 might have been too heterogeneous and that a model that focussed on those patients having resections for lung neoplasms would be more useful. The resulting model 2, labelled the European Society Objective Score (ESOS.01), shows promise, vindicating the decision to build this second model. ESSS.01 (the more clinically based model) could be regarded as a first evaluation while the more objective ESOS.01 could be appropriate for a final decision about surgery. It should be noted that, although the test data were not used directly in the development of ESOS.01, the decision to construct this model was made after the performance of model 1 amongst the test data has been assessed. Hence, we do not claim that the development of ESOS.01 was entirely independent of the characteristics of the test data set. That caveat aside, the performance of this model is encouraging.
As ever, caution is required in interpreting the prediction of a risk model in the case of an individual patient. Furthermore, the model here only deals with peri-operative mortality, which is only one factor in decision making. A better focus of performance monitoring would be the whole of the multidisciplinary team decision and its impact on long-term survival.
Acknowledgements
