-
PDF
- Split View
-
Views
-
Cite
Cite
Laura Matrajt, M Elizabeth Halloran, Rustom Antia, Successes and Failures of the Live-attenuated Influenza Vaccine: Can We Do Better?, Clinical Infectious Diseases, Volume 70, Issue 6, 15 March 2020, Pages 1029–1037, https://doi.org/10.1093/cid/ciz358
Close - Share Icon Share
Abstract
The effectiveness of the live-attenuated influenza vaccine (LAIV) can vary widely, ranging from 0% to 50%. The reasons for these discrepancies remain largely unclear.
We use mathematical models to explore how the efficacy of LAIV is affected by the degree of mismatch with the currently circulating influenza strain and interference with pre-existing immunity. The models incorporate 3 key antigenic distances: the distances between the vaccine strain, pre-existing immunity, and the challenge strain.
Our models show that an LAIV that is matched with the currently circulating strain is likely to have only modest efficacy. Our results suggest that the efficacy of the vaccine would be increased (optimized) if, rather than being matched to the circulating strain, it is antigenically slightly further from pre-existing immunity than the circulating strain. The models also suggest 2 regimes in which LAIV that is matched to circulating strains may be protective: in children before they have built immunity to circulating strains and in response to novel strains (such as antigenic shifts) which are at substantial antigenic distance from previously circulating strains. We provide an explanation for the variation in vaccine effectiveness between studies and countries of vaccine effectiveness observed during the 2014–2015 influenza season.
LAIV is offered to children across the world; however, its effectiveness significantly varies between studies. Here, we propose a mechanistic explanation to understand these differences. We further propose a way to select the LAIV strain that would have a higher chance of being protective.
Seasonal influenza viruses continue to pose significant disease and economic burden, with the Centers for Disease Control and Prevention (CDC) estimating between 12 000 and 56 000 deaths per year and between 9.2 and 35 million illnesses per year [1] in the United States. Due to the constant mutation of influenza viruses, the currently available influenza vaccines, the inactivated injectable influenza vaccine and a live-attenuated influenza vaccine (LAIV), are updated annually.
Early studies comparing the effectiveness of LAIV and inactivated influenza vaccine found the former to have a much better effectiveness in children than the latter [2–6], prompting the CDC’s Advisory Committee on Immunization Practices (ACIP) preferentially to recommend the use of LAIV in healthy 2- to 8-year-old children in 2014. The United Kingdom started a universal pediatric vaccination program with LAIV in 2013, and 1 year later, LAIV was offered in Finland to 2-year-olds for the first time. However, vaccine-effectiveness studies done in the United States showed mixed LAIV effectiveness during the 2013–2016 influenza seasons, ranging from 0% to 50% effectiveness [7–13]. As a result, the ACIP suspended the recommendation of LAIV for the next 2 seasons but resumed it for the 2018–2019 season. In contrast, studies done in Canada, the United Kingdom, and Finland told a very different story, with effectiveness ranging from 31% to 57.6% [14–18].
The reasons for these discrepancies remain largely unknown, with some attributing them to a reduction in fitness in the vaccine strain [19], problems with vaccine production [20], mismatches between the vaccine and the circulating (challenge) strain, or pre-existing immunity affecting the vaccine’s immunogenicity. The latter is called negative interference.
Negative interference has been well studied for inactivated influenza vaccines, with studies showing that, depending on the year and circulating serotype, people who have been vaccinated in the previous year(s) have a decreased vaccine efficacy compared with those who have not been vaccinated [21–23]. In a seminal paper in 1999, Smith et al [24] used a mathematical model to provide a quantification of negative interference for repeated influenza vaccination with inactivated vaccine. This phenomenon has been less studied for LAIV [21, 25]. Here, we use mathematical models to explore how the antigenic distance hypothesis can be used to explain differences in the vaccine effectiveness of LAIV. We hypothesize that differences seen in vaccine effectiveness across influenza seasons and across different countries arise from the interplay of 3 antigenic distances: the distances between the vaccine strain, pre-existing immunity, and the challenge strain.
METHODS
We developed nested mathematical models of increasing complexity describing the interaction between influenza virus and immune response [26] (Supplementary Figure S1). The adaptive immune response is generated by B-cell clones that produce antibodies, with different clones having different affinities to different viruses. The effectiveness of each of these clones depends on the antigenic distance between each clone and the virus. Clones having a higher affinity are stimulated more and generate larger numbers of B cells and antibodies. We utilized the antigenic distance given in Smith et al [24] and we assumed that once the antibodies and the antigen are approximately 20% different (Supplementary Figure S1), there is no cross-reactivity (similar to [17], see Supplementary Material). Hence, antigenic drift occurs in our models for parameter regimes where the antigenic distance between the challenge virus and previously circulating virus is in that range (20–30%). Because target-cell limitation models have been extensively used to describe within-host viral dynamics, we present here results for such a model (Supplementary Figure S2, Model 2) with 20 B-cell clones, but our results were consistent across a variety of model structures and insensitive to the number of clones (sensitivity analysis, Supplementary Figures S5–S16 and Supplementary Material).
We modeled pre-existing immunity as closest to the virus strain predominantly circulating in the population in the previous year, which, by simplicity, is assumed to be closest to B-cell clone 1. We then simulated vaccination with an LAIV vaccine by running the model for an attenuated virus (a vaccine strain can be attenuated in 2 ways in our model: either by reducing its growth rate and/or by increasing the rate at which antibodies remove virus). Finally, we simulated an epidemic challenge by running the model for a third, different virus. This is a within-host infection with viral replication taking place over time. The more replication there is, the higher the area under the growth curve will be. We use the area under the curve (AUC) for the (log) viral load curve for the infection with the challenge strain as an indication of immune control: if the AUC is less than 2, the infection with the challenge virus was deemed controlled by sterilizing immunity. Furthermore, we use this quantity to define a within-host vaccine effect, veω, that quantifies the extent to which the vaccine prevents further infections with that challenge strain, given by . A full description of the methods can be found in the Supplementary Material.
RESULTS
Influence of Pre-existing Immunity in Vaccination with LAIV
Our model recapitulates key features of primary influenza infection (Figure 1). If a vaccine strain is closely matched to pre-existing immunity, the model predicts that the pre-existing immunity will control the vaccine and no B-cell clone will be significantly boosted (Figure 2A and Figure 4), resulting in a poorly immunogenic vaccine. In this case, no new B-cell clone is stimulated and the antibodies matching the primary infection get a slight boost. However, once a vaccine strain is sufficiently different from pre-existing immunity (∼30% for our model parameters), the attenuated virus contained in the vaccine is no longer controlled by pre-existing immunity and this results in a high viral load and in the stimulation of B-cell clones and antibodies closest to the vaccine strain (Figure 2B and Figure 4). Interestingly, we find that the magnitude of the antibody response generated by B-cell clones stimulated during the primary infection is higher than that of clones that match the secondary challenge, consistent with the Original Antigenic Sin theory [28].
![Within-host simulation of the dynamics of an influenza primary infection (ie, with no pre-existing immunity). A, Uninfected cells (U) become infected (I) upon contact with virus (V). Viral load peaks around day 3, reaching well-established viral load values [27]. Immune response is modeled by including B-cell and antibody clones. For each clone, B-cell stimulation, antibody production, and the antibody’s ability to remove virus are modulated by a function that depends on the antigenic distance between that clone and the virus. The B-cell clones closest to the virus are stimulated the most, and the stimulation decays with distance (pie chart). These clones produce elevated levels of antibodies within 2–3 days of stimulation. Antibodies, in turn, clear virus. Pie charts: Contribution of each clone to the total B-cell and antibody response before (B) and after (C) the primary infection. The virus V was closest to clone 1 in this simulation with the parameters given in Supplementary Table S1. The model was run with 20 clones.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/cid/70/6/10.1093_cid_ciz358/4/m_ciz358f0001.jpeg?Expires=1750820222&Signature=NfSZFxKk98qCH0Yy9hIX8X3VD-b8LffHtkPnzE7n0TsIYjy7yQYs4zFSxdHe~oQCJciSo6rk3Qh51iwyOGOBmH8oG~waIJctQOL988SclkXl0A6xzctnhj0naNZFWoQbGlsig7aO-tCk8LKQFmbeW8MmTW95zX4s07iZgJDK243hfYJaL1aP3diqsV~NjHE4ulSYDNCpwdknmSkHbRj~ceMSPivek8nc6g6ZGlY7rwTBs-nBX7IbFQJC1arZ~CcAGoYYnNIulr1lqSsAqif32uROR0zG5hRFlD97Ip~IYq3trS1HtQhZU2FF4CXpj1DC2Ye28z8j~wkhli2o6hYmHA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Within-host simulation of the dynamics of an influenza primary infection (ie, with no pre-existing immunity). A, Uninfected cells (U) become infected (I) upon contact with virus (V). Viral load peaks around day 3, reaching well-established viral load values [27]. Immune response is modeled by including B-cell and antibody clones. For each clone, B-cell stimulation, antibody production, and the antibody’s ability to remove virus are modulated by a function that depends on the antigenic distance between that clone and the virus. The B-cell clones closest to the virus are stimulated the most, and the stimulation decays with distance (pie chart). These clones produce elevated levels of antibodies within 2–3 days of stimulation. Antibodies, in turn, clear virus. Pie charts: Contribution of each clone to the total B-cell and antibody response before (B) and after (C) the primary infection. The virus V was closest to clone 1 in this simulation with the parameters given in Supplementary Table S1. The model was run with 20 clones.
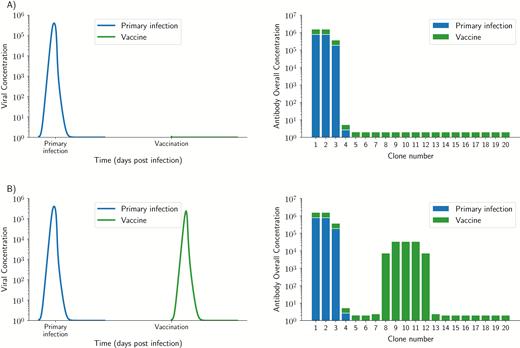
Simulated primary infection and vaccine dynamics for 2 vaccine strains: A, a slightly different strain, differing only 10% from pre-existing immunity (top row), and B, a substantially different strain with no cross-reactivity and a 45% difference from pre-existing immunity. For each row, the left panel shows the viral dynamics of primary infection followed by vaccination, and the right panel shows the overall antibody concentration after primary infection (blue) and after vaccination (green). Viruses that are too close to pre-existing immunity are immediately contained by pre-existing immunity resulting in no stimulation of any antibody clone (A). Once a vaccine escapes pre-existing immunity, it will result in the stimulation of the B cells and antibodies closest to the vaccine strain (B). However, for all cases, antibody clones closest to pre-existing immunity are always boosted in addition to those clones closest to the vaccine, and since they had the highest concentration, before vaccination this results in them still having the highest concentration after vaccination, which is consistent with the Original Antigenic Sin theory.
Optimal Vaccine Strain Selection
We now address the question of how a vaccine affects the dynamics following challenge with a new strain of influenza. To model prior exposure to influenza we begin by setting the pre-existing level of immunity to that generated by a primary infection as described above. We then consider how the severity of infection with a new virus strain (termed the challenge strain) can be reduced by vaccination. In particular, we consider how the severity of infection with the challenge strain depends both on its antigenic distance from pre-existing immunity as well as the antigenic distance of the vaccine from both pre-existing immunity and the challenge strain. We denote the distances between vaccine and pre-existing immunity, vaccine and challenge, and challenge and pre-existing immunity by d(V, PI), d(V, C) and d(C, PI), respectively. In Figure 3A we plot the extent to which viral replication with the challenge strain (defined as the AUC of the infection) depends on the distance from the challenge to pre-existing immunity and the distance from vaccine to pre-existing immunity. In Figure 3B we plot , the extent to which the vaccine reduces the severity of infection, and in particular, how veω depends on the antigenic distance from the vaccine strain to pre-existing immunity and the distance from the challenge to pre-existing immunity.
![A, Contour plot representing the AUC for the viral load following a challenge infection. If the AUC is less than 2, the infection with the challenge virus was deemed controlled (parameters described in Supplementary Table S1), where we assumed that an attenuated influenza virus will make the antibody killing rate 25 times more efficacious (kvac=25k, see Supplementary Materials for details). The diagonal line (black) represents a vaccine that was perfectly matched to the challenge strain [d(P,V) = 0], irrespective of their distance to pre-existing immunity. B, Contour plot representing the within-host vaccine effect veω as a function of the distance from the vaccine strain to pre-existing immunity and the distance from the challenge to pre-existing immunity. The within-host vaccine effect is a measure of the ability of the vaccine to prevent further infections. Abbreviation: AUC, area under the curve.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/cid/70/6/10.1093_cid_ciz358/4/m_ciz358f0003.jpeg?Expires=1750820222&Signature=5BCrLmZfIvekHN5p~nsklsEfTNcCXiqvim0DAljtyevheIvaf9sruDjpMmyMGze4YQRv0bliIRqGcHaI4wJ5EHRb1i0JfCNk2a5qhF~IRpMn4P90KQJEueDf1oe9zMLpywZfH1TmlP~H9Oj1DXMrhafRMRoHxPHXr2BID0-qU9PdjUMO3wvZRSTBfNW0EWGy08iHx6R7IBIQiFi5p9P5z0C6ankqtcjqR96kowtjp0Tt11a62xxv04CnbLWSRBvZa1~46tLRNtG8O8Tr1cnOIlHquXpvJoaCT6SDBRQs2fBN6fm1D75AlWwLdMNHx9hMgBKVeUm2z7TbU0Dcf6UjxA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
A, Contour plot representing the AUC for the viral load following a challenge infection. If the AUC is less than 2, the infection with the challenge virus was deemed controlled (parameters described in Supplementary Table S1), where we assumed that an attenuated influenza virus will make the antibody killing rate 25 times more efficacious (, see Supplementary Materials for details). The diagonal line (black) represents a vaccine that was perfectly matched to the challenge strain [d(P,V) = 0], irrespective of their distance to pre-existing immunity. B, Contour plot representing the within-host vaccine effect veω as a function of the distance from the vaccine strain to pre-existing immunity and the distance from the challenge to pre-existing immunity. The within-host vaccine effect is a measure of the ability of the vaccine to prevent further infections. Abbreviation: AUC, area under the curve.
We consider the following parameter regimes for the distance between pre-existing immunity and the challenge strain:
When the antigenic distance between pre-existing immunity and the challenge strain is small [d(C, PI) ≤ 20%]. Our model predicts that pre-existing immunity will prevent proliferation of a challenge virus. This can be seen in Figure 3A where we note that provided d(C, PI) is 20% or less the severity of the infection (its AUC) is very low, irrespective of the vaccine (Figure 3, Supplementary Figure S3A and S3B, and Supplementary Figure S4A and S4B). Consequently, the vaccine will have a very low veω as seen in Figure 3B since pre-existing immunity alone is sufficient to control the virus. At the population level, this corresponds to a scenario where the challenge strain is not significantly different from the previous year (a mild year). In this scenario, pre-existing immunity prevents infections in most individuals and it also prevents a matched vaccine from boosting the immune response. We also note that unless the vaccine is antigenically much more distant from pre-existing immunity than the challenge strain, pre-existing immunity will control the vaccine (Figure 3, Supplementary Figure S3B, and Supplementary Figure S4B). Regardless, the vaccine will have little efficacy against that year’s virus.
We then consider the regime where the antigenic distance between pre-existing immunity and the challenge strain is just a bit too large for pre-existing immunity to immediately clear the challenge strain [20% ≤ d(C, PI) ≤ 40%]. This scenario corresponds to seasonal antigenic drift with the challenge strain causing an infection. The ability of the vaccine to prevent further infections depends on the antigenic distance between the vaccine and pre-existing immunity. If the vaccine is antigenically closer to pre-existing immunity than the challenge strain [region where d(V, PI) ≤ 20% and to the left of the diagonal black line] then we find that the replication of the vaccine is controlled by pre-existing immunity and it does not boost immunity or affect subsequent infection with the challenge virus (Figure 3, Supplementary Figure S3C, and Supplementary Figure S4C). In this case, we expect to see low vaccine effectiveness. The best outcome is when the vaccine is antigenically a little more distant from pre-existing immunity than the challenge strain. In this regime, the vaccine boosts immunity that can help control the challenge strain (Figure 3, Supplementary Figure S3D, and Supplementary Figure S4D). Analogously, in Figure 3B, we see that the vaccine has optimal within-host vaccine effect when it is slightly more distant from pre-existing immunity than the challenge strain. At the population level, we expect to see a high vaccine effectiveness. When the vaccine is antigenically very distant from both pre-existing immunity and the challenge strain, then the response it elicits does not affect the challenge strain.
Finally we consider a scenario where the challenge strain is antigenically very distant from pre-existing immunity [eg, d(C, PI) > 40% in our model]. This corresponds to a year in which there is a major antigenic shift, such as the introduction of the 2009 H1N1 influenza A pandemic strain. In this situation, vaccine is most effective when it is antigenically matched to the challenge strain (Figure 3). In this parameter regime, pre-existing immunity has little effect on either vaccine or challenge virus.
We summarize these results in a diagram in Figure 4.
Application to the 2014–2015 Influenza Season
The 2014–2015 influenza season was characterized as a moderately severe season, with influenza A H3N2 being the dominant circulating strain in North America and Europe. While vaccine effectiveness studies done in the United States found contradictory results (vaccine effectiveness [VE] of –3%; 95% confidence interval [CI], –50% to 29%) in Zimmerman et al [12] versus a VE of 30% (95% CI, –6% to 54%) in McLean et al [11], studies done in the United Kingdom found LAIV to be 35% efficacious (95% CI, –29.9% to 67.5%) [15]. Skowronski et al [17] computed the antigenic distances between the vaccine, the previous year’s vaccine, and the epidemic challenge for the H3N2 strain for the 2014–2015 influenza season. The vaccine was identical to the previous year’s vaccine and they found that the antigenic distance between the vaccine and the epidemic challenge to be 4 (equivalent to 20% in our model, see Supplementary Material), so that d(V, PI) = 0 and d(V, C) = 20 = d(PI, C).
Children in the United States have been routinely vaccinated against seasonal influenza since 2008. The CDC estimates over 58% vaccination coverage of children in the United States from 2013 to 2017, so it is expected that, during the 2014–2015 influenza season, most of the children in the United States had some pre-existing immunity due to re-vaccination (and some due to natural infection). In contrast, the United Kingdom started a universal influenza vaccination program with the LAIV in 2013–2014. For the 2014–2015 season, children aged 2 to 4 years and school-age children were offered LAIV for the first time in some regions of the United Kingdom [16], with an estimated coverage of 33–41%. Hence, it is expected that children in the United Kingdom may not have received an influenza vaccine or exposure to circulating strains (because of their young age) prior to immunization. We then model 2 scenarios: (1) a child who has pre-existing immunity identical to the strain contained in the vaccine [d(V, PI) = 0, the American case] and (2) a child with no pre-existing immunity for whom the vaccine is her first exposure to influenza (the British case). Then, we modeled a challenge strain that is 20% different from the vaccine. For the American case, both the vaccine and the challenge strains are contained by pre-existing immunity (Figure 5A), preventing any B-cell response and a minimal antibody response (Figure 5C and 5D), obtaining a negligible within-host vaccine effect (veω = 0.00057). For the British case, the vaccine strain acts as a primary infection (Figure 5B), eliciting a strong immune response (Figure 5C and 5D) that will further control the epidemic challenge, achieving a very high within-host vaccine effect (veω = 0.99). If we translate the individual vaccine effects to population-level effects, we would expect to see no vaccine effectiveness in the American case but to observe vaccine effectiveness in the British case.
![Schematic diagram of expected VE as a function of the 3 antigenic distances: distance between epidemic challenge strain and pre-existing immunity [denoted d(C, PI)], vaccine strain and pre-existing immunity [denoted d(V, PI)], and between vaccine and epidemic challenge strain [denoted d(V, C)]. When d(C, PI) is small, pre-existing immunity controls the challenge strain, irrespective of the other 2 distances. If d(C, PI) is medium or large, then the expected VE depends on the other 2 distances as indicated here. Abbreviation: VE, vaccine effectiveness.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/cid/70/6/10.1093_cid_ciz358/4/m_ciz358f0004.jpeg?Expires=1750820222&Signature=Yr0LSgr-ewWGRd-mVPo8fC0tEQUunVSZ1bPByQNPHUswis1GIA0sPet8tK6vpFr6r2TMSEBADwEEioIf36tyyulIzvMrytrl9dwIlsAP6vgBx013uP4HBLIgfaVif3YE7kB5qq95sKYiNiGnhTQzOTlOdxXjRLz~CgWMj2VEkO7FcExGnVl8m52OD~bbDqg-9QnUlrNWUBvWfmkora~Dn4YW8IWljYyvWvrCoG5nguka9XZ6D9R7Z0MlqzEz7rBNfJZSlegfDywDXYmSVnaCExlWS7LO3h5T1zXbYdUPTtv~k3IguJGMqxv-NIHt20zfgBMs5vdT68je9gYbPCyyDg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Schematic diagram of expected VE as a function of the 3 antigenic distances: distance between epidemic challenge strain and pre-existing immunity [denoted d(C, PI)], vaccine strain and pre-existing immunity [denoted d(V, PI)], and between vaccine and epidemic challenge strain [denoted d(V, C)]. When d(C, PI) is small, pre-existing immunity controls the challenge strain, irrespective of the other 2 distances. If d(C, PI) is medium or large, then the expected VE depends on the other 2 distances as indicated here. Abbreviation: VE, vaccine effectiveness.
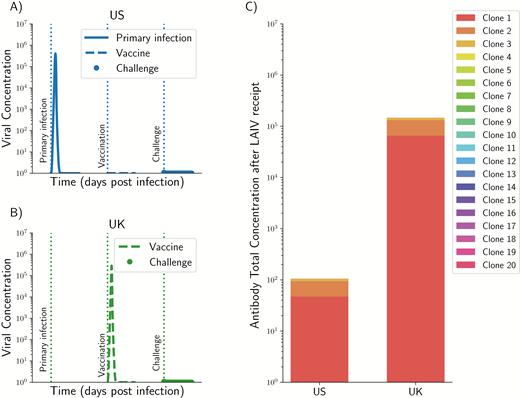
Application of our model to the 2014–2015 influenza season in the United States and in the United Kingdom. Viral dynamics (A and B) and magnitude of the overall antibody response (C) for a child in the United States (A) or in the United Kingdom (B). For a child in the United States, it was assumed that she or he had pre-existing immunity and the strain contained in the vaccine was identical to pre-existing immunity, so that pre-existing immunity controls the vaccine strain and the challenge (A and C). In contrast, for a child in the United Kingdom, it was assumed that she or he had no pre-existing immunity (B and C) and the vaccine is acting as a primary infection, resulting in the vaccine controlling the subsequent challenge. In both cases, it was assumed that the challenge strain was 20% different from pre-existing immunity and it is contained by the immune response. However, in the US case, the vaccine is also contained by pre-existing immunity. Abbreviation: LAIV, live-attenuated influenza vaccine.
DISCUSSION
Protection due to LAIV has exhibited considerable variability across populations and studies [10, 12–17, 29–32]. In this paper, we use mathematical models to explore a possible hypothesis to explain this phenomenon: interference due to pre-existing immunity. We defined a measure of within-host vaccine effect that allowed us to quantify our results. Furthermore, the results presented here provided us with parsimonious conditions under which the LAIV will be deemed to be efficacious. Our models indicate that there is a window within which LAIV will be successful at controlling a subsequent challenge infection with a drifted virus. This corresponds to the parameter regime where the vaccine is just distant enough from pre-existing immunity that it will successfully replicate and induce an immune response while being close enough to the circulating strain. Otherwise, the vaccine will be inefficacious, either because it is controlled by pre-existing immunity (and this prevents it boosting immunity) or if it is antigenically very distant and stimulates clones too distant from the challenge (a mismatched vaccine). For these cases, the vaccine did not confer any additional protection to the vaccinees, resulting in a poor within-host vaccine effect, and hence we would expect to see a low vaccine effectiveness. There are 2 additional scenarios that we consider. The first is in individuals such as very young children who have not been exposed to influenza. The second is following the emergence of a pandemic strain of influenza. In both of these scenarios there is little effect of pre-existing immunity and a matched vaccine is likely to be efficacious.
Influenza vaccines (inactivated and live-attenuated) have been extensively used in the United States over the past 2 decades and their use is on the rise in many countries. Inactivated influenza vaccines can be given to a wide population, since they are licensed for individuals aged 6 months or older. In contrast, LAIV has been used almost exclusively in young children. Because LAIV is administered nasally, children are more willing to accept it, making it more appealing to parents. Vaccine effectiveness for the inactivated vaccine has historically been more consistent than the effectiveness of LAIV. However, when LAIV results in adequate protection, it might provide a broader and longer protection than the inactivated vaccine. Further, in the event of the emergence of a new strain of influenza, where we expect no pre-existing immunity in the population, both vaccines, when matched to this strain, are likely to be highly efficacious in all age groups. In this case, the use of LAIV could be advantageous since LAIV can be produced at a faster rate.
Suggestions for Improvement of the LAIV
Our studies suggest that the current approach using a vaccine strain matched to the circulating strain is likely to be most effective only in very young children (who presumably have had little exposure to influenza) and potentially in individuals in areas where there is a relatively low attack rate from influenza. Instead, our models suggest that it would be optimal to choose a vaccine strain that is marginally farther away from pre-existing immunity as it is more likely to “take” in a larger fraction of the population. In this regard, our results are consistent with previous results presented for inactivated influenza vaccine [24, 34]. Phylogenetic tools [35, 36] can provide guidance on which direction to take. Ideally, different vaccine strains could be included in the live-attenuated vaccine for different populations depending on the particular strain that dominated the previous season. Further, one could envision a vaccination program that would systematically test individuals before and after vaccine receipt to ensure that it has mounted an adequate immune response.
Our results are also consistent with the current empirical studies and explain the discrepancies observed in the vaccine effectiveness studies done in the United States and in the United Kingdom for the 2014–2015 season. Our results showed that, for a child with pre-existing immunity, the LAIV would not be immunogenic, resulting in a poor within-host vaccine effect. In contrast, in children who are exposed to influenza via vaccination for the first time, the within-host vaccine effect would be very high. These results point to the need for more studies to measure LAIV immunogenicity. In an observational study in children aged 5–17 years assessing seroconversion and seroprotection for the inactivated influenza vaccine and the LAIV during the 2013–2014 influenza season, King et al [7] found that at most 8% of the participants seroconverted after vaccination with LAIV. In a similar study, Levine et al [37] found that only 3–5% of children seroconverted following receipt of LAIV. Our results suggest that a possible reason for these results could be interference with pre-existing immunity. This is in agreement with previous studies showing that pre-existing influenza antibodies can limit both the replication of the strains contained in the LAIV and the immune response generated by the vaccine [38].
Our model, like all models, involves a number of simplifications. We focus on the antibody response, which is critical to protection against influenza, and we do not consider T-cell responses to influenza. We simplify the potentially complex pattern of pre-existing immunity to multiple strains by a single infection. The antibody–virus affinity was modeled as a percentage of the antigenic distance between the antibody and the virus, thereby oversimplifying quite complex interactions. Furthermore, we based the antigenic distance on the serum hemagglutination inhibition assay, historically used to measure the immune response to inactivated influenza vaccine, but assays based on specific epitopes and measuring mucosal humoral responses might be better indicators of LAIV immunogenicity [39]. Integrating these complexities is a direction of future work.
LAIV is currently being offered to children across the world; however, its effectiveness significantly varies between studies. LAIV might have advantages over inactivated influenza vaccine, including higher acceptance, a potential slower waning, and higher production capabilities. Here, we proposed a mechanistic explanation to help understand these differences, and we further identify scenarios in which LAIV matched to the circulating strain will be protective, and when this is not the case we propose a way to select the LAIV strain that would have a higher chance of being protective.
Supplementary Data
Supplementary materials are available at Clinical Infectious Diseases online. Consisting of data provided by the authors to benefit the reader, the posted materials are not copyedited and are the sole responsibility of the authors, so questions or comments should be addressed to the corresponding author.
Notes
Acknowledgments. The authors thank 2 anonymous reviewers for their helpful comments.
Financial support. This work was supported by the National Institute of General Medical Sciences (grant number U54GM111274) and the National Institute of Allergy and Infectious Disease (grant number U19 AI117891) of the National Institutes of Health.
Potential conflicts of interest. The authors: No reported conflicts of interest. All authors have submitted the ICMJE Form for Disclosure of Potential Conflicts of Interest. Conflicts that the editors consider relevant to the content of the manuscript have been disclosed.




