Summary
A deterministic formula is commonly used to approximate the expected generation number of a population of growing cells. However, this can give misleading results because it does not allow for natural variation in the times that individual cells take to reproduce. Here we present more accurate approximations for both symmetric and asymmetric cell division. Based on the first two moments of the generation time distribution, these approximations are also robust. We illustrate the improved approximations using data that arise from monitoring individual yeast cells under a microscope and also demonstrate how the approximations can be used when such detailed data are not available.
1. Introduction
1.1 Illustrative Data and Malthusian Parameter
Individual cells vary in the times they take to reproduce and an illustration of this is given in Figure 1 for the single-celled budding yeast Saccharomyces cerevisiae. Cells of S. cerevisiae divide asymmetrically (Hartwell and Unger, 1977); the mother cell forms a bud that grows and then separates from the mother cell to produce a daughter cell. The mother cell can begin the reproductive process again immediately, but the daughter cell must first grow to maturity before it can produce a bud. The data in Figure 1 were obtained using time-lapse microscopy, which allows individual yeast cells to be observed and cell generation times to be accurately recorded.
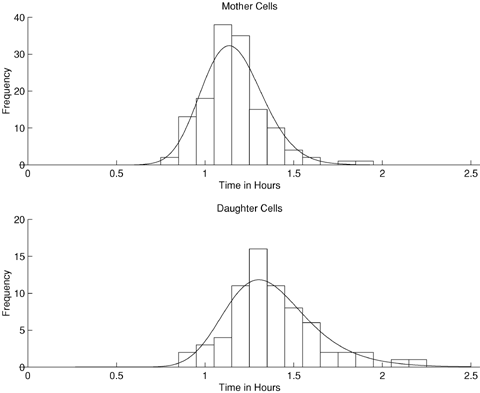
Histograms of the generation times of S.cerevisiae cells. The cells have been classified as either mother cells or daughter cells, the latter being those cells undergoing their first division. The fitted curves are the scaled gamma probability density function, for mother cells, and the scaled probability density function of a convolution of two gamma distributions for the daughter cells.
Despite the fact that cell reproduction is stochastic, a number of deterministic formulas for the growth of biological cell populations are in common use. For example, it is often stated that the growth rate, also called the Malthusian parameter, θ, is ln(2) divided by the mean cell generation time and that the time that a cell population takes to double in number is equal to the mean cell generation time. These assertions are only correct if there is no variation in cell generation times. Better approximations to the Malthusian parameter for populations of cells that reproduce by symmetric binary fission are given in Cowan (1985) and Ridout et al. (2006), and the latter extend the approximations to allow for asymmetric reproduction.
1.2 The Need to Estimate Expected Generation Number
In monitoring cellular processes over time in growing cells, researchers often need to estimate the mean number of cell divisions that occur over a time interval of length t, which we refer to as the expected generation number, E{G(t)}. For example, Eaglestone et al. (2000) needed to calculate the expected generation number of yeast cells, to compare the effect of two experimental treatments on cell growth. This was necessary because the cells were reproducing at different rates as one of the treatments involved the addition of ethanol to the culture medium. Similarly, Wu et al. (2005) used the number of cell divisions to evaluate the effect of the addition of the growth inhibition chemicals α-factor and farnesol to cultures of yeast cells. Another example is given by Cox, Ness, and Tuite (2003) who estimated the expected generation number both by directly counting cell numbers under the microscope and by plating cells onto agar and counting the numbers of colonies that arose at different times during the experiment; the estimated expected generation number was then used within a dilution model. A further example is given in Natarajan, Berry, and Gasche (2003), who used an estimate of expected generation number in estimating the mutation rate of cancer cells.
1.3 Approximations for the Expected Generation Number
The simplest commonly used approximation to the expected generation number at time t for a population of cells that reproduce by symmetric binary fission is
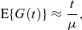
where μ is the mean cell generation time.
An alternative formula that can be used if measurements of the total number of cells (such as optical density measurements or cell/colony counts) are recorded is
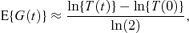
where T(t) is a measure of the total number of cells at time t. This expression is used by all four papers cited above. Under mild regularity assumptions E{T(t)}∝ exp(θt) as t→∞ (see, e.g., Kimmel and Axelrod 2002, Section 5.2). When cells have been growing for some time before experiments start, this result holds to a good approximation for small t as well. In these cases equation (2) becomes
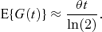
Equation (3) is equivalent to the expression for the expected generation number given in Williams (1969) for exponential generation time distributions. Evidently, if it is assumed that θ≈ ln(2) /μ then equation (3) reduces to equation (1).
It is shown by Samuels (1971) that, subject to certain regularity conditions, as t→∞, we should replace equation (1) by
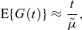
where
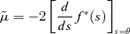
and f*(s) is the Laplace transform of the probability density function of the generation time. However, this expression does not lend itself to simple approximation by low-order moments, and so we adopt a different approach in what follows.
For comparison with moment-based approximations, in this article we will consider gamma and inverse Gaussian distributions as models for cell generation times. As we will see later, an important characteristic of cell generation time distributions is that the coefficient of variation is less than unity. Although we will on one occasion give an illustration for the exponential distribution, it is not a practical proposition.
In Section 2 we derive and evaluate a new approximation to the expected generation number. In Section 3 we extend this approximation to allow for the asymmetric cell division that occurs when budding yeast cells reproduce. Finally, in Section 4 we apply these approximations to data from time-lapse experiments on growing cells of the yeast S. cerevisiae and also show how the approximations can be used if time-lapse data are unavailable.
2. Symmetric Cell Division
2.1 Exact Expected Generation Number
For a cell chosen at random from the population at time t, the probability distribution of G(t) is given approximately by
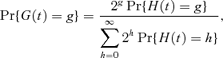
where H(t) denotes the number of cell divisions experienced by a single cell by time t. This formula is used by Morgan, Ridout, and Ruddock (2003) and Williams (1969). We consider H(t) to be an equilibrium renewal process, with renewals corresponding to cell divisions, because cells have usually been growing for some time before an experiment is started.
The expectation of G(t) is therefore,
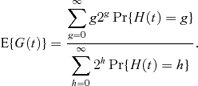
This expectation is shown by Samuels (1971) to be asymptotically equivalent to the expected generation number, as t→∞. We therefore refer to this expectation as the “exact” expectation for which we are seeking approximations. Details of how to evaluate 
and hence E{G(t)} are given in Morgan et al. (2003). However, numerical evaluation of equation (5) is complex, which motivates the need for simpler approximations to E{G(t)}.
2.2 Approximate Formulae for Expected Generation Number
From equation (5) we see that we can write E{G(t)}= EH (H 2H)/ EH (2H). If KH(ν) denotes the cumulant generating function of H(t), so that KH(ν) = ln [E{exp(νH)}], then E{G(t)} = K′H{ln(2)}. This gives
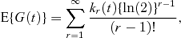
where kr(t) is the rth cumulant of H(t). As kr(t) ∼art + br as t→∞ (Smith, 1959), E{G(t)} is asymptotically a linear function of time, in agreement with the expressions of the last section. An approximation to E{G(t)} can be obtained from the first two terms of equation (6), because 
where σ2 is the variance of cell generation times and μ3 is the corresponding third central moment (Cox 1962, pages 40, 45–46, 55–58). This gives
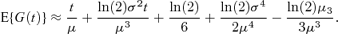
The last two terms of (7), taken together, are negligible for distributions that are realistic for cell division times, being − ln(2)CV4/6 for the gamma distribution and − ln(2)CV4/2 for the inverse Gaussian distribution, where CV denotes the coefficient of variation. Thus a simpler approximation is
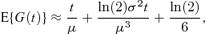
which is attractive as it is distribution free, and only requires μ and σ2. This expression shows clearly the inadequacy of approximation (1) in ignoring σ2.
2.3 Illustrations for Particular Distributions
We start with the case of an exponential distribution for cell generation times. When cell generation times follow an exponential distribution with mean 1/λ, equation (5) produces the exact result of E{G(t)}= 2 λt, whereas approximation (1) is E{G(t)}≈λt giving a relative error when compared with equation (5) of −0.5. Approximation (3) is E{G(t)}≈λt/ ln(2), giving a relative error when compared with equation (5) of − ln(2)/2 ≈− 0.28. Approximation (8) is E{G(t)}≈{1 + ln(2)}λt + ln(2)/6 with a relative error when compared with equation (5) that tends to −{1 − ln(2)}/2 ≈− 0.15; this may be improved by including a further term from equation (6) to give a relative error when compared with equation (5) that tends to 
.
When cell generation times are modeled by an inverse Gaussian distribution, the exact expected generation number is asymptotically 
, so that approximation (8) is exact in this case. When cell generation times follow a gamma distribution the exact expected generation number is asymptotically 
. Here the relative error for approximation (8) becomes very small when the coefficient of variation of cell generation times takes values typical of cell populations; examples are provided in Figure 2. Here two numerical examples are used to demonstrate the performance of approximations (1), (3), and (8) in comparison with the exact expected generation number, given by equation (5). In the examples, individual cell generation times follow a gamma distribution, with μ = 29.5 and σ2 = 36.0 for example A, and μ = 12.0 and σ2 = 48.0 for example B. (These are examples (i)a and (i)b from Cowan, 1985). We note that the expressions for exact generation number for both gamma and inverse Gaussian agree with the formula of Samuels (1971) from Section 1.2.
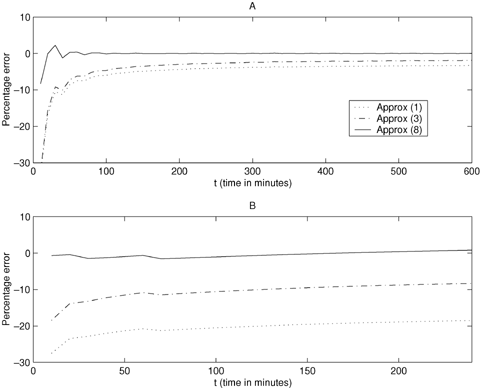
Percentage error when comparing the approximations for the expected generation number with the exact expected generation number for cells dividing symmetrically. Approx(1): 
; Approx(3): 
; Approx(8): 
. For example A we have μ = 29.5 and σ2 = 36.0, and for example B we have μ = 12.0 and σ2 = 48.0.
In order to use approximation (3) we employ the approximation for the Malthusian parameter provided by Ridout et al. (2006), namely, 
, which gives 
In these examples the approximation given by equation (8) is much better than the approximations (1) and (3) and is very close to the exact expected generation number. However, approximation (8) has the double advantage over the exact expected generation number of being more robust, requiring only the first two moments of the cell generation time distribution, rather than the full distribution, and being much easier to compute. Approximations (1) and (3) are not recommended. In the next section we show how the approach resulting in equation (8) can be generalized to allow for asymmetric cell division.
3. Asymmetric Cell Division
In this section we give an approximation for the expected generation number when cells reproduce by budding, as is the case with S. cerevisiae. We assume that mother cells take an average of μM hours to divide with variance σ2M, that daughter cells take, on average, an extra μD hours to divide, with variance σ2D and that the extra time that a daughter cell takes to divide is independent of the time the mother cell takes to divide. Therefore in total, daughter cells take an average of μM + μD hours to divide with variance σ2M + σ2D.
For this model, the population size again grows exponentially with rate θ for large t (Green, 1981). Therefore the approximation given by equation (3) still applies for asymmetric cell division, with the expression for θ that is appropriate to this case.
The probability distribution of G(t) is now given by
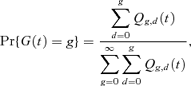
where Qg,d(t) is the expected number of cells at time t that, in their past history, have divided g times, d of which were daughter cell divisions (Cole et al., 2004). The exact expectation of G(t) is given by
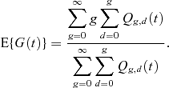
Cole et al. (2004) give details of how to calculate 
and the exact expected generation number.
We consider the random variable U with probability distribution 
, which has mean 
and variance 
where 
(see Web Appendix A). Therefore, as E{G(t)} = K′U(ln (2))), where KU(ν) is the cumulant-generating function of U, and following the same argument as before, we obtain
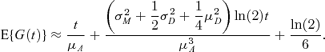
The approximation given by equation (9) reduces to the approximation given by equation (8) when μD = 0 and σ2D = 0.
4. Numerical Example
In this section we evaluate different approximations for the case of asymmetric cell division.
4.1 Time-Lapse Data
We consider four time-lapse experiments on the yeast S. cerevisiae, which track individual yeast cells and record how long mother and daughter cells take to reproduce. The experiments considered the effects of the chemical guanidine hydrochloride (GdnHCl) on the behavior of two different types of cell: petite cells, which contain defective mitochondria, and grande cells, which contain the normal complement of mitochondria. Petite cells grow more slowly than grande cells because they have a metabolic defect and both types of cells grow more slowly in the presence of GdnHCl (L. J. Byrne, unpublished data). Experiment 1 follows grande cells with no GdnHCl in the medium; experiment 2 follows petite cells with no GdnHCl in the medium; experiments 3 and 4 follow, respectively, grande and petite cells with added GdnHCl. The sample mean and variance of mother cell generation times and moment estimates of mean and variance for the extra daughter cell generation times are given in Table 1; these are used subsequently in calculating approximations. In order to provide a basis for comparison, gamma distributions are assumed for mother cell generation times and also the extra daughter cell generation times, as in the illustrations of Figure 1. In fact the data for experiment 1 are those illustrated in Figure 1, along with the curves showing the fitted gamma distributions described below.
Moment estimates of means and variances for mother cell generation time and the extra daughter cell generation time for four time-lapse experiments on yeast cells. Bootstrap standard errors are given in parentheses, and nM, nD denote sample sizes for respectively mother and daughter cells.
 |  |  |  | nM | nD | |
|---|---|---|---|---|---|---|
| Grande, no GdnHCl | 1.16 (0.015) | 0.22 (0.034) | 0.03 (0.0059) | 0.04 (0.0145) | 139 | 69 |
| Petite, no GdnHCl | 1.34 (0.020) | 0.40 (0.083) | 0.03 (0.0032) | 0.15 (0.0346) | 78 | 24 |
| Grande, + GdnHCl | 1.42 (0.034) | 0.79 (0.154) | 0.06 (0.0145) | 0.36 (0.2215) | 54 | 20 |
| Petite, + GdnHCl | 2.02 (0.112) | 1.87 (0.250) | 0.59 (0.2737) | 0.63 (0.5661) | 66 | 27 |
| | | | nM | nD | |
|---|---|---|---|---|---|---|
| Grande, no GdnHCl | 1.16 (0.015) | 0.22 (0.034) | 0.03 (0.0059) | 0.04 (0.0145) | 139 | 69 |
| Petite, no GdnHCl | 1.34 (0.020) | 0.40 (0.083) | 0.03 (0.0032) | 0.15 (0.0346) | 78 | 24 |
| Grande, + GdnHCl | 1.42 (0.034) | 0.79 (0.154) | 0.06 (0.0145) | 0.36 (0.2215) | 54 | 20 |
| Petite, + GdnHCl | 2.02 (0.112) | 1.87 (0.250) | 0.59 (0.2737) | 0.63 (0.5661) | 66 | 27 |
Moment estimates of means and variances for mother cell generation time and the extra daughter cell generation time for four time-lapse experiments on yeast cells. Bootstrap standard errors are given in parentheses, and nM, nD denote sample sizes for respectively mother and daughter cells.
| | | | nM | nD | |
|---|---|---|---|---|---|---|
| Grande, no GdnHCl | 1.16 (0.015) | 0.22 (0.034) | 0.03 (0.0059) | 0.04 (0.0145) | 139 | 69 |
| Petite, no GdnHCl | 1.34 (0.020) | 0.40 (0.083) | 0.03 (0.0032) | 0.15 (0.0346) | 78 | 24 |
| Grande, + GdnHCl | 1.42 (0.034) | 0.79 (0.154) | 0.06 (0.0145) | 0.36 (0.2215) | 54 | 20 |
| Petite, + GdnHCl | 2.02 (0.112) | 1.87 (0.250) | 0.59 (0.2737) | 0.63 (0.5661) | 66 | 27 |
| | | | nM | nD | |
|---|---|---|---|---|---|---|
| Grande, no GdnHCl | 1.16 (0.015) | 0.22 (0.034) | 0.03 (0.0059) | 0.04 (0.0145) | 139 | 69 |
| Petite, no GdnHCl | 1.34 (0.020) | 0.40 (0.083) | 0.03 (0.0032) | 0.15 (0.0346) | 78 | 24 |
| Grande, + GdnHCl | 1.42 (0.034) | 0.79 (0.154) | 0.06 (0.0145) | 0.36 (0.2215) | 54 | 20 |
| Petite, + GdnHCl | 2.02 (0.112) | 1.87 (0.250) | 0.59 (0.2737) | 0.63 (0.5661) | 66 | 27 |
The gamma means and variances are estimated for each of the four data sets by maximum likelihood. Using these estimates we can calculate the exact expected generation number at different times. This involves calculating Qg,d(t) (see Cole et al., 2004), which requires a complicated computer program. However, we need only the means and variances given in Table 1 to calculate the approximations to the expected generation number given by equations (3) and (9), and as in the symmetric case we need make no further assumptions about the mother and daughter distributions. The approximations can be calculated instantaneously and, unlike the exact expected generated number, do not require any special-purpose software. In order to use equation (3), the approximation that we use for the Malthusian parameter is given by
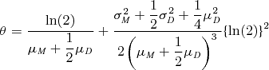
Figure 3 shows how the two approximations perform in comparison to the exact expected generation number. Displayed is the percentage error of the approximations to the exact expected generation number between t = 1 and t = 30 hours. The approximation given by equation (9) is closer to the exact expected generation number, and is clearly a good approximation in this case.
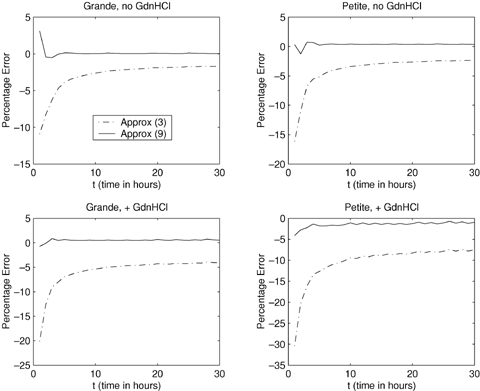
Percentage error when comparing the approximations to expected generation number with the exact expected generation number for cells dividing asymmetrically. Approx(3): 
; Approx(9): 
.
We can estimate standard errors by means of a bootstrap approach—see Table 2.
Estimates of the time coefficient in E{G(t)}; standard errors obtained from a bootstrap approach
| Approximation (9) | Approximation (3) | |
|---|---|---|
| Grande, no GdnHCl | 0.8072 (0.0097) | 0.7969 (0.0101) |
| Petite, no GdnHCl | 0.6753 (0.0149) | 0.6622 (0.0161) |
| Grande, + GdnHCl | 0.5995 (0.0176) | 0.5748 (0.0195) |
| Petite, + GdnHCl | 0.3912 (0.0143) | 0.3647 (0.0138) |
| Approximation (9) | Approximation (3) | |
|---|---|---|
| Grande, no GdnHCl | 0.8072 (0.0097) | 0.7969 (0.0101) |
| Petite, no GdnHCl | 0.6753 (0.0149) | 0.6622 (0.0161) |
| Grande, + GdnHCl | 0.5995 (0.0176) | 0.5748 (0.0195) |
| Petite, + GdnHCl | 0.3912 (0.0143) | 0.3647 (0.0138) |
Estimates of the time coefficient in E{G(t)}; standard errors obtained from a bootstrap approach
| Approximation (9) | Approximation (3) | |
|---|---|---|
| Grande, no GdnHCl | 0.8072 (0.0097) | 0.7969 (0.0101) |
| Petite, no GdnHCl | 0.6753 (0.0149) | 0.6622 (0.0161) |
| Grande, + GdnHCl | 0.5995 (0.0176) | 0.5748 (0.0195) |
| Petite, + GdnHCl | 0.3912 (0.0143) | 0.3647 (0.0138) |
| Approximation (9) | Approximation (3) | |
|---|---|---|
| Grande, no GdnHCl | 0.8072 (0.0097) | 0.7969 (0.0101) |
| Petite, no GdnHCl | 0.6753 (0.0149) | 0.6622 (0.0161) |
| Grande, + GdnHCl | 0.5995 (0.0176) | 0.5748 (0.0195) |
| Petite, + GdnHCl | 0.3912 (0.0143) | 0.3647 (0.0138) |
4.2 When Time-Lapse Data Are Unavailable
Time-lapse photography is technically difficult and time-consuming, and hence it is not possible to estimate both the mean(s) and variance(s) of individual cell generation times for every experiment. However, for a typical experiment it is usually possible to estimate the Malthusian parameter, θ, from measurements of the total number of cells. In this case it is still possible to use the approximation given by equation (3). In addition, in the symmetric case, if there is some prior knowledge of the coefficient of variation, CV = σ/μ (e.g., from a historical time-lapse experiment) and using the approximation for the Malthusian parameter given in Ridout et al. (2006) as 
, equation (8) can be rearranged as
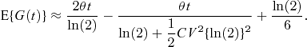
Similarly for asymmetric cell division, as the appropriate approximation for the Malthusian parameter is 
(Ridout et al., 2006) equation (9) can be rearranged to give
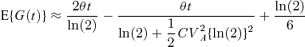
where 
.
Alternatively, if there is only prior knowledge of the mean cell generation time, μ, then for symmetric division, equation (8) can be expressed in terms of θ and μ as follows:
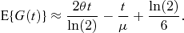
A prior estimate of μ might come from historical time-lapse data on generation times of individual cells. However, such data would typically also yield an estimate of the coefficient of variation, so that equation (10) could be used. The coefficient of variation is likely to be more stable across experiments than the mean, which can be sensitive to small differences, for example, between batches of media. Moreover, small errors in μ generally result in larger errors in E{G(t)} than do small errors in the coefficient of variation. Alternatively, one might estimate μ directly from θ, using the deterministic approximation μ = ln(2)/θ. In this case equation (12) becomes
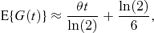
which is equivalent to approximation (10) if the coefficient of variation is set to zero and differs from approximation (3) only by the addition of the term ln(2)/6. This approximation can also be used for asymmetric cell division, but would be unlikely to perform as well as approximations (10) or (11).
An example of the application of equation (11) is given in Figure 4. An experiment on grande yeast cells grown in GdnHCl produced the number of colonies that arose at different time points, which gives an estimate of the total number of cells, T(t). By regressing ln{T(t)} on t an estimate of 
, with standard error 0.005 was obtained. Similarly, an experiment on petite yeast cells, grown in GdnHCl, resulted in an estimate of 
, with standard error 0.003. These estimates of θ are used to calculate approximations (3) and (13). Using assumed values of CV2A = 0.12 for the grande cells and CV2A = 0.20 for petite cells, derived from the time-lapse data, equation (11) is used to obtain an approximation to E{G(t)}; this is labeled Approx (11)a in Figure 4. As expected, approximation (13) does not perform as well as approximation (11).
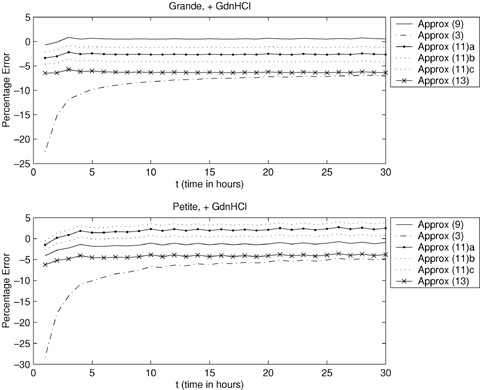
Percentage error when comparing the approximations to expected generation number, that can be used when no time lapse data are available, with the exact expected generation number. Approximation (9), which requires the availability of time-lapse data, is included for comparison. Approx(3): 
; Approx(9): 
; Approx(11): 
; the upper dotted line corresponds to CV2A + 0.05, and the lower dotted line corresponds to CV2A & − 0.05; Approx(13): 
.
Except when t < 10 for the case of petites in Figure 4, approximation (11) is not as good as approximation (9). However, it is much better than the viable alternatives, approximations (3) and (13). To demonstrate the effect of getting the prior knowledge of CV2A wrong, the figure also shows approximation (11) using CV2A± 0.05; these are labeled Approx (11)b and Approx (11)c in Figure 4. This shows that approximation (11) is still reasonable even if the assumed values of CV2A are slightly wrong.
5. Conclusion
By using results from renewal theory, we have developed simple approximations for expected generation number, for both symmetric and asymmetric cell division. These approximations are considerably easier to use than the exact calculation of expected generation number. They are also robust, depending only on the mean and variance, rather than an assumed form for generation time distributions. The simple algebraic expressions for the approximations allow one to appreciate the importance of taking account of variation in cell generation times, especially for large t. Although we derive approximations for large t, motivated by detailed studies of the case of exponential generation times, we speculate that the approximations may be used more generally, when cell numbers are sufficiently large, and this is a topic of current research.
In summary, when there is symmetric cell division we recommend formula (8), and formula (10) if data are not available on the mean and variance of the generation time distribution. For the asymmetric case we recommend (9) and (11), respectively. We do not recommend the use of approximations such as (3) or (13).
In common with other authors such as Kendall (1948), Cowan (1985), and Ridout et al. (2006), we have not considered the effect of cell death on expected generation number. This is because typically cells die when they are old, and as the population is made up of mostly young cells, cell death has only a negligible effect on the expected generation number. The conditions imposed by Samuels (1971) do not include the case of cell death, but as in Bühler (1972), we anticipate that conditioning on nonextinction of populations will allow the approximations of this article to be applied to the case of cell death that is not age-dependent, by replacing ln(2) by ln(2 − 2p) throughout, where p is the probability of a cell dying at any cell division.
6. Supplementary Materials
Web Appendix A, referenced in Section 3, is available under the Paper Information link at the Biometrics website http://www.tibs.org/biometrics.
Acknowledgements
The work of DJC and LJB was supported by the BBSRC project grant 96/E18382, awarded to MFT, BJTM, and MSR. We thank the editor, associate editor, and referee of the first version of the article, whose comments led to a clearer manuscript.
