-
PDF
- Split View
-
Views
-
Cite
Cite
Jin Liu, Xiang Wan, Shuangge Ma, Can Yang, EPS: an empirical Bayes approach to integrating pleiotropy and tissue-specific information for prioritizing risk genes, Bioinformatics, Volume 32, Issue 12, June 2016, Pages 1856–1864, https://doi.org/10.1093/bioinformatics/btw081
Close - Share Icon Share
Abstract
Motivation: Researchers worldwide have generated a huge volume of genomic data, including thousands of genome-wide association studies (GWAS) and massive amounts of gene expression data from different tissues. How to perform a joint analysis of these data to gain new biological insights has become a critical step in understanding the etiology of complex diseases. Due to the polygenic architecture of complex diseases, the identification of risk genes remains challenging. Motivated by the shared risk genes found in complex diseases and tissue-specific gene expression patterns, we propose as an Empirical Bayes approach to integrating Pleiotropy and Tissue-Specific information (EPS) for prioritizing risk genes.
Results: As demonstrated by extensive simulation studies, EPS greatly improves the power of identification for disease-risk genes. EPS enables rigorous hypothesis testing of pleiotropy and tissue-specific risk gene expression patterns. All of the model parameters can be adaptively estimated from the developed expectation–maximization (EM) algorithm. We applied EPS to the bipolar disorder and schizophrenia GWAS from the Psychiatric Genomics Consortium, along with the gene expression data for multiple tissues from the Genotype-Tissue Expression project. The results of the real data analysis demonstrate many advantages of EPS.
Availability and implementation: The EPS software is available on https://sites.google.com/site/liujin810822.
Contact: [email protected]
Supplementary information: Supplementary data are available at Bioinformatics online.
1 Introduction
As of April 2015, genome-wide association studies (GWAS) have identified more than 15 000 disease-associated single nucleotide polymorphisms (SNPs) at a genome-wide significance level (i.e. P-value ). Despite these discoveries, these SNPs can only explain a small fraction of the genetic contribution to diseases (Welter et al., 2014). It is widely agreed that this phenomenon is due to polygenicity of complex phenotypes and the large number of risk variants with weak effects that remain undiscovered (Visscher et al., 2012).
Growing evidence suggests that there are many genetic variants that may affect the multiple, seemingly different phenotypes (traits/diseases) (Solovieff et al., 2013). In fact, a term named ‘pleiotropy’ was introduced to describe such a phenomenon more than 100 years ago (Stearns, 2010). The original definition of ‘pleiotropy’ only concerns the nonzero effect of a locus on different phenotypes and allows the effect direction to be either the same (i.e. the risk allele increases the risk of two diseases) or different (i.e. the risk allele increases the risk of one disease while decreases the risk of another disease). For example, the G allele of rs6983267 increases the risk for prostate cancer and colorectal cancer (Thomas et al., 2008; Tomlinson et al., 2007) but the G allele of rs12720356 increases the risk for Crohn’s disease and decreases the risk for psoriasis (Franke et al., 2010, Genetic Analysis of Psoriasis Consortium and the Wellcome Trust Case Control Consortium 2 and others, 2010). A closely related but different concept is ‘genetic correlation’ (also known as ‘co-heritability’—Cross-Disorder Group of the Psychiatric Genomics Consortium, 2013a). This refers to the correlation between the genetic effect sizes of two phenotypes and thus the direction of these effects plays a role. To be clear, when referring to ‘pleiotropy’ in this article, we adopt its original definition. We are interested in the substantial overlap of genetic factors that underlie the multiple, seemingly different phenotypes. Fortunately, more GWAS results are becoming publicly available from GWAS repositories, such as the GWAS–GRASP (Eicher et al., 2015). This offers us an unprecedented opportunity to explore pleiotropic effects.
Besides an enormous amount of GWAS data, diverse data resources for biological processes at different layers are also becoming available (Civelek and Lusis, 2014). For example, the ongoing Genotype-Tissue Expression project (GTEx) is generating a comprehensive atlas of gene expression and regulation across multiple human tissues (Lonsdale et al., 2013). This provides abundant information to quantify biological processes that occur at the cellular level and thereby helps us to dissect the etiology of complex diseases. Moreover, the comprehensive gene expression data in multiple tissues may avoid the potential bias of the ‘candidate tissue approach’. For example, in the study of obesity, the affected tissue is fat, but the causal tissue is, in some cases, the hypothalamus (Loos et al., 2008). This suggests that the integration of GWAS data and gene expressions from multiple tissues may advance our understanding of complex diseases.
At present, the accumulating evidence on pleiotropy (Wang et al., 2015; Yang et al., 2015) and vast, publicly available data on tissue-specific gene expression [e.g. TiGER (Liu et al., 2008) and GTEx (Moore, 2013)] require novel statistical approaches to gain a deeper understanding of complex diseases (Ritchie et al., 2015). Statistical approaches that take pleiotropy into consideration have recently become very active (Solovieff et al., 2013), such as the conditional false discovery rate (FDR) approach (Andreassen et al., 2013), and linear mixed model-based approaches (Shriner, 2012; Zhou and Stephens, 2014). Various statistical methods have also been proposed to analyze tissue-specific gene expression data (Gutierrez-Arcelus et al., 2015), such as joint eQTL analysis in multiple tissues (Flutre et al., 2013) and covariate-modulated FDR (CMFDR) (Zablocki et al., 2014). More recently, a statistical approach named ‘GPA’ (Chung et al., 2014) was proposed to simultaneously integrate both pleiotropic information and functional annotation. Although GPA has demonstrated a very promising direction for the integration of multiple sources of genomic information, it does not fully account for the effects of linkage disequilibrium (LD) and only allows binary annotation as its input. These disadvantages may limit its use in the integrative analysis of large-scale genomic data.
In this article, we propose an Empirical Bayes approach to integrating Pleiotropy and Tissue-Specific (EPS) information for prioritizing risk genes. Compared with some existing approaches (Lee et al., 2015; Torres et al., 2014), EPS has several merits. First, EPS only requires the summary statistics at the gene level, rather than the genotype data at the individual level. The LD effects are carefully accounted for when grouping the SNP-level summary statistics into the gene level summary statistics by using reference panel data (e.g. 1000 genome data). Second, EPS is able to integrate both pleiotropy information and gene expression data (e.g. GTEx data), which greatly improves the power of risk gene prioritization. Third, EPS provides rigorous hypothesis testing to evaluate the significance of pleiotropy and tissue-specific patterns. These merits are demonstrated via extensive simulation studies and real data analysis.
2 EPS: basic model, algorithm and inference
2.1 Basic model
Suppose we have the P-values of all SNPs from one GWAS. Instead of working at the SNP level, we group the P-values at the SNP level into the P-values at the gene level using VEGAS (Liu et al., 2010). There are several advantages to working at the gene level. First, the signals at the gene level are often more visible than those at the SNP level (Li et al., 2011). Second, the gene itself is highly consistent across populations, which leads to more consistent results across a population and thus increases the replication rate (Neale and Sham, 2004). Third, it is more convenient to integrate expression data from multiple tissues with GWAS data at the gene level. We demonstrate these advantages in the real data analysis below.
Let us start with the simplest case. Consider P-values at the gene level: P1,…,Pg,…,PG, where G is the number of genes. We use the ‘two-group model’ (Efron et al., 2008) and assume that the P-values come from the mixture of a null and a non-null distribution, with a probability of π0 and , respectively. Let be the hidden variable indicating whether the P-value for the gth gene is from the null or non-null group, i.e. , and (a gene can be either null or non-null). Here, means that the gth gene is not associated with the trait (null) and means that the gth gene is associated (non-null) with the trait. Thus, we have and . Next, we model the conditional distribution of P-values given Z as: and , where is the uniform distribution on [0, 1], and is the Beta distribution with parameters α and 1, where .
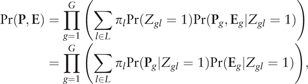
2.2 EM algorithm
Based on the complete likelihood, the -step and -step in the sth iteration of the EM algorithm involves the following calculations.
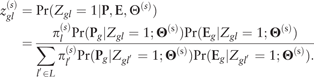
where and .
2.3 Statistical inference
2.3.1 False discovery rate
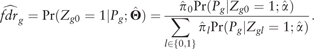
2.3.2 Hypothesis testing of risk genes differentially expressed in a tissue-specific manner
The LRT test statistic asymptotically follows the under the null.
2.3.3 Hypothesis testing of pleiotropy
2.3.4 Empirical null for inflated P-values
In the case that the P-values are inflated, it is inappropriate to assume that the P-values from null group follow Uniform distribution on [0, 1] (Schwartzman, 2008). Alternatively, we may use to accommodate the inflation. The parameters in null distribution can be estimated using P-values close to 1, e.g. P-value . Then we use to replace as the null distribution and keep unchanged during the EM updates. The strategy adopted here is similar to the one in the previous models (1) and (3) using the empirical null.
3 Extended model
3.1 Integrating a large number of tissues
If a large number of tissues are involved for gene expressions, the proposed model may not be appropriate because the number of parameters in increases quadratically with respect to the number of tissues T (see Equation (2)). To overcome this difficulty, we propose a stage-wise approach when T is large, where penalized LDA is used to regularize our model.
In this section, we describe this stage-wise approach. Let us begin with a single-GWAS analysis, with the extension to a joint analysis straightforward.
We fit the model only with the P-value vector from one GWAS and obtain the first-stage posterior probability for all G genes: , where .
Treating the first-stage posterior probability as a response matrix, we use the penalized LDA (Witten and Tibshirani, 2011) to find a sparse linear discriminant vector, denoted as , to separate the null () and non-null () group. The purpose here is to use a sparse discriminant vector to select the most useful tissue types and reduce the effects of irrelevant tissues. Using the discriminant vector , we can update the gene expression based on the sparse projection as . The details of our modified LDA are given in the following section.
We fit model (4) using , a sparse compression of gene expression, to replace the original high-dimensional gene expression (T is large), and then compute the second-stage posterior probability with as .
To extend the model to the joint analysis of two-GWAS, we need to find three sparse projection vectors because there are four groups . As a result, is a matrix. In this case, it is still applied to fit the model (4) using to replace .
3.2 Penalized LDA
We need to modify penalized LDA proposed by Witten and Tibshirani (2011) because here we only have the first-stage posterior probability () of each gene from the null and non-null groups with no knowledge of its exact group membership.
The remaining part is the same as the original paper (Witten and Tibshirani, 2011). For completeness, we describe more technical details of penalized LDA in the Supplementary materials.
4 Results
4.1 Simulation
First, we evaluated the type I errors of testing tissue-specific differential expression in a separate-GWAS analysis (9) and a joint-GWAS analysis (10), and the type I errors of testing pleiotropy (11). In this simulation, we set the number of genes G = 20 000, the number of tissues T = 5, the effect size , and the pleiotropy controlling parameter γ = 0. For simplicity, we chose (the smaller α, the stronger GWAS signals) and . For each parameter setting, we ran the EPS 500 times. The experimental results are shown in Figure 1. Clearly, all type I errors were well controlled at the nominal level (P = 0.05). We noticed that the test of pleiotropy was underpower when the GWAS signal was weak (e.g. ) and the proportion of risk genes was small (e.g. ). More detailed information on these three tests is summarized in the QQ-plots in Supplementary Figures S1 and S2.
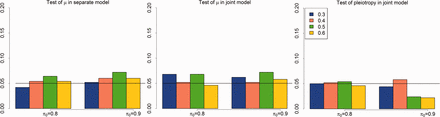
Evaluation of type I errors of testing pleiotropy (11) and testing enrichment in single-GWAS (9) and two-GWAS (10) with parameter setting: G = 20 000, T = 5, (Color version of this figure is available at Bioinformatics online.)
Next, we conducted a simulation to evaluate the power of the proposed method. We started with a small number of tissues, i.e. T = 5. We simulated , where the variance of ϵg was specified such that the signal-to-noise ratio (SNR) was controlled at around 2 (note that the SNR is defined as ). We varied γ to check the influence of pleiotropy on the performance of gene prioritization. To quantitatively evaluate the performance of EPS, we calculated the area under the curve (AUC) and the power with the global FDR controlled at 0.2. The results are shown in Figure 2. Comparing the red boxplots (separate-GWAS analysis with gene expression) with the blue ones (separate-GWAS analysis without gene expression), we observed a clear improvement after incorporating informative gene expression data from T tissues. The benefit of integrating pleiotropy was also confirmed by comparing the green boxplots (joint-GWAS analysis without gene expression) with the blue ones (separate-GWAS analysis without gene expression). Integrating both pleiotropy and gene expression from multiple tissues further improved the performance of EPS, as indicated by the yellow boxplots (joint-GWAS analysis with gene expression). However, there are two remaining concerns: how are the results of the joint analysis affected when there is no pleiotropy, and how is the analysis affected when all of the incorporated tissues are non-informative? For the first concern, as shown in Figure 2, the joint analysis in EPS showed comparable performance with a separate analysis in the absence of pleiotropy (γ = 0), suggesting that EPS can adapt to available pleiotropic information and avoid overfitting. To address the second concern, we performed a simulation study in which all of the tissues were non-information. As shown in Supplementary Figure S3, EPS performed robustly when a small number of non-informative gene expressions were incorporated into the analysis.
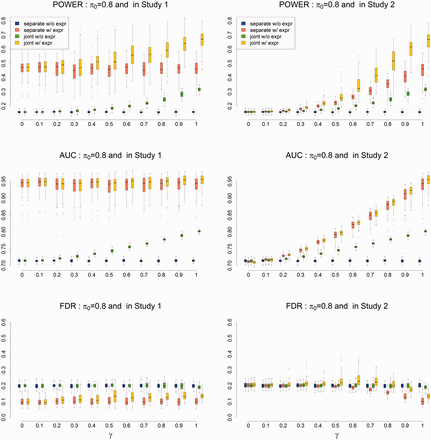
Power (upper panel), AUC (middle panel) and FDR (lower panel) of EPS for gene prioritization with parameter setting: G = 20 000, T = 5, and . The results are based on 500 simulations (Color version of this figure is available at Bioinformatics online.)
As observed in Fan and Fan (2008), inclusion of too many non-informative variables will generate too much noise, and thus degrade the performance. In such a case, we advocate using the extended model (Section 3), which uses penalized LDA to adaptively remove irrelevant tissues. To evaluate the performance of the extended model, we simulated gene expression from T = 100 tissues, only five of which were informative. The simulation results (Supplementary Fig. S4) suggest that the extended model performed very well for gene prioritization, even when most of the issues were non-informative. In addition to performance comparison, we investigated the accuracy of parameter estimation. These results are shown in Supplementary Figures S5 and S6. We compared EPS with CMFDR, which was designed to integrate one GWAS with functional annotation. The results shown in the left panel of Supplementary Figure S7 demonstrate that EPS performs better than CMFDR in terms of the AUC (top panel of Supplementary Fig. S7). CMFDR seems to have a greater power (middle panel of Supplementary Fig. S7), but it suffers from an uncontrolled FDR (lower panel of Supplementary Fig. S7).
Another issue with integrating multiple GWAS is the overlap of control samples. Although we did not take this issue into account in our analysis, we investigated its potential effects on EPS using simulation studies. The empirical results (shown in Supplementary Fig. S8) indicate that the FDR of EPS is indeed inflated in some extreme cases, but the inflation is small or moderate for the majority of cases (the true FDR is 0.3 where nominal FDR is 0.2). We plan to address this limitation in our future work.
4.2 Analysis of schizophrenia (SCZ) and bipolar disorder (BPD) with the GTEx data
In this section, we applied EPS to the analysis of BPD and SCZ. Previous studies have shown that BPD and SCZ share some common polygenic variation and susceptibility genes (Maier et al., 2006; Purcell et al., 2009). Therefore, it is ideal to jointly analyze BPD and SCZ by considering the pleiotropy between them. Detailed information about these GWAS is provided in Cross-Disorder Group of the Psychiatric Genomics Consortium (2013b). We downloaded the summary statistics for BPD and SCZ from the Psychiatric Genomics Consortium (PGC) website. There are 1 233 533 and 1 237 959 SNPs reported in the PGC GWAS for BPD and SCZ, respectively. We took the intersection of these available SNPs and obtained 1 219 805 overlapping SNPs and their P-values. As all of the samples are of European ancestry, we used VEGAS2 (Liu et al., 2010; Mishra and Macgregor, 2015) to combine P-values at the SNP level and obtained 17 763 P-values at the gene level, where 379 European ancestry samples in 1000 genome data served as the reference panel in the VEGAS method.
The GTEx (Lonsdale et al., 2013) provides an up-to-date resource for the gene expression data in multiple tissues (http://www.gtexportal.org/home/). As of April 2015, the gene expression data for 53 tissues from 2921 samples were available on GTEx. As the sample sizes of some tissues may have been too small to provide reliable analysis results, we only considered the tissues that had at least 16 samples. We collected gene expression data from 46 tissues for analysis. For each tissue, there were 25 208 gene Ensembl IDs. We matched these genes with the list of genes from the output of VEGAS, and ended up with gene expression data for 13 815 genes from 46 tissues and their P-values from SCZ and BPD at the gene level. We further performed quantile normalization of the gene expression data. In practice, the expression of genes may not be independent, i.e. the rows of matrix could be correlated. Because independence among genes is assumed in EPS, we performed additional simulation studies to evaluate the type I errors using this real data. The results shown in Supplementary Figures S7 and S8 indicate that EPS performed robustly in the presence of a correlation.
Next, we checked the distribution of the P-values from VEGAS and found that these gene-level P-values were inflated for both SCZ and BPD (the QQ-plots of these P-values are shown in Supplementary Fig. S9). Therefore, we chose to use the empirical null for the null distribution as described in Section 2.3.4. The parameters s were estimated to be 0.72 and 0.80 for SCZ and BPD, respectively.
To identify tissue-specific-enrichment patterns of a complex trait, we applied EPS to integrate multiple tissues with their P-values from GWAS and then evaluated whether risk genes were differentially expressed in a tissue-specific manner. We performed this analysis for all 46 tissues using hypothesis testing (9) (a complete list of the test results is given in Supplementary Table S1). The test results suggested that the risk genes for BPD are differentially expressed in brain–cerebellar hemisphere and brain–cerebellum. Although a number of studies have suggested that the cerebellum plays a critical role in emotion processing (Hoppenbrouwers et al., 2008), its importance in BPD is still uncertain (DelBello et al., 1999; Mills et al., 2005). A recent study based on quantitative T1ρ mapping (Johnson et al., 2015) investigated brain abnormalities in BPD and highlighted the critical role of the cerebellum in BPD, which is consistent with the result of our analysis. The risk genes for SCZ also showed differential expression in adrenal-gland, pituitary, EBV-ETL cells, spleen, testis and whole-blood, in addition to the brain cerebellum regions. The significance in both the adrenal-gland and pituitary supports the important role of the hypothalamic–pituitary–adrenal axis function in SCZ (Walker et al., 2008). The evidence that differential expression of SCZ risk genes in ‘Cell–EBV–ETL’ supports the recently discovered link between SCZ and the immune system (Schizophrenia Working Group of the Psychiatric Genomics Consortium, 2014). Although the biological explanation of the differentially expressed genes in the spleen, testis and whole blood remains elusive, our method suggests that they warrant significant consideration. We briefly explain the reason for this in the next paragraph where we discuss the gene prioritization results of our method.
The gene prioritization results with or without the inclusion of gene expression data are summarized using Manhattan plots in Figure 3. To control false positive findings, we use the local FDR as the criterion to report risk genes in the remainder of this section [the threshold for the local FDR, set at 0.1, is more stringent than the default setting of 0.2 in the classical local-FDR approach (Efron, 2010) (also see the ‘locfdr’ R package). In fact, setting the threshold for the local FDR at 0.1 often leads to a global FDR of around 0.05 (Efron, 2010)]. Without gene expression, EPS identified the same nine risk genes for both SCZ and BPD (see Supplementary Table S2 for details). For example, EPS identified two genes at 6p21-p22.1: NKAPL and PGBD1. These two genes have been identified as SCZ-risk genes in the Han Chinese population (Yue et al., 2011). In this Han Chinese population, rs2142731 is the most significant variant in PGBD1, while its P-value is 0.7387 based on the PGC samples from European ancestry. Similarly, the P-value of rs1635 in an exon of NKAPL is in the Han Chinese population, while its P-value is 0.7866 in the PGC samples. As genetic variants may have different allele frequencies and LD structures across different populations, it is difficult to replicate GWAS findings at the SNP level. However, genes can be highly consistent across ancestry (Neale and Sham, 2004). Here, EPS made use of the P-value at the gene level and successfully replicated these findings. According to the GTEx data, PGBD1 had a relatively high expression in the brain–cerebellum and brain–cortex, suggesting that PGBD1 may be more active in the brain than in other tissues. Another risk gene NKAPL had a relatively high expression in the testis, which explained why EPS detected some differentially expressed genes in the testis. These tissue-specific expression patterns of PGBD1 and NKAPL are shown in Supplementary Figures S10 and S11.
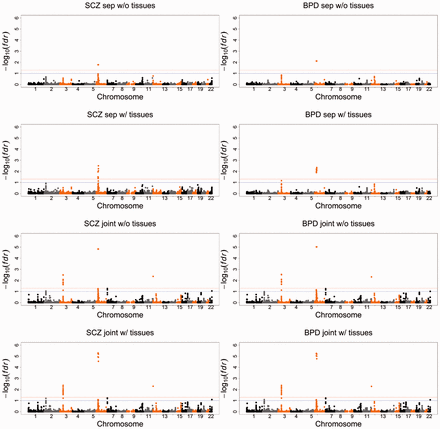
Manhattan plots of BPD and SCZ. From top to bottom: separate analysis of BPD and SCZ without the GTEx gene expression data; separate analysis of BPD and SCZ with the GTEx gene expression data. Joint analysis of BPD and SCZ without the GTEx gene expression data; joint analysis of BPD and SCZ with the GTEx gene expression data. The red and blue lines indicate local FDR = 0.05 and 0.1, respectively. See detailed explanation in the main text
When incorporating the gene expression data into our analysis, we did not use only the gene expression data from the significant tissues because using data twice may lead to a selection bias (Tibshirani and Efron, 2002). Instead, we incorporated the gene expression data from all tissues, and performed the analysis using penalized LDA as discussed in Section 3.2. The EPS results suggest that the gene FLOT1 may be a risk gene for SCZ, but not for BPD, which is consistent with a very recent large sample study (Andreassen et al., 2015). In fact, the GTEx data suggest that FLOT1 is highly expressed not only in the blood, but also in adrenal-gland, indicating that FLOT1 may be related to the functioning of the hypothalamic–pituitary–adrenal axis.
To demonstrate the possible benefits of leveraging the pleiotropic effects among different traits, we compared the separate GWAS analysis and the joint SCZ–BPD analysis without incorporating gene expression. In the joint analysis, EPS detected strong pleiotropy between SCZ and BPD, as indicated by the P-value [the estimated proportions are and , then the test statistic (12) equals 209.35]. Leveraging the pleiotropic effects enabled EPS to identify many more risk genes than the separate analyses of SCZ and BPD, as shown in Supplementary Table S2. For example, the identification of the gene CACNA1C in the joint analysis is consistent with a recent GWAS with a larger sample size (Schizophrenia Working Group of the Psychiatric Genomics Consortium, 2014) and a study using the conditional FDR (Andreassen et al., 2013). The gene CACNA1C, which encodes an alpha-1 subunit of a voltage-dependent calcium channel, has played an important role in the development of calcium antagonist drugs. As reported in Solovieff et al. (2013), this finding has been highlighted in clinical trials of calcium antagonist drugs, which are potentially effective in the treatment of psychiatric disorders.
Finally, we performed an integrative analysis of BPD–SCZ with the gene expression data from all tissues. As shown in Supplementary Table S2, the incorporation of the gene expression data enhanced the association signals of some genes. For example, FNDC4 and NT5DC2 were observed to be highly expressed in adrenal-gland, based on the GTEx data (Supplementary Figs S10 and S11). EPS also indicated that SCZ and BPD risk genes tend to be differentially expressed in the adrenal-gland. Combining all of these pieces of evidence, the strength of association between FNDC4 and NT5DC2 was adaptively enhanced by EPS. The association signals may also be weakened after incorporating gene expression data into the analysis. For example, HIST1H2BN is non-significant with a local FDR because its expression levels are very low in all of the tissues from the GTEx data. To the best of our knowledge, there is no strong evidence that HIST1H2BN is a risk gene for SCZ or BPD. By incorporating gene expression data, EPS was able to reduce the association strength and possibly avoid a false positive finding.
5 Conclusion
We have presented a statistical approach, named EPS, that can integrate pleiotropy information from GWAS data and tissue-specific gene expression data. Compared with some existing approaches, such as linear mixed models, which require genotype data at the individual level, EPS only requires summary statistics for analysis. More importantly, EPS provides statistically rigorous evaluations of tissue-specific gene expression patterns and pleiotropic effects via hypothesis testing. These merits make EPS an attractive and effective tool for the integrative analysis of GWAS data with gene expression data from multiple tissues. Despite the promising statistical improvements we have made, the biological implications need to be independently replicated. One limitation of EPS is that it does not take into account overlapping samples. Addressing this issue in integrating multiple GWAS is an important area for future work.
Funding
This work was supported in part by grant NO. 61501389 from National Natural Science Foundation of China (NSFC), grants HKBU_22302815 and HKBU_12202114 from Hong Kong Research Grant Council, and grants FRG2/14-15/069 and FRG2/14-15/077 from Hong Kong Baptist University, and Duke-NUS Medical School WBS: R-913-200-098-263.
Conflict of Interest: none declared.
References
Author notes
Associate Editor: Janet Kelso



