-
PDF
- Split View
-
Views
-
Cite
Cite
Jangsun Baek, Geoffrey J. McLachlan, Mixtures of common t-factor analyzers for clustering high-dimensional microarray data, Bioinformatics, Volume 27, Issue 9, May 2011, Pages 1269–1276, https://doi.org/10.1093/bioinformatics/btr112
Close - Share Icon Share
Abstract
Motivation: Mixtures of factor analyzers enable model-based clustering to be undertaken for high-dimensional microarray data, where the number of observations n is small relative to the number of genes p. Moreover, when the number of clusters is not small, for example, where there are several different types of cancer, there may be the need to reduce further the number of parameters in the specification of the component-covariance matrices. A further reduction can be achieved by using mixtures of factor analyzers with common component-factor loadings (MCFA), which is a more parsimonious model. However, this approach is sensitive to both non-normality and outliers, which are commonly observed in microarray experiments. This sensitivity of the MCFA approach is due to its being based on a mixture model in which the multivariate normal family of distributions is assumed for the component-error and factor distributions.
Results: An extension to mixtures of t-factor analyzers with common component-factor loadings is considered, whereby the multivariate t-family is adopted for the component-error and factor distributions. An EM algorithm is developed for the fitting of mixtures of common t-factor analyzers. The model can handle data with tails longer than that of the normal distribution, is robust against outliers and allows the data to be displayed in low-dimensional plots. It is applied here to both synthetic data and some microarray gene expression data for clustering and shows its better performance over several existing methods.
Availability: The algorithms were implemented in Matlab. The Matlab code is available at http://blog.naver.com/aggie100.
Contact: [email protected]
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
Model-based methods have been widely used for both clustering and classifying high-dimensional microarray data (McLachlan et al., 2002; Yeung et al., 2001). Thalamuthu et al. (2006) compared various clustering techniques and showed that model-based method performed well for microarray gene clustering. The finite normal mixture model with unrestricted component-covariance matrices is a highly parameterized model (McLachlan and Basford, 1988; McLachlan and Peel, 2000a). Banfield and Raftery (1993) introduced a parameterization of the component-covariance matrix based on a variant of the standard spectral decomposition, and its program MCLUST (Fraley and Raftery, 2003) has been often used. But if the number of genes p is large relative to the sample size n, it may not be possible to use this decomposition to infer an appropriate model for the component-covariance matrices. Even if it were possible, the results may not be reliable due to potential problems with near-singular estimates of the component-covariance matrices when p is large relative to n. In this case, mixtures of factor analyzers (MFA) is a useful model to reduce the number of parameters by allowing factor-analytic representation of the component-covariance matrices. Hinton et al. (1997) proposed the MFA adopting a finite mixture of factor analysis models, which was considered for the purposes of clustering by McLachlan and Peel (2000a, 2000b) and McLachlan et al. (2003, 2007). McLachlan et al. (2002, 2003) applied MFA to tissue samples with microarray gene expression data for clustering. Martella (2006) used MFA to classify microarray data successfully. Recently, Xie et al. (2010) proposed a penalized MFA to allow both selection of effective genes and clustering of high-dimensional data simultaneously. Zhou et al. (2009) has proposed another penalized model-based clustering method with unconstrained covariance matrices.
In practice, for example, where there are several different types of cancer, there is often the need to reduce further the number of parameters in the specification of the component-covariance matrices by factor-analytic representations. McNicholas and Murphy (2008) introduced some parsimonious MFA models, which include various MFA models with fewer parameters. Galimberti et al. (2009) proposed another parsimonious factor mixture model to allow both dimension reduction and variable selection. Baek and McLachlan (2008) and Baek et al. (2010) proposed the use of mixtures of factor analyzers with common component-factor loadings (MCFA) and applied it to a microarray dataset for clustering. The method considerably reduces further the number of parameters, and allows the data to be displayed in low-dimensional plots in a straightforward manner in contrast to MFA. Several analyses of many real datasets, however, have suggested that the empirical distribution of gene expression levels is approximately log-normal or sometimes with a slightly heavier tailed t-distribution depending on the biological samples under investigation (Li, 2002). In particular, Giles and Kipling (2003) applied the Shapiro–Wilks test to Affymetrix microarray expression data and concluded that non-normal distributions are common (up to 46% of probe sets). Lönnstedt and Speed (2002) also noted that outliers occur frequently in microarray experiments. Therefore, the above approaches are sensitive to both non-normality of the data and extreme expression levels as they are based on a mixture model in which the multivariate normal family of distributions is assumed for the component-error and factor distributions. McLachlan et al. (2007) extended MFA to incorporate the multivariate t-distribution for the component-error and factor distributions. In this article, we propose an extension of MCFA to incorporate the multivariate t-distribution to handle the data with tails longer than that of the normal distribution.
In the next section, we review briefly the MCFA approach as proposed by Baek and McLachlan (2008) and considered further in Baek et al. (2010). We then describe the mixtures of t-factor analyzers model with common factor loadings (MCtFA) and develop its implementation via the expectation-maximization (EM) algorithm. In Section 3, its application is demonstrated in the clustering of two microarray gene expression datasets. The results so obtained illustrate the improved performance of MCtFA over MCLUST, MFA and MCFA for these two datasets. A short discussion is given in Section 4.
2 METHODS
2.1 Mixtures of common t-factor analyzers and its EM algorithm
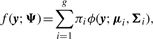
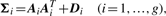
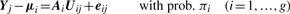
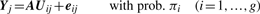
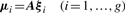
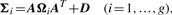
Comparison of MCLUST, MFA, MCFA and MCtFA models for implied clustering versus the true membership of Chowdary's 104 cancer tissues
| Model . | Factors . | BIC . | AWE . | ARI . | Error rate . |
|---|---|---|---|---|---|
| MCLUST . | VVI . | 242 872 . | . | 0.0657 . | 0.3462 . |
| MFA | 1 | 250 841 | 257 805 | 0.0296 | 0.3750 |
| 2 | 241 124 | 250 855 | 0.0296 | 0.3750 | |
| 3 | 234 888 | 247 371 | 0.5858 | 0.1154 | |
| 4 | 232 917 | 248 137 | 0.0386 | 0.3750 | |
| 5 | 230 485 | 248 426 | 0.0657 | 0.3462 | |
| 6 | 230 326 | 250 974 | 0.4726 | 0.1538 | |
| 7 | 230 461 | 253 800 | 0.2790 | 0.2308 | |
| 8 | 229 825 | 255 839 | 0.1431 | 0.2981 | |
| 9 | 229 433 | 258 107 | 0.1696 | 0.2885 | |
| MCFA | 1 | 261 337 | 264 164 | 0.6800 | 0.0865 |
| 2 | 253 301 | 257 532 | 0.0464 | 0.3654 | |
| 3 | 246 291 | 251 934 | 0.1282 | 0.3077 | |
| 4 | 243 084 | 250 139 | 0.0657 | 0.3462 | |
| 5 | 240 297 | 248 767 | 0.1587 | 0.2885 | |
| 6 | 236 654 | 246 539 | 0.0657 | 0.3462 | |
| 7 | 233 076 | 244 374 | 0.0657 | 0.3462 | |
| 8 | 232 083 | 244 795 | 0.2128 | 0.2596 | |
| 9 | 231 226 | 245 354 | 0.1240 | 0.3077 | |
| MCtFA | 1 | 234 450 | 237 278 | 0 | 0.4038 |
| 2 | 229 677 | 233 920 | 0.8505 | 0.0385 | |
| 3 | 228 106 | 233 764 | 0.8505 | 0.0385 | |
| 4 | 226 891 | 233 976 | 0.0675 | 0.3558 | |
| 5 | 225 387 | 233 876 | 0.5564 | 0.1250 | |
| 6 | 223 518 | 233 419 | 0.8867 | 0.0288 | |
| 7 | 222 455 | 233 772 | 0.6808 | 0.0865 | |
| 8 | 222 156 | 234 884 | 0.7465 | 0.0673 | |
| 9 | 221 134 | 235 276 | 0.4742 | 0.1538 | |
| Model . | Factors . | BIC . | AWE . | ARI . | Error rate . |
|---|---|---|---|---|---|
| MCLUST . | VVI . | 242 872 . | . | 0.0657 . | 0.3462 . |
| MFA | 1 | 250 841 | 257 805 | 0.0296 | 0.3750 |
| 2 | 241 124 | 250 855 | 0.0296 | 0.3750 | |
| 3 | 234 888 | 247 371 | 0.5858 | 0.1154 | |
| 4 | 232 917 | 248 137 | 0.0386 | 0.3750 | |
| 5 | 230 485 | 248 426 | 0.0657 | 0.3462 | |
| 6 | 230 326 | 250 974 | 0.4726 | 0.1538 | |
| 7 | 230 461 | 253 800 | 0.2790 | 0.2308 | |
| 8 | 229 825 | 255 839 | 0.1431 | 0.2981 | |
| 9 | 229 433 | 258 107 | 0.1696 | 0.2885 | |
| MCFA | 1 | 261 337 | 264 164 | 0.6800 | 0.0865 |
| 2 | 253 301 | 257 532 | 0.0464 | 0.3654 | |
| 3 | 246 291 | 251 934 | 0.1282 | 0.3077 | |
| 4 | 243 084 | 250 139 | 0.0657 | 0.3462 | |
| 5 | 240 297 | 248 767 | 0.1587 | 0.2885 | |
| 6 | 236 654 | 246 539 | 0.0657 | 0.3462 | |
| 7 | 233 076 | 244 374 | 0.0657 | 0.3462 | |
| 8 | 232 083 | 244 795 | 0.2128 | 0.2596 | |
| 9 | 231 226 | 245 354 | 0.1240 | 0.3077 | |
| MCtFA | 1 | 234 450 | 237 278 | 0 | 0.4038 |
| 2 | 229 677 | 233 920 | 0.8505 | 0.0385 | |
| 3 | 228 106 | 233 764 | 0.8505 | 0.0385 | |
| 4 | 226 891 | 233 976 | 0.0675 | 0.3558 | |
| 5 | 225 387 | 233 876 | 0.5564 | 0.1250 | |
| 6 | 223 518 | 233 419 | 0.8867 | 0.0288 | |
| 7 | 222 455 | 233 772 | 0.6808 | 0.0865 | |
| 8 | 222 156 | 234 884 | 0.7465 | 0.0673 | |
| 9 | 221 134 | 235 276 | 0.4742 | 0.1538 | |
The bold numbers are the optimal values of BIC, AWE, ARI and Error rate for each model.
Comparison of MCLUST, MFA, MCFA and MCtFA models for implied clustering versus the true membership of Chowdary's 104 cancer tissues
| Model . | Factors . | BIC . | AWE . | ARI . | Error rate . |
|---|---|---|---|---|---|
| MCLUST . | VVI . | 242 872 . | . | 0.0657 . | 0.3462 . |
| MFA | 1 | 250 841 | 257 805 | 0.0296 | 0.3750 |
| 2 | 241 124 | 250 855 | 0.0296 | 0.3750 | |
| 3 | 234 888 | 247 371 | 0.5858 | 0.1154 | |
| 4 | 232 917 | 248 137 | 0.0386 | 0.3750 | |
| 5 | 230 485 | 248 426 | 0.0657 | 0.3462 | |
| 6 | 230 326 | 250 974 | 0.4726 | 0.1538 | |
| 7 | 230 461 | 253 800 | 0.2790 | 0.2308 | |
| 8 | 229 825 | 255 839 | 0.1431 | 0.2981 | |
| 9 | 229 433 | 258 107 | 0.1696 | 0.2885 | |
| MCFA | 1 | 261 337 | 264 164 | 0.6800 | 0.0865 |
| 2 | 253 301 | 257 532 | 0.0464 | 0.3654 | |
| 3 | 246 291 | 251 934 | 0.1282 | 0.3077 | |
| 4 | 243 084 | 250 139 | 0.0657 | 0.3462 | |
| 5 | 240 297 | 248 767 | 0.1587 | 0.2885 | |
| 6 | 236 654 | 246 539 | 0.0657 | 0.3462 | |
| 7 | 233 076 | 244 374 | 0.0657 | 0.3462 | |
| 8 | 232 083 | 244 795 | 0.2128 | 0.2596 | |
| 9 | 231 226 | 245 354 | 0.1240 | 0.3077 | |
| MCtFA | 1 | 234 450 | 237 278 | 0 | 0.4038 |
| 2 | 229 677 | 233 920 | 0.8505 | 0.0385 | |
| 3 | 228 106 | 233 764 | 0.8505 | 0.0385 | |
| 4 | 226 891 | 233 976 | 0.0675 | 0.3558 | |
| 5 | 225 387 | 233 876 | 0.5564 | 0.1250 | |
| 6 | 223 518 | 233 419 | 0.8867 | 0.0288 | |
| 7 | 222 455 | 233 772 | 0.6808 | 0.0865 | |
| 8 | 222 156 | 234 884 | 0.7465 | 0.0673 | |
| 9 | 221 134 | 235 276 | 0.4742 | 0.1538 | |
| Model . | Factors . | BIC . | AWE . | ARI . | Error rate . |
|---|---|---|---|---|---|
| MCLUST . | VVI . | 242 872 . | . | 0.0657 . | 0.3462 . |
| MFA | 1 | 250 841 | 257 805 | 0.0296 | 0.3750 |
| 2 | 241 124 | 250 855 | 0.0296 | 0.3750 | |
| 3 | 234 888 | 247 371 | 0.5858 | 0.1154 | |
| 4 | 232 917 | 248 137 | 0.0386 | 0.3750 | |
| 5 | 230 485 | 248 426 | 0.0657 | 0.3462 | |
| 6 | 230 326 | 250 974 | 0.4726 | 0.1538 | |
| 7 | 230 461 | 253 800 | 0.2790 | 0.2308 | |
| 8 | 229 825 | 255 839 | 0.1431 | 0.2981 | |
| 9 | 229 433 | 258 107 | 0.1696 | 0.2885 | |
| MCFA | 1 | 261 337 | 264 164 | 0.6800 | 0.0865 |
| 2 | 253 301 | 257 532 | 0.0464 | 0.3654 | |
| 3 | 246 291 | 251 934 | 0.1282 | 0.3077 | |
| 4 | 243 084 | 250 139 | 0.0657 | 0.3462 | |
| 5 | 240 297 | 248 767 | 0.1587 | 0.2885 | |
| 6 | 236 654 | 246 539 | 0.0657 | 0.3462 | |
| 7 | 233 076 | 244 374 | 0.0657 | 0.3462 | |
| 8 | 232 083 | 244 795 | 0.2128 | 0.2596 | |
| 9 | 231 226 | 245 354 | 0.1240 | 0.3077 | |
| MCtFA | 1 | 234 450 | 237 278 | 0 | 0.4038 |
| 2 | 229 677 | 233 920 | 0.8505 | 0.0385 | |
| 3 | 228 106 | 233 764 | 0.8505 | 0.0385 | |
| 4 | 226 891 | 233 976 | 0.0675 | 0.3558 | |
| 5 | 225 387 | 233 876 | 0.5564 | 0.1250 | |
| 6 | 223 518 | 233 419 | 0.8867 | 0.0288 | |
| 7 | 222 455 | 233 772 | 0.6808 | 0.0865 | |
| 8 | 222 156 | 234 884 | 0.7465 | 0.0673 | |
| 9 | 221 134 | 235 276 | 0.4742 | 0.1538 | |
The bold numbers are the optimal values of BIC, AWE, ARI and Error rate for each model.
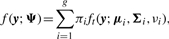
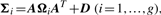
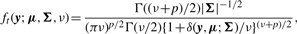
In order to fit the model (6) with the restriction (7), it is computationally convenient to exploit its link with factor analysis. Therefore, we assume that the distribution of yj of MCtFA is modelled as (3), where the joint distribution of the factor Uij and the error eij needs to be specified so that it is consistent with the t-mixture formulation (6) for the marginal distribution of yj. In the EM framework, the component label zj associated with the observation yj is introduced as missing data, where zij = (zj)i is one or zero according as yj belongs or does not belong to the i-th component of the mixture (i = 1,…, g; j = 1,…, n). The unobservable factors Uij are also introduced as missing data in the EM framework.
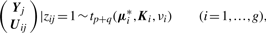
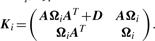
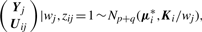
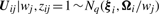
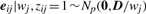
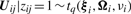
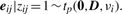
By adopting a common factor loading matrix and the t-distribution for the factors and error terms, the MCtF model has fewer parameters and is more robust against extreme observations, thus providing a better fit to data with skewed heavy tails.
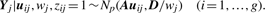
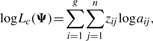
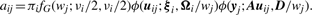
2.1.1 E-step
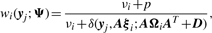

2.1.2 CM-step
We use two CM steps in the AECM algorithm, which correspond to the partition of Ψ into the two subvectors Ψ1 and Ψ2, where Ψ1 consists of the mixing proportions, the elements of ξi and the degrees of freedom νi(i = 1,…, g). The subvector Ψ2 consists of the elements of the common factor loadings matrix A, the Ωi and the diagonal matrix D.
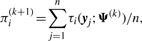
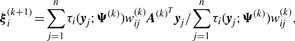
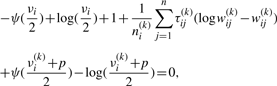
The estimate of Ψ is updated so that its current value after the first cycle is given by Ψ(k+1/2) = (Ψ1(k+1)T, Ψ2(k)T)T.
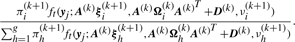
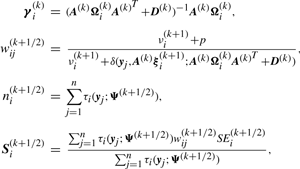
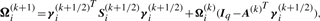

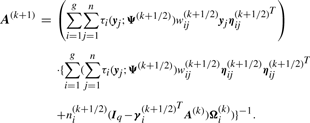
We have to specify an initial value for the vector Ψ of unknown parameters in the application of the EM algorithm. A random start is obtained by first randomly assigning the data into g groups. Using the sample mean and sample covariance matrix of each randomly partitioned data, the initial parameter estimates are obtained as described in the Appendix of Baek et al. (2010).
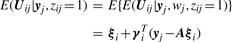
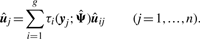
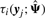 by
by 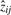 in (13).
in (13).3 RESULTS
Souto et al. (2008) compared different clustering methods for the analysis of 35 cancer gene expression datasets. For our experiment, we considered 2 of these 35 datasets. We applied MCtFA to cluster each of these two datasets, and compared its performance with other methods. We compare our method with MCLUST, MFA and MCFA. The performance is measured by the Adjusted Rand Index (ARI; Hubert and Arabie, 1985) and the error rate since the true membership of each observation is known.
MCLUST is a software package that implements Gaussian mixture models via EM algorithm and the Bayesian Information Criterion (BIC, Schwarz, 1978) for model-based clustering (Fraley and Raftery, 2003). In MCLUST, the component-covariance matrix Σi is parameterized by eigenvalue decomposition in the form Σi = ρiEiΛiEiT, where ρi is a constant, Ei is the matrix of eigenvectors, Λi is a diagonal matrix with elements proportional to the eigenvalues of Σi. Different conditions on ρi, Λi and Ei characterize the volume, shape and orientation of each component distribution in MCLUST. We deal with the 10 submodels of MCLUST: EII, VII, EEI, VEI, EVI, VVI, EEE, EEV, VEV, VVV (Fraley and Raftery, 2003, Table 1). For MFA, we assumed the covariance matrix of errors is equal for each component. We took advantage of the mclust software for R (Team RDC 2004) and the EMMIX program (McLachlan et al., 1999) for MFA, and developed programs for the MCFA and the MCtFA approaches, using the MATLAB language.
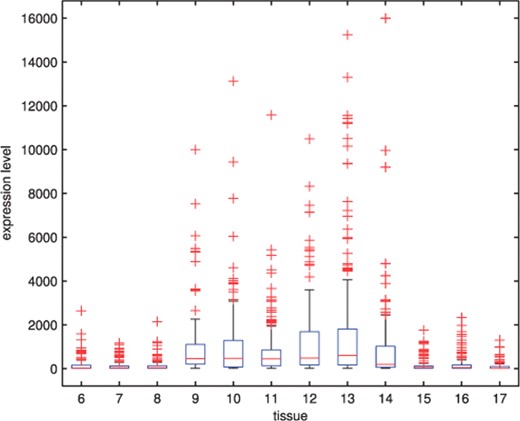
The first set concerns both breast and colon cancer data (Chowdary et al., 2006), which consists of 104 gene expressions for 52 matched tissue pairs of two different cancer types (32 pairs of breast tumour and 20 pairs of colon tumour). There are 22 283 genes in the original data, but Souto et al. (2008) selected 182 genes by filtering uninformative genes. It has been reported in many analyses of real datasets that the empirical distribution of gene expression levels is approximately log-normal or sometimes (on the log scale) with a slightly heavier tailed t-distribution depending on the biological samples under investigation (Li, 2002). Thus, these data may also have many extreme expressions for each gene. Figure 1 shows boxplots of the expression levels for the first 10 genes. The distribution of each gene is skewed and has a very long tail. The rest of the genes also have similar shaped distributions. In particular, gene 6 has very high expression levels for six particular tissues.
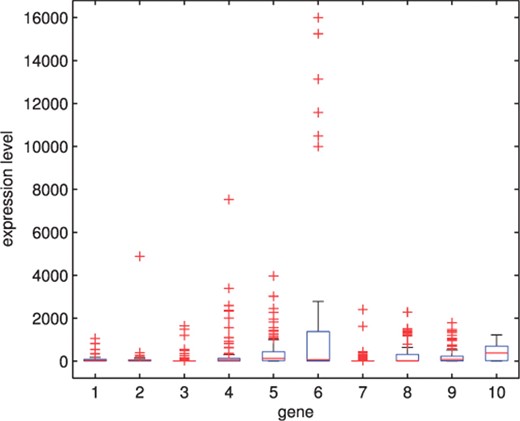
The boxplots for the first 10 genes in the cancer data of Chowdary et al. (2006).
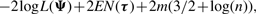
It can be seen that the lowest error rate (0.0288) and highest value (0.8867) of the ARI is obtained by using q = 6 factors with the MCtFA model, which coincides with the choice on the basis of AWE. The lowest error rate (0.1154) of the MFA model is obtained for q = 3 factors. The best result of MCFA model is obtained with its lowest error rate 0.0865 for q = 1 factor (AWE suggests using q = 7). MCLUST chose VVI model as its best and its error rate is 0.3462. It can be seen that the error rate and ARI for MCtFA are better than those for MCLUST, MFA and MCFA. We have also calculated BIC for all models. It can be seen that it failed to select the best model for each method. BIC reached its minimum for largest q (q = 9) of each method, so it selected a more complex model than the one with highest ARI and lowest error rate. In the case where the distribution from which the data arose is not in the collection of considered mixture models, BIC criterion tends to overestimate the correct size regardless of the separation of the clusters (Celeux, 2007).
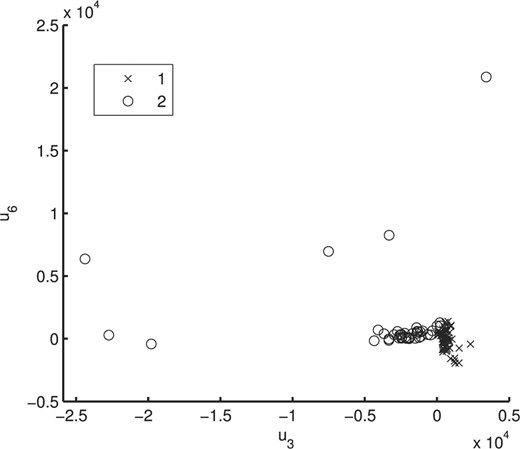
To illustrate the usefulness of the MCtFA approach for portraying the results of a clustering in low-dimensional space, we have plotted in Figure 2 the estimated factor scores ûj as defined by (13) with the implied cluster labels shown. In this plot, we used the third and sixth factors in the fit of the MCtFA model with q = 6 factors. It can be seen that the clusters are represented in this plot with very little overlap. The estimated factor scores were plotted according to the implied clustering labels. The degrees of freedom of the factor t-distributions for both groups were estimated as 1.0 and 1.0, which means their tails of the distributions are very thick and long. We can easily detect 6 distinct extreme tissues as shown in Figure 2, which are known to be the 9th–14th colon tumor tissue. Figure 3 shows the expression levels of all genes for the 6th–17th colon tumor tissues. In Figure 3, we observe that all of these 6 outliers are very different from others since they have extremely large expression levels not only of the 6th gene shown in Figure 1, but also of other genes.
Plot of the (estimated) posterior mean factor scores via the MCtFA approach based on the implied clustering for the cancer data of Chowdary et al. (2006).
The boxplots of expression levels of all genes for the 6th–17th colon tumor tissues.
The second dataset to which we applied our method is a lung cancer data (Bhattacherjee et al., 2001), for which the number of classes is not small (g = 5). It consists of 203 gene expressions partitioned into five subpopulations: four lung cancer types and normal tissues. Souto et al. (2008) selected 1543 informative genes from the original 12 600 genes. There are big differences among the class sizes of the data. The number of tissues for each class is 139, 17, 6, 21 and 20, respectively. Figure 4 shows the boxplots of the expressions of a gene plotted for each subpopulation. It can be seen that there exist skewed distributions mixed with symmetric distribution with or without extreme observations for five components in the plot. Since the selected (1543) genes are still too many for the mixture model, we grouped the genes into 50 clusters and selected the centroid from each cluster of genes. That is, we applied the k-means algorithm to the 1543 gene expressions and clustered them into 50 groups of similar characteristics. Then we extracted the centroid from each group to make 50 new features for the mixture models.
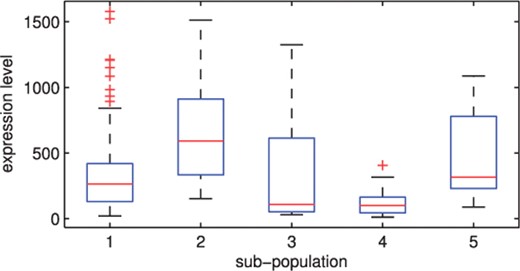
The boxplots for the expressions of a gene by subpopulation: the lung cancer data of Bhattacherjee et al. (2001).
We implemented the MCLUST, MFA, MCFA, and MCtFA approaches with g = 5 components for the number of factors q ranging from 1 to 10, using 50 starting values for the parameters. For each value of q, we computed the ARI and the error rate. The results are presented in Table 2. We have also listed in this table the values of BIC and AWE for each model with different levels of q. MCtFA attains its largest ARI (0.7322) and lowest error rate (0.1133) for q = 6, although AWE suggested the model with q = 7. We notice that there is little difference between the AWE values for q = 6 and for q = 7. The lowest error rate for MCFA is 0.2611 for q = 2 and the largest ARI is 0.4570 for q = 9. The error rate (NA) of MCFA for q = 1 was not able to be calculated since the estimated number of clusters was less than the true value 5. Neither BIC nor AWE indicated the best model for MCFA. MFA reached its best ARI (0.3487) and error rate (0.3498) for q = 7. The minimum BIC and AWE were obtained at q = 6, and at q = 1, respectively. The best model for MCLUST showed similar performance (ARI: 0.3021, error rate: 0.3350) to MFA. MCtFA again performed better than the other methods for this dataset.
We display the data using the estimated factor scores of our model in 3D space (Figure 5). In the latter, we used the second, the fourth and the fifth factors in the fit of the MCtFA model with q = 6 factors. The estimated factor scores were plotted according to the implied clustering labels. It can be seen that the five clusters are represented in this plot with very little overlap. The degrees of freedom of the factor t-distributions for the components were estimated as 1.1, 1.3, 7.8, 4.0 and 4.1. There are two distributions with long tails [ν1 = 1.1 (triangle), ν2 = 1.3 (circle)] in the plot. We have also given in Figure 6 the plot corresponding to that in Figure 5 with the true cluster labels shown. There are 23 misallocated tissues which can be seen in other's clusters, but as a whole there is a good agreement between the two plots.
Comparison of MCLUST, MFA, MCFA and MCtFA models for implied clustering versus the true membership of Bhattacharjee's 203 lung cancer tissues
| Model . | Factors . | BIC . | AWE . | ARI . | Error rate . |
|---|---|---|---|---|---|
| MCLUST . | VVI . | 135 023 . | . | 0.3021 . | 0.3350 . |
| MFA | 1 | 140 710 | 145 324 | 0.3100 | 0.4286 |
| 2 | 139 479 | 146 125 | 0.3219 | 0.3941 | |
| 3 | 139 313 | 147 955 | 0.3156 | 0.4089 | |
| 4 | 139 016 | 149 611 | 0.3013 | 0.4039 | |
| 5 | 139 068 | 151 573 | 0.3368 | 0.3645 | |
| 6 | 138 870 | 153 244 | 0.2445 | 0.4236 | |
| 7 | 139 358 | 155 561 | 0.3487 | 0.3498 | |
| 8 | 139 747 | 157 738 | 0.2616 | 0.4335 | |
| 9 | 140 207 | 159 943 | 0.2571 | 0.4433 | |
| 10 | 140 414 | 161 854 | 0.2368 | 0.4680 | |
| MCFA | 1 | 148 255 | 149 674 | 0.0721 | NA |
| 2 | 144 994 | 146 585 | 0.3348 | 0.2611 | |
| 3 | 142 978 | 145 042 | 0.3090 | 0.3300 | |
| 4 | 141 826 | 144 453 | 0.4376 | 0.2759 | |
| 5 | 140 943 | 144 139 | 0.3703 | 0.3153 | |
| 6 | 140 123 | 143 943 | 0.3269 | 0.3251 | |
| 7 | 139 362 | 143 800 | 0.3692 | 0.3153 | |
| 8 | 138 921 | 144 015 | 0.3775 | 0.3153 | |
| 9 | 138 420 | 144 194 | 0.4570 | 0.2709 | |
| 10 | 138 134 | 144 633 | 0.2418 | 0.4335 | |
| MCtFA | 1 | 144 424 | 145 607 | −0.1269 | 0.4384 |
| 2 | 142 708 | 144 294 | 0.3619 | 0.2413 | |
| 3 | 141 155 | 143 236 | 0.4735 | 0.2266 | |
| 4 | 139 683 | 142 334 | 0.6179 | 0.1527 | |
| 5 | 138 937 | 142 154 | 0.6657 | 0.1379 | |
| 6 | 138 194 | 142 025 | 0.7322 | 0.1133 | |
| 7 | 137 538 | 142 009 | 0.5875 | 0.1675 | |
| 8 | 136 973 | 142 105 | 0.6417 | 0.1773 | |
| 9 | 136 660 | 142 474 | 0.4408 | 0.2365 | |
| 10 | 136 431 | 142 967 | 0.3215 | 0.3153 | |
| Model . | Factors . | BIC . | AWE . | ARI . | Error rate . |
|---|---|---|---|---|---|
| MCLUST . | VVI . | 135 023 . | . | 0.3021 . | 0.3350 . |
| MFA | 1 | 140 710 | 145 324 | 0.3100 | 0.4286 |
| 2 | 139 479 | 146 125 | 0.3219 | 0.3941 | |
| 3 | 139 313 | 147 955 | 0.3156 | 0.4089 | |
| 4 | 139 016 | 149 611 | 0.3013 | 0.4039 | |
| 5 | 139 068 | 151 573 | 0.3368 | 0.3645 | |
| 6 | 138 870 | 153 244 | 0.2445 | 0.4236 | |
| 7 | 139 358 | 155 561 | 0.3487 | 0.3498 | |
| 8 | 139 747 | 157 738 | 0.2616 | 0.4335 | |
| 9 | 140 207 | 159 943 | 0.2571 | 0.4433 | |
| 10 | 140 414 | 161 854 | 0.2368 | 0.4680 | |
| MCFA | 1 | 148 255 | 149 674 | 0.0721 | NA |
| 2 | 144 994 | 146 585 | 0.3348 | 0.2611 | |
| 3 | 142 978 | 145 042 | 0.3090 | 0.3300 | |
| 4 | 141 826 | 144 453 | 0.4376 | 0.2759 | |
| 5 | 140 943 | 144 139 | 0.3703 | 0.3153 | |
| 6 | 140 123 | 143 943 | 0.3269 | 0.3251 | |
| 7 | 139 362 | 143 800 | 0.3692 | 0.3153 | |
| 8 | 138 921 | 144 015 | 0.3775 | 0.3153 | |
| 9 | 138 420 | 144 194 | 0.4570 | 0.2709 | |
| 10 | 138 134 | 144 633 | 0.2418 | 0.4335 | |
| MCtFA | 1 | 144 424 | 145 607 | −0.1269 | 0.4384 |
| 2 | 142 708 | 144 294 | 0.3619 | 0.2413 | |
| 3 | 141 155 | 143 236 | 0.4735 | 0.2266 | |
| 4 | 139 683 | 142 334 | 0.6179 | 0.1527 | |
| 5 | 138 937 | 142 154 | 0.6657 | 0.1379 | |
| 6 | 138 194 | 142 025 | 0.7322 | 0.1133 | |
| 7 | 137 538 | 142 009 | 0.5875 | 0.1675 | |
| 8 | 136 973 | 142 105 | 0.6417 | 0.1773 | |
| 9 | 136 660 | 142 474 | 0.4408 | 0.2365 | |
| 10 | 136 431 | 142 967 | 0.3215 | 0.3153 | |
The bold numbers are the optimal values of BIC, AWE, ARI and Error rate for each model. NA means Not Available.
Comparison of MCLUST, MFA, MCFA and MCtFA models for implied clustering versus the true membership of Bhattacharjee's 203 lung cancer tissues
| Model . | Factors . | BIC . | AWE . | ARI . | Error rate . |
|---|---|---|---|---|---|
| MCLUST . | VVI . | 135 023 . | . | 0.3021 . | 0.3350 . |
| MFA | 1 | 140 710 | 145 324 | 0.3100 | 0.4286 |
| 2 | 139 479 | 146 125 | 0.3219 | 0.3941 | |
| 3 | 139 313 | 147 955 | 0.3156 | 0.4089 | |
| 4 | 139 016 | 149 611 | 0.3013 | 0.4039 | |
| 5 | 139 068 | 151 573 | 0.3368 | 0.3645 | |
| 6 | 138 870 | 153 244 | 0.2445 | 0.4236 | |
| 7 | 139 358 | 155 561 | 0.3487 | 0.3498 | |
| 8 | 139 747 | 157 738 | 0.2616 | 0.4335 | |
| 9 | 140 207 | 159 943 | 0.2571 | 0.4433 | |
| 10 | 140 414 | 161 854 | 0.2368 | 0.4680 | |
| MCFA | 1 | 148 255 | 149 674 | 0.0721 | NA |
| 2 | 144 994 | 146 585 | 0.3348 | 0.2611 | |
| 3 | 142 978 | 145 042 | 0.3090 | 0.3300 | |
| 4 | 141 826 | 144 453 | 0.4376 | 0.2759 | |
| 5 | 140 943 | 144 139 | 0.3703 | 0.3153 | |
| 6 | 140 123 | 143 943 | 0.3269 | 0.3251 | |
| 7 | 139 362 | 143 800 | 0.3692 | 0.3153 | |
| 8 | 138 921 | 144 015 | 0.3775 | 0.3153 | |
| 9 | 138 420 | 144 194 | 0.4570 | 0.2709 | |
| 10 | 138 134 | 144 633 | 0.2418 | 0.4335 | |
| MCtFA | 1 | 144 424 | 145 607 | −0.1269 | 0.4384 |
| 2 | 142 708 | 144 294 | 0.3619 | 0.2413 | |
| 3 | 141 155 | 143 236 | 0.4735 | 0.2266 | |
| 4 | 139 683 | 142 334 | 0.6179 | 0.1527 | |
| 5 | 138 937 | 142 154 | 0.6657 | 0.1379 | |
| 6 | 138 194 | 142 025 | 0.7322 | 0.1133 | |
| 7 | 137 538 | 142 009 | 0.5875 | 0.1675 | |
| 8 | 136 973 | 142 105 | 0.6417 | 0.1773 | |
| 9 | 136 660 | 142 474 | 0.4408 | 0.2365 | |
| 10 | 136 431 | 142 967 | 0.3215 | 0.3153 | |
| Model . | Factors . | BIC . | AWE . | ARI . | Error rate . |
|---|---|---|---|---|---|
| MCLUST . | VVI . | 135 023 . | . | 0.3021 . | 0.3350 . |
| MFA | 1 | 140 710 | 145 324 | 0.3100 | 0.4286 |
| 2 | 139 479 | 146 125 | 0.3219 | 0.3941 | |
| 3 | 139 313 | 147 955 | 0.3156 | 0.4089 | |
| 4 | 139 016 | 149 611 | 0.3013 | 0.4039 | |
| 5 | 139 068 | 151 573 | 0.3368 | 0.3645 | |
| 6 | 138 870 | 153 244 | 0.2445 | 0.4236 | |
| 7 | 139 358 | 155 561 | 0.3487 | 0.3498 | |
| 8 | 139 747 | 157 738 | 0.2616 | 0.4335 | |
| 9 | 140 207 | 159 943 | 0.2571 | 0.4433 | |
| 10 | 140 414 | 161 854 | 0.2368 | 0.4680 | |
| MCFA | 1 | 148 255 | 149 674 | 0.0721 | NA |
| 2 | 144 994 | 146 585 | 0.3348 | 0.2611 | |
| 3 | 142 978 | 145 042 | 0.3090 | 0.3300 | |
| 4 | 141 826 | 144 453 | 0.4376 | 0.2759 | |
| 5 | 140 943 | 144 139 | 0.3703 | 0.3153 | |
| 6 | 140 123 | 143 943 | 0.3269 | 0.3251 | |
| 7 | 139 362 | 143 800 | 0.3692 | 0.3153 | |
| 8 | 138 921 | 144 015 | 0.3775 | 0.3153 | |
| 9 | 138 420 | 144 194 | 0.4570 | 0.2709 | |
| 10 | 138 134 | 144 633 | 0.2418 | 0.4335 | |
| MCtFA | 1 | 144 424 | 145 607 | −0.1269 | 0.4384 |
| 2 | 142 708 | 144 294 | 0.3619 | 0.2413 | |
| 3 | 141 155 | 143 236 | 0.4735 | 0.2266 | |
| 4 | 139 683 | 142 334 | 0.6179 | 0.1527 | |
| 5 | 138 937 | 142 154 | 0.6657 | 0.1379 | |
| 6 | 138 194 | 142 025 | 0.7322 | 0.1133 | |
| 7 | 137 538 | 142 009 | 0.5875 | 0.1675 | |
| 8 | 136 973 | 142 105 | 0.6417 | 0.1773 | |
| 9 | 136 660 | 142 474 | 0.4408 | 0.2365 | |
| 10 | 136 431 | 142 967 | 0.3215 | 0.3153 | |
The bold numbers are the optimal values of BIC, AWE, ARI and Error rate for each model. NA means Not Available.
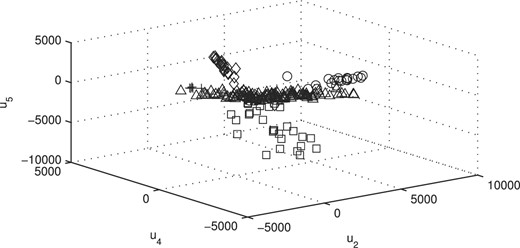
Plot of the (estimated) posterior mean factor scores via the MCtFA approach based on the implied clustering for the lung cancer data of Bhattacherjee et al. (2001).
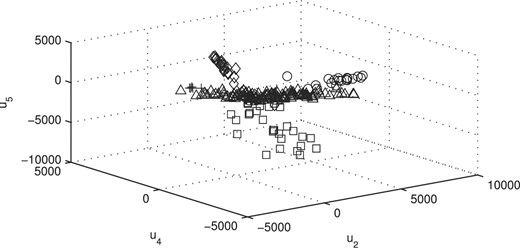
Plot of the (estimated) posterior mean factor scores via the MCtFA approach with the true labels shown for the lung cancer data of Bhattacherjee et al. (2001).
4 DISCUSSION
For clustering high-dimensional data such as microarray gene expressions, MFA is a useful technique since it can reduce the number of parameters through its factor-analytic representation of the component-covariance matrices. However, this approach is sensitive to outliers as it is based on a mixture model in which the multivariate normal family of distributions is assumed for the component factor and error distributions. McLachlan et al. (2007) extended MFA to incorporate t-distributions for the component factor and error in the mixture model for dealing with unusual extreme observations (MtFA). These methods, however, may not provide a sufficient reduction in the number of parameters, particularly when the number of clusters (subpopulations) is not small. In this article, we proposed a new mixture model which can reduce the number of parameters further in such instances and cluster the data containing outliers simultaneously by introducing a mixture of t-distributions with both component-mean and component covariance represented by common factor loadings. We call this approach mixtures of common t-factor analyzers (MCtFA). We describe the implementation of an EM algorithm for fitting the MCtFA. This approach also has the ability to portray the results of a clustering in low-dimensional space. We can plot the estimated posterior means of the factors ûj as defined by (13) with the implied cluster labels. On the other hand, the approaches MCLUST, MFA and MtFA cannot project high-dimensional objects in low-dimensional space. The applications of MCtFA to two cancer microarray datasets have demonstrated the usefulness and its relative superiority in clustering performance over MCLUST, MFA and MCFA. It has shown that our method works well for clustering data containing outliers. Moreover, it provides information on the distribution structure of each subpopulation by displaying the estimated factor scores in low-dimensional space. We observed also that the proposed approach fitted the experimental datasets better than the other approaches, and the performance difference between MCtFA and the others becomes even greater when the number of clusters is not small, such as in the case of second dataset (Section 1.1 of Supplementary Material).
Often BIC is used to provide a guide to the choice of the number of factors q and the number of components g to be used. However, it did not always lead to the correct choice of the best model. That is, BIC can lead to too simple or too complex model in practice, depending on the problem at hand. Simulation studies reported in Biernacki and Govaert (1997), Biernacki et al. (2000) and McLachlan and Peel (2000a) show that BIC will overrate the number of clusters under misspecification of the component density, whereas several alternative criteria such as the AWE and ICL criterion are able to identify the correct number of clusters even when the component densities are misspecified (Frühwirth-Schnatter and Pyne, 2010). In both of our real data applications, we observed that BIC did not choose the best q. An apparent explanation for this is that BIC tries to choose more complex model since some of the subpopulations of the datasets have skewed distributions and have several extreme outliers. On the other hand, AWE leads to the best or almost the best model with smallest error rate since it is more robust against misspecification of the component densities for the experimental datasets. Recently, Frühwirth-Schnatter and Pyne (2010) reported that AWE picked the correct model for both skew-t and skew-normal mixture distributions. Also a small simulation study confirms the better performance of the AWE over the BIC when the distribution of the data has skewed heavy tails due to some extreme observations (Section 1.2 of Supplementary Material). In future work, we wish to investigate the use of various model selection criteria on choosing the number of factors q and the number of components g in mixtures of t or skewed distributions.
Funding: Korea Research Foundation Grant funded by the Korean Government (MOEHRD, Basic Research Promotion Fund, KRF-2007-521-C00048 to J.B.). Australian Research Council (to G.J.M.).
Conflict of Interest: none declared.
REFERENCES
Author notes
Associate Editor: Trey Ideker



