-
PDF
- Split View
-
Views
-
Cite
Cite
Ami Levy-Moonshine, El-ad David Amir, Chen Keasar, Enhancement of beta-sheet assembly by cooperative hydrogen bonds potential, Bioinformatics, Volume 25, Issue 20, October 2009, Pages 2639–2645, https://doi.org/10.1093/bioinformatics/btp449
Close - Share Icon Share
Abstract
Motivation: The roughness of energy landscapes is a major obstacle to protein structure prediction, since it forces conformational searches to spend much time struggling to escape numerous traps. Specifically, beta-sheet formation is prone to stray, since many possible combinations of hydrogen bonds are dead ends in terms of beta-sheet assembly. It has been shown that cooperative terms for backbone hydrogen bonds ease this problem by augmenting hydrogen bond patterns that are consistent with beta sheets. Here, we present a novel cooperative hydrogen-bond term that is both effective in promoting beta sheets and computationally efficient. In addition, the new term is differentiable and operates on all-atom protein models.
Results: Energy optimization of poly-alanine chains under the new term led to significantly more beta-sheet content than optimization under a non-cooperative term. Furthermore, the optimized structure included very few non-native patterns.
Availability: The new term is implemented within the MESHI package and is freely available at http://cs.bgu.ac.il/∼meshi.
Contact: [email protected]
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
Hydrogen bonds are major constituents of protein structures (Backer and Hubbard, 1984; Huggins, 1971; McDonald and Thornton, 1994). All natural residues have the capacity to take part in hydrogen bonding (at least through the polar moieties of their backbones), and in native protein structures almost all of this potential is fulfilled through either inter- or intra-molecular hydrogen bonds (Fleming and Ros, 2005). This work focuses on backbone hydrogen bonds (BHBs), i.e. main chain to main chain hydrogen bonds. BHBs constitute the major class (63.2%) of intra-molecular hydrogen bonds in proteins (McDonald and Thornton, 1994). Most of them are organized in extensive networks of periodic patterns known as alpha helices and beta sheets. These networks are essential for the protein's structural stability, as they allow the burial of polar backbone moieties within the hydrophobic core. In this work, we developed an energy term that facilitates the formation not only of BHBs but also of native-like patterns of BHBs.
Ab initio protein structure predictions (Bonneau and Baker, 2001; Chivian et al., 2003; Yang et al., 2007) use optimization processes that gradually derive initial high-energy conformations toward lower energy ones. The initial conformations are typically poor in hydrogen bonds, which emerge and form extensive networks as the optimization process proceeds. To a somewhat lesser extent, this is also true for the refinement step of fold recognition (Krieger et al., 2003) and for homology modeling (Xiang, 2006), in which loop insertions may require remodeling of the hydrogen bond networks. For the optimization process to result in hydrogen bond formation, the hydrogen bonds should be rewarded by the energy function, either implicitly through a combination of electrostatic and van der Waals terms (Buck and Karplus, 2001; Cornell et al., 1995; Jorgensen and Tirado-Rives, 1988; Neria et al., 1996), or explicitly through specialized hydrogen bond terms (Brooks et al., 1983; Dahiyat et al., 1997; Kortemme and Baker, 2003; Mayo et al., 1990; Weiner et al., 1984). In both cases, the terms are typically sums of independent single hydrogen bond contributions. Thus, structures with a few sparse hydrogen bonds may constitute local minima, and the assembly of the network is likely to require the formation and breaking of numerous hydrogen bonds. Given a predefined secondary structure (i.e. from secondary structure prediction), the simple pattern of helix hydrogen bonds considerably eases the assembly of alpha helices. In contrast, the formation of beta sheets, which are characterized by more complex hydrogen bond patterns, remains a difficult task, even if the correct segments are defined as beta. The common treatment of hydrogen bonds by energy functions is thus a considerable contributor to the infamous ‘local minima problem’, which has annoyed predictors since the earliest days of this field (Burgess and Scheraga, 1975; Levitt and Warshel, 1975).
Cooperative terms for hydrogen bonds (Godzik et al., 1993; Keasar and Levitt, 2003; Kolinski and Skolnick, 1992, 1994; Liwo et al., 1998) attempt to ease this problem by shifting the focus from the individual hydrogen bond to patterns of hydrogen bonds. Specifically, they expand the basins of attraction of deep minima, which are characterized by organized hydrogen bond networks, at the expense of numerous shallow local minima with unstructured hydrogen bonds. In their pioneering work, Kolinski and Skolnick (1992, 1994) used this idea to improve the performance of lattice-based Monte Carlo simulations of simplified Cα protein models. Their cooperative energy term operated on six atoms at once (three consecutive Cα atoms in two distant fragments) and rewarded characteristic secondary structure patterns. Hydrogen bonds that did not take part in correct patterns were not rewarded. This idea was implemented later in off-lattice simulations with a united-residue force field (Liwo et al., 1998). In that study, it was demonstrated that the addition of a cooperative term improved the folding of short poly-alanine into an alpha helix. More recently, we revisited and extended this idea (Keasar and Levitt, 2003). Our energy function operated on all-atom models, took into account more subtle patterns, and was differentiable. With this energy term, we were able to form extensive secondary structures by downhill minimization.
The utility of this energy function was, however, limited by three factors: first, it was rule-based. The rules were manually hard-coded in the program, and after a large set of rules had been implemented, it was very difficult to add more rules. Second, the cooperative term took into consideration only the distances between the hydrogen and oxygen atoms. The orientation preferences of hydrogen bonds were not handled explicitly. The most severe problem, though, was the computational complexity and the memory requirements of the energy term. Both grew quadratically with protein length, thereby restricting the applicability of this term to small proteins.
The current study takes the cooperative approach three steps further. First, it is extendable. The hard-coded rules are replaced by an automatically generated database of patterns, which is queried in real time. Second, and most important, the proposed approach is computationally efficient, with computational complexity and memory requirements that are linearly proportional to protein length. Finally, it is accompanied by another term that imposes proper orientation on the hydrogen bonds. The current manuscript presents the new hydrogen bonds term and demonstrates its efficiency and usability.
2 METHODS
2.1 Dataset of native structures
The parameters and patterns for the energy term that we describe below were extracted from a subset of ASTRAL Version 1.63 (Brenner et al., 2000). This dataset includes 627 domain structures (∼100 000 residues). It is non-redundant, with only one representative for each SCOP family (Murzin et al., 1995), and includes only high-quality structures with a SPACI (Brenner et al., 2000) score above 0.62 (corresponding roughly to a resolution ≤1.6 Å) (available in the Supplementary Material).
2.2 Optimization methods
The differentiability of our energy function (below) allows employment of the LBFGS method for downhill minimization (Liu and Nocedal, 1989). Starting from an arbitrary conformation, this method uses a linear approximation of the energy's second derivatives matrix to find an efficient path to the nearest local minimum. In this work all minimizations were performed until convergence or for 100 000 steps.
For global optimization, we use Simulated Annealing (Kirkpatrick et al., 1983) Monte Carlo Minimization (MCM) method (Bradley et al., 2005; Li and Scheraga, 1987; Trosset and Scheraga, 1998) that iteratively hops between local minima, gradually converging to lower energy ones. In each iteration of MCM, a new local minimum structure is found by random perturbation of the previous conformation, followed by downhill minimization. Commonly, MCM implementations perturbed the conformations by a random rotation of a random torsion angle. Our implementation is softer, in the spirit of the ‘pushing potential’ of Levitt (Levitt, 1976; see also Gibson and Scheraga, 1969). In our new variant, the perturbation is achieved by downhill minimization of a randomly perturbed energy function. The perturbing minimization ends when it either converges or reaches a predefined RMS limit. In the current work all MCM simulations used a 7 Å RMS limit and 50 rounds of perturbation followed by minimization.
2.3 Energy terms
While this study focused on the hydrogen bond terms (see Section 3), it required several other energy terms. All the terms used are differentiable, and all non-bonded interactions are zero for atom distances above Rmax (=5.5 Å), ensuring that the length of the non-bonded list (NBL) is linear with the number of atoms (Maximova and Keasar, 2006).
The additional terms were: The total energy function used in this study is E = ∑ WiEi where each Ei is one of the energy terms specified above and the weights (Wi) are presented in the Supplementary Material.
Excluded volume and bonded terms (bond, angle, plane and out-of-plane) ensured the physical accuracy of the molecular structures.
A backbone torsion angles term (a simplified version of Amir et al., 2008) ensured proper backbone torsion angles.
Since the current work does not use any solvation term, it does not simulate hydrophobic interactions. We used the heavy atoms' radius of gyration as an energy term that forces the random initial configurations to collapse.
- During the perturbation steps of the MCM simulations, we used a special term that we call ‘inflate’. It pushes apart pairs (i, j) of adjacent (di,j≤Rmax) non-bonded atoms by a random and almost linear force that smoothly converges to zero when they reach Rmax.where 0 ≤randi,j≤ 1 is a random number chosen once in the initialization stage.

2.4 Computational experiments protocol
We tested the new cooperative energy term on a model system of poly-alanine chains with predefined secondary structure preferences. The lengths and secondary structure assignments of the chains were taken from a diverse set of mainly beta proteins (Table 1 and Supplementary Material).
| Protein PDB ID (Berman et al., 2000) . | CATH code (Orengo et al., 1997) . | Length . | Beta content (%)a . |
|---|---|---|---|
| 1WAPA | 2.60.40.50 | 68 | 42 |
| 1NPSA | 2.60.20.10 | 88 | 40 |
| 1FNA_ | 2.60.40.30 | 91 | 42 |
| 1WHO | 2.60.40.760 | 94 | 46 |
| 1TUL_ | 2.70.40.20 | 102 | 52 |
| 1SSPB | – | 112 | 62 |
| 1HDN | 3.30.1340.10 | 85 | 26 |
| 1RIS_ | 3.30.70.60 | 97 | 47 |
| 2ACY_ | 3.30.70.100 | 98 | 41 |
| 1FKB_ | 3.10.50.40 | 107 | 41 |
| 1KPEA | 3.30.428.10 | 113 | 25 |
| 1ACF | 3.30.450.30 | 125 | 41 |
| Protein PDB ID (Berman et al., 2000) . | CATH code (Orengo et al., 1997) . | Length . | Beta content (%)a . |
|---|---|---|---|
| 1WAPA | 2.60.40.50 | 68 | 42 |
| 1NPSA | 2.60.20.10 | 88 | 40 |
| 1FNA_ | 2.60.40.30 | 91 | 42 |
| 1WHO | 2.60.40.760 | 94 | 46 |
| 1TUL_ | 2.70.40.20 | 102 | 52 |
| 1SSPB | – | 112 | 62 |
| 1HDN | 3.30.1340.10 | 85 | 26 |
| 1RIS_ | 3.30.70.60 | 97 | 47 |
| 2ACY_ | 3.30.70.100 | 98 | 41 |
| 1FKB_ | 3.10.50.40 | 107 | 41 |
| 1KPEA | 3.30.428.10 | 113 | 25 |
| 1ACF | 3.30.450.30 | 125 | 41 |
The length and secondary structure of these proteins were assigned to the poly-alanine chains. The CATH classifications signify that all the proteins are mainly-beta, from the all-beta or alpha–beta categories, yet they belong to different folds. For 1SSPB there is no entry in the current version of CATH.
aThe beta content was determined by DSSP (Kabsch and Sander, 1983).
| Protein PDB ID (Berman et al., 2000) . | CATH code (Orengo et al., 1997) . | Length . | Beta content (%)a . |
|---|---|---|---|
| 1WAPA | 2.60.40.50 | 68 | 42 |
| 1NPSA | 2.60.20.10 | 88 | 40 |
| 1FNA_ | 2.60.40.30 | 91 | 42 |
| 1WHO | 2.60.40.760 | 94 | 46 |
| 1TUL_ | 2.70.40.20 | 102 | 52 |
| 1SSPB | – | 112 | 62 |
| 1HDN | 3.30.1340.10 | 85 | 26 |
| 1RIS_ | 3.30.70.60 | 97 | 47 |
| 2ACY_ | 3.30.70.100 | 98 | 41 |
| 1FKB_ | 3.10.50.40 | 107 | 41 |
| 1KPEA | 3.30.428.10 | 113 | 25 |
| 1ACF | 3.30.450.30 | 125 | 41 |
| Protein PDB ID (Berman et al., 2000) . | CATH code (Orengo et al., 1997) . | Length . | Beta content (%)a . |
|---|---|---|---|
| 1WAPA | 2.60.40.50 | 68 | 42 |
| 1NPSA | 2.60.20.10 | 88 | 40 |
| 1FNA_ | 2.60.40.30 | 91 | 42 |
| 1WHO | 2.60.40.760 | 94 | 46 |
| 1TUL_ | 2.70.40.20 | 102 | 52 |
| 1SSPB | – | 112 | 62 |
| 1HDN | 3.30.1340.10 | 85 | 26 |
| 1RIS_ | 3.30.70.60 | 97 | 47 |
| 2ACY_ | 3.30.70.100 | 98 | 41 |
| 1FKB_ | 3.10.50.40 | 107 | 41 |
| 1KPEA | 3.30.428.10 | 113 | 25 |
| 1ACF | 3.30.450.30 | 125 | 41 |
The length and secondary structure of these proteins were assigned to the poly-alanine chains. The CATH classifications signify that all the proteins are mainly-beta, from the all-beta or alpha–beta categories, yet they belong to different folds. For 1SSPB there is no entry in the current version of CATH.
aThe beta content was determined by DSSP (Kabsch and Sander, 1983).
The computational experiments used four energy optimization protocols: downhill-minimization with and without the cooperative hydrogen-bonds term and MCM, again with and without the cooperative term. All the protocols shared the same general scheme: the simulation started from a random extended-chain conformation (with pre-built helices—see Supplementary Material) and ended in a compact chain conformation (Fig. 1).
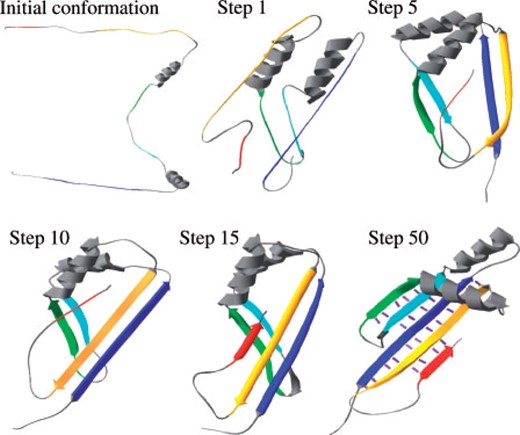
Sample snapshots from an MCM trajectory (with the cooperative term). The segments that were pre-defined as beta are colored from blue (N-terminus) to red (C-terminus) along the sequence. Purple lines represent the hydrogen bonds of the last conformation.
2.5 Secondary structure assignment and model evaluation
Given a protein structure (native or model), we used the DSSP program (Kabsch and Sander, 1983) to assign residues to secondary structure elements. Residues of the DSSP ‘H’ category were considered helices, and those of the ‘E’ category as beta. Residues of the DSSP ‘B’ category were considered beta if they were hydrogen bonded to an ‘E’ residue. Other residues were considered coil.
To evaluate the performance of the simulation protocols, we made use of preliminary knowledge on the secondary structure element assignment of each residue. We defined the success-score as the fractions (in percentages) of native-structure beta residues that were reproduced, i.e. the portions of the predefined beta residues that were identified as beta in the resulting model. Simulations with and without the cooperative term differ in their success-score distributions. The significance of this difference was tested using the Wilcoxon matched-pairs signed ranks test (Sokal and Rohlf, 1995) that compares the medians of two distributions (of paired experiments) and provide the probability (P-value) of an error when the null hypothesis of equal medians is rejected.
2.6 Implementation details
The new energy term was implemented in Java within the framework of MESHI (Kalisman et al., 2005). Adhering to the strict object-oriented guidelines of MESHI, the cooperative hydrogen bond energy term is implemented as three separate packages (energy.hydrogenBond; energy.hydrogenBondsPairs; energy.hydrogenBondsAngle). MESHI is freely available at http://cs.bgu.ac.il/∼meshi.
3 HYDROGEN BOND TERMS
3.1 Basic elements
The hydrogen bond energy terms presented here are intended to operate only on BHBs and on hydrogen-bond pairs (HBPs) and relay on predefined secondary structure assignment.
BHBs (Fig. 2a) are sets of four backbone atoms <Ni,Hi,Oj,Cj > from two non-neighbor residues i and j. At least one of these residues must be part of either a helix or a beta secondary structure element. Mixed BHBs between helix and beta residues are ignored. Only BHBs with an Hi−Oj distance ≤5.5 Å contribute to the energy. These atom pairs constitute a subset of the non-bonded (neighbor) list (Beck and Daggett, 2004; Verlet, 1967), whose size and maintenance time are linear with protein size (Heinz and Hünenberger, 2004; Levinthal, 1966; Maximova and Keasar, 2006; Yao et al., 2004).
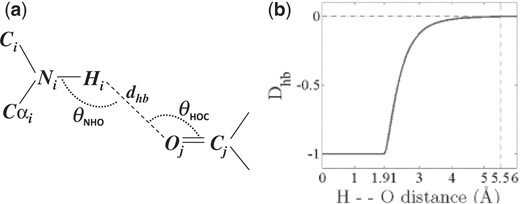
Hydrogen bond definitions. (a) An illustration of dhb, θNHO and θHOC, the three major measures that define a backbone hydrogen bond (BHB) in this work. (b) Chemical interpretation of the hydrogen bond distance dhb. The function Dhb (see the text) is the basis for both the cooperative and non-cooperative terms. It converges to zero at dhb of 5.5 Å.
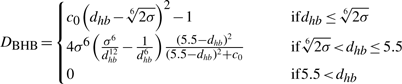
HBPs are simply pairs of two different BHBs <BHB1, BHB2> of the same secondary structure type and whose Hi−Oj distance is <5.5 Å. We characterize HBPs by their pattern of sequence separations: π(HBP) ≡ <SH1O1, SH2O2, SH1H2, SO1O2, SH1O2, SH2O1 > (Fig. 3a). We maintain a list of those HBPs for which at least two of SH1H2, SO1O2, SH1O2 and SH2O1 are five or lower (HBP-list). Under this condition each atom of at least one BHB is close in sequence to one of the atoms of the other. The number of such pairs of BHBs is bounded. Thus, the size and maintenance time of the HBP-list are also linear with protein size. The list is updated in real time whenever a new BHB is formed or an old one has broken.
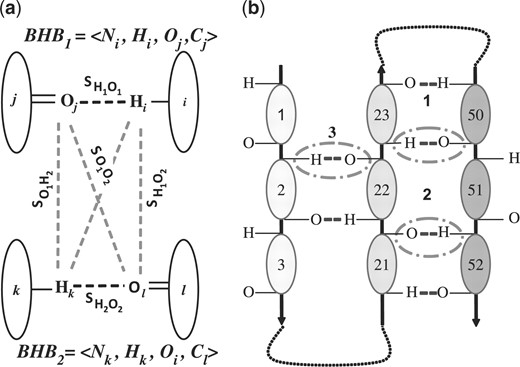
Definitions of hydrogen bond pairs (HBPs). (a) An HBP involving residues i, j, k and l and BHBs 1 and 2 is characterized by the six sequence separations SH1O1 =δ(i−j, 11), SH2O2 =δ(k−l, 11), SH1H2 =δ(i−k, 6), SO1O2 =δ(j−l, 6), SH1O2 =δ(i−l, 6) and SH2O1 =δ(k−j, 6), where δ(m, n) is −n if m≤−n; is n if m≥n; and is m otherwise. (b) An HBPs example: the three hydrogen bonds 1, 2 and 3 make three pairs. Two of these pairs <BHB1,BHB3> and <BHB2,BHB3> do not contribute to the energy, as each has three large inter-BHB separations. The pair <BHB1,BHB2> is associated with the sextuple <11,−11,6,−6,2,−2>.
3.2 The cooperative hydrogen bonds term
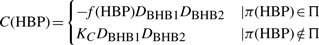
The cooperative energy term. (a) An HBP that often occurs in our dataset of native protein structures (top) and the associated energy function (bottom). The energy function promotes the formation of this pair. (b) An HBP that does not occur in our dataset (top) and the associated energy function (bottom) that prevents its formation.
Π, the set of HBP patterns, was extracted from the native structures dataset. For this purpose, only HBPs with Hi−Oj distances ≤2.5 Å and N–H–O angles above 150○ were considered (based on McDonald and Thornton, 1994). Further, to reduce the number of patterns that we take into account, SH1O1 and SH2O2 values above ten were clustered together, as were SH1H2, SO1O2, SH1O2 and SH2O1 values above five. If at least three of the latter separations were above five, the HBP was ignored (Fig. 3b). Under these restrictions, the numbers of native patterns were 729 and 113 for beta and helix patterns, respectively (Supplementary Material).
3.3 A non-cooperative hydrogen bonds energy term
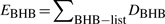
3.4 Hydrogen bonds geometry term

4 RESULTS
We performed two sets of simulations. The preliminary experiment, which used only the minimization protocol, tested the efficiency of our energy term and its implementation. The main experiment tested the efficacy of the new term, i.e. its contribution to the assembly of BHB networks during energy optimization.
4.1 The preliminary computational experiment
The design of the cooperative energy term ensured that its asymptotic time and memory consumptions would grow linearly with protein size. We wanted, however, to verify that this is also the case for short- and medium-size proteins, which are the major targets of protein structure prediction tasks. To this end, a series of 300 minimization simulations was performed on each of 19 different poly-alanine chains. The lengths and secondary structure assignments of these chains were taken from 19 mainly-beta proteins that cover a wide range (44–534) of lengths (the complete list is in the Supplementary Material).
During the simulations, we monitored the lengths of the BHB and HBP lists (Fig. 5a) and the number of insertion/deletion events on the two lists (Fig. 5b). All four parameters showed linear dependence on protein size. In addition, energy evaluation and pattern list query require constant time per HBP, and the latter is performed only when an HBP is created. Thus, both maintenance of the lists and energy evaluation require linear time and space. Moreover, in the simulations that we performed, the HBP-list changed slowly (Fig. 5), and its length was considerably smaller (<10%) than that of both the non-bonded and the bonded lists. Thus, the cooperative term amounted to no more than 2.4% of the total CPU time (Supplementary Material).
The memory and time consumption of the cooperative term are linear with protein size. (a) The average (over 100 simulations) sizes of the two dynamic lists maintained by the cooperative term. Both are linear with the number of beta residues and, hence, also with the protein size. (b) The average (over 100 simulations) number of insertion/deletion events per minimization step for the two lists. Again, both are linearly dependent on the number of beta residues. Even for large proteins, the numbers of these events are low, and hence their computational consumption is negligible.
4.2 Enhancement of native-like beta-sheet formation
The second and more significant experiment tested the efficacy of the cooperative hydrogen bonds energy term. To this end, we compared the performances of simulations under the cooperative term, with simulations under the non-cooperative one. Both simulation types produced well-structured beta sheets (including native-like side chain registration). For the sake of completeness, we also performed simulations without any hydrogen bond term, but as they did not produce any beta structures (data not shown) they will not be discussed further. In each case, we performed both downhill minimization and MCM simulation; qualitatively both protocols showed similar trends, although, as expected, the MCM simulations outperformed the minimizations. Thus, we focus here mainly on the MCM results. The complete set of minimization results may be found in the Supplementary Material.
The experiment was performed on a set of 12 poly-alanine chains (Table 1). The length and secondary structure assignments of these chains correspond to a diverse set of mainly beta proteins that have previously been used in a similar context (Bradley and Baker, 2006). At the end of each simulation, we counted the number of residues in each of the DSSP classes (‘E’, ‘B’ and ‘H’). Helices, which were augmented by the torsion angle term, were reproduced in almost all the simulations, including those without any hydrogen bond terms. Thus, we report and discuss only the beta residues that the new energy term aims to promote. In addition to the DSSP class, we also counted the numbers and types of the beta HBP-patterns.
4.2.1 The cooperative term results in higher success rates
Beta sheets emerged in all the simulation protocols and with all 12 chains. However, they were significantly more abundant when the cooperative term was applied (P < 0.03 for downhill minimizations and P < 0.0004 for MCM simulations) (Fig. 6). The patterns that the cooperative term enhanced included both parallel and anti-parallel beta sheets as well as beta hairpins and the relatively rare beta bulges. In addition, simulations with the cooperative terms ended with fewer sparse beta residues (a pair of DSSP ‘B’ type residues), which are rare in native protein structures, and fewer non-native patterns (Fig. 7).
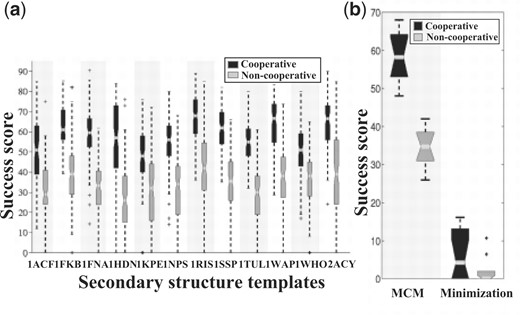
The cooperative term significantly enhances the formation of beta sheets (P < 0.03 for downhill minimization simulations and P < 0.0004 for MCM simulations). (a) Success rates of MCM optimizations of 12 poly-alanine chains that borrowed their secondary structure assignment from mainly beta proteins (Table 1). Each box presents the interquartile range (between the 25th and 75th percentiles) of 100 optimization simulations, with a notch representing the median value. The dashed lines represent the lowest and highest data still within 1.5 interquartile ranges below the lower quartile, and above the third quartile. The asterisks indicate outliers outside that range. (b) Summary of the median results of all 12 chains in both downhill-minimization and MCM simulations. Each box represents 12 median values.
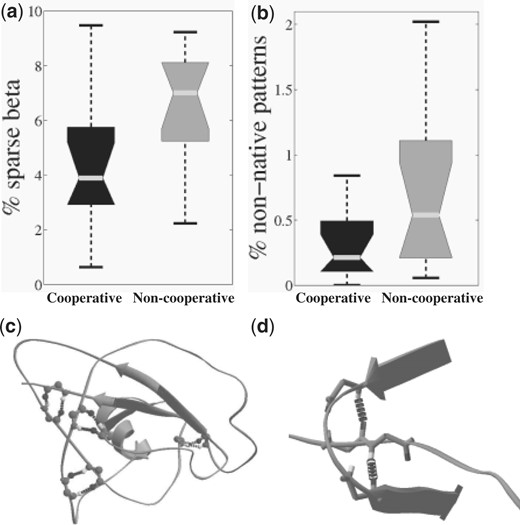
Local minima of simulations with the cooperative term include significantly fewer folding dead-ends (P <0.02). (a) Sparse hydrogen bonds that are not part of a beta sheet. (b) Hydrogen bond patterns that are not found in the database of native protein structures. (c) and (d) provide examples of these phenomena taken from low-energy minima of the non-cooperative term. (c) Sparse hydrogen bonds and (d) a non-native hydrogen bond pattern.
Both the cooperative and non-cooperative terms operate on predefined residues deriving their incorporation into secondary structure elements. Other residues, typically ones that immediately precede or follow these elements, are occasionally incorporated too. These events, however, amount to less than half a percent of the residues that were not predefined and were not included in the success statistics.
4.2.2 Correlation between the total energy and the success-score
Most of the protein structure prediction methods select the lowest-energy structures as their candidates. Hence, it is essential to provide significant enrichment of the number of beta elements in the lowest-energy structures. Although the new energy term was specifically designed to promote the formation of beta sheets, it operates on somewhat different entities, namely, HBPs. Thus, it is important to validate that the energy is correlated with the number of beta elements, which in this work is quantified by the success score (see ‘Methods’ section). Indeed, we observed some correlation between the energy and the success score in all our experiments (median correlation of −0.44). However, only with the cooperative term did we observe a significant (P < 10−4) correlation with all 12 chains (median correlation of −0.73; Fig. 8).
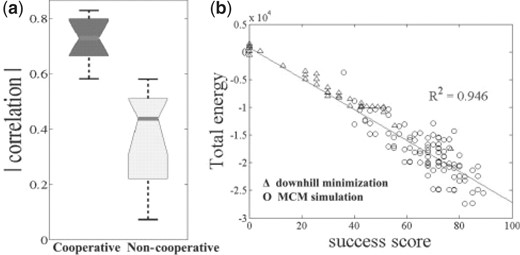
Correlation between the total energy value and the success score is significantly (P <0.05) stronger when the cooperative term is included. (a) Summary of median values of the correlations of all 12 chains with and without the cooperative term. (b) Specific example of the correlation in the simulations of 1RIS-like poly-alanine chains. Models resulting from both downhill-minimization and MCM simulations are presented.
5 DISCUSSION
In previous studies, cooperative hydrogen bond terms have been shown to facilitate the formation of secondary structure elements, most notably beta sheets (Godzik et al., 1993; Keasar and Levitt, 2003; Kolonski and Skolnick, 1992; Liwo et al., 1998). We presented here a new implementation of this concept that, for the first time, is both applicable to a full atom model and computationally very efficient. The efficacy of the new term in enhancing the formation of beta sheets was demonstrated by folding simulations performed on a model system. We showed that energy optimization under the new term consistently produced more beta sheets than a standard single hydrogen-bond term. Furthermore, preliminary results suggest that the new term also stabilizes protein native structures (Fig. 9).
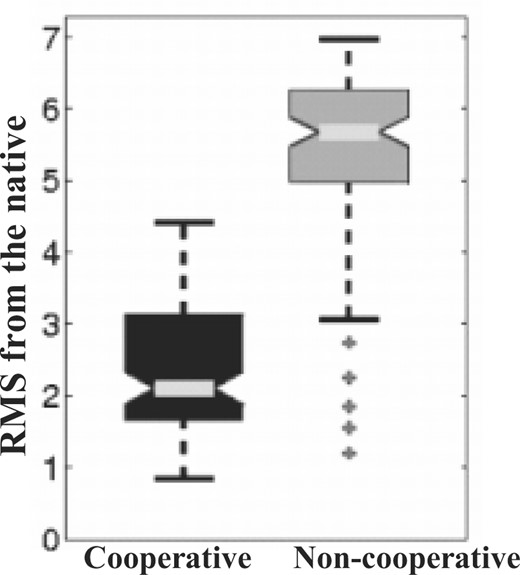
Aggregate results of energy minimization simulations under the random inflate term. Twelve native protein structures (Table 1) were perturbed 10 times each with both hydrogen bond terms. In these simulations, the energy function included, in addition to the above mentioned terms, an atomic pairwise term (Summa and Levitt, 2007) and cooperative solvation term (unpublished). Force constants were 1 and 10 for the cooperative and non-cooperative terms, respectively. The cooperative term stabilized the native structures much more than the non-cooperative one (P <0.0014 for each of the structures). Similar results were obtained with higher force constants for the non-cooperative term and very high values (i.e. 1000) induced severe backbone deformations (data not shown).
Like previous implementations, the new term operates on HBPs. Its efficiency stems from the restricted definition of these pairs and from the use of data structures that keep track only of those pairs that affect the energy. The number of these HBPs is small compared with the non-bonded atom pairs that need to be considered by excluded volume or Lennard–Jones terms. Thus, the CPU consumption of the new term is negligible. This is in sharp contrast to the previous all-atom implementation that was based on pre-compiled lists of all possible HBPs. That implementation required quadratic memory and time for maintenance and evaluation.
An important advantage of the current implementation over the previous, rule-based, methods is that it is based on a database of HBP patterns, which is queried in real-time. This feature allows the cooperative term to promote the formation of less common patterns, such as beta bulges and non-standard turns that were eliminated by the previous version. These patterns do occur within our minima, although they are rather rare, as expected.
How does a cooperative term facilitate the formation of beta sheets? We believe that a hint to the answer is offered in Figure 7. Without explicit cooperativity in the energy function, local minima often include non-native-like patterns and sparse hydrogen bonds that are folding dead ends. Once such a conformation is reached, any further improvement in energy requires the crossing of high-energy barriers. With the cooperative terms, these structures are either energy maxima (non-native-like patterns) or much shallower minima (sparse hydrogen bonds). Thus, we suggest that the cooperative term deepens the energy wells of native-like beta sheets and enlarges their radii of attraction. This suggestion is supported by inspection of the optimization trajectories. It appears that while the local minima with the cooperative term include, on average, more hydrogen bonds, the minimization trajectories include around ten times more hydrogen bond breakdown events.
Alongside the above advantages, an undesirable phenomenon is also evident from Figure 7. Though rare, HBP-patterns that are not observed in proteins do occur within the local minima of the cooperative energy function. These HBPs are recognized as ‘wrong’ and are penalized by the energy function, but the structures include enough native-like patterns to mask them. Increasing the penalty on the patterns that do not occur in proteins indeed removes them completely but at a heavy price—a dramatic reduction in the success rate (data not shown). The reason is that a non-native pattern starts to affect the energy when the two hydrogen bond distances are <5.5 Å. Many such patterns occur in native structures, as our lists of HBP-patterns were based on a 2.5 Å threshold. As long as the penalty on these patterns is low, the contribution of these HBPs to the energy is negligible. With heavier penalties, they become distractive. Thus, eliminating these non-native patterns is an obvious target for further work. One way to achieve this may be extension of the current approach to triplets or quadruplets of hydrogen bonds.
ACKNOWLEDGEMENTS
The authors thank Dr Nir Kalisman and Dr Tetyana Maximiva for their essential part in developing MESHI and for their great ideas and comments throughout the work. They also thank Ms Dotan-Cohen and Mr Avihoo for helpful discussions and technical assistance.
Funding: Israeli Science Foundation (grant no. 289/06); National Institute of Health (award no. 1R01 GM081712-01).
Conflict of interest: none declared.
REFERENCES
Author notes
Associate Editor: Anna Tramontano



