Search
Close
Search
Advanced Search
Search Menu
AI Discovery Assistant

Abstract

Discovering the relationships between long non-coding RNAs (lncRNAs) and diseases is significant in the treatment, diagnosis and prevention of diseases. However, current identified lncRNA-disease associations are not enough because of the expensive and heavy workload of wet laboratory experiments. Therefore, it is greatly important to develop an efficient computational method for predicting potential lncRNA-disease associations. Previous methods showed that combining the prediction results of the lncRNA-disease associations predicted by different classification methods via Learning to Rank (LTR) algorithm can be effective for predicting potential lncRNA-disease associations. However, when the classification results are incorrect, the ranking results will inevitably be affected. We propose the GraLTR-LDA predictor based on biological knowledge graphs and ranking framework for predicting potential lncRNA-disease associations. Firstly, homogeneous graph and heterogeneous graph are constructed by integrating multi-source biological information. Then, GraLTR-LDA integrates graph auto-encoder and attention mechanism to extract embedded features from the constructed graphs. Finally, GraLTR-LDA incorporates the embedded features into the LTR via feature crossing statistical strategies to predict priority order of diseases associated with query lncRNAs. Experimental results demonstrate that GraLTR-LDA outperforms the other state-of-the-art predictors and can effectively detect potential lncRNA-disease associations. Availability and implementation: Datasets and source codes are available at http://bliulab.net/GraLTR-LDA.

learning to rank, feature crossing statistical strategy, graph auto-encoder, lncRNA-disease associations

Introduction

Long non-coding RNAs (lncRNAs) play an important role in the processes of many human diseases. More and more evidences indicate that emergence and development of many diseases are related with gene expression regulated by several lncRNAs. For example, lncRNA LUCAT1 regulates microRNA-7-5p and reduces its expression to promote breast cancer development, which has been regarded as a potential therapeutic target [1]. With the development of high-throughput sequencing technology and the establishment of disease databases, many lncRNA sequence data and disease semantic information have been generated, which can be used to more comprehensively analyze associations between lncRNAs and diseases. In order to assist clinical diagnostics, many databases (LncRNADisease [2], Lnc2Cancer [3], etc.) have been established to record experimentally validated lncRNA-disease associations reported in the literature [4–6], based on which various computational methods were proposed to identify lncRNAs associated with diseases [7, 8]. In addition, the newly released database contains newly added associations between known lncRNAs and known diseases, indicating that many associations between lncRNAs and diseases have not been detected. Therefore, it is important to develop computational methods for predicting lncRNA-disease associations.

Existing computational methods can be divided into the following types: network-based methods, matrix factorization methods, random walk methods, machine learning (ML) methods and deep learning methods [9–13]. For network-based methods, LRLSLDA [14] is the first computational model and opens the door to research on the field of lncRNA-disease association identification from a computational perspective, which combined lncRNA-disease association network and lncRNA expression similarity network for identifying potential lncRNA-disease associations. Li et al. [15] introduced a model based on network consistency projection (NCPLDA) for lncRNA-disease association detection by integrating the lncRNA-disease association network, the disease similarity network and the lncRNA similarity network. For matrix factorization method, Lu et al. [16] designed an inductive matrix completion framework (SIMCLDA) for completing the association matrix by extracting primary feature vectors from the functional similarity network of diseases and interaction network of lncRNAs. For random walk methods, Xie et al. [17] implemented an unbalanced bi-random walk algorithm for predicting lncRNA-disease associations by the linear neighbor similarity reconstructed through lncRNA and disease network. However, network-based methods, matrix factorization methods and random walk methods cannot efficiently capture the complex non-linear connection between lncRNAs and diseases.

Machine learning methods treat lncRNA-disease association identification as a classification task. Guo et al. [18] applied auto-encoder neural network to obtain the optimal feature vectors of lncRNA-disease pairs, and then the feature vectors were fed into the rotating forest to predict potential lncRNA-disease associations (LDASR). Zhang et al. [19] fused multiple similarity data to construct feature vectors, and utilized Gradient Boosting to identify the associations between diseases and lncRNAs (LDNFSGB). Zhu et al. [20] proposed an incremental principal component analysis method to decrease the dimension of feature vectors, based on which a random forest predictor was trained to detect latent lncRNA-disease associations (IPCARF).

Deep learning methods have strong learning abilities by constructing complex neural networks. Zeng et al. [21] improved the prediction performance of lncRNA-disease associations by establishing a deep matrix factorization (DMFLDA). Wei et al. [22] combined convolution neural network framework and a 3D feature block based on similarity matrices to predict potential lncRNA-disease associations. Recently, inspired by the successful application of graph convolution neural network (GCN) [23] in the convolution operation of unstructured graph data, many methods combined the GCN-based deep learning algorithms and the graph to detect the associations between lncRNAs and diseases. Shi et al. [24] used graph auto-encoder to obtain graph embedding features and predicted potential lncRNA-disease associations (VAGELDA). Fan et al. [25] designed a graph convolutional matrix completion framework (GCRFLDA) to calculate the lncRNA-disease association score matrix by decoding embedding features extracted from the constructed lncRNA-disease graph. Lan et al. [26] predicted lncRNA-disease interactions by combining graph attention network and heterogeneous graph data of lncRNA and diseases (GANLDA). These GCN-based methods not only make great contributions to this field, but also reflect that GCN was particularly suitable for encoding graph nodes into low-dimensional, and has highly discriminative power embedded features. Besides, the related predictors for other similar tasks can contribute to identify lncRNA-disease associations, such as miRNA-disease association [27–29].

Learning to rank (LTR) [30] is a supervised algorithm, which is initially employed in retrieval tasks. In the field of web retrieval, LTR can rank the candidate websites according to the degree of correlation with queries [30]. LTR has been successfully applied to natural language processing and information retrieval, such as machine translation [31], recommender system [32], online advertisement [30], etc. For different application scenarios, LTR can be classified into three types: pointwise, pairwise and listwise. Listwise has been widely used in bioinformatics, such as human protein–phenotype association detection [33], protein remote homology prediction [34–36] and drug–target binding affinity prediction [37], etc. Recently, some methods treated lncRNA-disease association prediction as a search ranking problem, and consider the association between lncRNA and disease as an one-to-many relationship. LncRNAs and diseases can be regarded as query topics and documents, respectively. Therefore, LTR algorithm [30] can be used to predict latent lncRNA-disease associations. For example, Wu et al. [38] used the prediction results of the lncRNA-disease association predicted by different classification methods as the feature vectors of the lncRNA-disease pairs, which were fed into the supervised learning algorithm LTR [30] to re-calculate the relevant degree between lncRNAs and diseases (iLncDA-LTR). The experimental results showed that it has achieved the state-of-the-art performance. However, when the classification results are wrong, the ranking results will inevitably be affected, leading to the top predicted diseases unrelated to the query lncRNAs. In addition, directly fusing the final prediction results of the classification method as the ranking features may leave out important original information. As discussed above, embedded features can maximize the preservation of the topological information of the original graph. If so, can we use embedded features to replace classification results for solving the above shortcoming?

To answer this question, as shown in Figure 1, we treat the lncRNA-disease association prediction as a graph-based search task, which is similar as the searching task of searching associated movies for query actor in search engine. Graph-based knowledge storage is a kind of structured knowledge representation in knowledge graph. The current advanced search engines utilize the entity knowledge in the structured knowledge graph to find the entities associated with the query entities. For the lncRNA-disease association search task, the lncRNA-disease association graph is considered as biological knowledge graph.

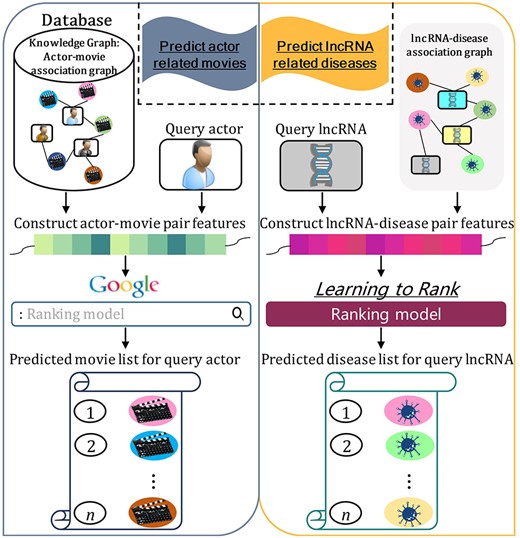
The similarities between the task of searching actor-movie associations in search engine combined with knowledge graph, and the graph-based lncRNA-disease association search task.
Figure 1

The similarities between the task of searching actor-movie associations in search engine combined with knowledge graph, and the graph-based lncRNA-disease association search task.

Open in new tabDownload slide

Therefore, we propose a new predictor called GraLTR-LDA to predict missing lncRNA-disease associations. GraLTR-LDA utilizes the feature crossing statistical method [32] to incorporate the embedded features into LTR to predict priority order of diseases related with query lncRNAs. In particular, we construct two kinds of graphs: (i) Homogeneous graph based on lncRNA sequence similarity and homogeneous graph based on disease semantic similarity. (ii) Heterogeneous graph combining lncRNA-disease association network and the above constructed homogeneous graphs. We combine graph auto-encoder [39] and attention mechanism [40] to obtain embedded features from the two kinds of graphs. Experimental results on independent dataset show that GraLTR-LDA outperforms the other existing methods for identifying missing lncRNA-disease associations.

Methods

Problem formulation

Given |$n$| lncRNAs |$\mathcal{L}=\{{l}_1,{l}_2,\dots, {l}_n\}$| and |$m$| diseases |$ \mathcal{D} =$||$\{{d}_1,{d}_2,\dots, {d}_m\}$|⁠, the lncRNA-disease association network is represented by an interaction matrix |$\mathrm{Y}\in{\mathbb{R}}^{n\times m}$|⁠. |$\mathrm{Y}(i,j)=1$| if lncRNA |${l}_i$| is verified related with disease |${d}_j$|⁠; otherwise, |$\mathrm{Y}(i,j)=0$|⁠. The purpose of our task is to predict missing associations between known lncRNAs and known diseases.

Methods overview

The framework of GraLTR-LDA with three main steps (construction of homogeneous graph and heterogeneous graph, feature representation and ranking diseases) is illustrated in Figure 2.

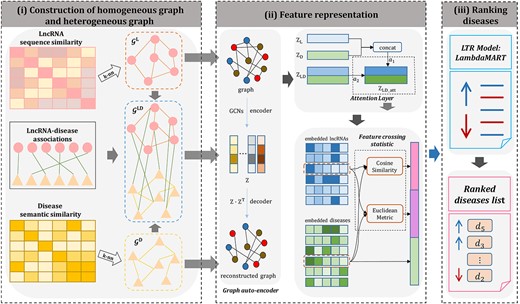
The overall framework of GraLTR-LDA. (i) Construction of homogenous graph and heterogeneous graph: homogeneous graphs ${\mathcal{G}}^{\mathrm{L}}$ and ${\mathcal{G}}^{\mathrm{D}}$ are constructed based on the top k most similarity information from calculated lncRNA sequence similarity matrix and disease semantic similarity matrix, respectively. Besides, the heterogeneous graph ${\mathcal{G}}^{\mathrm{LD}}$ is constructed by incorporating ${\mathcal{G}}^{\mathrm{L}}$, ${\mathcal{G}}^{\mathrm{D}}$ and lncRNA-disease associations network. (ii) Feature representation: the node embedding matrices are learned from ${\mathcal{G}}^{\mathrm{L}}$, ${\mathcal{G}}^{\mathrm{D}}$ and ${\mathcal{G}}^{\mathrm{LD}}$ by graph auto-encoder. Then, the attention layer is applied to integrate the embedding matrices from different graphs for constructing a global node embedding matrix ${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}$. For any lncRNA-disease pair, GraLTR-LDA integrates the two kinds of features computed based on the feature crossing statistical method and the embedded vectors of diseases as the final features. (iii) Ranking diseases: the final features are inputted into the ranking model LambdaMART, based on which the diseases related with query lncRNA are ranked according to the predicted lncRNA-disease association scores calculated by the ranking model.
Figure 2

The overall framework of GraLTR-LDA. (i) Construction of homogenous graph and heterogeneous graph: homogeneous graphs |${\mathcal{G}}^{\mathrm{L}}$| and |${\mathcal{G}}^{\mathrm{D}}$| are constructed based on the top k most similarity information from calculated lncRNA sequence similarity matrix and disease semantic similarity matrix, respectively. Besides, the heterogeneous graph |${\mathcal{G}}^{\mathrm{LD}}$| is constructed by incorporating |${\mathcal{G}}^{\mathrm{L}}$|⁠, |${\mathcal{G}}^{\mathrm{D}}$| and lncRNA-disease associations network. (ii) Feature representation: the node embedding matrices are learned from |${\mathcal{G}}^{\mathrm{L}}$|⁠, |${\mathcal{G}}^{\mathrm{D}}$| and |${\mathcal{G}}^{\mathrm{LD}}$| by graph auto-encoder. Then, the attention layer is applied to integrate the embedding matrices from different graphs for constructing a global node embedding matrix |${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}$|⁠. For any lncRNA-disease pair, GraLTR-LDA integrates the two kinds of features computed based on the feature crossing statistical method and the embedded vectors of diseases as the final features. (iii) Ranking diseases: the final features are inputted into the ranking model LambdaMART, based on which the diseases related with query lncRNA are ranked according to the predicted lncRNA-disease association scores calculated by the ranking model.

Open in new tabDownload slide

Graph construction

Construction of homogeneous graph

Because similar lncRNAs tend to be associated with similar diseases [16, 22], we utilize sequence information of lncRNA to construct the similarities among lncRNAs. The lncRNA sequences are available from Reference Sequence (RefSeq) database (https://ftp.ncbi.nlm.nih.gov/refseq/release/) [41]. Inspired by [22, 38], the lncRNA sequence similarity matrix (LSSM) is constructed by the Needleman–Wunsch alignment method [42].

Since similar diseases tend to be associated with similar lncRNAs [16, 22], disease semantic information is used to calculate disease similarities. The Disease Ontology database [43] is used to obtain term ‘DOID’ of diseases based on which the DOSE package [44] is used to construct the disease semantic similarity matrix (DSSM).

Based on the matrix LSSM and matrix DSSM, we can construct the homogeneous graph |${\mathcal{G}}^{\mathrm{L}}$| among lncRNAs, and the homogeneous graph |${\mathcal{G}}^{\mathrm{D}}$| among diseases. Moreover, the adjacency matrix of |${\mathcal{G}}^{\mathrm{L}}$| and |${\mathcal{G}}^{\mathrm{D}}$| can be defined as |${\mathrm{A}}^{\mathrm{L}}$| and |${\mathrm{A}}^{\mathrm{D}}$|⁠, respectively. They can be represented as follows:
(1)
(2)
where |${Nei}_{l_i}(k)$| (⁠|${Nei}_{d_i}(k)$|⁠) contained the top k sequence (semantic) most similarity lncRNAs (diseases) with lncRNA |${l}_i$| (disease |${d}_i$|⁠) containing itself. We empirically set k as 20.

Construction of heterogeneous graph

We integrate the graphs |${\mathcal{G}}^{\mathrm{L}}$|⁠, |${\mathcal{G}}^{\mathrm{D}}$| and the known lncRNA-disease association network to construct the heterogeneous graph |${\mathcal{G}}^{\mathrm{LD}}$|⁠, and its adjacency matrix |${\mathrm{A}}^{\mathrm{LD}}\in{\mathbb{R}}^{(n+m)\times (\mathrm{n}+m)}$| is defined as:
(3)
where |${\mathrm{Y}}^{\mathrm{T}}$| represents the transpose of the lncRNA-disease association matrix |$\mathrm{Y}$|⁠. In particular, the diagonal element values of adjacency matrix |${\mathrm{A}}^{\mathrm{LD}}$| are 1.
We define the initial feature matrices |${\mathrm{X}}_{\mathrm{L}}, {\mathrm{X}}_{\mathrm{D}}\ {\mathrm{and}}\ {\mathrm{X}}_{\mathrm{LD}}$| corresponding to the graphs |${\mathcal{G}}^{\mathrm{L}}, {\mathcal{G}}^{\mathrm{D}}\ {\mathrm{and}}\ {\mathcal{G}}^{\mathrm{LD}}$| as:
(4)
(5)
(6)

Feature representation

Encoder

GraLTR-LDA uses the graph auto-encoder [39] to learn embedded features of lncRNA and disease from graphs |${\mathcal{G}}^{\mathrm{L}}$|⁠, |${\mathcal{G}}^{\mathrm{D}}$| and |${\mathcal{G}}^{\mathrm{LD}}$|⁠. Graph auto-encoder model was proposed by Kipf et al. [39] to solve the link prediction problem. Graph auto-encoder includes encoding layers and decoding layers. For a given graph, the encoding layer combines with the graph convolutional network (GCN) [23, 45] to encode graph nodes into low-dimensional embedded features, and the decoding layer decodes the low-dimensional embedded features to reconstruct the original graph. The obtained low-dimensional embedded features are often used to support downstream tasks, such as node classification [39], link prediction [25], etc. In the encoding layer, the node embedding matrix of the target graph is calculated by using GCN [23, 45] encoding the adjacency matrix and the feature matrix of the target graph.

In this section, we use two-layer GCN to encode graphs |${\mathcal{G}}^{\mathrm{L}}$|⁠, |${\mathcal{G}}^{\mathrm{D}}$| and |${\mathcal{G}}^{\mathrm{LD}}$|⁠, respectively. The encoding processes of graph |${\mathcal{G}}^{\mathrm{L}}$| based on its adjacency matrix |${\mathrm{A}}^{\mathrm{L}}$| and feature matrix |${\mathrm{X}}_{\mathrm{L}}$| are [39]:
(7)
(8)
where |${\mathrm{Z}}_{\mathrm{L}}$| is the embedding matrix of graphs |${\mathcal{G}}^{\mathrm{L}}$| after two layers of GCN encoding, where each row represents the embedded features of an lncRNA. |$\mathrm{ReLU}(\cdot )$| is a linear rectification function. |${\mathrm{W}}_0^{\mathrm{L}}$| and |${\mathrm{W}}_1^{\mathrm{L}}$| are the first- and second-layer trainable weight matrices of GCN, respectively. |${\tilde{\mathrm{M}}}^{\mathrm{L}}$| and |${\mathrm{P}}_{\mathrm{L}}^{-\frac{1}{2}}$| are the symmetrically normalized adjacency matrices and degree matrices of |${\mathrm{A}}^{\mathrm{L}},$| respectively.
The encoding processes of graph |${\mathcal{G}}^{\mathrm{D}}$| based on its adjacency matrix |${\mathrm{A}}^{\mathrm{D}}$| and feature matrix |${\mathrm{X}}_{\mathrm{D}}$| are [39]:
(9)
(10)
where |${\mathrm{Z}}_{\mathrm{D}}$| is the embedding matrix of graphs |${\mathcal{G}}^{\mathrm{D}}$| after two layers of GCN encoding, where each row represents the embedded features of an disease. |$\mathrm{ReLU}(\cdot )$| is a linear rectification function. |${\mathrm{W}}_0^{\mathrm{D}}$| and |${\mathrm{W}}_1^{\mathrm{D}}$| are the first and second layer trainable weight matrices of GCN, respectively. |${\tilde{\mathrm{M}}}^{\mathrm{D}}$| and |${\mathrm{P}}_{\mathrm{D}}^{-\frac{1}{2}}$| are the symmetrically normalized adjacency matrices and degree matrices of |${\mathrm{A}}^{\mathrm{D}},$| respectively.
The encoding processes of graph |${\mathcal{G}}^{\mathrm{LD}}$| based on its adjacency matrix |${\mathrm{A}}^{\mathrm{LD}}$| and feature matrix |${\mathrm{X}}_{\mathrm{LD}}$| are [39]:
(11)
(12)
where |${\mathrm{Z}}_{\mathrm{LD}}$| is the embedding matrix of graphs |${\mathcal{G}}^{\mathrm{LD}}$| after two layers of GCN encoding, and the first n rows of the matrix represent the embedded features of all lncRNAs, and the last m rows represent embedded features of all diseases. |$\mathrm{ReLU}(\cdot )$| is a linear rectification function. |${\mathrm{W}}_0^{\mathrm{LD}}$| and |${\mathrm{W}}_1^{\mathrm{LD}}$| are the first and second layer trainable weight matrices of GCN, respectively. |${\tilde{\mathrm{M}}}^{\mathrm{LD}}$| and |${\mathrm{P}}_{\mathrm{LD}}^{-\frac{1}{2}}$| are the symmetrically normalized adjacency matrices and degree matrices of |${\mathrm{A}}^{\mathrm{LD}},$| respectively.

Decoder

To measure the quality of the embedded features obtained from encoding the target graph by the encoding layers, these embedded features are decoded by the decoding layer to reconstruct the target graph. By repeatedly training the graph auto-encoder model to reduce the difference between the target graph and the reconstruct target graph after decoding, we can obtain more accurate embedded features. In this section, the embedding matrix is decoded to reconstruct the target graph. For the encoded graphs, we decode embedding matrices to reconstruct adjacency matrices as [39]:
(13)
(14)
(15)
where |${\hat{\mathrm{M}}}_{\mathrm{L}}$|⁠, |${\hat{\mathrm{M}}}_{\mathrm{D}}$| and |${\hat{\mathrm{M}}}_{\mathrm{LD}}$| represent the reconstruct adjacency matrices. |${{\mathrm{Z}}_{\mathrm{L}}}^{\mathrm{T}}$|⁠,|${{\mathrm{Z}}_{\mathrm{D}}}^{\mathrm{T}}$| and |${{\mathrm{Z}}_{\mathrm{LD}}}^{\mathrm{T}}$| are the corresponding transposes of embedding matrices |${\mathrm{Z}}_{\mathrm{L}}$|⁠, |${\mathrm{Z}}_{\mathrm{D}}$| and |${\mathrm{Z}}_{\mathrm{LD}}$|⁠, respectively. |$\sigma$|(⁠|$\cdot $|⁠) represents the |$\mathrm{sigmoid}$| activation function. |${\mathrm{H}}_{\mathrm{L}}$|⁠, |${\mathrm{H}}_{\mathrm{D}}$| and |${\mathrm{H}}_{\mathrm{LD}}$| are the trainable weight matrix.

Attention layer

For each lncRNA, we have obtained different embedded representations from the heterogeneous graph |${\mathcal{G}}^{\mathrm{LD}}$| and the biological-sequence-similarity-based homogeneous graph |${\mathcal{G}}^{\mathrm{L}}$| by Graph auto-encoder. Because the heterogeneous graph |${\mathcal{G}}^{\mathrm{LD}}$| and the biological-sequence-similarity-based homogeneous graph |${\mathcal{G}}^{\mathrm{L}}$| contain different biological information, it is reasonable to assign different attention weights to the homogeneous graph and the heterogeneous graph to learn the global embedded representation of each lncRNA. The higher the weight is, the more important the corresponding feature in the heterogeneous graph is. For each disease, the attention weights also indicate the different importance of the features in the homogeneous graph |${\mathcal{G}}^{\mathrm{D}}$| and the heterogeneous graphs |${\mathcal{G}}^{\mathrm{LD}}$|⁠. Next, the multi-view graph attention mechanism [40] is introduced for learning the weights of different graphs, and then a comprehensive embedding matrix |${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}$| can be obtained. Specifically, |${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}$| can be used to reconstruct the matrix |${\mathrm{A}}^{\mathrm{LD}}$|⁠. The embedding matrices |${\mathrm{Z}}_{\mathrm{L}}$| and |${\mathrm{Z}}_{\mathrm{D}}$| can be combined to construct |${\mathrm{Z}}_{\mathrm{LDM}}$| as followings:
(16)
and then the embedding matrix |${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}$| is defined as [40]:
(17)
(18)
(19)
(20)
where |${v}^T$| and |${\mathrm{W}}_{\mathrm{a}}$| are the model parameters. tanh(⁠|$\cdot $|⁠) and exp(⁠|$\cdot $|⁠) are the hyperbolic tangent function and exponential function, respectively. |${a}_i$| represents the attention score of the ith matrix in the set |$Q$|⁠. In addition, we define the reconstruct adjacency matrix |${\hat{\mathrm{M}}}_{\mathrm{LD}\_\mathrm{att}}$| corresponding to the matrix |${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}$| as [39]:
(21)
where |${{\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}}^{\mathrm{T}}$| is the transpose of |${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}$|⁠. |$\sigma$|(⁠|$\cdot $|⁠) is the |$\mathrm{sigmoid}$| activation function. |${\mathrm{H}}_{\mathrm{LD}\_\mathrm{att}}$| is the trainable weight matrix.

Optimization

Because the embedding matrix |${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}$| comes from diverse graph, we minimize the overall loss function |$L$| to measure the difference between multiple reconstructed matrices and original matrices as [46]:
(22)
(23)
(24)
(25)
(26)

In addition, the Adam optimizer [47] is adopted as the optimizer.

Feature crossing statistical strategy

Previous studies [9, 24, 25, 48] indicated that features obtained from deep learning were widely used to predict potential lncRNA-disease associations. The embedding matrix |${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}$| extracted by homogeneous graph and heterogeneous graph cannot only reflect the association information of different type nodes, but also contains the similarity information of same type nodes. In the matrix |${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}$|⁠, the first n rows represent embedded features of all lncRNAs and the last m rows represent embedded features of all diseases. However, the relationship between the query lncRNA and feedback disease is not directly reflected by these features. Inspired by the idea of measuring the relationship between the query entity and the candidate entity in recommendation algorithm [32], we employed a feature crossing statistical method to measure this relationship as [32]:
(27)
(28)
where |${l}_q$| and |${d}_e$| denote the query lncRNA and the candidate disease, respectively. |${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}({l}_q)$| and |${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}({d}_e)$| represent the embedded feature vectors of lncRNA |${l}_q$| and disease |${d}_e$|⁠, respectively. The |$N$| is the length of the embedded feature vector. Specifically, crossing statistical features |${\mathrm{Y}}_1({l}_q,{d}_e)$| and |${\mathrm{Y}}_2({l}_q,{d}_e)$| are calculated by Cosine similarity and Euclidean metric, respectively.
Previous studies [25, 49, 50] have shown that combining the graph attribute features of disease can help to improve model performance for predicting potential lncRNA-disease associations. In this regard, we utilize |${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}({d}_e)$| to represent the graph attribute features of the disease |${d}_e$|⁠. Finally, the resulting feature vectors of pair between lncRNA |${l}_q$| and disease |${d}_e$| can be represented as:
(29)

Ranking diseases

LTR was widely used in the field of information retrieval, and the goal of LTR is to produce a permutation of a group of documents having the most relevant documents on the top of the result list [30, 51, 52]. At present, many bioinformatic problems can be solved by LTR, such as protein remote homology prediction [34–36], human protein–phenotype association detection [33], circRNA-disease association prediction [53] and drug–target binding affinity prediction [37]. LambdaMART algorithm [54] belongs to the listwise approach of LTR, which has been successfully applied to predict lncRNA-disease associations [38]. In this paper, we apply normalized discounted cumulative gain (NDCG) [55] as the loss function of LambdaMART algorithm to predict lncRNA-disease associations. The fixed data format {|$\mathrm{Y}$|(⁠|${l}_q,{d}_e$|⁠)|$, {l}_q$|⁠, |${\varphi}^{LTR}({l}_q,{d}_e)$|} is fed into the ranking model LambdaMART, where |${l}_q$| and |${d}_e$| denote the query lncRNA and the candidate disease, respectively. Finally, the disease list related to query lncRNA is ranked according to the predicted lncRNA-disease association scores by the ranking model.

Experiments

Data

In this paper, training set |${\mathbb{S}}_{\mathrm{training}}$| and independent set |${\mathbb{S}}_{\mathrm{independent}}$| are obtained from previous work [38], and they are used to simulate the scenario of identifying missing lncRNA-disease associations. Specifically, lncRNA-disease associations contained in the dataset |${\mathbb{S}}_{\mathrm{training}}$| come from LncRNADisease database (v2017) [2], and lncRNA-disease associations contained in the dataset |${\mathbb{S}}_{\mathrm{independent}}$| are from LncRNADisease v2.0 database [56]. Following previous studies [16, 20, 25, 57], if the lncRNA-disease associations are recorded in the LncRNADisease, they are considered as positive samples. Otherwise, they are negative samples. The statistical information of training set and independent set is listed in Table 1.

Table 1
Open in new tab

Statistical information of dataset |${\mathbb{S}}_{\mathrm{training}}$| and |${\mathbb{S}}_{\mathrm{independent}}$|⁠.

Date setLncRNADiseasePositiveNegative
|${\mathbb{S}}_{\mathrm{training}}$|404190104469,150
|${\mathbb{S}}_{\mathrm{independent}}$|169714636103
Date setLncRNADiseasePositiveNegative
|${\mathbb{S}}_{\mathrm{training}}$|404190104469,150
|${\mathbb{S}}_{\mathrm{independent}}$|169714636103
Table 1
Open in new tab

Statistical information of dataset |${\mathbb{S}}_{\mathrm{training}}$| and |${\mathbb{S}}_{\mathrm{independent}}$|⁠.

Date setLncRNADiseasePositiveNegative
|${\mathbb{S}}_{\mathrm{training}}$|404190104469,150
|${\mathbb{S}}_{\mathrm{independent}}$|169714636103
Date setLncRNADiseasePositiveNegative
|${\mathbb{S}}_{\mathrm{training}}$|404190104469,150
|${\mathbb{S}}_{\mathrm{independent}}$|169714636103

Metrics and parameter settings

Four metrics are used to evaluate the overall performance of different predictors: (i) area under the receiver operating characteristics curve (AUC) [58], (ii) area under the precision-recall curve (AUPR), (iii) ROCk [59] and (iv) NDCG@k [55]. AUC measures specificity and sensitivity, and AUPR more focuses on punishing false positives. ROCk and NDCG@k reflect the ranking quality of the recall results for information retrieval tasks [38, 55]. Higher ROCk and NDCG@k values indicate better ranking quality.

In this study, we implement GraLTR-LDA in Pytorch deep learning framework and Ranklib library. In the process of generation of the embedded representation, the dimensions of embedded features in the first layer GCN and the second layer GCN are set as 256 and 128, respectively. The dropout rate is set as 0.0005, and the initial learning rate is set to 0.01. The value of tree is the main parameter of the LambdaMART algorithm. We compare the performance changes of different numbers of trees of GraLTR-LDA by tenfold cross-validation on |${\mathbb{S}}_{\mathrm{training}}$|⁠. As shown in Figure 3, GraLTR-LDA obtains the best performance when tree is set as 50.

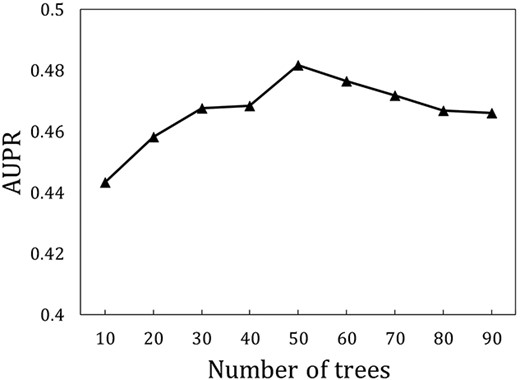
The AUPR values of GraLTR-LDA predictor with different number of trees via the ten-fold cross-validation on ${\mathbb{S}}_{\mathrm{training}}$.
Figure 3

The AUPR values of GraLTR-LDA predictor with different number of trees via the ten-fold cross-validation on |${\mathbb{S}}_{\mathrm{training}}$|⁠.

Open in new tabDownload slide

Comparison with the other methods

As discussed in the introduction section, several lncRNA-disease association identification methods have been proposed. In this section, we compare the performance of GraLTR-LDA with the state-of-the-art methods based on different theories on |${\mathbb{S}}_{\mathrm{independent}}$|⁠. Three machine-learning-based methods are selected, including LDASR [18], LDNFSGB [19] and IPCARF [20]. These methods employ different kinds of machine learning classifiers. Two network-based methods (SIMCLDA [16] and NCPLDA [15]) are also selected for comprehensive performance comparison. The deep-learning-based methods DMFLDA [21] is selected, and it only uses the known lncRNA-disease association for prediction. Three graph-based methods (VAGELDA [24], GCRFLDA [25] and GANLDA [26]) are selected, and they are the recently proposed computational methods based on graph neural network. The ranking method iLncDA-LTR [38] is selected as well. These comparison methods are reproduced by using the parameter settings and corresponding codes reported in the corresponding papers. All evaluation metrics are average values of all query lncRNAs, and the results of the comparison are shown in Table 2. We can see the followings: (i) The GraLTR-LDA predictor outperforms the iLncDA-LTR, indicating that combining the graph-based embedded features into the ranking framework (LTR) is a more efficient way for predicting lncRNA-disease associations. (ii) The performance of GraLTR-LDA is superior with the other graph-based methods (VAGELDA, GCRFLDA and GANLDA). The reason is that GraLTR-LDA further processes the attention-mechanism-based embedded features learned from homogeneous and heterogeneous graphs by using the feature crossing statistical method. (iii) GraLTR-LDA is comparable with these advanced computational methods. In particular, GraLTR-LDA achieves the best performance in terms of NDCG@10 and AUC. The GraLTR-LDA model is based on a supervised learning ranking framework, leading to excellent performance in terms of the NDCG@10 metric [38, 55]. We further compared the quality of the top ranked associations predicted by different prediction methods as shown in Figure 4. These results further indicate that the GraLTR-LDA predictor can effectively improve the predictive performance.

Table 2
Open in new tab

The performance comparison between GraLTR-LDA and the other methods on |${\mathbb{S}}_{\mathrm{independent}}$|⁠.

MethodsAUCAUPRNDCG@10
LDASR0.73420.27160.3970
LDNFSGB0.75200.23040.3640
IPCARF0.79560.34230.4682
SIMCLDA0.75350.17840.3135
NCPLDA0.81980.36800.4724
DMFLDA0.78560.30040.4305
VAGELDA0.72450.31730.4159
GCRFLDA0.76900.32670.4219
GANLDA0.71490.28720.4006
iLncDA-LTR0.78050.31740.4264
GraLTR-LDA0.83520.35970.5216
MethodsAUCAUPRNDCG@10
LDASR0.73420.27160.3970
LDNFSGB0.75200.23040.3640
IPCARF0.79560.34230.4682
SIMCLDA0.75350.17840.3135
NCPLDA0.81980.36800.4724
DMFLDA0.78560.30040.4305
VAGELDA0.72450.31730.4159
GCRFLDA0.76900.32670.4219
GANLDA0.71490.28720.4006
iLncDA-LTR0.78050.31740.4264
GraLTR-LDA0.83520.35970.5216

Note: These comparison methods are reproduced based on [15, 16, 18–21, 24–26, 38].

Table 2
Open in new tab

The performance comparison between GraLTR-LDA and the other methods on |${\mathbb{S}}_{\mathrm{independent}}$|⁠.

MethodsAUCAUPRNDCG@10
LDASR0.73420.27160.3970
LDNFSGB0.75200.23040.3640
IPCARF0.79560.34230.4682
SIMCLDA0.75350.17840.3135
NCPLDA0.81980.36800.4724
DMFLDA0.78560.30040.4305
VAGELDA0.72450.31730.4159
GCRFLDA0.76900.32670.4219
GANLDA0.71490.28720.4006
iLncDA-LTR0.78050.31740.4264
GraLTR-LDA0.83520.35970.5216
MethodsAUCAUPRNDCG@10
LDASR0.73420.27160.3970
LDNFSGB0.75200.23040.3640
IPCARF0.79560.34230.4682
SIMCLDA0.75350.17840.3135
NCPLDA0.81980.36800.4724
DMFLDA0.78560.30040.4305
VAGELDA0.72450.31730.4159
GCRFLDA0.76900.32670.4219
GANLDA0.71490.28720.4006
iLncDA-LTR0.78050.31740.4264
GraLTR-LDA0.83520.35970.5216

Note: These comparison methods are reproduced based on [15, 16, 18–21, 24–26, 38].

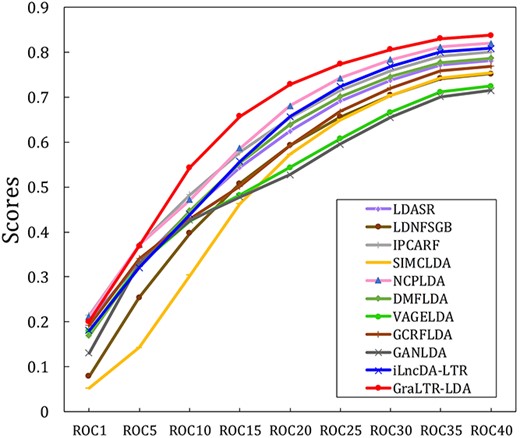
ROCk scores are obtained by different computational methods on ${\mathbb{S}}_{\mathrm{independent}}$.
Figure 4

ROCk scores are obtained by different computational methods on |${\mathbb{S}}_{\mathrm{independent}}$|⁠.

Open in new tabDownload slide

Feature analysis

In this paper, the feature crossing statistical method tightly couples the embedded features of lncRNA and the embedded features of disease to measure the correlation of lncRNA-disease pairs (Eqs (27) and (28)). The feature vector |${\varphi}^{LTR}({l}_q,{d}_e)$| of lncRNA-disease pair includes crossing statistical features |${\mathrm{Y}}_1({l}_q,{d}_e)$|⁠, |${\mathrm{Y}}_2({l}_q,{d}_e)$| and the graph attribute features of disease |${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}({d}_e)$|⁠. We explore the effectiveness of |${\mathrm{Y}}_1({l}_q,{d}_e)$|⁠, |${\mathrm{Y}}_2({l}_q,{d}_e)$| and |${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}({d}_e)$| on |${\mathbb{S}}_{\mathrm{independent}}$|⁠. As shown in Table 3, the model based on both features |${\mathrm{Y}}_1({l}_q,{d}_e)$| and |${\mathrm{Y}}_2({l}_q,{d}_e)$| performs better than the model based on only one feature. Furthermore, experimental results show that the model combining all the features outperforms the other models, which indicates that features of |${\mathrm{Y}}_1({l}_q,{d}_e),$||${\mathrm{Y}}_2({l}_q,{d}_e)$| and |${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}({d}_e)$| are complementary.

Table 3
Open in new tab

Predictive performance of various features on |${\mathbb{S}}_{\mathrm{independent}}$|⁠.

|${\mathrm{Y}}_1({l}_q,{d}_e)$||${\mathrm{Y}}_2({l}_q,{d}_e)$||${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}({d}_e)$|AUCAUPRNDCG@10
✔✗✗0.73140.28320.3837
✗✔✗0.55840.15480.2449
✔✔✗0.80690.30250.4659
✔✔✔0.83520.35970.5216
|${\mathrm{Y}}_1({l}_q,{d}_e)$||${\mathrm{Y}}_2({l}_q,{d}_e)$||${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}({d}_e)$|AUCAUPRNDCG@10
✔✗✗0.73140.28320.3837
✗✔✗0.55840.15480.2449
✔✔✗0.80690.30250.4659
✔✔✔0.83520.35970.5216
Table 3
Open in new tab

Predictive performance of various features on |${\mathbb{S}}_{\mathrm{independent}}$|⁠.

|${\mathrm{Y}}_1({l}_q,{d}_e)$||${\mathrm{Y}}_2({l}_q,{d}_e)$||${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}({d}_e)$|AUCAUPRNDCG@10
✔✗✗0.73140.28320.3837
✗✔✗0.55840.15480.2449
✔✔✗0.80690.30250.4659
✔✔✔0.83520.35970.5216
|${\mathrm{Y}}_1({l}_q,{d}_e)$||${\mathrm{Y}}_2({l}_q,{d}_e)$||${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}({d}_e)$|AUCAUPRNDCG@10
✔✗✗0.73140.28320.3837
✗✔✗0.55840.15480.2449
✔✔✗0.80690.30250.4659
✔✔✔0.83520.35970.5216

Comparison of two different disease features

The previous study indicated that integrating semantic attribute features of disease to construct the feature vectors of lncRNA-disease pairs can improve the performance of the ranking framework iLncDA-LTR [38]. However, disease features based on semantic similarity cannot fully reflect the associations between lncRNA-disease pairs. Compared to the DSSM(⁠|${d}_e$|⁠) (semantic attribute features of disease), the |${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}({d}_e)$| (graph attribute features of disease) are based on graph auto-encoder and attentional mechanism, which can learn more deep information from multiple graphs. We further compare the influence of two different disease features. For the GraLTR-LDA predictor, we replace |${\mathrm{Z}}_{\mathrm{LD}\_\mathrm{att}}({d}_e)$| in Eq. (29) by DSSM(⁠|${d}_e$|⁠) to get a new model GraLTR-LDA*. As shown in Table 4, GraLTR-LDA is superior with GraLTR-LDA*, indicating that the disease features based on graph attribute features are more critical than the disease semantic attribute features.

Table 4
Open in new tab

Performance comparison between GraLTR-LDA* and GraLTR-LDA on |${\mathbb{S}}_{\mathrm{independent}}$|⁠.

GraLTR-LDA*GraLTR-LDA
AUC0.75090.8352
AUPR0.24260.3597
NDCG@100.35990.5216
GraLTR-LDA*GraLTR-LDA
AUC0.75090.8352
AUPR0.24260.3597
NDCG@100.35990.5216
Table 4
Open in new tab

Performance comparison between GraLTR-LDA* and GraLTR-LDA on |${\mathbb{S}}_{\mathrm{independent}}$|⁠.

GraLTR-LDA*GraLTR-LDA
AUC0.75090.8352
AUPR0.24260.3597
NDCG@100.35990.5216
GraLTR-LDA*GraLTR-LDA
AUC0.75090.8352
AUPR0.24260.3597
NDCG@100.35990.5216

The impact of different k values on the performance of GraLTR-LDA

Construction of the similarity graph is the key of GraLTR-LDA. Therefore, we further analyze the influence of different k values on the performance of GraLTR-LDA for identifying lncRNA-disease associations in terms of AUPR (see Figure 5), from which we can see that GraLTR-LDA achieves stable performance and achieves the best performance when k is set as 20. The reason is that the smaller k values lead to sparse edges in the homogeneous graph resulting in insufficient model training, while the larger k values will introduce noise leading to performance decrement.

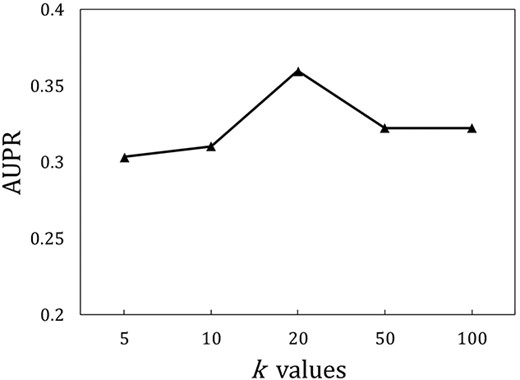
The influence of different k values on the performance of GraLTR-LDA on ${\mathbb{S}}_{\mathrm{independent}}$ in terms of AUPR.
Figure 5

The influence of different k values on the performance of GraLTR-LDA on |${\mathbb{S}}_{\mathrm{independent}}$| in terms of AUPR.

Open in new tabDownload slide

Case study

We implement two different case studies to further examine the performance of the GraLTR-LDA predictor. First, all lncRNA-disease associations on the above datasets are utilized to train the GraLTR-LDA for predicting potential lncRNA-disease pairs. The lncRNA-disease associations predicted by GraLTR-LDA not in LncRNADisease V2.0 database [56] may be correct. Table 5 lists several top predictions of the lncRNA-disease associations are supported by literature, but not in the LncRNADisease V2.0 database [56]. For example, the interaction between lncRNA NEAT1 and activating transcription factor 2 (ATF2) promoted the progression of lung adenocarcinoma [60]. LncRNA PVT1 regulated related downstream factors to promote the development in endometrial cancer [61]. We further provide the prediction results of the other lncRNA related diseases in the source code (http://bliulab.net/GraLTR-LDA).

Table 5
Open in new tab

Top predictions of lncRNA-disease associations with literature evidence

RankDiseaseLncRNAEvidence
9Lung cancerNEAT1PMID:32296457
10Lung adenocarcinomaPMID:33298086
16MelanomaPMID:33202380
20Pancreatic ductal adenocarcinomaPMID:34405022
10Lung adenocarcinomaPVT1PMID:32960438
17Endometrial cancerPMID:33948369
8Ovarian cancerTUSC7PMID:32706063
12Esophageal squamous cell carcinomaPMID:32897196
RankDiseaseLncRNAEvidence
9Lung cancerNEAT1PMID:32296457
10Lung adenocarcinomaPMID:33298086
16MelanomaPMID:33202380
20Pancreatic ductal adenocarcinomaPMID:34405022
10Lung adenocarcinomaPVT1PMID:32960438
17Endometrial cancerPMID:33948369
8Ovarian cancerTUSC7PMID:32706063
12Esophageal squamous cell carcinomaPMID:32897196
Table 5
Open in new tab

Top predictions of lncRNA-disease associations with literature evidence

RankDiseaseLncRNAEvidence
9Lung cancerNEAT1PMID:32296457
10Lung adenocarcinomaPMID:33298086
16MelanomaPMID:33202380
20Pancreatic ductal adenocarcinomaPMID:34405022
10Lung adenocarcinomaPVT1PMID:32960438
17Endometrial cancerPMID:33948369
8Ovarian cancerTUSC7PMID:32706063
12Esophageal squamous cell carcinomaPMID:32897196
RankDiseaseLncRNAEvidence
9Lung cancerNEAT1PMID:32296457
10Lung adenocarcinomaPMID:33298086
16MelanomaPMID:33202380
20Pancreatic ductal adenocarcinomaPMID:34405022
10Lung adenocarcinomaPVT1PMID:32960438
17Endometrial cancerPMID:33948369
8Ovarian cancerTUSC7PMID:32706063
12Esophageal squamous cell carcinomaPMID:32897196

In addition, to further demonstrate the practical ability of GraLTR-LDA for discovering potential lncRNA-disease associations, we use lncRNA MALAT1 as a typical example. We first removed the associations between lncRNA MALAT1 and the other diseases from all lncRNA-disease associations, and then used the remaining associations to train the GraLTR-LDA predictor. The trained predictor is used to re-predict the diseases related with lncRNA MALAT1. As shown in Table 6, top 10 predicted diseases associated with the lncRNA MALAT1 are recorded in the LncRNADisease V2.0 database [56] except for the fourth disease.

Table 6
Open in new tab

The top 10 MALAT1-associated diseases predicted by GraLTR-LDA

RankDiseaseEvidence
1AstrocytomaLncRNADiseaseV2.0
2Hepatocellular carcinomaLncRNADiseaseV2.0
3Gastric cancerLncRNADiseaseV2.0
4Hereditary hemorrhagic telangiectasiaUnconfirmed
5Colorectal cancerLncRNADiseaseV2.0
6Prostate cancerLncRNADiseaseV2.0
7Ovarian cancerLncRNADiseaseV2.0
8Non-small cell lung cancerLncRNADiseaseV2.0
9Breast cancerLncRNADiseaseV2.0
10Lung cancerLncRNADiseaseV2.0
RankDiseaseEvidence
1AstrocytomaLncRNADiseaseV2.0
2Hepatocellular carcinomaLncRNADiseaseV2.0
3Gastric cancerLncRNADiseaseV2.0
4Hereditary hemorrhagic telangiectasiaUnconfirmed
5Colorectal cancerLncRNADiseaseV2.0
6Prostate cancerLncRNADiseaseV2.0
7Ovarian cancerLncRNADiseaseV2.0
8Non-small cell lung cancerLncRNADiseaseV2.0
9Breast cancerLncRNADiseaseV2.0
10Lung cancerLncRNADiseaseV2.0
Table 6
Open in new tab

The top 10 MALAT1-associated diseases predicted by GraLTR-LDA

RankDiseaseEvidence
1AstrocytomaLncRNADiseaseV2.0
2Hepatocellular carcinomaLncRNADiseaseV2.0
3Gastric cancerLncRNADiseaseV2.0
4Hereditary hemorrhagic telangiectasiaUnconfirmed
5Colorectal cancerLncRNADiseaseV2.0
6Prostate cancerLncRNADiseaseV2.0
7Ovarian cancerLncRNADiseaseV2.0
8Non-small cell lung cancerLncRNADiseaseV2.0
9Breast cancerLncRNADiseaseV2.0
10Lung cancerLncRNADiseaseV2.0
RankDiseaseEvidence
1AstrocytomaLncRNADiseaseV2.0
2Hepatocellular carcinomaLncRNADiseaseV2.0
3Gastric cancerLncRNADiseaseV2.0
4Hereditary hemorrhagic telangiectasiaUnconfirmed
5Colorectal cancerLncRNADiseaseV2.0
6Prostate cancerLncRNADiseaseV2.0
7Ovarian cancerLncRNADiseaseV2.0
8Non-small cell lung cancerLncRNADiseaseV2.0
9Breast cancerLncRNADiseaseV2.0
10Lung cancerLncRNADiseaseV2.0

Conclusion

The previous method showed that combining the prediction results of different classification methods via LTR algorithm is effective for predicting potential lncRNA-disease associations [38]. However, once the classification results are wrong, the ranking results will inevitably be directly affected. Recently, the graph auto-encoder method was used to encode graph nodes into low-dimensional and has highly discriminative power embedded features.

Motivated by incorporating embedded features into the ranking methods, we propose a new predictor GraLTR-LDA for identifying missing lncRNA-disease associations. GraLTR-LDA has two main contributions: (i) Homogeneous and heterogeneous graphs are constructed by integrating multi-source biological information. GraLTR-LDA combines graph auto-encoder and attention mechanism to obtain embedded features from the constructed graphs. (ii) We employ a feature crossing statistical method to incorporate the embedded features into the LTR. LTR has been successfully applied to rank the candidate websites according to the degree of correlation with queries [30, 33]. The task of lncRNA-disease association identification is very similar with the task of searching actor-movie associations in search engine (see Figure 1), where one lncRNA can be associated with many diseases. Therefore, LTR works for lncRNA-disease association prediction. Experimental results show that GraLTR-LDA obviously outperforms the other state-of-the-art methods. In the future, we believe that GraLTR-LDA can be applied to the other similar tasks, such as protein–protein interaction prediction [62], drug–disease association prediction [63], etc. Because these problems can also be considered as the search tasks.

Key Points

  • GraLTR-LDA treats the lncRNA-disease association prediction as a graph-based search task, in which homogeneous graph and heterogeneous graph are constructed by integrating multi-source biological information.

  • GraLTR-LDA employs graph auto-encoder and multi-view attention mechanism to extract embedded features from the constructed graphs.

  • GraLTR-LDA is able to incorporate the embedded features into Learning to Rank framework via feature crossing statistical strategies to predict priority order of diseases associated with query lncRNAs.

Acknowledgments

We are very much indebted to the four anonymous reviewers, whose constructive comments are very helpful for strengthening the presentation of this paper.

Funding

This work was supported by the Beijing Natural Science Foundation (No. JQ19019) and National Natural Science Foundation of China (No. 62271049, U22A2039 and U21B2009).

Qi Liang is a master candidate at the School of Computer Science and Technology, Beijing Institute of Technology, Beijing, China. His expertise is in bioinformatics, nature language processing and machine learning.

Wenxiang Zhang is a doctoral candidate at the School of Computer Science and Technology, Beijing Institute of Technology, Beijing, China. His expertise is in bioinformatics, nature language processing and machine learning.

Hao Wu, PhD, is an experimentalist at the School of Computer Science and Technology, Beijing Institute of Technology, Beijing, China. His expertise is in bioinformatics, nature language processing and machine learning.

Bin Liu, PhD, is a professor at the School of Computer Science and Technology, Beijing Institute of Technology, Beijing, China. His expertise is in bioinformatics, nature language processing and machine learning.

References

1.

Xing
C
,
Sun
SG
,
Yue
ZQ
, et al.
Role of lncRNA LUCAT1 in cancer
.
Biomed Pharmacother
2021
;
134
:111158.

Google Scholar

OpenURL Placeholder Text

 
2.

Chen
G
,
Wang
Z
,
Wang
D
, et al.
LncRNADisease: a database for long-non-coding RNA-associated diseases
.
Nucleic Acids Res
2013
;
41
:
D983
–
6
.

Google Scholar

Crossref
Search ADS
PubMed

 
3.

Gao
Y
,
Shang
S
,
Guo
S
, et al.
Lnc2Cancer 3.0: an updated resource for experimentally supported lncRNA/circRNA cancer associations and web tools based on RNA-seq and scRNA-seq data
.
Nucleic Acids Res
2021
;
49
:
D1251
–
8
.

Google Scholar

Crossref
Search ADS
PubMed

 
4.

Zhang
J
,
Sun
Q
,
Liang
C
.
Prediction of lncRNA-disease associations based on robust multi-label learning
.
Current Bioinformatics
2021
;
16
:
1179
–
89
.

Google Scholar

Crossref
Search ADS

 
5.

Ramakrishnaiah
Y
,
Kuhlmann
L
,
Tyagi
S
.
Towards a comprehensive pipeline to identify and functionally annotate long noncoding RNA (lncRNA)
.
Comput Biol Med
2020
;
127
:104728.

Google Scholar

OpenURL Placeholder Text

 
6.

Ao
C
,
Yu
L
,
Zou
Q
.
Prediction of bio-sequence modifications and the associations with diseases
.
Brief Funct Genomics
2021
;
20
:
1
–
18
.

Google Scholar

Crossref
Search ADS
PubMed

 
7.

Chen
X
,
Yan
CC
,
Zhang
X
, et al.
Long non-coding RNAs and complex diseases: from experimental results to computational models
.
Brief Bioinform
2017
;
18
:
558
–
76
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
8.

Chen
X
,
Sun
YZ
,
Guan
NN
, et al.
Computational models for lncRNA function prediction and functional similarity calculation
.
Brief Funct Genomics
2019
;
18
:
58
–
82
.

Google Scholar

Crossref
Search ADS
PubMed

 
9.

Zhu
QQ
,
Fan
YX
,
Pan
XY
.
Fusing multiple biological networks to effectively predict miRNA-disease associations
.
Current Bioinformatics
2021
;
16
:
371
–
84
.

Google Scholar

Crossref
Search ADS

 
10.

Saxena
S
,
Achyuth
SB
,
Murthy
TPK
, et al.
Structural and functional analysis of disease-associated mutations in GOT1 gene: An in silico study
.
Comput Biol Med
2021
;
136
:104695.

Google Scholar

OpenURL Placeholder Text

 
11.

Lu
X
,
Gao
Y
,
Zhu
Z
, et al.
A constrained probabilistic matrix decomposition method for predicting miRNA-disease associations
.
Current Bioinformatics
2021
;
16
:
524
–
33
.

Google Scholar

Crossref
Search ADS

 
12.

Zhang
Y
,
Duan
G
,
Yan
C
, et al.
MDAPlatform: a component-based platform for constructing and assessing miRNA-disease association prediction methods
.
Current Bioinformatics
2021
;
16
:
710
–
21
.

Google Scholar

Crossref
Search ADS

 
13.

Rahaman
MM
,
Li
C
,
Yao
Y
, et al.
DeepCervix: A deep learning-based framework for the classification of cervical cells using hybrid deep feature fusion techniques
.
Comput Biol Med
2021
;
136
:
104649
.

Google Scholar

Crossref
Search ADS
PubMed

 
14.

Chen
X
,
Yan
GY
.
Novel human lncRNA-disease association inference based on lncRNA expression profiles
.
Bioinformatics
2013
;
29
:
2617
–
24
.

Google Scholar

Crossref
Search ADS
PubMed

 
15.

Li
G
,
Luo
J
,
Liang
C
, et al.
Prediction of LncRNA-disease associations based on network consistency projection
.
IEEE Access
2019
;
7
:
58849
–
56
.

Google Scholar

Crossref
Search ADS

 
16.

Lu
CQ
,
Yang
MY
,
Luo
F
, et al.
Prediction of lncRNA-disease associations based on inductive matrix completion
.
Bioinformatics
2018
;
34
:
3357
–
64
.

Google Scholar

Crossref
Search ADS
PubMed

 
17.

Xie
G
,
Jiang
J
,
Sun
Y
.
LDA-LNSUBRW: lncRNA-disease association prediction based on linear neighborhood similarity and unbalanced bi-random walk
.
IEEE/ACM Trans Comput Biol Bioinform
2022
;
19
:
989
–
97
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
18.

Guo
ZH
,
You
ZH
,
Wang
YB
, et al.
A learning-based method for LncRNA-disease association identification combing similarity information and rotation forest
.
iScience
2019
;
19
:
786
–
95
.

Google Scholar

Crossref
Search ADS
PubMed

 
19.

Zhang
Y
,
Ye
F
,
Xiong
D
, et al.
LDNFSGB: prediction of long non-coding rna and disease association using network feature similarity and gradient boosting
.
BMC Bioinformatics
2020
;
21
:
377
.

Google Scholar

Crossref
Search ADS
PubMed

 
20.

Zhu
R
,
Wang
Y
,
Liu
JX
, et al.
IPCARF: improving lncRNA-disease association prediction using incremental principal component analysis feature selection and a random forest classifier
.
BMC Bioinformatics
2021
;
22
:
175
.

Google Scholar

Crossref
Search ADS
PubMed

 
21.

Zeng
M
,
Lu
C
,
Fei
Z
, et al.
DMFLDA: a deep learning framework for predicting lncRNA-disease associations
.
IEEE/ACM Trans Comput Biol Bioinform
2021
;
18
:
2353
–
63
.

Google Scholar

Crossref
Search ADS
PubMed

 
22.

Wei
H
,
Liao
Q
,
Liu
B
.
iLncRNAdis-FB: identify lncRNA-disease associations by fusing biological feature blocks through deep neural network
.
IEEE/ACM Trans Comput Biol Bioinform
2021
;
18
:
1946
–
57
.

Google Scholar

Crossref
Search ADS
PubMed

 
23.

Kipf
TN
,
Welling
M
.
Semi-supervised classification with graph convolutional networks
.
arXiv preprint arXiv:1609.02907
, 2016.

24.

Shi
Z
,
Zhang
H
,
Jin
C
, et al.
A representation learning model based on variational inference and graph autoencoder for predicting lncRNA-disease associations
.
BMC Bioinformatics
2021
;
22
:
136
.

Google Scholar

Crossref
Search ADS
PubMed

 
25.

Fan
Y
,
Chen
M
,
Pan
X
.
GCRFLDA: scoring lncRNA-disease associations using graph convolution matrix completion with conditional random field
.
Brief Bioinform
2022
;
23
:bbab361.

Google Scholar

OpenURL Placeholder Text

 
26.

Lan
W
,
Wu
X
,
Chen
Q
, et al.
GANLDA: Graph attention network for lncRNA-disease associations prediction
.
Neurocomputing
2022
;
469
:
384
–
93
.

Google Scholar

Crossref
Search ADS

 
27.

Chen
X
,
Sun
LG
,
Zhao
Y
.
NCMCMDA: miRNA-disease association prediction through neighborhood constraint matrix completion
.
Brief Bioinform
2021
;
22
:
485
–
96
.

Google Scholar

Crossref
Search ADS
PubMed

 
28.

Chen
X
,
Li
TH
,
Zhao
Y
, et al.
Deep-belief network for predicting potential miRNA-disease associations
.
Brief Bioinform
2021
;
22
:bbaa186.

Google Scholar

OpenURL Placeholder Text

 
29.

Chen
X
,
Zhu
CC
,
Yin
J
.
Ensemble of decision tree reveals potential miRNA-disease associations
.
PLoS Comput Biol
2019
;
15
:e1007209.

Google Scholar

OpenURL Placeholder Text

 
30.

Li
H
.
Learning to rank for information retrieval and natural language processing
.
Synthesis Lectures on Human Language Technologies
2014
;
4
:
113
.

Google Scholar

OpenURL Placeholder Text

 
31.

Shen
L
,
Sarkar
A
,
Och
F
.
Discriminative reranking for machine translation
.
In HLT-NAACL
2004
;
77
:
177
–
84
.

Google Scholar

OpenURL Placeholder Text

 
32.

Huang
JZ
,
Zhang
W
,
Sun
YM
, et al.
Improving entity recommendation with search log and multi-task learning
.
Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence
2018
;
4107
–
14
.

Google Scholar

OpenURL Placeholder Text

 
33.

Liu
L
,
Huang
X
,
Mamitsuka
H
, et al.
HPOLabeler: improving prediction of human protein-phenotype associations by learning to rank
.
Bioinformatics
2020
;
36
:
4180
–
8
.

Google Scholar

Crossref
Search ADS
PubMed

 
34.

Liu
B
,
Chen
J
,
Wang
X
.
Application of learning to rank to protein remote homology detection
.
Bioinformatics
2015
;
31
:
3492
–
8
.

Google Scholar

Crossref
Search ADS
PubMed

 
35.

Liu
B
,
Zhu
Y
.
ProtDec-LTR3.0: protein remote homology detection by incorporating profile-based features into learning to rank, IEEE
.
Access
2019
;
7
:
102499
–
507
.

Google Scholar

Crossref
Search ADS

 
36.

Shao
J
,
Chen
J
,
Liu
B
.
ProtRe-CN: protein remote homology detection by combining classification methods and network methods via learning to rank
.
IEEE/ACM Trans Comput Biol Bioinform
2021
.

Google Scholar

OpenURL Placeholder Text

 
37.

Ru
X
,
Ye
X
,
Sakurai
T
, et al.
NerLTR-DTA: Drug-target binding affinity prediction based on neighbor relationship and learning to rank
.
Bioinformatics
2022
;
38
:1964–71.

Google Scholar

OpenURL Placeholder Text

 
38.

Wu
H
,
Liang
Q
,
Zhang
W
, et al.
iLncDA-LTR: Identification of lncRNA-disease associations by learning to rank
.
Comput Biol Med
2022
;
146
:105605.

Google Scholar

OpenURL Placeholder Text

 
39.

Kipf
TN
,
Welling
M
.
Variational graph auto-encoders
.
arXiv preprint arXiv:1611.07308
, 2016.

40.

Xie
Y
,
Zhang
Y
,
Gong
M
, et al.
MGAT: multi-view graph attention networks
.
Neural Netw
2020
;
132
:
180
–
9
.

Google Scholar

Crossref
Search ADS
PubMed

 
41.

O'Leary
NA
,
Wright
MW
,
Brister
JR
, et al.
Reference sequence (RefSeq) database at NCBI: current status, taxonomic expansion, and functional annotation
.
Nucleic Acids Res
2016
;
44
:
D733
–
45
.

Google Scholar

Crossref
Search ADS
PubMed

 
42.

Needleman
SB
,
Wunsch
CD
.
A general method applicable to the search for similarities in the amino acid sequence of two proteins
.
J Mol Biol
1970
;
48
:
443
–
53
.

Google Scholar

Crossref
Search ADS
PubMed

 
43.

Kibbe
WA
,
Arze
C
,
Felix
V
, et al.
Disease Ontology 2015 update: an expanded and updated database of human diseases for linking biomedical knowledge through disease data
.
Nucleic Acids Res
2015
;
43
:
D1071
–
8
.

Google Scholar

Crossref
Search ADS
PubMed

 
44.

Yu
G
,
Wang
LG
,
Yan
GR
, et al.
DOSE: an R/Bioconductor package for disease ontology semantic and enrichment analysis
.
Bioinformatics
2015
;
31
:
608
–
9
.

Google Scholar

Crossref
Search ADS
PubMed

 
45.

Jiang
H
,
Cao
P
,
Xu
M
, et al.
Hi-GCN: A hierarchical graph convolution network for graph embedding learning of brain network and brain disorders prediction
.
Comput Biol Med
2020
;
127
:
104096
.

Google Scholar

Crossref
Search ADS
PubMed

 
46.

Hao
Z
,
Wu
D
,
Fang
Y
, et al.
Prediction of synthetic lethal interactions in human cancers using multi-view graph auto-encoder
.
IEEE J Biomed Health Inform
2021
;
25
:
4041
–
51
.

Google Scholar

Crossref
Search ADS
PubMed

 
47.

Kingma
DP
,
Ba
J
.
Adam: a method for stochastic optimization
.
arXiv preprint arXiv:1412.6980
, 2014.

48.

La Salvia
M
,
Secco
G
,
Torti
E
, et al.
Deep learning and lung ultrasound for Covid-19 pneumonia detection and severity classification
.
Comput Biol Med
2021
;
136
:104742.

Google Scholar

OpenURL Placeholder Text

 
49.

Wu
QW
,
Xia
JF
,
Ni
JC
, et al.
GAERF: predicting lncRNA-disease associations by graph auto-encoder and random forest
.
Brief Bioinform
2021
;
22
:bbaa391.

Google Scholar

OpenURL Placeholder Text

 
50.

Sheng
N
,
Huang
L
,
Wang
Y
, et al.
Multi-channel graph attention autoencoders for disease-related lncRNAs prediction
.
Brief Bioinform
2022
;
23
:bbab604.

Google Scholar

OpenURL Placeholder Text

 
51.

Ru
X
,
Ye
X
,
Sakurai
T
, et al.
Application of learning to rank in bioinformatics tasks
.
Brief Bioinform
2021
;
22
:bbaa394.

Google Scholar

OpenURL Placeholder Text

 
52.

Ru
X
,
Wang
L
,
Li
L
, et al.
Exploration of the correlation between GPCRs and drugs based on a learning to rank algorithm
.
Comput Biol Med
2020
;
119
:103660.

Google Scholar

OpenURL Placeholder Text

 
53.

Wei
H
,
Xu
Y
,
Liu
B
.
iCircDA-LTR: identification of circRNA-disease associations based on Learning to Rank
.
Bioinformatics
2021
;
37
:3302–10.

Google Scholar

OpenURL Placeholder Text

 
54.

Burges
CJ
.
From ranknet to lambdarank to lambdamart: An overview
.
Learning
2010
;
11
:
81
.

Google Scholar

OpenURL Placeholder Text

 
55.

Järvelin
K
,
Kekäläinen
J
.
IR evaluation methods for retrieving highly relevant documents
.
ACM SIGIR Forum
2017
;
51
:
243
–
50
.

56.

Bao
Z
,
Yang
Z
,
Huang
Z
, et al.
LncRNADisease 2.0: an updated database of long non-coding RNA-associated diseases
.
Nucleic Acids Res
2019
;
47
:
D1034
–
7
.

Google Scholar

Crossref
Search ADS
PubMed

 
57.

Zhao
X
,
Zhao
X
,
Yin
M
.
Heterogeneous graph attention network based on meta-paths for lncRNA–disease association prediction
.
Brief Bioinform
2022
;
23
:bbab407.

Google Scholar

Crossref
Search ADS

 
58.

Zhao
C
,
Xu
N
,
Tan
J
, et al.
ILGBMSH: an interpretable classification model for the shRNA target prediction with ensemble learning algorithm
.
Brief Bioinform
2022
;bbac429.

Google Scholar

OpenURL Placeholder Text

 
59.

Gribskov
M
,
Robinson
NLJC
.
Use of receiver operating characteristic (ROC) analysis to evaluate sequence matching
.
Computers & chemistry
1996
;
20
:
25
–
33
.

60.

Liu
J
,
Li
K
,
Wang
R
, et al.
The interplay between ATF2 and NEAT1 contributes to lung adenocarcinoma progression
.
Cancer Cell Int
2020
;
20
:
594
.

Google Scholar

Crossref
Search ADS
PubMed

 
61.

Cong
R
,
Kong
F
,
Ma
J
, et al.
The PVT1/miR-612/CENP-H/CDK1 axis promotes malignant progression of advanced endometrial cancer
.
Am J Cancer Res
2021
;
11
:
1480
–
502
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
62.

Hu
L
,
Yang
S
,
Luo
X
, et al.
A distributed framework for large-scale protein-protein interaction data analysis and prediction using MapReduce
.
IEEE/CAA Journal of Automatica Sinica
2022
;
9
:
160
–
72
.

Google Scholar

Crossref
Search ADS

 
63.

Zhao
BW
,
Hu
L
,
You
ZH
, et al.
HINGRL: predicting drug-disease associations with graph representation learning on heterogeneous information networks
.
Brief Bioinform
2022
;
23
:bbab515.

Google Scholar

OpenURL Placeholder Text

 
© The Author(s) 2022. Published by Oxford University Press. All rights reserved. For Permissions, please email: [email protected]
This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)
Issue Section:
Problem solving protocol
Download all slides