-
PDF
- Split View
-
Views
-
Cite
Cite
Yongqing Zhang, Qiang Zhang, Jiliu Zhou, Quan Zou, A survey on the algorithm and development of multiple sequence alignment, Briefings in Bioinformatics, Volume 23, Issue 3, May 2022, bbac069, https://doi.org/10.1093/bib/bbac069
Close - Share Icon Share
Abstract
Multiple sequence alignment (MSA) is an essential cornerstone in bioinformatics, which can reveal the potential information in biological sequences, such as function, evolution and structure. MSA is widely used in many bioinformatics scenarios, such as phylogenetic analysis, protein analysis and genomic analysis. However, MSA faces new challenges with the gradual increase in sequence scale and the increasing demand for alignment accuracy. Therefore, developing an efficient and accurate strategy for MSA has become one of the research hotspots in bioinformatics. In this work, we mainly summarize the algorithms for MSA and its applications in bioinformatics. To provide a structured and clear perspective, we systematically introduce MSA’s knowledge, including background, database, metric and benchmark. Besides, we list the most common applications of MSA in the field of bioinformatics, including database searching, phylogenetic analysis, genomic analysis, metagenomic analysis and protein analysis. Furthermore, we categorize and analyze classical and state-of-the-art algorithms, divided into progressive alignment, iterative algorithm, heuristics, machine learning and divide-and-conquer. Moreover, we also discuss the challenges and opportunities of MSA in bioinformatics. Our work provides a comprehensive survey of MSA applications and their relevant algorithms. It could bring valuable insights for researchers to contribute their knowledge to MSA and relevant studies.
Introduction
Sequence alignment (SA) is one of the hotspots and critical steps in bioinformatics, which analyzes the essential biological characteristics between nucleotide or protein sequences by comparing the similarity, such as functional information, structural information and evolutionary information [1]. For example, in comparative genomic analysis, SA can identify conserved sequence motifs, estimate evolutionary differences among sequences and infer the historical relationship between genes and species [2].
SA is mainly used to determine the similarity of two or more sequences. As shown in Figure 1A, given two nucleotide sequences, it is only necessary to insert one gap in the 3rd position of the 2nd sequence to maximize the number of matched nucleotide columns between two sequences. According to the range of alignment, SA can be divided into global SA (shown as Figure 1A or B) and local SA (shown as Figure 1C) [3]. On the other hand, according to the number of sequences, SA can also be divided into pairwise sequence alignment [4] (PSA, shown as Figure 1A) and multiple sequence alignment [5] (MSA, shown as Figure 1B or C). SA makes the resulting sequences all have the same length and aligns the same or similar parts of each sequence by inserting gaps. At present, dynamic programming and the trace-back process can perfectly solve the problem of PSA, such as the Needleman–Wunsch algorithm for global alignment [6] and Smith–Waterman algorithm for local alignment [7]. However, compared with PSA, MSA is more complex. It is an NP (nondeterministic polynomial)-complete problem [8], there is no comprehensive solution for MSA [9].
There are currently many algorithms for MSA that can be roughly divided into progressive alignment algorithm, iterative algorithm, heuristics, machine learning and divide-and-conquer. Progressive alignment is a simple algorithm, which mainly includes two steps: constructing the guide tree and gradually constructing the alignment according to the guide tree [10]. The progressive alignment algorithm is more straightforward and faster. It is still widely used in various methods or programs of MSA after more than 30 years [11–13]. However, due to the lack of accuracy of progressive alignment algorithm, some methods introduced iterative algorithm into progressive alignment to solve this problem [14, 15]. These methods continuously optimize the alignment in the iterative process, but it is undeniable that the iterative algorithm comes with an additional time overhead. Recently, some researchers are pinning their hopes on heuristics [16, 17]. A heuristic algorithm is an iterative algorithm in a broad sense suitable for solving the NP problem such as MSA. However, unlike the traditional iterative algorithm, the heuristic algorithm may have different results each time due to its randomness. Although the application of machine learning to MSA is currently in its initial stage, there are still some valuable works on this subject [18–20]. These works show that machine learning-based methods for MSA perform better than traditional methods on some datasets. Moreover, divide-and-conquer is also widely used in MSA in recent years [21, 22]. It operates by dividing a group of sequences into multiple groups of subsequences for processing, which significantly improves the efficiency of the methods.
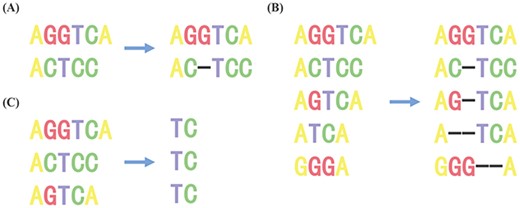
This figure shows various types of SA. (A) shows PSA and global SA, (B) shows MSA and global SA and (C) shows MSA and local SA.
With the development and extensive application of MSA, there have been many valuable works to review the research of MSA from several aspects. For example, Notredame described existing MSA algorithms and exposed the potential advantages and disadvantages of the widely used programs [23]. Furthermore, Chowdhury and Garai have shown different methods for SA and the latest trend of multi-objective genetic algorithms in MSA. Their research shows that there is excellent progress in improving the accuracy of the alignment [24]. Moreover, Chatzou et al. reviewed the development and performance of the algorithms for protein, DNA and RNA alignment. Importantly, they also explored the relationship between simulated and empirical data, which affect the development of the algorithm [8]. Bawono et al.’s work provided the background and considerations of MSA techniques, primarily focusing on the protein SA. Then, they reviewed existing MSA methods and summarized the specific strengths and limitations of these methods [5]. Xia et al. conducted the present situation of parallel local alignment, concentrating on the large-scale genomic alignment. Besides, they also surveyed the performance of typical methods and discussed the future directions [25]. However, due to the increasing sequences scale and the diversity and complexity of the approaches, these works are not systematic and comprehensive. There is an urgent demand to summarize the recent research of MSA clearly and systematically.
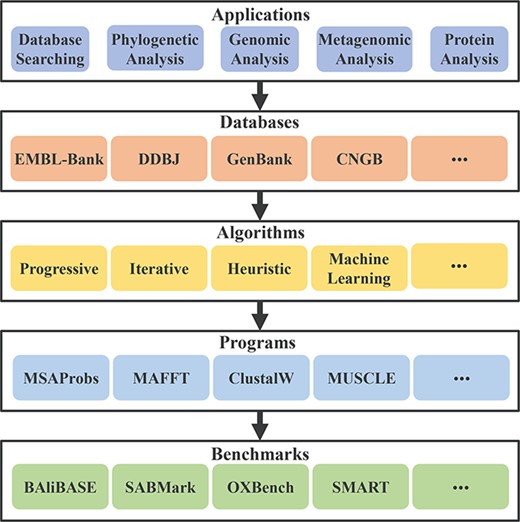
In this work, we provide a clear review of the research of MSA and its applications in several scenarios. Our study is mainly shown in Figure 2. We summarize the relevant knowledge of MSA from its application, database, algorithm, program and benchmark. Primarily, we introduce and classify the classical and latest algorithms for MSA in more detail. Furthermore, we also discuss the current challenges and opportunities for future directions of MSA. This work comprehensively reviews the research of MSA from several aspects, which aim to serve as a helpful guide for researchers. The contributions of this work can be summarized as follows: (1) summarize the research status of MSA systematically. (2) Classify and detail the classical and latest algorithms for MSA. (3) Discuss the current challenges and opportunities of MSA.
Applications of MSA
MSA plays a vital role in clarifying the biological patterns of multiple related sequences. For two or more sequences with high similarity, they may show similarity in function, evolution and structure [1]. For this reason, MSA has been widely used in sequence database searching, phylogenetic analysis, genomic analysis, protein analysis and metagenomic analysis [23].
Database searching
For a newly gene sequenced or protein sequenced, a vital clue to know its function is to search the known sequences homologous of similar to that sequence [26]. However, with the sustainable development of sequencing technology, the cumulative number of sequences has broken through the scope of human retrieval. Finding similar sequences from the sequence database has become one of the difficulties.
Sequence database search tools mainly include FASTA [27] and BLAST [26]. FASTA, derived from FASTAP, is the first program widely used in DNA and protein database searching. The search process of FASTA is as follows: firstly, build a dictionary of sequence fragments of |$ktup$|-length, then match the same or similar sequence fragments in the database. After the search, FASTA expands the matched fragments to obtain the best alignment between each matched sequence and the search sequence. In addition, BLAST is the most widely used tool at present. It has more improvements and faster speed than FASTA. The search process is similar to FASTA. It needs to establish a dictionary for the sequence fragments and expand on the matched fragments. The apparent difference is that BLAST introduces a fragment matching and expansion threshold. For different application scenarios, many derivative versions of BLAST have been born, including the latest BLASTP-ACC [28] and SMI-BLASE [29].
Phylogenetic analysis
Phylogenetic analysis is a critical key of many evolutionary studies. It reveals the phylogenetic relationship between different species and analyzes the major transitions in evolution [30]. MSA is the prerequisite in many studies of phylogenetic analysis, such as the construction of the phylogenetic tree. Such as, Khan et al. compute the alignment of 16S rRNA of seven muntjac species to determine the phylogenetic similarity among the muntjac using DNASTAR. And then construct the phylogenetic tree of these species based on the alignment. Finally, by analyzing the phylogenetic tree, they summarize the phylogenetic relationship among the selected species [31]. Furthermore, while investigating the Colletotrichum acutatum sensu lato, which causes leaf curl of celery, Liu et al. [32] align the genes of a collection of isolates from celery and non-celery using ClustalX and conduct a multilocus phylogenetic analysis based on the alignment. In addition, Wei et al. [33] and Hu et al. [34] used the MSA program MAFFT to construct the alignment for phylogenetic analysis.
Genomic analysis
Genomic analysis is an essential means of obtaining biological information, and it aims to analyze the gene functional, genetic, evolutionary or structural information contained in these genomes [35].
In early 2020, with the outbreak of SARS-CoV-2 (COVID-19), researchers paid particular attention to the virus [36, 37]. They constructed the MSA and the phylogenetic trees on the representative spike proteins of SARS-CoV and SARS-CoV-2 from various host sources. They analyzed the specificity required by SARS-CoV-2 spike proteins to cause human infection [38]. The results showed that N-terminal sequence regions MESEFR’ and SYLTPG’ were specific to human SARS-CoV-2. In the receptor-binding domain, two sequence regions, VGGNY’ and EIYQAGSTPCNGV’ and a disulfide bond connecting 480C and 488C are structural determinants for recognizing human ACE-2 receptors. The analysis of virus variants also depends on the MSA results. Through the study of base substitution, deletion, variation and single nucleotide polymorphisms (SNP) in the alignment, we can understand the evolution and classification of variants, which provides essential information for vaccine research about development and improvement [39].
In addition, MSA has been applied to many research fields, including the analysis of viral diseases of different species [40], the impact of enhancers on the evolution of mammals [41] and the study of genes encoding killer-cell immunoglobulin-like receptors [42].
Metagenomic analysis
The genomic analysis mainly analyzes the genome of a single species. In contrast, metagenomic analysis primarily studies the genome of all microbial communities in a specific environment and explores their genetic composition, community function and diversity [43].
Metagenomic analysis can be combined with MSA to quickly determine the genetic relationship between different organisms. In 2020, Zhou et al. collected the metagenomes of 227 bat samples and identified the new virus called RmYN02 through MSA. According to analysis, the virus has 93.3% nucleotide homology with SARS-CoV-2 and is the closest relative to SARS-SoV-2 found so far [44]. Furthermore, MSA is also often used in metagenomic classification. For example, the early metagenomic classifier uses BLAST to match each genome with all genomes in GenBank [45]. While now, to improve accuracy and efficiency, most classifiers prefer combining other algorithms based on MSA, such as k-mers [46] and Markov model [47].
Protein analysis
Similar to genomic analysis, protein sequence analysis mainly focuses on protein function analysis, homology analysis, structure prediction and residue contact prediction [23]. Primarily, protein structure prediction is one of the current research hotspots. In Protein Data Bank (PDB), the protein structure is mainly obtained by X-ray crystal diffraction, nuclear magnetic resonance and electron microscopy [48]. Because the cost of this structure acquisition method is too high, their respective limitations are relatively large. Therefore, to reduce the cost of obtaining protein structure, some researchers have proposed MSA combined with some prediction methods to predict protein structure. The main steps are as follows: give a group of protein sequences homologous to be tested and use the SA results to select an appropriate method to predict the structure [49]. A prediction accuracy combined with deep learning is proposed to improve the prediction accuracy. The core idea of this method is to map the amino acid sequence to the continuous space of adaptive learning with the help of natural language processing to input the whole alignment into the deep neural network for prediction. The results show that this method has good performance in different protein prediction problems [50].
Databases of biomolecules
The sequence database is mainly divided into gene, protein and comprehensive databases. In 1982, with sequencing technology development, biological sequences increased sharply. European Bioinformatics Institute established the first DNA sequence database, which is called European Molecular Biology Laboratory Bank (EMBL-Bank) [51]. In the same year, GeneBank was established by the National Institutes of Health and National Science Foundation [52]. After decades of development, the above databases have become a 1st-class comprehensive database [53]. To ensure data integrity, these databases share and exchange data. Therefore, from the perspective of data content, the resources stored in these databases are almost the same [54].
There are some deficiencies in the protein data in the above database. Therefore, databases dedicated to storing proteins have emerged, such as UniProt PDB. UniProt is the free protein database with the rich information and the most comprehensive resources. It integrates EMBL bank, the Swiss Institute of Bioinformatics and Protein Information Resource [55]. At present, UniProt is mainly composed of five sub-databases: Swiss-Prot, TrEMBL, UniParc, UniRef and Proteomes. The relationship of these data is shown in Figure 3. PDB mainly records the protein structural information and other biological macromolecules, such as polysaccharides and nucleic acids [48]. The structural information in PDB is mainly determined by X-ray crystal diffraction, nuclear magnetic resonance or electron microscope. It is expensive but has higher accuracy, so it is more suitable for research. The summary of the related database is shown in Table 1.
| Database . | Description . | References . |
|---|---|---|
| EMBL-Bank | Comprehensive database of Europe, top-level database. | [51] |
| DDBJ | Comprehensive database of Japan, top-level database. | [53] |
| GenBank | Comprehensive database of America, top-level database. | [52] |
| CNGB | Comprehensive database of China. | [56] |
| SRA | Comprehensive database, storing raw sequences. | [57] |
| RefSeq | Comprehensive database, storing non redundant sequences. | [58] |
| GDB | Genome database, storing human genome sequences. | [59] |
| MmtDB | Metazoa mtDNA variants specialized database. | [60] |
| MitBASE | Integrated mitochondrial DNA database. | [61] |
| SGD | Saccharomyces genome database. | [62] |
| AceDB | Caenorhabditis elegans sequence database. | [63] |
| dbSNP | Variant gene database. | [64] |
| OMIM | Online Mendelian inheritance in MA. | [65] |
| DGV | The database of genomic variants from healthy people. | [66] |
| UniProt | Protein database. | [55] |
| PDB | Protein structure database. | [48] |
| Database . | Description . | References . |
|---|---|---|
| EMBL-Bank | Comprehensive database of Europe, top-level database. | [51] |
| DDBJ | Comprehensive database of Japan, top-level database. | [53] |
| GenBank | Comprehensive database of America, top-level database. | [52] |
| CNGB | Comprehensive database of China. | [56] |
| SRA | Comprehensive database, storing raw sequences. | [57] |
| RefSeq | Comprehensive database, storing non redundant sequences. | [58] |
| GDB | Genome database, storing human genome sequences. | [59] |
| MmtDB | Metazoa mtDNA variants specialized database. | [60] |
| MitBASE | Integrated mitochondrial DNA database. | [61] |
| SGD | Saccharomyces genome database. | [62] |
| AceDB | Caenorhabditis elegans sequence database. | [63] |
| dbSNP | Variant gene database. | [64] |
| OMIM | Online Mendelian inheritance in MA. | [65] |
| DGV | The database of genomic variants from healthy people. | [66] |
| UniProt | Protein database. | [55] |
| PDB | Protein structure database. | [48] |
| Database . | Description . | References . |
|---|---|---|
| EMBL-Bank | Comprehensive database of Europe, top-level database. | [51] |
| DDBJ | Comprehensive database of Japan, top-level database. | [53] |
| GenBank | Comprehensive database of America, top-level database. | [52] |
| CNGB | Comprehensive database of China. | [56] |
| SRA | Comprehensive database, storing raw sequences. | [57] |
| RefSeq | Comprehensive database, storing non redundant sequences. | [58] |
| GDB | Genome database, storing human genome sequences. | [59] |
| MmtDB | Metazoa mtDNA variants specialized database. | [60] |
| MitBASE | Integrated mitochondrial DNA database. | [61] |
| SGD | Saccharomyces genome database. | [62] |
| AceDB | Caenorhabditis elegans sequence database. | [63] |
| dbSNP | Variant gene database. | [64] |
| OMIM | Online Mendelian inheritance in MA. | [65] |
| DGV | The database of genomic variants from healthy people. | [66] |
| UniProt | Protein database. | [55] |
| PDB | Protein structure database. | [48] |
| Database . | Description . | References . |
|---|---|---|
| EMBL-Bank | Comprehensive database of Europe, top-level database. | [51] |
| DDBJ | Comprehensive database of Japan, top-level database. | [53] |
| GenBank | Comprehensive database of America, top-level database. | [52] |
| CNGB | Comprehensive database of China. | [56] |
| SRA | Comprehensive database, storing raw sequences. | [57] |
| RefSeq | Comprehensive database, storing non redundant sequences. | [58] |
| GDB | Genome database, storing human genome sequences. | [59] |
| MmtDB | Metazoa mtDNA variants specialized database. | [60] |
| MitBASE | Integrated mitochondrial DNA database. | [61] |
| SGD | Saccharomyces genome database. | [62] |
| AceDB | Caenorhabditis elegans sequence database. | [63] |
| dbSNP | Variant gene database. | [64] |
| OMIM | Online Mendelian inheritance in MA. | [65] |
| DGV | The database of genomic variants from healthy people. | [66] |
| UniProt | Protein database. | [55] |
| PDB | Protein structure database. | [48] |
![The figure demonstrates the relationship among five sub-databases of UniProt [67].](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/bib/23/3/10.1093_bib_bbac069/1/m_bbac069f3.jpeg?Expires=1750222030&Signature=ZVdWSjWPH~l5mruJYR2SWiqOPhr4DVhirCuTbBVKBVGMk8cGcN0gzs~j7IoUjeE3JZdwi7hTv1Xjty8RBgaVO5VrgKag5bqJzO8oTx0zETFDndqXdxcMBWeS-mkP9eQmxfAjPVk5OKPU6RT~mGk7DJ6jZPlxIkmqHSIoUPGhhoEaCMfbYXZGCPkvnedpdAhvUmPJqCpGqzoTTb4r42anDx3zu5aauMPt9RTbbtP0m9cFKJm2Igg7Sv9mx7GY77VK2ZE7NTjcTD27X3xbRgpdYN8JJGUMm3Wy1aVKkz8QlxgR9xYJ8mhjF4vAB2YzSzpM~f3YYp-fUdJaJkpW7QZ-Vw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The figure demonstrates the relationship among five sub-databases of UniProt [67].
Algorithms for MSA
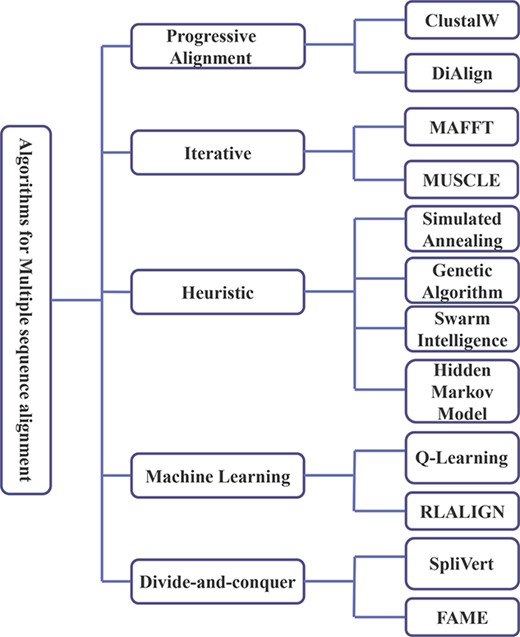
This section mainly introduces the widely used MSA algorithms, which are divided into the following five types according to the characteristics of the algorithm: progressive alignment algorithm, iterative algorithm, heuristic, machine learning and divide-and-conquer algorithm, as shown in Figure 4.
Progressive alignment algorithm
Hogeweg and Hesper [68] first proposed the progressive alignment algorithm in 1984. The progressive alignment algorithm is more straightforward, efficient and has lower memory consumption than other algorithms. However, it also has obvious defects, once a gap, always a gap’ meaning that the inserted gap cannot be changed after the alignment sequence is confirmed [69]. According to relevant research, the progressive alignment algorithm may cause information loss when calculating the distance matrix, making the algorithm unstable [70].
After more than 30 years of development, the progressive alignment algorithm has been widely used in various MSA methods, as shown in Table 2. Typically, Higgins et al. developed ClustalW, derived from ClustalV in 1994 [11], which uses the weighted sum-of-pairs (WSP) objective function and the neighbor-joining (NJ) method to build the guide tree, as shown in Figure 5. ClustalW is widely used in genome analysis, such as the study on the evolutionary relationship between banana subspecies [77], the rDNA barcoding identification of bacterial and fungal pathogens in vitreous fluids of endophthalmitis patients [78], and the study on the molecular variation of ABO in Chinese Han population [79].
| References . | Description . | Year . |
|---|---|---|
| [11] | ClustalW, guide tree, WSP | 1994 |
| [12] | DiAlign, segment-segment, probabilistic consideration | 1998 |
| [71] | T-Coffee, tree-based consistency objective | 2000 |
| [13] | Kalign, Wu-Manber character matching algorithm | 2005 |
| [72] | GramAlign, grammar-based distance | 2008 |
| [73] | MSAIndelFR, indel flanking region | 2015 |
| [74] | TM-Aligner, Wu-Manber and dynamic string matching algorithm | 2017 |
| [75] | ProPIP, dynamic programming | 2021 |
| [76] | Regressive algorithm | 2021 |
| References . | Description . | Year . |
|---|---|---|
| [11] | ClustalW, guide tree, WSP | 1994 |
| [12] | DiAlign, segment-segment, probabilistic consideration | 1998 |
| [71] | T-Coffee, tree-based consistency objective | 2000 |
| [13] | Kalign, Wu-Manber character matching algorithm | 2005 |
| [72] | GramAlign, grammar-based distance | 2008 |
| [73] | MSAIndelFR, indel flanking region | 2015 |
| [74] | TM-Aligner, Wu-Manber and dynamic string matching algorithm | 2017 |
| [75] | ProPIP, dynamic programming | 2021 |
| [76] | Regressive algorithm | 2021 |
| References . | Description . | Year . |
|---|---|---|
| [11] | ClustalW, guide tree, WSP | 1994 |
| [12] | DiAlign, segment-segment, probabilistic consideration | 1998 |
| [71] | T-Coffee, tree-based consistency objective | 2000 |
| [13] | Kalign, Wu-Manber character matching algorithm | 2005 |
| [72] | GramAlign, grammar-based distance | 2008 |
| [73] | MSAIndelFR, indel flanking region | 2015 |
| [74] | TM-Aligner, Wu-Manber and dynamic string matching algorithm | 2017 |
| [75] | ProPIP, dynamic programming | 2021 |
| [76] | Regressive algorithm | 2021 |
| References . | Description . | Year . |
|---|---|---|
| [11] | ClustalW, guide tree, WSP | 1994 |
| [12] | DiAlign, segment-segment, probabilistic consideration | 1998 |
| [71] | T-Coffee, tree-based consistency objective | 2000 |
| [13] | Kalign, Wu-Manber character matching algorithm | 2005 |
| [72] | GramAlign, grammar-based distance | 2008 |
| [73] | MSAIndelFR, indel flanking region | 2015 |
| [74] | TM-Aligner, Wu-Manber and dynamic string matching algorithm | 2017 |
| [75] | ProPIP, dynamic programming | 2021 |
| [76] | Regressive algorithm | 2021 |
![Given seven protein sequences. The distance matrix of paired sequences is calculated firstly, then the NJ algorithm is used to construct the guide tree, and finally, the progressive alignment is used to align the sequences gradually [11].](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/bib/23/3/10.1093_bib_bbac069/1/m_bbac069f5.jpeg?Expires=1750222030&Signature=fzVwcBTRMTrB0cFf8yfCHhmIQMX2WxlRn2t~yNSLVfu9UYDo1wgascDjAaec~KXmAk5h-fDaih6vRREitn94OnYCacMeutH-cCaFz8zFPQztwnQNNwpKTdqOJgEGp-vImozVV4eLGpKfHkxpXD6dm6YID2VEP6~ijKy131DHC5xu~i0p~ddWmVYDarHDA637KVjC1t8u4eFcIZyyCfGZb6e8ORJ~p9ujfkcy83ceFazj7CCSM4vQurK~ZaO-ilujTptmS9sBcwRsH0cPtGZz5ZykXWv8yI26di4BC1FAhU39Yxx6wCCtG8fUDKgJOzOreL7yVUDS0Eh4gbznthHygw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Given seven protein sequences. The distance matrix of paired sequences is calculated firstly, then the NJ algorithm is used to construct the guide tree, and finally, the progressive alignment is used to align the sequences gradually [11].
Recently, there has been some studies similar to ClustalW. For example, Kalign [13], developed by Lasmann and Sonnhammer in 2005, uses the Wu-Manber character matching algorithm when calculating distance matrix. GramAlign, proposed by Russell et al. [72], uses syntax based on Lempel–Ziv compression algorithm to compute distance matrix. In 2021, Maiolo et al. introduced the Poisson Indel Process (PIP) model and dynamic programming algorithm to calculate the distance matrix, which effectively reduced the complexity of the whole method [75]. In the optimization of the objective function, Al-Shatnawi adopts the objective process of variable gap penalty in the MSAIndelFR to improve the accuracy of alignment in 2015 [73].
To further improve the accuracy and avoid the severe pitfall caused by the greed, T-Coffee (Tree-based Consistency Objective Function For alignmEnt Evaluation) was presented by Notredame and Higginsin in 2000, which is based on progressive alignment algorithm and consistency [71]. The package of T-Coffee integrates a variety of MSA methods with different characteristics, such as low memory overhead or higher accuracy [80, 81]. For example, Garriga et al. [76] proposed an MSA method based on a T-Coffee regressive and progressive alignment algorithm. In their method, sequences are first clustered and then aligned starting from the most distant ones. Their experiments show that the technique can significantly improve alignment accuracy in large-scale datasets.
As the most classic algorithm, the progressive alignment algorithm has more clear and faster advantages. However, the progressive alignment algorithm’s accuracy is relatively unsatisfactory, and its performance is easily affected by the number of sequences. Therefore, in addition to the progressive alignment algorithm, most algorithms also use other methods to improve the accuracy of alignment, such as MUSCLE [15], MAFFT [14].
Iterative algorithm
The iterative algorithm is an algorithm that can continuously optimize the alignment to improve the accuracy until it converges. The iterative algorithm can generally be divided into deterministic and stochastic [23]. The calculation results of the deterministic iterative algorithm are the same every time. In contrast, the results of the stochastic iterative algorithm may be different due to the internal use of random values. In this section, we mainly discuss the deterministic iterative algorithm. As shown in Table 3, the table lists the MSA methods related to the deterministic iterative algorithm.
| References . | Description . | Year . |
|---|---|---|
| [82] | MultAlign, hierarchical clustering | 1988 |
| [14] | MAFFT, fast Fourier transform, refinement | 2002 |
| [15] | MUSCLE, unweighted pair-group method with arithmetic mean | 2004 |
| [83] | PRALINE, homology-extended, secondary structure | 2005 |
| [84] | Probalign, posterior probabilities | 2006 |
| [85] | SATé, minimizing tree-length, POY | 2009 |
| [86] | PASTA, large-scale, parallel technique | 2015 |
| [87] | VIRULIGN, reference-guide, codon-correct | 2019 |
| [88] | ViralMSA, reference-guide, real-time | 2021 |
| References . | Description . | Year . |
|---|---|---|
| [82] | MultAlign, hierarchical clustering | 1988 |
| [14] | MAFFT, fast Fourier transform, refinement | 2002 |
| [15] | MUSCLE, unweighted pair-group method with arithmetic mean | 2004 |
| [83] | PRALINE, homology-extended, secondary structure | 2005 |
| [84] | Probalign, posterior probabilities | 2006 |
| [85] | SATé, minimizing tree-length, POY | 2009 |
| [86] | PASTA, large-scale, parallel technique | 2015 |
| [87] | VIRULIGN, reference-guide, codon-correct | 2019 |
| [88] | ViralMSA, reference-guide, real-time | 2021 |
| References . | Description . | Year . |
|---|---|---|
| [82] | MultAlign, hierarchical clustering | 1988 |
| [14] | MAFFT, fast Fourier transform, refinement | 2002 |
| [15] | MUSCLE, unweighted pair-group method with arithmetic mean | 2004 |
| [83] | PRALINE, homology-extended, secondary structure | 2005 |
| [84] | Probalign, posterior probabilities | 2006 |
| [85] | SATé, minimizing tree-length, POY | 2009 |
| [86] | PASTA, large-scale, parallel technique | 2015 |
| [87] | VIRULIGN, reference-guide, codon-correct | 2019 |
| [88] | ViralMSA, reference-guide, real-time | 2021 |
| References . | Description . | Year . |
|---|---|---|
| [82] | MultAlign, hierarchical clustering | 1988 |
| [14] | MAFFT, fast Fourier transform, refinement | 2002 |
| [15] | MUSCLE, unweighted pair-group method with arithmetic mean | 2004 |
| [83] | PRALINE, homology-extended, secondary structure | 2005 |
| [84] | Probalign, posterior probabilities | 2006 |
| [85] | SATé, minimizing tree-length, POY | 2009 |
| [86] | PASTA, large-scale, parallel technique | 2015 |
| [87] | VIRULIGN, reference-guide, codon-correct | 2019 |
| [88] | ViralMSA, reference-guide, real-time | 2021 |
MultAlign is one of the earliest MSA methods using the iterative algorithm and progressive alignment developed by Corpet in 1988 [82]. MultAlign calculates the pairwise alignment and the distance matrix by FASTA. While constructing the guide tree, it uses a hierarchical clustering to cluster all similar sequences and generates a tree with leaf nodes. MUSCLE (MUltiple Sequence Comparison by Log-Expectation) is one of the widely used programs based on an iterative algorithm, which was developed by Edgar in 2004 [15]. The process of MUSCLE is mainly divided into the following three steps (As shown in Figure 6): (1) calculate the distance matrix D1, construct the guide tree TREE1 by UPGMA (Unweighted Pair-group Method with Arithmetic Mean) and produce an alignment MSA1 following TREE1. (2) Compute the Kimura distance matrix from MSA1 to produce a guide tree TREE2 and an accurate alignment. (3) Firstly, delete an edge near the root node on Tree2, generate two subtrees and calculate the subtree profiles [89]. Then, realign two profiles and obtain a new alignment. If the Sum-of-Pairs (SP) score of the alignment is higher than before, retain the alignment; otherwise, discard it. Finally, repeat this step until the accuracy reaches the criterion.
![The flow chart of MUSCLE [15].](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/bib/23/3/10.1093_bib_bbac069/1/m_bbac069f6.jpeg?Expires=1750222030&Signature=2EDvoYeF6gwQ6m6FJC7tswuIor6gAFgicjOjdkzMsbsg-6t6~4jIUBaWWuhHFxLMcmVzTG6PuqYh3EA6kkCvR2shQhhnH~N8d5J-9cWUsg6qILK~eKB39lLcwavTuO1iUM-s7FdChrQGD52onEsaGNBTFCf10ZocScONxVVZf8jsGLHay53~P0p6XTuwJLpPP4c33Tt1m44U6djYCiXKJ3lOnDLkkpKrAhbArn9cLqhsd6TI1qY6Nfn2Vi4Gg-7vp9vBGjA1ceNKwG57OUOmKOURv3p2Jg7pKhNR2WbwtrWydJvhlWe1w~428qnsZ5K~9929XjhlaNojKLfwx8i2Vg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
To reduce the time cost, Katoh et al. developed MAFFT (Multiple Alignment based on Fast Fourier Transform) in 2002 [14, 90]. MAFFT uses Fourier transform to convert the sequence into a vector for processing, which simplifies the calculation process of the algorithm. The most significant advantage is that it can quickly identify the homologous region and shorten the overall time of the program. The results demonstrate that MAFFT in iterative refinement mode is over 100 times faster than T-Coffee when more than 60 sequences are without accuracy.
Due to the lack of accuracy in phylogeny, Liu et al. [85] proposed SATé, which first applies the affine gap penalty to POY (a phylogenetic analysis program) in 2009. Compared with ClustalW, SATé has higher efficiency while searching short alignment or tree pairs. Besides, its constructed tree is also more accurate than ClustalW. Furthermore, Liu et al. [91] proposed the 2nd version of SATé in 2012. The method adopts a different divide-and-conquer from the previous one to produce smaller related subsets. Therefore, Saté-II is superior to SATé-I in both performance and accuracy. In 2015, Mirarabet et al. [86] proposed PASTA based on SATé, and this method adopts a parallel strategy to expand the scale of SA.
To fast construct the codon-correct alignment, Libin et al. proposed VIRULIGN [87] concerning the characteristics of mutual conversion between codons and amino acids in 2019. Specifically, firstly, VIRULIGN computes pairwise alignments between each target sequence and the reference sequence. Secondly, the same as the first step, calculate the alignment between the target sequence and the reference sequence represented by amino acid. Then adjust the target sequence according to the difference between the two alignments produced in the 1st and 2nd steps. Finally, repeat from the 2nd step until no more differences are detected. Recently, Moshiri proposed ViralMSA to adopt the reference-guide strategy [88], which aims to align the whole genome in real-time. Moshiri claims that ViralMSA is orders of magnitude faster than VIRULIGN.
Compared with the progressive alignment algorithm, the most significant advantage of the iterative algorithm is that it can improve the alignment result, has good robustness and is insensitive to the number of sequences. However, the drawback is that it is easy to fall into the local optimization.
Heuristics algorithm
A heuristics algorithm is a stochastic iterative algorithm in a broad sense. The main idea is to calculate each feasible solution of the combinatorial optimization problem within the acceptable range of time or space. Heuristics have good performance in solving NP-complete problems, and it can be roughly divided into the genetic algorithm, swarm intelligence, simulated annealing, hidden Markov model (HMM) and meta-heuristics [92].
Simulated annealing
Simulated annealing originates from the principle of solid annealing. When the stable temperature rises, the internal particles become disordered, and when the temperature drops, the particles will gradually become an ordered state. Therefore, a simulated annealing algorithm is often used in combinatorial optimization problems [93].
In 1993, Ishikawa et al. [94] first proposed using simulated annealing to solve MSA. The results demonstrate that the method can get a better solution in a specific time than the traditional progressive alignment algorithm. In addition, this method lays the foundation for the subsequent process based on simulated annealing. For example, Hernndez-Gua et al. [95] described another simulated annealing-based way in 2005. They use the mapping between MSA and Directed Polymer in a Random Media [96] to allow the insertion or deletion of gaps in the process of modifying alignment and expand the space of feasible solutions.
Due to the slow convergence speed of the simulated annealing algorithm, it is often necessary to combine genetic algorithms or swarm intelligence algorithms to improve efficiency.
Genetic algorithm
A genetic algorithm is a method to simulate biological evolution in nature. It transforms the problem-solving process into gene selection, crossover, mutation and other techniques similar to natural chromosomes and obtains better optimization results through multiple iterations [97]. The relative algorithms are shown in Table 4.
| References . | Description . | Year . |
|---|---|---|
| [16] | Affine gap penalty, crossover, mutation | 1996 |
| [98] | String, simultaneousness, automated processing | 1997 |
| [99] | Divide-and-conquer, dynamic programming | 2005 |
| [100] | Global criterion for SA, evolutionary computation | 2009 |
| [101] | Multi-objective, structural information, non-gaps percentage totally conserved columns | 2013 |
| [102] | Multi-objective, affine gap penalty, similarity, support maximization | 2014 |
| [103] | Chaotic sequences, logistic map | 2016 |
| [104] | Chemical reaction optimization, single-point operator | 2019 |
| [105] | Optimization algorithm, gap insertion mutation, gap removal mutation | 2020 |
| [106] | Bi-objective, integer coding, Wilcoxon sign test | 2020 |
| References . | Description . | Year . |
|---|---|---|
| [16] | Affine gap penalty, crossover, mutation | 1996 |
| [98] | String, simultaneousness, automated processing | 1997 |
| [99] | Divide-and-conquer, dynamic programming | 2005 |
| [100] | Global criterion for SA, evolutionary computation | 2009 |
| [101] | Multi-objective, structural information, non-gaps percentage totally conserved columns | 2013 |
| [102] | Multi-objective, affine gap penalty, similarity, support maximization | 2014 |
| [103] | Chaotic sequences, logistic map | 2016 |
| [104] | Chemical reaction optimization, single-point operator | 2019 |
| [105] | Optimization algorithm, gap insertion mutation, gap removal mutation | 2020 |
| [106] | Bi-objective, integer coding, Wilcoxon sign test | 2020 |
| References . | Description . | Year . |
|---|---|---|
| [16] | Affine gap penalty, crossover, mutation | 1996 |
| [98] | String, simultaneousness, automated processing | 1997 |
| [99] | Divide-and-conquer, dynamic programming | 2005 |
| [100] | Global criterion for SA, evolutionary computation | 2009 |
| [101] | Multi-objective, structural information, non-gaps percentage totally conserved columns | 2013 |
| [102] | Multi-objective, affine gap penalty, similarity, support maximization | 2014 |
| [103] | Chaotic sequences, logistic map | 2016 |
| [104] | Chemical reaction optimization, single-point operator | 2019 |
| [105] | Optimization algorithm, gap insertion mutation, gap removal mutation | 2020 |
| [106] | Bi-objective, integer coding, Wilcoxon sign test | 2020 |
| References . | Description . | Year . |
|---|---|---|
| [16] | Affine gap penalty, crossover, mutation | 1996 |
| [98] | String, simultaneousness, automated processing | 1997 |
| [99] | Divide-and-conquer, dynamic programming | 2005 |
| [100] | Global criterion for SA, evolutionary computation | 2009 |
| [101] | Multi-objective, structural information, non-gaps percentage totally conserved columns | 2013 |
| [102] | Multi-objective, affine gap penalty, similarity, support maximization | 2014 |
| [103] | Chaotic sequences, logistic map | 2016 |
| [104] | Chemical reaction optimization, single-point operator | 2019 |
| [105] | Optimization algorithm, gap insertion mutation, gap removal mutation | 2020 |
| [106] | Bi-objective, integer coding, Wilcoxon sign test | 2020 |
Notredame and Higgins [16] first proposed and developed Sequence Alignment by Genetic Algorithm (SAGA) based on genetic algorithm in 1996. The method continuously optimizes the alignment through crossover and insertion operations until the alignment does not change, as shown in Figure 7. The result indicates that SAGA is suitable for most objective functions and can achieve better alignment. Different from SAGA, Chen et al. proposed a method combining genetic algorithm, divide-and-conquer algorithm and dynamic programming [99]. The method divides the sequences vertically into multiple subsequences by a genetic algorithm. Then compute the sub-alignments of all subsequences using dynamic programming. Finally, splice the sub-alignments into a complete alignment.
![The figure explains how to use the existing alignment to generate a better alignment in SAGA. Given two alignments, two new alignments are combined by crossing and inserting gaps. Finally, the better one is selected to join the next generation [16].](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/bib/23/3/10.1093_bib_bbac069/1/m_bbac069f7.jpeg?Expires=1750222030&Signature=P0adFw2K0nl9t202IIZg12yo~Uku-9sTC0US6cvVOdcaYYvQ4-acNUIVhK-f2vXCsz4CSHkuEu5zPC7eE9Jt6gZ8GbBHU4Tslg~JALOVEyywHiHtnXZgxZ9e5F1r9DlbzOP~cL-StaHiTqrRIo2qA4sdgvDJwGYtczQXwvfWI72gFMo4uDdrq2IJRxpSi3O~5iZHKEmt4lGHGvRZDY-a7FkgY3UHYHcIM5IrEszw8tGUHs-LCqxAY6yJNGB0-8KOF2DocI9YYWS2kh1Wjq5HrLuOnEFZ9iqEEgfBGojR7qO1DQ8n4tbb6A0bhbSHeJl-eXo0ZxWDRFBdd8z3MeqVrQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The figure explains how to use the existing alignment to generate a better alignment in SAGA. Given two alignments, two new alignments are combined by crossing and inserting gaps. Finally, the better one is selected to join the next generation [16].
Some efforts also focus on the objective function to improve genetic algorithm. For example, Arenas-Daz and Ochoterena proposed a new objective function GLObal Criterion for Sequence Alignment (GLOCSA), in 2009. Experiments show that GLOCSA can effectively improve the performance of the alignment [100]. Later, Ortuno applied a multi-objective function to the genetic algorithm, and the result indicates that the genetic algorithm with multi-objective function has more obvious advantages than the traditional genetic algorithm [101].
Moreover, Gao et al. adopted a chaos algorithm to optimize the genetic algorithm in 2016., the premature phenomenon in the genetic algorithm is effectively solved Using the ergodicity and inherent randomness of chaotic iteration [103]. Different from Gao’s method, Chatterjee uses a chemical reaction optimization algorithm to optimize the population in the evolution process, thus improving the efficiency [104]. In addition, there also are some genetic algorithm-based methods, such as Mishra et al. [105] present progressive technique to enhance the value of the alignment, and Chowdhury et al. [106] combine with bi-objective function to optimize the selection.
The genetic algorithm can give feasible solutions in a particular time, but the most feasible solutions are local optimal solutions. Therefore, the genetic algorithm needs to be combined with other algorithms to improve stability and accuracy.
Swarm intelligence algorithm
Swarm intelligence algorithm simulates the biological behavior of groups such as insects, animals or birds in nature. By definition, any algorithm or strategy inspired by natural behavior can be regarded as a swarm intelligence algorithm. Since the advent of the swarm intelligence algorithm, dozens of algorithms have been derived, including ant colony algorithm, particle swarm optimization (PSO) and artificial bee colony. In the field of MSA, swarm intelligence optimization is also applied, as shown in Table 5.
| References . | Description . | Year . |
|---|---|---|
| [107] | Binary SAGA | 2009 |
| [108] | Dispersion graph, ant colony | 2009 |
| [109] | Ant colony, genetic algorithm, planar graph | 2010 |
| [110] | SAGA | 2011 |
| [111] | Artificial fish swarm | 2014 |
| [112] | Bacterial foraging optimization, genetic algorithm | 2017 |
| [113] | SAGA, simulated annealing | 2018 |
| [114] | Multi-strategy artificial bee colony | 2018 |
| [115] | Flower pollination algorithm, profile algorithm | 2019 |
| [116] | Multi-objective, artificial fish swarm | 2020 |
| [117] | WOAMSA, whale optimization algorithm | 2020 |
| [118] | Meta-heuristic, dynamic programming, dynamic simulated SAGA | 2021 |
| References . | Description . | Year . |
|---|---|---|
| [107] | Binary SAGA | 2009 |
| [108] | Dispersion graph, ant colony | 2009 |
| [109] | Ant colony, genetic algorithm, planar graph | 2010 |
| [110] | SAGA | 2011 |
| [111] | Artificial fish swarm | 2014 |
| [112] | Bacterial foraging optimization, genetic algorithm | 2017 |
| [113] | SAGA, simulated annealing | 2018 |
| [114] | Multi-strategy artificial bee colony | 2018 |
| [115] | Flower pollination algorithm, profile algorithm | 2019 |
| [116] | Multi-objective, artificial fish swarm | 2020 |
| [117] | WOAMSA, whale optimization algorithm | 2020 |
| [118] | Meta-heuristic, dynamic programming, dynamic simulated SAGA | 2021 |
| References . | Description . | Year . |
|---|---|---|
| [107] | Binary SAGA | 2009 |
| [108] | Dispersion graph, ant colony | 2009 |
| [109] | Ant colony, genetic algorithm, planar graph | 2010 |
| [110] | SAGA | 2011 |
| [111] | Artificial fish swarm | 2014 |
| [112] | Bacterial foraging optimization, genetic algorithm | 2017 |
| [113] | SAGA, simulated annealing | 2018 |
| [114] | Multi-strategy artificial bee colony | 2018 |
| [115] | Flower pollination algorithm, profile algorithm | 2019 |
| [116] | Multi-objective, artificial fish swarm | 2020 |
| [117] | WOAMSA, whale optimization algorithm | 2020 |
| [118] | Meta-heuristic, dynamic programming, dynamic simulated SAGA | 2021 |
| References . | Description . | Year . |
|---|---|---|
| [107] | Binary SAGA | 2009 |
| [108] | Dispersion graph, ant colony | 2009 |
| [109] | Ant colony, genetic algorithm, planar graph | 2010 |
| [110] | SAGA | 2011 |
| [111] | Artificial fish swarm | 2014 |
| [112] | Bacterial foraging optimization, genetic algorithm | 2017 |
| [113] | SAGA, simulated annealing | 2018 |
| [114] | Multi-strategy artificial bee colony | 2018 |
| [115] | Flower pollination algorithm, profile algorithm | 2019 |
| [116] | Multi-objective, artificial fish swarm | 2020 |
| [117] | WOAMSA, whale optimization algorithm | 2020 |
| [118] | Meta-heuristic, dynamic programming, dynamic simulated SAGA | 2021 |
Long et al. [107] described an MSA method based on binary SAGA in 2009. This method starts with multiple alignments and then continuously modifies each alignment until convergence. The results show that most of the alignment scores of their ways are better than ClustalW, DiAlign, SAGA and T-Coffee. Besides, Chaabane proposed Particle Swarm Optimization and Simulated Annealing (PSOSA) hybrid model in 2018 [113], which combines PSO and simulated annealing to fully use the former’s exploration ability and the latter’s development ability. The experiment shows that the performance is better than MUSCLE, MAFFT and ClustalW programs.
In addition to PSO, there are many optimization algorithms based on animal behavior in MSA. For example, in 2009, Chen et al. proposed an ant colony algorithm-based method [108]. They use a dispersion graph to represent the alignment and then an ant colony algorithm to find an optimal path. The experimental results show that this method can obtain a better solution than ClustalX. Meanwhile, Xiang et al. [109] proposed a similar approach based on genetic algorithm and planar graph to optimize the search path. Kuang et al. [114] proposed an artificial bee colony-based method that adopts a multi-strategy to balance the global exploration and the local exploitation in 2018. The strategies include the following three aspects: tent chaos initialization population, neighborhood search and tournament selection. The results show that this method has better performance and biological characteristics and has strong robustness.
Some studies also adopt less commonly used algorithms. In 2017, Manikandan and Duraisamy proposed a method combining a bacterial foraging algorithm and genetic algorithm based on the dispersion optimization principle of the individual and population of Escherichia coli[112]. They obtain individuals with higher fitness through bacterial foraging behavior to improve accuracy and speed. The result shows that this method is better than other swarm intelligence algorithms on multiple benchmarks. In 2019, Hussein et al. adopted the flower pollination algorithm to optimize the MSA [115]. Besides, they also proposed a new profile algorithm to improve alignment quality. Finally, compared with other methods, this method is superior to other ways except for the MSAProbs.
Hidden Markov model
The HMM) is a statistical analysis model, which is used to describe a Markov process with unknown parameters [119]. In short, HMM can calculate the state transition probability matrix by analyzing the object’s previous and current observable states and inferring the next state of the object through the probability matrix. Due to the Markov property of MSA, some researchers proposed several MSA methods based on HMM, as shown in Table 6.
| References . | Description . | Year . |
|---|---|---|
| [17] | ProbCons, probabilistic consistency-based | 2005 |
| [120] | MUMMALS, local structural information | 2006 |
| [121] | PROMALS, database search, secondary structure prediction | 2007 |
| [122] | MSAProbs, partition function | 2010 |
| [123] | Clustal Omega, mBed, profile | 2011 |
| [124] | RDPSO, SAGA | 2014 |
| [125] | ProbPFP, SAGA | 2019 |
| References . | Description . | Year . |
|---|---|---|
| [17] | ProbCons, probabilistic consistency-based | 2005 |
| [120] | MUMMALS, local structural information | 2006 |
| [121] | PROMALS, database search, secondary structure prediction | 2007 |
| [122] | MSAProbs, partition function | 2010 |
| [123] | Clustal Omega, mBed, profile | 2011 |
| [124] | RDPSO, SAGA | 2014 |
| [125] | ProbPFP, SAGA | 2019 |
| References . | Description . | Year . |
|---|---|---|
| [17] | ProbCons, probabilistic consistency-based | 2005 |
| [120] | MUMMALS, local structural information | 2006 |
| [121] | PROMALS, database search, secondary structure prediction | 2007 |
| [122] | MSAProbs, partition function | 2010 |
| [123] | Clustal Omega, mBed, profile | 2011 |
| [124] | RDPSO, SAGA | 2014 |
| [125] | ProbPFP, SAGA | 2019 |
| References . | Description . | Year . |
|---|---|---|
| [17] | ProbCons, probabilistic consistency-based | 2005 |
| [120] | MUMMALS, local structural information | 2006 |
| [121] | PROMALS, database search, secondary structure prediction | 2007 |
| [122] | MSAProbs, partition function | 2010 |
| [123] | Clustal Omega, mBed, profile | 2011 |
| [124] | RDPSO, SAGA | 2014 |
| [125] | ProbPFP, SAGA | 2019 |
ProCons (Probabilistic Consistency) is the first program to use HMM for MSA, developed by Do et al. in 2005 [17]. ProCons adopts a novel objective function based on probability consistency, which combines the posterior probability matrix derived from HMM and the alignment consistency to integrate the conservative information of sequences. From the results, ProCons is more accurate than Align-m, ClustalW, MUSCLE and other programs. In 2006, Roshan and Livesay made some improvements based on ProCons and proposed Probalign (Probabilistic alignment) [84]. The difference is that ProCons uses the matched partition function interested of HMM to calculate the posterior probability matrix.
Efficient computation with high accuracy is an urgent need. Therefore, to solve this problem, Liu et al. [122] developed a program, MASProbs based on ProCons and Proalign. To enhance the performance, MSAProbs calculates the weight of the sequence, which participates in the calculation of probability consistency score and progressive alignment. The result shows that MASProbs has higher accuracy than ClustalW, MAFFT, MUSCLE, ProCons and Probalign. Since then, the author proposed MSAProbs-MPI, which introduces parallel and distributed memory based on MSAProbs and can cope with larger datasets [126, 127]. In 2019, Zhan et al. [125] proposed the ProbPFP method, which mainly refers to the above techniques. However, ProbPFP is unique in that it introduces PSO to optimize the parameters of HMM model.
ClustalW has great limitations in large-scale data; therefore, Sievers et al. developed Clustal Omega in 2011. Clustal Omega is based on the mBed algorithm and HMM. Clustal Omega can process tens of thousands of sequences, and its accuracy is greatly improved. Besides, to improve the alignment efficiency, Clustal Omega can use the existing alignment in the database to assist new sequences alignment [123, 128]. In 2020, Pachetti et al. [129] applied clustal Omega to the MSA of genomes of SARS-CoV-2 and found eight new recurrent mutations of virus.
Machine learning
Machine learning is still in the initial stage in MSA. In 2016, Mircea et al. [18] first proposed an MSA method based on reinforcement learning. This method is similar to the progressive alignment algorithm to find an optimal alignment order and then align the sequences in order. They use a reinforcement learning method based on dynamic programming–Q-learning to calculate the optimal alignment order of sequences and use this order to construct the alignment gradually. In 2019, Jafari et al. [20] replaced Q-learning with the A3C (Asynchronous Advantage Actor Critic) model in deep reinforcement learning based on Mircea, which improved the convergence speed and reduced the possibility of falling into local optimum to a certain extent.
Then, Ramakrishnan et al. [19] proposed an MSA method based A3Cin 2018, called RLALIGN. Unlike Mircea’s method, RLALIGN takes the current alignment as the state and the moving direction of the nucleotide in the alignment as the action. Although this method can better align some small datasets, the process may not converge with the sequence number or length increase.
Machine learning has valuable achievements in many fields of bioinformatics, but there is more work to be done across MSA. In particular, there are three challenges: (1) lack of sufficient optimal alignment samples for learning. (2) There is no suitable loss function. (3) It is challenging to build a generalized model due to the variability of the length and quantity of sequences.
Divide-and-conquer algorithm
Divide-and-conquer is a relatively simple algorithm whose idea is to break down a whole problem into multiple independent sub-problems of the related or same type for processing. The divide-and-conquer algorithm is a standard solution for solving MSA, and the relevant methods are shown in Table 7.
Zhan et al. [21] proposed an optimization method for MSA based on splitting and splicing in 2020, which is called SpliVert (Splitting-splicing Vertically). The process is as shown in Figure 8. Firstly, obtain an alignment by other MSA methods. Second, divide the alignment into three parts from the vertical direction and then remove the gap in the middle part and realign the part. Finally, merge the three regions and obtain the refined alignment. The experiment shows that the alignment optimized is better than those obtained by the original MSA method or program.
![This picture explains the optimization process of SpliVert. The general process can be summarized to four steps: compute the alignment, split the alignment, realign the middle part and merge these parts into alignment [21].](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/bib/23/3/10.1093_bib_bbac069/1/m_bbac069f8.jpeg?Expires=1750222030&Signature=wApx2euKsORoTaSzTKGvhnnEh~uU8N2sg7s33qSpasarr13raFoc0VJOlch8t5KWZkIyN6OVftsI8adXucJIqbyDjzpY1xOLD~snCtFzAwcqUCBO0HpN0Oks7FHLi55L1j5jy5d88oHvXvRrohwGUo01-EMY~tHKsFgY~l5-EqU-IMdMLxkmMapBaJxLkTkgFwg7kQdlyJIw9XlG3u104SyngwKURR22lWwX9tPQuqDlV64DoJvQeVuAMVmUX-KvkMr-dIIN1jZm3bMv~~VZkhzAxaXvs2ozShdyOgJI-bu2cn2TxBj1KH551AJOkGkQywFvTd0fNMfSvD2XCJwXPw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
This picture explains the optimization process of SpliVert. The general process can be summarized to four steps: compute the alignment, split the alignment, realign the middle part and merge these parts into alignment [21].
To reduce the time and memory consumption of long SA, Naznooshsadat et al. [22] proposed FAME (FAst and MEmory), an MSA method based on splitting and splicing. Its process consists of the following three steps: (1) divide the set of sequences into groups of subsequences vertically and maintain the order of these subsequences on the original sequences. (2) Align the subsequence at common regions and align the unaligned subsequence with other MSA methods. (3) Merge all aligned subsequences. The results show that the FAME can process large-scale data four times faster than the original method.
The alignment method for large-scale sequences has always been a hot spot. For example, Smirnov et al. [130] proposed an MSA method based on graph clustering and divide-and-conquer algorithm—MAGUS (MSA using Graph clUStering) in 2021. This method is similar to PASTA. It also introduces divide-and-conquer to construct the alignment. The difference between PASTA and MAGUS lies in the merging stage of the subset. Smirnov uses a merging strategy of combining disjoint alignment—GMC (Graph Clustering Merge) to merge subsets. In addition, benefit from GMC, MAGUS does not need iteration to improve accuracy like PASTA. Their experiments show that the method has strong robustness, and it not only improves the accuracy and exceeds PASTA in speed. Furthermore, Shen et al. [132] introduced HMM based on Smirnov’s work to further enhance the accuracy of alignment in 2021.
What’s more, Liu et al. proposed a technique, FMAlign, which is based on divide-and-conquer and FM-index. Their method has four steps: 1. building FM-index; 2. querying anchors; 3. finding optimal chain; 4. breaking sequence and aligning. Compared with MAFFT, Halign and FAME, FMAlign has a shorter running time and higher accuracy on long sequences. Besides, their results show that FMAlign is applicable to large-scale sequences alignment [131].
Because divide-and-conquer can divide a whole problem into multiple sub-problems that can be handled directly, its performance has apparent advantages over other algorithms. In addition, the algorithm can flexibly combine with parallel techniques to further improve performance because these sub-problems have the same or similar types and are independent.
Objective functions
The total column (TC) score is a relatively simple evaluation metric indicating the similarity between two alignments. The score is the ratio of correctly aligned columns between the test alignment and the reference alignment to the total number of columns in the reference alignment [134]. Take two alignments in Figure 9 as an example. There are three correctly aligned columns (1st, 2nd and 5th) and six TCs. Therefore, the TC score is 0.5 (3 divided by 6). The value range of the TC score is |$[0,1]$|. The higher the value, the more agreement the test alignment with the reference alignment.
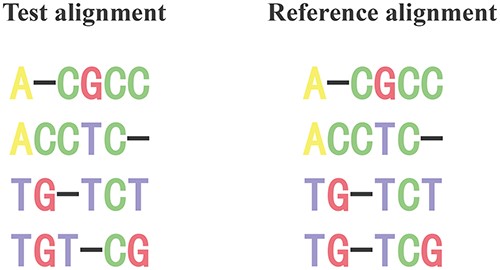
Two alignments for illustrating the calculation of TC score. In this figure, there are three correctly aligned columns (1st, 2nd and 5th) and six TCs. Therefore, TC score is 0.5 (3 divided by 6).
Programs
The commonly used programs for MSA include ClustalW, MUSCLE, MAFFT and T-Coffee, which are shown in Table 8.
| Programs . | Year . | Website . |
|---|---|---|
| ClustalW | 1994 | http://www.clustal.org/ |
| DiAlign | 1998 | http://dialign.gobics.de/ |
| T-Coffee | 2000 | http://tcoffee.crg.cat/ |
| MAFFT | 2002 | https://mafft.cbrc.jp/alignment/software/ |
| MUSCLE | 2004 | http://www.drive5.com/muscle/ |
| ProbCons | 2005 | http://probcons.stanford.edu/ |
| Kalign | 2005 | https://www.ebi.ac.uk/Tools/msa/kalign/ |
| Probalign | 2006 | http://probalign.njit.edu/standalone.html |
| PRANK | 2008 | http://wasabiapp.org/software/prank/ |
| MSAProbs | 2010 | http://msaprobs.sourceforge.net/ |
| NX4 | 2019 | https://www.nx4.io |
| FAME | 2020 | http://github.com/naznoosh/msa |
| Programs . | Year . | Website . |
|---|---|---|
| ClustalW | 1994 | http://www.clustal.org/ |
| DiAlign | 1998 | http://dialign.gobics.de/ |
| T-Coffee | 2000 | http://tcoffee.crg.cat/ |
| MAFFT | 2002 | https://mafft.cbrc.jp/alignment/software/ |
| MUSCLE | 2004 | http://www.drive5.com/muscle/ |
| ProbCons | 2005 | http://probcons.stanford.edu/ |
| Kalign | 2005 | https://www.ebi.ac.uk/Tools/msa/kalign/ |
| Probalign | 2006 | http://probalign.njit.edu/standalone.html |
| PRANK | 2008 | http://wasabiapp.org/software/prank/ |
| MSAProbs | 2010 | http://msaprobs.sourceforge.net/ |
| NX4 | 2019 | https://www.nx4.io |
| FAME | 2020 | http://github.com/naznoosh/msa |
| Programs . | Year . | Website . |
|---|---|---|
| ClustalW | 1994 | http://www.clustal.org/ |
| DiAlign | 1998 | http://dialign.gobics.de/ |
| T-Coffee | 2000 | http://tcoffee.crg.cat/ |
| MAFFT | 2002 | https://mafft.cbrc.jp/alignment/software/ |
| MUSCLE | 2004 | http://www.drive5.com/muscle/ |
| ProbCons | 2005 | http://probcons.stanford.edu/ |
| Kalign | 2005 | https://www.ebi.ac.uk/Tools/msa/kalign/ |
| Probalign | 2006 | http://probalign.njit.edu/standalone.html |
| PRANK | 2008 | http://wasabiapp.org/software/prank/ |
| MSAProbs | 2010 | http://msaprobs.sourceforge.net/ |
| NX4 | 2019 | https://www.nx4.io |
| FAME | 2020 | http://github.com/naznoosh/msa |
| Programs . | Year . | Website . |
|---|---|---|
| ClustalW | 1994 | http://www.clustal.org/ |
| DiAlign | 1998 | http://dialign.gobics.de/ |
| T-Coffee | 2000 | http://tcoffee.crg.cat/ |
| MAFFT | 2002 | https://mafft.cbrc.jp/alignment/software/ |
| MUSCLE | 2004 | http://www.drive5.com/muscle/ |
| ProbCons | 2005 | http://probcons.stanford.edu/ |
| Kalign | 2005 | https://www.ebi.ac.uk/Tools/msa/kalign/ |
| Probalign | 2006 | http://probalign.njit.edu/standalone.html |
| PRANK | 2008 | http://wasabiapp.org/software/prank/ |
| MSAProbs | 2010 | http://msaprobs.sourceforge.net/ |
| NX4 | 2019 | https://www.nx4.io |
| FAME | 2020 | http://github.com/naznoosh/msa |
Among the MSA programs, Clustal is the earliest program used for MSA and now, its improved version ClustalW is still commonly used. ClustalW adopts a simple progressive alignment algorithm [11], which can not guarantee the optimal alignment. MUSCLE is an MSA program based on progressive and iterative algorithm [15], which is also one of the fastest MSA programs at present. MUSCLE is better than ClustalW in speed and accuracy. For example, for 10 000 sequences with a length of 350|$bp$|, MUSCLE can compute the alignment in >10 min, whereas ClustalW may take 1 year.
MAFFT is the first program to adopt fast Fourier transform in MSA. The first version of MAFFT was released in 2002 [14]. MAFFT adds various options and alignment modes, such as FFT-NS-1, FFT-NS-2 and FFT-NS-i and researchers can select appropriate options for different occasions. In alignment accuracy, MAFFT is higher than MUSCLE. T-Coffee is one of the most popular programs [71], which has high scalability and abundant functions. T-Coffee can integrate various sequences information during alignment, so its accuracy is more elevated than ClustalW, MUSCLE and MAFFT.
Benchmarks
Benchmark is the golden criterion for judging the MSA method. Table 9 [123] lists the benchmarking results of the popular MSA programs on BAliBASE (Benchmark Alignment dataBASE) [135]. BAliBASE consists of five groups of references, containing 82, 41, 30 and 16 alignments, respectively. Besides, the first group is divided into two subgroups, R1-1 and R1-2, which contain 38 and 44 alignments, respectively. In Table 9. the TC scores of each reference are in columns 2–7. The average TC score general references are given in the second last column and the total run time for all references is given in the last column. The value range of the TC score is |$[0,1]$| and the higher the value, the more agreement the result of the program with the benchmark. As can be seen from the table, MSAProbs has the highest accuracy, but its run time is higher than most programs. Kalign has the shortest run time, but the accuracy is not satisfactory. The worst program is PRANK, which runs much longer than other programs and has a lower score and run time.
Summary of the benchmarking results of several MSA program on BAliBASE 3.0 [123]
| Program . | R1-1 . | R1-2 . | R2 . | R3 . | R4 . | R5 . | Avg Score . | Tot time(s) . |
|---|---|---|---|---|---|---|---|---|
| MSAProbs [122] | 0.441 | 0.865 | 0.464 | 0.607 | 0.622 | 0.608 | 0.607 | 12382.00 |
| Probalign [84] | 0.453 | 0.862 | 0.439 | 0.566 | 0.603 | 0.549 | 0.589 | 10095.20 |
| MAFFT [14] | 0.439 | 0.831 | 0.450 | 0.581 | 0.605 | 0.591 | 0.588 | 1475.40 |
| Probcons [17] | 0.417 | 0.855 | 0.406 | 0.544 | 0.532 | 0.573 | 0.558 | 13086.30 |
| Clustal Omega [123] | 0.358 | 0.789 | 0.450 | 0.575 | 0.579 | 0.533 | 0.554 | 539.91 |
| T-Coffee [71] | 0.410 | 0.848 | 0.402 | 0.491 | 0.545 | 0.587 | 0.551 | 81041.50 |
| Kalign [72] | 0.365 | 0.790 | 0.360 | 0.476 | 0.504 | 0.435 | 0.501 | 21.88 |
| MUSCLE [15] | 0.318 | 0.804 | 0.350 | 0.409 | 0.450 | 0.460 | 0.475 | 789.57 |
| FSA [136] | 0.270 | 0.818 | 0.187 | 0.259 | 0.474 | 0.398 | 0.419 | 53648.10 |
| DiAlign [12] | 0.265 | 0.696 | 0.292 | 0.312 | 0.441 | 0.425 | 0.415 | 3977.44 |
| PRANK [137] | 0.223 | 0.680 | 0.257 | 0.321 | 0.360 | 0.356 | 0.376 | 128355.00 |
| ClustalW [11] | 0.227 | 0.712 | 0.220 | 0.272 | 0.396 | 0.308 | 0.374 | 766.47 |
| Program . | R1-1 . | R1-2 . | R2 . | R3 . | R4 . | R5 . | Avg Score . | Tot time(s) . |
|---|---|---|---|---|---|---|---|---|
| MSAProbs [122] | 0.441 | 0.865 | 0.464 | 0.607 | 0.622 | 0.608 | 0.607 | 12382.00 |
| Probalign [84] | 0.453 | 0.862 | 0.439 | 0.566 | 0.603 | 0.549 | 0.589 | 10095.20 |
| MAFFT [14] | 0.439 | 0.831 | 0.450 | 0.581 | 0.605 | 0.591 | 0.588 | 1475.40 |
| Probcons [17] | 0.417 | 0.855 | 0.406 | 0.544 | 0.532 | 0.573 | 0.558 | 13086.30 |
| Clustal Omega [123] | 0.358 | 0.789 | 0.450 | 0.575 | 0.579 | 0.533 | 0.554 | 539.91 |
| T-Coffee [71] | 0.410 | 0.848 | 0.402 | 0.491 | 0.545 | 0.587 | 0.551 | 81041.50 |
| Kalign [72] | 0.365 | 0.790 | 0.360 | 0.476 | 0.504 | 0.435 | 0.501 | 21.88 |
| MUSCLE [15] | 0.318 | 0.804 | 0.350 | 0.409 | 0.450 | 0.460 | 0.475 | 789.57 |
| FSA [136] | 0.270 | 0.818 | 0.187 | 0.259 | 0.474 | 0.398 | 0.419 | 53648.10 |
| DiAlign [12] | 0.265 | 0.696 | 0.292 | 0.312 | 0.441 | 0.425 | 0.415 | 3977.44 |
| PRANK [137] | 0.223 | 0.680 | 0.257 | 0.321 | 0.360 | 0.356 | 0.376 | 128355.00 |
| ClustalW [11] | 0.227 | 0.712 | 0.220 | 0.272 | 0.396 | 0.308 | 0.374 | 766.47 |
Several benchmarking results on BAliBASE 3.0 are summarized. This table presents total column (TC) scores for six references, average TC scores on all references, and total running times. The best results in each column are put in bold.
Summary of the benchmarking results of several MSA program on BAliBASE 3.0 [123]
| Program . | R1-1 . | R1-2 . | R2 . | R3 . | R4 . | R5 . | Avg Score . | Tot time(s) . |
|---|---|---|---|---|---|---|---|---|
| MSAProbs [122] | 0.441 | 0.865 | 0.464 | 0.607 | 0.622 | 0.608 | 0.607 | 12382.00 |
| Probalign [84] | 0.453 | 0.862 | 0.439 | 0.566 | 0.603 | 0.549 | 0.589 | 10095.20 |
| MAFFT [14] | 0.439 | 0.831 | 0.450 | 0.581 | 0.605 | 0.591 | 0.588 | 1475.40 |
| Probcons [17] | 0.417 | 0.855 | 0.406 | 0.544 | 0.532 | 0.573 | 0.558 | 13086.30 |
| Clustal Omega [123] | 0.358 | 0.789 | 0.450 | 0.575 | 0.579 | 0.533 | 0.554 | 539.91 |
| T-Coffee [71] | 0.410 | 0.848 | 0.402 | 0.491 | 0.545 | 0.587 | 0.551 | 81041.50 |
| Kalign [72] | 0.365 | 0.790 | 0.360 | 0.476 | 0.504 | 0.435 | 0.501 | 21.88 |
| MUSCLE [15] | 0.318 | 0.804 | 0.350 | 0.409 | 0.450 | 0.460 | 0.475 | 789.57 |
| FSA [136] | 0.270 | 0.818 | 0.187 | 0.259 | 0.474 | 0.398 | 0.419 | 53648.10 |
| DiAlign [12] | 0.265 | 0.696 | 0.292 | 0.312 | 0.441 | 0.425 | 0.415 | 3977.44 |
| PRANK [137] | 0.223 | 0.680 | 0.257 | 0.321 | 0.360 | 0.356 | 0.376 | 128355.00 |
| ClustalW [11] | 0.227 | 0.712 | 0.220 | 0.272 | 0.396 | 0.308 | 0.374 | 766.47 |
| Program . | R1-1 . | R1-2 . | R2 . | R3 . | R4 . | R5 . | Avg Score . | Tot time(s) . |
|---|---|---|---|---|---|---|---|---|
| MSAProbs [122] | 0.441 | 0.865 | 0.464 | 0.607 | 0.622 | 0.608 | 0.607 | 12382.00 |
| Probalign [84] | 0.453 | 0.862 | 0.439 | 0.566 | 0.603 | 0.549 | 0.589 | 10095.20 |
| MAFFT [14] | 0.439 | 0.831 | 0.450 | 0.581 | 0.605 | 0.591 | 0.588 | 1475.40 |
| Probcons [17] | 0.417 | 0.855 | 0.406 | 0.544 | 0.532 | 0.573 | 0.558 | 13086.30 |
| Clustal Omega [123] | 0.358 | 0.789 | 0.450 | 0.575 | 0.579 | 0.533 | 0.554 | 539.91 |
| T-Coffee [71] | 0.410 | 0.848 | 0.402 | 0.491 | 0.545 | 0.587 | 0.551 | 81041.50 |
| Kalign [72] | 0.365 | 0.790 | 0.360 | 0.476 | 0.504 | 0.435 | 0.501 | 21.88 |
| MUSCLE [15] | 0.318 | 0.804 | 0.350 | 0.409 | 0.450 | 0.460 | 0.475 | 789.57 |
| FSA [136] | 0.270 | 0.818 | 0.187 | 0.259 | 0.474 | 0.398 | 0.419 | 53648.10 |
| DiAlign [12] | 0.265 | 0.696 | 0.292 | 0.312 | 0.441 | 0.425 | 0.415 | 3977.44 |
| PRANK [137] | 0.223 | 0.680 | 0.257 | 0.321 | 0.360 | 0.356 | 0.376 | 128355.00 |
| ClustalW [11] | 0.227 | 0.712 | 0.220 | 0.272 | 0.396 | 0.308 | 0.374 | 766.47 |
Several benchmarking results on BAliBASE 3.0 are summarized. This table presents total column (TC) scores for six references, average TC scores on all references, and total running times. The best results in each column are put in bold.
Currently, the most used benchmark is BAliBASE [135], which provides multiple reference sets that have been optimized. Up to now, BAliBASE has three versions. The 1st version provides four reference sets, each containing multiple reference alignments. The 2nd version provides eight reference sets, and the 3rd version adds an update protocol to allow online updates of the reference set. In addition to BAliBASE, other common benchmark sets include SABMark (Sequence Alignment BenchMark) [138], OXBench (OXford Benchmark) [139], SMART (Simple Modular Architecture Research Tool) [140], PREFAB (Protein REFerence Alignment Benchmark) [15] and QuanTest [141].
Challenges and opportunities
Although the existing methods for MSA can cope with the most alignment tasks, these methods are not good enough to provide comprehensive solutions for any analysis scenario in any condition. There are still some challenges and opportunities for future directions.
Scale of sequence
Compared with small-scale and straightforward data in most bioinformatics fields, the MSA data may have a large discrepancy in the scale of each alignment. At the same time, with the rapid accumulation of sequences, MSA may face hyper-scale sequences. For example, Koyama et al. [142] collected >10 000 genomes to analyze the variation of SARS-CoV-2. However, the existing MSA methods are challenging to cope with hyper-scale sequences. Even if possible, these methods have low accuracy or high consumption of memory and time. This problem is a big challenge to develop a technique that can deal with hyper-scale sequences while ensuring accuracy and consumption.
Design of method
Most MSA methods are flexible and complicated. Various efforts are made to improve accuracy and performance, and several works adopt more complex machine learning, such as reinforcement learning and natural language processing. In real-life sequence analysis scenarios, the scale and length of sequences may differ, requiring that the method has good generalization ability and robustness to ensure accuracy. In addition, using friendly visualization technology is also essential for users. Making the MSA method more reliable and usable is a promising issue.
Correctness of alignment
The correctness-sensitive biological sequence analysis scenarios put forward higher requirements for the biological correctness of alignment. The most existing MSA methods are difficult to predict the evolution process of sequences correctly and lack explanations. For these problems, there are three main reasons as follows: the randomness of the evolutionary process, the limitations of the bioinformatics method and the lack of an accurate evolutionary model [143]. Therefore, focusing on the above points is more helpful for applying MSA to biological sequence analysis scenarios.
Conclusion
MSA is widely used in many bioinformatics scenarios because it can extract potential information from sequences. In this work, we introduced the base knowledge of MSA from several aspects. Furthermore, we described representative applications of MSA for database searching, phylogenetics, genomics, metagenomics and proteomics. We also categorize and analyze the classical and state-of-the-art algorithms for MSA, such as progressive alignment, iterative algorithm, heuristics, machine learning and divide-and-conquer. Finally, We further discussed the challenges of this field and promising directions. This review will provide valuable insight and serve as a starting point for studying MSA in future research.
As many biomedical sequences have been accumulated, MSA is widely applied to extract knowledge from these massive sequences, such as evolution, structure and function.
We systematically introduce MSA’s knowledge from several aspects, including background, application, database, algorithm, metric, program and benchmark.
We also list and discuss the current challenges and opportunities for future directions in bioinformatics.
As a comprehensive review of current works, this paper will provide valuable insight and serve as a launching point for researchers in their studies.
Funding
National Natural Science Foundation of China (Grant No. 61922020).
Author Biographies
Yongqing Zhang He is an associate professor in the School of Computer Science at the Chengdu University of Information Technology. He is a senior member of CCF. His research interests include machine learning and bioinformatics.
Qiang Zhang He is a graduate student in the School of Computer Science at the Chengdu University of Information Technology. His research interests include deep learning and bioinformatics.
Jiliu Zhou He is a professor in the School of Computer Science at the Chengdu University of Information Technology. His research interests include intelligent computing and image processing.
Quan Zou He is a professor in the Institute of Fundamental and Frontier Science at the University of Electronic Science and Technology of China. He is a senior member of IEEE and ACM. His research interests include bioinformatics and machine learning.


