Search
Close
Search
Advanced Search
Search Menu
AI Discovery Assistant

Abstract

Motivation

The developmental process of epithelial-mesenchymal transition (EMT) is abnormally activated during breast cancer metastasis. Transcriptional regulatory networks that control EMT have been well studied; however, alternative RNA splicing plays a vital regulatory role during this process and the regulating mechanism needs further exploration. Because of the huge cost and complexity of biological experiments, the underlying mechanisms of alternative splicing (AS) and associated RNA-binding proteins (RBPs) that regulate the EMT process remain largely unknown. Thus, there is an urgent need to develop computational methods for predicting potential RBP-AS event associations during EMT.

Results

We developed a novel model for RBP-AS target prediction during EMT that is based on inductive matrix completion (RAIMC). Integrated RBP similarities were calculated based on RBP regulating similarity, and RBP Gaussian interaction profile (GIP) kernel similarity, while integrated AS event similarities were computed based on AS event module similarity and AS event GIP kernel similarity. Our primary objective was to complete missing or unknown RBP-AS event associations based on known associations and on integrated RBP and AS event similarities. In this paper, we identify significant RBPs for AS events during EMT and discuss potential regulating mechanisms. Our computational results confirm the effectiveness and superiority of our model over other state-of-the-art methods. Our RAIMC model achieved AUC values of 0.9587 and 0.9765 based on leave-one-out cross-validation (CV) and 5-fold CV, respectively, which are larger than the AUC values from the previous models. RAIMC is a general matrix completion framework that can be adopted to predict associations between other biological entities. We further validated the prediction performance of RAIMC on the genes CD44 and MAP3K7. RAIMC can identify the related regulating RBPs for isoforms of these two genes.

Availability and implementation

The source code for RAIMC is available at https://github.com/yushanqiu/RAIMC.

Contact

[email protected] online.

Introduction

Epithelial–mesenchymal transition (EMT) is a developmental process where epithelial cells lose their cell–cell adhesion and apical-basal polarity, thus gaining the migratory and invasive properties characteristic of mesenchymal cells [1]. Tumor cells frequently hijack the EMT developmental process to invade surrounding tissues and migrate to distant organs during metastasis [2]. Genome-wide alternative splicing (AS) analyses have revealed that dynamic changes in AS occur during EMT [3, 4]. AS is a ubiquitous regulatory mechanism of gene expression, whereby more than one unique mRNA sequences is generated from a single gene. Nearly all human genes undergo AS, and alternatively, spliced isoforms have been shown to play distinct functional roles in cells [5, 6]. AS is a complicated process in which numerous interacting components are at work, including |$cis$|-acting elements, such as exonic/intronic splicing enhancers/silencers (ESE/S, ISE/S) and |$trans$|-acting factors, such as serine arginine-rich (SR) proteins and heterogeneous nuclear ribonucleoproteins (hnRNPs), transcription, chromatin modification and RNA secondary structure, and is further guided by the functional coupling between transcription and splicing [7–9]. The |$cis$|-elements are recognized and bounded by cognate RNA-binding proteins (RBPs) to influence splice site recognition by the spliceosome. Splicing-regulatory RBPs promote or inhibit the inclusion of alternative exons in transcribed mRNAs and they frequently form complexes to modulate splicing regulatory action [7–9]. Thus, RBP-AS event associations are highly context-dependent; deciphering the ‘splicing code’ remains a challenge. The development of mathematical models and computational methods to understand RBP-AS event associations during the EMT process is urgently needed.

Until now, only a few models have been developed to predict RBP-AS event associations. Damianov et al. [10] found that hnRNPM and ESRP1 co-regulate a set of cassette exon events during EMT and Ying et al. [11] shown that RBP AKAP8 suppresses tumor metastasis by antagonizing EMT-associated AS. Shen et al. [15] used robust regression to test the correlation between RBPs and |$229$| survival associated AS events and performed a gene-exon co-expression network analysis. Qiu et al. [12] proposed to integrate bipartite network and community detection method to investigate the regulating relationships between the selected |$22$| RBPs and |$25$| AS events during EMT. However, all these methods only focused on limited RBPs or AS events to investigate their associations, a comprehensive regulating mechanism between RBPs and AS events requires further exploration. To this end, we formulate comprehensive RBP-AS event relationship prediction as a two biological entities association prediction problem. And the associations prediction for other biological entities (such as lncRNA-disease and microRNA-disease) has achieved a remarkable results and a great number of computational models have been proposed to identify potential lncRNA-disease associations [13–18]. The prediction models for lncRNA-disease association can be classified into three categories. (1) Methods that utilize machine learning models to predict potential associations. For example, Harvey et al. [13] proposed a semi-supervised learning method called LRLSLDA to identify potential lncRNA-disease associations based on Laplacian regularized least squares. This method requires a combination of two classifiers that are reasonably matched. Hu et al. [14] proposed the use of a bagging support vector machine classifier and the fusion of different data sources to predict possible lncRNA-disease associations. However, the question of how to fuse different lncRNA kernels remains a challenging problem. (2) Methods based on the assumption that similar diseases tend to be associated with functionally similar lncRNAs and vice versa [15]. For example, Qiu et al. [16] used a random walk with restart to infer lncRNA-disease associations and Chen and Yan [17] designed a heterogeneous random walk on a constructed multi-level network that integrated lncRNAs, genes and phenotypes. However, these methods use only the most important feature vector, that is, the maximum eigenvector of the known information. (3) Methods that use biological information associated with lncRNAs, such as expression profiles, genome locations and tissue specificity, to predict lncRNA-disease associations. For example, Lan et al. [18] predicted potential lncRNA-disease associations by integrating lncRNA tissue specificity and gene-lncRNA co-expression. Wu et al. [19] adopted the KATZ measure to identify potential associations that integrated lncRNA expression profiles, disease semantic similarities and a Gaussian interaction profile (GIP) kernel. However, low levels and tissue-specific expression of lncRNA limit the ability of these methods to predict all lncRNAs. Recently, Sun et al. [20] proposed an inductive matrix completion (IMC) method to predict lncRNA-disease associations (SIMCLDA) which formulated lncRNA-disease associations prediction as a recommendation system problem. SIMCLDA used the primary feature vectors based on disease–gene, gene–gene ontology and known lncRNA-disease associations to complete the association matrix and the experimental results have confirmed the superiority and reliability of SIMCLDA. However, other biological information related with lncRNA-disease associations (such as lncRNA–protein interaction) have not included in the model which may help understand biological molecular mechanisms of disease.

Although these methods have achieved remarkable results, they each have different limitations and restrictions. For instance, most of the existing models are based on the assumption that lncRNAs share high similarity will be associated with similar diseases. Furthermore, when constructing lncRNA and disease similarity kernels, most researchers use functional similarity and GIP kernel similarity for lncRNAs and semantic similarity and GIP kernel similarity for diseases. To integrate these two similarity kernels, most researchers simply accumulate them or use the corresponding averages [21, 22]. These approaches implicitly assume that each similarity contributes equally to target association prediction and does not differentiate among the quality of the different similarity kernels. Therefore, the development of effective methods for integrating multiple lncRNA and disease similarities is of great importance. In addition, it is also a challenging problem for integrating multiple RBP and AS event similarities for the RBP-AS event association prediction.

Here, we propose a new computational method for predicting RBP-AS event associations for the EMT process to understand how and to what extent RBPs regulating AS events. The development of an effective and efficient model for predicting RBP-AS event associations is a completely new challenge. Instead of equally combining the similarity matrix for RBPs and AS events, we explored how to best integrate known RBP-AS events, RBP regulating similarities, AS event module similarities and GIP kernel similarities because different sources of similarity kernels could have different impacts on the target prediction task. First, we extracted the RBP regulating similarity and GIP kernel similarity for RBPs and the AS event module similarity and GIP kernel similarity for AS events. We then employed the fast kernel learning (FKL) method to combine the similarity matrices into one single RBP similarity and AS event similarity matrix, and we used the sparse kernel model to eliminate noise for the integrated similarity matrix for RBPs and AS events, respectively. Finally, we developed modified IMC (RAIMC) using known RBP-AS event associations, integrated RBP similarity and integrated AS event similarity, to predict RBP-AS event associations.

The main contributions of this study are the following. First, we provide a novel perspective on the comprehensive determination of RBP-AS event associations during EMT. Second, we developed a novel method based on IMC with the integration of RBP regulating similarity, AS event module similarity and GIP kernel similarity. We use the FKL model and a sparse similarity model to eliminate noise in the integrated similarity kernel to predict RBP-AS event associations. Third, important RBP-AS event associations are identified and an appropriate modeling mechanism is determined. Finally, experimental results have shown that RAIMC has excellent predictive and generalization ability.

Methods

We represented the RBPs as |$RBP=\{r_i\}_{i=1}^m$| and the AS events as |$AS=\{a_j\}_{j=1}^{n}$|⁠, where |$m$| and |$n$| are the number of RBPs and AS events, respectively. The known RBP-AS event associations that we used in this study can be downloaded from [12]. The associations between |$m$| RBPs and |$n$| AS events are represented by a binary matrix |$Y\in \mathcal{R}^{m\times n}$|⁠, where each row corresponds to an RBP and each column represents an AS event. |$Y_{i,j}$| is 1 if RBP |$r_i$| is associated with AS event |$a_j$| and |$Y_{i,j}$| is 0 if the RBP-AS event relationship is unknown. Thus, predicting potential RBP-AS event associations during EMT is deemed as completing matrix |$Y$|⁠, which makes it a problem of matrix completion.

Methods overview

To infer potential RBP-AS event associations during EMT, we developed the RAIMC method based on IMC [23]. RAIMC consists of the five major steps depicted in Figure 1. Step 1: RBP regulating similarity and AS event module similarity matrices are extracted. Step 2: GIP kernels are calculated for RBPs and AS events. Step 3: the FKL method is used to combine the similarity matrices into a new integrated matrix for RBPs and AS events. Step 4: the top-|$k$| nearest neighbor model is used to eliminate noise in the integrated similarity matrix and generate the final RBP similarity and AS event similarity. Step 5: the association matrix is completed with IMC using the known RBP-AS event associations, and the final RBP similarity and AS event similarity.

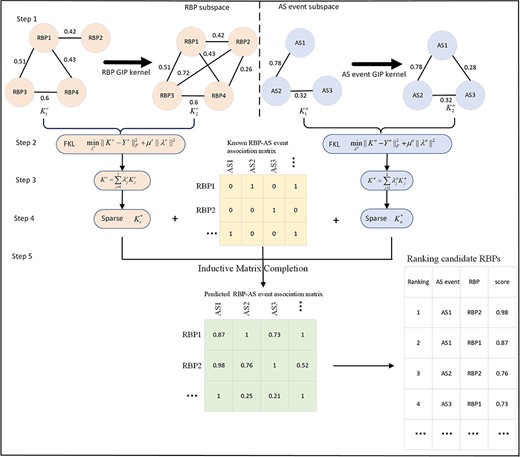
Flowchart of the RAIMC model to predict potential RBP-AS event associations. Step 1: construct RBP regulating similarity and AS event module similarity. Step 2: compute GIP for RBPs and AS events. Step 3: use FKL to combine similarity matrices. Step 4: employ top-$k$ nearest neighbor model to denoise the integrated similarity matrix. Step 5: complete the association matrix with IMC.
Figure 1

Flowchart of the RAIMC model to predict potential RBP-AS event associations. Step 1: construct RBP regulating similarity and AS event module similarity. Step 2: compute GIP for RBPs and AS events. Step 3: use FKL to combine similarity matrices. Step 4: employ top-|$k$| nearest neighbor model to denoise the integrated similarity matrix. Step 5: complete the association matrix with IMC.

Open in new tabDownload slide

RBP regulating similarity

Splicing regulating RBPs can have positive or negative effects on the inclusion of alternative exons and they frequently interact with one another in complexes to regulate splicing regulating actions [7, 8, 10]. Motivated by this, RBP regulating similarity was determined by assuming that interacting RBPs (treated as a complex) tend to regulate the same AS events and vice versa. To obtain the RBP–RBP interaction information, we imported a list of 1532 RBP names (downloaded from [24]) to the STRING database (https://string-db.org/) and generated an RBP–RBP interaction network. We extracted combined score for each interaction as RBP regulating similarity score. The STRING database is a publicly accessible database that provides comprehensive information about protein–protein interaction networks. We used the network data to construct a |$m\times m$| matrix |$K_1^r$| to represent the RBP regulating similarity network, in which |$K_1^r(r(i),r(j))$| defines the regulating similarity score between RBP |$r(i)$| and RBP |$r(j)$|⁠.

AS event module similarity

The AS event similarity was calculated by assuming that if the isoforms share the same module, the corresponding functions of the AS events would be similar. We retrieved the AS event modules from IIIDB [25], which constructs isoform–isoform interaction network clusters and catalogs 1025 isoform modules. We defined the similarity score of AS event |$A$| as
(1)
where |$M(A)$| is the set of all modules including AS event |$A$| and the contribution score of AS event |$a$| in module(A) to AS event |$A$| was defined as
(2)
Assuming that two AS events in the same module have high similarity scores, we denote the AS event module similarity as |$K_1^a\in \mathcal{R}^{n\times n}$| and the similarity score between AS event |$a(i)$| and AS event |$a(j)$| as
$$\begin{align*} &K_1^a(a(i),a(j))=\frac{\sum_{k\in M(a(i))\cap M(a(j))}(S_{a(i)}(k)+S_{a(j)}(k))}{AS(a(i))+AS(a(j))}.\end{align*}$$

GIP similarity for RBPs and AS events

Assuming that functionally similar RBPs exhibit similar interaction patterns with AS events and vice versa [10, 12, 20], we calculated GIP kernel similarity to denote the RBP latent feature space including a feature matrix. The row vector |$IP(r(i))\in \mathcal{R}^{1\times n}$| is the |$i$|-th row of the association matrix |$Y$| that is used to represent the interaction profiles of RBP |$r(i)$| by observing whether or not there is known associations between RBP |$r(i)$| and each AS event. Then, the distance between any two row vectors is computed as the GIP kernel of their corresponding RBPs as
(3)
where |$\gamma _r$| is the parameter used to control kernel bandwidth, which is normalized by the average number of associations with AS events for all RBPs and is calculated as
(4)
Similarly, GIP kernel similarity between AS event |$a(i)$| and |$a(j)$| is defined as
(5)
(6)

Integrated similarity of RBPs and AS events

Considering the fact that a single similarity matrix cannot cover all information between RBPs, we integrated |$K_1^r, K_2^r$| to get a new integrated similarity matrix |$K_r\in \mathcal{R}^{m\times m}$| using the FKL method proposed by [26]. We defined the new similarity matrix for RBPs as |$K^r$|⁠:
(7)
We considered that |$K^r$| should be close to the RBP association similarity, which is calculated as follows:
(8)
Then, we find |$\lambda ^r\in \mathcal{R}^{1\times 2}$| by minimizing the distance between |$K^r$| and |$Y^r$| as
(9)
To avoid over-fitting in the learning procedure, we added a regularization term to the above equation as
(10)
where |$\mu ^r$| is set as |$200$|⁠. To solve this optimization problem, we used the Matlab R2018a CVX to get the integrated parameter |$\lambda ^r\in \mathcal{R}^{1\times 2}$| for RBP regulating similarity and RBP GIP similarity. Similarly, we obtained the integrated parameter |$\lambda ^a\in \mathcal{R}^{1\times 2}$| for AS event module similarity and AS event GIP kernel similarity using the FKL model and defined the integrated AS event similarity as
(11)

Sparse similarity model

To further reduce noise in the integrated similarity matrix, we used the top-|$k$| nearest neighbor model to obtain a denoised sparse RBP similarity matrix. That is, we constructed a weight matrix |$w_r\in \mathcal{R}^{m\times m}$| for |$K^r$| with elements being defined as
(12)
where |$T(k,i)$| is the |$k$|-th largest element of |$i$|-th row in |$K^r$| and |$T(k,j)$| is the |$k$|-th largest element of |$j$|-th column in |$K^r$|⁠. Then, the denoised RBP similarity matrix was calculated as
(13)
Similarity, we obtained the denoised similarity matrix |$K_a^*\in R^{n\times n}$| for AS events.

The RAIMC model

Given a pair of similarity matrices for RBP |$K_r^\star $| and AS event |$K_a^\star $|⁠, the main idea of RAIMC is to recover a matrix |$Score\in \mathcal{R}^{m\times n}$| using the known entries (i.e. the known RBP-AS event association matrix |$Y$|⁠). The form of |$Score$| is |$Score=K_a^\star (i)WH^TK_r^{\star T}(j)$|⁠, where |$W\in \mathcal{R}^{m\times r}$| and |$H\in \mathcal{R}^{n\times r}$| and |$r$| is the desired rank that is equal to min(rank(W),rank(H)). The parameter |$r$| will affect the convergence speed of the IMC algorithm, but the impact on the results is very small. Then, matrices |$W$| and |$H$| are obtained by solving the following optimization problem:
(14)
where |$\alpha ,\beta $| are regularization parameters that are usually set as the Frobenius norm of matrix |$\alpha =\beta =1||\bf{\cdot }||_F$|⁠. The first part of objective function |$\frac{1}{2}||Y-K_a^\star WH^TK_r^{\star T}||_F^2$| is the least squares cost function, and |$\frac{1}{2}\alpha ||W||_F^2$| and |$\frac{1}{2}\beta ||H||_F^2$| are set to overcome the over-fitting problem using the method proposed by [23] to obtain |$W$| and |$H$|⁠. Initially, |$W$| and |$H$| are assumed to be random dense matrices that are then updated using an iterative operator that stops when convergence is reached. Details of the algorithm steps with the iterative equation are summarized in Figure 1.

In this way, the RAIMC model can predict a new AS event |$newa(i)$| that has no known related RBPs. Therefore, as long as we have the feature vector of AS event |$newa(i)$|⁠, the entry |$Score(new(a(i),j)$| can be computed for all RBPs.

Results and Discussions

Data collection

We collected 1532 RBP genes that were expressed in all the breast cancer samples in a recent census of human RBPs [24]. Integrating the gene expression levels in breast cancer from TCGA, we can extract the expression level of RBPs. For the AS events, we retrieved the raw junction reads from level 3 The Cancer Genome Atlas BRCA data from GDC legacy archive (https://portal.gdc.cancer.gov/legacy-archive). Known AS events can be provided by the splicing analysis tool MISO (mixture-of-isoforms) database downloaded from (https://miso.readthedocs.io/en/fastmiso/) [27]. The percent spliced-in value of AS, events can be calculated by the formula |$PSI=\frac{I/L_I}{I/L_I+S/L_S}$| where |$I$| represents the exon inclusion reads which are from the upstream splice junction and downstream splice junction, |$S$| represents the exon skipping reads which are from the skipping splice junction connecting the upstream exon to the downstream exon. The association matrix is typically very sparse because only strong correlations are set as 1.

Evaluation criteria

To evaluate the prediction accuracy of our method, we implemented 5-fold cross-validation (CV) and leave-one-out cross-validation (LOOCV). In the 5-fold CV, all RBP-AS event associations were divided randomly into five uncrossed groups; four were used for the training set and one was used as the testing set. In the LOOCV, for a given AS event the |$a(i)$| of each known RBP associated with |$a(i)$| was left out in turn as the testing sample, and the other known verified RBPs associated with |$a(i)$| were used as the training sample. All the RBPs with no known association with |$a(i)$| were considered as candidate samples and were ranked using the predicted score.

Area under the receiver operating characteristic curve (ROC AUC) was used to establish the measuring criteria for evaluating the prediction performance of our method. The AUC plot is created by plotting the true positive rate against the false positive rate. An AUC value of 1 indicates perfect performance, whereas an AUC value of 0.5 implies random performance, that is, high AUC values indicate the good performance of a prediction method.

Effects of parameters

Effects of |$\mu ^r$| and |$\mu ^a$|

The |$\mu ^r$| from Equation 10 and |$\mu ^a$| are the regularization coefficients of FKL. We use different |$\mu ^r$| and |$\mu ^a$| values to integrate two RBP similarity kernels and two AS event similarity kernels. We use a grid searching strategy in the range |$\{0,200,\cdots ,1000\}$| to find the optimal |$\mu ^r$| and |$\mu ^a$| values. Figure 2 shows that the AUC values have only small fluctuations between 0 to 1,000, which indicate that FKL method was insensitive to the regularization parameters, and hence we set |$\mu ^r=200$| and |$\mu ^a=200$| as the default values for RAIMC.

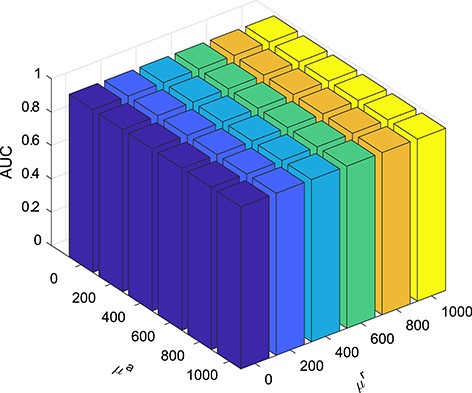
AUC values obtained by RAIMC with the with grid search strategy for different $\mu ^r$ and $\mu ^a$ values ($\{0,200,\cdots ,1000\}$) by 5-fold CV.
Figure 2

AUC values obtained by RAIMC with the with grid search strategy for different |$\mu ^r$| and |$\mu ^a$| values (⁠|$\{0,200,\cdots ,1000\}$|⁠) by 5-fold CV.

Open in new tabDownload slide

Effect of |$k$| value

The |$k$| value in Equation 12 is used in the sparse similarity model and plays a vital role in constructing the final integrated RBP and AS event similarity matrix. To investigate the performance of different |$k$| values, we used values from 20 to 200 in steps of 10 and determined the distribution of AUC values by 5-fold CV. Figure 3 clearly shows that the sparse kernel process has a positive effect on the discovery of potential RBP-AS event associations. We found that the AUC values gradually decreased with increasing |$k$|⁠; therefore, we set |$k=20$| as the default.

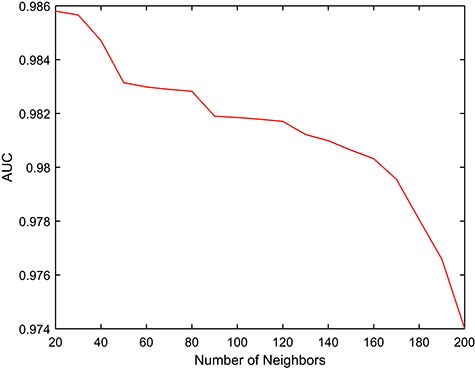
AUC values obtained by RAIMC for different $k$ by 5-fold CV.
Figure 3

AUC values obtained by RAIMC for different |$k$| by 5-fold CV.

Open in new tabDownload slide

Comparison of RAIMC with other related methods

We conducted both LOOCV and 5-fold CV to compare the performance of RAIMC with the performances of four other state-of-the-art computational methods, namely IMCMDA ([28]), MFLDA ([29]), LAPRLS ([30]) and SIMCLDA ([20]), by calculating AUC values.

For the LOOCV, an ROC curve was plotted using the LOOCV results in Figure 4(A). We calculated the AUC values from the ROC curve to evaluate the performance of the models. Figure 4(A) shows that RAIMC gives an AUC of |$0.9587$|⁠, whereas the AUC values for IMCMDA, MFLDA, LAPRLS and SIMCLDA are 0.8852, 0.8518, 0.8081 and |$0.6902$|⁠, respectively. These results confirm that the RAIMC model performed better than the other methods in predicting RBP-AS event associations.

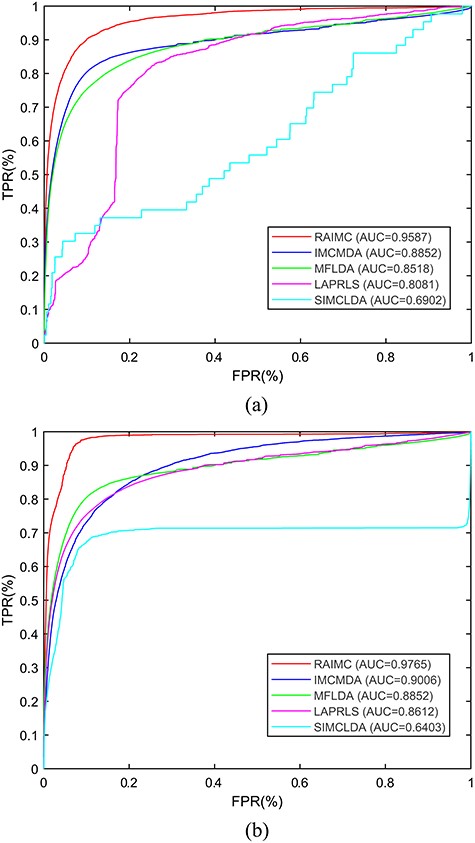
Comparison of RAIMC with four other state-of-the-art methods by leave-one-out cross-validation (LOOCV) (A) and 5-fold CV (B). The X-axis shows the true positive rate (TPR$\%$) and the Y-axis shows the false positive rate (FPR$\%$).
Figure 4

Comparison of RAIMC with four other state-of-the-art methods by leave-one-out cross-validation (LOOCV) (A) and 5-fold CV (B). The X-axis shows the true positive rate (TPR|$\%$|⁠) and the Y-axis shows the false positive rate (FPR|$\%$|⁠).

Open in new tabDownload slide
Comparison of predicting methods in de novo prediction for RBP-AS event associations.
Figure 5

Comparison of predicting methods in de novo prediction for RBP-AS event associations.

Open in new tabDownload slide
Table 1
Open in new tab

Top 10 predicted RBPs associated with CD44v

RBPEffect on variable exonsEvidence (PMID)Rank
ESRP2Promote exon inclusion28991261 ([34])1
ESRP1Promote exon inclusion28991261 ([10, 34])2
AKAP8Promote exon inclusion31980632([11])3
LARP4BUnknownNo evidence4
HNRNPMPromote exon skipping28825698 ([10])5
QKIUnknownNo evidence6
CELF2UnknownNo evidence7
ZCCHC24UnknownNo evidence8
PTBP1Promote exon inclusion31980632([11])9
SAMD4AUnknownNo evidence10
RBPEffect on variable exonsEvidence (PMID)Rank
ESRP2Promote exon inclusion28991261 ([34])1
ESRP1Promote exon inclusion28991261 ([10, 34])2
AKAP8Promote exon inclusion31980632([11])3
LARP4BUnknownNo evidence4
HNRNPMPromote exon skipping28825698 ([10])5
QKIUnknownNo evidence6
CELF2UnknownNo evidence7
ZCCHC24UnknownNo evidence8
PTBP1Promote exon inclusion31980632([11])9
SAMD4AUnknownNo evidence10
Table 1
Open in new tab

Top 10 predicted RBPs associated with CD44v

RBPEffect on variable exonsEvidence (PMID)Rank
ESRP2Promote exon inclusion28991261 ([34])1
ESRP1Promote exon inclusion28991261 ([10, 34])2
AKAP8Promote exon inclusion31980632([11])3
LARP4BUnknownNo evidence4
HNRNPMPromote exon skipping28825698 ([10])5
QKIUnknownNo evidence6
CELF2UnknownNo evidence7
ZCCHC24UnknownNo evidence8
PTBP1Promote exon inclusion31980632([11])9
SAMD4AUnknownNo evidence10
RBPEffect on variable exonsEvidence (PMID)Rank
ESRP2Promote exon inclusion28991261 ([34])1
ESRP1Promote exon inclusion28991261 ([10, 34])2
AKAP8Promote exon inclusion31980632([11])3
LARP4BUnknownNo evidence4
HNRNPMPromote exon skipping28825698 ([10])5
QKIUnknownNo evidence6
CELF2UnknownNo evidence7
ZCCHC24UnknownNo evidence8
PTBP1Promote exon inclusion31980632([11])9
SAMD4AUnknownNo evidence10
Table 2
Open in new tab

Top 10 predicted RBPs associated with MAP3K7v

RBPEffect on variable exonsEvidence (PMID)Rank
PTCD3UnknownNo evidence1
RBM47Promote exon inclusion32467311 ([12])2
QKIPromote exon skipping32467311([12])3
RBMS2UnknownNo evidence4
BIRC3Promote exon inclusion30368883([36])5
LARP6UnknownNo evidence6
C2ortf15UnknownNo evidence7
ESRP1Promote exon inclusion32467311 ([12])8
NOVA2UnknownNo evidence9
ZCCHC24UnknownNo evidence10
RBPEffect on variable exonsEvidence (PMID)Rank
PTCD3UnknownNo evidence1
RBM47Promote exon inclusion32467311 ([12])2
QKIPromote exon skipping32467311([12])3
RBMS2UnknownNo evidence4
BIRC3Promote exon inclusion30368883([36])5
LARP6UnknownNo evidence6
C2ortf15UnknownNo evidence7
ESRP1Promote exon inclusion32467311 ([12])8
NOVA2UnknownNo evidence9
ZCCHC24UnknownNo evidence10
Table 2
Open in new tab

Top 10 predicted RBPs associated with MAP3K7v

RBPEffect on variable exonsEvidence (PMID)Rank
PTCD3UnknownNo evidence1
RBM47Promote exon inclusion32467311 ([12])2
QKIPromote exon skipping32467311([12])3
RBMS2UnknownNo evidence4
BIRC3Promote exon inclusion30368883([36])5
LARP6UnknownNo evidence6
C2ortf15UnknownNo evidence7
ESRP1Promote exon inclusion32467311 ([12])8
NOVA2UnknownNo evidence9
ZCCHC24UnknownNo evidence10
RBPEffect on variable exonsEvidence (PMID)Rank
PTCD3UnknownNo evidence1
RBM47Promote exon inclusion32467311 ([12])2
QKIPromote exon skipping32467311([12])3
RBMS2UnknownNo evidence4
BIRC3Promote exon inclusion30368883([36])5
LARP6UnknownNo evidence6
C2ortf15UnknownNo evidence7
ESRP1Promote exon inclusion32467311 ([12])8
NOVA2UnknownNo evidence9
ZCCHC24UnknownNo evidence10

For the 5-fold CV, Figure 4(B) clearly shows that RAIMC almost always achieves the highest true positive rates under the same false negative rates with an AUC of |$0.9765$|⁠.

SIMCLDA predicts RBP-AS event associations using an IMC framework and the primary feature vectors from constructed feature matrices. Its performance was much lower than that of RAIMC (Figure 4), possibly because it does not integrate prior information about RBPs and AS events (i.e. RBP similarity and AS event similarity as the features of RBPs and AS events), which produces biased predicted scores.

LAPRLS combines two RBP similarity kernels and two disease similarity kernels into a single kernel using the FKL model, and it uses a sparse kernel to eliminate noise in the integrated similarity kernel. Then, the Laplacian regularized least squares is used to predict the association between RBPs and AS events. Its performance was lower than that of RAIMC (Figure 4) with AUC values of |$0.8081$| for the LOOCV and |$0.8612$| for the 5-fold CV. Finding the optimal solution using an alternating gradient decent algorithm guarantees the reliability of the RBP eigenvectors. However, LAPRLS does not integrate the final RBP and AS event similarities as features of RBPs and AS events to infer potential associations, which may explain its lower performance.

IMCMDA integrates RBP similarity and AS events similarity based on RBP regulating similarity, AS event module similarity and GIP kernel similarity to infer RBP-AS event associations. However, these features may contain noise or outliers. Furthermore, to integrate similarity kernels, IMCMDA directly accumulates the similarity kernels and does not look for the optimal combination. IMCMDA did not perform as well as RAIMC with AUC values of |$0.8852$| for the LOOCV and |$0.9006$| for the 5-fold CV.

Unlike SIMCLDA, LAPRLS and IMCMDA, MFLDA integrates heterogeneous data sources and decomposes the matrices of heterogeneous data sources into low-rank matrices using matrix tri-factorization to explore intrinsic structure. MFLDA did not perform as well as RAIMC with AUC values of |$0.8518$| for the LOOCV and |$0.8852$| for the 5-fold CV. The data sources used by MFLDA include lncRNA–gene, miRNA–disease, gene–disease and gene–drug associations, which may contain noise and outliers. RAIMC may better exploit inherent data structures and alleviate the impact of noise or outliers in the constraint matrix.

These results confirm that integrating RBP similarity and AS event similarity greatly improves the prediction of RBP-AS event associations. In addition, integrating the similarity kernels using FKL and sparse similarity models is essential because it weights the different sources of the similarity kernels and eliminates noise for the integrated matrix.

De novo RBP-AS event prediction

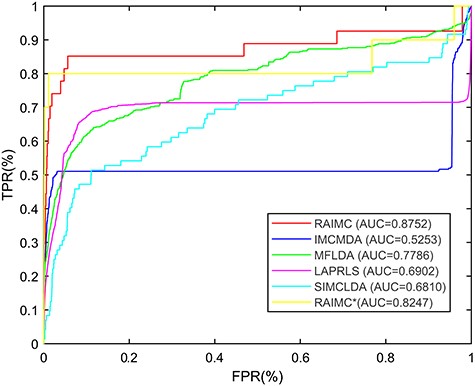
To evaluate the performance of RAIMC in predicting potential associations for new RBPs, we conducted a de novo prediction test. For each queried RBP, we removed all known AS events for this RBP and applied our proposed model to predict its association. In order to evaluate the effectiveness of integrating similarity matrices, we performed analysis on the one without using the FKL to get the optimal integration for similarity matrices and called it as RAIMC|$^*$|⁠. Then, we compare the performance of RAIMC, IMCMDA, MFLDA, LAPRLS, SIMCLDA and RAIMC|$^*$| in terms of AUC value. As we can see from the Figure 5, RAIMC achieves the AUC values of |$0.8752$|⁠, whereas the AUC values for IMCMDA, MFLDA, LAPRLS, SIMCLDA and RAIMC|$^*$| are |$0.5253, 0.7786, 0.6902, 0.6810$| and |$0.8247$|⁠, respectively. Thus, we can conclude that the performance of RAIMC is superior to the other methods in the de novo experiments. Moreover, we can see that finding the optimal integration for similarity matrices is an effective way for improving the prediction performance.

Validation of RBP-AS event associations predicted by RAIMC

We selected two important genes (CD44 and MAP3K7) that undergo AS events during EMT to further validate the predictive power of RAIMC. We kept the optimal parameter set and used RAIMC to integrate RBP regulating similarity and RBP GIP kernel, and we used AS event module similarity and AS event GIP kernel to predict novel RBP-AS event associations. We checked the predicted RBP-AS event associations manually in PubMed to identify supportive literature. The standard splice isoform of CD44 (CD44s) is reported to be positively associated with the gene signatures of cancer stem cells, whereas the variant splice isoform (CD44v) has a negative association [31]. Additionally, CD44s was found to be the predominant isoform expressed in breast cancer stem cells [31, 32]. Mesenchymal splice isoform of CD44 (CD44s) promotes EMT/invasion and imparts stem-like properties to ovarian cancer cells [33] Thus, RBPs that regulate CD44v expression may be important in EMT. We selected the top 10 RBPs associated with CD44 and looked for supporting evidence in the literature. We found supporting evidence for 5 of the 10 selected RBPs as shown in Table 1, which further verified the effectiveness and reliability of our method. The predicted novel associations for which no evidence was found need to be validated in future studies.

MAP3K7 plays an important role for enhancing the response of tumors to anticancer therapies [35]. Previous work have been conduced to design inhibitors of MAP3K7 activity, which could be used to reverse MAP3K7-mediated chemoresistance. The activity of these inhibitors has been tested in preclinical studies, proving the efficacy of MAP3K7 inhibition in reducing tumor growth and survival following chemotherapy administration.

We found supporting evidence for four of the ten selected RBPs, as shown in Table 2, which again confirms the effectiveness of our model. The predicted novel associations for which no evidence was found can be further investigated, thereby possibly reducing the number of time-consuming and costly validations that are often required.

RAIMC for predicting other biological entities associations

To test the generalization ability of RAIMC, we further applied it to predict other biological entities (such as microRNA-disease) associations. We also compared the performance of RAIMC with the performance of the other four related methods with the new data set. Figure 6 shows that RAIMC performed better than the other four methods in predicting microRNA-disease associations. Among the four methods, LAPRLS produced the best performance with an AUC value of |$0.9535$| for the 5-fold CV; the AUC value for RAIMC was slightly higher. Therefore, we can conclude that our proposed method has an excellent predictive and generalization ability.

Conclusions

Predicting RBP-AS event associations is helpful not only for understanding the regulating relationships between RBPs and AS events in the EMT process but also for tumor metastasis diagnosis, prognosis and prevention. We developed an effective and reliable novel computational method (RAIMC) to uncover potential RBP-AS event associations. The RAIMC model outperforms previous methods as determined by 5-fold CV and LOOCV. Known RBP-AS event associations and integrated RBP similarity and AS event similarity were combined to calculate the prediction scores of RBP-AS event pairs. Unlike the average kernel method, RAIMC integrates the FKL method to combine the kernel matrices and the sparse similarity model has a positive effect on noise elimination in the similarity network. RAIMC achieves AUC values of 0.9765 and 0.9587 by 5-fold CV and LOOCV, respectively, which confirms that our method is reliable and superior to the other methods tested. RAIMC predicts RBP-AS event associations using the low-rank IMC algorithm, which may be the basis of its reliable performance. A major advantage of IMC is that it uses RBP similarity and AS event similarity as features of RBPs and AS events to complete missing RBP-AS event associations, so the feature vector of a new AS event can be used without any known related RBPs to predict the association scores between the new AS event and all RBPs. We also adopt an alternative gradient descent algorithm to search for the optimal solution, which further guarantees the reliability of the RBP and AS event eigenvectors. Furthermore, integrating the FKL and sparse similarity models helps to identify important features for RBPs and AS events and thus improves the prediction performance of RAIMC. Nonetheless, RAIMC does have some limitations that influence its prediction performance. Some detailed information is lost in the FKL process when handling a new AS event without known associations with RBPs. Furthermore, we did not conduct wet-laboratory experiments to verify predictions because of limited laboratory resources. In future work, we will attempt to construct additional similarity kernels using different sources of information, such as gene-AS event and disease–disease associations. In addition, if we could collect the expression level of RBPs and AS events in other data sets (such as neuron development and drug resistance), we can further explore the significant RBP and AS event associations in such scenarios. Finally, this study only focused on the association of RBPs and skipping exon events; the relationship between RBPs and other four types of AS events can be further analyzed.

Key Points

  • The paper provided a novel perspective on the comprehensive determination of RBP-AS event associations during EMT.

  • The paper developed a novel method (RAIMC) and compared the state-of-the-art models of the RBP-AS event association prediction. Aiming at the shortcoming of their models, a novelty model was designed.

  • Important RBP-AS event associations are identified and an appropriate EMT regulating mechanism is determined.

  • Experimental results have shown that RAIMC has excellent predictive and generalization ability.

Acknowledgments

The authors are deeply grateful to the anonymous reviewers for their helpful and constructive comments.

Funding

This work was supported by the National Natural Science Foundation of China (62002234); the Guangdong Basic and Applied Basic Research Foundation (2019A1515111180); the Natural Science Foundation of SZU (827-000393); the Natural Science Foundation of Guangdong (2019A1515011917); the Natural Science Foundation of Shenzhen (JCYJ20190808173603590); the HKRGC GRF (17301519); and the IMR and RAE Research Fund from the Faculty of Science, HKU.

Quan Zou is a professor in University of Electronic Science and Technology of China. He is a senior member of IEEE and ACM. He majors in bioinformatics, machine learning and algorithms. His email is [email protected].

Yushan Qiu is an assistant professor in Shenzhen University. Her research interest are bioinformatics and machine learning. Her email is [email protected]

Wai-Ki Ching is a professor in The University of Hong Kong. His research interest are bioinformatics and matrix computation. His email is [email protected]

References

1.

Thiery
JP
,
Acloque
H
,
Huang
RYJ
, et al.
Epithelial-mesenchymal transitions in development and disease
.
Cell
2009
;
139
(
5
):
871
–
90
.

Google Scholar

Crossref
Search ADS
PubMed

 
2.

Thiery
JP
,
Sleeman
JP
.
Complex networks orchestrate epithelial–mesenchymal transitions
.
Nat Rev Mol Cell Biol
2006
;
7
(
2
):
131
–
42
.

Google Scholar

Crossref
Search ADS
PubMed

 
3.

Shapiro
IM
,
Cheng
AW
,
Flytzanis
NC
, et al.
An EMT-driven alternative splicing program occurs in human breast cancer and modulates cellular phenotype
.
PLoS Genet
2011
;
7
(
8
):
e1002218
.

Google Scholar

Crossref
Search ADS
PubMed

 
4.

Yang
Y
,
Park
JW
,
Bebee
TW
, et al.
Determination of a comprehensive alternative splicing regulatory network and combinatorial regulation by key factors during the epithelial-to-mesenchymal transition
.
Mol Cell Biol
2016
;
36
(
11
):
1704
–
19
.

Google Scholar

Crossref
Search ADS
PubMed

 
5.

Wang
ET
,
Sandberg
R
,
Luo
S
, et al.
Alternative isoform regulation in human tissue transcriptomes
.
Nature
2008
;
456
(
7221
):
470
–
6
.

Google Scholar

Crossref
Search ADS
PubMed

 
6.

Nilsen
TW
,
Graveley
BR
.
Expansion of the eukaryotic proteome by alternative splicing
.
Nature
2010
;
463
(
7280
):
457
–
63
.

Google Scholar

Crossref
Search ADS
PubMed

 
7.

Damianov
A
,
Yi
Y
,
Lin
C-H
, et al.
Rbfox proteins regulate splicing as part of a large multiprotein complex LASR
.
Cell
2016
;
165
(
3
):
606
–
19
.

Google Scholar

Crossref
Search ADS
PubMed

 
8.

Ying
Y
,
Wang
X-J
,
Vuong
CK
, et al.
Splicing activation by Rbfox requires self-aggregation through its tyrosine-rich domain
.
Cell
2017
;
170
(
2
):
312
–
23
.

Google Scholar

Crossref
Search ADS
PubMed

 
9.

Qiu
Y
,
Jiang
H
,
Ching
W-K
, et al.
On predicting epithelial mesenchymal transition by integrating RNA-binding proteins and correlation data via L1/2-regularization method
.
Artif Intell Med
2019
;
95
:
96
–
103
.

Google Scholar

Crossref
Search ADS
PubMed

 
10.

Harvey
SE
,
Xu
Y
,
Lin
X
, et al.
Coregulation of alternative splicing by hnRNPM and ESRP1 during EMT
.
RNA
2018
;
24
(
10
):
1326
–
38
.

Google Scholar

Crossref
Search ADS
PubMed

 
11.

Hu
X
,
Harvey
SE
,
Zheng
R
, et al.
The RNA-binding protein AKAP8 suppresses tumor metastasis by antagonizing EMT-associated alternative splicing
.
Nat Commun
2020
;
11
(
1
):
1
–
15
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
12.

Qiu
Y
,
Lyu
J
,
Dunlap
M
, et al.
A combinatorially regulated RNA splicing signature predicts breast cancer EMT states and patient survival
.
RNA
2020
;
26
(
9
):
1257
–
67
.

Google Scholar

Crossref
Search ADS
PubMed

 
13.

Chen
X
,
Yan
G-Y
.
Novel human lncRNA-disease association inference based on lncRNA expression profiles
.
Bioinformatics
2013
;
29
(
20
):
2617
–
24
.

Google Scholar

Crossref
Search ADS
PubMed

 
14.

Lan
W
,
Li
M
,
Zhao
K
, et al.
LDAP: a web server for lncRNA-disease association prediction
.
Bioinformatics
2017
;
33
(
3
):
458
–
60
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
15.

Wu
X
,
Jiang
R
,
Zhang
MQ
, et al.
Network-based global inference of human disease genes
.
Mol Syst Biol
2008
;
4
(
1
):
189
.

Google Scholar

Crossref
Search ADS
PubMed

 
16.

Sun
J
,
Shi
H
,
Wang
Z
, et al.
Inferring novel lncRNA-disease associations based on a random walk model of a lncRNA functional similarity network
.
Mol Biosyst
2014
;
10
(
8
):
2074
–
81
.

Google Scholar

Crossref
Search ADS
PubMed

 
17.

Yao
Q
,
Wu
L
,
Li
J
, et al.
Global prioritizing disease candidate lncRNAs via a multi-level composite network
.
Sci Rep
2017
;
7
(
1
):
1
–
13
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
18.

Liu
M-X
,
Chen
X
,
Chen
G
, et al.
A computational framework to infer human disease-associated long noncoding RNAs
.
PLoS One
2014
;
9
(
1
):
e84408
.

Google Scholar

Crossref
Search ADS
PubMed

 
19.

Chen
X
.
KATZLDA: KATZ measure for the lncRNA-disease association prediction
.
Sci Rep
2015
;
5
:
16840
.

Google Scholar

Crossref
Search ADS
PubMed

 
20.

Lu
C
,
Yang
M
,
Luo
F
, et al.
Prediction of lncRNA-disease associations based on inductive matrix completion
.
Bioinformatics
2018
;
34
(
19
):
3357
–
64
.

Google Scholar

Crossref
Search ADS
PubMed

 
21.

Fu
L
,
Peng
Q
.
A deep ensemble model to predict miRNA-disease association
.
Sci Rep
2017
;
7
(
1
):
1
–
13
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
22.

You
Z-H
,
Huang
Z-A
,
Zhu
Z
, et al.
PBMDA: a novel and effective path-based computational model for miRNA-disease association prediction
.
PLoS Comput Biol
2017
;
13
(
3
):
e1005455
.

Google Scholar

Crossref
Search ADS
PubMed

 
23.

Jain
P
,
Dhillon
IS
.
Provable inductive matrix completion
.
arXiv preprint arXiv:1306.0626
.
2013
.

24.

Gerstberger
S
,
Hafner
M
,
Tuschl
T
.
A census of human RNA-binding proteins
.
Nat Rev Genet
2014
;
15
(
12
):
829
–
45
.

Google Scholar

Crossref
Search ADS
PubMed

 
25.

Tseng
Y-T
,
Li
W
,
Chen
C-H
, et al.
IIIDB: a database for isoform–isoform interactions and isoform network modules
.
BMC Genomics
2015
;
16
:
S10
.
Springer
.

Google Scholar

Crossref
Search ADS
PubMed

 
26.

He
J
,
Chang
S-F
,
Xie
L
.
Fast kernel learning for spatial pyramid matching
. In:
2008 IEEE Conference on Computer Vision and Pattern Recognition
.
Columbia: IEEE
,
2008
,
1
–
7
.

Google Scholar

OpenURL Placeholder Text

 
27.

Katz
Y
,
Wang
ET
,
Airoldi
EM
, et al.
Analysis and design of RNA sequencing experiments for identifying isoform regulation
.
Nat Methods
2010
;
7
(
12
):
1009
–
15
.

Google Scholar

Crossref
Search ADS
PubMed

 
28.

Chen
X
,
Wang
L
,
Qu
J
, et al.
Predicting miRNA-disease association based on inductive matrix completion
.
Bioinformatics
2018
;
34
(
24
):
4256
–
65
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
29.

Fu
G
,
Wang
J
,
Domeniconi
C
, et al.
Matrix factorization-based data fusion for the prediction of lncRNA-disease associations
.
Bioinformatics
2018
;
34
(
9
):
1529
–
37
.

Google Scholar

Crossref
Search ADS
PubMed

 
30.

Jiang
L
,
Xiao
Y
,
Ding
Y
, et al.
FKL-Spa-LapRLS: an accurate method for identifying human microRNA-disease association
.
BMC Genomics
2018
;
19
(
10
):
11
–
25
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
31.

Zhang
H
,
Brown
RL
,
Wei
Y
, et al.
CD44 splice isoform switching determines breast cancer stem cell state
.
Genes Dev
2019
;
33
(
3–4
):
166
–
79
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
32.

Xu
Y
,
Gao
XD
,
Lee
J-H
, et al.
Cell type-restricted activity of hnRNPM promotes breast cancer metastasis via regulating alternative splicing
.
Genes Dev
2014
;
28
(
11
):
1191
–
203
.

Google Scholar

Crossref
Search ADS
PubMed

 
33.

Bhattacharya
R
,
Mitra
T
,
Ray Chaudhuri
S
, et al.
Mesenchymal splice isoform of CD44 (CD44s) promotes EMT/invasion and imparts stem-like properties to ovarian cancer cells
.
J Cell Biochem
2018
;
119
(
4
):
3373
–
83
.

Google Scholar

Crossref
Search ADS
PubMed

 
34.

Jeong
HM
,
Han
J
,
Lee
SH
, et al.
ESRP1 is overexpressed in ovarian cancer and promotes switching from mesenchymal to epithelial phenotype in ovarian cancer cells
.
Oncogenesis
2017
;
6
(
10
):
e389
–
9
.
This article has been corrected since advance online publication and an erratum is also printed in this issue
.

Google Scholar

Crossref
Search ADS
PubMed

 
35.

Santoro
R
,
Carbone
C
,
Piro
G
, et al.
TAK-ing aim at chemoresistance: the emerging role of map3k7 as a target for cancer therapy
.
Drug Resist Update
2017
;
33
:
36
–
42
.

Google Scholar

OpenURL Placeholder Text

 
36.

Fu
P-Y
,
Hu
B
,
Ma
X-L
, et al.
New insight into birc3: a novel prognostic indicator and a potential therapeutic target for liver cancer
.
J Cell Biochem
2019
;
120
(
4
):
6035
–
45
.

Google Scholar

Crossref
Search ADS
PubMed

 
© The authors 2021. Published by Oxford University Press. All rights reserved. For Permissions, please email: [email protected]
This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)
Issue Section:
Articles
Download all slides