Search
Close
Search
Advanced Search
Search Menu
AI Discovery Assistant

Abstract

The long non-coding RNAs (lncRNAs) are subject of intensive recent studies due to its association with various human diseases. It is desirable to build the artificial intelligence-based models for prediction of diseases or tissues based on the lncRNAs data, which will be useful in disease diagnosis and therapy. The accuracy and robustness of existing models based on the machine learning techniques are subject to further improvement. In this study, we propose a deep learning model, called Multi-Label Classifications with Deep Forest, termed MLCDForest, to address multi-label classification on tissue prediction for a given lncRNA, which can be regarded as an implementation of the deep forest model in multi-label classification. The MLCDForest is a sequential multi-label-grained scanning method, which distinguishes from the standard deep forest model. It is proposed to train in sequential of multi-labels with label correlation considered. A systematic comparison using the lncRNA-disease association datasets demonstrates that our method consistently shows superior performance over the state-of-the-art methods in disease prediction. Considering label correlation in the sequential multi-label-grained scanning, our model provides a powerful tool to make multi-label classification and tissue prediction based on given lncRNAs.

cascade forest, deep learning, multi-label classification, lncRNAs, disease association and prediction

Introduction

Long non-coding RNAs (lncRNAs) are very critical in many biological processes [1] and associated with a wide range of human diseases, such as diabetes [2], cardiovascular diseases [3], HIV [4], neurological disorders [5] and cancers including lung cancer [6], breast cancer [7] and prostate cancer [8]. To understand, disease- or tissue-associated lncRNAs will provide a new perspective on deciphering disease mechanisms, novel drug development and personalized medications [9].

The known association between lncRNA and disease is rare. Compared to the experimental methods for identification of associations between lncRNAs and diseases, computational approach is much more efficient [10, 11]. The methods for prediction of lncRNA-disease associations are categorized into two groups: network models [12, 13], which based on a network representation to identify novel associations between lncRNAs and diseases, and machine learning [9–11, 14–18], such as dual-network integrated logistic matrix factorization [11], LRSLDA with semi-supervised learning [16], SVM based on the similarity between two lncRNAs and similarity of disease [17], and NCPHLDA based on network consistency projection [18]. In general, all these approaches are based on the combination of classification algorithms of machine learning and prior knowledge to diseases. However, more than 227 human diseases are associated with 266 lncRNAs [19], which means that the association between lncRNA and disease is a multi-label classification problem. Although many modified models have been proposed to ease these challenges in the past few years, more accurate and robust methods need to be further developed for multi-label classification.

As one of the supervised learning algorithms, multi-label classification is used for the problem that an instance is associated with one or more labels [20]. Currently, multi-label classification algorithms can be categorized into two main groups: problem transformation and algorithm adaptation. The problem transformation methods convert the problem into a series of single-label single-class or a single-label multi-class classification task [21]. The most representative models in problem transformation are binary relevance (BR) method and label powerset (LP) [21]. The random k-labelsets (RAkEL) method divides a large set of labels into a number of small random subsets. Then, LP is utilized to train an easier single-label multi-class classifier on each small subset [22]. In algorithm adaptation methods, multi-label k-nearest neighbor (ML-kNN) and back-propagation multi-label learning (BPMLL) [20] are widely applied in various applications.

Deep neural network (DNN) is a hot topic that has reached great success in natural language processing and visual recognitions. With the high requirements of the size of training data and hyperparameter tuning skills, the application of DNN in multi-label classification will be limited. gcForest is proposed as an alternative approach for DNN, which is a multiple-layer cascade frame with multiple random forest in each layer [23]. Two ensemble components, which are multi-grained scanning and cascade forest, have been employed in the frame. To overcome the limitation of gcForest in biology data, manually defining different types of forests may increase the risk of overfitting, and the importance of feature is ignored. Boosting cascade deep forest (BCDForest) [24] has been proposed for multiple class classification of cancer subtypes. In BCDForest, multi-class-grained scanning strategy is implemented from the multi-grained scanning to improve the diversity of ensemble with different training data of classes considered. And in each layer, the importance of features in forest learning is considered with the boosting strategy.

In this study, a further implemented deep forest in multi-label classification (MLCDForest) has been proposed for prediction of lncRNA-tissue associations considering label correlations as prior information [25, 26]. In each layer, the estimated class distribution is employed in the training of each forest. Finally, the voting results of multiple weak classifiers are used to determine which class a test sample should belong to. The experimental results show that the proposed method performs better on the dataset than the other machine learning methods.

The rest of this paper is organized as follows. In Section 2, we describe our method, MLCDForest and how it considers label correlations as prior information in detail. In Section 3, we introduce the experiment process and results. Finally, the summaries and conclusions are given.

Methods

In this section, details of the proposed method MLCDForest will be presented. The problem of multi-label classification will be defined first. Then the correlation between labels will be introduced. Lastly, the proposed models will be detailed with implementation to gcForest with label correlation considered.

Multi-label classification

As the basic information of a multi-label classification dataset |$(X,Y)$|⁠, |$n$| is the number of instances, |$X$| stands for the attributes and |$Y$| is the label. Given the label space |$Y=\{{Y}_1,{Y}_2,\cdots, {Y}_m\}$|⁠, an instance of |${x}_i$| with |$k$| lncRNA features is assigned by a subset of y in the label space |$Y$|⁠.

Label correlations and concurrence

Label correlations

For multinomial sample on the |$r\times c$| contingency table, Cramér’s V statistics [27, 28] is a popular association measure for nominal random variables with the following formula:
(1)
in which mean square contingency |${\phi}^2$| is estimated as
(2)
and the estimated proportion in cell |$(i,j)$| is |${p}_{ij}$|⁠, and |${p}_{i+}$| and |${p}_{+j}$| are summation over that subscript.
To correct the bias of Cramér’s V statistics, correlated Cramér’s V statistics [29] is proposed as
(3)
in which |${\overset{\sim }{\phi}}_{+}^2=\max (0,{\hat{\phi}}^2-\frac{1}{n-1}(r-1)(c-1))$|⁠, |$\overset{\sim }{r}=r-\frac{1}{n-1}(r-1)(c-1)$| and |$\overset{\sim }{c}=c-\frac{1}{n-1}(r-1)(c-1)$|⁠.

Correlated Cramér’s V statistics is employed in this study to evaluate the association between each of these two labels.

Label concurrence

The level of imbalance between different labels can be measured by the imbalance ratio [30]. |$\mathrm{SCUMBLE}$| [30, 31] is another measurement, considering both the imbalance ratio and sparsity of the labels. The formula for |$\mathrm{SCUMBLE}$| is as follows:
(4)
in which
|${\mathrm{labelset}}_i$| is for any subset of full label set |$Y$|⁠. The significance of |$\mathrm{SCUMBLE}$| can be measured with standard coefficient of variation (CV) of |$\mathrm{SCUMBLE}$|⁠. The larger standard CV means the higher differences in concurrence among instances.
In the data for multi-label classification, most of these labels are imbalance. In most of common practice, imbalance ratio is used to measure the imbalance. And the overall imbalance of these labels is measured as |$\mathrm{Mean} IR$| [32], which is based on the mean of imbalance ratios among all labels from |$Y$|⁠. And standard coefficient of variation (CV) is to measure of significance of |$\mathrm{Mean} IR$|⁠. Formulas to |$\mathrm{Mean} IR$| and the standard can be checked as follows:
(5)
and
(6)

Framework of the proposed methodology

As an alternative to the deep neural network (DNN), deep forest tries to employ the class distribution features by multi-grained scanning and cascade forest.

Multi-grained scanning

In the first step, multi-grained scanning is based on the window sliding approach, which is to obtain class distribution based on the generated low-dimensional feature vectors [33]. It has been proven to be an effective approach in the recognition of local feature. In the multi-grained scanning, as shown in Figure 1A and B, suppose there are |$n$| instances with 100 raw features from 4 labels in the training data, and each label is binary class (in the multi-level labels, approach from [24]), multi-grained scanning is performed for each label to generate a 50-dimensional feature vector by sliding the window by one feature. Considering the correlation between different labels, multi-grained scanning for the first label is performed based on the input features and other three labels, and 54 feature vectors are produced. Fifty-three feature vectors are generated for each of the rest three labels. The extracted instances will be trained with a completely random tree forest and a random forest to generate a class vector, leading to an 852 (⁠|$(54+53+53+53)\times 2\times 2$|⁠)-dimensional transformed feature vector.

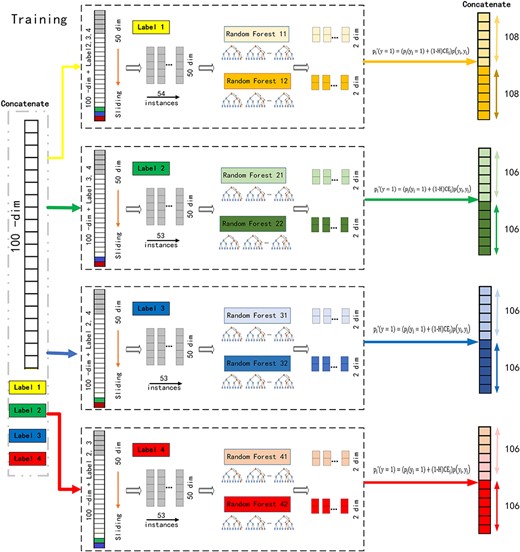
(A) Illustration of multi-grained scanning in training. Suppose there are four labels, raw features are 100-dim, and sliding window is 50-dim in the training of the first label. (B) Illustration of multi-grained scanning in predicting. Suppose there are four labels, raw features are 100-dim, and sliding window is 50-dim in the predicting of the first label.
Figure 1

(A) Illustration of multi-grained scanning in training. Suppose there are four labels, raw features are 100-dim, and sliding window is 50-dim in the training of the first label. (B) Illustration of multi-grained scanning in predicting. Suppose there are four labels, raw features are 100-dim, and sliding window is 50-dim in the predicting of the first label.

Open in new tabDownload slide
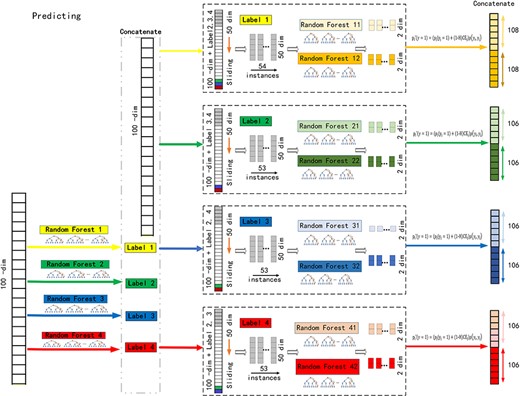
Continued.
Figure 1

Continued.

Open in new tabDownload slide
Considering the joint probabilities of labels and input of |$x$|⁠, the inference model to binary classification is
(7)
in which |${y}_i\in 0,1$|⁠, the probability of the independent binary classification to label |$i$| is |$p({y}_i|x)$|⁠, |$k,j\in \{i|{y}_i=1\}$|⁠, and |$p({y}_i|x)$| is the pairwise probability of each pair of labels, which is based on the correlation coefficient. The probability will be discounted when pair of labels is co-dependent. Multi-grained scanning for each label should be combined in the classification and prediction of each label. In order to enhance classification performance, the loss from each classifier may be transmitted when the predicted probability is incorporated in the classification of the label. The correlated loss (CL) can be computed when label |$j$|’s prediction is incorporated to the classification of label |$i$|⁠:
(8)
|$p({y}_i,{y}_j)$| is the correlation coefficient between label i and label j and calculated with correlated Cramér’s V statistics. |${\mathrm{CE}}_j$| is the cross-entropy loss [34] to label j, described as follows:
(9)
in which p is the expected output and q is the actual output:
(10)
H is a transform gate to control the rate of correlated loss which may be transformed from label j.

As shown in Figure 1B, in the prediction phase, probability is predicted first with traditional random forest for each label and concatenated to raw features. Probability of each label in the test data is predicted in the sequence of concurrence. Label with low concurrence rate is trained first.

Cascade forest

In the layer-wise cascade forest, the powerful classifier, random forest, is ensembled in each layer. In the classification to each label, the feature importance is considered assuming that the discriminative features should take higher weights. In the most correlated labels, this discriminative feature may also contribute to the classification of other labels. Boost class distribution vectors are generated by two random forests (one for complete random forest, the other for partial random forest) for both multi-grained scanning and cascade forest periods. The performance of each layer is evaluated with k-fold cross-validation [35, 36] to overcome the risk of overfitting. And in the cascade forest, the propagation will be terminated when there is no significant improvement to the performance of the whole cascade on validation set.

Overall procedure of MLCDForest

As the gcForest, there are two main components in the framework of MLCDForest. In the multi-grained scanning part, the corresponding transformed feature representation is classified according to different forests. And in the cascade forest, layer-wise random forest is to get more discriminative representations. The example of MLCDForest is illustrated for the first label in Figure 2. Two window sizes (50, 80) are used in multi-grained scanning for the data with 100 dimensions. |$(54+53+53+53)\times 2\times 2$| and |$(24+23+23+23)\times 2\times 2$| dimensional feature vectors are obtained for the window size of 50 and 80，respectively. Combining these feature vectors to different labels together with the correlation statistics, a 1224-dimensional transformed feature vector is available here if there are only four labels. In the cascade forest, the cascade-wise random forest is learnt with such 1224-dimensional feature vector, and the process will be terminated when the performance of the validation set is not significantly improved.

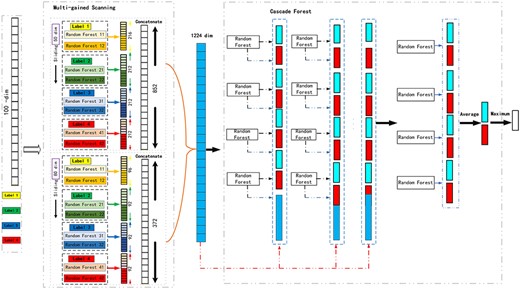
Overall procedure of MLCDForest. Suppose there are two classes, raw features are 100-dim, and sliding windows are 50-dim and 80-dim.
Figure 2

Overall procedure of MLCDForest. Suppose there are two classes, raw features are 100-dim, and sliding windows are 50-dim and 80-dim.

Open in new tabDownload slide

In any test instance, a 1224-dimensional representation vector, generated with multi-grained scanning, is the input data to the cascade forest to get its final prediction to each label by taking its class according to the maximum aggregated value.

Performance measures

Performance of different methods in multi-label classification is evaluated from the example-based, label-based and ranking-based [31]. In order to evaluate the generalization ability of MLCDForest, we utilized cross-validation in this study.

Example-based performance evaluation

With performance evaluation practice from Madjarov [37], accuracy, precision, recall, |$F- measure$|⁠, hamming loss and subset accuracy will be adopted in this study to compare the example-based performance evaluation of different methods for multi-label lncRNA-disease association classification:
(11)
(12)
(13)
(14)
(15)
(16)
in which|$\cap$| is for the intersection of two sets, |$\cup$| is the union of two sets and |$\Delta$| is for the symmetric difference between predicted and true labels. |${Y}_i$| is the subset of subset predicted labels for the|$i$|-instance, and |${Z}_i$| is the true subset labels |$[[ {Y}_i={Z}_i]] =1$| if |${Y}_i={Z}_i$| is TRUE and 0 otherwise.

Label-based performance evaluation

There are two methods to aggregate values of the labels: macro-average and micro-average approach. Macro-average is to compute the average of evaluation for each label independently. In micro-average approach, the evaluation is based on the count for true positive (TP), false positive (FP), true negative (TN) and false negative (FN) computed for all labels. These two evaluations can be calculated as follows:
(17)
(18)
in which evaluation matrix precision, recall and |$F- measure$| are considered here in |$evaluateMatric(\ast )$|⁠.

Ranking-based performance evaluation

In the ranking-based performance evaluation, One error, Coverage and Average Precision will be adopted here and can be computed as follows:
(19)
(20)
(21)
in which |$\mathit{\operatorname{rank}}({x}_i,y)$| refers to the rank of the position of label |$y$| in the |${x}_i$| instance and |${Y}_i$| is the subset of subset predicted labels for the|$i$|-instance.

Experiments and results

To evaluate the effectiveness of our proposed method, MLCDForest was compared with other multi-label classification methods: Deep Back-Propagation Neural Network (DBPNN) [38,39], RAkEL [22], MLkNN, BR and BPMLL [20] over this lncRNA dataset [40].

Datasets and hyperparameters

Data to associations between specific disease and lncRNAs [40] was employed in the construction of the proposed method. In the data downloaded from http://biomecis.uta.edu/∼ashis/res/csps2014/suppl/, 7566 lncRNA transcripts with 22 tissue labels were selected from the Human Body Map Project [41] with annotation and expression information of these 21,626 distinct lncRNAs. Eighty-nine composition-based features and 21 secondary structure-based features were identified with tissue-specificity threshold and as the input feature for different tissue classification. The detail information can be checked in [40].

In the experiments the division of the data in training and test set, which follows stratified approach [42], is in ratio of 80% versus 20%. Multi-grained scanning was based on 500 trees in each forest, and there were 1000 trees in the cascade forest as the default. In both multi-grained scanning and cascade forest, two completely random forests and two partial random forests were used in the training and prediction. In the two partial random forests, |$\sqrt{d}$| of features were selected as the candidates and separated with gini values. Fivefold cross-validation is used to evaluate the overall accuracy to overcome over-fitting. Comparing MLCDForest with DBPNN, which is conducted with Meka [39] and set the base classifier as random forest, other hyperparameters are the same as recommended in Meka. In [40], BR and RAkEL are based on sequential minimal optimization with support vector machines (SVMs) as base classifier. The number of nearest neighbors is 10 in MLkNN. And 10-fold cross-validation was conducted.

One major advantage of multi-label learning framework is to explore label correlations. Bias-corrected Cramér’s V statistics was calculated for all the label in label pairs and depicted them in a heat map (Figure 3A). Label concurrence is depicted in Figure 3B and Supplementary Table S1. Twenty out of 22 tissues are with standard CV of |$\mathrm{SCUMBLE}<0.8$|⁠, 14 tissues are with standard CV of |$\mathrm{SCUMBLE}<0.75$|⁠, and 8 tissues are with standard CV of |$\mathrm{SCUMBLE}<0.7$|⁠. Tissues Foreskin_R and LF_r2 take the standard CV of 0.366 and 0.157 correspondingly. Details about the standard CV of |$\mathrm{SCUMBLE}$| can be found in Supplementary Table S1. Details about the pairwise corrected Cramér’s V statistics and pairwise intersections plot between all the labels are appended as Supplementary Table S2 and Supplementary Figure S1.

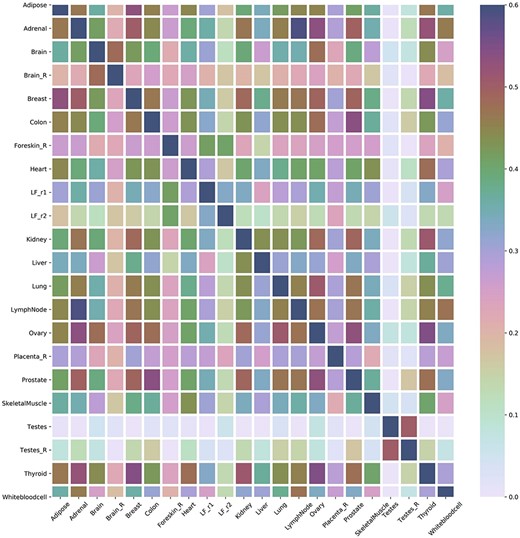
(A) Heat map of the correlation between tissues. (B) Concurrence to tissues based on SCUMBLE.
Figure 3

(A) Heat map of the correlation between tissues. (B) Concurrence to tissues based on SCUMBLE.

Open in new tabDownload slide
Continued.
Figure 3

Continued.

Open in new tabDownload slide

Performance comparison

Performance comparison of the MLCDForest and other multi-label classifiers are presented in Tables 1–3. The MLCDForest achieved the best performance. In example-based evaluation from Table 1, it has achieved about 13% improvement in accuracy compared to MLkNN [40] and 16% in the precision compared to BR [40]. It is about 10% improvement in the label-based evaluation (Table 2) and similar performance in ranking-based evaluation (Table 3). As the performance of standard gcForest presented in [23] for single-label classification, neural network has shown to be better in the precision from example-based and label-based evaluation, but did not have similar performance from any evaluation aspect when compared to MLCDForest. This is because the dataset [40] is a small-scale biology data and deep neural network is highly dependent on the scale of dataset.

Label-wise evaluation

With the multi-label learning models, label-wise manner was also performed to check the performance for each label. Performance of MLCDForest can be checked in Table 4, which was conducted in 5-fold cross-validation.

Table 1
Open in new tab

Example-based evaluation of the predictive performance of different multi-label classifiers

Hamming lossAccuracyPrecisionRecallF1-measureSubset accuracy
MLCDForest0.11450.69780.84020.74000. 69780.3347
DBPNN0.21180.48110.82580.49990.59970.1636
RAkEL [36]0.20320.54710.77810.61330.64090.1980
MLkNN [36]0.19700.56100.75990.64860.66270.1807
BR [36]0.20480.54410.78040.60500.64050. 1965
BPMLL [36]0.22410.51910.69000.66600.64120.1006
Hamming lossAccuracyPrecisionRecallF1-measureSubset accuracy
MLCDForest0.11450.69780.84020.74000. 69780.3347
DBPNN0.21180.48110.82580.49990.59970.1636
RAkEL [36]0.20320.54710.77810.61330.64090.1980
MLkNN [36]0.19700.56100.75990.64860.66270.1807
BR [36]0.20480.54410.78040.60500.64050. 1965
BPMLL [36]0.22410.51910.69000.66600.64120.1006
Table 1
Open in new tab

Example-based evaluation of the predictive performance of different multi-label classifiers

Hamming lossAccuracyPrecisionRecallF1-measureSubset accuracy
MLCDForest0.11450.69780.84020.74000. 69780.3347
DBPNN0.21180.48110.82580.49990.59970.1636
RAkEL [36]0.20320.54710.77810.61330.64090.1980
MLkNN [36]0.19700.56100.75990.64860.66270.1807
BR [36]0.20480.54410.78040.60500.64050. 1965
BPMLL [36]0.22410.51910.69000.66600.64120.1006
Hamming lossAccuracyPrecisionRecallF1-measureSubset accuracy
MLCDForest0.11450.69780.84020.74000. 69780.3347
DBPNN0.21180.48110.82580.49990.59970.1636
RAkEL [36]0.20320.54710.77810.61330.64090.1980
MLkNN [36]0.19700.56100.75990.64860.66270.1807
BR [36]0.20480.54410.78040.60500.64050. 1965
BPMLL [36]0.22410.51910.69000.66600.64120.1006
Table 2
Open in new tab

Label-based evaluation of the predictive performance of different multi-label classifiers

Micro-avgMacro-avg
PrecisionRecallF1PrecisionRecallF1
MLCDForest0.86030.79470.82620.84960.71700.7682
DBPNN0.85560.45860.59710.76100.31600.3726
RAkEL [36]0.76800.62190.68720.66250.49480.5494
MLkNN [36]0.76980.64390.70110.69980.52370.5804
BR [36]0.77660.60290.67880.57870.45880.5058
BPMLL [36]0.70430.64970.67540.57530.48270.4700
Micro-avgMacro-avg
PrecisionRecallF1PrecisionRecallF1
MLCDForest0.86030.79470.82620.84960.71700.7682
DBPNN0.85560.45860.59710.76100.31600.3726
RAkEL [36]0.76800.62190.68720.66250.49480.5494
MLkNN [36]0.76980.64390.70110.69980.52370.5804
BR [36]0.77660.60290.67880.57870.45880.5058
BPMLL [36]0.70430.64970.67540.57530.48270.4700
Table 2
Open in new tab

Label-based evaluation of the predictive performance of different multi-label classifiers

Micro-avgMacro-avg
PrecisionRecallF1PrecisionRecallF1
MLCDForest0.86030.79470.82620.84960.71700.7682
DBPNN0.85560.45860.59710.76100.31600.3726
RAkEL [36]0.76800.62190.68720.66250.49480.5494
MLkNN [36]0.76980.64390.70110.69980.52370.5804
BR [36]0.77660.60290.67880.57870.45880.5058
BPMLL [36]0.70430.64970.67540.57530.48270.4700
Micro-avgMacro-avg
PrecisionRecallF1PrecisionRecallF1
MLCDForest0.86030.79470.82620.84960.71700.7682
DBPNN0.85560.45860.59710.76100.31600.3726
RAkEL [36]0.76800.62190.68720.66250.49480.5494
MLkNN [36]0.76980.64390.70110.69980.52370.5804
BR [36]0.77660.60290.67880.57870.45880.5058
BPMLL [36]0.70430.64970.67540.57530.48270.4700
Table 3
Open in new tab

Ranking-based evaluation of the predictive performance of different multi-label classifiers

One errorCoverageAverage Precision
MLCDForest0.150312.55200.8024
DBPNN0.205215.47860.7249
RAkEL [36]0.286514.28690.7382
MLkNN [36]0.107511.58040.8155
BR [36]0.295914.57130.7274
BPMLL [36]0.103412.56040.7867
One errorCoverageAverage Precision
MLCDForest0.150312.55200.8024
DBPNN0.205215.47860.7249
RAkEL [36]0.286514.28690.7382
MLkNN [36]0.107511.58040.8155
BR [36]0.295914.57130.7274
BPMLL [36]0.103412.56040.7867
Table 3
Open in new tab

Ranking-based evaluation of the predictive performance of different multi-label classifiers

One errorCoverageAverage Precision
MLCDForest0.150312.55200.8024
DBPNN0.205215.47860.7249
RAkEL [36]0.286514.28690.7382
MLkNN [36]0.107511.58040.8155
BR [36]0.295914.57130.7274
BPMLL [36]0.103412.56040.7867
One errorCoverageAverage Precision
MLCDForest0.150312.55200.8024
DBPNN0.205215.47860.7249
RAkEL [36]0.286514.28690.7382
MLkNN [36]0.107511.58040.8155
BR [36]0.295914.57130.7274
BPMLL [36]0.103412.56040.7867
Table 4
Open in new tab

Label-wise analysis of MLCDForest

TissueAccuracyPrecisionRecallF1 scoreROCAUC
Adipose0.89020.87880.74770.80800.8375
Adrenal0.89360.90660.85730.88130.8845
Brain0.86010.85550.80540.82970.7770
Brain_R0.93930.90160.64450.75170.5561
Breast0.87510.83030.85940.84460.8501
Colon0.87050.83020.74830.78710.8236
Foreskin_R0.95030.82050.45070.58180.7215
Heart0.89020.88750.70580.78630.6596
LF_r10.89940.88680.54650.67630.6556
LF_r20.97400.77270.32080.45330.7186
Kidney0.84800.85850.76650.80990.7995
Liver0.87280.80620.53470.64300.5528
Lung0.82310.74840.82230.78360.8439
Lymph node0.87510.83180.83930.83560.9018
Ovary0.84800.90480.74320.81600.7531
Placenta_R0.91040.80950.51130.62670.7615
Prostate0.85490.83270.85570.84410.8825
Skeletal muscle0.89540.83200.61030.70410.6988
Testes0.89360.89220.99440.94050.8336
Testes_R0.90290.92880.92970.92920.9601
Thyroid0.86990.85770.84200.84980.8661
White blood cell0.86470.81870.63810.71720.7342
TissueAccuracyPrecisionRecallF1 scoreROCAUC
Adipose0.89020.87880.74770.80800.8375
Adrenal0.89360.90660.85730.88130.8845
Brain0.86010.85550.80540.82970.7770
Brain_R0.93930.90160.64450.75170.5561
Breast0.87510.83030.85940.84460.8501
Colon0.87050.83020.74830.78710.8236
Foreskin_R0.95030.82050.45070.58180.7215
Heart0.89020.88750.70580.78630.6596
LF_r10.89940.88680.54650.67630.6556
LF_r20.97400.77270.32080.45330.7186
Kidney0.84800.85850.76650.80990.7995
Liver0.87280.80620.53470.64300.5528
Lung0.82310.74840.82230.78360.8439
Lymph node0.87510.83180.83930.83560.9018
Ovary0.84800.90480.74320.81600.7531
Placenta_R0.91040.80950.51130.62670.7615
Prostate0.85490.83270.85570.84410.8825
Skeletal muscle0.89540.83200.61030.70410.6988
Testes0.89360.89220.99440.94050.8336
Testes_R0.90290.92880.92970.92920.9601
Thyroid0.86990.85770.84200.84980.8661
White blood cell0.86470.81870.63810.71720.7342
Table 4
Open in new tab

Label-wise analysis of MLCDForest

TissueAccuracyPrecisionRecallF1 scoreROCAUC
Adipose0.89020.87880.74770.80800.8375
Adrenal0.89360.90660.85730.88130.8845
Brain0.86010.85550.80540.82970.7770
Brain_R0.93930.90160.64450.75170.5561
Breast0.87510.83030.85940.84460.8501
Colon0.87050.83020.74830.78710.8236
Foreskin_R0.95030.82050.45070.58180.7215
Heart0.89020.88750.70580.78630.6596
LF_r10.89940.88680.54650.67630.6556
LF_r20.97400.77270.32080.45330.7186
Kidney0.84800.85850.76650.80990.7995
Liver0.87280.80620.53470.64300.5528
Lung0.82310.74840.82230.78360.8439
Lymph node0.87510.83180.83930.83560.9018
Ovary0.84800.90480.74320.81600.7531
Placenta_R0.91040.80950.51130.62670.7615
Prostate0.85490.83270.85570.84410.8825
Skeletal muscle0.89540.83200.61030.70410.6988
Testes0.89360.89220.99440.94050.8336
Testes_R0.90290.92880.92970.92920.9601
Thyroid0.86990.85770.84200.84980.8661
White blood cell0.86470.81870.63810.71720.7342
TissueAccuracyPrecisionRecallF1 scoreROCAUC
Adipose0.89020.87880.74770.80800.8375
Adrenal0.89360.90660.85730.88130.8845
Brain0.86010.85550.80540.82970.7770
Brain_R0.93930.90160.64450.75170.5561
Breast0.87510.83030.85940.84460.8501
Colon0.87050.83020.74830.78710.8236
Foreskin_R0.95030.82050.45070.58180.7215
Heart0.89020.88750.70580.78630.6596
LF_r10.89940.88680.54650.67630.6556
LF_r20.97400.77270.32080.45330.7186
Kidney0.84800.85850.76650.80990.7995
Liver0.87280.80620.53470.64300.5528
Lung0.82310.74840.82230.78360.8439
Lymph node0.87510.83180.83930.83560.9018
Ovary0.84800.90480.74320.81600.7531
Placenta_R0.91040.80950.51130.62670.7615
Prostate0.85490.83270.85570.84410.8825
Skeletal muscle0.89540.83200.61030.70410.6988
Testes0.89360.89220.99440.94050.8336
Testes_R0.90290.92880.92970.92920.9601
Thyroid0.86990.85770.84200.84980.8661
White blood cell0.86470.81870.63810.71720.7342

Discussion

As an alternative to deep learning, deep forest has been proven to be very powerful in the single-label classification in practice. However, most of practical biology classifications are multi-label classification problem. As one of the novel implementations and application of the standard deep forest model (gcForest), we emphasize the correlation and concurrence of labels in the data transformation. It is shown to be an effective method in the multi-label classification to lncRNA-disease associations. Our MLCDForest method provides an effective option to investigate multi-label classification by using deep learning on small-scale biology datasets.

Based on the data to associations between specific disease and lncRNAs [40], MLCDForest is compared with other multi-label classification approaches in the performance metrics. The proposed model has achieved the best performance on the dataset with original features. In the present study, we made an initial and rough attempt to incorporate the label correlation in sequential manner into the deep forest framework. In further study, we will test our proposed approach on more strictly experimental settings and apply it on more similar bioinformatics problems. Based on various types of association between ncRNAs, ncRNAs and disease, ncRNA and drug targets, small molecules and ncRNAs, genome analysis applications, etc. [43–48], we should perform further evaluation based on other independent dataset (i.e., association between miRNA–circRNA associations).

Key Points

  • Predicting lncRNA-tissue association using computational methods is very important in disease diagnosis and therapy.

  • Label correlation is considered in multi-label classification with frame of MLCDForest

Funding

Dong-Qing Wei is supported by the grants from the Key Research Area Grant 2016YFA0501703 of the Ministry of Science and Technology of China, the National Natural Science Foundation of China (Contract no. 61832019, 61503244), the Science and Technology Commission of Shanghai Municipality (Grant: 19430750600), the Natural Science Foundation of Henan Province (162300410060) and Joint Research Funds for Medical and Engineering and Scientific Research at Shanghai Jiao Tong University (YG2017ZD14). The computations were partially performed at the Peng Cheng Lab and the Center for High-Performance Computing, Shanghai Jiao Tong University.

Wei Wang is a PhD student at the School of Mathematical Sciences, Shanghai Jiao Tong University. He works on statistical learning algorithm for the drug discovery.

Qiuying Dai is a PhD student at the School of Life Sciences and Biotechnology, Shanghai Jiao Tong University. She works on predicting circRNA-disease associations through machine learning methods.

Fang Li is a lecturer at the School of Life Sciences and Biotechnology, Shanghai Jiao Tong University. She works on drug discovery through machine learning methods and molecular simulation.

Yi Xiong is an associate professor at the School of Life Sciences and Biotechnology, Shanghai Jiao Tong University. His main research interests focus on machine learning algorithms and their applications in the protein sequence–structure–function relationship and biomedicine.

Dong-Qing Wei is a full professor at the School of Life Sciences and Biotechnology, Shanghai Jiao Tong University, State Key Laboratory of Microbial Metabolism and Joint Laboratory of International Cooperation in Metabolic and Developmental Sciences, Ministry of Education, Shanghai Jiao Tong University and Peng Cheng Laboratory, Vanke Cloud City Phase I Building 8, Xili Street, Nanshan District, Shenzhen, Guangdong. His main research areas include structural bioinformatics and biomedicine.

References

1.

Guttman
M
,
Amit
I
,
Garber
M
, et al.
Chromatin signature reveals over a thousand highly conserved large non-coding RNAs in mammals
.
Nature
2009
;
458
:
223
–
7
.

Google Scholar

Crossref
Search ADS
PubMed

 
2.

Pasmant
E
,
Sabbagh
A
,
Vidaud
M
, et al.
ANRIL, a long, noncoding RNA, is an unexpected major hotspot in GWAS
.
FASEB J
2011
;
25
:
444
–
8
.

Google Scholar

Crossref
Search ADS
PubMed

 
3.

Congrains
A
,
Kamide
K
,
Oguro
R
, et al.
Genetic variants at the 9p21 locus contribute to atherosclerosis through modulation of ANRIL and CDKN2A/B
.
Atherosclerosis
2012
;
220
:
449
–
55
.

Google Scholar

Crossref
Search ADS
PubMed

 
4.

Zhang
Q
,
Chen
C-Y
,
Yedavalli
VSRK
, et al.
NEAT1 long noncoding RNA and paraspeckle bodies modulate HIV-1 posttranscriptional expression
.
MBio
2013
;
4
:
e00596
–
12
.

Google Scholar

Crossref
Search ADS
PubMed

 
5.

Johnson
R
.
Long non-coding RNAs in Huntington’s disease neurodegeneration
.
Neurobiol Dis
2012
;
46
:
245
–
54
.

Google Scholar

Crossref
Search ADS
PubMed

 
6.

Ji
P
,
Diederichs
S
,
Wang
W
, et al.
MALAT-1, a novel noncoding RNA, and thymosin beta4 predict metastasis and survival in early-stage non-small cell lung cancer
.
Oncogene
2003
;
22
:
8031
–
41
.

Google Scholar

Crossref
Search ADS
PubMed

 
7.

Gupta
RA
,
Shah
N
,
Wang
KC
, et al.
Long non-coding RNA HOTAIR reprograms chromatin state to promote cancer metastasis
.
Nature
2010
;
464
:
1071
–
6
.

Google Scholar

Crossref
Search ADS
PubMed

 
8.

Széll
M
,
Bata-Csörgo
Z
,
Kemény
L
.
The enigmatic world of mRNA-like ncRNAs: their role in human evolution and in human diseases
.
Semin Cancer Biol
2008
;
18
:
141
–
8
.

Google Scholar

Crossref
Search ADS
PubMed

 
9.

Chen
X
,
Yan
CC
,
Zhang
X
, et al.
Long non-coding RNAs and complex diseases: from experimental results to computational models
.
Brief Bioinform
2017
;
18
:
558
–
76
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
10.

Fan
XN
,
Zhang
SW
,
Zhang
SY
, et al.
Prediction of lncRNA-disease associations by integrating diverse heterogeneous information sources with RWR algorithm and positive pointwise mutual information
.
BMC Bioinform
2019
;
20
:
87
.

Google Scholar

Crossref
Search ADS

 
11.

Li
Y
,
Li
J
,
Bian
N
.
DNILMF-LDA: prediction of lncrna-disease associations by dual-network integrated logistic matrix factorization and Bayesian optimization
.
Genes (Basel)
2019
;
10
:
608
. doi:
10.3390/genes10080608
.

Google Scholar

Crossref
Search ADS

 
12.

Zhang
J
,
Zhang
Z
,
Chen
Z
, et al.
Integrating multiple heterogeneous networks for novel LncRNA-disease association inference
.
IEEE/ACM Trans Comput Biol Bioinform
2019
;
16
:
396
–
406
.

Google Scholar

Crossref
Search ADS
PubMed

 
13.

Yang
X
,
Gao
L
,
Guo
X
, et al.
A network based method for analysis of lncRNA-disease associations and prediction of lncRNAs implicated in diseases
.
PLoS One
2014
;
9
:
1
–
10
. doi:
10.1371/journal.pone.0087797
.

Google Scholar

Crossref
Search ADS

 
14.

Sun
J
,
Shi
H
,
Wang
Z
, et al.
Inferring novel lncRNA-disease associations based on a random walk model of a lncRNA functional similarity network
.
Mol Biosyst
2014
;
10
:
2074
–
81
.

Google Scholar

Crossref
Search ADS
PubMed

 
15.

Ou-Yang
L
,
Huang
J
,
Zhang
XF
, et al.
LncRNA-disease association prediction using two-side sparse self-representation
.
Front Genet
2019
;
10
:
476
. doi:
10.3389/fgene.2019.00476
.

Google Scholar

Crossref
Search ADS
PubMed

 
16.

Chen
X
,
Yan
G-Y
.
Novel human lncRNA–disease association inference based on lncRNA expression profiles
.
Bioinformatics
2013
;
29
:
2617
–
24
.

Google Scholar

Crossref
Search ADS
PubMed

 
17.

Fu
G
,
Wang
J
,
Domeniconi
C
, et al.
Matrix factorization-based data fusion for the prediction of lncRNA-disease associations
.
Bioinformatics
2018
;
34
:
1529
–
37
.

Google Scholar

Crossref
Search ADS
PubMed

 
18.

Xie
G
,
Huang
Z
,
Liu
Z
, et al.
NCPHLDA: a novel method for human lncRNA-disease association prediction based on network consistency projection
.
Mol Omi
2019
;
15
:
442
–
50
.

Google Scholar

Crossref
Search ADS

 
19.

Chen
G
,
Wang
Z
,
Wang
D
, et al.
LncRNADisease a database for long-non-coding RNA-associated diseases
.
Nucleic Acids Res
2013
;
41
:
983
–
6
.

Google Scholar

Crossref
Search ADS

 
20.

Tsoumakas
G
,
Katakis
I
.
Multi-label classification: an overview
.
INT J DATA Warehous Min
2007
;
2007
:
1
–
13
.

Google Scholar

OpenURL Placeholder Text

 
21.

Zhang
ML
,
Zhou
ZH
.
A review on multi-label learning algorithms
.
IEEE Trans Knowl Data Eng
2014
;
26
:
1819
–
37
.

Google Scholar

Crossref
Search ADS

 
22.

Tsoumakas
G
,
Vlahavas
I
.
Random k-Labelsets: An Ensamble Method for Multilabel Classification, ECML’07 Proceedings of the 18th European conference on Machine Learning
,
2007
.

23.

Zhou
ZH
,
Feng
J
. Deep forest: Towards an alternative to deep neural networks. In:
IJCAI International Joint Conference on Artificial Intelligence
,
2017
.

24.

Guo
Y
,
Liu
S
,
Li
Z
, et al.
BCDForest: a boosting cascade deep forest model towards the classification of cancer subtypes based on gene expression data
.
BMC Bioinform
2018
;
19
:
118
. doi:
10.1186/s12859-018-2095-4
.

Google Scholar

Crossref
Search ADS

 
25.

Yu
Y
,
Pedrycz
W
,
Miao
D
.
Multi-label classification by exploiting label correlations
.
Expert Syst Appl
2014
;
41
:
2989
–
3004
.

Google Scholar

Crossref
Search ADS

 
26.

Huang
S-J
,
Zhou
Z-H
.
Multi-label learning by exploiting label correlations locally
.
AAAI
2012
;
949
–
955
.

Google Scholar

OpenURL Placeholder Text

 
27.

Cramér
H
.
Mthematical Methods of Statitics
.
Princeton
:
Princeton University Press
,
1946
.

Google Scholar

OpenURL Placeholder Text

 
28.

Sheskin
D.
Handbook of Parametric and Nonparametric Statistical Procedures
. Boca Raton: Chapman & Hall/CRC,
2011
.

29.

Bergsma
W
.
A bias-correction for Cramér’s V and Tschuprow’s T
.
J Korean Stat Soc
2013
;
42
:
323
–
8
.

Google Scholar

Crossref
Search ADS

 
30.

Charte
F
,
Rivera
A
,
Del Jesus
MJ
, et al. Concurrence among imbalanced labels and its influence on multilabel resampling algorithms. In:
Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics)
, Vol.
8480
.
LNAI
:
Springer Verlag
,
2014
,
110
–
21
.

Google Scholar

OpenURL Placeholder Text

 
31.

Charte
F
,
Charte
D
.
Working with multilabel datasets in R: the mldr package
.
R J
2015
;
7
:
149
–
62
.

Google Scholar

Crossref
Search ADS

 
32.

Charte
F
,
Rivera
AJ
,
del
Jesus
MJ
, et al.
Addressing imbalance in multilabel classification: measures and random resampling algorithms
.
Neurocomputing
2015
;
163
:
3
–
16
.

Google Scholar

Crossref
Search ADS

 
33.

Zhou
Z-H
,
Feng
J
.
Deep Forest: Towards an Alternative to Deep Neural Networks.
In:
Proceedings of the 26th International Joint Conference on Artificial Intelligence
, IJCAI’17: Melbourne, Australia,
2017
,
3553
–
3559
.

34.

De Boer
P-T
,
Kroese
DP
,
Rubinstein
RY
.
A Tutorial on the Cross-Entropy Method
.
Annals of Operations Research
,
2005
;
134
:
19
–
67
.

35.

Rao
RB
,
Fung
G
,
Rosales
R
.
On the Dangers of Cross-Validation. An Experimental Evaluation.
In: Society for Industrial and Applied Mathematics - 8th SIAM International Conference on Data Mining 2008, Proceedings in Applied Mathematics
, Vol.
2
.
2008
,
588
–
596
. doi:
10.1137/1.9781611972788.54
.

36.

Hastie
T
,
Tibshirani
R
,
Friedman
J
.
Elements of statistical learning 2nd ed
.
Elements
2009
;
27
:
745
.

Google Scholar

OpenURL Placeholder Text

 
37.

Madjarov
G
,
Kocev
D
,
Gjorgjevikj
D
, et al.
An extensive experimental comparison of methods for multi-label learning
.
Pattern Recognition
2012
;
45
:
3084
–
104
.

Google Scholar

Crossref
Search ADS

 
38.

Hinton
GE
,
Salakhutdinov
RR
.
Reducing the dimensionality of data with neural networks
.
Science (80-)
2006
;
313
:
504
–
7
.

Google Scholar

Crossref
Search ADS

 
39.

Read
J
,
Reutemann
P
,
Pfahringer
B
, et al.
MEKA: a multi-label/multi-target extension to WEKA
.
J Mach Learn Res
2016
;
17
:
1
–
5
.

Google Scholar

OpenURL Placeholder Text

 
40.

Biswas
AK
,
Zhang
B
,
Wu
X
, et al. A multi-label classification framework to predict disease associations of long non-coding RNAs (IncRNAs). In:
Lecture Notes in Electrical Engineering
, Vol.
322
.
Springer Verlag: Cham, Switzerland
,
2015
,
821
–
30
.

Google Scholar

OpenURL Placeholder Text

 
41.

Cabili
M
,
Trapnell
C
,
Goff
L
, et al.
Integrative annotation of human large intergenic noncoding RNAs reveals global properties and specific subclasses
.
Genes Dev
2011
;
25
:
1915
–
27
.

Google Scholar

Crossref
Search ADS
PubMed

 
42.

Szymański
P
,
Kajdanowicz
T
.
Scikit-multilearn: a scikit-based python environment for performing multi-label classification
.
J Mach Learn Res
2019
;
20
:
209
–
30
.

Google Scholar

OpenURL Placeholder Text

 
43.

Fang
Z
,
Lei
X
.
Prediction of miRNA-circRNA associations based on k-NN multi-label with random walk restart on a heterogeneous network
.
Big Data Min Anal
2019
;
2
:
261
–
72
.

Google Scholar

Crossref
Search ADS

 
44.

Yu
N
,
Li
Z
,
Yu
Z
.
Survey on encoding schemes for genomic data representation and feature learning—from signal processing to machine learning
.
Big Data Min Anal
2018
;
1
:
191
–
210
.

Google Scholar

OpenURL Placeholder Text

 
45.

Chen
X
,
Guan
N-N
,
Sun
Y-Z
, et al.
MicroRNA-small molecule association identification: from experimental results to computational models
.
Brief Bioinform
2018
;
21
:
47
–
61
. doi:
10.1093/bib/bby098
.

Google Scholar

Crossref
Search ADS

 
46.

Lin
YC
,
Lee
YC
,
Chang
KL
, et al.
Analysis of common targets for circular RNAs
.
BMC Bioinformatics
2019
;
20
:
372
.

Google Scholar

Crossref
Search ADS
PubMed

 
47.

Wang
WT
,
Han
C
,
Sun
YM
, et al.
Noncoding RNAs in cancer therapy resistance and targeted drug development
.
J Hematol Oncol
2019
;
12
:
1
–
15
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
48.

Ling
H
,
Fabbri
M
,
Calin
GA
.
MicroRNAs and other non-coding RNAs as targets for anticancer drug development
.
Nat Rev Drug Discov
2013
;
12
:
847
–
65
.

Google Scholar

Crossref
Search ADS
PubMed

 
© The Author(s) 2020. Published by Oxford University Press. All rights reserved. For Permissions, please email: [email protected]
This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)
Issue Section:
Problem solving protocol
Download all slides
  • Supplementary data

    • Supplementary data

    MLCDF_bbaa104 - docx file