Search
Close
Search
Advanced Search
Search Menu
AI Discovery Assistant

Abstract

Linkage analysis has played an important role in understanding genome structure and evolution. However, two-point linkage analysis widely used for genetic map construction can rarely chart a detailed picture of genome organization because it fails to identify the dependence of crossovers distributed along the length of a chromosome, a phenomenon known as crossover interference. Multi-point analysis, proven to be more advantageous in gene ordering and genetic distance estimation for dominant markers than two-point analysis, is equipped with a capacity to discern and quantify crossover interference. Here, we review a statistical model for four-point analysis, which, beyond three-point analysis, can characterize crossover interference that takes place not only between two adjacent chromosomal intervals, but also over multiple successive intervals. This procedure provides an analytical tool to elucidate the detailed landscape of crossover interference over the genome and further infer the evolution of genome structure and organization.

multi-point linkage analysis, crossover interference, EM algorithm, high-order crossover interference

Introduction

Linkage, a phenomenon by which adjacent genes on the same chromosomal region tend to be inherited together, has been extensively investigated since its first discovery by several pioneering geneticists [1]. By measuring the frequency with which a single chromosomal crossover (chiasmata) takes place between two genes during meiosis, known as the recombination fraction, linkage analysis has served as a primary tool of gene localization and ordering. The past several decades have seen the tremendous application of linkage analysis to mapping and identifying causal genes that affect Mendelian diseases or quantitative traits [2–5]. Although linkage mapping was largely replaced by genome-wide association studies during the past few years, its potential to identify genes involved in disease etiology has been recognized and reactivated by the increasing availability of family-based exome and whole-genome sequence data [6, 7]. Apart from its application for gene mapping, linkage analysis has been instrumental for comparative analysis of genome structure and organization from which the evolution of sexually reproducing organisms in response to environmental changes can be inferred [8]. For example, heterochiasmy, i.e. differences between female and male recombination fractions, regarded as an important evolutionary force shaping the nucleotide landscape of sex-specific genomes, can well be studied through linkage analysis [9].

Two-point analysis is the most basic approach for linkage analysis and has been extended to multi-point analysis that analyzes information from many markers simultaneously [2, 4]. Multi-point analysis has been widely used to construct genetic linkage maps that describe the frequency and distribution of meiotic crossovers along a chromosome within a population. However, traditional multi-point analysis ignores crossover interference [4], although the assumption may not conform to the actual existence of interference. As a phenomenon by which the occurrence of one crossing-over interferes with the coincident occurrence of another crossing-over in the same pair of chromosomes [10], crossover interference has been recognized to play a more important role in evolution and speciation than previously appreciated [11–18]. A new three-point analysis that analyzes simultaneously the linkage relationship among three adjacent markers has been developed to estimate the magnitude and distribution of crossover interference along a chromosome [19–21]. This approach can also improve the gene ordering and the estimation precision of linkage for dominant-inherited markers [22], and it has been modified to accommodate the different types of populations including controlled crosses [22], natural human family populations [23] and open-pollinated plant populations [24, 25].

Three-point analysis has an adequate degree of freedom that allows it not to rely on the hypothesis that the recombination events between two adjacent marker intervals are independent, thus providing a possibility to estimate crossover interference [26, 27]. Nevertheless, it is possible that interference occurs simultaneously between more than two marker intervals in marker-dense chromosomal regions to form high-order crossover interference (Figure 1). Despite its importance, this issue has not been reviewed and assessed in the literature. In this article, we argue that well-developed three-point analysis can be extended to perform linkage analysis using more than three markers. Such an extension opens an avenue to estimate and test crossover interference that may take place along multiple intervals across a chromosome. We show that four-point analysis can not only preserve the statistical properties of parameter estimation characteristic of two- and three-point analysis, but also provide additional information about how multiple marker intervals interfere with each other to affect genome structure.

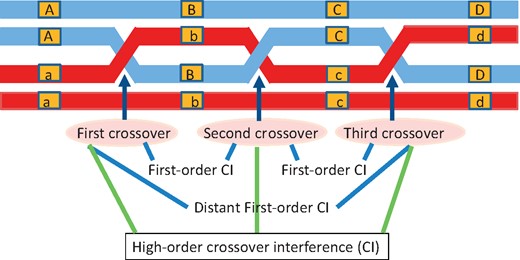
Diagram of the occurrence of crossover interference (CI) of different orders among markers A–D over a chromosome.
Figure 1

Diagram of the occurrence of crossover interference (CI) of different orders among markers A–D over a chromosome.

Open in new tabDownload slide

Four-point analysis for the backcross

Estimation

Suppose there is a backcross mapping population of n progeny in which a suite of molecular markers was generated. Consider four-order markers, A-B-C-D, with alleles A versus a, B versus b, C versus c and D versus d, respectively. Thus, backcross ABCD/abcd × abcd/abcd generates 16 marker genotypes in the progeny, each exactly corresponding to its gamete genotype contributed by the heterozygote F1. During meiosis, two homologous chromosomes of the F1 each duplicate into sister chromatids that crossover between markers A and B (first crossover), between markers B and C (second crossover) and between markers C and D (third crossover) (Figure 1). Crossover interference may occur if the occurrence of one crossover affects the occurrence of other crossovers nearby. In this four-marker case, crossover interference takes place between the first and the second crossover, between the second and the third crossover, between the first and the third crossover and jointly among the three crossovers. The first two crossover interferences have been explored in the genetic literature, but we are ignorant of the last two. Four-point analysis can reveal these two unexplored types of crossover interference.

By denoting the capital allele by 1 and the lower-case allele by 0 for a particular gamete produced by the heterozygote F1 (Figure 1), we define the observations of each progeny genotype (Table 1). All 16 distinguishable gametes produced by heterozygote F1 are classified into eight types based on the numbers of crossovers between marker pairs A and B, B and C and C and D (Table 1). These eight types are as follows:
Table 1
Open in new tab

Eight gamete types and their frequencies at four ordered markers A-B-C-D produced by the heterozygous F1 parent in a backcross population of n progeny, along with observations of each genotype

No.Gamete typeNumber of crossoversGamete typeFrequencyDiplotypeGenotypeObservation
A-BB-CC-D
1ABCD000g000ABCD|abcdAaBbCcDdn1111
abcdabcd|abcdaabbccddn0000
2ABCd001g001ABCd|abcdAaBbCcddn1110
abcDabcD|abcdaabbccDdn0001
3ABcd010g010ABcd|abcdAaBbccddn1100
abCDabCD|abcdaabbCcDdn0011
4ABcD011g011ABcD|abcdAaBbccDdn1101
abCdabCd|abcdaabbCcddn0010
5Abcd100g100Abcd|abcdAabbccddn1000
aBCDaBCD|abcdaaBbCcDdn0111
6AbcD101g101AbcD|abcdAabbccDdn1001
aBCdaBCd|abcdaaBbCcddn0110
7AbCD110g110AbCD|abcdAabbCcDdn1011
aBcdaBcd|abcdaaBbccddn0100
8AbCd111g111AbCd|abcdAabbCcddn1010
aBcDaBcD|abcdaaBbccDdn0101
No.Gamete typeNumber of crossoversGamete typeFrequencyDiplotypeGenotypeObservation
A-BB-CC-D
1ABCD000g000ABCD|abcdAaBbCcDdn1111
abcdabcd|abcdaabbccddn0000
2ABCd001g001ABCd|abcdAaBbCcddn1110
abcDabcD|abcdaabbccDdn0001
3ABcd010g010ABcd|abcdAaBbccddn1100
abCDabCD|abcdaabbCcDdn0011
4ABcD011g011ABcD|abcdAaBbccDdn1101
abCdabCd|abcdaabbCcddn0010
5Abcd100g100Abcd|abcdAabbccddn1000
aBCDaBCD|abcdaaBbCcDdn0111
6AbcD101g101AbcD|abcdAabbccDdn1001
aBCdaBCd|abcdaaBbCcddn0110
7AbCD110g110AbCD|abcdAabbCcDdn1011
aBcdaBcd|abcdaaBbccddn0100
8AbCd111g111AbCd|abcdAabbCcddn1010
aBcDaBcD|abcdaaBbccDdn0101
Table 1
Open in new tab

Eight gamete types and their frequencies at four ordered markers A-B-C-D produced by the heterozygous F1 parent in a backcross population of n progeny, along with observations of each genotype

No.Gamete typeNumber of crossoversGamete typeFrequencyDiplotypeGenotypeObservation
A-BB-CC-D
1ABCD000g000ABCD|abcdAaBbCcDdn1111
abcdabcd|abcdaabbccddn0000
2ABCd001g001ABCd|abcdAaBbCcddn1110
abcDabcD|abcdaabbccDdn0001
3ABcd010g010ABcd|abcdAaBbccddn1100
abCDabCD|abcdaabbCcDdn0011
4ABcD011g011ABcD|abcdAaBbccDdn1101
abCdabCd|abcdaabbCcddn0010
5Abcd100g100Abcd|abcdAabbccddn1000
aBCDaBCD|abcdaaBbCcDdn0111
6AbcD101g101AbcD|abcdAabbccDdn1001
aBCdaBCd|abcdaaBbCcddn0110
7AbCD110g110AbCD|abcdAabbCcDdn1011
aBcdaBcd|abcdaaBbccddn0100
8AbCd111g111AbCd|abcdAabbCcddn1010
aBcDaBcD|abcdaaBbccDdn0101
No.Gamete typeNumber of crossoversGamete typeFrequencyDiplotypeGenotypeObservation
A-BB-CC-D
1ABCD000g000ABCD|abcdAaBbCcDdn1111
abcdabcd|abcdaabbccddn0000
2ABCd001g001ABCd|abcdAaBbCcddn1110
abcDabcD|abcdaabbccDdn0001
3ABcd010g010ABcd|abcdAaBbccddn1100
abCDabCD|abcdaabbCcDdn0011
4ABcD011g011ABcD|abcdAaBbccDdn1101
abCdabCd|abcdaabbCcddn0010
5Abcd100g100Abcd|abcdAabbccddn1000
aBCDaBCD|abcdaaBbCcDdn0111
6AbcD101g101AbcD|abcdAabbccDdn1001
aBCdaBCd|abcdaaBbCcddn0110
7AbCD110g110AbCD|abcdAabbCcDdn1011
aBcdaBcd|abcdaaBbccddn0100
8AbCd111g111AbCd|abcdAabbCcddn1010
aBcDaBcD|abcdaaBbccDdn0101

  1. Gametes ABCD and abcd:there are no crossovers for each pair,

  2. Gametes ABCd and abcD: there is only a crossover from the third pair,

  3. Gametes ABcd and abCD: there is only a crossover from the second pair,

  4. Gametes ABcD and abCd: there are crossovers from the second and third pair,

  5. Gametes Abcd and aBCD: there is only a crossover from the first pair,

  6. Gametes AbcD and aBCd: there are crossovers from the first and third pair,

  7. Gametes AbCD and aBcd: there are crossovers from the first and second pair,

  8. Gametes AbCd and aBcD: there are crossovers for each pair.

Denote g000, …, g111 as the frequencies of these gamete types where the subscript stands for the number of crossovers between a particular pair of markers. From these gamete-type frequencies, we can express the recombination fractions of each marker pair, denoted by rAB, rBC, rCD, rAC, rBD and rAD, as follows:
(1)
with g’s ≥ 0 and 0 ≤ r’s ≤ 0.5.
As we have known, the recombination events occurring between different marker intervals are not independent [18, 21]. Denote the coefficients of coincidence (a measure of crossover interference) between double marker intervals A-B and B-C, double marker intervals B-C and C-D, double marker intervals A-B and C-D and triple marker intervals A-B, B-C and C-D by C1, C2, C3 and C4, respectively. It is not difficult to derive the expression of coincidence from the relationship between the gamete-type frequencies and recombination fractions as follows:
(2a)
(2b)
(2c)
(2d)
For any two markers that are separated by an intermediate marker, their recombination fraction is contributed by only one recombinant that occurs either between the left marker and intermediate marker or between the intermediate marker and right marker. Under the crossover interference, we obtain the recombination fractions between any two separated markers as follows:
(3a)
(3b)
(3c)
Under the assumption of independence, i.e. no crossover interference, Equations (3a)–(3c) are reduced as follows:
(4a)
(4b)
(4c)
To estimate the recombination fractions and coefficients of coincidence, we need first to estimate the gamete-type frequencies. From Table 1, it is straightforward to formulate the log-likelihood,
from which the maximum likelihood estimate of gamete-type frequencies can be obtained as follows:
(5)
where n…. denotes the observation of a gamete (and therefore genotype) subscripted by the allele type (1 for the capital allele and 0 for the lowercase allele) at a particular marker.

Hypothesis tests

After r’s and C’s are estimated, we need to make a few important hypothesis tests. First, hypotheses should be made to test whether a particular pair of markers is linked. The null hypotheses for this test (there is no linkage) are written as follows:
(6a)
(6b)
(6c)
(6d)
(6e)
(6f)
The estimation of g’s under each of these null hypotheses can be made through a constraint obtained from Equation (1). The log-likelihood ratios under the null and alternative hypotheses are calculated and compared against the critical threshold obtained from a chi-square distribution with one degree of freedom.
Second, we need to test whether and how crossover interference occurs. This can be done by formulating the null hypotheses for the coefficients of coincidence:
(7a)
(7b)
(7c)
(7d)
The rejection of any of the null hypotheses mentioned above suggests that crossovers between two corresponding marker intervals are not independent, i.e. there is crossover interference. The estimation of g’s under null hypotheses (7a)–(7d) is obtained by constructing a constraint from Equations (2a)–(2d), respectively. In addition, by testing whether C is equal to 0, we can characterize whether there is an occurrence of triple crossovers (C4 ≠ 0) and double crossovers (C1, C2 or C3 ≠ 0).

Evaluation by computer simulation

Simulation studies were carried out to test statistical properties of the four-point analysis model. Consider four ordered markers in a backcross population, which were simulated by assuming recombinant fractions rAB = 0.05, rBC = 0.15 and rCD = 0.3 with coefficients of coincidence C1 = 2, C2 = 0, C3 = 1 and C4 = 0, 1 or 2. This simulation design covers several typical situations, i.e. strong versus week linkage, interference versus no interference and double recombination versus no double recombination. Depending on the value of C4, this design has three scenarios: (i) there is a strong high-order interference (C4 = 2), (ii) there is a triple recombination (C4 = 0) and (iii) there is no high-order interference (C4 = 1). Two different sample sizes, n = 200 or n = 400, were considered. From these parameters, we obtained gamete-type frequencies using the following expressions:
from which we can obtain the numbers of each backcross genotype.

Table 2 gives the results about parameter estimation by four-point analysis. In general, the recombination fractions can be reasonably well estimated for a moderate sample size (n = 200), regardless of the degree of linkage and crossover interference. Notably, the estimation of low-order crossover interference can be well estimated with a moderate sample size, but the estimation precision of high-order crossover interference hinges more strongly on sample size. A large sample size (n = 400) is needed to obtain precise estimation of high-order crossover interference. The estimation of the recombination fraction is not affected by the occurrence of crossover interference (Table 2); that is, the linkage can be well estimated, regardless of whether there is a crossover interference.

Table 2
Open in new tab

Simulation results under different scenarios of occurrence of high-order crossover interference for a backcross of different sample sizes estimated by four-point analysis, in comparison with those by two- and three-point analysis. The standard errors of parameter estimates are given in parentheses

Scenario 1
Scenario 2
Scenario 3
MethodsTruen = 200n = 400Truen = 200n = 400Truen = 200n = 400
Four-point Analysis
 rAB0.050.041(0.013)0.042(0.099)0.050.051(0.016)0.049(0.009)0.050.044(0.014)0.046(0.010)
 rBC0.150.155(0.026)0.157(0.016)0.150.146(0.024)0.152(0.017)0.150.154(0.024)0.149(0.019)
 rCD0.30.309(0.030)0.302(0.021)0.30.302(0.038)0.300(0.025)0.30.302(0.038)0.300(0.020)
 rAC0.170.165(0.026)0.169(0.019)0.170.168(0.027)0.171(0.018)0.170.170(0.025)0.162(0.020)
 rBD0.450.455(0.033)0.450(0.025)0.450.449(0.040)0.453(0.025)0.450.452(0.038)0.443(0.024)
 rAD0.4580.453(0.034)0.449(0.024)0.440.438(0.041)0.442(0.026)0.4490.445(0.040)0.436(0.023)
 C122.455(1.141)2.301(0.818)22.040(1.087)2.042(0.694)22.080(1.140)2.367(0.755)
 C200.091(0.100)0.093(0.066)00.000(0.000)0.000(0.000)00.041(0.060)0.065(0.058)
 C311.218(0.564)1.217(0.388)11.084(0.493)1.003(0.347)11.154(0.605)1.169(0.395)
 C422.390(2.746)2.161(1.405)00.000(0.000)0.000(0.000)10.934(1.442)1.425(1.283)
Two-point Analysis
 rAB0.050.039(0.014)0.043(0.011)0.050.048(0.017)0.048(0.010)0.050.047(0.016)0.043(0.011)
 rBC0.150.146(0.024)0.155(0.019)0.150.152(0.025)0.150(0.018)0.150.152(0.024)0.150(0.018)
 rCD0.30.306(0.037)0.302(0.023)0.30.301(0.033)0.300(0.024)0.30.305(0.036)0.300(0.021)
 rAC0.170.158(0.026)0.166(0.021)0.170.172(0.026)0.170(0.019)0.170.170(0.026)0.165(0.017)
 rBD0.450.443(0.039)0.448(0.027)0.450.453(0.035)0.446(0.026)0.450.453(0.039)0.444(0.025)
 rAD0.4580.444(0.040)0.446(0.028)0.440.443(0.035)0.437(0.026)0.4490.447(0.038)0.437(0.025)
 C12––2––2––
 C20––0––0––
 C31––1––1––
 C42––0––1––
Three-point Analysis
 rAB0.050.043(0.016)0.041(0.010)0.050.049(0.016)0.052(0.012)0.050.044(0.014)0.048(0.011)
 rBC0.150.147(0.021)0.154(0.018)0.150.151(0.026)0.152(0.019)0.150.156(0.024)0.152(0.016)
 rCD0.30.307(0.031)0.300(0.024)0.30.300(0.034)0.298(0.022)0.30.300(0.032)0.297(0.023)
 rAC0.170.158(0.025)0.164(0.019)0.170.172(0.027)0.172(0.021)0.170.170(0.024)0.168(0.019)
 rBD0.450.444(0.034)0.444(0.026)0.450.447(0.038)0.450(0.024)0.450.448(0.031)0.445(0.025)
 rAD0.4580.445(0.033)0.444(0.025)0.440.437(0.038)0.440(0.025)0.4490.442(0.031)0.438(0.025)
 C12––2––2––
 C20––0––0––
 C31––1––1––
 C42––0––1––
Scenario 1
Scenario 2
Scenario 3
MethodsTruen = 200n = 400Truen = 200n = 400Truen = 200n = 400
Four-point Analysis
 rAB0.050.041(0.013)0.042(0.099)0.050.051(0.016)0.049(0.009)0.050.044(0.014)0.046(0.010)
 rBC0.150.155(0.026)0.157(0.016)0.150.146(0.024)0.152(0.017)0.150.154(0.024)0.149(0.019)
 rCD0.30.309(0.030)0.302(0.021)0.30.302(0.038)0.300(0.025)0.30.302(0.038)0.300(0.020)
 rAC0.170.165(0.026)0.169(0.019)0.170.168(0.027)0.171(0.018)0.170.170(0.025)0.162(0.020)
 rBD0.450.455(0.033)0.450(0.025)0.450.449(0.040)0.453(0.025)0.450.452(0.038)0.443(0.024)
 rAD0.4580.453(0.034)0.449(0.024)0.440.438(0.041)0.442(0.026)0.4490.445(0.040)0.436(0.023)
 C122.455(1.141)2.301(0.818)22.040(1.087)2.042(0.694)22.080(1.140)2.367(0.755)
 C200.091(0.100)0.093(0.066)00.000(0.000)0.000(0.000)00.041(0.060)0.065(0.058)
 C311.218(0.564)1.217(0.388)11.084(0.493)1.003(0.347)11.154(0.605)1.169(0.395)
 C422.390(2.746)2.161(1.405)00.000(0.000)0.000(0.000)10.934(1.442)1.425(1.283)
Two-point Analysis
 rAB0.050.039(0.014)0.043(0.011)0.050.048(0.017)0.048(0.010)0.050.047(0.016)0.043(0.011)
 rBC0.150.146(0.024)0.155(0.019)0.150.152(0.025)0.150(0.018)0.150.152(0.024)0.150(0.018)
 rCD0.30.306(0.037)0.302(0.023)0.30.301(0.033)0.300(0.024)0.30.305(0.036)0.300(0.021)
 rAC0.170.158(0.026)0.166(0.021)0.170.172(0.026)0.170(0.019)0.170.170(0.026)0.165(0.017)
 rBD0.450.443(0.039)0.448(0.027)0.450.453(0.035)0.446(0.026)0.450.453(0.039)0.444(0.025)
 rAD0.4580.444(0.040)0.446(0.028)0.440.443(0.035)0.437(0.026)0.4490.447(0.038)0.437(0.025)
 C12––2––2––
 C20––0––0––
 C31––1––1––
 C42––0––1––
Three-point Analysis
 rAB0.050.043(0.016)0.041(0.010)0.050.049(0.016)0.052(0.012)0.050.044(0.014)0.048(0.011)
 rBC0.150.147(0.021)0.154(0.018)0.150.151(0.026)0.152(0.019)0.150.156(0.024)0.152(0.016)
 rCD0.30.307(0.031)0.300(0.024)0.30.300(0.034)0.298(0.022)0.30.300(0.032)0.297(0.023)
 rAC0.170.158(0.025)0.164(0.019)0.170.172(0.027)0.172(0.021)0.170.170(0.024)0.168(0.019)
 rBD0.450.444(0.034)0.444(0.026)0.450.447(0.038)0.450(0.024)0.450.448(0.031)0.445(0.025)
 rAD0.4580.445(0.033)0.444(0.025)0.440.437(0.038)0.440(0.025)0.4490.442(0.031)0.438(0.025)
 C12––2––2––
 C20––0––0––
 C31––1––1––
 C42––0––1––
Table 2
Open in new tab

Simulation results under different scenarios of occurrence of high-order crossover interference for a backcross of different sample sizes estimated by four-point analysis, in comparison with those by two- and three-point analysis. The standard errors of parameter estimates are given in parentheses

Scenario 1
Scenario 2
Scenario 3
MethodsTruen = 200n = 400Truen = 200n = 400Truen = 200n = 400
Four-point Analysis
 rAB0.050.041(0.013)0.042(0.099)0.050.051(0.016)0.049(0.009)0.050.044(0.014)0.046(0.010)
 rBC0.150.155(0.026)0.157(0.016)0.150.146(0.024)0.152(0.017)0.150.154(0.024)0.149(0.019)
 rCD0.30.309(0.030)0.302(0.021)0.30.302(0.038)0.300(0.025)0.30.302(0.038)0.300(0.020)
 rAC0.170.165(0.026)0.169(0.019)0.170.168(0.027)0.171(0.018)0.170.170(0.025)0.162(0.020)
 rBD0.450.455(0.033)0.450(0.025)0.450.449(0.040)0.453(0.025)0.450.452(0.038)0.443(0.024)
 rAD0.4580.453(0.034)0.449(0.024)0.440.438(0.041)0.442(0.026)0.4490.445(0.040)0.436(0.023)
 C122.455(1.141)2.301(0.818)22.040(1.087)2.042(0.694)22.080(1.140)2.367(0.755)
 C200.091(0.100)0.093(0.066)00.000(0.000)0.000(0.000)00.041(0.060)0.065(0.058)
 C311.218(0.564)1.217(0.388)11.084(0.493)1.003(0.347)11.154(0.605)1.169(0.395)
 C422.390(2.746)2.161(1.405)00.000(0.000)0.000(0.000)10.934(1.442)1.425(1.283)
Two-point Analysis
 rAB0.050.039(0.014)0.043(0.011)0.050.048(0.017)0.048(0.010)0.050.047(0.016)0.043(0.011)
 rBC0.150.146(0.024)0.155(0.019)0.150.152(0.025)0.150(0.018)0.150.152(0.024)0.150(0.018)
 rCD0.30.306(0.037)0.302(0.023)0.30.301(0.033)0.300(0.024)0.30.305(0.036)0.300(0.021)
 rAC0.170.158(0.026)0.166(0.021)0.170.172(0.026)0.170(0.019)0.170.170(0.026)0.165(0.017)
 rBD0.450.443(0.039)0.448(0.027)0.450.453(0.035)0.446(0.026)0.450.453(0.039)0.444(0.025)
 rAD0.4580.444(0.040)0.446(0.028)0.440.443(0.035)0.437(0.026)0.4490.447(0.038)0.437(0.025)
 C12––2––2––
 C20––0––0––
 C31––1––1––
 C42––0––1––
Three-point Analysis
 rAB0.050.043(0.016)0.041(0.010)0.050.049(0.016)0.052(0.012)0.050.044(0.014)0.048(0.011)
 rBC0.150.147(0.021)0.154(0.018)0.150.151(0.026)0.152(0.019)0.150.156(0.024)0.152(0.016)
 rCD0.30.307(0.031)0.300(0.024)0.30.300(0.034)0.298(0.022)0.30.300(0.032)0.297(0.023)
 rAC0.170.158(0.025)0.164(0.019)0.170.172(0.027)0.172(0.021)0.170.170(0.024)0.168(0.019)
 rBD0.450.444(0.034)0.444(0.026)0.450.447(0.038)0.450(0.024)0.450.448(0.031)0.445(0.025)
 rAD0.4580.445(0.033)0.444(0.025)0.440.437(0.038)0.440(0.025)0.4490.442(0.031)0.438(0.025)
 C12––2––2––
 C20––0––0––
 C31––1––1––
 C42––0––1––
Scenario 1
Scenario 2
Scenario 3
MethodsTruen = 200n = 400Truen = 200n = 400Truen = 200n = 400
Four-point Analysis
 rAB0.050.041(0.013)0.042(0.099)0.050.051(0.016)0.049(0.009)0.050.044(0.014)0.046(0.010)
 rBC0.150.155(0.026)0.157(0.016)0.150.146(0.024)0.152(0.017)0.150.154(0.024)0.149(0.019)
 rCD0.30.309(0.030)0.302(0.021)0.30.302(0.038)0.300(0.025)0.30.302(0.038)0.300(0.020)
 rAC0.170.165(0.026)0.169(0.019)0.170.168(0.027)0.171(0.018)0.170.170(0.025)0.162(0.020)
 rBD0.450.455(0.033)0.450(0.025)0.450.449(0.040)0.453(0.025)0.450.452(0.038)0.443(0.024)
 rAD0.4580.453(0.034)0.449(0.024)0.440.438(0.041)0.442(0.026)0.4490.445(0.040)0.436(0.023)
 C122.455(1.141)2.301(0.818)22.040(1.087)2.042(0.694)22.080(1.140)2.367(0.755)
 C200.091(0.100)0.093(0.066)00.000(0.000)0.000(0.000)00.041(0.060)0.065(0.058)
 C311.218(0.564)1.217(0.388)11.084(0.493)1.003(0.347)11.154(0.605)1.169(0.395)
 C422.390(2.746)2.161(1.405)00.000(0.000)0.000(0.000)10.934(1.442)1.425(1.283)
Two-point Analysis
 rAB0.050.039(0.014)0.043(0.011)0.050.048(0.017)0.048(0.010)0.050.047(0.016)0.043(0.011)
 rBC0.150.146(0.024)0.155(0.019)0.150.152(0.025)0.150(0.018)0.150.152(0.024)0.150(0.018)
 rCD0.30.306(0.037)0.302(0.023)0.30.301(0.033)0.300(0.024)0.30.305(0.036)0.300(0.021)
 rAC0.170.158(0.026)0.166(0.021)0.170.172(0.026)0.170(0.019)0.170.170(0.026)0.165(0.017)
 rBD0.450.443(0.039)0.448(0.027)0.450.453(0.035)0.446(0.026)0.450.453(0.039)0.444(0.025)
 rAD0.4580.444(0.040)0.446(0.028)0.440.443(0.035)0.437(0.026)0.4490.447(0.038)0.437(0.025)
 C12––2––2––
 C20––0––0––
 C31––1––1––
 C42––0––1––
Three-point Analysis
 rAB0.050.043(0.016)0.041(0.010)0.050.049(0.016)0.052(0.012)0.050.044(0.014)0.048(0.011)
 rBC0.150.147(0.021)0.154(0.018)0.150.151(0.026)0.152(0.019)0.150.156(0.024)0.152(0.016)
 rCD0.30.307(0.031)0.300(0.024)0.30.300(0.034)0.298(0.022)0.30.300(0.032)0.297(0.023)
 rAC0.170.158(0.025)0.164(0.019)0.170.172(0.027)0.172(0.021)0.170.170(0.024)0.168(0.019)
 rBD0.450.444(0.034)0.444(0.026)0.450.447(0.038)0.450(0.024)0.450.448(0.031)0.445(0.025)
 rAD0.4580.445(0.033)0.444(0.025)0.440.437(0.038)0.440(0.025)0.4490.442(0.031)0.438(0.025)
 C12––2––2––
 C20––0––0––
 C31––1––1––
 C42––0––1––

The simulated marker data were further analyzed by two- and three-point analysis. It can be seen that these approaches can also provide good estimates of the recombination fractions (Table 2), again suggesting that crossover interference does not affect the identification of linkage by two- or three-point analysis. The power of linkage analysis has been investigated previously (Lu et al. 2004). Here, we focus on the power analysis of detecting crossover interference, which is based on hypothesis tests of Equations (7a)–(7d). In general, the power of detecting low-order crossover interference (C1, C2 or C3) is high, reaching 0.95 or higher, even with a moderate sample size. However, to detect high-order crossover interference (C4), a larger sample size, such as 400, is needed.

For those unsequenced genomes, we do not know the order of their genes. However, gene order can be inferred from genotypic data. We performed simulation studies based on the above scenario to examine the power of gene ordering by four-point analysis. For a given set of markers, we considered all possible orders under each of which the likelihood of observations is calculated. The maximum likelihood corresponds to a most likely gene order. We found that four-point analysis can provide full power to correctly detect the optimal gene order with a moderate sample size (n = 200). Such power decreases slightly for three- and two-point analysis (Table 3). With a large sample size (n = 400), all approaches give full power. Compared with two-point analysis, the computing time of three- and four-point analysis is 1.5 and 2.5 times more, respectively.

Table 3
Open in new tab

Empirical power of correctly detecting an optimal order of genes with varying recombination fractions and interference degrees under different sample sizes

Methodsn = 200n = 400
Two-point analysis98%100%
Three-point analysis99%100%
Four-point analysis100%100%
Methodsn = 200n = 400
Two-point analysis98%100%
Three-point analysis99%100%
Four-point analysis100%100%
Table 3
Open in new tab

Empirical power of correctly detecting an optimal order of genes with varying recombination fractions and interference degrees under different sample sizes

Methodsn = 200n = 400
Two-point analysis98%100%
Three-point analysis99%100%
Four-point analysis100%100%
Methodsn = 200n = 400
Two-point analysis98%100%
Three-point analysis99%100%
Four-point analysis100%100%

Four-point analysis for a full-sib family: a mixture model

The backcross is the simplest design for linkage analysis that contains a full amount of marker segregation information. For the backcross, we can derive explicit estimators for the linkage and the genetic interference. However, for more complex designs, such as the F2, in which genotypes may not be consistent with diplotype, a more sophisticated expectation-maximization (EM) algorithm should be implemented. Two heterozygous F1, ABCD/abcd × ABCD/abcd, are crossed to generate a segregating F2 population. Here, each F1 parent generates 16 gametes, which are divided into eight types (Table 1). Their cross generates 136 diplotypes collapsed into 81 distinguishable genotypes. Table 3 provides the genotype frequencies of the F2 progeny expressed in terms of products of gamete-type frequencies from the two heterozygous parents. It can be seen that the frequencies of heterozygous genotypes at two or more markers are a mix of products of gamete-type frequencies.

By formulating a mixture model-based likelihood by considering missing information for heterozygote genotypes, Wu and group have derived a closed form of the EM algorithm for estimating the linkage and other parameters in complex designs like the ones given in Table 2 [22–25, 28]. According to Wu’s algorithm, we first calculate the expected numbers of crossover events contained within a particular F2 genotype (E step) and then implement these numbers to estimate the recombination fraction from genotypic observations (M step). For example, genotype AABBCCDD or aabbccdd, each due to the union of two same gametes ABCD or abcd, respectively, contains two g000 but nothing for other gamete types. This is the simplest case for counting g’s. The most complex case is genotype AaBbCcDd that has eight possible diplotypes, ABCD|abcd, ABCd|abcD, ABcd|abCD, ABcD|abCd, Abcd|aBCD, AbcD|aBCd, AbCD|aBcd and AbCd|aBcD. Thus, its frequency is expressed as g0002+g0012+g0102+g0112+g1002+g1012+g1102+g1112. The expected number of g000 is calculated as following:
(8)
The expected numbers of the other g’s within genotype AaBbCcDd can be similarly obtained. Those numbers for other genotypes are given in the footnote of Table 4.
Table 4
Open in new tab

Four-marker genotype observations and expected frequencies composed of gamete-type frequencies produced by each parent in an F2 population. The expected numbers of each gamete type within each genotype are also given

CCDDCCDdCCddCcDDCcDdCcddccDDccDdccdd
AABBFrequencyg00022g000g001g00122g000g0112(g000g010+g001g011)2g001g010g01122g011g010g0102
Observationn2222n2221n2220n2212n2211n2210n2202n2201n2200
g0002101φ30000
g00101201-φ31000
g0100000φ31012
g01100011-φ30210
g100000000000
g101000000000
g110000000000
g111000000000
AABbFrequency2g000g1102(g000g111+g001g110)2g001g1112(g000g101+g011g110)2(g000g100+g001g101+ g010g110+g011g111)2(g001g100+g010g111)2g011g1012(g010g101 + 2g011g100)2g010g100
Observationn2122n2121n2120n2112n2111n2110n2102n2101n2100
g0001φ100φ7φ60000
g00101-φ1010φ16φ15000
g0100000φ231-φ150φ221
g0110001-φ7φ27011-φ220
g1000000φ6φ1501-φ221
g101000φ7φ1601φ220
g11011-φ1001-φ7φ230000
g1110φ1010φ271-φ15000
AAbbFrequencyg11022g110g111g11122g011g1012(g110g100+g111g101)2g111g100g10122g101g100g1002
Observationn2022n2021n2020n2012n2011n2010n2002n2001n2000
g000000000000
g001000000000
g010000000000
g011000000000
g1000000φ301012
g10100011-φ300210
g1102101φ300000
g11101201-φ301000
AaBBFrequency2g000g1002(g000g101+g001g011)2g001g1012(g000g111+g011g100)2(g000g110+g001g111+ g010g100+g011g101)2(g001g110+g010g101)2g011g1112(g010g111+g011g110)2g010g110
Observationn1222n1221n1220n1212n1211n1210n1202n1201n1200
g0001φ80φ11φ90000
g00101-φ810φ18φ17000
g0100000φ211-φ170φ241
g01101-φ801-φ11φ26011-φ240
g1001001-φ11φ210000
g1010φ810φ261-φ17000
g1100000φ9φ1701-φ241
g111000φ11φ1801φ240
AaBbFrequency2(g000g010+ g110g100)2(g000g011+g001g010+g110g101+g111g100)2(g001g011+ g111g101)2(g000g001+g011g010+g110g111+g101g100)g0002+g0012+g0102+g0112+g1002+g1012+g1102+g11122(g000g001+g011g010+g110g111+g101g100)2(g001g011+g111g101)2(g000g011+g001g010+g110g101+g111g100)2(g000g010+g110g100)
Observationn1122n1121n1120n1112n1111n1110n1102n1101n1100
g000φ4φ50φ22φ1φ20φ5φ4
g0010φ13φ14φ22φ12φ2φ14φ130
g010φ4φ130φ202φ19φ200φ13φ4
g0110φ5φ14φ202φ25φ20φ14φ50
g1001-φ4φ310φ292φ28φ290φ311-φ4
g1010φ331-φ14φ292φ32φ291-φ14φ330
g1101-φ4φ330φ352φ34φ350φ331-φ4
g1110φ311-φ14φ352φ36φ351-φ14φ310
AabbFrequency2g010g1102(g010g111+g011g110)2g011g1112(g001g110+g010g101)2(g000g110+g001g111+ g010g100+g011g101)2(g000g111+g011g100)2g001g1012(g000g101+g001g011)2g000g100
Observationn1022n1021n1020n1012n1011n1010n1002n1001n1000
g0000000φ9φ110φ81
g001000φ17φ18011-φ80
g0101φ2401-φ17φ210000
g01101-φ2410φ261-φ1101-φ80
g1000000φ211-φ11001
g1010001-φ17φ2601φ80
g110g111101-φ240φ17φ90000
φ2410φ18φ11000
aaBBFrequencyg10022g101g100g10122g111g1002(g110g100+g111g101)2g110g101g11122g110g111g1102
Observationn0222n0221n0220n0212n0211n0210n0202n0201n0200
g000000000000
g001000000000
g010000000000
g011000000000
g1002101φ300000
g10101201-φ301000
g1100000φ301012
g11100011-φ300210
aaBbFrequency2g010g1002(g010g101+g011g100)2g011g1012(g001g100+g010g111)2(g000g100+g001g101+ g010g110+g011g111)2(g000g101+g011g110)2g001g1112(g000g111+g001g110)2g000g110
Observationn0122n0121n0120n0112n0111n0110n0102n0101n0100
g0000000φ6φ70φ101
g001000φ15φ16011-φ100
g0101φ2201-φ15φ230000
g01101-φ2210φ271-φ7000
g10011-φ220φ15φ60000
g1010φ2210φ16φ7000
g1100000φ231-φ701-φ101
g1110001-φ15φ2701φ100
aabbFrequencyg01022g011g010g01122g001g0102(g000g010+g001g011)2g000g011g00122g000g001g0002
Observationn0022n0021n0020n0012n0011n0010n0002n0001n0000
g0000000φ31012
g00100011-φ30210
g0102101φ30000
g01101201-φ31000
g100000000000
g101000000000
g110000000000
g111000000000
CCDDCCDdCCddCcDDCcDdCcddccDDccDdccdd
AABBFrequencyg00022g000g001g00122g000g0112(g000g010+g001g011)2g001g010g01122g011g010g0102
Observationn2222n2221n2220n2212n2211n2210n2202n2201n2200
g0002101φ30000
g00101201-φ31000
g0100000φ31012
g01100011-φ30210
g100000000000
g101000000000
g110000000000
g111000000000
AABbFrequency2g000g1102(g000g111+g001g110)2g001g1112(g000g101+g011g110)2(g000g100+g001g101+ g010g110+g011g111)2(g001g100+g010g111)2g011g1012(g010g101 + 2g011g100)2g010g100
Observationn2122n2121n2120n2112n2111n2110n2102n2101n2100
g0001φ100φ7φ60000
g00101-φ1010φ16φ15000
g0100000φ231-φ150φ221
g0110001-φ7φ27011-φ220
g1000000φ6φ1501-φ221
g101000φ7φ1601φ220
g11011-φ1001-φ7φ230000
g1110φ1010φ271-φ15000
AAbbFrequencyg11022g110g111g11122g011g1012(g110g100+g111g101)2g111g100g10122g101g100g1002
Observationn2022n2021n2020n2012n2011n2010n2002n2001n2000
g000000000000
g001000000000
g010000000000
g011000000000
g1000000φ301012
g10100011-φ300210
g1102101φ300000
g11101201-φ301000
AaBBFrequency2g000g1002(g000g101+g001g011)2g001g1012(g000g111+g011g100)2(g000g110+g001g111+ g010g100+g011g101)2(g001g110+g010g101)2g011g1112(g010g111+g011g110)2g010g110
Observationn1222n1221n1220n1212n1211n1210n1202n1201n1200
g0001φ80φ11φ90000
g00101-φ810φ18φ17000
g0100000φ211-φ170φ241
g01101-φ801-φ11φ26011-φ240
g1001001-φ11φ210000
g1010φ810φ261-φ17000
g1100000φ9φ1701-φ241
g111000φ11φ1801φ240
AaBbFrequency2(g000g010+ g110g100)2(g000g011+g001g010+g110g101+g111g100)2(g001g011+ g111g101)2(g000g001+g011g010+g110g111+g101g100)g0002+g0012+g0102+g0112+g1002+g1012+g1102+g11122(g000g001+g011g010+g110g111+g101g100)2(g001g011+g111g101)2(g000g011+g001g010+g110g101+g111g100)2(g000g010+g110g100)
Observationn1122n1121n1120n1112n1111n1110n1102n1101n1100
g000φ4φ50φ22φ1φ20φ5φ4
g0010φ13φ14φ22φ12φ2φ14φ130
g010φ4φ130φ202φ19φ200φ13φ4
g0110φ5φ14φ202φ25φ20φ14φ50
g1001-φ4φ310φ292φ28φ290φ311-φ4
g1010φ331-φ14φ292φ32φ291-φ14φ330
g1101-φ4φ330φ352φ34φ350φ331-φ4
g1110φ311-φ14φ352φ36φ351-φ14φ310
AabbFrequency2g010g1102(g010g111+g011g110)2g011g1112(g001g110+g010g101)2(g000g110+g001g111+ g010g100+g011g101)2(g000g111+g011g100)2g001g1012(g000g101+g001g011)2g000g100
Observationn1022n1021n1020n1012n1011n1010n1002n1001n1000
g0000000φ9φ110φ81
g001000φ17φ18011-φ80
g0101φ2401-φ17φ210000
g01101-φ2410φ261-φ1101-φ80
g1000000φ211-φ11001
g1010001-φ17φ2601φ80
g110g111101-φ240φ17φ90000
φ2410φ18φ11000
aaBBFrequencyg10022g101g100g10122g111g1002(g110g100+g111g101)2g110g101g11122g110g111g1102
Observationn0222n0221n0220n0212n0211n0210n0202n0201n0200
g000000000000
g001000000000
g010000000000
g011000000000
g1002101φ300000
g10101201-φ301000
g1100000φ301012
g11100011-φ300210
aaBbFrequency2g010g1002(g010g101+g011g100)2g011g1012(g001g100+g010g111)2(g000g100+g001g101+ g010g110+g011g111)2(g000g101+g011g110)2g001g1112(g000g111+g001g110)2g000g110
Observationn0122n0121n0120n0112n0111n0110n0102n0101n0100
g0000000φ6φ70φ101
g001000φ15φ16011-φ100
g0101φ2201-φ15φ230000
g01101-φ2210φ271-φ7000
g10011-φ220φ15φ60000
g1010φ2210φ16φ7000
g1100000φ231-φ701-φ101
g1110001-φ15φ2701φ100
aabbFrequencyg01022g011g010g01122g001g0102(g000g010+g001g011)2g000g011g00122g000g001g0002
Observationn0022n0021n0020n0012n0011n0010n0002n0001n0000
g0000000φ31012
g00100011-φ30210
g0102101φ30000
g01101201-φ31000
g100000000000
g101000000000
g110000000000
g111000000000
Note: We denote an F2 genotype by the number of its capital type at each marker. For example, n2222 denotes the observation of genotype AABBCCDD that contains two capital alleles at marker A, B, C and D in order. The expected numbers of g’s within each genotype are given, with
.
Table 4
Open in new tab

Four-marker genotype observations and expected frequencies composed of gamete-type frequencies produced by each parent in an F2 population. The expected numbers of each gamete type within each genotype are also given

CCDDCCDdCCddCcDDCcDdCcddccDDccDdccdd
AABBFrequencyg00022g000g001g00122g000g0112(g000g010+g001g011)2g001g010g01122g011g010g0102
Observationn2222n2221n2220n2212n2211n2210n2202n2201n2200
g0002101φ30000
g00101201-φ31000
g0100000φ31012
g01100011-φ30210
g100000000000
g101000000000
g110000000000
g111000000000
AABbFrequency2g000g1102(g000g111+g001g110)2g001g1112(g000g101+g011g110)2(g000g100+g001g101+ g010g110+g011g111)2(g001g100+g010g111)2g011g1012(g010g101 + 2g011g100)2g010g100
Observationn2122n2121n2120n2112n2111n2110n2102n2101n2100
g0001φ100φ7φ60000
g00101-φ1010φ16φ15000
g0100000φ231-φ150φ221
g0110001-φ7φ27011-φ220
g1000000φ6φ1501-φ221
g101000φ7φ1601φ220
g11011-φ1001-φ7φ230000
g1110φ1010φ271-φ15000
AAbbFrequencyg11022g110g111g11122g011g1012(g110g100+g111g101)2g111g100g10122g101g100g1002
Observationn2022n2021n2020n2012n2011n2010n2002n2001n2000
g000000000000
g001000000000
g010000000000
g011000000000
g1000000φ301012
g10100011-φ300210
g1102101φ300000
g11101201-φ301000
AaBBFrequency2g000g1002(g000g101+g001g011)2g001g1012(g000g111+g011g100)2(g000g110+g001g111+ g010g100+g011g101)2(g001g110+g010g101)2g011g1112(g010g111+g011g110)2g010g110
Observationn1222n1221n1220n1212n1211n1210n1202n1201n1200
g0001φ80φ11φ90000
g00101-φ810φ18φ17000
g0100000φ211-φ170φ241
g01101-φ801-φ11φ26011-φ240
g1001001-φ11φ210000
g1010φ810φ261-φ17000
g1100000φ9φ1701-φ241
g111000φ11φ1801φ240
AaBbFrequency2(g000g010+ g110g100)2(g000g011+g001g010+g110g101+g111g100)2(g001g011+ g111g101)2(g000g001+g011g010+g110g111+g101g100)g0002+g0012+g0102+g0112+g1002+g1012+g1102+g11122(g000g001+g011g010+g110g111+g101g100)2(g001g011+g111g101)2(g000g011+g001g010+g110g101+g111g100)2(g000g010+g110g100)
Observationn1122n1121n1120n1112n1111n1110n1102n1101n1100
g000φ4φ50φ22φ1φ20φ5φ4
g0010φ13φ14φ22φ12φ2φ14φ130
g010φ4φ130φ202φ19φ200φ13φ4
g0110φ5φ14φ202φ25φ20φ14φ50
g1001-φ4φ310φ292φ28φ290φ311-φ4
g1010φ331-φ14φ292φ32φ291-φ14φ330
g1101-φ4φ330φ352φ34φ350φ331-φ4
g1110φ311-φ14φ352φ36φ351-φ14φ310
AabbFrequency2g010g1102(g010g111+g011g110)2g011g1112(g001g110+g010g101)2(g000g110+g001g111+ g010g100+g011g101)2(g000g111+g011g100)2g001g1012(g000g101+g001g011)2g000g100
Observationn1022n1021n1020n1012n1011n1010n1002n1001n1000
g0000000φ9φ110φ81
g001000φ17φ18011-φ80
g0101φ2401-φ17φ210000
g01101-φ2410φ261-φ1101-φ80
g1000000φ211-φ11001
g1010001-φ17φ2601φ80
g110g111101-φ240φ17φ90000
φ2410φ18φ11000
aaBBFrequencyg10022g101g100g10122g111g1002(g110g100+g111g101)2g110g101g11122g110g111g1102
Observationn0222n0221n0220n0212n0211n0210n0202n0201n0200
g000000000000
g001000000000
g010000000000
g011000000000
g1002101φ300000
g10101201-φ301000
g1100000φ301012
g11100011-φ300210
aaBbFrequency2g010g1002(g010g101+g011g100)2g011g1012(g001g100+g010g111)2(g000g100+g001g101+ g010g110+g011g111)2(g000g101+g011g110)2g001g1112(g000g111+g001g110)2g000g110
Observationn0122n0121n0120n0112n0111n0110n0102n0101n0100
g0000000φ6φ70φ101
g001000φ15φ16011-φ100
g0101φ2201-φ15φ230000
g01101-φ2210φ271-φ7000
g10011-φ220φ15φ60000
g1010φ2210φ16φ7000
g1100000φ231-φ701-φ101
g1110001-φ15φ2701φ100
aabbFrequencyg01022g011g010g01122g001g0102(g000g010+g001g011)2g000g011g00122g000g001g0002
Observationn0022n0021n0020n0012n0011n0010n0002n0001n0000
g0000000φ31012
g00100011-φ30210
g0102101φ30000
g01101201-φ31000
g100000000000
g101000000000
g110000000000
g111000000000
CCDDCCDdCCddCcDDCcDdCcddccDDccDdccdd
AABBFrequencyg00022g000g001g00122g000g0112(g000g010+g001g011)2g001g010g01122g011g010g0102
Observationn2222n2221n2220n2212n2211n2210n2202n2201n2200
g0002101φ30000
g00101201-φ31000
g0100000φ31012
g01100011-φ30210
g100000000000
g101000000000
g110000000000
g111000000000
AABbFrequency2g000g1102(g000g111+g001g110)2g001g1112(g000g101+g011g110)2(g000g100+g001g101+ g010g110+g011g111)2(g001g100+g010g111)2g011g1012(g010g101 + 2g011g100)2g010g100
Observationn2122n2121n2120n2112n2111n2110n2102n2101n2100
g0001φ100φ7φ60000
g00101-φ1010φ16φ15000
g0100000φ231-φ150φ221
g0110001-φ7φ27011-φ220
g1000000φ6φ1501-φ221
g101000φ7φ1601φ220
g11011-φ1001-φ7φ230000
g1110φ1010φ271-φ15000
AAbbFrequencyg11022g110g111g11122g011g1012(g110g100+g111g101)2g111g100g10122g101g100g1002
Observationn2022n2021n2020n2012n2011n2010n2002n2001n2000
g000000000000
g001000000000
g010000000000
g011000000000
g1000000φ301012
g10100011-φ300210
g1102101φ300000
g11101201-φ301000
AaBBFrequency2g000g1002(g000g101+g001g011)2g001g1012(g000g111+g011g100)2(g000g110+g001g111+ g010g100+g011g101)2(g001g110+g010g101)2g011g1112(g010g111+g011g110)2g010g110
Observationn1222n1221n1220n1212n1211n1210n1202n1201n1200
g0001φ80φ11φ90000
g00101-φ810φ18φ17000
g0100000φ211-φ170φ241
g01101-φ801-φ11φ26011-φ240
g1001001-φ11φ210000
g1010φ810φ261-φ17000
g1100000φ9φ1701-φ241
g111000φ11φ1801φ240
AaBbFrequency2(g000g010+ g110g100)2(g000g011+g001g010+g110g101+g111g100)2(g001g011+ g111g101)2(g000g001+g011g010+g110g111+g101g100)g0002+g0012+g0102+g0112+g1002+g1012+g1102+g11122(g000g001+g011g010+g110g111+g101g100)2(g001g011+g111g101)2(g000g011+g001g010+g110g101+g111g100)2(g000g010+g110g100)
Observationn1122n1121n1120n1112n1111n1110n1102n1101n1100
g000φ4φ50φ22φ1φ20φ5φ4
g0010φ13φ14φ22φ12φ2φ14φ130
g010φ4φ130φ202φ19φ200φ13φ4
g0110φ5φ14φ202φ25φ20φ14φ50
g1001-φ4φ310φ292φ28φ290φ311-φ4
g1010φ331-φ14φ292φ32φ291-φ14φ330
g1101-φ4φ330φ352φ34φ350φ331-φ4
g1110φ311-φ14φ352φ36φ351-φ14φ310
AabbFrequency2g010g1102(g010g111+g011g110)2g011g1112(g001g110+g010g101)2(g000g110+g001g111+ g010g100+g011g101)2(g000g111+g011g100)2g001g1012(g000g101+g001g011)2g000g100
Observationn1022n1021n1020n1012n1011n1010n1002n1001n1000
g0000000φ9φ110φ81
g001000φ17φ18011-φ80
g0101φ2401-φ17φ210000
g01101-φ2410φ261-φ1101-φ80
g1000000φ211-φ11001
g1010001-φ17φ2601φ80
g110g111101-φ240φ17φ90000
φ2410φ18φ11000
aaBBFrequencyg10022g101g100g10122g111g1002(g110g100+g111g101)2g110g101g11122g110g111g1102
Observationn0222n0221n0220n0212n0211n0210n0202n0201n0200
g000000000000
g001000000000
g010000000000
g011000000000
g1002101φ300000
g10101201-φ301000
g1100000φ301012
g11100011-φ300210
aaBbFrequency2g010g1002(g010g101+g011g100)2g011g1012(g001g100+g010g111)2(g000g100+g001g101+ g010g110+g011g111)2(g000g101+g011g110)2g001g1112(g000g111+g001g110)2g000g110
Observationn0122n0121n0120n0112n0111n0110n0102n0101n0100
g0000000φ6φ70φ101
g001000φ15φ16011-φ100
g0101φ2201-φ15φ230000
g01101-φ2210φ271-φ7000
g10011-φ220φ15φ60000
g1010φ2210φ16φ7000
g1100000φ231-φ701-φ101
g1110001-φ15φ2701φ100
aabbFrequencyg01022g011g010g01122g001g0102(g000g010+g001g011)2g000g011g00122g000g001g0002
Observationn0022n0021n0020n0012n0011n0010n0002n0001n0000
g0000000φ31012
g00100011-φ30210
g0102101φ30000
g01101201-φ31000
g100000000000
g101000000000
g110000000000
g111000000000
Note: We denote an F2 genotype by the number of its capital type at each marker. For example, n2222 denotes the observation of genotype AABBCCDD that contains two capital alleles at marker A, B, C and D in order. The expected numbers of g’s within each genotype are given, with
.
After the expected numbers of g’s are obtained in the E step, we estimate gamete-type frequencies in the M step using the following formulas:
where n1=n2222+n0000,n2=n2221+n0001, …,n41=n2222+n0000 (see Table 4 for the definition of these observations).

Iterations that contain both E (8) and M steps (9) are repeated until the difference of the estimated g values between two successive iterations is less than a small value, such as e−8. The maximum likelihood estimates of the recombinant fractions and coincident coefficients are then obtained from the final estimates of g’s.

Model validation by a worked example

Four-point analysis was used to analyze a real data set collected from a controlled cross of two heterozygous trees ‘Fenban’ and ‘Kouzi Yudie’ from mei (Prunus mume), an ornamental woody plant [29, 30]. This cross contains 190 segregating F1 progeny, which, along with the two parents, were genotyped for 2342 polymorphic single-nucleotide polymorphisms over eight mei chromosomes. These markers are either testcross markers that are segregating because of only one of the parents (backcross type) or intercross markers whose segregation results from both parents (F2 type). By estimating the recombination fraction for all possible pairs and determining an optimal diplotype for each pair [22, 28], we constructed a genetic linkage map that covers the eight chromosomes. The Haldane map function was used to convert the recombination fraction to genetic distance.

By scanning this linkage map, we performed four-point analysis successively for every four markers, which provided the estimates of the recombination fraction for each marker pair, two first-order crossover interferences for two adjacent marker intervals, one first-order crossover interference for two marker intervals that is separated by one interval and one second-order crossover interference. Figure 2 illustrates the genome landscape of crossover interference for mei. It was seen that crossover interferences for two adjacent marker intervals are distributed pervasively throughout the entire genome, although the strength of crossover interference varies along the length of chromosome (Figure 2A). The interference between two non-adjacent marker intervals is sporadically distributed, with a much lower frequency of occurrence (Figure 2B). It is interesting to see that high-order crossover interference is substantially strong and has a widespread distribution over the genome (Figure 2C). It appears that chromosome 3 harbors a high-density distribution of high-order crossover interference.

The distribution of crossover interference over the mei genome composed of eight chromosomes estimated from a full-sib family of two different cultivars. (A) The first-order crossover interference between two adjacent marker intervals (C1 and C2). (B) The first-order crossover interference between two non-adjacent marker intervals (C3). (C) The second-order crossover interference over three successive marker intervals.
Figure 2

The distribution of crossover interference over the mei genome composed of eight chromosomes estimated from a full-sib family of two different cultivars. (A) The first-order crossover interference between two adjacent marker intervals (C1 and C2). (B) The first-order crossover interference between two non-adjacent marker intervals (C3). (C) The second-order crossover interference over three successive marker intervals.

Open in new tabDownload slide

Discussion

Crossover interference, a feature of meiosis that governs the genome-wide distribution of recombination events, has been observed to pervade most (if not all) organisms [18]. In eukaryotes, interference may act over megabase lengths of DNA. For example, in the nematode Caenorhabditis elegans, interference can exert its effect across a fusion chromosome of 50 Mb [15]. Several approaches have been proposed to explore the strength and distribution of interference. Lian et al. [17] used immunofluorescence, combined with fluorescence in situ hybridization of testicular biopsies, to analyze and to identify the frequency and location of crossovers in specific chromosomes of pachytene cells and to further estimate the strength of crossover interference by fitting the frequency distribution of inter-crossover distances to the gamma model. By assuming crossover interference as a quasi-uniform, rather than exponential, distribution of intercrossover map distances, Lam et al. [16] capitalized on tetrad analysis based on the quartet mutation [31] to identify a mixture of interference-sensitive and interference-insensitive recombination events on chromosomes 1, 3 and 5 of Arabidopsis. Many of these approaches used some strict assumption, e.g. the frequency and magnitude of interference decrease with increasing distance from the initial crossover along the chromosome [15]. However, extensive chromosome fusion and bisection studies suggested that interference within a specific chromosome region may vary, depending on the overall size and structure of the chromosome. From these previous studies, there is a pressing need to develop an approach that can identify crossover interference without the assumption of interference distribution.

In this article, we have demonstrated that the extension of traditional linkage analysis to analyzing multiple markers simultaneously provides a powerful tool to identify and estimate crossover interference. The use of three-point linkage analysis to characterize crossover interference has well been documented in the literature [19, 20, 22, 27]. We showed that high-dimensional linkage analysis of more than three markers can find its implication for genome research. First, it can estimate the recombination fraction between two adjacent markers as precisely as can two-point analysis. Second, like three-point analysis, it can estimate and identify the strength of genetic interference occurring between adjacent marker intervals along a chromosome. Third, this approach can particularly find interference over multiple marker intervals, providing additional information about genome structure and organization. Furthermore, high-dimensional linkage analysis can determine the order of genes with more power than two-point analysis. These advantages have been well validated through simulation studies. Actual analysis of marker data collected from a controlled cross of mei trees has not only well supported the usefulness of the model, but also glean insight into the structure and function of the mei genome.

Increasing studies have been conducted to investigate the recombination events of homologous chromosomes as an adaptive process by which the organism responds to environmental perturbations [8]. As an important fuel to generate genetic diversity, the frequency and the distribution of recombination achieved via crossovers are determined by genetic background, sex and many environmental factors, such as temperature and age [9, 17]. Crossover interference that tends to increase spacing between crossover events plays a pivotal role in affecting and regulating the event of recombination [18, 32]. For example, crossover interference may have significantly contributed to sex differences of recombination rates, known as heterochiasmy, a phenomenon that has been widely observed in eukaryotes [9]. Multi-locus linkage analysis described in this article provides a useful guidance to design evolutionary experiments of recombination and interference [33].

Jing Wang is a PhD candidate in the Center for Computational Biology at Beijing Forestry University. Her research interest is in plant genetics and genomics.

Lidan Sun is a lecturer in ornamental genetics in the National Engineering Research Center for Floriculture at Beijing Forestry University. She studies the population genetics of ornamental plants using molecular techniques.

Libo Jiang is a PhD candidate in the Center for Computational Biology at Beijing Forestry University. His research interest is in computational genetics and genomics.

Mengmeng Sang is a PhD student in the Center for Computational Biology at Beijing Forestry University. His research interest is in computational genetics and genomics.

Meixia Ye is a lecturer in the Center for Computational Biology at Beijing Forestry University. She studies the genetics and genomics of complex traits.

Tangren Cheng is an associate professor of ornamental genetics and the executive director of National Engineering Research Center for Floriculture at Beijing Forestry University. He is interested in the molecular ecology of ornamental plants.

Qixiang Zhang is a professor of ornamental genetics and the director of National Engineering Research Center for Floriculture at Beijing Forestry University and vice president of Beijing Forestry University. He directs a national program of ornamental genetics and breeding in China.

Rongling Wu is Changjiang Scholars Professor of genetics and the director of the Center for Computational Biology at Beijing Forestry University. He is also a distinguished professor of biostatistics and bioinformatics at The Pennsylvania State University. His interest is to unravel the genetic roots for the outcome of a biological trait by dissecting the trait into its biochemical and developmental pathways.

Acknowledgements

The authors thank Dr. Wei Hou for his contribution to this work and three anonymous reviewers for their constructive comments.

Funding

This work is supported by National Natural Science Foundation of China (Grant No.31401900), grant 201404102 from the State Administration of Forestry of China, the Changjiang Scholars Award and ‘One-thousand Person Plan’ Award.

Key Points

  • Crossover interference is a phenomenon by which a chromosomal crossover in one interval affects the occurrence of additional crossovers nearby.

  • Because of its biological significance, crossover interference has been extensively studied by genetic and cytological approaches.

  • We review and assess a four-point linkage analysis approach that can characterize the pattern and the degree of crossover interference based on recombination events.

  • This approach can discern high-order crossover interference if more than three markers are analyzed simultaneously.

References

1

Lobo
I
,
Shaw
K.
Discovery and types of genetic linkage
.
Nat Ed
2008
;
1
(
1
):
139.

Google Scholar

OpenURL Placeholder Text

 
2

Lathrop
GM
,
Lalouel
JM
,
Julier
C
, et al.
Strategies for multilocus linkage analysis in humans
.
Proc Natl Acad Sci
1984
;
81
:
3443
–
6
.

Google Scholar

Crossref
Search ADS
PubMed

 
3

Dupuis
J
,
Siegmund
D.
Statistical methods for mapping quantitative trait loci from a dense set of markers
.
Genetics
1999
;
151
:
373
–
86
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
4

Lande
ES
,
Green
P.
Construction of multilocus genetic linkage maps in humans
.
Proc Natl Acad Sci
1987
;
84
:
2363
–
7
.

Google Scholar

Crossref
Search ADS
PubMed

 
5

MacArthur
DG
,
Manolio
TA
,
Dimmock
DP
, et al.
Guidelines for investigating causality of sequence variants in human disease
.
Nature
2014
;
508
:
469
–
76
.

Google Scholar

Crossref
Search ADS
PubMed

 
6

Bailey-Wilson
JE
,
Wilson
AF.
Linkage analysis in the next-generation sequencing era
.
Hum Hered
2011
;
72
:
228
–
36
.

Google Scholar

Crossref
Search ADS
PubMed

 
7

Ott
J
,
Wang
J
,
Leal
SM.
Genetic linkage analysis in the age of whole-genome sequencing
.
Nat Rev Genet
2015
;
16
:
275
–
84
.

Google Scholar

Crossref
Search ADS
PubMed

 
8

Bomblies
K
,
Higgins
JD
,
Yant
L.
Meiosis evolves: adaptation to internal and external environments
.
New Phytol
2015
;
208
:
306
–
23
.

Google Scholar

Crossref
Search ADS
PubMed

 
9

Phillips
D
,
Jenkins
G
,
Macaulay
M
, et al.
The effect of temperature on the male and female recombination landscape of barley
.
New Phytol
2015
;
208
:
421
–
9
.

Google Scholar

Crossref
Search ADS
PubMed

 
10

Muller
HJ.
The mechanism of crossing over
.
Am Nat
1916
;
50
:
193
–
221
.

Google Scholar

Crossref
Search ADS

 
11

Broman
KW
,
Weber
JL.
Characterization of human crossover interference
.
Am J Hum Genet
2000
;
66
:
1911
–
26
.

Google Scholar

Crossref
Search ADS
PubMed

 
12

Copenhaver
GP
,
Housworth
EA
,
Stahl
FW.
Crossover interference in Arabidopsis
.
Genetics
2002
;
160
:
1631
–
9
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
13

van Veen
JE
,
Hawley
RS.
Meiosis: when even two is a crowd
.
Curr Biol
2003
;
13
:
R831
–
3
.

Google Scholar

Crossref
Search ADS
PubMed

 
14

Bishop
DK
,
Zickler
D.
Early decision; meiotic crossover interference prior to stable strand exchange and synapsis
.
Cell
2004
;
117
:
9
–
15
.

Google Scholar

Crossref
Search ADS
PubMed

 
15

Hillers
KJ.
Crossover interference
.
Cur Biol
2004
;
14
:
R1036
–
7
.

Google Scholar

Crossref
Search ADS

 
16

Lam
SY
,
Horn
SR
,
Radford
SJ
, et al.
Crossover interference on nucleolus organizing region-bearing chromosomes in Arabidopsis
.
Genetics
2005
;
170
:
807
–
12
.

Google Scholar

Crossref
Search ADS
PubMed

 
17

Lian
J
,
Yin
Y
,
Oliver-Bonet
M
, et al.
Variation in crossover interference levels on individual chromosomes from human males
.
Hum Mol Genet
2008
;
17
:
2583
–
94
.

Google Scholar

Crossref
Search ADS
PubMed

 
18

Campbell
CL
,
Furlotte
NA
,
Eriksson
N
, et al.
Escape from crossover interference increases with maternal age
.
Nat Commun
2015
;
6
:
6260.

Google Scholar

Crossref
Search ADS
PubMed

 
19

Zhao
LP
,
Thompson
E
,
Prentice
R.
Joint estimation of recombination fractions and interference coefficients in multilocus linkage analysis
.
Am J Hum Genet
1990
;
47
:
255
–
65
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
20

Weeks
DE
,
Ott
J
,
Lathrop
GM.
Detection of genetic interference: simulation studies and mouse data
.
Genetics
1994
;
136
:
1217
–
26
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
21

Ott
J.
Analysis of Human Genetic Linkage
.
John Hopkins University Press, Maryland
,
1999
;
3
:
78
–
9
.

Google Scholar

OpenURL Placeholder Text

 
22

Lu
Q
,
Cui
YH
,
Wu
R.
A multilocus likelihood approach to joint modeling of linkage, parental diplotype and gene order in a full-sib family
.
BMC Genet
2004
;
5
:
20.

Google Scholar

Crossref
Search ADS
PubMed

 
23

Li
Q
,
Wu
R.
A multilocus model for constructing a linkage disequilibrium map in human populations
.
Stat Appl Genet Mol Biol
2009
;
8
:
Article 18
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
24

Hou
W
,
Liu
T
,
Li
Y
, et al.
Multilocus genomics of outcrossing populations
.
Theor Pop Biol
2009
;
76
:
68
–
76
.

Google Scholar

Crossref
Search ADS

 
25

Sun
LD
,
Zhu
XL
,
Bo
WH
, et al.
An open-pollinated design for mapping imprinting genes in natural populations
.
Brief Bioinform
2015
;
16
:
449
–
60
.

Google Scholar

Crossref
Search ADS
PubMed

 
26

Sall
T
,
Bengtsson
BO.
Apparent negative interference due to variation in recombination frequencies
.
Genetics
1989
;
122
:
935
–
42
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
27

Wu
R
,
Ma
C
,
Casella
G.
Statistical Genetics of Quantitative Traits: Linkage, Maps and QTL
.
New York
:
Springer
,
2007
.

Google Scholar

OpenURL Placeholder Text

 
28

Wu
R
,
Ma
CX
,
Painter
I
, et al.
Simultaneous maximum likelihood estimation of linkage and linkage phases in outcrossing species
.
Theor Pop Biol
2002
;
61
:
349
–
63
.

Google Scholar

Crossref
Search ADS

 
29

Sun
L
,
Yang
W
,
Zhang
Q
, et al.
Genome-wide characterization and linkage mapping of simple sequence repeats in mei (Prunus mume Sieb. et Zucc.)
.
PloS One
2013
;
8
(
3
):
e59562.

Google Scholar

Crossref
Search ADS
PubMed

 
30

Sun
LD
,
Wang
YQ
,
Yan
XL
, et al.
Genetic control of juvenile growth and botanical architecture in an ornamental woody plant, Prunus mume Sieb. et Zucc., as revealed by a high-density linkage map
.
BMC Genet
2014
;
15(Suppl 1)
:
S1.

Google Scholar

PubMed
OpenURL Placeholder Text

 
31

Preuss
D
,
Rhee
SY
,
Davis
RW.
Tetrad analysis possible in Arabidopsis with mutation of the QUARTET (QRT) genes
.
Science
1994
;
264
:
1458
–
60
.

Google Scholar

Crossref
Search ADS
PubMed

 
32

Petkov
PM
,
Broman
KW
,
Szatkiewicz
JP
, et al.
Crossover interference underlies sex differences in recombination rates
.
Trends Genet
2007
;
23
:
539
–
42
.

Google Scholar

Crossref
Search ADS
PubMed

 
33

Sun
LD
,
Zhu
XL
,
Zhang
QX
, et al.
A unifying experimental design for dissecting tree genomes
.
Trends Plant Sci
2015
;
20
:
473
–
6
.

Google Scholar

Crossref
Search ADS
PubMed

 

Author notes

Jing Wang, Lidan Sun and Libo Jiang authors contributed equally to this work.

© The Author 2016. Published by Oxford University Press. All rights reserved. For Permissions, please email: [email protected]
This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/about_us/legal/notices)
Issue Section:
Papers
Download all slides