Allotetraploid and autotetraploid models of linkage analysis

Abstract

INTRODUCTION

Because of their biological and economic importance, genetic analysis of polyploids has received a surge of interest in the recent years [1–5]. Tremendous efforts have been made to develop statistical models for linkage analysis used to study the genome structure and organization of polyploids and map quantitative trait loci for polyploid traits [6–13]. These models can be biologically relevant only when they have taken into account cytological properties of meiosis characterized by polyploids, which are qualitatively different from those in diploids.

According to their different origins, polyploids can be classified into two groups, allopolyploids and autopolyploids [1]. Wu et al. [12,13] have for the first time developed a series of models for linkage analysis in allopolyploids arising from hybridization of two different species. Allopolyploids frequently display bivalent pairings of chromosomes at meiosis, in which more similar chromosomes pair with each other at a higher likelihood than less similar chromosomes. Wu et al.’s models incorporated a parameter that describes this cytological property, called the preferential pairing factor [14], into the linkage analysis framework, increasing the biological interpretation of linkage mapping models [15].

For autopolyploids derived from genome combinations of different species, chromosomes pair among more than two homologous copies at meiosis [16,17], leading to a phenomenon called double reduction, i.e. two sister chromatids of a chromosome sort into the same gamete [18]. Thus, models for autopolyploid linkage analysis are qualitatively different from those for allopolyploids, because the double reduction affects the relative proportions of recombinant and non-recombinant gametes in a way differently from the preferential pairing factor. Fisher [19] was the first who pioneered a conceptual model that characterizes the individual probabilities of 11 different modes of gamete formation for an autotetraploid in terms of the recombination fraction between two different loci and their double reductions. By assuming that the chromosomal distribution of double reduction follows a particular pattern, Luo et al. [9] was able to develop linkage analysis models for autotetraploids. Wu et al. [10] derived the EM algorithm for simultaneous estimation of the linkage and double reductions based on Fisher’s model, with no assumption about the genomic distribution of double reduction. This algorithm was extended to analyse simplex or multiplex markers [11] and three-point linkage relationships [20].

Owing to the implementation of unique meiotic properties of polyploids, these algorithms have been shown to perform better than traditional approaches derived from the recombination event alone [10–13]. Despite this, the existing algorithms aimed at allotetraploid and autotetraploid characteristics have not well been used in most linkage analysis for this group of species partly because of their statistical complexities. For example, in a recent well-designed study for Arabidopsis, Pecinka et al. [5] attempted to detect the evolutionary merit of polyploidization by estimating and comparing the recombination frequencies of two dominant markers among segregating populations of diploids, allotetraploids and autotetraploids. They used a traditional diploid model to perform linkage analysis for all these three types of populations, which may inevitably lead to an imprecise inference about the linkage for the two tetraploid populations. In this Note, we modify the existing tetraploid linkage analysis algorithms to accommodate dominant markers and use them to reanalyse marker data for Arabidopsis by Pecinka et al. [5]. We have not only corrected the estimates of the recombination frequency in the tetraploid populations, but also provided a recommendation for the choice of informative molecular markers used to study the evolutionary significance of polyploids.

MODEL

Allotetraploid model

Consider an allotetraploid plant derived from the chromosomal combination of distinct genomes and subsequent chromosomal doubling [14]. Four sets of chromosomes for the allotetraploid are labelled as 1, 2, 3 and 4, respectively. There are three different homologous patterns:

• Chromosomes 1 and 2 are homologous while chromosomes 3 and 4 are homologous. Chromosomes from different homologous pairs, i.e. 1 and 3, 1 and 4, 2 and 3 and 2 and 4, are homoeologous.

• Chromosomes 1 and 3 and, therefore, chromosomes 2 and 4 are homologous. Chromosome pairs, 1 and 2, 1 and 4, 2 and 3 and 3 and 4, are homoeologous.

• Chromosomes 1 and 4 and, therefore, chromosomes 2 and 3 are homologous. Chromosome pairs, 1 and 2, 1 and 3, 2 and 4 and 3 and 4, are homoeologous.

The affinity of chromosomal pairing may be higher between homologous pairs than between the homoeologues. Two-third of this difference is defined as the preferential pairing factor (p) [14]. By considering all possible pairs, i.e. 1 pairs with 2, then 3 must pair 4; if 1 pairs with 3, then 2 must pair 4; if 1 pairs 4, then 2 must pair 3. Of the three possibilities, the first is homologous and the rest are homoeologous for the first configuration. The homologous combination has a probability of and the two homoeologous combinations each have a probability of ⁠. If p = ⁠, then homoeologous chromosomes do not pair, i.e. chromosomal pairings happen strictly between the homologues. When p = 0, then all the four chromosomes act as if they are homologous, and they will pair randomly. Thus, the value of p ranges from 0 to ⁠.

Consider a heterozygous allotetraploid that undergoes bivalent pairings during meiosis. A fully informative codominant marker has four alleles, labelled as 1, 2, 3 and 4, that locate on chromosomes 1, 2, 3 and 4, respectively. If meiotic pairing strictly occurs between two homologous chromosomes, we will have four diploid gametes 13, 14, 23 and 24 under homologous pattern I where chromosomes 1 and 2 are homologous and chromosomes 3 and 4 are homologous. Because homoeologous chromosomes may also pair, but with a lesser extent compared with homologous pairing, we essentially have six diploid gametes 12, 13, 14, 23, 24 and 34 with frequencies ⁠, ⁠, ⁠, ⁠, and ⁠, respectively.

For a particular allelic configuration of two given markers and homologous pattern, Wu et al. [12] derived the frequencies of 36 two-marker gametes for the allotetraploid in terms of θ₁, θ₂ and the recombination frequency between the two markers. When two markers are dominant markers, 36 gametes are collapsed into four genotypically distinguishable groups. In this case, the preferential pairing factor (p) either disappears or is impossible to be estimated so that only the recombination frequency (r) can be estimated. An optimal combination of allelic configuration and homologous pattern corresponds to one in which the smallest estimate of r is obtained.

Autotetraploid model

For an autotetraploid with genotype 1234 at a fully informative codominant marker, it generates 10 gametes through multivalent pairing, i.e. 11, 22, 33, 44, 12, 13, 14, 23, 24 and 34. The first four are the gametes resulting from double reduction and the second six are those from non-double reduction. Fisher [19] classified gamete formation for two codominant markers into 11 types distributed within four blocks of a 10 × 10 gamete matrix expressed in Matrix (2) of Wu et al. [10]. Block one is composed of two gamete formations resulting from double reduction at both markers, block two composed of two gamete formations resulting from double reduction at the first marker and non-double reduction at the second marker, block three composed of two gamete formations resulting from double reduction at the second marker and non-double reduction at the first marker, and block four composed of five gamete formations resulting from non-double reduction at both markers. However, in block four only three gametes can be observed, two of which each include two gamete formations. In total, 11 gamete formations can be observed in terms of nine distinguishable gametes whose frequencies are defined as f₁,…, f₉ (see [10]).

For two dominant markers in autotetraploid, the frequencies of gamete genotypes with allele configuration produces can be derived by collapsing the frequencies of indistinguishable gametes (see [11]). Let 1 denote dominant allele and 0 denote recessive allele. Thus, the collapsed gamete frequencies are expressed as

(1)

with the linear constraint

(2)

Let α and β denote the coefficients of double reduction at two markers, respectively. Then, we have

(3)

We now write the frequency matrix H as

(4)

where

(5)

For a progeny derived from crossing two autotetraploids ×⁠, we can obtain the frequencies of genotypes at the two dominant markers through merging the elements of matrix H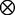H with the same genotypes, expressed as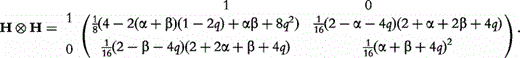

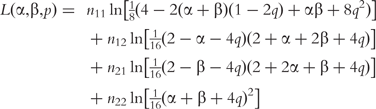
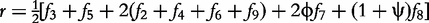
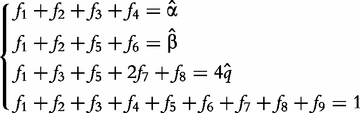
(6)

Therefore, the log likelihood of parameters α, β and q can be expressed as

(7)

where n_ij is the counts of genotype ij in the progeny of the two autotetraploids. The maximum-likelihood estimates of the three parameters can be obtained by non-linear optimization tools, such as fmincon in MATLAB. Dominant markers have not enough information to uniquely estimate the f_is and, therefore, the recombination frequency between the two markers (r). However, the range of the estimate of r can be found by the iterative formula,

(8)

where ϕ and ψ are the proportions of the gametes that contain the recombination events to a total amount of the 7th and 8th gametes, respectively [10,11], with linear constrains as follows:

(9)

For a cross of two heterozygous tetraploids, there are four possible combinations of tetraploid configurations, i.e. ×⁠, ×⁠, × and ×⁠.

An optimal allelic configuration combination corresponds to one in which the lowest estimate of r is obtained.

RESULTS

To investigate whether polyploidization increases the frequency of meiotic recombination and, therefore, the genetic variation of a species as a fuel for evolution, Pecinka et al. [5] genotyped two genetically linked transgenes that provide seed-specific green and red fluorescence, respectively, for the progeny derived from diploid and tetraploid Arabidopsis plants. Staring with a diploid plant that is homozygous for green and red transgenes, they made three different crosses (see Figure 1 in [5]). First, this homozygote (parent 1) was crossed with a homozygous wild-type (parent 2) that was not inserted by the transgenic genes, producing the F₁ heterozygotes. The F₁ was then selfed to generate an F₂ population and backcrossed with the second parent to generate a backcross population, in both of which four types of seed colors were observed, green, red, merged color and normal (because the transgenic genes are dominant to wild types). Second, the transgenic plant was polyploidized to form a homozygous tetraploid, which was crossed with a homozygous non-transgenic tetraploid of the same species, producing a heterozygous F₁ autotetraploid. The selfing and backcrossing of this F₁ produce a segregating population with four different types of colors. Third, the polyploidized tetraploid was crossed with a homozygous wild-type tetraploid of a different species, producing a heterozygous F₁ allotetraploid. By selfing and backcrossing, the F₂ and backcross populations were generated with four different types of colors. To examine the effect of sex on meiotic recombination frequencies, reciprocal matings for each backcross cross were made.

The linkage between the two transgenes was analysed for each cross derived from diploids, autotetraploids or allotetraploids using the data supplied in Table 1 of Pecinka et al. [5]. According to their cross experiment, the allelic configuration for the individual that generates segregating progeny populations is known, which is for the diploids, for the allotetraploids and for the autotetraploids. The allotetraploid model that incorporates the preferential pairing factor for an allopolyploid’s meiosis was used to estimate the recombination frequency for the two backcrosses and F₂. Because of insufficient information of segregation from the two dominant markers, we could not estimate this factor. In this case, our allotetraploid model is reduced to the traditional diploid model. However, as the principle that leads to the occurrence of preferential pairings has been considered, our estimate of the recombination frequency, r, for codominant markers is biologically more relevant. It turns out that our estimate of r for each backcross population is the same as those obtained by Pecinka et al. [5] but for the selfed F₂ population is different from their result (Table 1). Our estimate in the F₂ is 0.2770 ± 0.0110, in a contrast of 0.241 ± 0.018. This difference is owing to their incorrect use of the backcross model to analyse the F₂ data.

We used our autotetraploid model to estimate the linkage between the same pair of markers for the progeny derived from the autotetraploid parent. It is found that our estimates are different from those obtained by the original authors who simply used the traditional backcross linkage model (Table 1). Our method allows the estimation and test of double reduction at individual transgenes. There is a significant double reduction (6–9%, P < 0.05) for the green transgene in all backcrosses and F₂ populations, but non-significant double reduction is observed (P > 0.05) at the red transgene for the female parent-derived backcross and F₂. The autotetraploid model provides the estimates of the interval of the recombination frequency between the two transgenes, with the lower bound strikingly larger than the estimates obtained by Pecinka et al. [5].

Pecinka et al. [5] used a backcross diploid model to estimate the F₂ diploid population for dominant markers, which provided an incorrect result. Using the EM algorithm given in Wu et al. [21], we estimated the recombination frequency as 0.1643 ± 0.0062, different from their estimate 0.0154 ± 0.009 (Table 1).

DISCUSSION

The estimation of meiotic recombination frequencies between different markers in polyploids is challenging because their meiotic properties complicate the pattern of genotypic segregation. A set of statistical models has been available in the literature [6–13], which integrate parametric aspects of polyploidy meiotic behavior into a linkage analysis framework. For example, the preferential pairing factor that specifies bivalent pairing in allotetraploids is embedded in the derivation of gamete frequencies [12,13]. In autotetraploids, double reduction resulting from multivalent pairing is integrated [10,11]. However, many studies in polyploidy linkage mapping have not well used these cytologically more meaningful models partly owing to the complexity of the models.

In this Note, we describe two basic frameworks for linkage analysis in allotetraploids and autotetraploids and demonstrate their usefulness by reanalysing a published data set for diploid and tetraploid Arabidopsis plants by Pecinka et al. [5]. In particular, we pinpoint the limitation of the results obtained by inappropriate linkage analysis models, making the conclusions more precise and appealing for biological interpretations.

The dominant feature of the two transgenes used by Pecinka et al. [5] loses much information for linkage analysis. However, the autotetraploid model can still provide informative estimates of double reduction for dominant genes. By producing more gametes, double reduction may play a significant role in the maintenance of genetic diversity that favours evolution under natural populations. Thus, the estimation of double reduction becomes essential for shedding light on the genetic variation and organization of natural populations in autopolyploids [22]. Based on our previous computer simulation, the estimation of the linkage among markers would be biased for a progeny of autotetraploids that undergo double reduction if double reduction was neglected during the estimation procedure [10,11].

Although it is impossible to provide a point estimate of the recombination fraction between dominant markers in an autotetraploid population, the autotetraploid model can obtain an estimate of the interval for the recombination fraction, facilitating the widespread use of dominant markers to study the genetic variation of autotetraploid populations. The use of this model to reanalyse the data of dominant markers in an autotetraploid of Arabidopsis [5] has well validated its practical application. Our estimates of the recombination frequency are different from those reported in the original article, but the conclusion that polyploidization leads to an increase of meiotic recombination frequencies does not change. Indeed, to precisely address this fundamental question related to polyploidization, we recommend the use of codominant markers that will contain more informativeness for the estimation of the recombination frequencies and double reduction in autotetraploids [10,11].

Our models focus on the derivations of tetraploids, but the idea behind can be used for model development in polyploids at higher ploidy levels, such as hexaploid (i.e. wheat, kiwifruit), octaploid (i.e. dahlias), decaploid (i.e. strawberries) and dodecaploid (i.e. plumed cockscomb). Although polyploidy is more common in plants than in animals, linkage analysis of animal polyploids, such as sturgeon and the uganda clawed frog, can gain additional insight into evolution and speciation. All the models described can also find their immediate applications in animals as long as their segregating populations are available. With a set of models available for linkage analysis of polyploids at any ploidy level, we are in a better position to study the genetics and evolution of polyploids [23]. In addition, despite their importance, statistical models for mapping quantitative trait loci (QTLs) in polyploids are still in their infancy (but see [24–26]). Li et al. [24] has presented a first model that incorporates Fisher’s [18] gamete classification patterns into a QTL mapping framework, allowing the QTLs for autotetraploids that experience double reduction to be characterized. This incorporation provides a powerful tool for QTL mapping and understanding the genetic control of a quantitative trait in a multivalent autotetraploid.

The statistical model for allotetraploid and autotetraploid linkage analysis described in this article has been packed into an R platform, available at http://statgen.psu.edu/software.html. By inputting marker data for segregating population from allotetraploids or autotetraploids, this platform provides users with the estimates of pair-wise recombination fractions and the standard errors of these estimates. The platform allows the recombination fraction, preferential pairing factor and double reduction to be tested.

Acknowledgments

This work is partially supported by NSF/IOS-0923975, Changjiang Scholars Award and ‘Thousand-person Plan’ Award.

References

Author notes