https://orcid.org/0000-0002-7294-3812
In Annals of Botany in 1949, E. J. H. Corner laid out two general principles of plant architecture: (1) stouter stems support larger and more complicated appendages and (2) denser branching corresponds with smaller branches and smaller appendages. These principles have come to be known as Corner’s rules. Interest in both rules has largely focused on small and terminal branches (twigs) of woody plants and the first principle has generally been broadened to state that stems with greater cross-sectional area (cs) support greater leaf areas (la) in addition to larger individual leaves. These simple rules have compelled a handful of researchers over the decades to ask: what are the exact relationships between leaf and stem dimensions? Are these relationships universal and why do they exist? At the heart of Corner’s rule is a probable coordination between light interception, hydraulic supply/demand, metabolic demands and mechanical stability, tempered by developmental constraints. For example, larger leaves increase photosynthetic area but also increase transpiration area and mechanical loading from wind, precipitation and gravity (Fig. 1). There is no question about whether the stem bearing a larger leaf area should coordinate its mechanical and hydraulic properties to meet these demands, but exactly how this is achieved continues to draw interest.
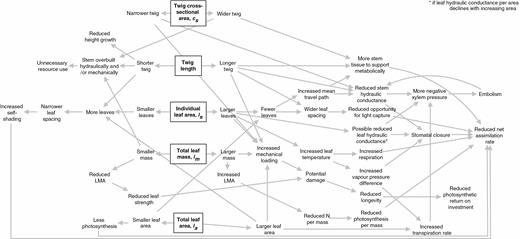
Possible negative consequences of changing individual leaf size, total leaf area, total leaf mass, stem cross-sectional area and stem length (boxed items) of terminal branches (twigs) while keeping all else constant. Functional coordination probably drives structural coordination between leaves and stems, and understanding the trade-offs will aid in our understanding of seasonal spatial, and interspecific coordination of structure.
An la–cs relationship has been found across species (e.g. White, 1983) and within species (e.g. Smith et al 2017). Stem and leaf dimensions vary not only spatially within plants but also temporally through growth. During this growth, are stem and leaf dimensions coordinated just as they are coordinated between stems? In this issue, Fajardo et al. (2020) asked this question and found in four of six study species that la–cs scaling was isometric across the season and at each measured point throughout the season. It is remarkable that such coordination exists given that leaf growth is biphasic with cell proliferation preceding cell expansion (Fajardo et al., 2020) and that growth occurs during seasonal changes in environmental conditions and, therefore, changes in opportunities and demands. A compelling follow-up question would address how the functions of the organs change through this time. For example, results from Fajardo et al. (2020) suggest a structural equivalence between early- and late-season shoots with the same cs, but are these shoots also hydraulically, mechanically and photosynthetically equivalent? In two of their six study species, the la–cs relationship was isometric at a given point in time but not across time, suggesting that individual shoots grow allometrically while maintaining isometry across shoots. Determining how and why this allometry occurs will add insight into the functional coordination of shoots.
Reproductive structures add to the balance of light interception, hydraulic transport, metabolism and mechanical stability. Flowers can have comparable transpiration rates to those of leaves (Lambrecht, 2013) and add mechanical strain yet do not contribute carbon as leaves do. Reproductive shoots may be expected to support smaller leaf areas compared with vegetative shoots of the same cs, but in the conspicuously flowered Embothrium coccineum, Fajardo et al. (2020) found no difference in slope or intercept of la–cs scaling. However, as stem mass increased, vegetative shoots increased leaf mass faster than reproductive shoots, thus falling more in line with expectations. How do these shoots simultaneously support and contradict the expectation? Two non-exclusive possibilities are that (1) as la increases, leaf mass increases more quickly in vegetative shoots due to increasing leaf mass per area (LMA) relative to reproductive shoots, or (2) as cs increases, stem mass increases more slowly in vegetative shoots due to declining stem density or declining total length relative to reproductive shoots. Fajardo et al. (2020) found support for these differences in LMA and if reproductive E. coccineum shoots branch more than vegetative shoots, then this last option seems plausible as well.
While studies on Corner’s rule have often dealt with current-year shoots, leaves of course may persist for longer, providing function and requiring support for multiple years, thus raising the question of whether leaf and stem traits should coordinate differently according to leaf longevity. Leaves that persist for longer should be mechanically tougher (e.g. via greater LMA) to avoid damage (Wright & Westoby, 2002), but more massive leaves, in turn, require stems to support this mass. Meanwhile, greater mechanical strength may reduce nitrogen content per mass. Due to these requirements, evergreen and deciduous species may be expected to differ in their la–cs scaling relationships and yet scant work has been done to address this. Fajardo et al. (2020) compared evergreen and deciduous congeneric species and showed that la–cs scaling does indeed differ with leaf persistence. The deciduous species generally supported more leaf area for a given cross-sectional area but this difference diminished as cs increased.
Arguably, one challenge in finding functional explanations for Corner’s first rule is the multi-functional nature of stems. When stem cross-sectional area is the composite of multiple tissues and each tissue plays multiple roles, it is no wonder that separating roles is difficult. The approach taken by Fajardo et al. (2020) to study species with contrasting statures (shrubs to trees), leaf habits (deciduous vs. angiosperm) and shoot type (reproductive vs. vegetative) provides a starting point to help tease apart different functions. We may further dissect functions by studying plants with additional contrasts such as where one or more demands on twigs are amplified or reduced. Plants with reduced mechanical loads are perhaps the most common option for such contrasts. Examples may be found in lianas, mistletoes, aquatics and prostrate herbaceous plants. Do these plants have isometric la–cs relationships? At the very least, we would expect their la–csy-intercepts to be greater than for fully self-supporting plants, provided that relaxing mechanical demands does not lead to stem tissue being co-opted for other purposes such as storage. We may find contrasting hydraulic properties looking at very tall trees such as Sequoia sempervirens where leaves become increasingly small and scale-like as height increases and have low water potentials due to long hydraulic path lengths and where gravitational effects limit cellular expansion (Koch et al., 2004). Osada (2011) has touched on this, showing that la/cs of leader shoots declined with increasing tree height when assessed in trees up to ~13 m tall. If Corner’s first rule is thought to result from matching hydraulic supply to demand so as to avoid excessively negative xylem pressures and loss of conductivity due to embolism, then would we expect to see a relaxation of Corner’s rule in species maintaining a very wide safety margin between midday leaf pressure and the stem xylem pressure causing 50 % loss of conductivity? For example, Actinostrobus acuminatus has been observed to have a safety margin of nearly 9 MPa beyond its midday leaf pressure around −5 MPa (Choat et al., 2012). Does this species coordinate stem and leaf dimensions more weakly than species with smaller safety margins? In contrast, we may study Corner’s rule in plants where hydraulic transport and photosynthesis are largely decoupled in time, such as in plants with CAM photosynthesis. We may expect a weak role of hydraulic transport in these plants but perhaps stem and leaf coordination remains strong for other reasons. Lastly, studies on Corner’s rule have mostly been limited to woody species with very few studies on herbaceous species (e.g. Schnablová et al., 2017), although Corner (1949) specifically mentioned them. Is Corner’s first rule followed similarly in herbaceous species despite their minimal or absent secondary growth and the often short-lived nature of their shoots? Studying these edge-case scenarios and species whose traits stray from the ‘typical’ species in other studies of Corner’s rule has the potential to add important insights.
Continued interest in Corner’s rules more than 70 years after their introduction shows that behind such seemingly simple observations about plant architecture lies a complex coordination of functions that we do not yet fully understand. By investigating how structural coordination changes seasonally, Fajardo et al. (2020) have shown that individual shoots manage this coordination on a temporal scale, and this opens up an avenue to answer how such coordination occurs developmentally and how function follows this structural coordination. Continuing along this avenue will further aid our understanding of how plants have evolved to efficiently and perhaps optimally balance multiple functions and constraints at the individual shoot level.
LITERATURE CITED
